②. 中国石油塔里木油田公司勘探开发研究院, 新疆库尔勒 841000
②. Research Institute of Exploration and Development, Tarim Oilfield Company, PetroChina, Korla, Xinjiang 841000, China
柯东构造带位于塔里木盆地西南坳陷昆仑山前,受西昆仑造山带多期构造运动的强烈影响及多次挤压—逆冲作用,形成了该区南北分带、东西分段的构造特征。同时,地表山体覆盖巨厚黄土,地形起伏大,近地表速度变化快,属于“双复杂”勘探区域。柯东构造带是西昆仑山前重要的油气勘探接替领域,2010年,柯东1井在下白垩统获得高产油气流,表明西昆仑山前冲断带具有巨大的油气勘探前景[1]。然而,在柯东构造带部署的后续钻井相继失利,表明西昆仑山前冲断带的构造十分复杂,研究人员对该区的构造认识尚不清晰。
复杂的地形和近地表结构,使地震波传播路径不满足一致性假设,因此,基于垂向时移的基准面校正加上水平地表偏移成像方法无法满足精细勘探的要求。理论上,基于起伏地表的叠前偏移是解决“双复杂”区地震资料成像问题的最佳方法。Rajasekaran等[2]利用初至层析成像估算近地表速度,采用起伏地表速度扫描、反射层析等方法建立深层速度模型,应用双程波有限差分逆时偏移方法实现起伏地表的偏移成像。杨勤勇等[3]讨论了浅层和中深层速度融合技术,建立了用于从起伏地表直接偏移成像的各向同性深度域速度模型和处理流程,并实现了起伏地表的叠前深度偏移。刘少勇等[4]通过选择适当光滑的基准面,提出了一套Kirchhoff叠前深度偏移方法在起伏地表的应用流程。在实际应用中,射线类方法(Kirchhoff积分法和束偏移法)相较于单程波和双程波方法,对复杂的近地表条件具有更强的适应性,对速度模型依赖性较弱,而且具有更高的计算效率,因而在生产中得到广泛的应用。
偏移速度建模是一个综合分析迭代的过程,主要包括叠前深度偏移和成像道集偏移速度分析两个环节。偏移速度分析依据不同的判别标准,主要形成了深度聚焦分析法和剩余曲率分析法。Faye等[5]、Mackay等[6]利用波动方程成像过程中的聚焦深度和成像深度的差异做速度分析。Al-Yahya[7]提出了剩余曲率分析法,利用偏移后的共成像点(CIP)道集拉平程度更新速度,该方法成熟、高效,简单易行,是目前应用最广泛的偏移速度分析方法。
层析反演方法能够恢复速度模型的高频信息,提高速度模型的精度,成为速度建模的重要技术,获得了广泛应用。射线层析反演方法通过最小化观测旅行时与计算旅行时之间的差值计算速度扰动、更新速度模型[8-9],具有高效、稳健、成本低的特点。Cerveny等[10]提出了更符合地震波实际传播规律的菲涅耳体射线追踪方法,是传统射线层析和波动方程层析方法的折中,降低了射线追踪误差。Marque-ring等[11]、Spetzler等[12-13]研究了第一菲涅耳体范围内的层析核函数,发展了菲涅耳体层析反演方法。
大量的研究表明,地层的各向异性对偏移成像的影响不可忽略[14-16]。Meadows等[17-18]实现了椭圆各向异性介质的Stolt偏移和TI介质的相移法偏移。Alkhalifah等[19]在VTI介质的速度分析中提出了一个反映各向异性综合响应的等效参数,进一步推动了各向异性理论的实际应用。各向异性速度建模和偏移技术在西部山地复杂构造成像方面获得了较好的应用效果[20-22]。
东方地球物理公司成功研制了深度域速度建模系统GeoEast-Diva (Depth Image Velocity Analysis),具备构造解释、初始建模、速度更新、深度偏移、可视化质控五大功能模块。根据实际地震资料品质,分别开发了速度扫描、垂向速度分析、沿层速度分析和层析反演等四种模型更新的关键技术,并配套了积分法和波束法叠前深度偏移技术,满足了“双复杂”条件下的地震速度建模和成像需求[23]。本文针对柯东巨厚黄土山区的地震成像难点,应用GeoEast-Diva软件完成了起伏地表条件下TTI各向异性介质全深度速度建模和偏移,明显改善了成像效果。
1 成像难点柯东构造带地表主要为巨厚黄土山,低、降速层的速度和厚度变化大,山区地表海拔接近3000m,最大黄土层厚度超过600m,表层静校正问题突出且地震波能量衰减严重,地震资料信噪比极低。该区总体构造格架表现为,在背斜构造背景下,被高角度基底卷入式断裂复杂化的断背斜模式。
该区断裂发育,地层倾角变化大,波场复杂,速度横向变化剧烈,地层的各向异性较强,导致处理、解释难度很大,无论是求取叠加速度还是偏移速度都非常困难,复杂构造难以准确成像[24-25]。其典型地震剖面如图 1所示,浅部呈杂乱反射,下盘为断块或断背斜。地质、钻井资料表明,白垩系分布与下伏上古生界古地貌关系密切,呈角度不整合接触,但在剖面上表现不明显,不利于白垩系分布分析。因此,厚黄土覆盖区极低信噪比地震资料的准确速度建模和偏移成像是制约塔西南地区油气勘探的关键。

|
图 1 柯东构造带典型地震剖面 TE、TK分别为白垩系顶、底界反射。深度从海拔0起算,下同 |
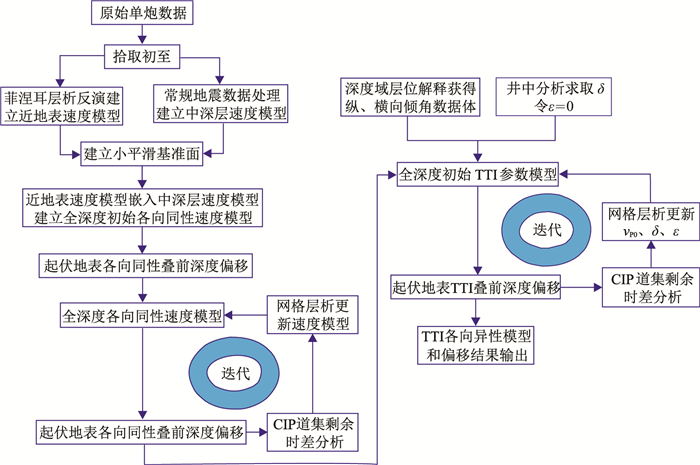
处理流程以地表小平滑面作为基准面建立各向异性全深度速度模型。建模分为两个阶段,一是建立起伏地表各向同性速度模型,其中,近地表模型采用菲涅耳体层析反演方法获得,并将其嵌入中深层速度模型。镶嵌时浅层速度模型需要进行编辑、平滑等处理,同时要设计一个过渡带,以使合并后不留痕迹。二是采用井震联合的方式求取三维各向异性参数,建立各向异性参数模型(图 2)。
|
图 2 起伏地表TTI各向异性速度建模流程 |
对于柯东地区地形高陡、黄土层厚度和速度变化快的特点,常规的初至波射线层析必然会造成射线密度不均匀,存在不适定性。菲涅耳体层析考虑了射线路径上第一菲涅耳带范围内介质对地震波传播速度的影响,较常规的射线层析可更精细、更稳定地描述复杂地表剧烈变化情况下近地表速度分布。因此,本文采用基于散射积分的初至波菲涅耳体层析方法建立近地表速度模型。
根据地震波传播的有限频理论[11],对于某个特定震相的观测信息,不仅射线路径上的点对该信息具有影响,中心射线邻域上的其他点对接收信息也具有影响,而且不同位置的点对接收信息的影响程度不同。这种影响可以用核函数表达。因此,在连续慢度场s(x)中,有限频地震波传播的旅行时t可以表示为
| $ t=\int_V K(\boldsymbol{x}) s(\boldsymbol{x}) \mathrm{d} \boldsymbol{x} $ | (1) |
式中:K (x)是旅行时层析核函数;V为中心射线附近对初至信息贡献最大的邻域范围,即菲涅耳体;x为空间位置。刘玉柱等[26]给出了单频菲涅耳体层析核函数的表达式
| $ K(\boldsymbol{x}, \omega)=\frac{2 \omega}{v(\boldsymbol{x})} \cdot \operatorname{Im}\left[\frac{G(\boldsymbol{g}, \boldsymbol{x}) u(\boldsymbol{x}, \boldsymbol{S})}{u(\boldsymbol{g}, \boldsymbol{S})}\right] $ | (2) |
式中:ω为圆频率;v (x)为当前速度场;G (g,x)为源点在x处、接收点在g处的格林函数;u (g,S)为源点在S、接收点在g处的地震波场;Im(·)表示取复数的虚部。
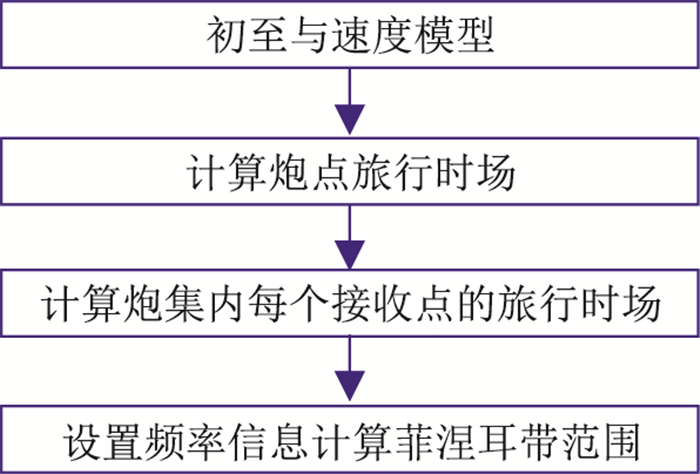
根据上述理论,计算菲涅耳体的实现流程如图 3所示。
|
图 3 菲涅耳体计算流程 |
本文采用改进的散射积分初至波菲涅耳体层析反演[27],其基本原理如下。
首先建立如下的最小二乘目标函数
| $ \varPhi(s)=\frac{1}{2}\left\|t_0-t\right\|_2^2 \rightarrow \min $ | (3) |
式中:t表示在当前模型下计算出的理论旅行时;t0表示实际观测到的旅行时。然后在有限频条件下,将式(1)离散化,得到n个初至波旅行时数据,m个空间未知数的方程组
| $ \mathit{\boldsymbol{t}}{\rm{ = }}\mathit{\boldsymbol{K s}} $ | (4) |
式中:K为n×m维的敏感核函数(式(2)的单频菲涅耳体层析核函数);t为旅行时向量;s为慢度模型向量。慢度模型的修改量可以表示为修改方向p与步长α的乘积。通过对式(3)进行二阶泰勒级数展开,可得模型参数的修改方向
| $ \boldsymbol{p}=-\left(\frac{\partial^2 \varPhi}{\partial s^2}\right)^{-1} \frac{\partial \varPhi}{\partial \boldsymbol{s}}=\boldsymbol{H}^{-1} \boldsymbol{K}^{\mathrm{T}} \Delta \boldsymbol{t} $ | (5) |
式中:Δt表示实际观测旅行时与当前模型下理论计算旅行时之差;H为准确的Hessian矩阵,是目标函数对慢度参数的二阶导数。模型参数的修改步长为
| $ \alpha=\frac{\boldsymbol{p}^{\mathrm{T}} \boldsymbol{K}^{\mathrm{T}} \Delta \boldsymbol{t}}{\boldsymbol{p}^{\mathrm{T}} \boldsymbol{H} \boldsymbol{p}} $ | (6) |
对于第j次迭代,可利用式(5)求得模型参数修改方向,用式(6)计算步长,从而对模型进行更新
| $ \boldsymbol{s}_{j+1}=\boldsymbol{s}_j+\alpha_j \boldsymbol{p}_j $ | (7) |
在小平滑面基础上,将菲涅耳体层析反演获得的近地表速度模型嵌入中深层速度模型,建立全深度速度模型。其中,中深层速度模型是利用时间域均方根速度场,通过约束速度反演(CVI)得到时间域层速度。约束速度反演过程首先是在解释人员提供的构造模型和测井资料约束下,应用Dix公式将时间域均方根速度转换为时间域层速度,然后利用趋势函数[28]
| $v_{\mathrm{T}}(t)=\frac{v_{\mathrm{a}} v_{\infty}}{v_{\mathrm{a}}+\Delta v \exp \left(-k_{\mathrm{a}} t v_{\infty} / \Delta v\right)} $ | (8) |
约束该层速度,使层速度模型更平滑,速度趋势更符合地层结构。式中:va为小平滑面处的初始瞬时速度,根据测井资料取值;v∞是无限深度处的渐进速度,实际取值为6500m/s;ka为速度垂向梯度;Δv= v∞-va。最后,通过时深转换获得深度域层速度模型,并加以编辑和平滑,作为叠前深度偏移的初始速度模型。
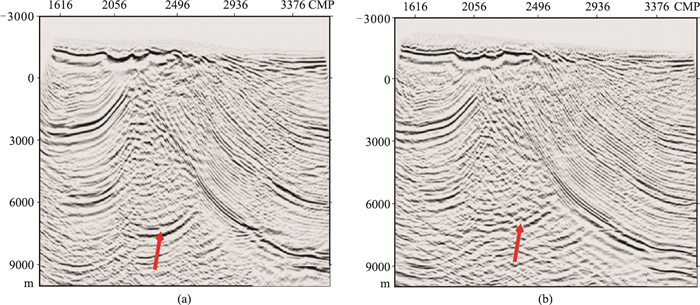
2.2.2 速度模型更新各向同性速度模型更新采用偏移与速度分析迭代的方式完成。与以往不同的是,本文联合采用了Kirchhoff积分法和高斯束法进行偏移迭代。柯东地区古近系以上地层结构相对简单,地震资料信噪比较高,古近系以下的古生界地质结构复杂,地震资料信噪比较低。实际处理中,古近系以上地层采用积分法偏移进行速度分析,古近系以下地层采用高斯束法偏移进行速度分析,有利于提高速度分析的道集质量[29-30]。图 4为Kirchhoff积分法和高斯束法联合与纯粹Kirchhoff积分法速度分析的偏移剖面对比,可见前者对古近系以下老地层的成像效果更好(红色箭头所示)。
|
图 4 Kirchhoff积分法和高斯束法联合(a)与纯粹Kirchhoff积分法(b)速度分析的偏移剖面对比 |
CIP道集速度分析采用由浅至深逐层分析方法。古近系以上的层状地层采用沿层谱速度分析方法,对于局部速度结构复杂、信噪比较低的区域采用速度扫描和垂向谱速度分析方法。通过校平CIP道集中的反射波同相轴,达到速度模型更新和提高成像质量的目的。
垂向谱速度分析是基于单个CIP道集进行速度分析,其实现过程是:①选择CIP道集,计算相关谱,并基于CIP道集和相关谱拾取残差;②通过一维层析反演把每个道集的残差转化为深度—速度对;③在CIP道集之间插值深度—速度对,更新层速度。沿层谱速度分析把单道集速度更新变成了沿层速度更新,沿层相关谱能够更直观地展示残差的横向变化趋势,其实现过程与垂向谱速度分析法类似。
速度扫描是低信噪比资料初始速度建模与更新的有效工具,其实现过程是:①扫描单层速度,得到不同百分比的速度场;②对每个速度场进行目标线深度偏移,得到叠加剖面和CIP道集;③分析深度剖面的成像质量、CIP道集的同相轴校平情况和剩余速度谱,在选定的CIP道集上挑选合适的速度插值,完成整个层位的更新。不同扫描速度的成像结果在深度上变化很大,不利于叠加剖面和CIP道集的快速对比。为此,在速度扫描法中引入了等效深度概念[23],将不同速度模型的偏移结果校正到统一深度,便于速度分析。
网格层析方法根据拾取的深度残差和射线路径建立方程,采用反演方法优化速度模型。与前面三种速度分析方法相比,该方法能够恢复速度场的高频信息,更有利于对古近系以下老地层的速度场进行优化,有助于研究新、老地层的角度不整合。其实现过程是:①根据初始的深度域偏移数据及其连续性,提取构造倾角体和质量因子;②利用质量因子选取拾取位置,在CIP道集上拾取深度残差;③根据速度模型、残差和倾角等信息,从地下面元向上进行射线追踪,得到射线路径和旅行时;④建立包含多层位的全局网格层析成像矩阵;⑤求解矩阵,沿着射线路径,获得每个网格的速度修改量,将其平滑后更新速度场。
2.3 各向异性参数建模业界各向异性速度建模广泛采用Thomsen的VTI介质模型
| $ v_{\mathrm{P}}(\theta)=v_{\mathrm{P} 0}\left(1+\delta \sin ^2 \theta \cos ^2 \theta+\varepsilon \sin ^4 \theta\right) $ | (9) |
式中:θ是地震射线与垂直对称轴的夹角;δ、ε是各向异性参数,分别对应中等角度、大角度的速度影响因素;vP0是地震波垂直地层传播的速度,与动校正速度vnmo满足
| $ v_{\mathrm{nmo}}=v_{\mathrm{P} 0} \sqrt{1+2 \delta} $ | (10) |
对于三维数据体,TTI各向异性叠前深度偏移还需要地层的倾角和方位角信息。
上述5个参数中,速度、倾角、方位角参数主要控制构造的形态,对构造成像的影响较大,δ和ε主要控制井震误差和改善同相轴成像的连续性。GeoEast-Diva软件中,倾角和方位角参数可以转换为Inline方向的倾角和Crossline方向的倾角。具体的各向异性参数建模步骤如下。
(1) 将2.2中获得的各向同性深偏速度模型作为各向异性叠前深度偏移的初始速度模型。
(2) 解释各向同性深度域层位,求取Inline倾角和Crossline倾角体,利用测井分层数据通过求取对应层位的δ
| $ \delta_i=\frac{1}{2}\left(\frac{Z_i^{\mathrm{m}}}{Z_i^{\mathrm{r}}}-1\right) $ | (11) |
式中:Zim为从偏移剖面获得的第i层厚度;Zir是从测井分层数据获得的第i层厚度。使ε=0(因为ε值通常较小),从而建立初始各向异性参数模型。
(3) 基于初始各向异性全深度参数模型进行起伏地表叠前深度偏移,采用网格层析反演的方法迭代更新参数模型,最后得到准确合理的起伏地表TTI叠前深度偏移参数模型。
速度更新过程中,利用钻、测资料控制深度和倾角,同时利用中、远炮检距道集是否拉平来判断参数模型更新是否合理。
3 应用效果分析抽取柯东工区一条过井剖面进行试处理。图 5为试处理测线菲涅耳体层析反演建立的近地表速度模型。采用本文的起伏地表TTI各向异性全深度速度建模方法建立的各向同性和各向异性叠前深度偏移速度模型如图 6所示,图 7是对应的各向异性参数剖面。

|
图 5 菲涅耳层析反演建立的近地表速度模型 |

|
图 6 各向同性(a)与各向异性(b)深度域速度模型对比 |
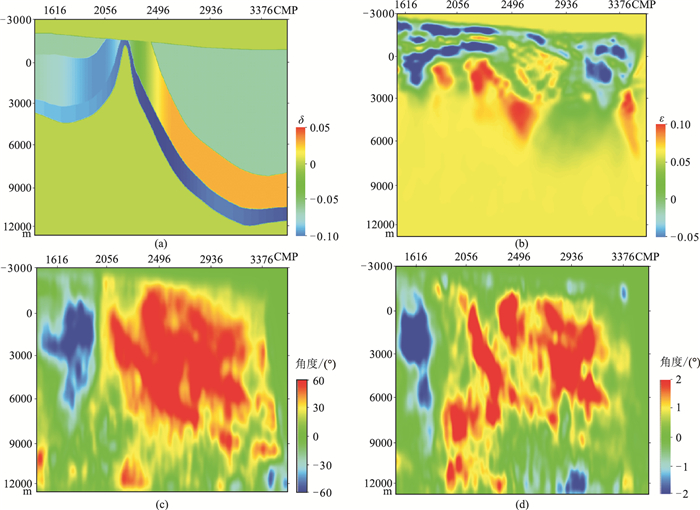
|
图 7 各向异性参数及倾角剖面 (a)δ;(b)ε;(c)Inline方向倾角;(d)Crossline方向倾角 |
图 8a是基于各向同性起伏地表速度模型的Kirchhoff叠前深度偏移剖面,图 8b是各向异性起伏地表速度模型获得的Kirchhoff叠前深度偏移剖面。从偏移效果看,后者(图 8b)的成像效果明显优于前者(图 8a)。在图 8b上,陡倾地层反射同相轴更连续,红色箭头处清晰展示了白垩系与下伏老地层的角度不整合接触关系,而图 8a的红色箭头处同相轴交叉,接触关系不清晰。同时,图 8b的深部老地层的同相轴的连续性和信噪比也更高(蓝色箭头处)。与图 1相比,图 8的成像效果明显改善。

|
图 8 不同速度模型的起伏地表Kirchhoff叠前深度偏移剖面对比 (a)各向同性速度模型偏移结果;(b)各向异性速度模型偏移结果。红色竖线表示钻井位置,蓝色横线表示区域标准层白垩系顶的钻遇深度,绿色短线表示白垩系顶在剖面上井点处的成像深度。紫色层位TE为白垩系顶,绿色层位TK为白垩系底。 |
另外,TTI各向异性叠前深度偏移剖面的目的层(古近系底)的成像深度与钻井更吻合(表 1)。
|
|
表 1 不同模型古近系底成像误差对比 |
针对塔西南复杂探区的速度建模难题,应用GeoEast-Diva建模系统综合多种信息建立了精度较高的起伏地表各向异性叠前深度偏移速度模型,为柯东复杂构造带高精度地震成像提供了保障。
(1) 菲涅耳体初至波层析反演方法利用大炮初至建立精确的起伏地表近地表速度模型,是全深度速度建模的基础。
(2) 联合利用积分法和高斯束法偏移迭代以及多种速度分析工具,提高了各向同性全深度速度模型的精度。
(3) 通过井震联合的方法获取各向异性参数,联合倾角和方位角信息建立了初始TTI各向异性全速度模型。采用起伏地表TTI介质Kirchhoff叠前深度偏移进行偏移成像时,自动拾取CIP道集中的剩余时差,利用网格层析反演实现各向异性速度模型的更新,多次迭代后获得了比较理想的成像结果。
(4) 与各向同性起伏地表叠前深度偏移结果相比,基于TTI各向异性起伏地表速度模型的叠前深度偏移结果基本消除了复杂构造与各向异性的影响,偏移结果与钻井更吻合,构造形态合理,新、老地层角度不整合接触关系更清晰。
| [1] |
杨海军, 王步清, 杨芝林, 等. 塔里木盆地西南坳陷柯东构造建模与油气勘探[J]. 地质科学, 2011, 46(2): 456-465. YANG Haijun, WANG Buqing, YANG Zhilin, et al. Structure modeling and hydrocarbon exploration of Kedong structural belt in southwestern Tarim Basin[J]. Chinese Journal of Geology, 2011, 46(2): 456-465. DOI:10.3969/j.issn.0563-5020.2011.02.014 |
| [2] |
RAJASEKARAN S, MCMECHAN G A. Prestack processing of land data with complex topography[J]. Geophysics, 1995, 60(6): 1875-1886. DOI:10.1190/1.1443919 |
| [3] |
杨勤勇, 方伍宝. 复杂地表复杂地下地区地震成像技术研究[J]. 石油与天然气地质, 2008, 29(5): 676-682, 689. YANG Qinyong, FANG Wubao. A study on seismic imaging techniques in complex surface and subsurface areas[J]. Oil & Gas Geology, 2008, 29(5): 676-682, 689. DOI:10.3321/j.issn:0253-9985.2008.05.017 |
| [4] |
刘少勇, 王华忠, 张兵. 起伏地表Kirchhoff积分法叠前深度偏移方法研究与应用[J]. 岩性油气藏, 2010, 22(7): 49-54. LIU Shaoyong, WANG Huazhong, ZHANG Bing. Kirchhoff integral PSDM for rugged topography: technology and application[J]. Lithologic Reservoirs, 2010, 22(7): 49-54. |
| [5] |
FAYE J P, JEANNOT J P. Prestack migration velo-cities from depth focusing analysis[J]. SEG Technical Program Expanded Abstracts, 1986, 5: 438-440. |
| [6] |
MACKAY S, ABMA R. Imaging and velocity estimation with depth-focusing analysis[J]. Geophysics, 1992, 57(12): 1608-1622. DOI:10.1190/1.1443228 |
| [7] |
AL-YAHYA K. Velocity analysis by iterative profile migration[J]. Geophysics, 1989, 54(6): 718-729. DOI:10.1190/1.1442699 |
| [8] |
BISHOP T N, BUBE K P, CUTLER R T, et al. Tomographic determination of velocity and depth in la-teral varying media[J]. Geophysics, 1985, 50(4): 903-923. |
| [9] |
杨文采. 地球物理反演的理论与方法[M]. 北京: 地质出版社, 1997.
|
| [10] |
CERVENY V, SOARES J E P. Fresnel volume ray tracing[J]. Geophysics, 1992, 52(7): 902-915. |
| [11] |
MARQUERING H, DAHLEN F A, NOLET G. Three-dimensional waveform sensitivity kernels for finite-frequency traveltimes: the banana doughnut pa-radox[J]. Geophysical Journal International, 1999, 137(3): 805-815. DOI:10.1046/j.1365-246x.1999.00837.x |
| [12] |
SPETZLER J, SNIEDER R. The effect of small-scale heterogeneity on the arrival time of waves[J]. Geophysical Journal International, 2001, 145(3): 786-796. DOI:10.1046/j.1365-246x.2001.01438.x |
| [13] |
SPETZLER J, SNIEDER R. The Fresnel volume and transmitted waves[J]. Geophysics, 2004, 69(3): 653-663. DOI:10.1190/1.1759451 |
| [14] |
BALL G. Estimation of anisotropy and anisotropic 3D prestack depth migration, offshore Zaire[J]. Geophysics, 1995, 60(5): 1495-1513. DOI:10.1190/1.1443883 |
| [15] |
YAN L L, LINES L R, LAWTON D C. Influence of seismic anisotropy on prestack depth migration[J]. The Leading Edge, 2004, 23(1): 30-36. DOI:10.1190/1.1645453 |
| [16] |
ZHANG J F, VERSCHUUR D J, WAPENAAR C P A. Depth migration of shot records in heterogeneous, transversely isotropic media using optimum explicit operators[J]. Geophysical Prospecting, 2001, 49(3): 287-299. DOI:10.1046/j.1365-2478.2001.00255.x |
| [17] |
MEADOWS M, COEN S, LIU G M. F-K migration in elliptically anisotropic media[J]. Geophysics, 1986, 55(11): 2031-2050. |
| [18] |
MEADOWS M, ABRIEL W L. 3-D poststack phase-shift migration in transversely isotropic media[C]. SEG Technical Program Expanded Abstracts, 1994, 13: 1205-1208.
|
| [19] |
ALKHALIFAH T, TSVANKIN I. Velocity analysis for transversely isotropic media[J]. Geophysics, 1995, 60(5): 1550-1566. DOI:10.1190/1.1443888 |
| [20] |
王延光, 尚新民, 赵胜天, 等. 山前带联合层析反演地震成像[J]. 石油地球物理勘探, 2021, 56(4): 782-791. WANG Yanguang, SHANG Xinmin, ZHAO Shengtian, et al. Joint tomography for foothills seismic imaging[J]. Oil Geophysical Prospecting, 2021, 56(4): 782-791. |
| [21] |
杨宗青, 李宏伟, 欧居刚, 等. TTI介质各向异性参数优化提取方法[J]. 石油地球物理勘探, 2020, 55(1): 111-116. YANG Zongqing, LI Hongwei, OU Jugang, et al. An optimized method for extracting anisotropic parameters in TTI media[J]. Oil Geophysical Prospecting, 2020, 55(1): 111-116. |
| [22] |
吴超, 许安明, 尚江伟, 等. TTI各向异性叠前深度偏移技术在库车复杂山地的应用[J]. 新疆石油地质, 2019, 40(1): 103-107. WU Chao, XU Anming, SHANG Jiangwei, et al. Application of TTI anisotropic prestack depth migration technology in complex mountain areas of Kuqa depression[J]. Xinjiang Petroleum Geology, 2019, 40(1): 103-107. |
| [23] |
程玉坤, 刘建红, 周振晓, 等. 速度建模特色技术的实际应用[J]. 石油地球物理勘探, 2017, 52(增刊2): 110-115. CHENG Yukun, LIU Jianhong, ZHOU Zhenxiao, et al. Depth-domain velocity model building for prestack depth imaging[J]. Oil Geophysical Prospecting, 2017, 52(S2): 110-115. |
| [24] |
杜治利, 师骏, 曾昌民, 等. 柯东构造带柯东段中新世以来两期构造变形与油气成藏[J]. 新疆地质, 2012, 30(2): 192-195. DU Zhili, SHI Jun, ZENG Changmin, et al. 2-stage deformation and its exploration significance since Miocene in the east section of Kedong thrust belt[J]. Xinjiang Geology, 2012, 30(2): 192-195. |
| [25] |
周翼, 李道善, 师骏, 等. 塔西南柯东构造带二维资料叠前深度偏移处理、解释[J]. 中国石油勘探, 2011, 16(5): 14-18, 48. ZHOU Yi, LI Daoshan, SHI Jun, et al. Prestack depth migration processing and interpretation of 2D seismic data in Kedong tectonic zone, southwest of Tarim Basin[J]. China Petroleum Exploration, 2011, 16(5): 14-18, 48. |
| [26] |
刘玉柱, 董良国, 李培明, 等. 初至波菲涅尔体地震层析成像[J]. 地球物理学报, 2009, 52(9): 2310-2320. LIU Yuzhu, DONG Liangguo, LI Peiming, et al. Fresnel volume tomography based on the first arrival of the seismic wave[J]. Chinese Journal of Geophy-sics, 2009, 52(9): 2310-2320. |
| [27] |
李勇德, 董良国, 刘玉柱. 基于改进的散射积分算法的初至波走时层析[J]. 地球物理学报, 2016, 59(10): 3820-3828. LI Yongde, DONG Liangguo, LIU Yuzhu. First arrival traveltime tomography based on an improved scatte-ringintegral algorithm[J]. Chinese Journal of Geophysics, 2016, 59(10): 3820-3828. |
| [28] |
KOREN Z, RAVVE L. Constrained Dix inversion[J]. Geophysics, 2006, 71(6): 113-130. |
| [29] |
李振春, 岳玉波, 郭朝斌, 等. 高斯波束共角度保幅深度偏移[J]. 石油地球物理勘探, 2010, 45(3): 360-365. LI Zhenchun, YUE Yubo, GUO Chaobin, et al. Gaussian beam common angle preserved-amplitude migration[J]. Oil Geophysical Prospecting, 2010, 45(3): 360-365. |
| [30] |
刘强, 张敏, 李振春, 等. 各向异性介质共炮域高斯束偏移[J]. 石油地球物理勘探, 2016, 51(5): 930-937. LIU Qiang, ZHANG Min, LI Zhenchun, et al. Com mon-shot domain Gaussian beam migration in aniso-tropic media[J]. Oil Geophysical Prospecting, 2016, 51(5): 930-937. |



 李忠, 四川省成都市天府新区滨河路一段95号东方地球物理公司物探技术研究中心成都分中心, 610213。Email:
李忠, 四川省成都市天府新区滨河路一段95号东方地球物理公司物探技术研究中心成都分中心, 610213。Email: 