2. 中国地质调查局南海地质科学院, 海南三亚 572025;
3. 中国石油辽河油田分公司, 辽宁盘锦 124010
2. Academy of South China Sea Geological Science, China Geological Survey, Sanya, Hainan 572025, China;
3. PetroChina Liaohe Oilfield Company, Panjin, Liaoning 124010, China
天然气水合物又称“可燃冰”,是天然气与水在高压、低温条件下形成的类冰状结晶物质,通常分布于深海沉积物或陆域永久冻土带中。与不含水合物的地层相比,含天然气水合物的地层具有高电阻率、高纵波速度、高横波速度、高拉梅系数、略低泊松比及低氯离子浓度等特征。这些参数的大小主要与水合物饱和度有关。饱和度也是资源量估算的一个关键参数[1]。目前,利用井资料计算水合物饱和度的方法主要有速度法、电阻率法、碳氧比能谱法及孔隙水氯离子浓度法[2-5]等,利用地震资料计算水合物饱和度的方法主要是速度法[6-10]。
研究区位于中国某海域外陆坡深水区。该区域隆升构造发育且缺少陆源物质注入。从研究区地质特征来看,温压条件、气源条件、构造条件及沉积条件均满足天然气水合物成藏与保存。分析地震资料可知,研究区存在较可靠的似海底反射(Bottom Simulating Reflection,BSR),具有良好的天然气水合物资源前景。研究区与其以北的已发现水合物的区域地质背景不同,这使得研究区成为水合物研究的新领域。
研究表明,水合物的微观赋存模式主要有三种,即悬浮模式、颗粒接触模式及胶结模式。目前已有多种理论或实验模型可把水合物饱和度与地震速度联系起来,用于估算天然气水合物饱和度。常用的声波速度方程主要有三种:①伍德方程[11-12],适用于悬浮状填充物孔隙流体介质;②李权重方程[13-15],主要适用于颗粒接触模式;③时间平均方程[16],主要适用于胶结模式[17]。与声波速度方程不同,等效介质方程主要通过限定条件描述三种赋存模式的纵波速度与水合物饱和度的关系[18-19]。以上几种应用地震速度计算水合物饱和度的方法均需要利用骨架颗粒速度与密度、流体速度与流体密度等实测资料才能相对准确地求取水合物饱和度。研究区目的层缺乏实测数据,无法直接利用理论公式计算水合物饱和度。另外,由于目的层无钻探取样,无法对水合物饱和度与纵波阻抗关系进行标定。因此,尽管研究区具备纵波阻抗数据体,也无法利用关系式法直接求取水合物饱和度。
研究区稳定带内的浅部地层为深海—半深海沉积[20],沉积相对稳定,地层岩性及厚度横向变化小。从地震剖面看,地震同相轴横向连续性强,推测纵波阻抗剖面中异常高值仅是地层中水合物矿体引起的。因此,本研究尝试利用水合物地层纵波阻抗与不含水合物地层纵波阻抗的比值(称为波阻抗增大系数)求取水合物饱和度。
本研究基于东方地球物理公司开发的GeoEast解释系统,形成了一套特定地质条件下的水合物饱和度评价技术方案。可靠的水合物饱和度数据为区域资源量的评价奠定了基础。
1 水合物饱和度计算原理水合物主要以悬浮模式、颗粒接触模式及胶结模式三种方式赋存于沉积物孔隙中[21],不同的微观模式会呈现出不同的水合物地层岩石物理特征。水合物聚散过程模拟实验[22-23]表明:游离态甲烷形成的水合物主要以胶结模式赋存于沉积物颗粒间;溶解态甲烷形成的水合物颗粒较小,主要以悬浮模式赋存于沉积物颗粒间。通过研究区地震资料及成矿条件分析可知,研究区水合物矿体源自溶解态甲烷,因此,本研究采用悬浮模式水合物模型进行饱和度分析。
三相介质Wood方程适合于悬浮模式,其表达式[11-12]如下
| $ \frac{1}{\rho V_{\mathrm{p}}^2}=\frac{\phi\left(1-S_{\mathrm{h}}\right)}{\rho_{\mathrm{w}} V_{\mathrm{w}}^2}+\frac{\phi S_{\mathrm{h}}}{\rho_{\mathrm{h}} V_{\mathrm{h}}^2}+\frac{1-\phi}{\rho_{\mathrm{m}} V_{\mathrm{m}}^2} $ | (1) |
式中:Vp为沉积层纵波速度;Vm为骨架颗粒速度,研究区内灰岩速度为6410m/s,黏土速度为3400m/s;Vh为纯水合物的纵波速度,取值3650m/s;Vw为孔隙中流体纵波速度,取值1500m/s;ρw为流体密度,取值1.000g/cm3;ρh为纯水合物密度,取值0.917g/cm3;ρm为岩石骨架密度,研究区灰岩骨架密度为2.710g/cm3,砂岩骨架密度为2.650g/cm3,泥岩骨架密度为2.600g/cm3;ρ为沉积物密度;ϕ为孔隙度;Sh为水合物饱和度。
采用如下组分加权平均公式计算沉积物的整体等效密度
| $ \rho=(1-\phi) \rho_{\mathrm{m}}+\left(1-S_{\mathrm{h}}\right) \phi \rho_{\mathrm{w}}+S_{\mathrm{h}} \phi \rho_{\mathrm{h}} $ | (2) |
根据研究区稳定带以下的测井和录井资料及海底表层采样资料,推测稳定带内岩性为灰质泥岩或泥质灰岩,但无法确定灰质颗粒或黏土颗粒的含量。假设地层骨架颗粒组分为四种组合:灰岩0,黏土100%;灰岩30%,黏土70%;灰岩70%,黏土30%;灰岩100%,黏土0。浅部未成岩地层孔隙度较大,孔隙度分别设定为40%、50%及60%。
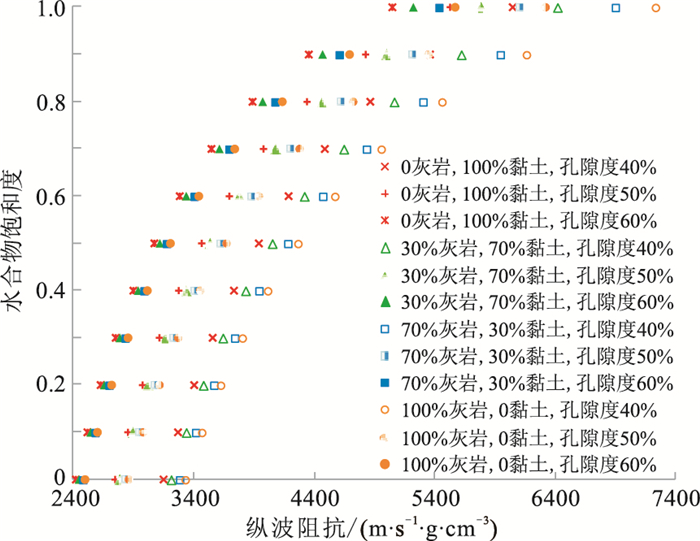
应用Wood方程计算纵波阻抗与水合物饱和度的关系(见图 1),可以看出,对于前述四种不同地层骨架颗粒组分与三种孔隙度的组合(后文称每种组合为一个系列),地层纵波阻抗均随饱和度增大而增大,且各系列相对较分散。当地层骨架颗粒组成及水合物饱和度相同时,地层纵波阻抗随孔隙度增大而减小。当地层孔隙度及水合物饱和度相同时,灰岩颗粒含量越高,地层纵波阻抗越大。因此,在研究区水合物储层骨架颗粒含量及孔隙度无法确定的情况下,无法应用纵波阻抗与饱和度的关系直接进行水合物饱和度的定量计算。
|
图 1 研究区纵波阻抗与水合物饱和度关系图 |
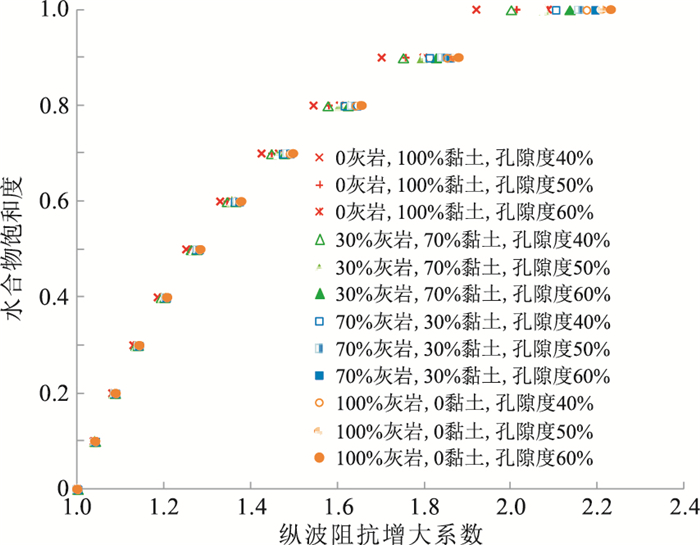
为解决以上问题,尝试用图 1中每个系列数据点的纵波阻抗除以该系列饱和度为0时的纵波阻抗,得到各系列纵波阻抗增大系数与水合物饱和度的关系(图 2)。可以看出,水合物饱和度随纵波阻抗增大系数的增大而增大,且在饱和度小于60%时,不同骨架颗粒组分和不同孔隙度的各系列相对较收敛,即无论骨架颗粒组分及孔隙度如何变化,水合物饱和度与纵波阻抗增大系数之间的关系基本不变。因此,纵波阻抗增大系数与饱和度的关系法优于传统的纵波阻抗与饱和度关系法,前者可忽略骨架颗粒组分及孔隙度对饱和度计算结果带来的影响,使水合物饱和度计算结果更可靠。
|
图 2 研究区纵波阻抗增大系数与水合物饱和度关系 |
不难发现,纵波阻抗增大系数与水合物饱和度的关系类似于阿尔奇公式[24-26]
| $ I=\frac{R_{\mathrm{t}}}{R_0}=\frac{b}{S_{\mathrm{w}}{ }^n} $ | (3) |
式中:I为电阻增大系数;Rt为含油气岩石的电阻率;R0为地层完全含水时的电阻率;b为与岩性相关的系数,一般取b=1;n为水合物饱和度指数;Sw为含水饱和度。
参考阿尔奇公式,建立含水合物地层纵波阻抗和纯含水地层纵波阻抗比值与含水饱和度关系
| $ I_{\mathrm{R}}=\frac{Z_{\mathrm{P}_{\mathrm{t}}}}{Z_{\mathrm{P}_0}}=\frac{x}{{S_{\mathrm{w}}}^y} $ | (4) |
式中:IR为纵波阻抗增大系数;Zpt为含水合物地层的纵波阻抗;Zp0为纯含水地层的纵波阻抗;x为与地层相关的系数;y为与饱和度相关的系数。当地层不含水合物时,即Zpt/Zp0=1,此时Sw=1,则式中x=1,将关系式Sh=1-Sw代入式(4),整理得到
| $ S_{\mathrm{h}}=1-I_{\mathrm{R}}^{-\frac{1}{y}} $ | (5) |
将图 2中饱和度小于60%的所有系列数据点代入式(5)进行拟合,得到饱和度相关系数y=0.34237,即
| $ S_{\mathrm{h}}=1-I_{\mathrm{R}}^{-\frac{1}{0.34237}} $ | (6) |
该公式的相关系数的平方(y2)为0.994,只适用于水合物微观赋存状态为悬浮模式且地层岩性为灰质泥岩或泥质灰岩且水合物饱和度小于60%的情况。
2 实例分析通过分析研究区BSR与地层的关系,发现BSR基本分布于莺二下段(T12-T2)内,相比邻近的原状地层(不含水合物地层),BSR出现的地层地震波形发生明显改变。由于研究区远离陆源,区域内沉积稳定,浅部地层岩性和厚度横向变化小,因此可认为波形和纵波阻抗的改变仅是地层中充填了水合物造成的。
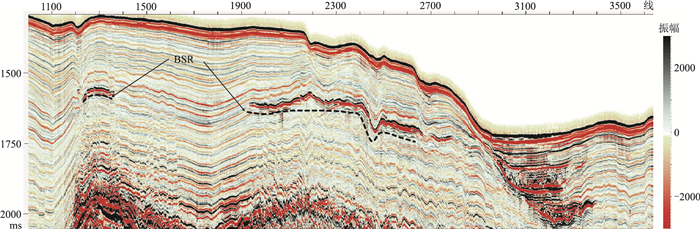
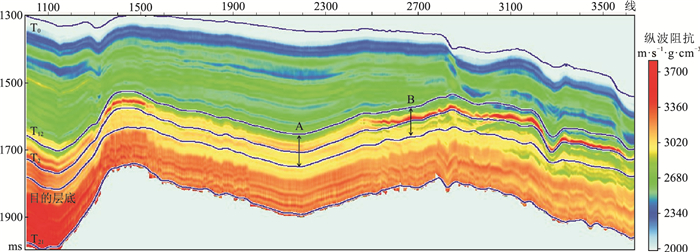
以图 3所示过BSR的典型剖面为例。可以看出,浅部地层同相轴横向连续性较好,BSR局部有穿层现象。图 4为对应的纵波阻抗剖面。可以看出,由于水合物的存在,BSR强反射之上地层相比围岩纵波速度明显增大,呈薄层连片状发育。
|
图 3 研究区过BSR的地震剖面 |
|
图 4 图 3对应的纵波阻抗剖面 |
本文求取水合物饱和度的流程如下:首先,利用GeoEast反演模块对地震数据进行反演,得到纵波阻抗数据体,确定原状地层目的层段纵波阻抗平均值与其埋深的关系;其次,确定研究区目的层段原状地层参考点的波阻抗曲线;最后,利用GeoEast平台的Custom Calculation模块对研究区纵波阻抗数据进行处理,得到研究区原状地层波阻抗数据体,进而计算得到纵波阻抗数据体与原状地层纵波阻抗数据体的比值,求得纵波阻抗增大系数体。利用纵波阻抗增大系数与水合物饱和度的关系式可计算研究区水合物的饱和度[27-29]。
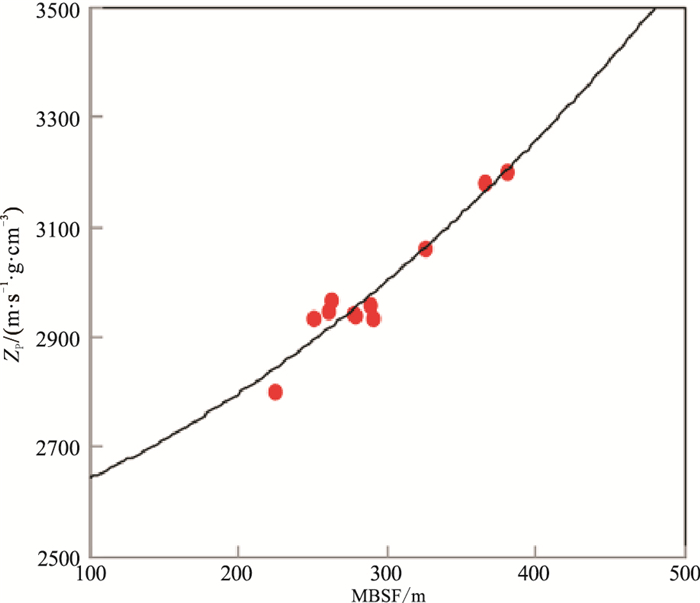
2.1 确定原状地层目的层段纵波阻抗平均值与埋深的关系在研究区选定11个典型的采样点,统计目的层段(T12-RB,RB为目的层底界)原状地层纵波阻抗平均值ZP与海底以下埋深(MBSF)的关系(表 1),可知采样点目的层段内纵波阻抗平均值随埋深增加而增大(图 5),其拟合关系式为
| $ \begin{aligned} Z_{\mathrm{P}}= & 0.0025 \times \mathrm{MBSF}^2+ \\ & 0.7955 \times \mathrm{MBSF}+2537.6 \end{aligned} $ | (7) |
|
|
表 1 工区目的层段MBSF与ZP统计结果 |
|
图 5 原状地层目的层段MBSF与ZP关系图 |
式中相关系数平方y2=0.9281。
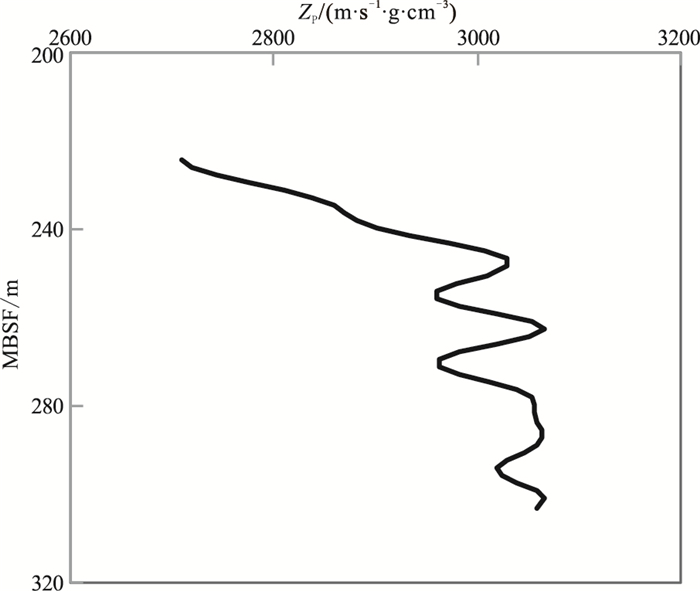
2.2 确定目的层段纵波阻抗标准曲线通过综合分析原状地层11个采样点在目的层段的波阻抗曲线,最终选定3号样点(图 4中A点)的波阻抗曲线(图 6)作为研究区原状地层波阻抗计算的标准曲线。研究区其他位置目的层段的原状地层纵波阻抗曲线均参照此标准曲线求取。
|
图 6 3号样点(A点)目的层段纵波阻抗曲线 |
以图 4中B点为例说明原状地层波阻抗求取方法,具体步骤如下。
首先,确定B点原状地层埋深为210m,将埋深值代入式(7)求得目的层段原状地层纵波阻抗为2815 m·s-1·g·cm-3。已知标准样点A的目的层段纵波阻抗平均值为2967 m·s-1·g·cm-3(表 1),得到B点目的层段纵波阻抗与A点目的层段的纵波阻抗的比值为0.949,即B点目的层段原状地层纵波阻抗值均为A点纵波阻抗曲线的0.949倍。将图 6中的A点的纵波阻抗乘以0.949,即得到B点目的层段原状地层波阻抗。
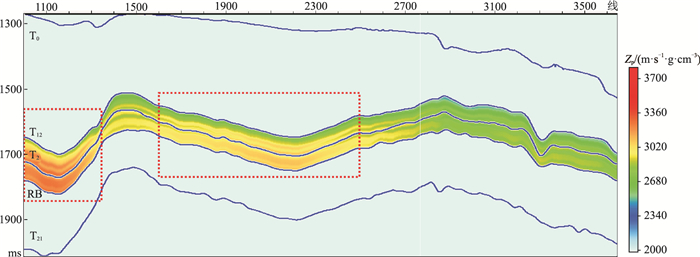
然后,将上述方法应用于研究区所有点,得到研究区原状地层纵波阻抗数据体(图 7)。可以看出,剖面中部(右边红色虚线框)纵波阻抗值与图 4中反演纵波阻抗剖面中的原状地层纵波阻抗值基本一致,说明计算得到的原状地层纵波阻抗值较准确。图 7中剖面左侧目的层段(左边红色虚线框)相较于图 4中同一层段纵波阻抗值偏大,这是该点地层埋深较大造成的。
|
图 7 研究区原状地层纵波阻抗剖面 |
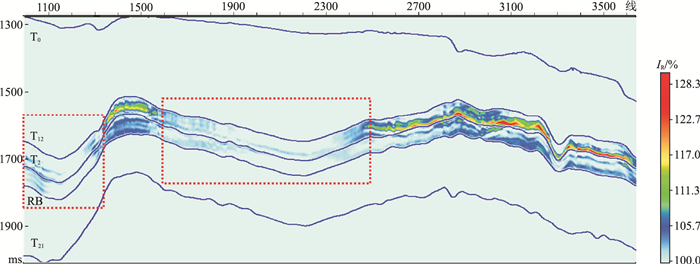
最后,计算反演纵波阻抗与原状地层纵波阻抗的比值,得到研究区纵波阻抗增大系数(图 8)。可以看出,剖面左侧及中部原状地层位置的纵波阻抗增大系数约等于1,这与原状地层中几乎不含水合物是吻合的;含水合物地层的纵波阻抗增大系数局部大于1,这与地层中含水合物相吻合,说明预测结果合理、可靠。
|
图 8 研究区纵波阻抗增大系数剖面 |
利用波阻抗增大系数与水合物饱和度的关系计算得到研究区饱和度数据体(图 9)。可以看出,原状地层目地层内(右边红色虚线框)水合物饱和度整体上低于5%,与原状地层中几乎不含水合物相吻合,误差在允许范围内。BSR之上、靠近BSR地层(左边红色虚线框)的水合物饱和度较高,向上逐渐降低,纵向上水合物饱和度曲线表现为漏斗状。

|
图 9 研究区水合物饱和度剖面 |
本文基于GeoEast软件平台,采用波阻抗增大系数法实现了特定地质条件下水合物饱和度的定量求取,为后续资源量计算奠定了基础。
3 结论与认识研究区为深海—半深海沉积,沉积稳定,目的层地震同相轴连续性好,这是本研究开展水合物饱和度求取的前提条件。
本文利用Wood方程建立适于研究区的波阻抗增大系数方程。相比传统纵波阻抗法,该方程收敛性强,可以有效消除岩性及孔隙度对饱和度计算结果的影响。
在研究区目的层段缺少井资料及岩石物理参数的情况下,本文建立了一套仅依靠波阻抗数据实现水合物饱和度评价的方法。该方法亦可应用到类似研究区地质条件的其他区域。
受地震分辨率及反演纵波阻抗精度的限制,本方法计算的水合物饱和度尚需录井、测井或取心资料进一步验证。
| [1] |
王秀娟, 吴时国, 刘学伟, 等. 基于测井和地震资料的神狐海域天然气水合物资源量估算[J]. 地球物理学进展, 2010, 25(4): 1288-1297. WANG Xiujuan, WU Shiguo, LIU Xuewei, et al. Estimation of gas hydrates resources based on well log data and seismic data in Shenhu area[J]. Progress in Geophysics, 2010, 25(4): 1288-1297. |
| [2] |
冯凯, 李敏锋, 刘竣川, 等. 天然气水合物和游离气层的弹性参数异常特征及其在饱和度估算中的应用[J]. 石油地球物理勘探, 2008, 43(4): 430-436. FENG Kai, LI Minfeng, LIU Junchuan, et al. Anomalous feature of elastic parameters in sediments with gas-hydrate and free gas and application in estimation of saturation[J]. Oil Geophysical Prospecting, 2008, 43(4): 430-436. |
| [3] |
王秀娟, 吴时国, 郭璇, 等. 南海陆坡天然气水合物饱和度估计[J]. 海洋地质与第四纪地质, 2005, 25(3): 89-95. WANG Xiujuan, WU Shiguo, GUO Xuan, et al. Estimation of gas hydrate saturation in the continental slope, the South China Sea[J]. Marine Geology & Quaternary Geology, 2005, 25(3): 89-95. |
| [4] |
宋海斌, 耿建华, WANG H K, 等. 南海北部东沙海域天然气水合物的初步研究[J]. 地球物理学报, 2001, 44(5): 687-695. SONG Haibin, GENG Jianhua, HOW-KING W, et al. A preliminary study of gas hydrates in Dongsha region, North of South China Sea[J]. Chinese Journal of Geophysics, 2001, 44(5): 687-695. |
| [5] |
王秀娟, 靳佳澎, 郭依群, 等. 南海北部天然气水合物富集特征及定量评价[J]. 地球科学, 2021, 46(3): 1038-1057. WANG Xiujuan, JIN Jiapeng, GUO Yiqun, et al. The characteristics of gas hydrate accumulation and quantitative estimation in the North slope of South China Sea[J]. Earth Science, 2021, 46(3): 1038-1057. |
| [6] |
ZHANG Z J, HAN D H, YAO Q L. Quantitative interpretation for gas hydrate accumulation in the eas-tern Green Canyon Area, Gulf of Mexico using seismic inversion and rock physics transform[J]. Geophy-sics, 2011, 76(4): B139-B150. |
| [7] |
LU S M, MCMECHAN G A. Estimation of gas hydrate and free gas saturation, concentration, and distribution from seismic data[J]. Geophysics, 2002, 67(2): 582-593. DOI:10.1190/1.1468619 |
| [8] |
李子坤, 王赟, 陆敬安, 等. 海洋天然气水合物地震探测技术进展——从单纵波到多波[J]. 石油物探, 2021, 60(1): 92-104. LI Zikun, WANG Yun, LU Jing'an, et al. Seismic exploration of marine gas hydrates: A review of P-wave and multi-wave technologies[J]. Geophysical Prospecting for Petroleum, 2021, 60(1): 92-104. |
| [9] |
MINDLIN R D. Compliance of elastic bodies in contact[J]. Journal of Applied Mechanics, 1949, 16(3): 259-268. DOI:10.1115/1.4009973 |
| [10] |
NUR A, MAVKO G, DVORKIN J, et al. Critical porosity: a key to relating physical properties to porosity in rocks[J]. The Leading Edge, 1998, 17(3): 357-362. DOI:10.1190/1.1437977 |
| [11] |
WOOD W T, STOFFA P L, SHIPLEY T H. Quantitative detection of methane hydrate through high-reso-lution seismic velocity analysis[J]. Journal of Geophysical Research: Solid Earth, 1994, 99(B5): 9681-9695. |
| [12] |
WOOD W T, HOLBROOK S W, HOSKINS H. In situ measurements of P-wave attenuation in the me-thane hydrate- and gas-bearing sediments of the Blake Ridge[J]. Proceedings of the Ocean Drilling Program, Scientific Results, 2000, 164: 265-272. |
| [13] |
LEE M W, HUTCHINSON D R, COLLETT T S, et al. Seismic velocities for hydrate-bearing sediments using weighted equation[J]. Journal of Geophysical Research: Solid Earth, 1996, 101(B9): 20347-20358. |
| [14] |
LEE M W, WAITE W F. Amplitude loss of sonic waveform due to source coupling to the medium[J]. Geophy-sical Research Letters, 2007, 34(5): L05303. |
| [15] |
LEE M W. Biot-Gassmann theory for velocities of gas hydrate-bearing sediments[J]. Geophysics, 2002, 67(6): 1711-1719. |
| [16] |
WYLLIE M R J, GREGORY A R, GARDNER L W. Elastic wave velocities in heterogeneous and porous media[J]. Geophysics, 1956, 21(1): 41-70. |
| [17] |
孙春岩, 章明昱, 牛滨华, 等. 天然气水合物地震似海底反射现象AVO正演模型研究[J]. 现代地质, 2003, 17(3): 337-344. SUN Chunyan, ZHANG Mingyu, NIU Binhua, et al. Study of modeling seismic bottom simulating reflector for nature gas hydrate[J]. Geoscience, 2003, 17(3): 337-344. |
| [18] |
DVORKIN J, NUR A. Elasticity of high-porosity sandstones: Theory for two North Sea data sets[J]. Geophysics, 1996, 61(5): 1363-1370. |
| [19] |
DVORKIN J, UDEN R. Seismic wave attenuation in a methane hydrate reservoir[J]. The Leading Edge, 2004, 23(8): 730-732. |
| [20] |
KVENVOLDEN K A. Methane hydrate-A major reservoir of carbon in the shallow geosphere?[J]. Chemical Geology, 1988, 71(1-3): 41-51. |
| [21] |
ECKER C. Seismic Characterization of Methane Hydrate Structures[D]. US Stanford University, San Francisco, California, USA, 2001.
|
| [22] |
梁金强, 张光学, 陆敬安, 等. 南海东北部陆坡天然气水合物富集特征及成因模式[J]. 天然气地球科学, 2016, 36(10): 157-162. LIANG Jinqiang, ZHANG Guangxue, LU Jing'an, et al. Accumulation characteristics and genetic models of natural gas hydrate reservoirs in the NE slope of the South China Sea[J]. Natural Gas Industry, 2016, 36(10): 157-162. |
| [23] |
ZATSEPINA O Y, BUFFETT B A. Phase equilibrium of gas hydrate: Implications for the formation of hydrate in the deep sea floor[J]. Geophysical Research Letters, 1997, 24(13): 1567-1570. |
| [24] |
ARCHIE G E. The electrical resistivity log as an aid in determining some reservoir characteristic[J]. Trans, 1942, 146(1): 54-62. |
| [25] |
ARCHIE G E. Electrical resistivity, an aid in core-analysis interpretation[J]. AAPG Bulletin, 1947, 31(2): 350-366. |
| [26] |
张志松. 阿尔奇公式的理论本原[J]. 地球物理学进展, 2020, 35(4): 1514-1522. ZHANG Zhisong. Theoretical roots of Archie formulas[J]. Progress in Geophysics, 2020, 35(4): 1514-1522. |
| [27] |
韩建光, 于常青, 张晓波, 等. 陆域冻土区天然气水合物多波地震数值模拟研究[J]. 地质学报, 2016, 90(9): 2502-2512. HAN Jianguang, YU Changqing, ZHANG Xiaobo, et al. Multi-wave seismic numerical simulation study on terrestrial gas hydrate in permafrost area[J]. Acta Geologica Sinica, 2016, 90(9): 2502-2512. |
| [28] |
徐华宁, 张光学, 郑晓东, 等. 井震联合分析预测神狐海域天然气水合物可能的垂向分布[J]. 地球物理学报, 2014, 57(10): 3364-3372. XU Huaning, ZHANG Guangxue, ZHENG Xiaodong, et al. Integrated analysis of well logs and seismic data to deduce the possible distribution in depth of gas hydrate in Shenhu Area, South China Sea[J]. Chinese Journal of Geophysics, 2014, 57(10): 3364-3372. |
| [29] |
刘洁, 张建中, 孙运宝, 等. 基于地震谱反演的地层速度估算方法及应用[J]. 石油地球物理勘探, 2016, 51(5): 909-915. LIU Jie, ZHANG Jianzhong, SUN Yunbao, et al. Seismic velocities estimation method based on spectral inversion[J]. Oil Geophysical Prospecting, 2016, 51(5): 909-915. |



 毛爽, 辽宁省盘锦市兴隆台区石油大街76号辽河油田分公司经济技术研究院, 124010。Email:
毛爽, 辽宁省盘锦市兴隆台区石油大街76号辽河油田分公司经济技术研究院, 124010。Email: 