随着准噶尔盆地油气勘探的不断发展,勘探目标日趋转向更复杂、更隐蔽的油气藏,相带精细划分、薄储层识别、小断裂刻画等均对地震资料分辨率提出了更高要求。然而,准噶尔盆地山前带近地表条件复杂,普遍存在较厚的未成岩地层。当地震波在疏松介质中传播时,高频成分迅速衰减,导致地震资料分辨率降低,严重影响了最终的岩性解释和储层描述。目前常用的消除近地表吸收影响的方法包括地表一致性反褶积、Q补偿等。
地表一致性反褶积是地震资料处理的常规流程。该方法将地震道分解为震源项、检波器项、炮检距项和地层脉冲响应项的褶积。通过消除震源项、检波器项、炮检距项的影响,即可得到地层脉冲响应。地表一致性反褶积属于一种统计方法,可解决近地表因素引起的地震子波横向变化问题。该方法存在一系列假设,例如假设地震子波为最小相位, 反射系数具有白噪特征,地震子波形态只与震源和检波器位置有关,而与地震波具体传播路径无关等。在实际生产中,这些假设均难以满足,因此该方法的保真度一直存在争议[1]。
与地表一致性反褶积方法相比,近地表Q补偿属于一种确定性的补偿技术,通过炮点Q值、检波点Q值、地震波旅行时计算得到空变的补偿因子,完成对地震数据的补偿。Q补偿的关键在于建立准确的Q场,目前计算Q值方法有许多。于承业等[2]利用双井微测井资料估算近地表Q值;武银婷等[3]利用VSP资料反演近地表Q值;裴江云等[4]利用面波衰减计算近地表Q值;蒋立等[5]通过谱比法计算炮、检点Q值并完成Q补偿;李庆忠[6]通过纵波速度与Q值的经验关系计算Q值;叶秋焱等[7]使用广义S变换求取Q值;许李囡等[8]使用S变换与变分法克服Q值计算对地震子波类型及窗函数长度的依赖;杨登锋等[9]使用加权谱比法提升Q值计算的稳定性。经验公式法Q值计算存在区域限制,不同区域参数差异较大;微测井实测Q值虽然精度很高,但受成本因素影响,测点过于稀疏;通过地震资料计算Q值要求地震资料具有较的高信噪比。
本文采用双井微测井获取实测Q值和频移法计算相对Q值,建立准确Q场并进行Q补偿。在准噶尔盆地南缘山前带的实际应用效果表明,本文的近地表Q补偿技术可以有效消除近地表差异吸收对地震资料的影响,提高地震资料的分辨率。
1 原理 1.1 双井微测井Q值计算常规基于微测井的表层Q调查方式包括三类:井中激发井中接收、井中激发地表接收、地表激发井中接收。在获得初至信息后,采用谱比法或频移法计算Q值。但在实际应用中,发现这三类调查方式存在如下问题:①当表层较厚时,井中的震源、检波器难以有效耦合;②在进行Q值计算时,未考虑地震波的传播路径。
针对以上问题,本文采用了一种新的微测井调查方式,即炮、检点对称的双激发微测井,如图 1所示。在野外施工时,采取双井激发、地面接收的采集方式,其关键在于激发点、接收点呈对称分布。
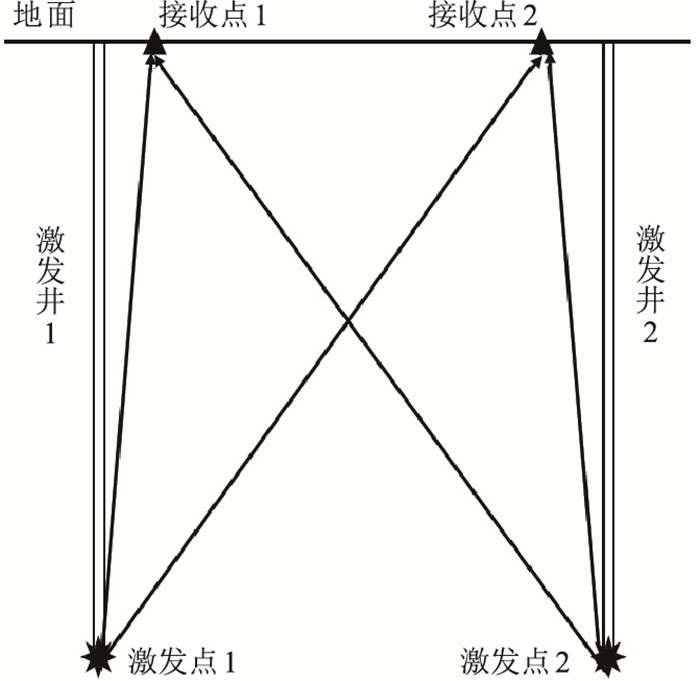
|
图 1 炮、检点对称的双激发微测井观测示意图 |
实际地震信号可以看作理想地震信号、激发点耦合效应、接收点耦合效应的综合结果。在频率域,有
| $ y_{11}(f)=x_{11}(f) \times s_1(f) \times r_1(f) $ | (1) |
| $ y_{12}(f)=x_{12}(f) \times s_1(f) \times r_2(f) $ | (2) |
| $ y_{21}(f)=x_{21}(f) \times s_2(f) \times r_1(f) $ | (3) |
| $ y_{22}(f)=x_{22}(f) \times s_2(f) \times r_2(f) $ | (4) |
式中:s1(f)、s2(f)分别表示激发点1和激发点2的耦合响应,其中f为频率;r1(f)、r2(f)分别表示接收点1和接收点2的耦合响应;xij表示i点激发、j点接收的理想地震信号;yij表示受炮、检点耦合响应影响的地震信号。
通过对来自相同炮点、不同检波点的信号进行谱比运算,可以消除检波点耦合因素的影响,即
| $ \begin{aligned} A_1(f)= & \ln \frac{y_{11}(f)}{y_{12}(f)}=\ln x_{11}(f)-\ln x_{12}(f)+ \\ & \ln r_1(f)-\ln r_2(f) \end{aligned} $ | (5) |
| $ \begin{aligned} A_2(f)= & \ln \frac{y_{22}(f)}{y_{21}(f)}=\ln x_{22}(f)-\ln x_{21}(f)+ \\ & \ln r_2(f)-\ln r_1(f) \end{aligned} $ | (6) |
式中:A1(f)为针对激发点1的两个接收点的谱比对数;A2(f)为针对激发点2的两个接收点的谱比对数。对式(5)、式(6)取平均,即可消除检波点耦合因素的影响
| $ \begin{aligned} & A(f)=\frac{A_1(f)+A_2(f)}{2}= \\ & \quad \frac{\ln x_{11}(f)-\ln x_{12}(f)+\ln x_{22}(f)-\ln x_{21}(f)}{2} \end{aligned} $ | (7) |
式中A(f)为消除炮、检点耦合影响的谱比对数。
在获得A(f)后,对多组数据点(A(f), f)使用线性回归分析获得谱比对数的斜率,再计算近地表Q值
| $ A(f)=a f+b $ | (8) |
| $ Q=\pi \times \tau / a $ | (9) |
式中:a为斜率;b为截距;τ为地震波从激发点到两个接收点的传播时间差。
1.2 频移法Q值计算近地表Q补偿的前提是建立精确Q场。通过比较现有Q场的计算方法,本文选用准确度和稳定性都较高的质心频移法。质心频移法主要包括三步:①计算各地震道质心频率;②计算各炮集、检波点道集内所有地震道的质心频率平均值;③计算各炮、检点Q值。
在计算地面各地震道质心频率时,首先需要选取适当的时窗,该时窗可根据初始叠加剖面上稳定反射层所对应的时间进行确定;其次对所选时窗内的数据进行傅里叶变换,将数据转换到频率域;最后计算各地震道的质心频率fc
| $ f_{\mathrm{c}}=\frac{\int_0^{\infty} f S(f) \mathrm{d} f}{\int_0^{\infty} S(f) \mathrm{d} f} $ | (10) |
式中S(f)为地震道的振幅谱。
在完成各地震道质心频率计算后,对各炮集、检波点集所包含的地震道计算质心频率平均值,将其作为该炮、检点的主频
| $ f_1=\frac{1}{n} \sum\limits_{k=1}^n f_{\mathrm{c}}(k) $ | (11) |
式中n为道数。
再根据频移法求取每个炮、检点的品质因子
| $ Q=\frac{\pi f_1 \Delta t f_{\mathrm{m}}^2}{2\left(f_{\mathrm{m}}^2-f_1^2\right)} $ | (12) |
式中:f1为炮检点主频值;fm为期望输出主频,该值由处理人员自行确定,一般在炮检点主频最大值的基础上增加3~5Hz;Δt为近地表旅行时,即地震波从近地表模型表面传播到模型底界的单程旅行时,该近地表模型可通过层析反演等方法进行构建。
通过地震资料获取的相对Q值精度相对较低,因此用实测Q值对相对Q值进行约束,提高Q场精度,具体做法为:首先获取微测井处实测Q值与相对Q值的差值;其次,根据这些差值,使用插值方法建立整个工区范围内的差值分布趋势;最后根据该分布趋势对相对Q值进行校正。
1.3 表层Q补偿本文采用Wang等[10-12]所提方法完成表层Q补偿。其振幅补偿因子和相位校正因子分别为
| $ A(\omega)=\frac{\beta(\omega)+\sigma^2}{\beta^2(\omega)+\sigma^2} $ | (13) |
| $ \varPhi(\omega)=\exp \left[\mathrm{i}\left(\frac{\omega}{\omega_{\mathrm{h}}}\right)^{-\gamma} \omega \Delta t-\mathrm{i} \omega \Delta t\right] $ | (14) |
| $ \sigma^2=\exp [-(0.23 G+1.63)] $ | (15) |
| $ \beta(\omega)=\exp \left[-\left(\frac{\omega}{\omega_{\mathrm{h}}}\right)^{-\gamma} \frac{\omega}{2 Q} \Delta t\right] $ | (16) |
| $ \gamma=\frac{2}{\pi} \tan ^{-1} \frac{1}{2 Q} $ | (17) |
式中:ω为圆频率;ωh为相位校正参考频率;G为振幅增益控制参数。
由Q补偿原理可知,该方法可避免地表一致性反褶积所需要的一系列假设,如地震子波最小相位、反射系数具有白噪特征等假设,因此其保真度较高。
2 应用实例以准噶尔盆地南缘X工区为例。该工区地表环境复杂,有农田、山地、河流、城镇等多种地形;工区整体地势较为平坦,但山区地表起伏较大(图 2)。
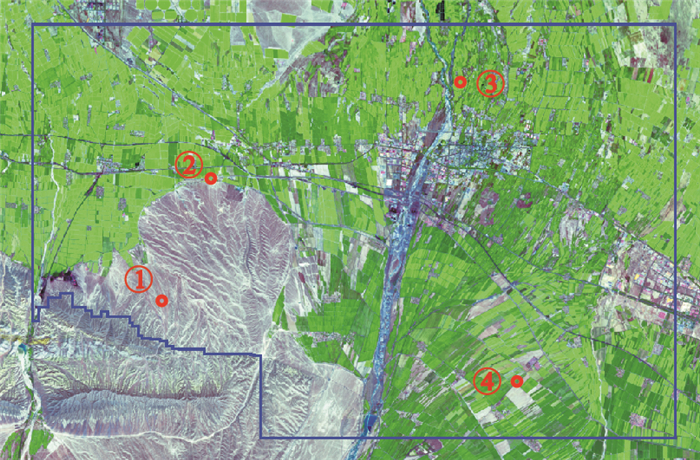
|
图 2 准噶尔盆地南缘X工区卫星图片 |
在工区内共布设四对Q表层调查微测井(图 1红圈所示)。对采集的四对微测井数据应用式(5)~式(7)进行处理,可获得各微测井的谱比对数曲线,其中第④对井的谱比对数曲线如图 3所示。由图可知,在谱比对数取平均后,曲线的线性关系明显改善,炮、检点耦合效应得到有效消除,Q值计算精度得到提升。
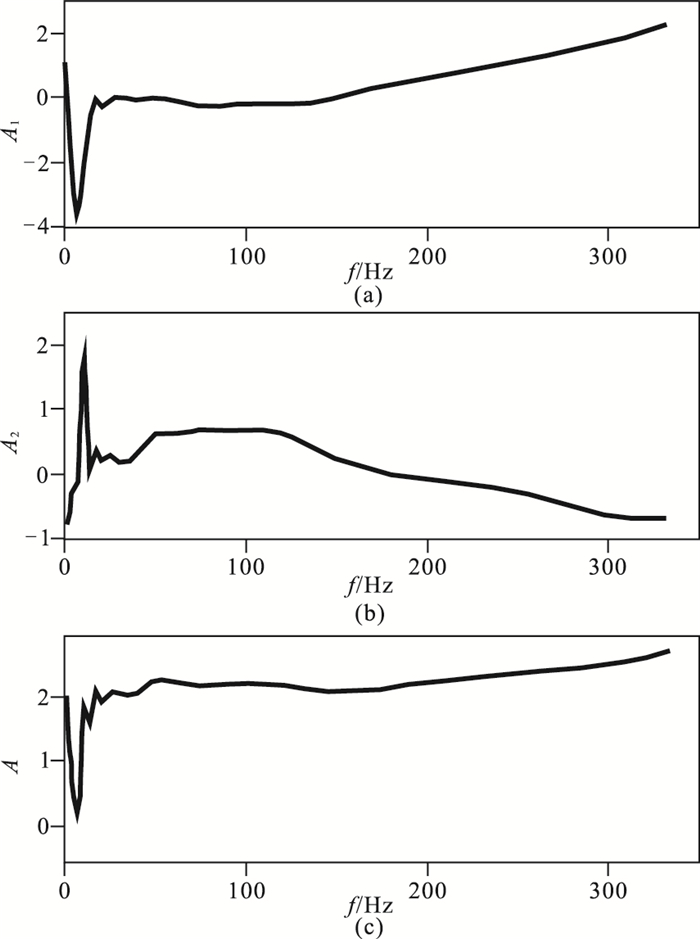
|
图 3 双激发微测井谱比对数曲线 (a)激发点1;(b)激发点2;(c)平均值 |
针对该工区,采用频移法计算相对Q值,再使用实测Q值对相对Q值进行约束。约束前、后的近地表Q场如图 4所示,可见约束后Q异常值显著减少,平面分布整体更趋平缓;同时Q值整体增大,Q值范围从0.1~10上升为0.1~13,与实测Q值更接近。
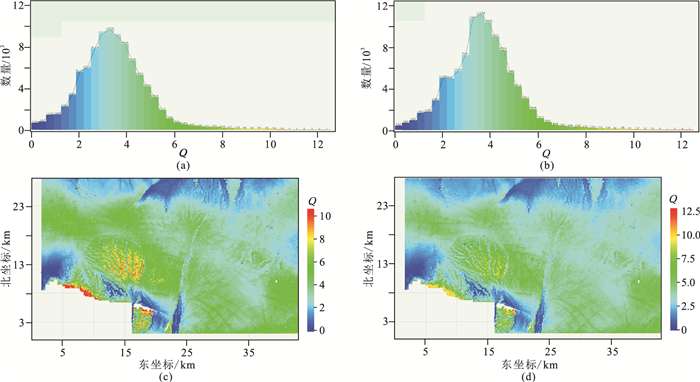
|
图 4 微测井约束前、后的近地表Q值分布 (a)约束前统计柱状图;(b)约束后统计柱状图;(c)约束前平面分布;(d)约束后平面分布 |
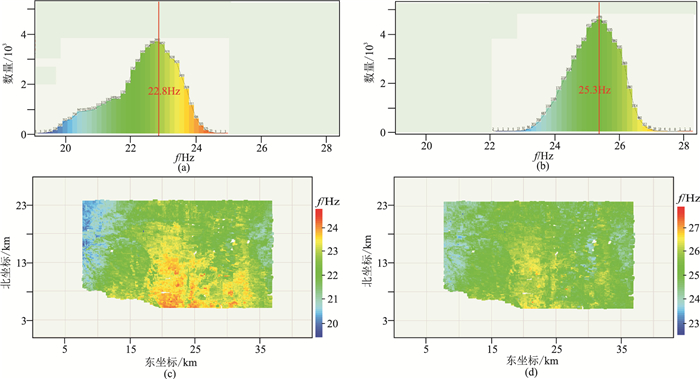
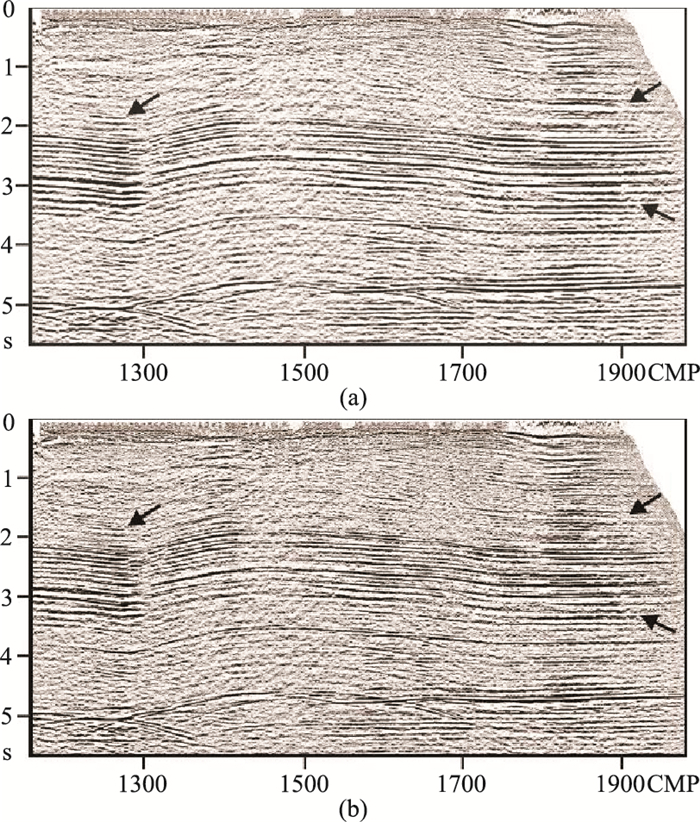
在获得近地表Q场后,即可对地震资料进行Q补偿。对比补偿前、后的质心频率分布(图 5)可知,经过表层Q补偿以后,炮点质心频率分布更加均衡,同时主频整体抬升2~3Hz。对比补偿前、后的叠加剖面(图 6)可知,经过表层Q补偿以后,叠加剖面整体分辨率明显提升,同相轴更加连续,剖面质量大幅改善,其中尤以箭头所指处效果最为明显。
|
图 5 Q补偿前、后炮点主频分布 (a)补偿前统计柱状图;(b)补偿后统计柱状图;(c)补偿前平面分布;(d)补偿后平面分布 |
|
图 6 Q补偿前(a)、后(b)叠加剖面对比 |
通过对准噶尔盆地南缘工区的地震资料的分析,结合实测Q值对相对Q值进行约束,并完成Q补偿,得到以下结论。
(1) 当近地表地层较厚时,井中震源、检波器难以有效耦合,严重影响实测Q值的计算精度;通过采用炮、检点对称的双井激发微测井测量Q值,可有效消除耦合因素的影响。
(2) 微测井实测Q值精度很高,但限于成本因素井位稀疏;而地震资料计算得到的相对Q值精度较低,通过使用实测Q值对相对Q值进行约束,可以有效提高近地表Q场的精度。
(3) 通过采用近地表Q补偿技术,可以有效消除近地表差异吸收对地震资料的影响,提高地震资料的分辨率。
| [1] |
渥·伊尔马兹. 地震资料分析[M]. 北京: 石油工业出版社, 2006.
|
| [2] |
于承业, 周志才. 利用双井微测井资料估算近地表Q值[J]. 石油地球物理勘探, 2011, 46(1): 89-92. YU Chengye, ZHOU Zhicai. Estimation of near surface Q value based on the datasets of the uphole survey in double hole[J]. Oil Geophysical Prospecting, 2011, 46(1): 89-92. |
| [3] |
武银婷, 朱光明, 刘伊克, 等. 零偏VSP反演Q值CFS方法及影响因素研究[J]. 地球物理学进展, 2010, 25(6): 1897-1904. WU Yinting, ZHU Guangming, LIU Yike, et al. Study on CFS method in Q inversion using zero-offset VSP data[J]. Progress in Geophysics, 2010, 25(6): 1897-1904. DOI:10.3969/j.issn.1004-2903.2010.06.003 |
| [4] |
裴江云, 陈树民, 刘振宽, 等. 近地表Q值求取及振幅补偿[J]. 地球物理学进展, 2001, 16(4): 18-22. PEI Jiangyun, CHEN Shumin, LIU Zhenkuan, et al. Near surface Q value extraction and amplitude compensation[J]. Progress in Geophysics, 2001, 16(4): 18-22. |
| [5] |
蒋立, 王晓涛, 谭佳, 等. 沙漠区近地表和中深层一体化Q模型的建立及应用[J]. 新疆石油地质, 2017, 38(1): 91-95. JIANG Li, WANG Xiaotao, TAN Jia, et al. Establishment and application of integrated near-surface and subsurface Q model in desert area[J]. Xinjiang Petroleum Geology, 2017, 38(1): 91-95. |
| [6] |
李庆忠. 走向精确勘探的道路[M]. 北京: 石油工业出版社, 1993.
|
| [7] |
叶秋焱, 崔宏良, 叶玮, 等. 一种基于叠前数据的综合Q值求取及应用[J]. 石油地球物理勘探, 2017, 52(2): 304-308. YE Qiuyan, CUI Hongliang, YE Wei, et al. Integra-ted Q-value estimation based on prestack seismic data[J]. Oil Geophysical Prospecting, 2017, 52(2): 304-308. |
| [8] |
许李囡, 高静怀, 杨阳, 等. 基于S变换和变分法的品质因子Q估计方法[J]. 石油地球物理勘探, 2022, 57(1): 82-90. XU Linan, GAO Jinghuai, YANG Yang, et al. Quality factor Q estimation based on S transform and variational method[J]. Oil Geophysical Prospecting, 2022, 57(1): 82-90. |
| [9] |
杨登锋, 刘军, 吴静, 等. 加权谱比法Q值估计[J]. 石油地球物理勘探, 2022, 57(3): 593-601. YANG Dengfeng, LIU Jun, WU Jing, et al. Q factor estimation by weighted spectral ratio method[J]. Oil Geophysical Prospecting, 2022, 57(3): 593-601. |
| [10] |
WANG Y H. A stable and efficient approach of inverse Q filtering[J]. Geophysics, 2002, 67(2): 657-663. |
| [11] |
WANG Y H. Inverse Q-filter for seismic resolution enhancement[J]. Geophysics, 2006, 71(3): V51-V60. |
| [12] |
WANG Y H. Quantifying the effectiveness of stabilized inverse Q filtering[J]. Geophysics, 2003, 68(1): 337-345. |



 马凯, 新疆自治区乌鲁木齐市北京北路397号新疆油田公司勘探开发研究院地球物理研究所, 830013。Email:
马凯, 新疆自治区乌鲁木齐市北京北路397号新疆油田公司勘探开发研究院地球物理研究所, 830013。Email: 