② 有色资源与地质灾害探查湖南省重点实验室, 湖南长沙 41008;
③ 中南大学有色金属成矿预测与地质环境监测教育部重点实验室, 湖南长沙 410083;
④ 自然资源部覆盖区深部资源勘查工程技术创新中心, 安徽合肥 230001
② Hunan Key Laboratory of Nonferrous Resources and Geological Disaster Exploration, Changsha, Hunan 410083, China;
③ Key Laboratory of Metallogenic Prediction of Nonferrous Metals and Geological Environment Monitoring (Central South University), Ministry of Education, Changsha, Hunan 410083, China;
④ Technical Innovation Center of Coverage Area Deep Resources Exploration, Ministry of Natural Resources, Hefei, Anhui 230001, China
大地电磁测深(MT)通过观测地表相互正交的电磁场分量获取地下电性结构相关信息,具有不受高阻层屏蔽、对高导层分辨能力强、横向电性差异分辨能力较强、勘探深度大、勘探费用低、施工方便、资料处理和解释技术成熟等优势,广泛应用于区域地质调查、资源勘探和工程勘探等领域[1-3]。近年来,随着研究涉及的地质构造复杂程度明显增加,对大地电磁测深资料的处理解释要求亦更高[4]。当近地表存在几何尺寸远远小于电磁波趋肤深度的三维电性不均匀小异常体时,观测数据会受到电流型畸变的影响,若不消除这种影响,会影响后续的反演解释[5-10]。
阻抗张量分解方法是目前常用的大地电磁数据处理分析方法,可以去除局部畸变带来的影响,获得真实的区域阻抗、构造方位角、构造维性等信息。Swift [11]提出了经典的阻抗张量分解方法,具体做法是:旋转阻抗张量,寻找阻抗张量反对角元素最大时或者主对角元素最小时所对应的角度,该角度即为所求的电性主轴方向。但是,此方法获得的电性主轴方向存在90°的多解性,故需要依据实际地质信息进一步判断。该方法为后续的阻抗分解方法奠定了坚实的基础。Berdichevsky等[12]研究了水平电性非均匀性引起的畸变问题,并将畸变划分为感应型畸变和电流型畸变。Bahr [13]根据局部畸变的观测阻抗的同一列元素相位相等的特性进行了畸变校正,提出了Bahr分解方法,但是对非严格意义上的三维/二维构造效果不理想。Bahr[14]在此方法的基础上提出了Bahr相位偏差法,即阻抗张量同一列元素的阻抗相位存在一个角度差,这个角度差称为相位偏差角,并定义了与维性密切相关的表征参数。Groom等[15]提出了经典的GB分解法,将局部畸变分为可确定部分(剪切因子和扭曲因子)和不可确定部分(各向异性因子和静位移因子),然而GB分解得到的模型是一个欠定问题:8个已知参数(4个复数形式的观测阻抗张量元素),9个未知参数(电性主轴角,4个实数形式的畸变矩阵元素,2个复数形式的区域阻抗张量元素)。需要特别强调的是,尽管GB分解方法得到了广泛应用,取得了很好的效果,但实际应用中往往忽略了其应用前提,即地下介质为二维或近似二维的电性结构[16]。Caldwell等[17]提出了相位张量的概念,基于相位张量不受电场畸变的影响这一特点,从观测阻抗中提取区域阻抗的构造电性主轴方向以及二维偏度等表征构造属性的参数,是目前最常用的维性分析方法之一。Bibby等[18]分析了阻抗张量畸变与相位张量的关系,将相位张量用于局部畸变校正。蔡军涛等[19]提出一种共轭阻抗变换法(CCZ),通过对大地电磁阻抗张量做共轭阻抗变换,求取畸变因子和最佳电性主轴方位角,该方法具有与相位张量分解相似的优点,即不受局部电场畸变的影响,且无需假设区域维性。尹曜田等[5]将遗传算法引入GB分解的求解过程,通过实际资料处理证明了该算法的有效性。谢成良等[20]使用相位张量分解获得电性主轴方位角,将旋转后的区域阻抗作为GB分解区域阻抗元素的初值,并将各向异性参数引入目标函数,采用共轭梯度法进行模型最优化求解,提高了GB算法的稳定性及可靠性。
但前人工作大多集中于二维区域构造。对于三维区域结构,一些学者已经开展了一些研究。Utada等[21]利用观测阻抗张量和观测地磁传递函数(即倾子)确定畸变参数,压制电流型畸变,获得三维区域电性构造。Garcia等[22]假设相邻测点的区域电性结构变化不大但受畸变的影响不同,提出了一种类似于GB分解且适用于三维区域的畸变校正方法,使用牛顿法求解三维区域结构中的畸变参数。Bibby等[18]利用不受电流型畸变影响的相位张量获得地下维度信息,进而采用低维度数据求解畸变参数。这些方法只适用于特定条件,对于更一般的三维/三维模型不适用。Neukirch等[23]提出了与相位张量互补的振幅张量,利用“相位张量和振幅张量反映同样的地下介质信息,且所有电流型畸变信息都保存在振幅张量中”这一假说,采用遗传算法实现了畸变校正,该方法的实测效果及理论效果均较好[24]。
本文借鉴Neukirch等[24]的研究成果,基于阻抗振幅张量与相位张量的联合分解,采用改进粒子群算法求解畸变参数,对三维模型正演数据和安徽省霍山地区中生代火山岩盆地实测MT数据进行处理。
1 大地电磁振幅相位张量分解基本理论 1.1 GB分解理论对于三维/二维电性结构模型,Groom等[15]只考虑电流型畸变影响,不考虑磁场感应型畸变,将区域构造主轴坐标系顺时针旋转角度θ到测量坐标系,则观测阻抗Zm为
| $ \begin{aligned} \boldsymbol{Z}_{\mathrm{m}} & =\boldsymbol{R}(\theta) \boldsymbol{C}\boldsymbol{Z}_{2 \mathrm{D}} \boldsymbol{R}^{\mathrm{T}}(\theta) \\ & =\boldsymbol{R}(\theta) g \boldsymbol{T} \boldsymbol{S} \boldsymbol{A} \boldsymbol{Z}_{2 \mathrm{D}} \boldsymbol{R}^{\mathrm{T}}(\theta) \end{aligned} $ | (1) |
式中:R(θ)为单位旋转矩阵; C为畸变矩阵;Z2D为区域阻抗矩阵;g表示增益因子;T表示扭曲角矩阵;S表示剪切角矩阵;A表示各向异性因子矩阵。畸变矩阵C可表示为
| $ \left\{\begin{array}{l} \boldsymbol{C}=g^{\prime}\left[\begin{array}{cc} 1 & -t \\ t & 1 \end{array}\right]\left[\begin{array}{ll} 1 & e \\ e & 1 \end{array}\right]\left[\begin{array}{cc} 1+s & 0 \\ 0 & 1-s \end{array}\right] \\ g^{\prime}=\frac{g}{\sqrt{\operatorname{det}(\boldsymbol{T}) \operatorname{det}(\boldsymbol{S}) \operatorname{det}(\boldsymbol{A})}} \end{array}\right. $ | (2) |
式中:扭曲因子t=tanϕt,其中ϕt∈[-90°, 90°]为扭曲角;剪切因子e=tanϕe,其中ϕe∈[-45°, 45°]为剪切角;各向异性因子s=tanϕs,其中ϕs∈[-45°, 45°]为各向异性因子角。
GB分解把畸变矩阵分解为可确定部分(扭曲角矩阵T、剪切角矩阵S)和不确定部分(各向异性因子矩阵A与增益因子g的乘积),并将不确定部分并入区域阻抗矩阵Z2D,得到
| $ \boldsymbol{Z}_{2 \mathrm{D}}^{\prime}=\left[\begin{array}{cc} 0 & g^{\prime}(1+s) Z_{\mathrm{TE}} \\ g^{\prime}(1-s) Z_{\mathrm{TM}} & 0 \end{array}\right] $ | (3) |
式中ZTE和ZTM分别表示二维区域构造下TE模式和TM模式的阻抗张量元素。此时,式(1)变为
| $ \boldsymbol{Z}_{\mathrm{m}}=\boldsymbol{R}(\theta) \boldsymbol{T}\boldsymbol{S} \boldsymbol{Z}^{\prime}{ }_{2 \mathrm{D}} \boldsymbol{R}^{\mathrm{T}}(\theta) $ | (4) |
上式中右边8个参数(观测阻抗的实部、虚部)为已知,7个参数(畸变参数t、e、θ和区域阻抗反对角元素的实部、虚部)为未知,利用最优化求解即可获得其解。可以看出,对于三维介质,阻抗张量的区域阻抗对角元素中也存在未知数,未知数为11个,故传统的GB分解无法适用于三维介质的情况。使用GB分解的前提是区域构造为二维,对于三维区域构造不再适用,因为三维区域构造增加了4个未知数,此时的未知数个数大于方程个数,传统的阻抗分解方法失效,需要探索新的方法求解畸变参数。
1.2 相位张量大地电磁阻抗张量Z为一个复数张量,既含有电阻率信息,也含有相位信息,可以表示为Z=X+iY,这里X和Y分别表示阻抗张量的实部和虚部。根据Caldwell等[17]对相位张量的定义,相位张量Φ的表达式为
| $ \begin{aligned} \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}& = {\mathit{\boldsymbol{X}}^{ - 1}}\mathit{\boldsymbol{Y}} = \left[ {\begin{array}{*{20}{l}} {{\mathit{\Phi }_{11}}}&{{\mathit{\Phi }_{12}}}\\ {{\mathit{\Phi }_{21}}}&{{\mathit{\Phi }_{22}}} \end{array}} \right] = \\ & \frac{{\left[ {\begin{array}{*{20}{l}} {{X_{22}}{Y_{11}} - {X_{12}}{Y_{21}}}&{{X_{22}}{Y_{12}} - {X_{12}}{Y_{22}}}\\ {{X_{11}}{Y_{21}} - {X_{21}}{Y_{11}}}&{{X_{11}}{Y_{22}} - {X_{21}}{Y_{12}}} \end{array}} \right]}}{{\det (\mathit{\boldsymbol{X}})}} \end{aligned} $ | (5) |
式中:Xpq、Ypq分别表示阻抗张量元素的实部和虚部,其中p=1、2,q=1、2;det (X)=X11X22-X12X21;Φpq表示相位张量Φ的元素。
只考虑电场畸变影响时,畸变矩阵C是一个与频率无关的实数矩阵,观测阻抗Zm可以写为
| $ \boldsymbol{Z}_{\mathrm{m}}=\boldsymbol{C} \boldsymbol{Z}=\boldsymbol{C}(\boldsymbol{X}+\mathrm{i} \boldsymbol{Y}) $ | (6) |
记
| $ \boldsymbol{X}_{\mathrm{m}}=\boldsymbol{C X} $ | (7) |
| $ \boldsymbol{Y}_{\mathrm{m}}=\boldsymbol{C} \boldsymbol{Y} $ | (8) |
根据式(6),若能求得畸变矩阵C,即可计算得到未畸变的阻抗张量Z
| $ \boldsymbol{Z}=\boldsymbol{C}^{-1} \boldsymbol{Z}_{\mathrm{m}} $ | (9) |
根据相位张量的定义,此时的观测相位张量Φm可根据下式求得
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\rm{m}}} = \mathit{\boldsymbol{X}}_{\rm{m}}^{ - 1}{\mathit{\boldsymbol{Y}}_{\rm{m}}} = {(\mathit{\boldsymbol{CX}})^{ - 1}}{\mathit{\boldsymbol{Y}}_{\rm{m}}} = {\mathit{\boldsymbol{X}}^{ - 1}}{\mathit{\boldsymbol{C}}^{ - 1}}\mathit{\boldsymbol{CY}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} $ | (10) |
由上式可以看出,相位张量不受局部电场畸变的影响,因此可广泛应用于区域构造走向的研究和维度分析。相位张量概念的提出对于阻抗张量分解具有里程碑式的意义,为大地电磁数据分析提供了新的思路和方法。但同时也意味着采用相位张量无法判断测点受畸变的程度,因而只采用不含振幅信息的相位张量进行反演,会很大程度增加反演的非唯一性,导致反演不稳定。
1.3 振幅张量通过相位张量的定义发现,相位张量是阻抗相位的混合,只包括阻抗的相位信息,仅是阻抗张量信息的一半,这对于测点本就稀疏、数据不足的大地电磁来说,是一项非常大的损失。Neukirch等[23]为了提取振幅信息,创造性地提出了类似于相位张量的振幅张量。
根据Neukirch等[23]的研究成果,一个复数M可用欧拉公式展开为一个实数L和一个角度β的函数
| $ M=L \mathrm{e}^{\mathrm{i} \beta}=L(\cos \beta+\mathrm{i} \sin \beta) $ | (11) |
按照式(11)的形式,可将单个复数扩展到二阶复数张量的形式,则阻抗张量Z可以表示为
| $ \mathit{\boldsymbol{Z}} = \mathit{\boldsymbol{P}}{{\rm{e}}^{{\rm{i}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}} = \mathit{\boldsymbol{P}}[\cos (\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}) + {\rm{i}}\sin (\mathit{\boldsymbol{ \boldsymbol{\varPhi} }})] $ | (12) |
式中:为了书写方便,cos(·)和sin(·)表示对一个矩阵的各元素分别求余弦和正弦;P为振幅张量。由于采用张量表示形式,下面给出振幅张量的具体求取方法。
张量下的约束条件为
| $ \cos (\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}){[\cos (\mathit{\boldsymbol{ \boldsymbol{\varPhi} }})]^{\rm{T}}} + \sin (\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}){[\sin (\mathit{\boldsymbol{ \boldsymbol{\varPhi} }})]^{\rm{T}}} = \mathit{\boldsymbol{I}} $ | (13) |
式中I为二阶单位矩阵。通过式(13)和式(5)可得
| $ \cos (\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}) = {\left( {\mathit{\boldsymbol{I}} + \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}} \right)^{ - \frac{1}{2}}} $ | (14) |
| $ \sin (\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}) = {\left( {\mathit{\boldsymbol{I}} + \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}} \right)^{ - \frac{1}{2}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} $ | (15) |
| $ \begin{aligned} \mathrm{e}^{\mathrm{i} \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}} & =\cos (\mathit{\boldsymbol{ \boldsymbol{\varPhi} }})+\mathrm{i} \sin (\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}) \\ & =\left(\boldsymbol{I}+\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\mathrm{T}}\right)^{-\frac{1}{2}}+\mathrm{i}\left(\boldsymbol{I}+\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\mathrm{T}}\right)^{-\frac{1}{2}} \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \end{aligned} $ | (16) |
将式(16)代入式(12),便可得到振幅张量P的唯一表示形式
| $ \mathit{\boldsymbol{P}} = \mathit{\boldsymbol{Z}}{\left[ {{{\left( {\mathit{\boldsymbol{I}} + \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}} \right)}^{ - \frac{1}{2}}} + {\rm{i}}{{\left( {\mathit{\boldsymbol{I}} + \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}} \right)}^{ - \frac{1}{2}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}} \right]^{ - 1}} $ | (17) |
Booker[25]提出了一种相位张量参数化分解方法,把相位张量的奇异值分解与区域构造走向、维度等地质信息联系起来,这种分解方法同样适用于同为实数矩阵的振幅张量。振幅张量和相位张量都是地下介质、构造信息的反映,在某种程度上其表现形式相似,而且相位张量不受电流型畸变的影响,所有的畸变信息都隐含在振幅张量里,通过寻找与相位张量相似性最高的振幅张量,便可实现大地电磁的畸变校正。其中,畸变矩阵C为待求参数,采用式(9)对观测张量阻抗Zm进行校正,根据式(17)获得振幅张量P,根据式(5)获得相位张量Φ,并对这个张量进行分解。求解畸变参数C时,振幅张量P的分解参数与相位张量Φ的分解参数最相似。因此,根据以上思路构建了关于畸变参数的求解策略,将畸变求解问题转化为一个最优化问题。
相位张量矩阵使用奇异值分解可表示为[25]
| $ \begin{aligned} \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}& = \left[ {\begin{array}{*{20}{l}} {{\mathit{\Phi }_{11}}}&{{\mathit{\Phi }_{12}}}\\ {{\mathit{\Phi }_{21}}}&{{\mathit{\Phi }_{22}}} \end{array}} \right] = {\mathit{\boldsymbol{V}}_\mathit{\Phi }}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_\mathit{\Phi }}\mathit{\boldsymbol{W}}_\mathit{\Phi }^{\rm{T}}\\ & = \mathit{\boldsymbol{R}}\left( { - {\theta _\mathit{\Phi }}} \right)\left[ {\begin{array}{*{20}{c}} {{\phi _1}}&0\\ 0&{{\phi _2}} \end{array}} \right]\mathit{\boldsymbol{R}}\left( {{\psi _\mathit{\Phi }}} \right)\mathit{\boldsymbol{R}}\left( {{\theta _\mathit{\Phi }}} \right) \end{aligned} $ | (18) |
式中VΦ=R(-θΦ)、ΣΦ和WΦ=R(-ψΦ-θΦ)是奇异值分解后的三个矩阵,其中旋转矩阵R的表达式为
| $ \boldsymbol{R}(\delta)=\left[\begin{array}{rr} \cos \delta & \sin \delta \\ -\sin \delta & \cos \delta \end{array}\right] $ | (19) |
θΦ=arccos[Tr(VΦ)/2]表示笛卡尔坐标与矩阵坐标之间的角度,这里Tr(·)表示求矩阵的迹,在二维情况下,θΦ表示区域构造走向;ϕ1和ϕ2是对角矩阵ΣΦ的奇异值;偏离角ψΦ可表示为
| $ \psi_\mathit{\Phi }= \begin{cases}\arctan \frac{\mathit{\Phi }_{12}-\mathit{\Phi }_{21}}{\mathit{\Phi }_{11}+\mathit{\Phi }_{22}} & 0 \leq\left|\mathit{\Phi }_{12}-\mathit{\Phi }_{21}\right| \leq\left|\mathit{\Phi }_{11}+\mathit{\Phi }_{22}\right| \neq 0 \\ \operatorname{arccot} \frac{\mathit{\Phi }_{11}+\mathit{\Phi }_{22}}{\mathit{\Phi }_{12}-\mathit{\Phi }_{21}} & \left|\mathit{\Phi }_{12}-\mathit{\Phi }_{21}\right|>\left|\mathit{\Phi }_{11}+\mathit{\Phi }_{22}\right| \text { 且 } \frac{\mathit{\Phi }_{11}+\mathit{\Phi }_{22}}{\mathit{\Phi }_{12}-\mathit{\Phi }_{21}} \geq 0 \\ \operatorname{arccot} \frac{\mathit{\Phi }_{11}+\mathit{\Phi }_{22}}{\mathit{\Phi }_{12}-\mathit{\Phi }_{21}}-\pi & \left|\mathit{\Phi }_{12}-\mathit{\Phi }_{21}\right|>\left|\mathit{\Phi }_{11}+\mathit{\Phi }_{22}\right| \text { 且 } \frac{\mathit{\Phi }_{11}+\mathit{\Phi }_{22}}{\mathit{\Phi }_{12}-\mathit{\Phi }_{21}}<0\end{cases} $ | (20) |
同样地,对振幅张量进行上述分解,可以得到与相位张量分解参数相对应的各个分解参数。
为了使相位张量与振幅张量的奇异值具有可比性,Neukirch等[23]定义了相位相对各向异性参数ηϕ和振幅相对各向异性参数ηP,其表达式分别为
| $ \eta_\phi=\frac{1}{2}\left(\tan ^{-1} \phi_1-\tan ^{-1} \phi_2\right) $ | (21) |
| $ \eta_P=\frac{1}{2}\left(\operatorname{In} P_1-\operatorname{In} P_2\right) $ | (22) |
式中P1和P2分别是振幅张量奇异值分解的两个奇异值。
假设某一测点有N个观测频率,且其电流型畸变与频率无关。可先求得这N个频率的振幅张量和相位张量,然后进行上述分解,得到各频点相应的偏离角ψ、相位相对各向异性参数ηϕ和振幅相对各向异性参数ηP,所有频率同一分解参数皆可组成1×N 阶矩阵。为了对振幅张量和相位张量的分解参数进行对比,定义目标函数
| $ \begin{gathered} F(\boldsymbol{C})=\operatorname{In}\left|\boldsymbol{\psi}_P \boldsymbol{W}_\psi \boldsymbol{\psi}_P^{\mathrm{T}}\right|+\operatorname{In}\left|\boldsymbol{\Delta} \boldsymbol{W}_\psi \boldsymbol{\Delta}^{\mathrm{T}}\right|+ \\ \quad \ \left|\operatorname{In}\left(\boldsymbol{\eta}_\phi \boldsymbol{W}_\eta \boldsymbol{\eta}_\phi^{\mathrm{T}}\right)-\operatorname{In}\left(\boldsymbol{\eta}_P \boldsymbol{W}_\eta \boldsymbol{\eta}_P^{\mathrm{T}}\right)\right| \end{gathered} $ | (23) |
式中:Wψ/η=diag(fi2/δψ/η, j2ffT)为N×N阶的权重矩阵,其中频率矩阵f=[f1, f2, …,fi, …,fN],i=1, 2,…,N,δψ/η, j2表示测点i所有频点的相位张量偏离角ψ或者相位相对各向异性参数ηϕ的方差,由于高频段数据的相位张量与未畸变的振幅张量的相似程度最高,故该权重矩阵优先考虑高频数据。该目标函数是一个多目标优化问题,为了求得最优解,可对每个子目标赋予权重,转化为单一目标函数问题;ψP、Δ、ηϕ-ηP是目标函数的三个子目标函数:第一项ψP={π/2-ψP,i}是1×N 阶矩阵,表示归一化后的振幅张量偏离角矩阵,分析发现,未畸变的振幅张量分解得到的归一化偏离角几乎为0°,故将其作为稳定项;第二项Δ=ψP-ψϕ是1×N阶矩阵,其中ψϕ是相位张量偏离角矩阵;第三项是振幅相对各向异性参数矩阵ηϕ与相位相对各向异性参数矩阵ηP之差,即ηϕ-ηP,也是1×N阶矩阵,对子目标分别取对数可以加速收敛。由于相位张量走向角θϕ与振幅张量走向角θP之差不稳定,会影响后续的计算结果,故通过去除走向角之差(θϕ-θP)这一子目标函数实现对Neukirch等[24]提出的目标函数的改进。
通过目标函数值的大小可以衡量相位张量与振幅张量的相似程度,从而通过求目标函数的最小值寻找与相位张量相似程度最高的振幅张量,进而得到未畸变阻抗张量,实现畸变校正。
2.2 粒子群优化算法为了求取目标函数(式(23))的最小值,可以使用简单有效的粒子群优化算法,将式(23)的值作为粒子适应度,此问题只有三个未知数,使用粒子群算法能够有效求解。
粒子群算法(Particle Swarm Optimization,PSO)是由Kennedy等[26]提出的一种基于群体智能进化的计算方法。在给定粒子个数后,随机初始化粒子的位置和速度,然后通过迭代方法优化问题。每一次迭代中,粒子通过跟踪两个“极值”更新自身的位置和速度:一个是粒子本身所找到的最优解,即个体极值Pbest,另一个是整个粒子群中所有粒子在历代搜索过程中所达到的最优解,即全局极值Gbest。每个粒子都不断地改变自身在解空间中的速度,当找到这两个最优解后,可进一步实现PSO中最重要的“加速”过程,以尽可能地朝Pbest和Gbest所指向的区域“飞”去。
假设对于M个粒子,在一个D维空间进行搜索,粒子i的信息可用两个D维向量表示,即位置向量xi和速度向量vi
| $ \boldsymbol{x}_i=\left(x_{i 1}, x_{i 2}, \cdots, x_{i D}\right)^{\mathrm{T}} $ | (24) |
| $ \boldsymbol{v}_i=\left(v_{i 1}, v_{i 2}, \cdots, v_{i D}\right)^{\mathrm{T}} $ | (25) |
通过测试发现,使用标准PSO算法容易陷入局部极小,不能很好地求解畸变参数。为了提高种群多样性,避免产生早熟收敛现象,本文对Clerc[27]提出的具有收缩因子的PSO算法进行了改进。找到Pbest和Gbest后,粒子即可根据下式更新速度和位置
| $ \begin{aligned} v_{i d}= & k\left[v_{i d}+c_1 r_1\left(P_{\text {best }, d}-x_{i d}\right)+\right. \\ & \left.c_2 r_2\left(G_{\text {best }, d}-x_{i d}\right)\right] \end{aligned} $ | (26) |
| $ \begin{aligned} & x_{i d}=x_{i d}+v_{i d} \\ & i=1, 2, \cdots, M ; \quad d=1, 2, \cdots, D \end{aligned} $ | (27) |
式中r1和r2是区间[0, 1]的两个随机数;
| $ c_1=c_2=2.0+\operatorname{rand}(0, 0.5) $ | (28) |
通过改进学习因子,收缩因子k在每一次迭代中也会相应改变,这样既可以增强粒子的活性,加强算法的全局探索能力,也可以避免因选取的收缩因子过大而错过最优值。
数值实验结果表明,当粒子群体数量M为32时,速度限制为[-3, 3],针对此场景问题表现出了良好的效果[28]。
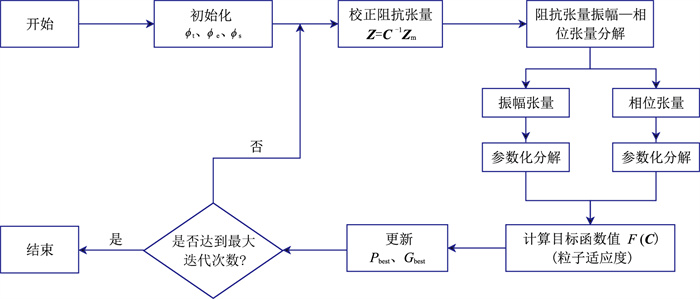
2.3 计算流程增益因子g的求解非常困难,到目前为止并没有一个特别好的求解策略,因此本文将增益因子g并入区域阻抗,只考虑扭曲因子t、剪切因子e和各向异性因子s。利用本文方法进行畸变校正的流程见图 1,具体求解过程如下。
|
图 1 本文方法畸变校正流程 |
(1) 给定32个初始粒子,随机初始化每个粒子的空间位置x(ϕt, ϕe, ϕs)和速度v,空间位置的三维坐标与求解的畸变参数扭曲角ϕt、剪切角ϕe和各向异性因子角ϕs一一对应,需同时给定畸变参数的取值范围;
(2) 利用生成粒子的位置信息生成畸变矩阵的逆C-1,利用式(9)校正阻抗张量Zm,然后利用式(5)和式(17)计算振幅张量P和相位张量Φ;
(3) 对振幅张量P和相位张量Φ进行参数化分解,根据分解得到的参数计算式(23)目标函数的值F(C),将得到的目标函数值作为粒子的适应度;
(4) 根据步骤(3)计算得到的值不断更新粒子的位置x(ϕt, ϕe, ϕs)和速度v,直到达到预设条件,迭代达到最优,迭代终止。
本文迭代终止条件设置为固定的迭代次数。经过数值实验,迭代次数设置为1000可以满足此问题的求解。由于求解参数只有3个,故无需考虑求解速度。
3 模型实验和实例分析 3.1 理论模型为了验证方法的可靠性,设计了一组三维模型,对三维阻抗张量进行畸变校正。图 2所示为三维电阻率模型及测点分布图。在100Ω·m的均匀半空间中分布着三个电阻率异常体,其电阻率分别为1000、5000、10Ω·m。点距为200m,共25个测点,测点site01~site25从左到右测点号依次增大,计算频率为0.01~1000Hz,19个频点对数等间隔分布。使用MT3D软件进行正演计算[29]。

|
图 2 三维理论模型及测点示意图 (a)侧视图;(b)俯视图及测点分布 |
对正演得到的数据施加局部电场畸变影响,即人为添加畸变[30-31]。选取8个点位分布比较典型的测点(site01、site05、site08、site10、site13、site15、site19、site23),随机生成了各测点的畸变参数。使用本文方法对其中4个测点(site10、site13、site15和site19)畸变数据进行校正,结果如图 3所示。

|
图 3 三维理论模型测点site10(a)、site13(b)、site15(c)、site19(d)畸变数据校正前、后视电阻率(上)和相位(下)对比 Zxy和Zyx分别表示未加畸变的视电阻率和相位,Dis-Zxy、Dis-Zyx分别表示添加畸变后的电阻率和相位,Cor-Zxy、Cor-Zyx分别表示经本文方法校正的视电阻率和相位。图 6同 |
由图 3可见,施加局部电场畸变对相位的影响明显弱于对视电阻率的影响,且视电阻率曲线首支出现不同程度的分离;校正后的视电阻率曲线与未施加畸变的视电阻率曲线几乎重合,可见很好地恢复了区域电性结构,证明此方法对于恢复除静位移因子外的其他三个畸变参数(t、e和s)是有效的。所选取测点随机生成的畸变参数及恢复的参数如表 1所示。可见,除site19受畸变严重的点恢复效果有所欠缺外,其他3个测点各畸变参数相对误差都小于3%,对于人为添加畸变数据利用本文方法恢复效果良好。
|
|
表 1 三维理论模型畸变参数表 |
安徽霍山—舒城盆地位于金寨断裂南侧,属山间拗陷盆地(图 4),呈东西向,基底除见有少量卢镇关岩群、佛子岭岩群变质岩外,多为中、晚侏罗世三尖铺组、凤凰台组山间磨拉石建造,盆地充填物中有毛坦厂组火山岩[32]。对霍山地区中生代火山岩盆地的1条测线上的15个MT测点(图 4中红框区域)实测数据应用本文方法进行校正。

|
图 4 安徽霍山地区MT测点分布图 蓝色圆点和标注为测点及其编号,红框内为MT01测线 |
MT数据的采集使用加拿大凤凰公司生产的MTU-5A系统,该系统配备MTC-30磁传感器,实际测量中最低频率为0.00055Hz,最高频率为320Hz,共40个频点。
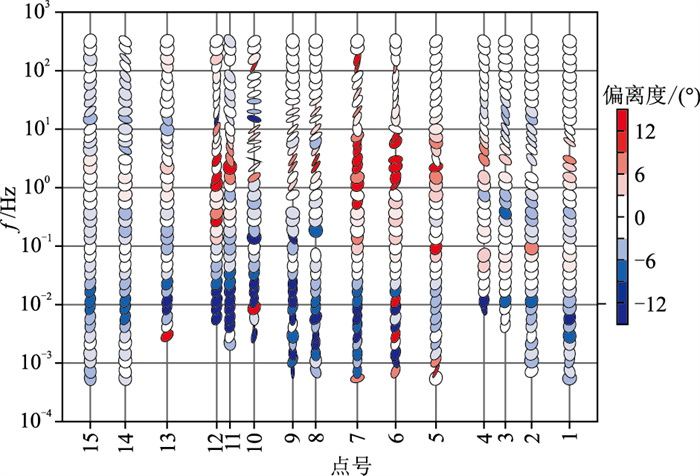
由于测区存在强烈的电磁干扰,需要对MT数据进行精细的整理和处理。首先对工区内MT01测线上的15个MT测点都进行了时间域及频率域数据预处理,对干扰严重的点进行了功率谱挑选、飞点剔除、曲线拟合等处理,然后使用相位张量方法对这15个测点进行了维性分析,图 5所示为该测线相位张量分析图[33]。
|
图 5 安徽霍山地区MT01测线相位张量分析结果 |
一般地,当二维偏离度小于3°时,表明地下构造为二维或准二维,反之则趋向于三维。分析MT01测线相位张量图,发现该剖面10Hz以下频段的二维偏离度高于其阈值3°,即表现出明显的三维性,因而传统的阻抗分解方法不适用于该剖面。在大地电磁勘探中,由于第四系沉积物的存在,一般表现为一维电性结构,理论上其阻抗张量满足一维地电模型条件下的特征,即TE和TM模式视电阻率曲线的首支重合,实际上这也是判断资料是否存在畸变的一个重要标准[19],故可以通过对比校正前、后视电阻率曲线的首支是否重合评价校正结果。
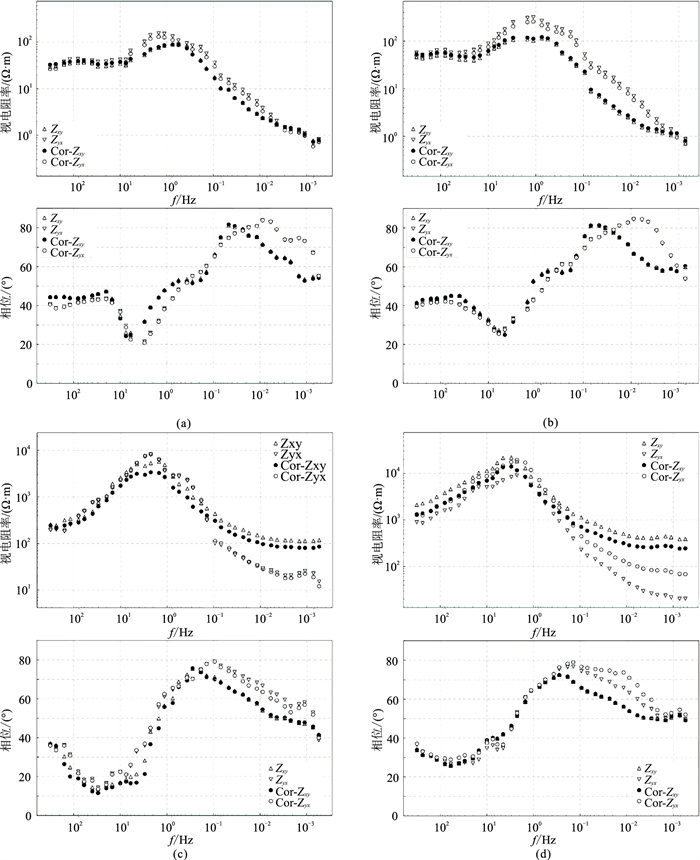
以测点site01、site02、site07、site15为例分析校正效果。图 6为这4个测点经本文方法校正前、后视电阻率和相位的对比。可见,校正前的测点site01和测点site02的XY和YX模式视电阻率偏离较小;校正后首支近乎重合,测点site01视电阻率曲线在10Hz附近分离,测点site02视电阻率曲线在50Hz附近分离,这与图 5的相位张量分析结果一致,在相应的重合频段呈现近圆形,分离的频段相位张量椭圆率增大。测点site07同样具有这种特征。测点site15的原始视电阻率曲线首支分离程度较大,校正后首支重合,这在一定程度上佐证了本文方法的有效性。
|
图 6 测点site01(a)、site02(b)、site07(c)、site15(d)经本文方法校正前、后视电阻率(上)、相位(下)曲线对比 |
传统阻抗分解算法一般是对区域构造进行一维或者二维假设,然后选择相应的方法进行校正,对于三维区域构造,传统的阻抗分解方法失效。在前人的研究基础上,本文提出基于大地电磁振幅—相位张量分解进行大地电磁阻抗畸变校正,无需进行区域构造维性假设,对三维构造MT数据的畸变校正适用。此外,本文方法无需将各向异性参数并入区域阻抗,通过改进粒子群算法实现了畸变参数的可靠求取。理论模型和实测数据计算结果分析表明本文方法能够有效进行大地电磁阻抗张量畸变校正。
本文算法存在以下不足:畸变校正只针对单一测点,若实际观测数据受噪声影响严重,则校正结果不够理想,有待在后续研究中改进,进一步讨论多站点、其他条件约束下的畸变校正方法。
| [1] |
杨长福, 林长佑, 徐世浙. 大地电磁GB张量分解法的改进[J]. 地球物理学报, 2002, 45(增刊): 356-364. YANG Changfu, LIN Changyou, XU Shizhe. The improvement of the Groom-Baily's tensor decomposition in magnetotellurics[J]. Chinese Journal of Geophy-sics, 2002, 45(S1): 356-364. |
| [2] |
晋光文, 孙洁, 白登海, 等. 川西—藏东大地电磁资料的阻抗张量畸变分解[J]. 地球物理学报, 2003, 46(4): 547-552. JIN Guangwen, SUN Jie, BAI Denghai, et al. Impedance tensor distortion decomposition of magnetotelluric data from West Sichuan-East Xizang[J]. Chinese Journal of Geophysics, 2003, 46(4): 547-552. DOI:10.3321/j.issn:0001-5733.2003.04.018 |
| [3] |
胡玉平, 鲍光淑, 贾继标. 基于畸变3个因子的MT畸变曲线改正方法与应用[J]. 地质与勘探, 2005, 41(6): 75-79. HU Yuping, BAO Guangshu, JIA Jibiao. A method to correct MT curve on 3 distortion factors and its application[J]. Geology and Prospecting, 2005, 41(6): 75-79. DOI:10.3969/j.issn.0495-5331.2005.06.014 |
| [4] |
张翔, 严良俊, 苏朱刘, 等. 山区MT资料处理新技术及效果[J]. 石油地球物理勘探, 2007, 42(4): 454-456, 473. ZHANG Xiang, YAN Liangjun, SU Zhuliu, et al. New technology and effects of mountainous MT data processing[J]. Oil Geophysical Prospecting, 2007, 42(4): 454-456, 473. DOI:10.3321/j.issn:1000-7210.2007.04.018 |
| [5] |
尹曜田, 魏文博, 叶高峰, 等. 基于遗传算法的大地电磁阻抗张量分解方法研究[J]. 地球物理学报, 2012, 55(2): 671-682. YIN Yaotian, WEI Wenbo, YE Gaofeng, et al. An improved GB decomposition method based on genetic algorithm[J]. Chinese Journal of Geophysics, 2012, 55(2): 671-682. |
| [6] |
王书明, 李德山, 胡浩. 三维/三维构造下大地电磁相位张量数值模拟[J]. 地球物理学报, 2013, 56(5): 1745-1752. WANG Shuming, LI Deshan, HU Hao. Numerical modeling of magnetotelluric phase tensor in the context of 3D/3D formation[J]. Chinese Journal of Geophysics, 2013, 56(5): 1745-1752. |
| [7] |
吕庆田, 张晓培, 汤井田, 等. 金属矿地球物理勘探技术与设备: 回顾与进展[J]. 地球物理学报, 2019, 62(10): 3629-3664. LYU Qingtian, ZHANG Xiaopei, TANG Jingtian, et al. Review on advancement in technology and equipment of geophysical exploration for metallic deposits in China[J]. Chinese Journal of Geophysics, 2019, 62(10): 3629-3664. DOI:10.6038/cjg2019N0056 |
| [8] |
周聪, 汤井田, 原源, 等. 大地电磁多参考站阵列数据处理方法[J]. 石油地球物理勘探, 2020, 55(6): 1373-1382. ZHOU Cong, TANG Jingtian, YUAN Yuan, et al. Multi-reference array MT data processing method[J]. Oil Geophysical Prospecting, 2020, 55(6): 1373-1382. DOI:10.13810/j.cnki.issn.1000-7210.2020.06.023 |
| [9] |
LÜ Q T, MENG G X, ZHANG K, et al. The lithospheric architecture of the Lower Yangtze Metallogenic Belt, East China: insights into an extensive Fe-Cu mineral system[J]. Ore Geology Reviews, 2021, 132: 103989. DOI:10.1016/j.oregeorev.2021.103989 |
| [10] |
李永博, 吴琼, 王刚, 等. 海岸效应对大地电磁响应的影响及校正方法[J]. 石油地球物理勘探, 2021, 56(3): 631-644. LI Yongbo, WU Qiong, WANG Gang, et al. Study on the influence and correction method of coast effect on magnetotelluric responses[J]. Oil Geophysical Prospecting, 2021, 56(3): 631-644. DOI:10.13810/j.cnki.issn.1000-7210.2021.03.022 |
| [11] |
SWIFT C M. A Magnetotelluric Investigation of An Electrical Conductivity Anomaly in the Southwestern United States[D]. Massachusetts Institute of Technology, Boston, Massachusetts, 1967.
|
| [12] |
BERDICHEVSKY M N, DMITRIEV V I. Basic Principles of Interpretation of Magnetotelluric Soun-ding Curves[M]. Geoelectric and Geothermal Studies, Akademiai Kiado, Budapest, 1976, 163-221.
|
| [13] |
BAHR K. Interpretation of the magnetotelluric impedance tensor: regional induction and local telluric distortion[J]. Journal of Geophysics, 1988, 62: 119-127. |
| [14] |
BAHR K. Geological noise in magnetotelluric data: a classification of distortion types[J]. Physics of the Earth and Planetary Interiors, 1991, 66(1-2): 24-38. DOI:10.1016/0031-9201(91)90101-M |
| [15] |
GROOM R W, BAILEY R C. Decomposition of magnetotelluric impedance tensors in the presence of local three-dimensional galvanic distortion[J]. Journal of Geophysical Research (Solid Earth), 1989, 94(B2): 1913-1925. DOI:10.1029/JB094iB02p01913 |
| [16] |
蔡纲, 陈乐寿, 马涛. 华北平原GB大地电磁剖面的二维解释[J]. 石油地球物理勘探, 1987, 22(2): 169-179. CAI Gang, CHEN Leshou, MA Tao. The 2-D interpretation of GB magnetotelluric sounding profile on North China Plain[J]. Oil Geophysical Prospecting, 1987, 22(2): 169-179. |
| [17] |
CALDWELL T G, BIBBY H M, BROWN C. The magnetotelluric phase tensor[J]. Geophysical Journal International, 2004, 158(2): 457-469. DOI:10.1111/j.1365-246X.2004.02281.x |
| [18] |
BIBBY H M, CALDWELL T G, BROWN C. Determinable and non-determinable parameters of galvanic distortion in magnetotellurics[J]. Geophysical Journal International, 2005, 163(3): 915-930. |
| [19] |
蔡军涛, 陈小斌, 赵国泽. 大地电磁资料精细处理和二维反演解释技术研究(一)——阻抗张量分解与构造维性分析[J]. 地球物理学报, 2010, 53(10): 2516-2526. CAI Juntao, CHEN Xiaobin, ZHAO Guoze. Refined techniques for data processing and two-dimensional inversion in magnetotelluric Ⅰ: tensor decomposition and dimensionality analysis[J]. Chinese Journal of Geophysics, 2010, 53(10): 2516-2526. |
| [20] |
谢成良, 魏文博, 金胜, 等. 相位张量分析约束下的大地电磁测深阻抗张量分解方法研究[J]. 地球物理学进展, 2013, 28(3): 1208-1218. XIE Chengliang, WEI Wenbo, JIN Sheng, et al. Study of magnetotelluric impedance tensor decomposition under the constraint of analysis of phase tensor[J]. Progress in Geophysics, 2013, 28(3): 1208-1218. |
| [21] |
UTADA H, MUNEKANE H. On galvanic distortion of regional 3-D MT impedances on galvanic distortion of regional three-dimensional magnetotelluric impe-dances[J]. Geophysical Journal International, 2000, 140(2): 385-398. |
| [22] |
GARCIA X, JONES A G. Chapter 13 decomposition of three-dimensional magnetotelluric data[J]. Methods in Geochemistry and Geophysics, 2002, 35: 235-250. |
| [23] |
NEUKIRCH M, RUDOLF D, GARCIA X, et al. Amplitude-phase decomposition of the magnetotelluric impedance tensor[J]. Geophysics, 2019, 84(5): E301-E310. |
| [24] |
NEUKIRCH M, GALIANA S, GARCIA X. Appraisal of magnetotelluric galvanic electric distortion by optimizing amplitude and phase tensor relations[J]. Geophysics, 2020, 85(3): E79-E98. |
| [25] |
BOOKER J R. The magnetotelluric phase tensor: a critical review[J]. Surveys in Geophysics, 2014, 35(1): 7-40. |
| [26] |
KENNEDY J, EBERHART R. Particle swarm optimization[C]. Proceedings of International Conference on Neural Networks, Perth, WA, Australia, 1995, 1942-1948.
|
| [27] |
CLERC M. The swarm and the queen: towards a deterministic and adaptive particle swarm optimization[C]. Proceedings of the 1999 Congress on Evolutionary Computation, Washington, DC, USA, 1999, 1951-1957.
|
| [28] |
REN Z Y, KALSCHEUER T, GREENHALGH S, et al. A goal-oriented adaptive finite-element approach for plane wave 3-D electromagnetic modelling[J]. Geophysical Journal International, 2013, 194(2): 700-718. |
| [29] |
李鑫, 白登海, 闫永利, 等. 考虑电流型畸变的大地电磁三维反演[J]. 地球物理学报, 2016, 59(6): 2302-2315. LI Xin, BAI Denghai, YAN Yongli, et al. Three-dimensional inversion of magnetotelluric resistivity model with galvanic distortion[J]. Chinese Journal of Geophysics, 2016, 59(6): 2302-2315. |
| [30] |
MCNEICE G W, JONES A G. Multisite, multi-frequency tensor decomposition of magnetotelluric data[J]. Geophysics, 2001, 66(1): 158-173. |
| [31] |
薛怀民, 马芳, 宋永勤, 等. 江南造山带东段新元古代花岗岩组合的年代学和地球化学: 对扬子与华夏地块拼合时间与过程的约束[J]. 岩石学报, 2010, 26(11): 3215-3244. XUE Huaimin, MA Fang, SONG Yongqin, et al. Geochronology and geochemistry of the Neoproterozoic granitoid association from eastern segment of the Jiangnan orogen, China: constraints on the timing and process of amalgamation between the Yangtze and Cathaysia blocks[J]. Acta Petrologica Sinica, 2010, 26(11): 3215-3244. |
| [32] |
KRIEGER L, PEACOCK J R. MTPy: a python toolbox for magnetotellurics[J]. Computers & Geosciences, 2014, 72: 167-175. |
| [33] |
KIRKBY A, ZHANG F, PEACOCK J R, et al. The MTPy software package for magnetotelluric data analysis and visualisation[J]. Journal of Open Source Software, 2019, 4(35): 1358-1364. |



 肖晓, 湖南省长沙市麓山南路932号中南大学校本部地学楼,410083。Email:
肖晓, 湖南省长沙市麓山南路932号中南大学校本部地学楼,410083。Email: 