② 中国石油大学(北京)地球物理学院, 北京 102249
② College of Geophysics, China University of Petroleum (Beijing), Beijing 102249, China
近年来,频谱激发极化(Spectral Induced Polarization,SIP)已广泛应用于金属矿藏、水文地质、环境科学等领域[1-5]。针对不同的研究对象,在现场及实验室中测量SIP数据时所采用的频率范围不尽相同,影响其激发极化特征的微观机理也不同[6]。在油气勘探领域,储层岩石激发极化主要受离子双电层及界面极化效应的影响,测量SIP数据所采用的频率较低。对于泥质含量较低的储层,当测量频率为10~10MHz时,离子双电层的影响可以忽略,SIP主要受低频界面极化效应的影响[7]。
储层岩石低频界面极化效应微观机理研究是储层SIP技术应用的基础,大量的SIP测量结果表明储层岩石SIP数据在评价孔隙度、渗透率、饱和度、矿化度及润湿性方面优势明显[8-12]。然而,部分储层岩石是典型的多孔介质,其孔隙结构复杂、非均质性较强,因此仅根据实验测量数据难以定量表征储层的微观孔隙特征,目前为止还没有可用于有效解释岩石低频界面极化效应的理论模型。
为了有效分析和研究岩石低频界面极化效应,学者们提出了一系列等效电路模型。Cole等[13]对Debye模型进行了修正,提出了实际应用中更加精确的频散模型。对于宽频范围的岩石介电频谱,Pelton等[14]提出了二阶Cole-Cole模型,以分别表征流体与岩石骨架交界面的界面极化和盐水中偶极极化,取得了较好应用效果。然而Cole-Cole类型的模型均属于经验模型,无法定量描述岩石电阻率频散的物理机理[15]。Dias[16]提出一种新的等效电路模型,并基于双电层形变理论对模型参数的物理含义进行了详细说明。Vinegar等[17]提出了泥质砂岩导电模型,该模型考虑了泥质砂岩中泥岩矿物的附加导电性对激发极化数据的影响。Revil等[18]修订了Vinegar等[17]的等效电路模型,并基于离子双电层理论阐述了低频及高频电导率激发极化效应的微观机理。Tong等[19]提出了能准确预测非均质介质的直流电阻率和极化率的MGEMTIP模型,该模型适用于表征高矿化度、低孔隙度及低渗透率岩石的极化现象。迄今为止,大多数等效电路模型只能对岩石电频散特征进行定性分析,为了定量评价和分析岩石的电频散特性,还需要建立一种可定量表征岩石电频散特性的等效电路模型。
本文基于储层岩石孔隙毛管模型,推导了岩石宏观物性参数与微观孔隙流体导电性质及介电性质的定量关系,对岩石低频界面极化效应的各项影响因素进行了数值模拟,建立了定量评价岩石低频界面极化效应各项影响因素的模型,为岩石低频界面极化微观机理的研究提供了理论基础及数值模型。
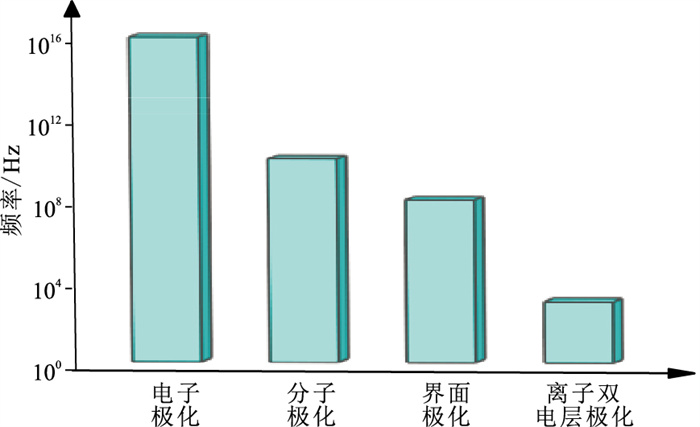
1 油气储层频率域激发极化效应 1.1 低频界面极化效应微观机理在地球物理勘探领域,针对不同的研究对象,频率域激发极化测量所采用的频率各不相同。在0.001~10GHz频率范围,控制频率域激发极化特征的微观机理是变化的,不同的微观机理具有各自所主导的频率范围。如图 1所示,将储层岩石样品置于外加电场中进行频率域激发极化测量时,控制其激发极化特征的主要机理从低频到高频分别为:离子双电层极化、界面极化、分子极化及电子极化等[20]。测量过程中,具体哪种极化机理占主导作用取决于外部电场的频率。由于分子摩擦力及静电场力的作用,每种极化机理起主导作用的频率范围都是有限的。本文中,频率域激发极化数值模拟所采用的频率范围为10~10MHz,在此范围内控制含油岩石激发极化效应的主要机理为界面极化效应。
|
图 1 多孔介质频率域激发极化频带范围 |
在分析频率域电频谱数据极化效应时,通常在位移电流D的表达式中引入宏观极化矢量P[21]
| $ \boldsymbol{D}=\varepsilon_0 \boldsymbol{E}+\boldsymbol{P}=\varepsilon_0 \varepsilon_{\mathrm{r}} \boldsymbol{E} $ | (1) |
式中:E为电场强度;εr表示相对介电常数;ε0=8.85×10-12F·m-1为真空介电常数。基于安培定律,磁场强度H与位移电流D和电流密度j的关系为
| $ \nabla \times \boldsymbol{H}=\frac{\partial \boldsymbol{D}}{\partial t}+\boldsymbol{j} $ | (2) |
式中t表示时间。在时谐电磁场中,将上式中对时间的导数和电流密度分别替换为-iω和σE,则式(2)可改写为
| $ \nabla \times \boldsymbol{H}=-\mathrm{i} \omega\left(\varepsilon_{\mathrm{r}}+\mathrm{i} \frac{\sigma}{\omega \varepsilon_0}\right) \boldsymbol{E} $ | (3) |
式中:σ表示电导率;ω=2πf表示频率域激发极化实验所采用的角频率,其中f表示频率。
在频率域激发极化测量中,岩石样品可等效为具有复介电常数的电容,在角频率为ω的外加电磁场中,岩石复介电常数为
| $ \varepsilon^*(\omega)=\varepsilon_{\mathrm{r}}+\mathrm{i} \frac{\sigma}{\omega \varepsilon_0} $ | (4) |
类似地,在同样的交变电磁场条件下,如果岩石样品被等效为具有复电导率的导体,则其复电导率σ*(ω)可以表示为
| $ \sigma^*(\omega)=\sigma-\mathrm{i} \omega \varepsilon_0 \varepsilon_{\mathrm{r}} $ | (5) |
在频率域激发极化测量中,岩石的复电阻率同样可以表示为
| $ \rho^*(\omega)=\frac{\sigma}{\sigma^2+\left(\omega \varepsilon_0 \varepsilon_{\mathrm{r}}\right)^2}-\mathrm{i} \frac{\omega \varepsilon_0 \varepsilon_{\mathrm{r}}}{\sigma^2+\left(\omega \varepsilon_0 \varepsilon_{\mathrm{r}}\right)^2} $ | (6) |
当σ*(ω)、ρ*(ω)和ε*(ω)中任意两个参数已知时,其余参数可根据式(4)~式(6)计算得到。因此,传统评价介电激发极化效应的方法和模型也同样适用于电阻率激发极化效应的研究。
1.2 油气储层孔隙毛管模型经典孔隙毛管模型广泛应用于研究多孔介质宏观物性参数与微观孔隙结构的关系。在储层孔隙结构研究中,通常将孔隙网络等效为多条毛细管组成的孔隙毛细管模型。当储层孔隙由半径及长度恒定的毛细管组成时,其部分宏观物性参数可由Darcy定律和Hagen-Poiseuille定律表述[22]
| $ \phi =n_0 \pi r_0^2 $ | (7) |
| $ K =\frac{n_0 \pi r_0^4}{8} $ | (8) |
| $ F=\frac{1}{\phi}=\frac{1}{n_0 \pi r_0^2} $ | (9) |
式中:ϕ表示孔隙度;K表示渗透率;F表示地层因素;r0表示毛管半径;n0表示单位截面积上的毛管数。基于式(7)~式(9),岩心部分宏观物性参数可由经典的孔隙毛管模型定量表征。然而,实际岩心的孔隙网络常常由不同尺寸的孔隙及喉道组成,基于传统的单一尺寸的孔隙毛管模型难以准确表征实际岩心的孔隙结构,计算得到的宏观物性参数也会偏离真实值。
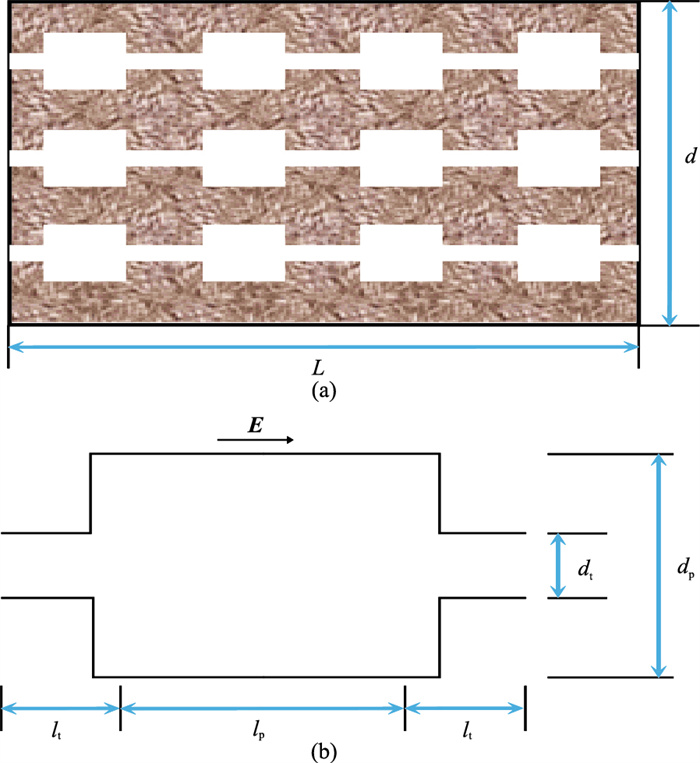
为了克服上述局限性,本文引入一种新型孔隙毛管模型[23](图 2)。沿着外加电场E的方向,模型中每条毛管束由多个相同的孔隙单元组成。假设岩心长度为L,岩心直径为d,孔隙及喉道直径分别为dp和dt,每个孔隙单元中的孔隙长度lp及喉道尺寸lt可以单独设置,每个孔隙单元的长度le=lp+lt。
|
图 2 毛管孔隙网络(a)及基本孔隙单元(b)示意图 |
根据式(7)~式(9),本文孔隙毛管模型的岩心宏观物性参数可表示为
| $ \phi=n_0 \pi r_{\mathrm{e}}^2=\frac{n_0 \pi}{4} \frac{1+x^2 y}{1+y} d_{\mathrm{t}}^2 $ | (10) |
| $ K=\frac{n_0 \pi r_{\mathrm{e}}^4}{8}=\frac{n_0 \pi}{128}\left(\frac{1+x^2 y}{1+y}\right)^2 d_{\mathrm{t}}^4 $ | (11) |
| $ F=\frac{1}{n_0 \pi r_{\mathrm{e}}^2}=\frac{4}{n_0 \pi} \frac{1+y}{1+x^2 y} \frac{1}{d_{\mathrm{t}}^2} $ | (12) |
式中:令x=dp/dt和y=lp/lt,目的是简化表达式;等效毛管半径re可表示为
| $ r_{\mathrm{e}}^2=\frac{1+x^2 y}{1+y}\left(\frac{d_{\mathrm{t}}}{2}\right)^2 $ | (13) |
上述岩心宏观物性参数真实值可由实验测量获取,对于均匀介质,x≈y。此外,基于岩心宏观物性参数测量结果,可以确定式(10)~式(12)中的其他参数
| $ d_{\mathrm{t}}^2=\frac{32 K}{\phi} \frac{1+y}{1+x^2 y} $ | (14) |
| $ n_0=\frac{\phi^2}{8 \pi K} $ | (15) |
确定了所有参数后,即可建立本文孔隙毛管模型。该孔隙毛管模型不仅可以研究传统的宏观物性参数与微观几何参数的关系,还可为储层岩石频率域激发极化数据的定量解释提供理论模型。
2 油气储层频率域激发极化效应评价模型在岩石频率域激发极化测量中,岩石的宏观电性特征源于骨架和孔隙流体两部分的贡献。为了评价频率域激发极化效应对岩石电频散或者介电频散的影响,需构建油气储层频率域激发极化效应评价模型。在评价频率域激发极化效应的众多模型中,等效电路模型通常将岩石骨架及孔隙流体分别等效为电路中的电阻或电容等电子元器件,这类模型已广泛应用于评价频率域岩石激发极化效应。
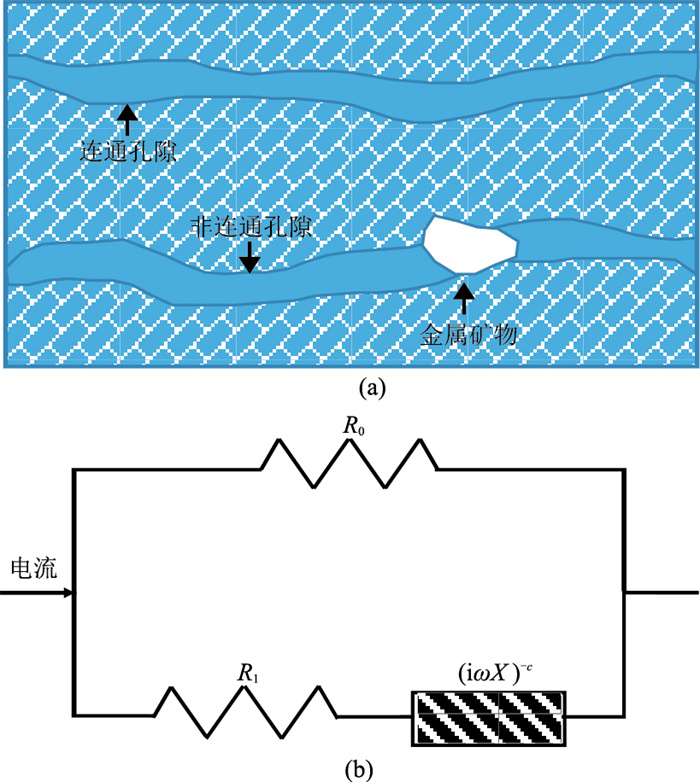
2.1 传统Cole-Cole模型Cole-Cole模型是经典Debye模型的扩展模型,最初用于表征图 3a所示的含金属矿物地层的介电特性[24]。基于此模型,建立图 3b所示的Cole-Cole模型含金属矿物岩石等效电路,其中(iωX)-c表征金属颗粒和导电离子的复阻抗(X表示虚部阻抗值,c是频率相关系数),R0表征允许传导电流通过的连通孔隙通道的电阻,R1表征不连通孔隙中盐溶液的电阻。
|
图 3 含金属矿物岩石的Cole-Cole模型示意图 (a)孔隙结构;(b)等效电路 |
作为一种简单的经验模型,Cole-Cole模型已广泛应用于岩石、土壤等离子导电介质的频率域激发极化效应的评价。尽管还有一些等效电路模型也具有类似的响应特征,但是Cole-Cole模型可提供图 3所示的比较直观的岩石孔隙结构的类比关系,且模型参数较少(仅4个),更适用于分析频率域激发极化实测数据。尽管实际的岩石孔隙形态比Cole-Cole模型中的孔隙结构复杂得多,但是大量的实际应用结果表明,Cole-Cole模型足以表征频率域激发极化数据的主要特征。描述岩石复电阻率频率域激发极化特征时,Cole-Cole模型对应的复电阻率表达式为
| $ \rho(\omega)=\rho_0\left\{1-m\left[1-\frac{1}{1+(\mathrm{i} \omega \tau)^c}\right]\right\} $ | (16) |
式中:ρ0是直流电阻率;m=1-ρ∞/ρ0表示极化率,其中ρ∞是高频电阻率;τ是弛豫时间。在应用Cole-Cole模型评价岩石频率域激发极化数据时,主要目标是反演获得上述模型参数(即ρ0、m、τ及c),使Cole-Cole模型能较好地拟合实测数据[25]。
综上所述,Cole-Cole模型可以很好地拟合岩石频率域激发极化数据,模型参数也可用于岩石频率域激发极化数据的宏观属性的定性解释。但是,对于Cole-Cole模型,并不是所有的参数都具有明确的物理意义,因而Cole-Cole模型并不适合于岩石频率域激发极化数据的定量分析。
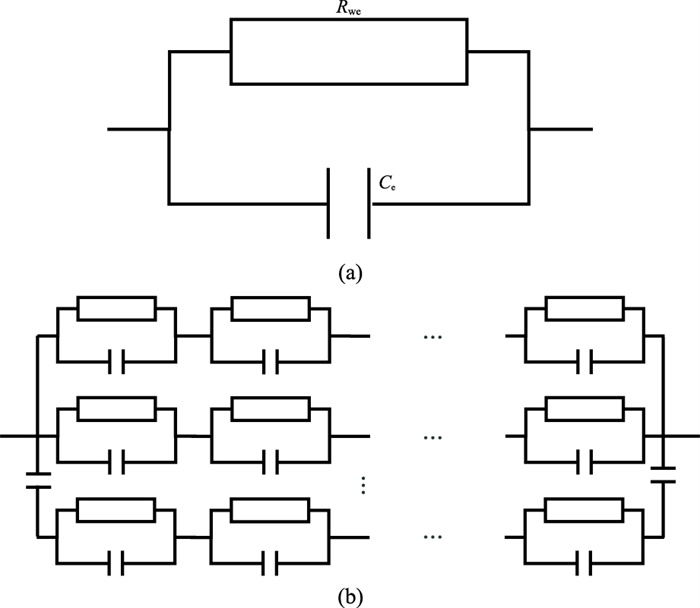
2.2 基于毛管孔隙网络的等效电路模型为了对岩石频率域激发极化数据进行定量分析,本文基于图 2所示孔隙毛管模型建立一种等效电路模型,如图 4所示。在该等效电路模型中,岩石的激发极化特征主要来自孔隙流体的贡献,图 2中每个孔隙单元可被等效为一个电阻Rwe与电容Ce并联的电路单元,每条孔隙毛管束可以表示为多个电路单元的串联,进而整个岩石的等效电路则可表征为许多毛管束对应的电路并联的结果。
|
图 4 基于毛管孔隙网络的等效电路模型示意图 (a)孔隙流体微观导电网络;(b)岩石宏观导电模型 |
与传统的Cole-Cole等效电路模型不同,图 4所示模型不仅考虑了孔隙流体的阻抗特征,也兼顾其容抗特征。根据界面极化微观机理,该模型将连通孔隙空间(通常是喉道)中的流体电阻等效为Rwe,将未连通孔隙空间(通常是孔隙表面)中的流体电容等效为Ce。根据孔隙毛管模型中孔隙单元的几何结构,可计算出含油岩石孔隙单元连通孔隙空间流体的等效电阻为
| $ R_{\mathrm{we}}=\rho_{\mathrm{w}} \frac{l_{\mathrm{e}}}{A_{\mathrm{e}} S_{\mathrm{w}}} $ | (17) |
式中:Sw是孔隙单元的含水饱和度;Ae是孔隙喉道截面积;ρw是孔隙流体电阻率。当孔隙中含有油、水两相流体时,不考虑极性分子的极化情况,孔隙流体电阻率可表示为[26]
| $ \rho_{\mathrm{w}}=\frac{1+\frac{3 \times 10^5}{C_{\mathrm{NaCl}}^{1 / 1.05}}}{1.8 T+39} $ | (18) |
式中:CNaCl是孔隙流体中NaCl溶液的矿化度;T是孔隙流体的温度。
在岩石频率域激发极化分析时,可将垂直于外电场方向的孔隙表面视为平行板电容,孔隙单元内两相流体的电容可表示为
| $ C_{\mathrm{e}}=\pi \frac{\left(\frac{d_{\mathrm{p}}}{2}\right)^2-\left(\frac{d_{\mathrm{t}}}{2}\right)^2}{l_{\mathrm{p}}}\left[\varepsilon_{\mathrm{water}} S_{\mathrm{w}}+\varepsilon_{\mathrm{oil}}\left(1-S_{\mathrm{w}}\right)\right] $ | (19) |
式中εwater和εoil分别表示孔隙中盐溶液和油的介电常数。
基于上述Rwe(式(17))和Ce(式(19))的表达式,单个孔隙单元的电阻抗Ze(ω)可表示为
| $ Z_{\mathrm{e}}(\omega)=\frac{R_{\mathrm{we}} \times \frac{1}{\mathrm{i} \omega C_{\mathrm{e}}}}{R_{\mathrm{we}}+\frac{1}{\mathrm{i} \omega C_{\mathrm{e}}}}=\frac{R_{\mathrm{we}}-\mathrm{i} \omega R_{\mathrm{we}}^2 C_{\mathrm{e}}}{1+\left(\omega R_{\mathrm{we}} C_{\mathrm{e}}\right)^2} $ | (20) |
对于由多个串联孔隙单元组成的毛细管,可通过叠加得到总电阻抗。单条毛细管的总阻抗表达式为
| $ Z_{\text {le }}(\omega)=n_{\mathrm{e}} Z_{\mathrm{e}}(\omega) L $ | (21) |
式中ne表示每条毛细管中的孔隙单元数。对于岩石样品,孔隙网络由若干相同的平行毛管组成,其总电阻抗可表示为
| $ Z_{\text {core }}(\omega)=\frac{Z_{\text {le }}(\omega)}{A n_0}=\frac{n_{\mathrm{e}}}{n_0} \frac{L}{A} \frac{R_{\mathrm{we}}-\mathrm{i} \omega R_{\mathrm{we}}^2 C_{\mathrm{e}}}{1+\left(\omega R_{\mathrm{we}} C_{\mathrm{e}}\right)^2} $ | (22) |
式中A为岩心样品截面积。结合岩样宏观物性参数,主要受界面极化效应影响的岩样复电阻率的实部和虚部分别为[27]
| $ \begin{aligned} \rho_{\mathrm{r}}(\omega) & =\frac{A}{L} \times \operatorname{Re}\left[Z_{\text {core }}(\omega)\right] \\ & =\frac{n_{\mathrm{e}}}{n_0} \times \operatorname{Re}\left[\frac{R_{\mathrm{we}}-\mathrm{i} \omega R_{\mathrm{we}}^2 C_{\mathrm{e}}}{1+\left(\omega R_{\mathrm{we}} C_{\mathrm{e}}\right)^2}\right] \end{aligned} $ | (23) |
| $ \begin{aligned} \rho_{\mathrm{x}}(\omega) & =\frac{A}{L} \times \operatorname{Im}\left[Z_{\text {core }}(\omega)\right] \\ & =\frac{n_{\mathrm{e}}}{n_0} \times \operatorname{Im}\left[\frac{R_{\mathrm{we}}-\mathrm{i} \omega R_{\mathrm{we}}^2 C_{\mathrm{e}}}{1+\left(\omega R_{\mathrm{we}} C_{\mathrm{e}}\right)^2}\right] \end{aligned} $ | (24) |
式中Re(·)、Im(·)分别表示取实部和虚部。
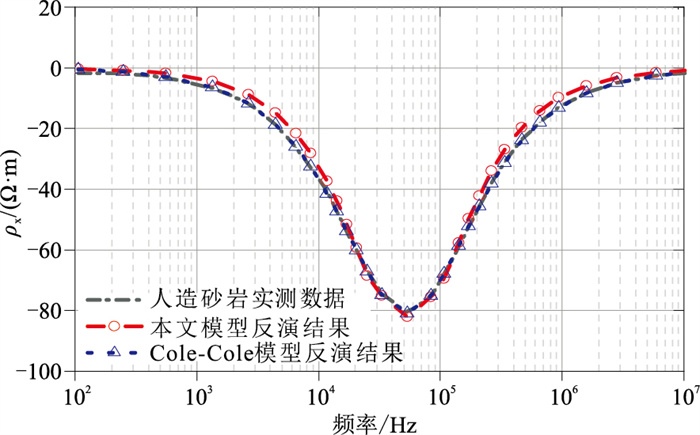
为验证式(23)和式(24)的准确性,基于人造砂岩数据进行了反演拟合,将反演结果与传统Cole-Cole模型反演结果进行对比。如图 5所示,基于传统Cole-Cole模型和本文模型的反演结果与实测数据吻合较好,本文模型反演结果与传统Cole-Cole模型反演结果相比存在一定的差异,这是由于本文模型是基于均一孔隙毛管模型建立的,与真实岩石孔隙结构存在一定偏差,但二者均能较好地表征虚部电阻率实测数据频散特征。同时,基于式(17)~式(24),本文等效电路模型建立了含油岩石宏观物性参数与微观孔隙流体导电性质和介电性质之间的定量关系,这是其他传统等效电路模型目前无法实现的。
|
图 5 人造砂岩不同导电模型电频谱虚部反演结果对比 |
在界面极化所主导的电频散频率范围内,岩石复电阻率是与孔隙度ϕ、渗透率K、含水饱和度Sw、温度T和流体矿化度Cw等因素相关的复杂函数。为定量分析这些因素对岩石低频界面极化的影响,本文数值模拟所用岩心的长度L及直径d分别为2in和1in,并假设岩石孔隙网络由均匀毛管孔隙单元组成(即式(13)中x≈y),分别对盐水饱含岩石和含油岩石两种情况进行数值模拟和分析。
3.1 盐水饱含岩石激发极化效应对于NaCl溶液完全饱和的岩心样品,孔隙和喉道均被NaCl溶液充填,若不考虑骨架导电性的影响,岩石低频界面极化效应主要由孔隙中NaCl溶液的阻抗和电容特性决定。由式(11)可知,毛管孔隙模型孔隙度由孔喉尺寸及孔喉比λ共同决定。但是,当岩石孔隙度变化时,难以同时表征孔喉尺寸和孔喉比的变化规律,本文主要研究孔喉比λ对岩石电频散特征的影响。
图 6为不同孔喉比条件下的完全饱和NaCl溶液岩样的虚部电频谱曲线。设岩石平均孔喉半径为10μm,岩心孔喉比λ的变化范围为20~80。根据式(18)计算地层水电阻率ρw时,岩心孔隙中饱和NaCl溶液的温度T和矿化度Cw分别为25℃和5000ppm。由图 6可见,在低频范围(1k~10M Hz)内,虚部电阻率幅值随孔喉比λ的增大而明显增大,且虚部电阻率极小值的模值ρi对应的特征频率(即虚部电阻率极小值点对应的频率)随孔喉比λ的增大明显减小,与马雪瑞等[28]关于不同孔隙度人造岩心电频谱实测结果一致。

|
图 6 不同孔喉比λ饱和岩样电频谱虚部电阻率曲线 |
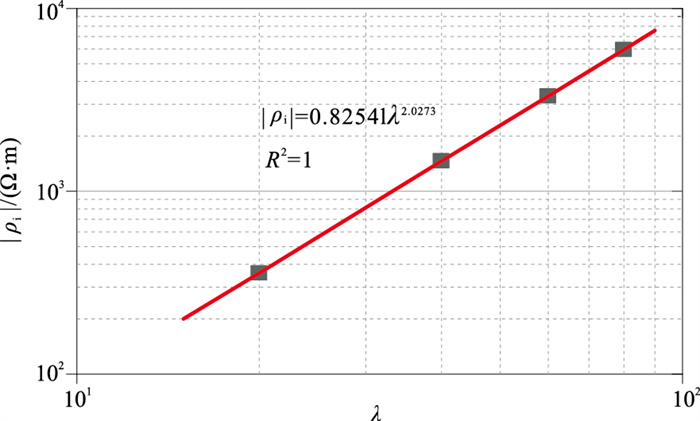
图 7为孔喉比λ与|ρi|的交会图,可见|ρi|随孔喉比λ的增大呈幂指数增大。
|
图 7 虚部电阻率极小值模值|ρi|与孔喉比λ相关曲线 |
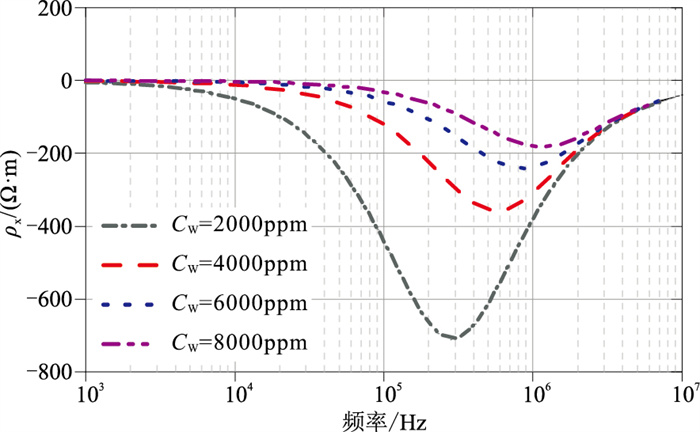
对于饱和样品,本文除考虑孔喉比的影响,还模拟了NaCl溶液矿化度Cw对低频界面极化的影响。图 8为不同Cw条件下完全饱和NaCl溶液岩样虚部电频谱曲线。假设岩心孔隙饱和NaCl溶液的矿化度Cw分别为2000、4000、6000、8000ppm,平均喉道直径为10μm,孔喉比λ为20,岩心孔隙度ϕ为0.1,岩心孔隙中饱和NaCl溶液温度T为25℃。根据式(18)可计算地层水电阻率。从图 8可见,在低频范围(1k~10MHz)内,虚部电阻率幅值随NaCl溶液矿化度Cw的增大明显减小,虚部电阻率极小值模值|ρi|对应的特征频率则随着矿化度Cw的增大呈幂指数增大。
|
图 8 不同NaCl溶液矿化度Cw饱和岩样电频谱虚部电阻率曲线 |
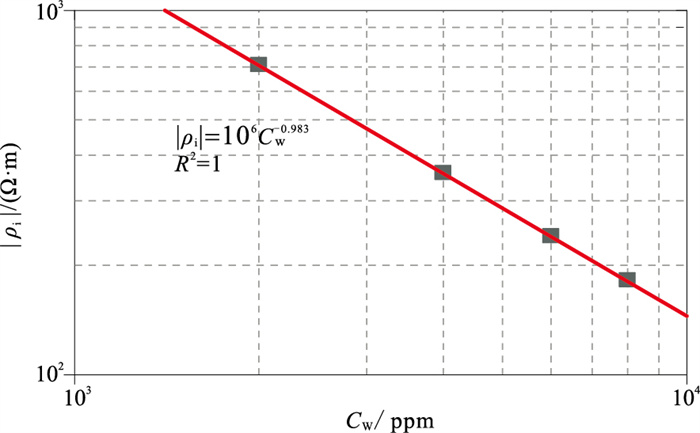
图 9为NaCl溶液矿化度CW与|ρi|的交会图。由图可见,|ρi|随CW的增大呈幂指数减小。
|
图 9 虚部电阻率极小值模值|ρi|与NaCl溶液矿化度Cw交会图 |
本文模型数值模拟结果表明,虚部电阻率模值与实部电阻率一样,可用于评价矿化度对岩石导电性的影响,这一结论与Niu等[29]关于人造砂岩样品的电频谱测量结果一致,且该文献中得到的电阻率虚部与矿化度的拟合关系式与本文结果基本一致。
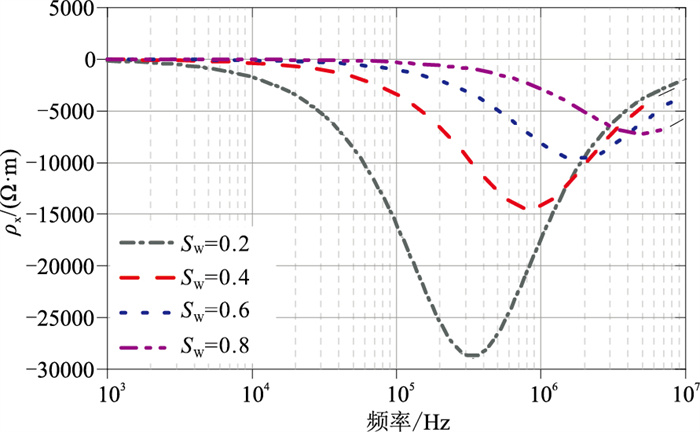
3.2 含油岩石激发极化效应对于含油岩石样品,其孔隙空间常同时存在多相流体。孔隙流体的饱和度,尤其是盐水含水饱和度会直接影响岩石的导电特性。图 10所示为部分饱和相同矿化度NaCl溶液的含油岩样虚部电频谱曲线,其中岩心含水饱和度Sw分别取值0.2、0.4、0.6、0.8,地层流体矿化度Cw为1000ppm,平均喉道直径dt为10μm,孔喉比λ为40,储层温度T为25℃。
|
图 10 不同含水饱和度Sw岩样电频谱虚部曲线 |
由图可见,虚部电阻率极小值模值|ρi|随地层水含水饱和度Sw的增大明显减小,且|ρi|对应的特征频率随着含水饱和度Sw的增大明显增大。
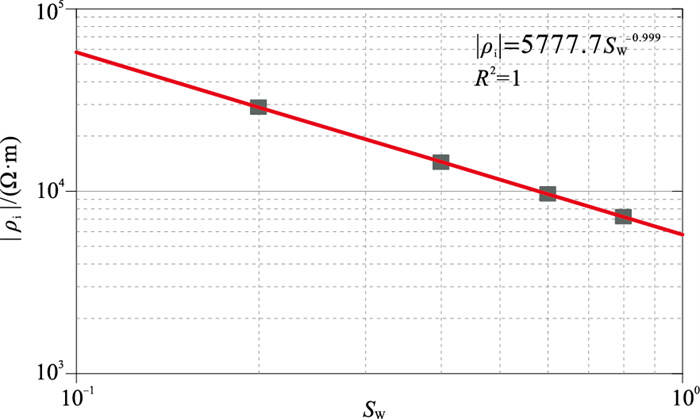
图 11为含水饱和度与虚部电阻率极小值模值|ρi|的交会图。可见|ρi|随含水饱和度Sw增大呈幂指数减小,表明利用低频界面极化效应评价储层含油饱和度是可行的,文献[30]中关于含油砂岩、碳酸盐岩样品的电频谱实验结果也证明了这一结论。另外,Schmutz等[31]的实际测量结果也验证了图中的拟合趋势。
|
图 11 虚部电阻率极小值模值|ρi|与含水饱和度Sw交会图 |
基于岩石孔隙毛管模型,本文建立了岩石微观孔隙流体导电特性及介电特性与电子元器件之间的等效关系,从而构建了一种评价岩石低频界面极化效应的等效电路模型。相对于传统的等效电路模型,该等效电路模型参数具有更加明确的物理含义,引入低频界面极化效应的机理更加清晰,并首次建立了等效电路与岩石宏观物性参数间的定量关系,为定量分析岩石低频界面极化效应奠定了理论基础。
利用本文所构建等效电路模型,开展了岩石低频界面极化效应微观机理研究,对盐水饱和岩样及含油岩样低频界面极化效应的各项影响因素进行了数值模拟。模拟结果表明,随着孔喉比的增大、孔隙流体矿化度的减小及含油饱和度的增大,岩石虚部电阻率幅度值增大,界面极化效应影响更大;反之,则岩石虚部电阻率幅度值减小,界面极化效应影响更小。
为了定量评价各项因素对岩石低频界面极化效应的影响,本文引入虚部电阻率极小值模值|ρi|对各项影响因素进行了回归分析。结果表明,在双对数坐标系下,|ρi|与孔喉比λ、矿化度Cw及含水饱和度Sw均呈幂指数关系,且|ρi|随λ的增大而增大,随Cw或Sw的增大而减小。
本文数值模拟结果为利用岩石低频界面极化效应微观机理研究和储层含油气性定量评价提供了理论基础和模型基础。然而,由于本文模型的孔隙结构均一,且未考虑岩石骨架导电性的影响,该模型的应用效果还需要进一步的研究和论证。
| [1] |
伍操为, 邹长春, 吴涛, 等. 基于激发极化弛豫时间谱的浸染型海底多金属硫化物岩石物性评价方法[J]. 地球物理学报, 2022, 65(1): 393-403. WU Caowei, ZOU Changchun, WU Tao, et al. A physical property evaluation method of disseminated seafloor polymetallic sulfide rocks based on time domain induced polarization relaxation time spectra[J]. Chinese Journal of Geophysics, 2022, 65(1): 393-403. |
| [2] |
MARTIN T, GVNTHER T, OROZCO A F, et al. Evaluation of spectral induced polarization field mea-surements in time and frequency domain[J]. Journal of Applied Geophysics, 2020, 180: 104141. DOI:10.1016/j.jappgeo.2020.104141 |
| [3] |
向葵, 严良俊, 胡华, 等. 四川盆地前寒武系重磁电物性特征与建模[J]. 石油地球物理勘探, 2020, 55(5): 1160-1168. XIANG Kui, YAN Liangjun, HU Hua, et al. Physical properties and modeling of density, susceptibility and resistivity of Pre-Cambrian system in Sichuan Basin[J]. Oil Geophysical Prospecting, 2020, 55(5): 1160-1168. |
| [4] |
杜炳锐, 白大为, 裴发根, 等. 水合物沉积物介电特性测量实验[J]. 石油地球物理勘探, 2019, 54(1): 118-126. DU Bingrui, BAI Dawei, PEI Fagen, et al. An experimental study on dielectric properties of hydrate sediments in radar wave propagation[J]. Oil Geophysical Prospecting, 2019, 54(1): 118-126. |
| [5] |
李静和, 何展翔, 穆桐. 接触式激发极化法油气储层压裂监测有限元模拟[J]. 石油地球物理勘探, 2022, 57(3): 719-727. LI Jinghe, HE Zhanxiang, MU Tong. Finite element simulation for fracturing monitoring of oil and gas reservoirs by using contact induced polarization me-thod[J]. Oil Geophysical Prospecting, 2022, 57(3): 719-727. |
| [6] |
王云梅, 潘保芝, 栗猛, 等. 三种孔隙水的导电和介电性质及其频散特征[J]. 地球物理学进展, 2018, 33(5): 1989-1996. WANG Yunmei, PAN Baozhi, LI Meng, et al. Electrical and dielectric properties of three types of pore water and their frequency dispersion characteristics[J]. Progress in Geophysics, 2018, 33(5): 1989-1996. |
| [7] |
XIAO Z S, ZHANG S W, ZHANG T X, et al. Experi-mental research on the rock electrical parameter dispersion properties in the displacement process[J]. Geophysical Prospecting, 2009, 57(6): 1027-1033. DOI:10.1111/j.1365-2478.2009.00812.x |
| [8] |
JIANG M, KE S Z, KANG Z M. Measurements of complex resistivity spectrum for formation evaluation[J]. Measurement, 2018, 124: 359-366. DOI:10.1016/j.measurement.2018.01.041 |
| [9] |
JIA J, KE S Z, REZAEE R, et al. The frequency exponent of artificial sandstone's complex resistivity spectrum[J]. Geophysical Prospecting, 2021, 69(4): 856-871. DOI:10.1111/1365-2478.13072 |
| [10] |
LI J J, KE S Z, YIN C F, et al. A laboratory study of complex resistivity spectra for predictions of reservoir properties in clear sands and shaly sands[J]. Journal of Petroleum Science and Engineering, 2019, 177: 983-994. DOI:10.1016/j.petrol.2019.01.061 |
| [11] |
REVIL A, COPEREY A, MAO D Q, et al. Induced polarization response of porous media with metallic particles-Part 8:Influence of temperature and salinity[J]. Geophysics, 2018, 83(6): E435-E456. DOI:10.1190/geo2018-0089.1 |
| [12] |
潘保芝, 阿茹罕, 郭宇航, 等. 裂缝性岩石低频下复电阻率与饱和度关系研究[J]. 地球物理学报, 2021, 64(10): 3774-3787. PAN Baozhi, A Ruhan, GUO Yuhang, et al. Study on the relationship between complex resistivity and water saturation in fractured rock at low frequency[J]. Chinese Journal of Geophysics, 2021, 64(10): 3774-3787. DOI:10.6038/cjg2021O0084 |
| [13] |
COLE K S, COLE R H. Dispersion and absorption in dielectrics. I: Alternating current characteristics[J]. Journal of Chemical Physics, 1941, 9(4): 341-351. DOI:10.1063/1.1750906 |
| [14] |
PELTON W H, WARD S H, HALLOF P G, et al. Mineral discrimination and removal of inductive coupling with multi-frequency IP[J]. Geophysics, 1978, 43(3): 588-609. DOI:10.1190/1.1440839 |
| [15] |
MAJOR J, SILIC J. Restrictions on the use of Cole-Cole dispersion models in complex resistivity interpretation[J]. Geophysics, 1981, 46(6): 916-931. |
| [16] |
DIAS C A. Developments in a model to describe low-frequency electrical polarization of rocks[J]. Geophysics, 2000, 65(2): 437-451. |
| [17] |
VINEGAR H J, WAXMAN M H. Induced polarization of shaly sands[J]. Geophysics, 1984, 49(8): 1267-1287. |
| [18] |
REVIL A, COPEREY A, DENG Y P, et al. Complex conductivity of tight sandstones[J]. Geophysics, 2018, 83(2): E55-E74. |
| [19] |
TONG X L, YAN L J, XIANG K. Modifying the generalized effective-medium theory of induced polarization model in compacted rocks[J]. Geophysics, 2020, 85(4): MR245-MR255. |
| [20] |
GARROUCH A A, SHARMA M M. Dielectric dispersion of partially saturated porous media in the frequency range 10 Hz to 10 MHz[J]. The Log Analyst, 1998, 39(3): 48-53. |
| [21] |
JACKSON J D. Classical Electrodynamics[M]. New York: Springer Press, 1998.
|
| [22] |
TOUMELIN E, TORRES-VERDIN C. 2D pore-scale simulation of wide-band electromagnetic dispersion of saturated rocks[J]. Geophysics, 2007, 72(3): F97-F110. |
| [23] |
程媛媛, 关继腾, 王殿生. 基于毛管模型的含油储层岩石激发极化特性[J]. 石油地球物理勘探, 2013, 48(3): 467-473. CHENG Yuanyuan, GUAN Jiteng, WANG Dian-sheng. Induced polarization effects of oil-bearing re-servoir rocks based on the capillary model[J]. Oil Geophysical Prospecting, 2013, 48(3): 467-473. |
| [24] |
关继腾, 程媛媛, 于华. 利用等效电路模型研究泥质砂岩复电阻率频散特性[J]. 测井技术, 2011, 35(6): 512-517. GUAN Jiteng, CHENG Yuanyuan, YU Hua. On the frequency dispersion characteristics of complex resistivity in shaly sandstone based on equivalent circuit model[J]. Well Logging Technology, 2011, 35(6): 512-517. |
| [25] |
林小稳, 柯式镇, 贺秋丽, 等. 岩石复电阻率频谱反演研究[J]. 测井技术, 2016, 40(2): 142-146. LIN Xiaowen, KE Shizhen, HE Qiuli, et al. Inversion study on complex resistivity spectrum of rocks[J]. Well Logging Technology, 2016, 40(2): 142-146. |
| [26] |
XIANG J, JONES N B, CHENG D, et al. Direct inversion of the apparent complex-resistivity spectrum[J]. Geophysics, 2001, 66(5): 1399-1404. |
| [27] |
雍世和, 张超谟. 测井数据处理与综合解释[M]. 山东东营: 石油大学出版社, 1996.
|
| [28] |
马雪瑞, 柯式镇, 贺秋利, 等. 人工岩心电频谱实验及饱和度评价模型研究[J]. 石油科学通报, 2019, 4(2): 134-144. MA Xuerui, KE Shizhen, HE Qiuli, et al. A study of complex resistivity experiments and a saturation mo-del of rock[J]. Petroleum Science Bulletin, 2019, 4(2): 134-144. |
| [29] |
NIU Q F, REVIL A, SAIDIAN M. Salinity depen-dence of the complex surface conductivity of the Portland sandstone[J]. Geophysics, 2016, 81(2): D125-D140. |
| [30] |
XU W, KE S Z, YIN C F, et al. Measurement and inversion of complex resistivity spectra for different core samples[C]. SEG Technical Program Expanded Abstracts, 2014, 33: 469-472.
|
| [31] |
SCHMUTZ M, BLONDEL A, REVIL A. Saturation dependence of the quadrature conductivity of oil-bearing sands[J]. Geophysical Research Letters, 2012, 39(3): 2-7. |



 许巍, 湖北省武汉市蔡甸区蔡甸大街大学路111号长江大学地球物理与石油资源学院,430100。Email:
许巍, 湖北省武汉市蔡甸区蔡甸大街大学路111号长江大学地球物理与石油资源学院,430100。Email: 