测井数据是进行地下储层解释与评价的重要基础,对于指导油气藏勘探、开发具有重要意义。在实际测井过程中,测井仪器故障、井壁垮塌等因素导致测井数据失真或者缺失。由于重新测井成本高昂,且对于许多已做过固井的油气井来说,重新测井工程难度极大。测井数据失真或缺失给油气藏开发和评价带来了巨大挑战。因此,如何重构失真或缺失的测井曲线已成为新挑战[1-3]。
近年来,许多数据驱动方法被提出来并应用于地质参数估计及油藏描述等方面,如人工神经网络(Artificial Neural Network,ANN)[4-5]、模糊逻辑模型(Fuzzy Logic Model,FLM)[6]、决策树(Decision- making Tree,DT)[7]和支持向量机(Support Vector Machine,SVM)[8]等。由于测井数据具有明显的时间或空间序列特征,数据之间存在长序列依赖关系,上述机器学习方法无法有效提取测井数据的依赖关系,且存在计算效率低或易过拟合等缺点[8],因此它们在一定程度上不能完全适用于基于测井资料的地质建模或岩性识别[9]。
随着人工智能技术的发展,循环神经网络(Recurrent Neural Network,RNN)在地球科学各领域的良好应用而受到广泛关注[10]。由于RNN需要为每一步保持一个激活向量,容易在训练阶段出现梯度爆炸和消失问题[11]。长短时记忆(Long Short-Term Memory,LSTM)神经网络是一种特殊的RNN结构[12],通过正则化项约束权值范数,使其不至于过大,在一定程度上遏制了RNN的梯度爆炸和消失问题的发生。考虑到测井数据通常在同一岩性段内呈现平滑变化特征,测井数据与LSTM网络之间有天然的内在匹配特性,因此LSTM网络已被应用于测井数据重构方法研究[13-14]。由于单向LSTM网络方法只考虑数据信息在单方向序列的相关性,忽略了缺失点后序数据的影响,不利于对测井数据的精准预测。
于是,双向长短时记忆(Bidirectional LSTM,Bi-LSTM)神经网络[15-18]应运而生,它利用另一个在序列中向后移动的LSTM完成双向时序学习,该结构既能表征过去的趋势,也能预测未来发展方向,对于整段测井数据缺失的情况,具有天然的双向时序数据重构优势。周雪晴等[19]提出基于Bi-LSTM网络的流体高精度识别新方法,利用Bi-LSTM网络提取井下测井曲线随深度的变化趋势及前后关联特征,提高流体识别能力。周欣等[20]提出一种基于双向门控循环单元神经网络的声波测井曲线重构技术,充分利用测井数据中的前后序列关联性补全缺失的声波测井曲线。王俊等[21]提出基于深度双向RNN的储层孔隙度预测方法,利用双向RNN建立测井数据与储层孔隙度之间的非线性映射关系,提高了模型预测的准确性。但上述方法在具体应用时,都存在一定缺陷:一是每次预测多条曲线,待测曲线之间干扰较大。二是模型缺乏灵活性和适应性,一旦模型训练完成,无法将当前井已补全的测井曲线用于剩余测井曲线的补全。不能充分考虑当前井测井曲线之间的影响关系,即模型无法在补全过程中做优化。
为此,本文提出一种串级双向长短时记忆(CBi-LSTM)网络的测井数据重构方法,利用缺失数据点的前趋与后继之间的双向关联性,提取缺失数据点的前趋与后继中的关键特征信息对缺失数据点进行重构,采用串级更新策略,将获得的估计值与已知测井曲线合并为新的输入,完成对缺失测井数据块的重构。
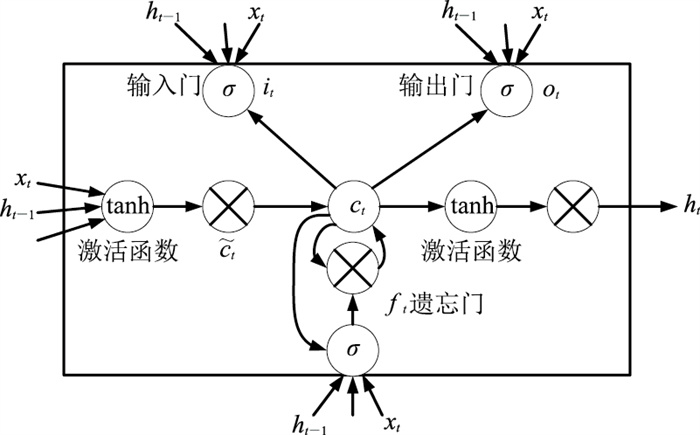
1 基于Bi-LSTM网络的数据重构法原理 1.1 长短时记忆网络LSTM网络是RNN的改进算法,通过门机制将短期记忆与长期记忆结合起来,弥补RNN只能记忆短期的历史输入信息而无法实现长期记忆的缺陷,在一定程度上解决了网络的梯度消失和梯度爆炸。LSTM网络保留了RNN的链式结构,由一系列递归链接的记忆区块的子网络构成,其中关键结构为交互层中的3个门层,即输入门、输出门、遗忘门(图 1)。
|
图 1 LSTM模型示意图 |
图 1中:it为输入门,由前一时刻的短期记忆ht-1和当前输入xt经激活函数σ计算得到;ft为遗忘门,决定丢弃哪些信息;ot为输出门,输出当前隐态结果;
利用上述结构,在各时间点t都可得到对应的隐藏层状态序列,从而获得每一个时间步输出的结果。由于LSTM网络只能单方向地处理数据,无法考虑缺失点后面数据的影响。另外,模型缺乏鲁棒性,使用过程无法利用当前井补全的缺失曲线和已知曲线作为新的输入,来补全剩余缺失曲线,且无法充分考虑当前井曲线之间相关性。
1.2 双向长短时记忆网络在实际测井时,采样间隔往往较小,通常可低至0.1m。然而从地层角度而言,不同深度地层之间相互影响的范围高达30m,甚至50m[22]。因此,每个数据点周围相互有影响的范围包含数据点可多达240~400个,不仅包括当前地层以上部分,还包括当前地层以下部分,这就意味着测井曲线重构是典型的具有长期双向(空间)相关性的序列数据分析问题。相对LSTM模型,Bi-LSTM模型更适合处理这类问题。为了将当前地层以下的测井数据信息的影响考虑到建模中,本文使用Bi-LSTM网络,它由一个前向LSTM模型与一个后向LSTM模型连接组成。作为时序相反的两个LSTM网络,前向LSTM网络可获取缺失序列之前储层段的信息,后向LSTM网络可获取缺失序列之后储层段的信息。该模型能从前、后两方面充分提取上、下储层段的信息,从而提高模型效果。
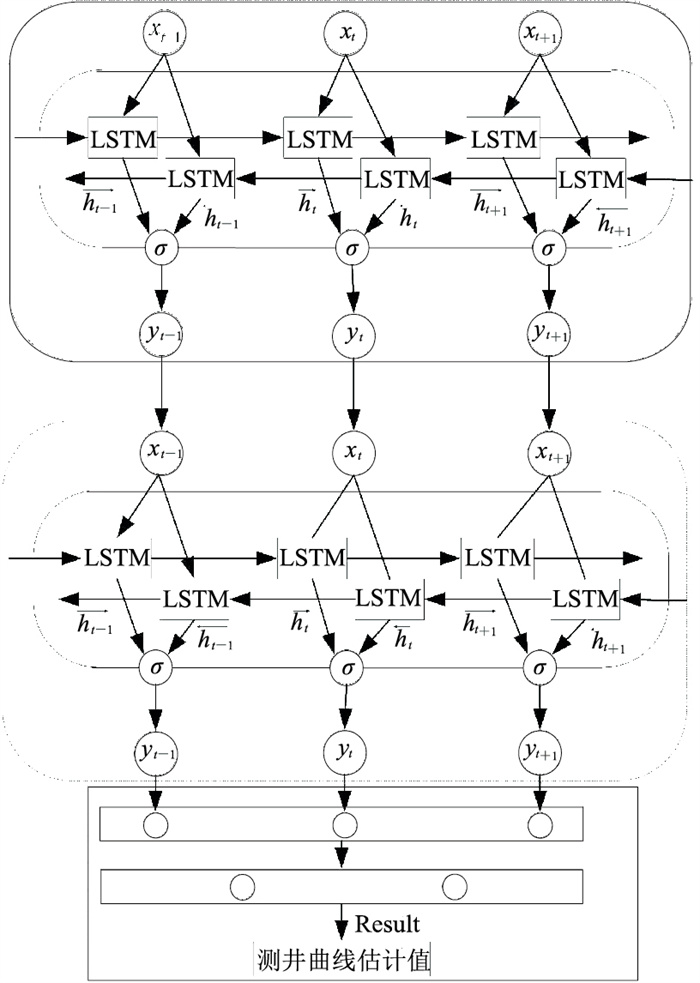
图 2为Bi-LSTM模型示意图,从中可看出Bi-LSTM网络是由两层LSTM网络组成:第一层认左边作为起始输入,在测井曲线重构时可理解成从当前采样点前一段序列开始输入;第二层是认右边作为起始输入,在测井曲线重构时可理解成从当前采样点后一段序列作为输入,反向开展与第一层相同的处理。此时,yt-1、yt及yt+1为前、后两个LSTM网络共同作用的结果。

|
图 2 Bi-LSTM模型示意图 |
在将Bi-LSTM网络应用到测井曲线数据的重构过程中,虽然Bi-LSTM网络完美地解决了LSTM网络只能按照从前到后的顺序处理数据,无法融合后序数据信息的问题,但模型缺乏灵活性。模型一旦训练完成,在补全过程中无法进行优化,且未能利用当前井补全的测井曲线数据继续补全剩余曲线,导致模型缺乏适应性。
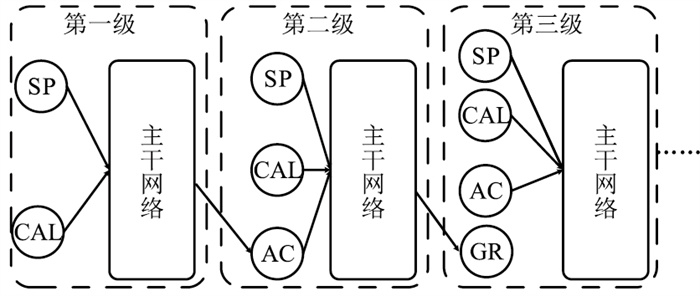
1.3 串级双向长短时记忆神经网络针对Bi-LSTM网络存在的问题,提出了CBi-LSTM网络,其原理如图 3所示。
|
图 3 CBi-LSTM测井曲线重构模型框架 |
CBi-LSTM网络模型借鉴串级控制系统思想,每次补全缺失曲线中的一条。在第一级,利用完整的测井曲线自然电位(SP)和井径(CAL)测井数据完成缺失曲线声波时差(AC)的补全;在第二串级将补全的AC与已知的SP及CAL测井曲线结合,作为新的输入,补全自然伽马(GR)缺失曲线;最后,完成所有缺失曲线的重构。
可看出使用串级控制系统思想有以下优点。
(1) 每次只补全缺失的一条曲线,减少了待重构曲线之间的相互干扰。
(2) 提高模型的输入兼容性。在每一级,可将补全的数据和已知数据进行合并作为新的输入,利用当前井补全的测井曲线数据继续补全剩余曲线中的一条,进一步提高了模型的适应性。
(3) 模型训练完成后,可从中间步直接进行下一条缺失曲线的重构。
(4) 补全过程中,网络共享各级的重构数据,每级只保留当前级预测数据,避免了数据冗余。
在引入串级系统的基础上,对其中主干网络结构进行改进,特征提取使用两层Bi-LSTM网络,并增加三层全连接层,进一步增强模型的表达能力。主干网络结构如图 4所示,采用两个隐状态分别为80和100维的Bi-LSTM网络和三层全连接层,采用丢弃操作,概率为30%。
|
图 4 主干网络结构框架 xt为t时刻输入,t时刻输出yt由前输出 |
当前串级计算过程如下:
(1) 向前计算t时刻的输出
| $ \overrightarrow{i_t}=\sigma\left(\overrightarrow{w_i} x_t+\vec{w}_i \overrightarrow{h_{t-1}}+\vec{b}_i\right) $ | (1) |
| $ \overrightarrow{f_t}=\sigma\left(\overrightarrow{w_f} x_t+\overrightarrow{w_f} \overrightarrow{h_t}+\overrightarrow{b_f}\right) $ | (2) |
| $ \overrightarrow{o_t}=\sigma\left(\overrightarrow{w_o} x_o+\overrightarrow{w_o} \overrightarrow{h_{t-1}}+\overrightarrow{b_o}\right) $ | (3) |
| $ \overrightarrow{\widetilde{c}_t}=\tanh \left(\overrightarrow{w_c} x_t+\overrightarrow{w_c} \overrightarrow{h_{t-1}}+\overrightarrow{b_c}\right) $ | (4) |
| $ \overrightarrow {{c_t}} = \overrightarrow {{f_t}} *\overrightarrow {{c_{t - 1}}} + \overrightarrow {{i_t}} *\overrightarrow {{{\tilde c}_t}} $ | (5) |
| $ \overrightarrow {{h_t}} = \overrightarrow {{o_t}} *\tanh \left( {\overrightarrow {{c_t}} } \right) $ | (6) |
式中
(2) 向后计算t时刻的输出
| $ \overleftarrow{i_t}=\sigma\left(\overleftarrow{w_i}x_t+\overleftarrow{w_i} \overleftarrow{h_{t-1}}+\overleftarrow{b_i}\right) $ | (7) |
| $ \overleftarrow{f_t}=\sigma\left(\overleftarrow{w_f} x_t+\overleftarrow{w_f} \overleftarrow{h_t}+\overleftarrow{b_f}\right) $ | (8) |
| $ \overleftarrow{o_t}=\sigma\left(\overleftarrow{w_0}x_0+\overleftarrow{w_0} \overleftarrow{h_{t-1}}+\overleftarrow{b_o}\right) $ | (9) |
| $ \overleftarrow {{{\tilde c}_t}} = \tanh \left( {\overleftarrow {{w_c}} {x_t} + \overleftarrow {{w_c}} \overleftarrow {{h_{t - 1}}} + \overleftarrow {{b_c}} } \right) $ | (10) |
| $ \overleftarrow {{c_t}} = \overleftarrow {{f_t}} *\overleftarrow {{c_{t - 1}}} + \overleftarrow {{i_t}} *\overleftarrow {{{\tilde c}_t}} $ | (11) |
| $ \overleftarrow {{h_t}} = \overleftarrow {{o_t}} *\tanh \left( {\overleftarrow {{c_t}} } \right) $ | (12) |
式中
(3) 将t时刻前向
| $ y_t\left(\overrightarrow{h_t}, \overleftarrow{h_t}\right)=\left[\begin{array}{c} \overrightarrow{h_1} \\ \overrightarrow{h_2} \\ \vdots \\ \overrightarrow{h_n} \end{array}\right] \odot\left[\begin{array}{c} \overleftarrow{h_1} \\ \overleftarrow{h_2} \\ \vdots \\ \overleftarrow{h_n} \end{array}\right]=\left[\begin{array}{c} \overrightarrow{h_1} \overleftarrow{h_1} \\ \overrightarrow{h_2} \overleftarrow{h_2} \\ \vdots \\ \overrightarrow{h_n} \overleftarrow{h_n} \end{array}\right] $ | (13) |
(4) 完成两个隐状态计算结果后,将结果转化成一维数据(yt)并传入全连接层进行计算,过程为
| $ \operatorname{Net}_i=\sum\limits_{i=1}^n w_{l 1} * y_i $ | (14) |
| $ \operatorname{result}_i=f\left(\mathrm{Net}_i\right) $ | (15) |
| $ E_k=\frac{1}{2} \sum\limits_{i=1}^n\left(\text {result}_i-\text {result}_{\mathrm{r}}\right)^2 $ | (16) |
式中:Neti为激活函数f的输入;wl1和wl2为全连接层待训练权重;resulti为预测值;resultr为真实值。然后利用均方误差Ek更新参数,优化网络。
(5) 最后传入曲线的预测所缺失的值resulti。到下一级并和已知数据合并为新的输入预测剩余缺失曲线中的一条,重复上述计算过程。
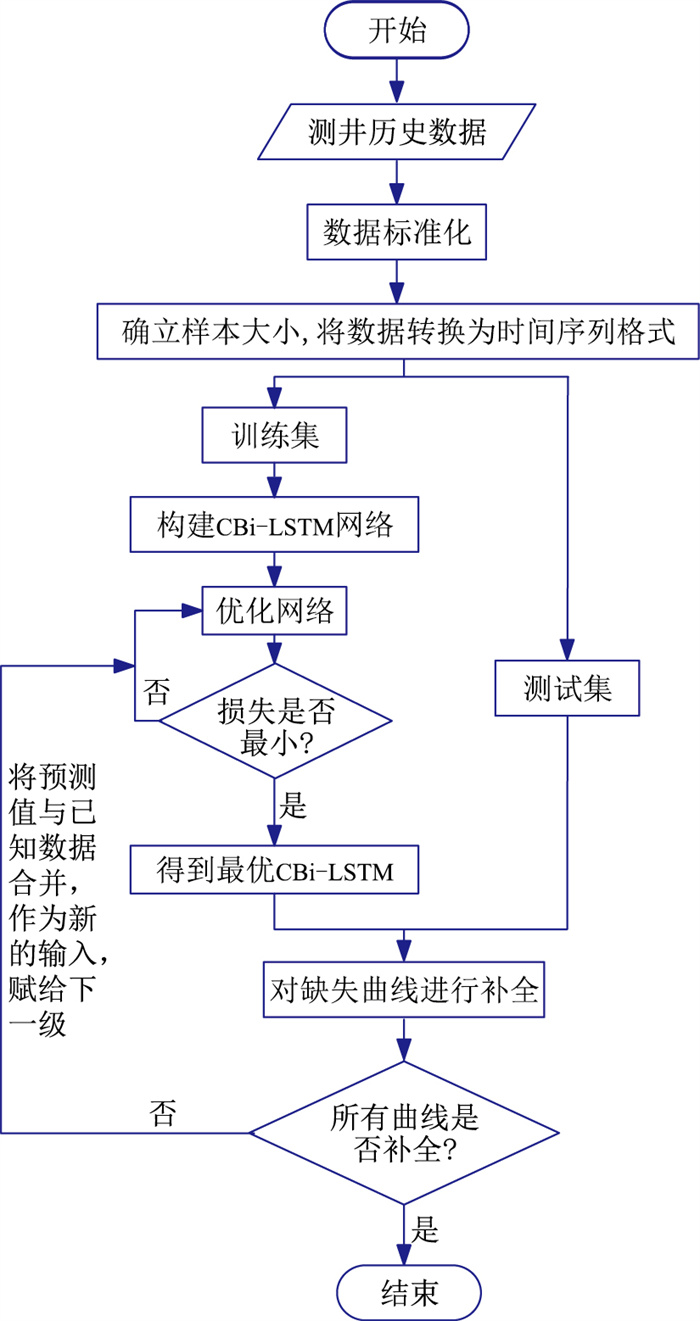
在CBi-LST网络结构中,首先根据已知测井曲线训练模型估计未知测井曲线中的1条,然后将获得的估计值与已知测井曲线合并为新的输入,作为下一级的输入,再据此输入估计剩余未知测井曲线中的1条。缺失曲线重构过程如图 5所示。
|
图 5 曲线重构流程图 |
采用苏里格气田4口直井测井数据开展实验。这些井都记录了多种测井数据,如AC、CAL、CNL(补偿中子)、GR、SP、TH(放射性钍)、U(铀)、K(钾)等。为了验证模型对测井数据的重构能力,实验基于留一法补充相关文献,即进行四次实验,每次实验将一口井作为实验,其余三口井作为训练数据,对模型进行训练,最终用模型生成实验井的测井曲线。
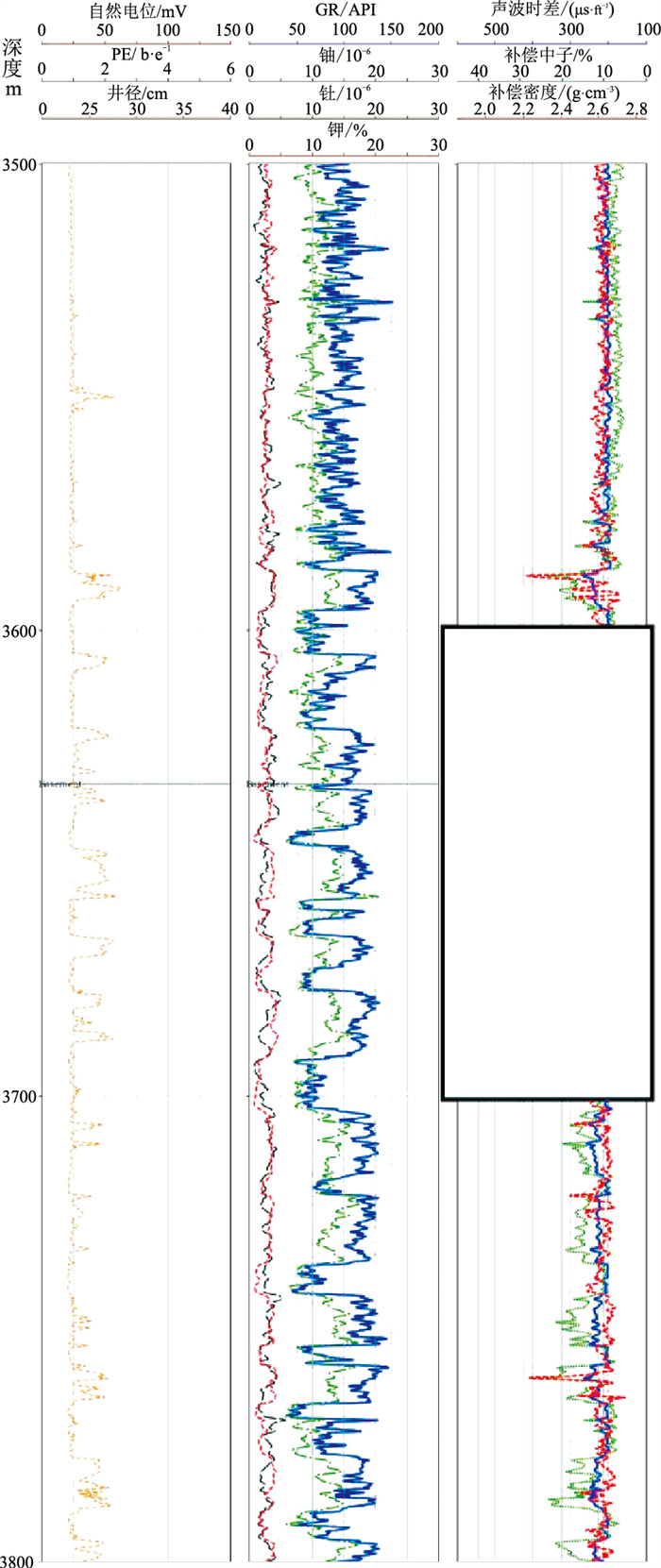
实验中直井的探测深度为3300~3800m,对应该深度范围的AC和GR测井曲线被人工删除,用于模拟缺失部分的测井曲线(图 6)。
|
图 6 测井曲线缺失图 |
本次实验中,数据的采样间隔为0.125m。从地层角度而言,不同深度地层之间相互可产生影响的深度范围可高达30m,甚至50m。因此,在测井问题中,每个数据点周围相互有影响的范围包含的数据点可多达240~400个。因此,网络模型中每个训练样本的序列长度设置为240。最终制作的训练集一共有20000组训练数据,每组数据的序列长度为240,用于补全3300~3800m深度区间缺失的测井数据。模型第一级输入变量为CAL、SP,输出为AC;第二级输入变量为CAL、SP、AC,输出为GR。
2.2 模型评估指标CBi-LSTM网络模型属于回归模型的一种,采用均方误差(MSE)、均方根误差(RMSE)及平均绝对误差(MAE)作为模型的评估标准。MSE是指参数估计值与参数真实值之差点期望值,可用于评价数据点变化程度,MSE值越小,则模型预测结果越精确。RMSE用于衡量数据的波动性,RMSE值越小,则模型的泛化能力和稳定性就越强。MAE是计算每一个样本的预测值与真实值的差的绝对值,然后求和再取平均值。用于评估预测结果与真实数据集的接近程度,其值越小说明拟合效果越好。计算公式如下
| $ \mathrm{MSE}=\frac{1}{N} \sum\limits_{i=1}^N\left(\text { result}_i-\text { result}_{\mathrm{r}}\right)^2 $ | (17) |
| $ \mathrm{RMSE}=\sqrt{\frac{1}{N} \sum\limits_{i=1}^N\left(\text { result}_i-\text { result}_{\mathrm{r}}\right)^2} $ | (18) |
| $ \mathrm{MAE}=\frac{1}{N} \sum\limits_{i=1}^N \mid\left(\text { result}_i-\text { result}_{\mathrm{r}}\right)^2 \mid $ | (19) |
每口井都有多组测井曲线,在构建模型之前需对测井曲线做相关性分析。使用统计学中的皮尔逊相关系数度量两个变量之间的相关性程度,各条测井曲线的响应值看成一个矩阵。以AC和GR为例,其对应矩阵命名为XAC及XGR,则平均值为
| $ \begin{aligned} & r\left(X_{\mathrm{AC}}, X_{\mathrm{GR}}\right)= \\ & \ \ \frac{\sum\limits_{i=1}^n\left(X_{\mathrm{AC}}, i-\bar{X}_{\mathrm{AC}}\right)\left(X_{\mathrm{GR}}-\bar{X}_{\mathrm{GR}}\right)}{\left[\sum\limits_{i=1}^n\left(X_{\mathrm{AC}}, i-\bar{X}_{\mathrm{AC}}\right)^2 \sum\limits_{j=1}^n\left(X_{\mathrm{GR}}-\bar{X}_{\mathrm{GR}}\right)^2\right]^{1 / 2}} \end{aligned} $ | (20) |
式中:n为每列的长度;r(XAC,XGR)为曲线XAC与XGR的相关系数,范围是-1~1,其中1表示完全正相关,-1表示完全负相关,0表示两属性无关。
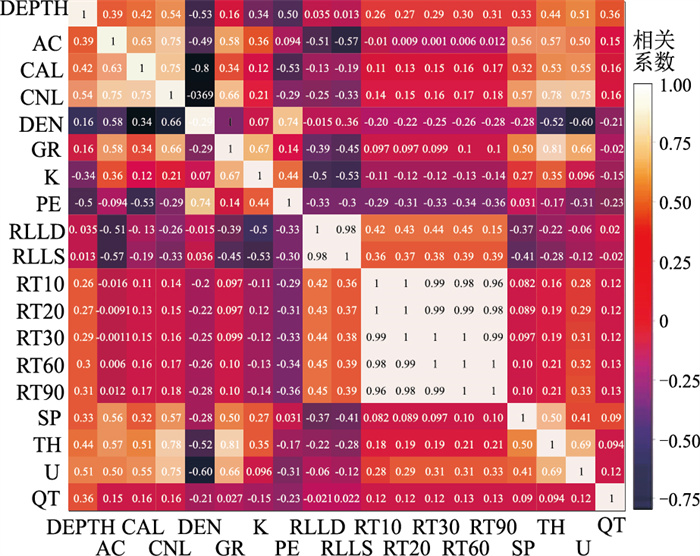
图 7为19条测井曲线之间的相关系数计算结果。从该图可见:对AC影响较大的有CAL、GR、SP等,且相关系数大于0.5;对GR影响较大的有AC、CAL、SP等。
|
图 7 测井曲线相关度热力图 文中未提及测井简称:DEN,密度;PE,有效光电吸收截面指数;RLLD,深侧向;RLLS,浅侧向;RT**,地层电阻率;QT,总流量 |
对于非地层因素CAL,在实际钻井过程中,CAL会因为地层地质的变化发生形变:砂岩质地坚硬,在钻井钻头经过后由于弹性形变会恢复原来形状,造成井径缩小(缩径);泥岩质地疏松,会发生井壁垮塌并造成井径扩大(扩径)。因此,井径是判断地下岩石岩性的重要参数之一。
所以,在地层数据发生变化时,采集到的井径数据会由于地层地质数据的变化而变化。因此,把CAL作为辅助因素与地层数据进行合并,作为新的数据进行测井实验。
3 实验对比分析 3.1 模型重构结果分析为了对比每一种算法重构测井曲线的能力,分别建立了基于LSTM、Bi-LSTM及改进的CBi- LSTM网络的重构测井曲线重构模型。对训练数据做归一化处理并采用了批训练方法。批尺寸设置为200,即每次选取200组训练数据。训练样本长度均为240。为充分验证每一种模型对测井曲线缺失部分重构的能力,分别对每种模型进行4次实验,每次实验任选1口井进行测试。
为分析LSTM、Bi-LSTM及CBi-LSTM网络生成的人工测井曲线的效果,对4口井中预测结果最好的A1井的人工曲线进行绘制(图 8)。
|
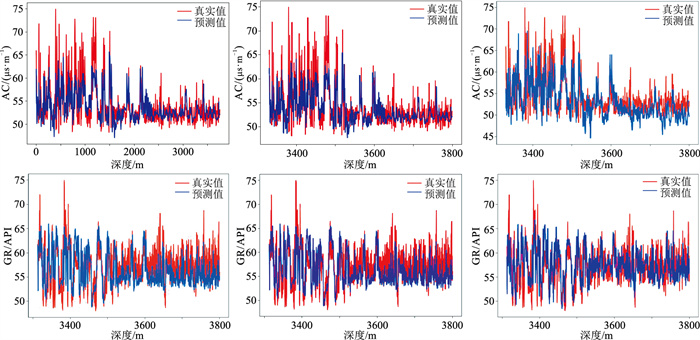
图 8 基于LSTM (左)、Bi-LSTM(中)和CBi-LSTM(右)网络生成的A1井的声波时差(上)、自然伽马(下)测井曲线 |
观察三种方法得到的缺失AC曲线和GR曲线的重构结果(图 8),可见在A1井3300~3460m深度范围(图 8上),随着模型的不断改进,AC拟合曲线(蓝线)与参照曲线(红线)之间的误差逐渐变小,两条曲线的走势基本吻合。接着观察A1井3600~3800m范围的GR曲线(图 8下),对比可知,在3600~3650m区间,红线呈现阶跃式变化。常规LSTM网络及Bi-LSTM网络在3600~3650m区间都无法准确预测目标曲线的趋势变化,而所提CBi-LSTM网络模型却能准确地拟合出目标曲线的变化趋势。
通过分析图 8中测井曲线重构结果,可知本文的CBi-LSTM网络能综合分析预测点前的数据和预测点输入的影响,弥补了LSTM网络及Bi-LSTM网络在进行测井曲线重构过程中存在的不足,准确预测出目标曲线的趋势性变化。因此,本文的CBi-LSTM网络对于测井曲线这种序列数据具有更好的重构能力。
3.2 模型结果量化分析为了量化评价LSTM、Bi-LSTM及本文的CBi-LSTM三种模型重构测井曲线的能力,针对苏里格气田4口直井采用此三种模型进行对比实验。基于皮尔逊算法对测井曲线进行特征分析,利用与AC和GR相关性高的测井曲线分别对AC和GR进行数据重构,并对重构结果进行量化评估。
表 1展示了三种方法测井曲线的估计值的均方误差、均方根误差及绝对值差。由表 1可知,首先利用LSTM网络重构测井曲线并取得较好效果,但还存在上述两点缺陷。因此引入Bi-LSTM网络构建出考虑测井曲线的变化趋势即上下数据相关关系的数据重构模型,并将实验结果量化。通过对比表 1中的数据可见,Bi-LSTM网络整个模型鲁棒性和泛化能力比LSTM网络更稳定。但针对第二个问题,仍然无法解决。因此,为了进一步提高模型的灵活性及适应性,将串级系统与Bi-LSTM网络相结合,利用本文的CBi-LSTM网络对测井曲线进行了重构,通过对比表 1量化数据可知,本文的网络模型取得了更好的成绩。不仅如此,整个模型的鲁棒性和泛化能力不仅得到了提高,而且模型在曲线重构的过程中,具有了动态优化及自适应动态重构测井曲线的能力。
|
|
表 1 不同模型生成人工测井曲线模型数据评估 |
本文提出一种基于改进CBi-LSTM神经网络的测井数据重构方法。将Bi-LSTM与串级系统相结合,通过利用Bi-LSTM网络提取缺失数据前后序列数据的关键特征信息对缺失数据点进行预测,然后将获得的估计值与已知测井曲线合并为新的输入,采用串级更新策略完成对缺失数据块的重构。充分考虑当前井测井曲线之间相关性,提高了模型的适应性及灵活性。针对苏里格气田4口井测井数据进行处理重构,并与LSTM和Bi-LSTM模型做对比分析,结果表明改进的CBi-LSTM模型对测井数据具有更高重构精度。
| [1] |
何旭, 李忠伟, 刘昕, 等. 应用卷积神经网络识别测井相[J]. 石油地球物理勘探, 2019, 54(5): 1159-1165. HE Xu, LI Zhongwei, LIU Xin, et al. Log facies re-cognition based on convolutional neural network[J]. Oil Geophysical Prospecting, 2019, 54(5): 1159-1165. DOI:10.13810/j.cnki.issn.1000-7210.2019.05.024 |
| [2] |
张岩, 李新月, 王斌, 等. 基于深度学习的鲁棒地震数据去噪[J]. 石油地球物理勘探, 2022, 57(1): 12-25. ZHANG Yan, LI Xinyue, WANG Bin, et al. Robust seismic data denoising based on deep learning[J]. Oil Geophysical Prospecting, 2022, 57(1): 12-25. |
| [3] |
匡立春, 刘合, 任义丽, 等. 人工智能在石油勘探开发领域的应用现状与发展趋势[J]. 石油勘探与开发, 2021, 48(1): 1-11. KUANG Lichun, LIU He, REN Yili, et al. Application and development trend of artificial intelligence in petroleum exploration and development[J]. Petroleum Exploration and Development, 2021, 48(1): 1-11. |
| [4] |
韩明亮, 邹志辉, 马锐. 利用反射地震资料和多尺度训练集的深度学习速度建模[J]. 石油地球物理勘探, 2021, 56(5): 935-946. HAN Mingliang, ZOU Zhihui, MA Rui. Deep lear-ning-driven velocity modeling based on seismic reflection data and multi-scale training sets[J]. Oil Geophysical Prospecting, 2021, 56(5): 935-946. |
| [5] |
常德宽, 雍学善, 王一惠, 等. 基于深度卷积神经网络的地震数据断层识别方法[J]. 石油地球物理勘探, 2021, 56(1): 1-8. CHANG Dekuan, YONG Xueshan, WANG Yihui, et al. Seismic fault interpretation based on deep convolutional neural networks[J]. Oil Geophysical Prospecting, 2021, 56(1): 1-8. |
| [6] |
HE S M, LIU L W. Using the improved genetic BP neural network algorithm for lithologic identification[J]. Advanced Materials Research, 2014, 1037: 389-392. |
| [7] |
LUO H, LAI F Q, DONG Z, et al. A lithology identification method for continental shale oil reservoir based on BP neural network[J]. Journal of Geophy-sics and Engineering, 2018, 15(3): 895-908. |
| [8] |
刘为付, 朱筱敏. 利用模糊数学识别鄂尔多斯盆地气藏岩性[J]. 断块油气田, 2005, 12(5): 7-9. LIU Weifu, ZHU Xiaomin. Identifying lithology of natural gas pool by fuzzy mathematics in Ordos basin[J]. Fault-block Oil & Gas Field, 2005, 12(5): 7-9. |
| [9] |
李洪奇, 谭锋奇, 许长福, 等. 基于决策树方法的砾岩油藏岩性识别[J]. 测井技术, 2010, 34(1): 16-21. LI Hongqi, TAN Fengqi, XU Changfu, et al. Lithology identification of conglomerate reservoir based on decision tree method[J]. Well Logging Technology, 2010, 34(1): 16-21. |
| [10] |
DENG C X, PAN H P, FANG S N, et al. Support vector machine as an alternative method for lithology classification of crystalline rocks[J]. Journal of Geophysics and Engineering, 2017, 14(2): 341-349. |
| [11] |
周游, 张广智, 高刚, 等. 核主成分分析法在测井浊积岩岩性识别中的应用[J]. 石油地球物理勘探, 2019, 54(3): 667-675. ZHOU You, ZHANG Guangzhi, GAO Gang, et al. Application of kernel principal component analysis in well logging turbidite lithology identification[J]. Oil Geophysical Prospecting, 2019, 54(3): 667-675. |
| [12] |
ZHENG J, LIU J R, PENG S P, et al. An automatic microseismic or acoustic emission arrival identification scheme with deep recurrent neural networks[J]. Geophysical Journal International, 2018, 212(2): 1389-1397. |
| [13] |
XIE Y X, ZHU C Y, ZHOU W, et al. Evaluation of machine learning methods for formation lithology identification: A comparison of tuning processes and model performances[J]. Journal of Petroleum Science and Engineering, 2018, 160: 182-193. |
| [14] |
JAIN G, SHARMA M, AGARWAL B. Spam detection in social media using convolutional and long short term memory neural network[J]. Annals of Mathematics and Artificial Intelligence, 2019, 85(1): 21-44. |
| [15] |
LI H, MISRA S. Long short-term memory and variational autoencoder with convolutional neural networks for generating NMR T2 distributions[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 16(2): 192-195. |
| [16] |
PALANGI H, DENG L, SHEN Y L, et al. Deep sentence embedding using long short-term memory networks: analysis and application to information retrie-val[J]. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2016, 24(4): 694-707. |
| [17] |
ATEF S, ELTAWIL A B. Assessment of stacked unidirectional and bidirectional long short-term me-mory networks for electricity load forecasting[J]. Electric Power Systems Research, 2020, 187(5): 106489. |
| [18] |
BHASKAR N, SUCHETHA M, PHILIP N Y. Time series classification-based correlational neural network with bidirectional LSTM for automated detection of kidney disease[J]. IEEE Sensors Journal, 2021, 21(4): 4811-4818. |
| [19] |
周雪晴, 张占松, 朱林奇, 等. 基于双向长短时记忆网络的流体高精度识别新方法[J]. 中国石油大学学报(自然科学版), 2021, 45(1): 69-76. ZHOU Xueqing, ZHANG Zhansong, ZHU Linqi, et al. A new method for high-precision fluid identification in bidirectional long short-term memory network[J]. Journal of China University of Petroleum (Edition of Natural Science), 2021, 45(1): 69-76. |
| [20] |
周欣, 曹俊兴, 王兴建, 等. 基于双向门控循环单元神经网络的声波测井曲线重构技术[J]. 地球物理学进展, 2022, 37(1): 357-366. ZHOU Xin, CAO Junxing, WANG Xingjian, et al. Acoustic log reconstruction based on bidirectional gated recurrent unit neural network[J]. Progress in Geophysics, 2022, 37(1): 357-366. |
| [21] |
王俊, 曹俊兴, 周欣. 基于深度双向循环神经网络的储层孔隙度预测[J]. 地球物理学进展, 2022, 37(1): 267-274. WANG Jun, CAO Junxing, ZHOU Xin. Reservoir porosity prediction based on deep bidirectional recurrent neural network[J]. Progress in Geophysics, 2022, 37(1): 267-274. |
| [22] |
陈云天. 基于机器学习的测井曲线补全与生成研究[D]. 北京: 北京大学, 2020. CHEN Yuntian. Research on Well Log Completion and Generation Based on Machine Learning[D]. Peking University, Beijing, 2020. |



 周伟, 重庆市沙坪坝区大学城东路20号重庆科技学院智能技术与工程学院,401331。Email:
周伟, 重庆市沙坪坝区大学城东路20号重庆科技学院智能技术与工程学院,401331。Email: