中国陆相油田大多处于特高含水开发阶段,剩余油分布极度零散,高效挖潜难度大,储层描述的重点是搞清楚不同类型砂体的井间分布特征及相互接触关系,进而为剩余油精确描述、挖潜措施调整及不同井网综合利用提供数据基础,而高精度三维地质建模是陆相储层精细表征的重要手段之一[1-2]。大量研究结果表明,由地质模式指导、井信息控制的砂体三维表征是决定地质模型精度的关键因素[3-6]。因此,地质模式约束的多点地质统计学模拟方法越来越受到关注,主要集中在理论研究和方法试验阶段,并初步用于勘探与开发过程[7-10],并获得了一定的效果。
多点地质统计学方法是为弥补传统两点地质统计学方法在储层表征中的不足而产生的建模方法。传统两点地质统计学建模方法通过变差函数描述储层两点间的关系,而无法精细模拟陆相复杂地质体。多点地质统计学方法采用“训练图像”替代变差函数描述地质体的空间分布特征,在建模过程中通过训练图像模拟目标地质体的尺寸、形状及其空间组合关系等,相当于将沉积模式认识融入建模运算过程,因此能够精细表征不同沉积环境地质体的特征[11-12]。为满足油田生产对地质建模的需求,在理论研究方面,人们通过建立从训练图像获取信息并用于模拟过程的高效算法,保证了建模效率和效果满足储层模拟需求。在应用方面,将储层特点与建模原理相结合,应用类比、目标体模拟等方法获取训练图像,采用分区、分级等建模策略表征不同类型储层。同时,为降低模型不确定性,充分利用地震数据体空间密集采样的特点,开展地震约束建模,将地震属性体、反演体加入模型模拟和优选过程,并根据井震数据匹配程度、模型地质特征等信息确定约束权重与最优成果,进而提高模型精度[13]。然而,陆相油田储层强非均质特点及深度开发油田储层预测精度较高的要求增加了建模难度。因此,陆相河流—三角洲相特征训练图像的建立以及建模过程中地震资料的有效利用仍是限制多点地质统计学方法在油田开发中规模应用的重要原因。
本文以陆相大庆长垣油田BGX区块为研究对象,建立了长垣油田河流—三角洲相典型河道的5种训练图像模式,在此基础上形成了以地震反演为约束、密井网控制的井震结合多点地质统计学方法,建立了BGX区块高精度储层三维模型,并在剩余油挖潜中得到规模应用,展现了该方法较大的应用前景。
1 研究区概况BGX区块位于大庆长垣油田北部,面积约为20km2,有2100余口油水井。目的层萨二(SⅡ)油层组主要为三角洲分流平原和内前缘相沉积,主要发育水上、水下分流河道砂体,河道砂体宽度为200~600m,垂向厚度为2~5m,河道规模较小,非均质性严重。2007年采集的高密度地震资料的面元为10m×10m,主频约为45Hz,频带宽度为6~80Hz。地震资料品质较好,为开展井震结合多点地质统计学三维建模研究及应用提供了较好的数据基础。
大庆长垣油田主力产层萨(S)、葡(P)、高油层属大型河流—三角洲的砂、泥岩薄互层沉积,砂体规模小,纵向划分为100多个沉积单元。经过60多年持续开采,已进入特高含水、密井网、细分层开采阶段。油层深度为700~1100m,沉积总厚度约为380m,划分为8个油层组,包含35个砂岩组,细分为114个沉积单元(图 1)。
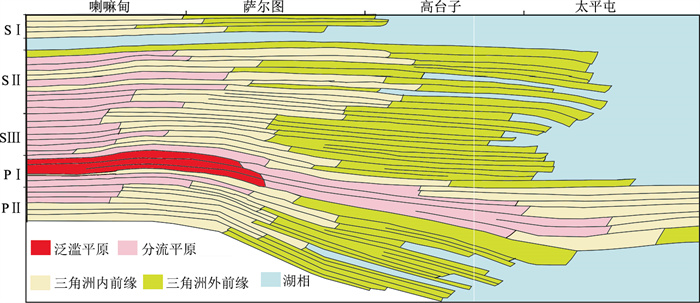
|
图 1 大庆长垣河流—三角洲相砂体发育模式(部分油层) |
传统两点地质统计学以变差函数为主要建模工具,变差函数描述了空间两点间的相关性。多点地质统计学是为了弥补仅用两点描述空间元素的相关性的不足而提出的,表达了多个点间的相关性,并用数据事件表述这一概念。假设dn={L(uα)=Lkα, α=1, 2, …,n}为以u为中心、n个已知点确定的几何形态(数据样板)及相应的数值构成的数据事件,对于k类岩相Lk(k=1, 2, …, n),由多点地质统计学得到dn出现的概率为P{dn},即数据点L(u1), L(u2), …, L(un)分别为Lk1, Lk2, …Lkn时的概率P{L(uα)},也即为n个数据指示值I(uα; kα)乘积的期望,即
| $ \begin{aligned} P\left\{d_n\right\} & =P\left\{L\left(u_\alpha\right)=L_{k_\alpha}, \alpha=1, \cdots, n\right\} \\ & =E\left[\prod\limits_{\alpha=1}^n I\left(u_\alpha ; k_\alpha\right)\right] \end{aligned} $ | (1) |
图 2为多点地质统计建模示意图。由图可见,在储层建模过程中,难以利用井信息获取上述概率,只能采用扫描训练图像的方式获取待估点的条件概率分布函数。利用给定的样板数据扫描训练图像,通过分析样本数据在训练图像中的重复率确定未知点u处为不同岩相出现的概率。当用定义的数据样板(图 2a)扫描训练图像(图 2b)时,总共得到7次重复,其中未知点为河道的重复5次,未知点为非河道的重复2次,则未知点为河道的概率等于5/7(0.7143),未知点为非河道的概率等于2/7(0.2857)。
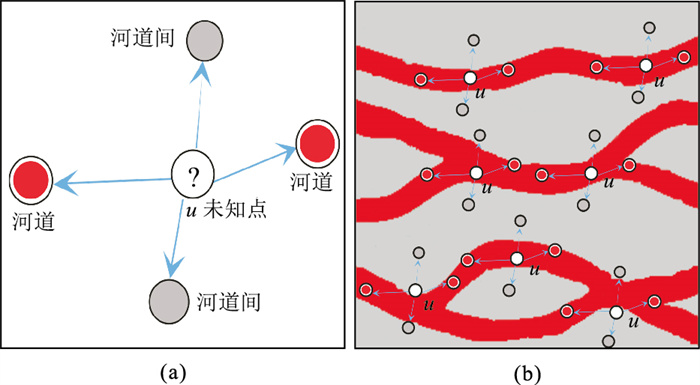
|
图 2 多点地质统计建模示意图 (a)数据样板;(b)训练图像 |
反演约束的多点地质统计学建模流程如下:首先,建立三维网格模型训练图像,并按某个随机路径确定一个以待估点为中心的数据样板,用数据样板扫描训练图像获得待估点的条件概率分布函数;然后,从待估点处的条件概率分布函数获取一个值作为待估点的模拟值;最后,将获得的模拟值作为已知点,沿先前的随机路径进入下一个待估点进行模拟,直至完成所有节点的模拟,从而建立初始模型。在上述过程中,利用地震波阻抗反演结果约束初始模型并反复迭代模型,直至模型结果符合反演结果的趋势,从而提高最终模型精度(图 3)。
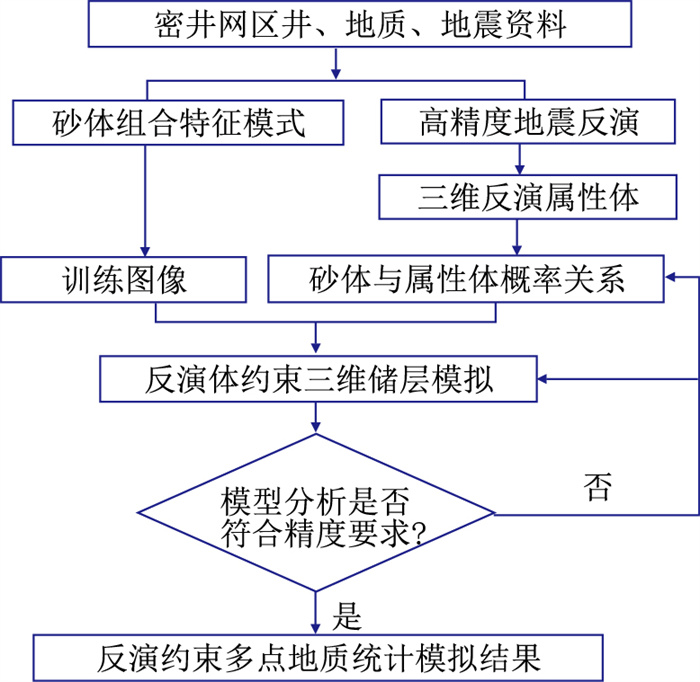
|
图 3 反演约束的多点地质统计学建模流程 |
多点地质统计学通过扫描训练图像建模。训练图像是表达储层结构特征、几何形态及其分布形态的数字化图像,是一种先验的地质概念模式,是对砂体形态、类型及相互接触关系模式的概括[14-15]。因此,建模之前首先要研究砂体分布特征及组合模式,通过剖析密井网资料,建立适用于陆相河流—三角洲沉积体系的训练图像。
目的层河道砂体主要发育低弯曲、顺直型、网状型、枝状分叉型、单一连续型等5种沉积模式,根据不同的特征建立了3种分流河道砂体和2种非河道砂体平面组合模式(图 4)。其中,在三角洲平原环境中主要发育分叉枝状(图 4b)、交织网状(图 4c)的组合模式,在水下分流河道中主要以交织网状(图 4c)、孤立窄带(图 4a)的组合模式为主。对于分流间砂体,主要分为2种组合模式。根据砂体与河道的关系分为河间溢岸类、决口类和末端扇类(图 4d、图 4e)。溢岸类包括天然堤和溢岸砂,在河道两侧平行发育;决口类包括决口水道和决口扇,与河道斜交或垂直发育,当决口类砂体达到一定规模,可形成决口三角洲砂体组合模式;末端扇主要分布于河道末端,是在河流惯性作用下形成的末端扇状薄层砂体。在建模过程中,依据各单元具体的沉积特征确定不同的训练图像,从而确保模型结果能够反映不同沉积类型的砂体特征。
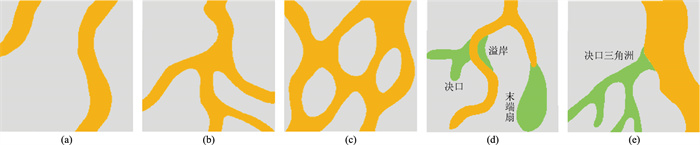
|
图 4 分流河道砂体和非河道砂体平面组合模式 (a)孤立窄带组合;(b)分叉枝状组合;(c)交织网状组合;(d) 河道与河间组合1;(e) 河道与河间组合2 |
利用地震反演三维数据体在三维空间密集分布、能反映地下储层信息的特性约束多点地质统计学建模过程,其中训练图像具有模式引导作用,地震反演数据控制使模型结果符合反演结果的趋势,从而提高最终模型的精度。
文中采用纵波阻抗波形指示反演方法,即基于井点处的纵波阻抗曲线与地震波形的相关性,以井间地震波形为指引,依据统计学规律实现纵波阻抗空间赋值,以建立纵波阻抗数据模型。其基本思想是在筛选统计样本时参照波形相似性和空间距离两个因素,在保证样本结构特征一致性的基础上按照分布距离对样本排序,从而使反演结果在空间上体现沉积相带的约束,在平面上更符合沉积规律和特点[16-21]。
具体步骤包括:①按照地震波形特征分析已知井数据,优选与待判别道波形关联度高的井样本建立初始模型,并统计其纵波阻抗作为先验信息;②将初始模型与地震频带阻抗进行匹配滤波,以计算似然函数;③在贝叶斯框架下联合似然函数分布和先验分布得到后验概率分布,并将其作为目标函数,通过不断扰动模型参数,使后验概率分布函数最大时的解作为有效的随机实现。通过以上过程增强反演结果低频段的确定性,同时约束了高频段的取值范围,使反演结果从完全随机到逐步确定。
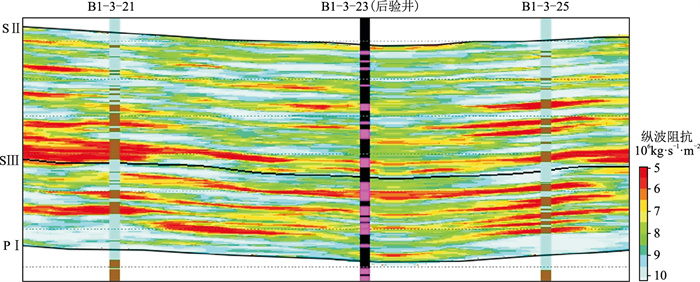
图 5为纵波阻抗反演剖面,可见其预测结果与井点(参与井、后验井)岩性结果一致,表明纵波阻抗反演结果的可靠性较高。
|
图 5 纵波阻抗反演剖面 纵波阻抗低值区指示砂岩,高值区指示泥岩 |
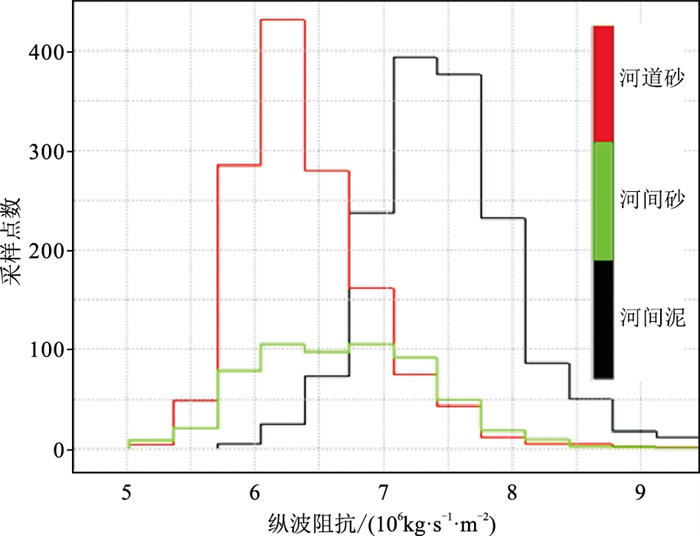
利用井点纵波阻抗曲线和沉积微相解释结果,明确了不同沉积微相的纵波阻抗特征(图 6),为地震反演约束的多点沉积微相建模提供了基础。利用高精度速度场,将反演数据体转换到深度域,并采样至三维地质网格模型,采用地震反演约束的多点建模方法,建立了BGX区块沉积微相三维地质模型(图 7)。
|
图 6 不同沉积微相的纵波阻抗特征 纵波阻抗低值指示河道砂体,纵波阻抗高值指示河间泥,河间砂的纵波阻抗值介于河道砂体和河间泥之间 |

|
图 7 BGX区块沉积微相三维地质模型 |
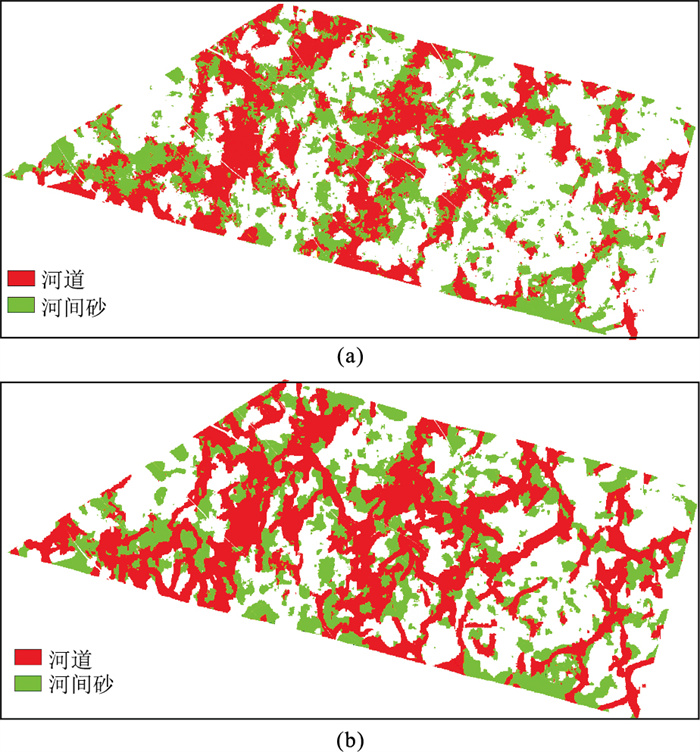
基于反演约束的多点地质统计学模型可以提取各单元的平面沉积相图。图 8为基于不同建模方法的SⅡ13+14b单元沉积微相。由图可见:序贯指示建模(图 8a)和多点地质统计建模(图 8b)的预测结果的整体趋势一致,河道砂体呈南北走向;在图 8a中局部砂体平面接触关系不清晰、砂体连续性较差,碎片化现象较严重;图 8b清晰地刻画了河道特征,展示了河道几何形态、宽度以及交汇方式,并且砂体的平面接触关系也较清楚。
|
图 8 基于不同建模方法的SⅡ13+14b单元沉积微相 (a)序贯指示建模;(b)多点地质统计学建模 |
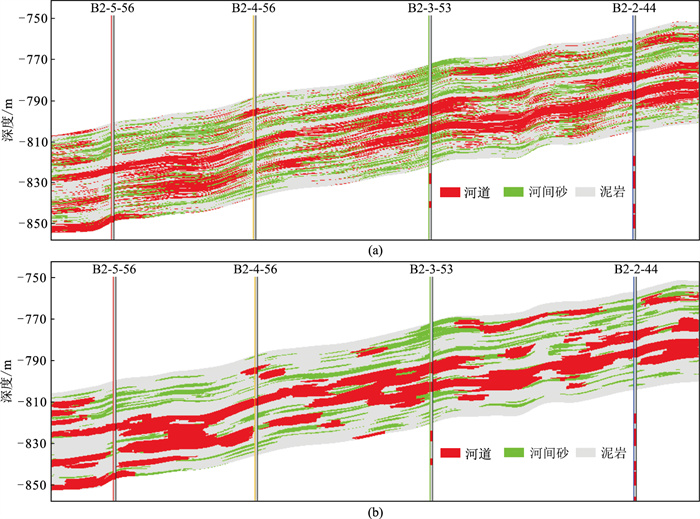
图 9为基于不同建模方法得到的储层沉积微相连井剖面。由图可见:序贯指示模拟结果(图 9a)的砂体垂向接触关系不清晰,不同砂体之间的连通关系不明确,不利于判断储层动用状况;多点地质统计学模拟结果(图 9b)较清晰地反映了不同砂体之间的连通部位、范围及其纵向组合关系。
|
图 9 基于不同建模方法得到的储层沉积微相连井剖面 (a)序贯指示建模;(b)多点地质统计学建模 |
为进一步对比、分析两点统计学和多点统计学建模方法的储层表征精度,利用无效网格砂体对模型进行统计分析。无效网格砂体定义:与其他砂体不接触、孤立的、相距大于50m的单个网格内的砂体,该砂体不是由沉积作用形成的,而是由建模算法本身的稳定性决定的。通过统计17个沉积单元的无效网格与单元网格总数的比值发现,多点地质统计学方法产生无效网格的数量明显少于序贯指示模拟方法(图 10)。
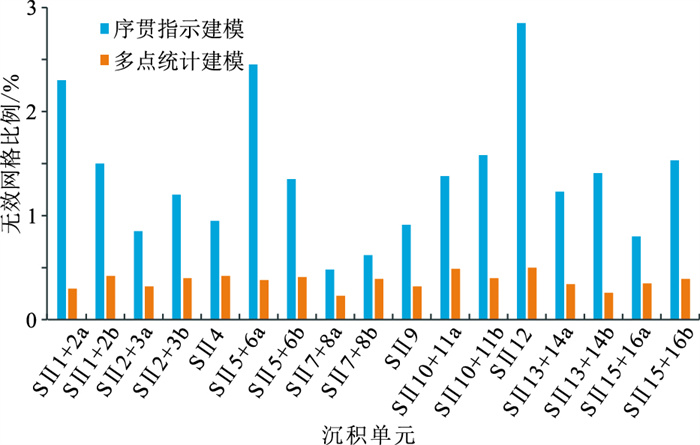
|
图 10 基于不同建模方法产生的无效网格统计 |
在BGX区块均匀选择45口后验井检验储层模型精度,但不参与序贯指示和多点地质统计学建模过程。从45口后验井中抽取17个单元(共361个数据点)进行统计,按厚度将河道分为3个级别(厚度分别小于2m、2~3m及大于3m),统计发现多点地质统计学模拟的河道砂体模型精度明显高于序贯指示模拟,河道砂体平均预测精度由79.6%提高至86.1%(图 11)。因此,基于反演约束的多点地质统计学模拟方法具有较高精度,在精细描述陆相油田砂体时较常规建模方法具有明显优势,可用于陆相老油田剩余油开发方案的编制。
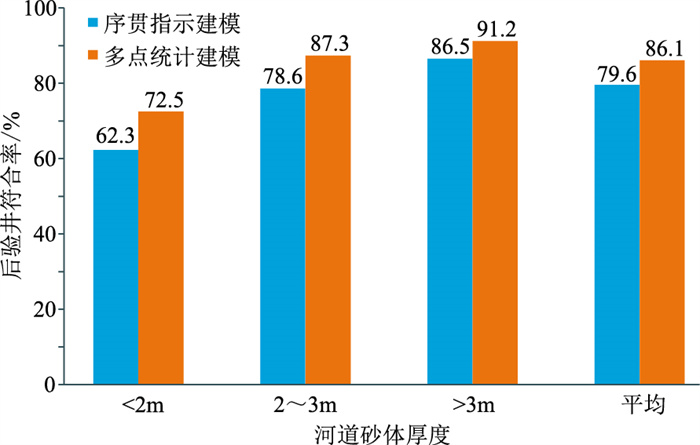
|
图 11 基于不同建模方法的河道砂体预测精度对比 |
目前陆相老油田普遍面临剩余油分布零散、挖潜难度大等问题,对井间砂体的描述精度要求高,通过反演约束的多点地质统计学建模,重新认识了砂体展布特征,结合注采关系,指导BGX区块剩余油开发方案编制。
图 12为基于不同建模方法得到的河道砂体分布特征图。由图可见,序贯指示模拟结果表明3-143井(注入井)与D4-37井(采出井)间的河道砂体不连通(图 12a),而反演约束的多点地质统计学模拟结果指示砂体注采连通,3-143井能够有效驱动D4-37井,在D4-37井周边的剩余油潜力较大。因此对D4-37井进行补孔,补孔后初期日增油4.1t,含水率下降5.2%,取得了较好的增油效果。
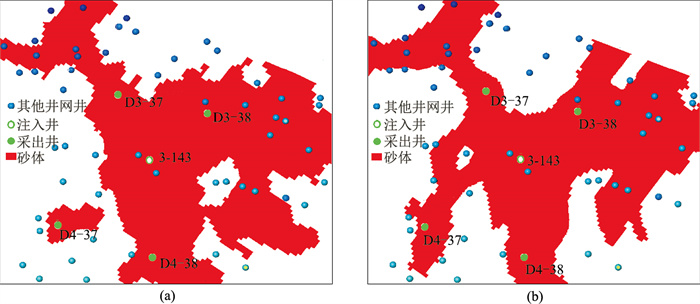
|
图 12 基于不同建模方法得到的河道砂体分布特征图 (a)序贯指示建模;(b)多点地质统计学建模 |
图 13为采用反演约束的多点地质统计学建模得到的过井剖面砂体分布图。由图可见,60-29井(注入井)与60-28井(采出井)为开采相同层位的同套井网,在两口井的井间SⅡ7+8a单元河道砂体与河间砂相连,为二类连通。分析认为在井间存在由河间薄层砂物性差异形成的“井网控制不住型”剩余油。因此对60-28井压裂和补孔,日增油达1.8t,含水率降低2.9%。
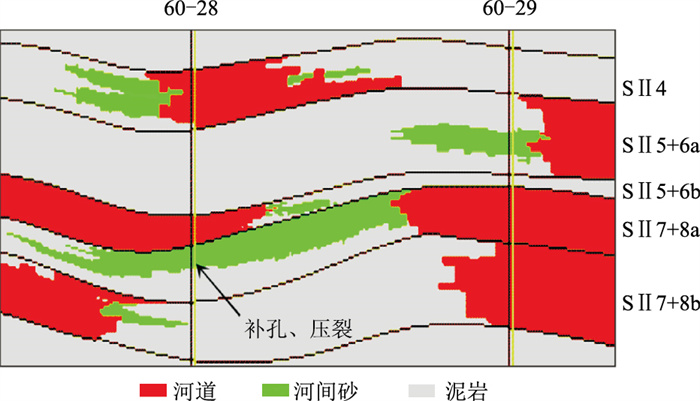
|
图 13 采用反演约束的多点地质统计学建模得到的过井剖面砂体分布图 |
BGX区块确定了11个注采不完善造成的剩余油富集部位,对6口井压裂、5口井补孔,均见到较好效果(表 1),展示了反演约束的多点地质统计学建模方法具有较好的应用前景。
|
|
表 1 措施效果统计表 |
反演约束的多点地质统计学方法弥补了传统两点地质统计学方法在储层表征中的缺陷。利用训练图像替代变差函数,将地质沉积模式认识融入建模运算过程,并结合地震数据横向采样密集的优势,适用于表征陆相河流—三角洲沉积环境的地质体特征。
(1) 根据河流—三角洲沉积特征,建立了3种分流河道砂体和2种非河道砂体平面组合模式。在三角洲平原环境中主要发育分叉枝状、交织网状组合模式,在水下分流河道中主要以交织网状、孤立窄带组合模式为主。对于分流间砂体,主要划分为2种组合模式。
(2) 利用井点纵波阻抗曲线和沉积微相解释结果,明确了不同沉积微相的纵波阻抗特征。纵波阻抗低值反映了河道砂体,高值反映了河间泥,而河间砂的纵波阻抗值介于河道砂体和河间泥之间;运用纵波阻抗波形指示反演得到了纵波阻抗数据体,为地震反演约束的多点沉积微相建模提供了基础。
(3) 反演约束的多点地质统计学模拟方法具有较高精度。相对于序贯指示模拟方法,反演约束的多点地质统计学方法更清晰地描述了河道的几何形态、宽度及砂体接触关系,砂体间连通关系更明确、无效网格更少,河道砂体平均预测精度由79.6%提高至86.1%。
(4) 反演约束的多点地质统计学模拟方法能够满足陆相油田储层精细描述及剩余油精准挖潜需求,具有较好的应用前景。利用研究区储层精细建模结果,进一步确定了注采关系不完善造成的剩余油潜力部位,制定了相应挖潜措施,在已实施的11口措施井中均见到良好效果。
| [1] |
韩大匡. 关于高含水油田二次开发理念、对策和技术路线的探讨[J]. 石油勘探与开发, 2010, 37(5): 583-591. HAN Dakuang. Discussions on concepts, countermeasures and technical routes for the redevelopment of high water-cut oilfields[J]. Petroleum Exploration and Development, 2010, 37(5): 583-591. |
| [2] |
邹拓, 左毅, 孟立新, 等. 地质建模技术在复杂断块老油田二次开发中的应用[J]. 石油与天然气地质, 2014, 35(1): 143-147. ZOU Tuo, ZUO Yi, MENG Lixin, et al. Application of geological modeling technology in secondary development of old and complex fault block oilfields[J]. Oil & Gas Geology, 2014, 35(1): 143-147. |
| [3] |
石石, 初广震, 万玉金, 等. 油气藏开发阶段储层地质模型的建立及优选方法[J]. 辽宁工程技术大学学报(自然科学版), 2011, 30(4): 493-496. SHI Shi, CHU Guangzhen, WAN Yujin, et al. Reservoir geological modeling and optimum seeking method in the development phase of the oil and gas field[J]. Journal of Liaoning Technical University(Natural Science), 2011, 30(4): 493-496. |
| [4] |
夏吉庄, 张玉晓, 吕德灵. 多资料匹配融合储层建模技术[J]. 石油地球物理勘探, 2016, 51(2): 350-354. XIA Jizhuang, ZHANG Yuxiao, LYU Deling. Reservoir model building with multi-data fusion[J]. Oil Geophysical Prospecting, 2016, 51(2): 350-354. |
| [5] |
吴胜和, 张一伟, 李恕军, 等. 提高储层随机建模精度的地质约束原则[J]. 石油大学学报(自然科学版), 2001, 25(1): 55-58. WU Shenghe, ZHANG Yiwei, LI Shujun, et al. Geological constraint principles in reservoir stochastic modeling[J]. Journal of the University of Petroleum, China, 2001, 25(1): 55-58. |
| [6] |
徐立恒, 宋宝权, 韩嵩, 等. 变尺度构造模型在地质统计学反演储层预测中的应用[J]. 石油学报, 2019, 40(2): 190-196, 239. XU Liheng, SONG Baoquan, HAN Song, et al. Application of variable-scale structure model on geostatistics inversion reservoir prediction[J]. Acta Petrolei Sinica, 2019, 40(2): 190-196, 239. |
| [7] |
付斌, 石林辉, 江磊, 等. 多点地质统计学在致密砂岩气藏储集层建模中的应用: 以s48-17-64区块为例[J]. 断块油气田, 2014, 21(6): 726-729. FU Bin, SHI Linhui, JIANG Lei, et al. Application of multiple-point geostatistics method in reservoir mode-ling of tight sandstone gas reservoir: Taking Block s48-17-64 as an example[J]. Fault-Block Oil & Gas Field, 2014, 21(6): 726-729. |
| [8] |
王鸣川, 段太忠, 计秉玉. 多点统计地质建模技术研究进展与应用[J]. 古地理学报, 2017, 19(3): 557-566. WANG Mingchuan, DUAN Taizhong, JI Bingyu. Research progress and application of multipoint statistics geological modeling technology[J]. Journal of Palaeogeography, 2017, 19(3): 557-566. |
| [9] |
张伟, 林承焰, 董春梅. 多点地质统计学在秘鲁D油田地质建模中的应用[J]. 中国石油大学(自然科学版), 2008, 32(4): 24-28. ZHANG Wei, LIN Chengyan, DONG Chunmei. App-lication of multiple-point geostatistics in geological modeling of D Oilfield in Peru[J]. Journal of China University of Petroleum, 2008, 32(4): 24-28. |
| [10] |
朱亚军, 李进步, 陈龙, 等. 苏里格气田大井组立体开发关键技术[J]. 石油学报, 2018, 39(2): 208-215. ZHU Yajun, LI Jinbu, CHEN Long, et al. Key technology of large-well-group stereoscopic development in Sulige gasfield[J]. Acta Petrolei Sinica, 2018, 39(2): 208-215. |
| [11] |
尹艳树, 张昌民, 李少华, 等. 一种基于沉积模式的多点地质统计学建模方法[J]. 地质论评, 2014, 60(1): 216-221. YIN Yanshu, ZHANG Changmin, LI Shaohua, et al. A pattern-based multiple point geostatistics method[J]. Geological Review, 2014, 60(1): 216-221. |
| [12] |
韩继超, 王夕宾, 孙致学, 等. 利用多点地质统计学模拟河流相沉积微相[J]. 特种油气藏, 2011, 18(6): 48-51. HAN Jichao, WANG Xibin, SUN Zhixue, et al. Simulation of fluvial sedimentary microfacies using multiple-point geostatistics[J]. Special Oil and Gas Reservoirs, 2011, 18(6): 48-51. |
| [13] |
罗红梅, 杨培杰, 王长江, 等. 基于多点地质统计学多数据联合约束的岩相模拟[J]. 石油地球物理勘探, 2015, 50(1): 162-169. LUO Hongmei, YANG Peijie, WANG Changjiang, et al. Lithofacies simulation based on multi-point geostatistics multiple data joint constraints[J]. Oil Geophy-sical Prospecting, 2015, 50(1): 162-169. |
| [14] |
ZHANG T F. Incorporating geological conceptual models and interpretations into reservoir modeling using multiple-point geostatistics[J]. Earth Science Frontiers(China University of Geosciences, Beijing; Peking University), 2008, 15(1): 26-35. |
| [15] |
王凯其, 肖凡. 多点地质统计学的理论、方法、应用及发展现状[J]. 地质科技情报, 2019, 38(6): 256-268. WANG Kaiqi, XIAO Fan. Multiple-ponits geostatistics: A review of theories, methods and application[J]. Geological Science and Technology Information, 2019, 38(6): 256-268. |
| [16] |
孙思敏, 彭仕宓. 地质统计学反演方法及其在薄层砂体预测中的应用[J]. 西安石油大学学报(自然科学版), 2007, 22(1): 41-48. SUN Simin, PENG Shimi. Geostatistical inversion method and its application in the prediction of thin reservoirs[J]. Journal of Xi'an Shiyou University(Na-tural Science Edition), 2007, 22(1): 41-48. |
| [17] |
刘张聚, 童思友, 方云峰, 等. 基于时域加权的拉普拉斯—频率域弹性波全波形反演[J]. 石油地球物理勘探, 2021, 56(2): 302-312, 331. LIU Zhangju, TONG Siyou, FANG Yunfeng, et al. Full elastic waveform inversion in Laplace-Fourier domain based on time domain weighting[J]. Oil Geophysical Prospecting, 2021, 56(2): 302-312, 331. |
| [18] |
JOHNSTON D H. Methods and Applications in Re-servoir Geophysics: Investigations in Geophysics Serise NO. 15[M]. SEG, 2010.
|
| [19] |
王朋岩, 李耀华, 赵荣. 叠后MCMC法岩性反演算法研究[J]. 地球物理学进展, 2015, 30(4): 1918-1925. WANG Pengyan, LI Yaohua, ZHAO Rong. Algorithm research of post-stack MCMC lithology inversion method[J]. Progress in Geophysics, 2015, 30(4): 1918-1925. |
| [20] |
周爽爽, 印兴耀, 裴松, 等. 地震波形约束的蒙特卡洛—马尔科夫链随机反演方法[J]. 石油地球物理勘探, 2021, 56(3): 543-554, 592. ZHOU Shuangshuang, YIN Xingyao, PEI Song, et al. Monte Carlo-Markov Chain stochastic inversion constrained by seismic waveform[J]. Oil Geophysical Prospecting, 2021, 56(3): 543-554, 592. |
| [21] |
撒利明, 杨午阳, 姚逢昌, 等. 地震反演技术回顾与展望[J]. 石油地球物理勘探, 2015, 50(1): 184-202. SA Liming, YANG Wuyang, YAO Fengchang, et al. Past, present, and future of geophysical inversion[J]. Oil Geophysical Prospecting, 2015, 50(1): 184-202. |



 黄勇, 黑龙江省大庆市让胡路区科苑路18号大庆油田勘探开发研究院,163712。Email:
黄勇, 黑龙江省大庆市让胡路区科苑路18号大庆油田勘探开发研究院,163712。Email: