② 成都理工大学地球勘探与信息技术教育部重点实验室, 四川成都 610059
② Key Lab of Earth Exploration & Information Techniques of Ministry of Education, Chengdu University of Technology, Chengdu, Sichuan 610059, China
随着油气勘探、开发不断深入,面对的油气储集层的形态愈加复杂,勘探目标逐渐向岩性油气藏和隐蔽油气藏转移。传统的AVO技术基于叠前地震数据,运用Zoeppritz方程计算反射系数并厘清界面上、下岩层的纵、横波速度及密度之间的关系,通过研究弹性参数变化对地震振幅的影响预测含油气储层[1]。Chapman等[2-4]基于喷射流理论提出了动态等效介质模型,阐述了岩石中流体活动引起的地震波速度频散与衰减效应引起的频率依赖的AVO响应,即地震反射系数不仅与入射角有关而且随频率变化;Smith等[5]首次提出将纵、横波速度的组合作为流体因子进行岩石属性估算及含气检测;Whitcombe等[6]提出了横波弹性阻抗的概念;Castagna等[7]逐步研究了用以识别岩性和油气异常的AVO属性交会技术;Connolly[8]利用弹性阻抗识别岩石中的流体。随着弹性阻抗反演技术应用愈加成熟,研究发现敏感流体因子对流体识别的作用也十分重要。Russell等[9]基于多孔弹性介质岩石物理理论,提出了反映岩隙流体弹性效应的Gassmann流体项和Russell流体因子,都对流体有着高敏感度;Wilson等[10]、吴小羊[11]将传统的AVO技术与时频分析技术相结合,发展形成了依赖频率的AVO分析技术;张世鑫等[12]提出了纵波速度频散属性反演方法;程冰洁等[13]基于纵、横波速度频散属性提出了频变AVO含气性识别技术;Chen等[14]基于依赖频率的AVO数值模拟方法研究了储层流体流度变化引起的地震响应异常;高刚[15]详细分析了含流体孔隙介质的地震响应特征,并利用纵、横波频散属性识别流体;罗鑫等[16]基于Gray反射系数实现了依赖频率的AVO反演;钟晗等[17]研究了依赖频率的AVO的影响因素;Li等[18]、Wu等[19]基于依赖频率的AVO方法,利用数值模拟以及实际资料定量估算岩层含气饱和度;Chen等[20]利用地震波的频散反演定量计算含气饱和度。
利用地震波在含流体储层传播时的频散和衰减属性进行储层流体识别一直是重点研究的问题。目前,基于叠前地震数据的频散属性反演技术取得了较大的进展,而利用叠前地震数据反演储层的衰减参数也同样重要。本文通过推导逆品质因子与速度的最佳正弦拟合解析公式,定义依赖频率的纵、横波衰减参数,构建了利用叠前角道集和岩石模量反演衰减参数的算法;然后基于实际地震数据反演分析纵、横波衰减参数的敏感度,从而预测高含气饱和度有效储层。实验表明,纵、横波衰减参数对高含气储层的敏感性高,能够准确识别高含气有效储层的位置。本文算法为预测高含气储层提供了较为可靠的新方法。
1 方法原理 1.1 逆品质因子与速度的一般关系式地震波在含流体孔隙介质中传播时,纵、横波速度和逆品质因子均是与频率有关的函数,逆品质因子与纵、横波速度的函数关系为[2]
| $ \left\{\begin{array}{l} V(f)=\frac{1}{\operatorname{Re}[1 / v(f)]} \\ \frac{1}{Q(f)}=\frac{\operatorname{Im}\left[v^2(f)\right]}{\operatorname{Re}\left[v^2(f)\right]} \end{array}\right. $ | (1) |
式中:f为频率;1/Q(f)为逆品质因子;V(f)为依赖频率的相速度;v(f)为复纵、横波速度;Re[·]和Im[·]分别指对复数求实部和虚部。
由式(1)可知,逆品质因子的计算考虑到纵、横波速度的虚部,但实际运用中,虚部的测量难以实现,无法直接利用叠前地震数据反演求得储层衰减参数,因而需要一个更直接的关系式表述纵、横波逆品质因子。
首先,建立纵、横波逆品质因子与纵、横波速度的映射拟合解析公式。令依赖频率的纵、横波速度分别为vP(f)和vS(f),通过正弦拟合分别与纵、横波品质因子QP(f)和QS(f)建立如下关系
| $ \frac{1}{Q_{\mathrm{w}}(f)}=\alpha \sin \left[v_{\mathrm{w}}(f)+\beta\right] $ | (2) |
式中:vw(f)可以是vP(f)或vS(f);Qw(f)是对应的QP(f)或QS(f);且有控制参数
| $ \left\{\begin{array}{l} \alpha=\max \left[\frac{1}{Q(f)}\right] \\ \beta=\frac{\pi\left[1-v_{\min }(f)\right]}{v_{\max }(f)-v_{\min }(f)+1} \end{array}\right. $ | (3) |
式中:α为逆品质因子的最大值;vmax(f)为vw(f)的最大值,vmin(f)为vw(f)的最小值。
以下通过地质模型数值分析详细说明式(2)的可靠性,并验证控制参数α和β的精度。
根据Chapman的动态等效介质理论[2]设计的两层储层初始模型(参数见表 1),第一层为不发生频散的页岩,第二层为发生速度频散的砂岩。
|
|
表 1 初始模型参数 |
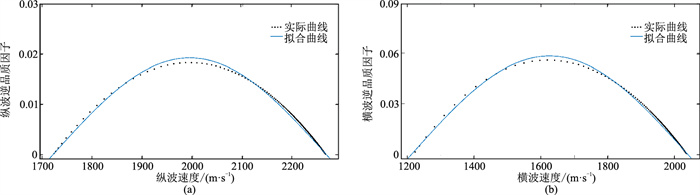
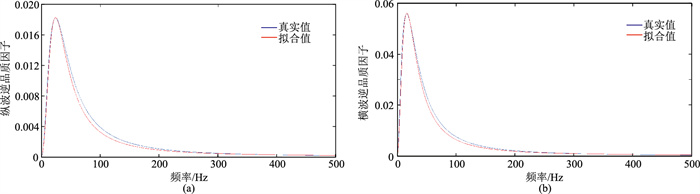
将基于初始模型计算的纵、横波逆品质因子与对应的纵、横波速度在频率域进行拟合(图 1),拟合曲线均为正弦曲线。图 2是初始模型逆品质因子真实值与式(2)计算出的拟合值的对比,由图可见,真实值与拟合值曲线的形态一致,误差小且主要集中于频率较高的区域(50~190Hz),满足实际地震资料反演要求。
|
图 1 初始模型逆品质因子与速度拟合曲线对比 (a)纵波;(b)横波 |
|
图 2 逆品质因子真实值与拟合值对比 (a)纵波;(b)横波 |
改变模型的岩层密度、流体种类、孔隙度、裂隙密度、裂缝密度、流体松弛时间、裂缝半径、裂缝尺度、纵横波速度、裂隙纵横比等岩石物理参数,并对相应参数改变模型的纵、横波逆品质因子与纵、横波速度进行多次拟合,以验证式(2)。通过实验发现岩石物理参数在合理范围内变化时,不影响纵、横波逆品质因子与纵、横波速度的拟合关系。
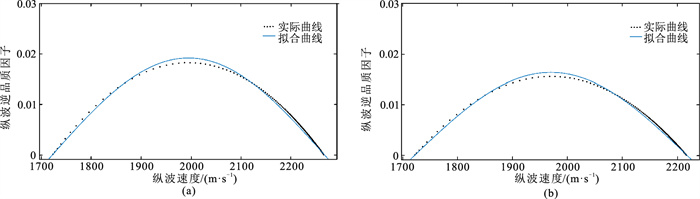
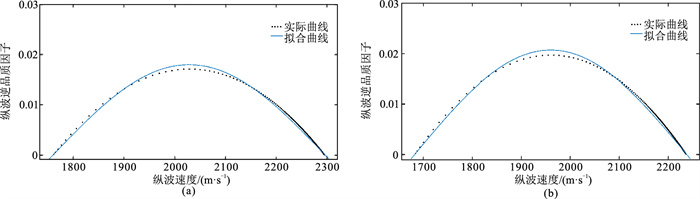
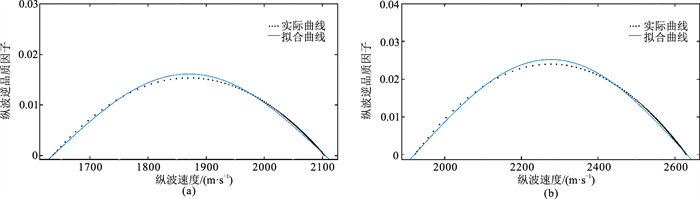
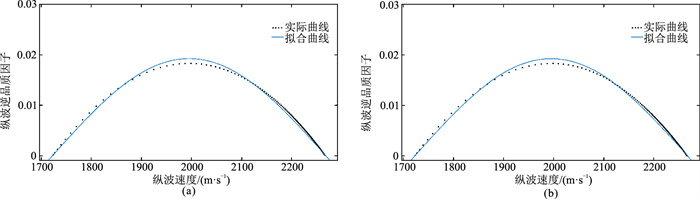
图 3是储层流体分别为水和气时,纵波逆品质因子与纵波速度的拟合曲线;图 4是将孔隙度由25%改变为20%(图 4a)、30%(图 4b)时的拟合图像,可见拟合趋势仍然是典型的正弦曲线;图 5是当裂隙密度变为0.08(图 5a)、0.15(图 5b)时的拟合曲线;当裂隙纵横比为0.0002、0.0004时(图 6),拟合曲线同样为正弦曲线形态。
|
图 3 不同储层流体时(孔隙度为25%)纵波逆品质因子与纵波速度的拟合曲线对比 (a)储层饱含水;(b)储层饱含气 |
|
图 4 不同孔隙度时纵波逆品质因子与纵波速度的拟合曲线对比 (a)孔隙度为20%;(b)孔隙度为30% |
|
图 5 不同裂隙密度时纵波逆品质因子与纵波速度的拟合曲线对比 (a)裂隙密度为0.08;(b)裂隙密度为0.15 |
|
图 6 不同裂隙纵横比时纵波逆品质因子与纵波速度的拟合曲线对比 (a)裂隙纵横比为0.0002;(b)裂隙纵横比为0.0004 |
从上述实验结果可以看出,当改变其他岩石物理参数,如裂缝密度、裂缝半径、松弛时间及纵、横波速度时,拟合曲线均满足纵、横波逆品质因子与纵、横波速度的一般关系式,证明了式(2)的可靠性及准确性,并且式(2)中控制参数α、β的定义式满足实验要求。
引入和方差(SSE)、均方根误差(RMSE)评价拟合效果,计算公式为
| $ \left\{\begin{array}{l} \mathrm{SSE}=\sum\limits_{i=1}^N w_i\left(y_i-\hat{y}_i\right)^2 \\ \mathrm{RMSE}=\sqrt{\frac{\mathrm{SSE}}{N}}=\sqrt{\frac{1}{N} \sum\limits_{i=1}^N w_i\left(y_i-\hat{y}_i\right)^2} \end{array}\right. $ | (4) |
式中:N为拟合数据个数;yi为真实值;
SSE和RMSE的值越接近0,说明模型选择与拟合效果越好,数据预测越成功。根据式(4)计算得到拟合曲线与实际曲线的SSE小于0.00004,RMSE小于0.0002,证明该公式实用性较强。
1.2 衰减参数反演算法实现将式(2)进行等式变换可得
| $ v(f)=\arcsin \left[\frac{1}{\alpha Q(f)}\right]-\beta $ | (5) |
在Smith等[5]提出的AVO二项近似表达式的基础上引入速度参数,将常规AVO反射系数转换成与时间t、地震波入射角θ和频率f都有关的函数R(t, θ, f),即
| $ R(t, \theta, f)=A(t, \theta) \frac{\Delta v_{\mathrm{P}}(t, f)}{v_{\mathrm{P}}(t, f)}+B(t, \theta) \frac{\Delta v_{\mathrm{S}}(t, f)}{v_{\mathrm{S}}(t, f)} $ | (6) |
其中
| $ \left\{\begin{array}{l} A(t, \theta)=\frac{5}{8}-\frac{1}{2} \frac{V_{\mathrm{S}}^2(t)}{V_{\mathrm{P}}^2(t)} \sin ^2 \theta+\frac{1}{2} \tan ^2 \theta \\ B(t, \theta)=-4 \frac{V_{\mathrm{S}}^2(t)}{V_{\mathrm{P}}^2(t)} \sin ^2 \theta \end{array}\right. $ | (7) |
式中:VP(t)、VS(t)分别为测井获取的纵、横波速度;ΔvP(t, f)和ΔvS(t, f)分别为反射界面上、下地层与频率有关的纵、横波速度差。
引入逆品质因子构建纵、横波衰减参数,将式(5)代入式(6)变换可得
| $ R(t, \theta, f)=A(t, \theta) P(t, f)+B(t, \theta) S(t, f) $ | (8) |
其中
| $ \left\{\begin{array}{l} P(t, f)=\frac{\Delta Q_{\mathrm{P}}(t, f)}{\sqrt{\frac{1}{\alpha_{\mathrm{P}}^2}-Q_{\mathrm{P}}(t, f)^2}\left\{\arcsin \left[\alpha_{\mathrm{P}} Q_{\mathrm{P}}(t, f)\right]-\beta_{\mathrm{P}}\right\}} \\ S(t, f)=\frac{\Delta Q_{\mathrm{S}}(t, f)}{\sqrt{\frac{1}{\alpha_{\mathrm{S}}^2}-Q_{\mathrm{S}}(t, f)^2}\left\{\arcsin \left[\alpha_{\mathrm{S}} Q_{\mathrm{S}}(t, f)\right]-\beta_{\mathrm{S}}\right\}} \end{array}\right. $ | (9) |
在参考频率f0处分别对式(9)中的P(t, f)和S(t, f)项进行泰勒展开,并舍去高阶项,则式(8)变换为
| $ \begin{aligned} R(t, \theta, f) \approx & A(t, \theta) P(t, f)+\left(f-f_0\right) A(t, \theta) \times \\ & \frac{\mathrm{d} P(t, f)}{\mathrm{d} f}+B(t, \theta) S(t, f)+ \\ & \left(f-f_0\right) B(t, \theta) \frac{\mathrm{d} S(t, f)}{\mathrm{d} f} \end{aligned} $ | (10) |
式(10)是本文纵、横波品质因子频散属性反演的基础。本文将地震纵波衰减参数属性FP(t)和横波衰减参数属性FS(t)分别定义为
| $ \left\{\begin{array}{l} F_{\mathrm{P}}(t)=\frac{\mathrm{d} P(t, f)}{\mathrm{d} f} \\ F_{\mathrm{S}}(t)=\frac{\mathrm{d} S(t, f)}{\mathrm{d} f} \end{array}\right. $ | (11) |
假设叠前角道集的道数为n,每道样点数为nt,道集可表示为
| $ d(t, j) t=1, 2, \cdots, n_t ; j=1, 2, \cdots, n $ | (12) |
采用广义S变换[21]进行时频谱分析,将频谱分解后频率fi对应的振幅谱记为Dfi(t, j),则瞬时谱加权因子为
| $ W\left(f_i, j\right)=\frac{\max \left[D_{f 0}(j)\right]}{\max \left[D_{f i}(j)\right]} $ | (13) |
式中:Df0(j)为第j道参考频率f0对应的振幅谱;Dfi(j)为第j道频率fi对应的振幅谱。则均衡处理后的谱可表示为
| $ D_{f i}^{\mathrm{b}}(t, j)=W\left(f_i, j\right) D_{f_i}(t, j) $ | (14) |
参考频率的选取很重要,它会直接影响反演的效果,通常选择地震子波的主频作为参考频率。许迪等[22]提出一种通过交会分析确定参考频率的方法,此方法可基于实际资料准确地确定参考频率,进而提升反演的准确度。
在参考频率f0处,P(t, f0)和S(t, f0)满足以下矩阵
| $ \left( {\begin{array}{*{20}{l}} {P\left( {t, {f_0}} \right)}\\ {S\left( {t, {f_0}} \right)} \end{array}} \right) = {\left( {\begin{array}{*{20}{c}} {A(t, 1)}&{}&{B(t, 1)}\\ {}& \vdots &{}\\ {A(t, n)}&{}&{B(t, n)} \end{array}} \right)^{ - 1}}\left( {\begin{array}{*{20}{c}} {D_{{f_0}}^{\rm{b}}(t, 1)}\\ \vdots \\ {D_{{f_0}}^{\rm{b}}(t, n)} \end{array}} \right) $ | (15) |
根据下式计算FP(t)和FS(t)
| $ \left(\begin{array}{l} F_P(t) \\ F_{\mathrm{S}}(t) \end{array}\right)=\left(\boldsymbol{e}^{\mathrm{T}} \boldsymbol{e}\right)^{-1} \boldsymbol{e}^{\mathrm{T}} \boldsymbol{r} $ | (16) |
式中r定义为m×n行(m为频率个数)的列向量;e定义为m×n行的2列矩阵,有
| $ \boldsymbol{r}=\left(\begin{array}{c} R\left(t, \theta_1, f_1\right)-A\left(t, \theta_1\right) P\left(t, f_0\right)-B\left(t, \theta_1\right) S\left(t, f_0\right) \\ \vdots \\ R\left(t, \theta_1, f_m\right)-A\left(t, \theta_1\right) P\left(t, f_0\right)-B\left(t, \theta_1\right) S\left(t, f_0\right) \\ \vdots \\ R\left(t, \theta_n, f_1\right)-A\left(t, \theta_n\right) P\left(t, f_0\right)-B\left(t, \theta_n\right) S\left(t, f_0\right) \\ \vdots \\ R\left(t, \theta_n, f_m\right)-A\left(t, \theta_n\right) P\left(t, f_0\right)-B\left(t, \theta_n\right) S\left(t, f_0\right) \end{array}\right) $ | (17) |
| $ \mathit{\boldsymbol{e}} = \left( {\begin{array}{*{20}{c}} {\left( {{f_1} - {f_0}} \right)A\left( {t, {\theta _1}} \right)}&{}&{\left( {{f_1} - {f_0}} \right)B\left( {t, {\theta _1}} \right)}\\ {}& \vdots &{}\\ {\left( {{f_m} - {f_0}} \right)A\left( {t, {\theta _1}} \right)}&{}&{\left( {{f_m} - {f_0}} \right)B\left( {t, {\theta _1}} \right)}\\ {}& \vdots &{}\\ {\left( {{f_1} - {f_0}} \right)A\left( {t, {\theta _n}} \right)}&{}&{\left( {{f_1} - {f_0}} \right)B\left( {t, {\theta _n}} \right)}\\ {}& \vdots &{}\\ {\left( {{f_m} - {f_0}} \right)A\left( {t, {\theta _n}} \right)}&{}&{\left( {{f_m} - {f_0}} \right)B\left( {t, {\theta _n}} \right)} \end{array}} \right) $ | (18) |
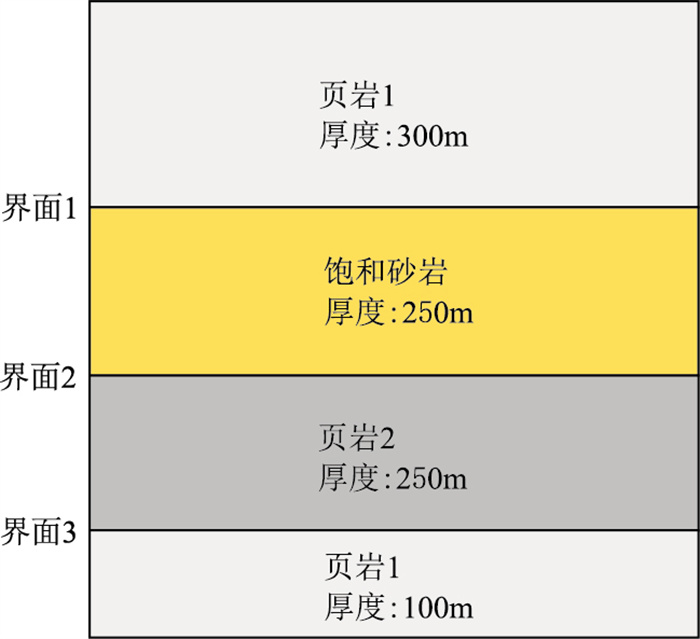
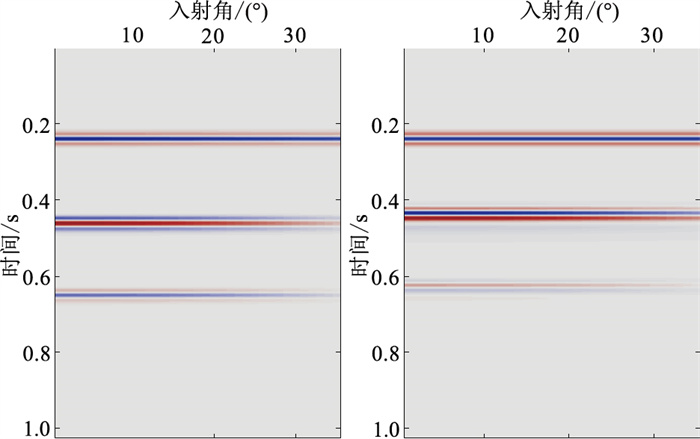
本文讨论了储层饱和含气或饱和含水两种流体状况下纵、横波衰减参数属性变化情况。设计一个4层地质模型(图 7),其中第2层为饱含流体层。具体模型参数见表 2。采用主频为40Hz的合成子波,通过相移法波动方程模拟该地质模型在不同流体情况下的地震角道集(图 8)。并选用40Hz作为参考频率,分别对两个角道集数据开展纵、横波衰减参数属性反演。
|
图 7 4层地质模型 |
|
|
表 2 4层地质模型参数 |
|
图 8 饱含水(左)、饱含气(右)模型地震角道集 |
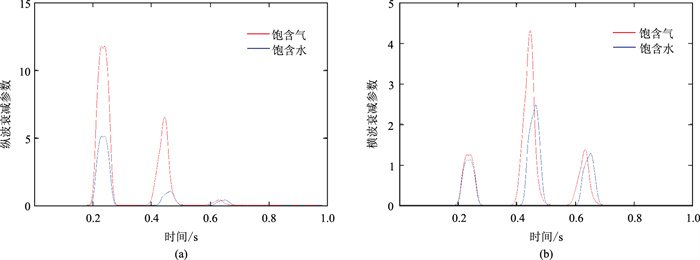
图 9为不同流体模型纵、横波衰减参数反演结果对比。由图可见,饱和含气砂岩顶、底界面的纵、横波衰减参数属性变化均大于饱和含水砂岩,且纵波衰减参数属性的变化更明显(图 9a)。分析认为,因饱和含流体砂岩内地震波存在依赖频率的衰减,使下部地层的反射发生了纵、横波衰减参数变化异常,据此可间接预测含流体砂岩储层。
|
图 9 不同流体模型衰减参数反演结果对比 (a)纵波;(b)横波 |
将本文方法应用到某工区实际三维地震资料,分析说明纵、横波衰减参数属性对高含气饱和度有效储层的预测效果。工区面积约为150km2,Inline范围1~1000,Xline范围1~1000。图 10为沿目的层提取的原始地震数据振幅切片,图中可见well-1~well-5井的分布位置,振幅异常受背景影响较严重,较难预测其范围。

|
图 10 沿目的层提取的地震振幅切片 |
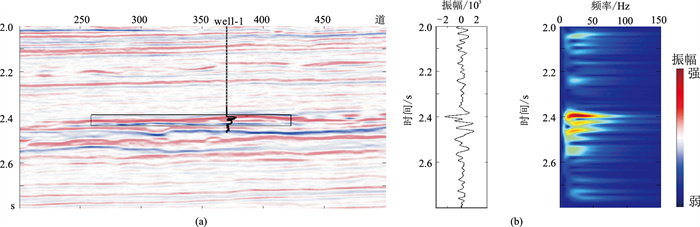
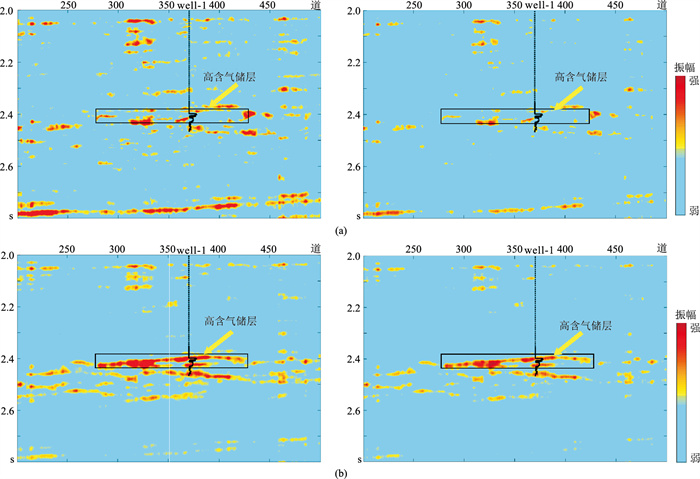
图 11为过well-1井地震剖面及井旁道时频分析结果,图中黑色矩形区域为高含气目标储层,时间延续范围为2.38~2.45s(图 11a)。从时频分析结果(图 11b)可看出,在2.38~2.55s的振幅较强,且气层的主频集中在25Hz附近。选取地震资料的主频(25Hz)为地震反演的参考频率,反演得到该数据纵、横波速度频散属性及衰减参数属性剖面(图 12),图中黑色矩形标记处指示高含气有效储层,黑色曲线为测井含气饱和度曲线。由图 12a可见,横波频散和横波衰减参数变化受背景干扰严重,杂乱信息较多,对高含气储层的敏感性较差,且横波频散受背景干扰更严重。由图 12b可见,纵波衰减参数变化受背景干扰较轻,杂乱信息较少,对高含气储层敏感性强,纵波频散有着相似的表现,但纵波频散受背景干扰更强。分析得出,与横波衰减参数相比,纵波衰减参数变化属性可清楚地刻画高含气储层位置。
|
图 11 过well-1井地震剖面(a)和井旁道时频分析结果(b) |
|
图 12 过well-1井频散(左)、衰减参数(右)属性反演剖面 (a)横波;(b)纵波 |
在实际应用中,通过构建纵、横波衰减参数,对两者进行联合对比分析,能够提高对高含气储层识别的准确性。
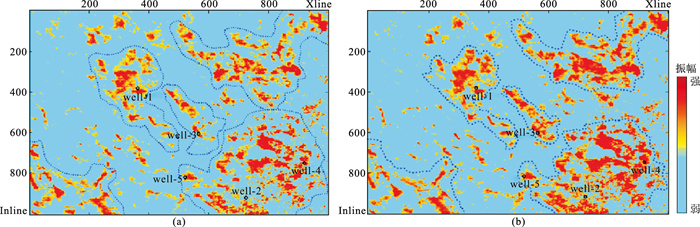
进而对整个工区有效三维资料进行纵波衰减参数的反演处理,得到纵波衰减参数反演属性体,提取沿目的层衰减参数属性切片(图 13a)和沿目的层下方5ms的衰减参数属性切片(图 13b),对比可见,根据反演衰减参数属性异常可有效地识别出高含气饱和度储层,图中蓝色虚线区域为有利高含气饱和度储层范围,实际钻探的5口井均包含在反演得到的高含气饱和度储层范围内,符合率极高。图 13b显示目的层下5ms的时窗区域仍有明显属性异常,预测该区域油气丰富度良好。
|
图 13 衰减参数属性切片 (a)沿目的层提取;(b)沿目的层+5ms提取 |
图 14连井反演属性剖面显示,well-1、well-3、well-5、well-2井的高含气饱和度位置均出现强衰减参数异常,低含气饱和度位置表现为弱衰减参数异常,并且背景异常干扰小,能够准确地刻画高含气饱和度储层的位置和空间分布。上述分析进一步证明了衰减参数反演在实际地震数据反演中的可行性,丰富了地震反演方法的思路。
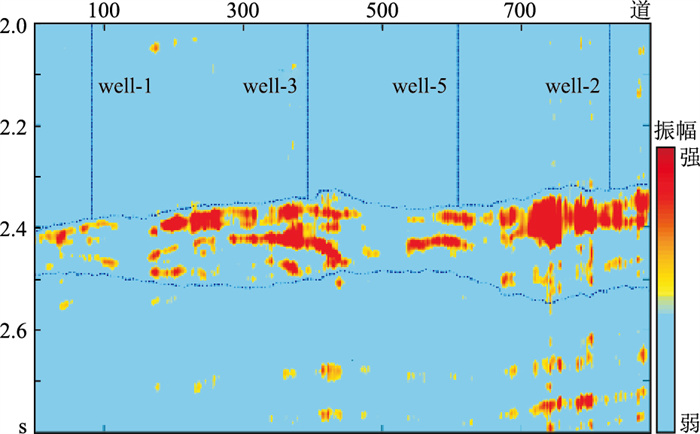
|
图 14 连井衰减参数属性反演剖面 |
基于频率域推导了纵、横波逆品质因子与纵、横波速度的最佳正弦拟合公式,进而构建了纵、横波衰减参数进行地震数据属性反演算法,再利用谱均衡等处理对数据进行优化,提高反演精度。通过模型试算和实际地震资料应用,得到以下认识:
(1) 模型试算分析结果表明,纵、横波衰减参数变化属性对储层含流体的敏感性存在差异,纵波衰减参数变化属性对流体的敏感性更强,且受背景干扰小,可以优于横波衰减参数属性更为精确地识别高含气储层;
(2) 实际地震资料反演结果进一步证明了建立的纵、横波品质因子与纵、横波速度关系式的有效性,在此基础上构建纵、横波衰减参数开展地震数据属性反演可有效识别储层流体。为利用纵、横波衰减参数进行储层流体识别和预测提供了一条新的途径。
| [1] |
OSTRANDER W J. Plane-wave reflection coefficients for gas sands at nonnormal angles of incidence[J]. Geophysics, 1984, 49(10): 1637-1648. |
| [2] |
CHAPMAN M, ZATSEPIN S V, CRAMPIN S. De-rivation of a microstructural poroelastic model[J]. Geophysical Journal International, 2002, 151(2): 427-451. DOI:10.1046/j.1365-246X.2002.01769.x |
| [3] |
CHAPMAN M, LIU E R, LI X Y. The influence of abnormally high reservoir attenuation on the AVO signature[J]. The Leading Edge, 2005, 24(11): 1120-1125. DOI:10.1190/1.2135103 |
| [4] |
CHAPMAN M, LIU Enru, LI X Y. The influence of fluid sensitive dispersion and attenuation on AVO analysis[J]. Geophysical Journal International, 2006, 167(1): 89-105. DOI:10.1111/j.1365-246X.2006.02919.x |
| [5] |
SMITH G C, GIDLOW P M. Weighted stacking for rock property estimation and detection of gas[J]. Geophysical Prospecting, 1987, 35(9): 993-1014. |
| [6] |
WHITCOMBE D N, CONNOLLY P A, REAGAN R L. Extended elastic impedance for fluid and lithology prediction[J]. Geophysics, 2002, 67(1): 63-67. DOI:10.1190/1.1451337 |
| [7] |
CASTAGNA J P, SWAN H W, FOSTER J D. Framework for AVO gradient and intercept interpretation[J]. Geophysics, 1998, 63(3): 948-956. DOI:10.1190/1.1444406 |
| [8] |
CONNOLLY P. Elastic impedance[J]. The Leading Edge, 1999, 18(4): 438-452. DOI:10.1190/1.1438307 |
| [9] |
RUSSELL B H, HEDLIN K, HILTERMAN F J. Fluid-property discrimination with AVO: a Biot-Gassmann perspective[J]. Geophysics, 2003, 68(1): 29-39. DOI:10.1190/1.1543192 |
| [10] |
WILSON A, CHAPMAN M, LI X Y. Frequency-dependent AVO inversion[C]. SEG Technical Program Expanded Abstracts, 2009, 28: 341-345.
|
| [11] |
吴小羊. 基于频谱分析技术的频散AVO反演研究[D]. 湖北武汉: 中国地质大学(武汉), 2010. WU Xiaoyang. Frequency Dependent AVO Inversion Using Spectral Decomposition Techniques[D]. China University of Geosciences(Wuhan), Wuhan, Hubei, 2010. |
| [12] |
张世鑫, 印兴耀, 张广智, 等. 纵波速度频散属性反演方法研究[J]. 石油物探, 2011, 50(3): 219-224. ZHANG Shixin, YIN Xingyao, ZHANG Guangzhi, et al. Inversion method for the velocity dispersion-dependent attribute of P-wave[J]. Geophysical Prospecting for Petroleum, 2011, 50(3): 219-224. DOI:10.3969/j.issn.1000-1441.2011.03.002 |
| [13] |
程冰洁, 徐天吉, 李曙光. 频变AVO含气性识别技术研究与应用[J]. 地球物理学报, 2012, 55(2): 608-613. CHENG Bingjie, XU Tianji, LI Shuguang. Research and application of frequency dependent AVO analysis for gas recognition[J]. Chinese Journal of Geophy-sics, 2012, 55(2): 608-613. |
| [14] |
CHEN X H, HE Z H, GAO G, et al. A fast combined method for fluid flow related frequency-dependent AVO modeling[C]. SEG Technical Program Expanded Abstracts, 2013, 32: 3454-3459.
|
| [15] |
高刚. 含流体孔隙介质地震响应特征分析及流体识别方法[D]. 四川成都: 成都理工大学, 2013. GAO Gang. Analysis of Seismic Response Characte-ristics in Fluid-Saturated Porous Media and Study on Fluid Identification Method[D]. Chengdu University of Technology, Chengdu, Sichuan, 2013. |
| [16] |
罗鑫, 陈学华, 吕丙南, 等. 基于Gray反射系数的频变AVO反演[J]. 石油物探, 2018, 57(2): 292-301. LUO Xin, CHEN Xuehua, LYU Bingnan, et al. Frequency-dependent AVO inversion based on Gray reflection coefficient formula[J]. Geophysical Prospecting for Petroleum, 2018, 57(2): 292-301. DOI:10.3969/j.issn.1000-1441.2018.02.015 |
| [17] |
钟晗, 刘洋. 频变AVO影响因素分析[J]. 石油地球物理勘探, 2017, 52(4): 783-796. ZHONG Han, LIU Yang. Influence factors on frequency-dependent AVO[J]. Oil Geophysical Prospecting, 2017, 52(4): 783-796. |
| [18] |
LI X Y, WU X Y, SURVEY B G, et al. Quantitative estimation of gas saturation by frequency dependent AVO: numerical, physical modelling and field studies[C]. International Petroleum Technology Confe-rence, 2013, 1-10.
|
| [19] |
WU X Y, CHAPMAN M, LI X Y, et al. Quantitative gas saturation estimation by frequency-dependent amplitude-versus-offset analysis[J]. Geophysical Prospecting, 2014, 62(6): 1224-1237. DOI:10.1111/1365-2478.12179 |
| [20] |
CHEN S Q, CHAPMAN M, WU X Y, et al. The application of quantitative gas saturation estimation based on the seismic wave dispersion inversion[J]. Journal of Applied Geophysics, 2015, 120: 81-95. |
| [21] |
陈学华, 贺振华, 黄德济. 广义S变换及其时频滤波[J]. 信号处理, 2008, 24(1): 28-31. CHEN Xuehua, HE Zhenhua, HUANG Deji. Genera-lized S transform and its time-frequency filtering[J]. Signal Processing, 2008, 24(1): 28-31. |
| [22] |
许迪. 基于叠前数据反演的流体识别新方法[D]. 四川成都: 成都理工大学, 2015. XU Di. The New Inversion Method for Fluid Identification Based on Pre-stack Seismic Data[D]. Chengdu University of Technology, Chengdu, Sichuan, 2015. |



 陈学华, 四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院5301室,610059。Email:
陈学华, 四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院5301室,610059。Email: