② 油气资源与探测国家重点实验室, 北京 102249
② State Key Laboratory of Petroleum Resources and Prospecting, Beijing 102249, China
地震反演技术是提取地层属性的有效手段之一,其基本过程是根据地表接收的地震数据反推地层的物理参数,从而预测储层及识别流体[1]。根据所使用的地震数据体,地震反演分为叠后反演和叠前反演两大类[2-4]。
叠后波阻抗(acoustic impedance, AI)反演是地震反演中的一种重要技术,首次被Lindseth[5]提出,随后在地球物理反演领域得到快速发展[6-8]。根据实现方式的不同,AI反演主要分为稀疏脉冲反演、基于模型约束的反演、递归反演以及有色反演四类,不同方法各有其适用条件及应用范围[2, 9]。尽管AI反演历经多年且得到很大发展,但仍存在诸多问题,如反问题求解的不适定性、常规反演算法对地层边界刻画不清晰以及递归反演中的误差累积等[10-11]。
对于反问题求解的不适定问题,人们进行了研究并提出了相应的解决办法[12-15]。早在1973年,Claerbout等[16]分析了L2范数和L1范数在反问题求解中的作用。基于L2范数约束,Tikhonov等[17]提出了一套完整的正则化方法解决不适定问题,其基本思想是在满足数据残差最小的条件下找到一个使模型的L2范数最小的解。尽管Tikhonov正则化很好地解决了不适定问题,但基于Tikhonov正则化获得的解较平滑,难以满足地学界对反演分辨率的要求。Buland等[18]将贝叶斯理论引入地球物理反问题,为基于概率的反演方法提供了数学基础。Tarantola[19]给出了反问题求解的一些算法细节,包括蒙特卡洛方法以及最小二乘离散问题等。此后,各种范数被提出以在解决不适定问题的同时获得较高分辨率的反演结果,包括L1范数[20]、Lp范数[21]以及L1-2范数等。L1-2范数作为一种稀疏度量,近年来广泛用于地球物理反演[11, 22]。
此外,常规的递归反演算法首先利用叠后地震数据反演反射系数,然后利用道积分技术计算地层波阻抗信息。这种波阻抗反演算法存在两个问题:一是对初始波阻抗依赖过高,如果第一层的波阻抗给定不准确,那么所有的波阻抗反演结果都会产生偏差;二是道积分中存在误差累积,如果某些反演的反射系数存在误差,那么这种误差会累积到该目标层之后的所有波阻抗计算结果上。
为了解决波阻抗反演中存在的这些问题,本文提出了基于L1-2正则化的地震波阻抗“块”反演方法。在前人的基础上,将L1-2正则化引入基于模型的波阻抗反演,通过借鉴全变分(Total Variation, TV)正则化的思想,利用叠后地震数据直接获得波阻抗反演结果。首先,推导线性化的波阻抗正演近似公式并分析精度。然后,基于贝叶斯理论,引入L1-2正则化构建波阻抗反演的目标函数,利用迭代重加权最小二乘算法(IRLS)求解目标函数,获得波阻抗反演结果。由于波阻抗反演为单道反演算法,反演多道数据时道与道之间会产生空间不连续现象,因此文中对反演结果执行f-x域空间预测滤波,改善由噪声和单道反演算法带来的空间不连续性[23-24]。最后,利用合成数据和实际资料反演验证所提方法的有效性和可行性。
1 线性化波阻抗正演公式基于褶积模型,地震数据可以表示为反射系数和地震子波褶积的形式
| $ d(t) = \int_{ - \infty }^{ + \infty } w (\tau )r(t - \tau ){\rm{d}}\tau + e(t) $ | (1) |
式中:d(t)为地震数据,t为时间;w(τ)为地震子波,τ为时移量;r(t-τ)为地层反射系数;e(t)为噪声。将式(1)写为矩阵形式,有
| $ \mathit{\boldsymbol{D}} = \mathit{\boldsymbol{WR}} + \mathit{\boldsymbol{e}} $ | (2) |
式中的变量分别为式(1)变量的矩阵形式。根据定义,当地下为多层水平介质时,任意第i个界面的反射系数为
| $ {r_i} = \frac{{{Z_{i + 1}} - {Z_i}}}{{{Z_{i + 1}} + {Z_i}}} $ | (3) |
式中Zi和Zi+1分别为第i层和第i+1层的波阻抗。将式(3)代入式(2)即可获得由地层波阻抗得到地震数据的公式。不难看出,式(3)中反射系数与地层波阻抗之间为非线性关系,当与地震子波褶积后,得到的地震记录与地层波阻抗之间的关系显然也是非线性的,这种非线性关系会增加反演方程的计算复杂度,也会增强反演的不稳定性。因此需要将式(3)进行线性化近似。根据等价无穷小代换ex~1+x,由式(3)可得[25]
| $ \frac{{{Z_{i + 1}}}}{{{Z_i}}} = \frac{{1 + {r_i}}}{{1 - {r_i}}} \approx \frac{{{{\rm{e}}^{{r_i}}}}}{{{{\rm{e}}^{ - {r_i}}}}} = {{\rm{e}}^{2{r_i}}} $ | (4) |
则有
| $ {r_i} = \frac{1}{2}\left( {\ln {Z_{i + 1}} - \ln {Z_i}} \right) $ | (5) |
将式(5)代入式(2)可得波阻抗正演公式
| $ \mathit{\boldsymbol{D}} = \mathit{\boldsymbol{WSZ}} + \mathit{\boldsymbol{e}} $ | (6) |
式中:Z=ln(Z1, Z2, …, Znt)T为地层波阻抗的自然对数, nt为波阻抗采样点数;S为差分算子,可表示为
| $ \mathit{\boldsymbol{S}} = \frac{1}{2}\left( {\begin{array}{*{20}{c}} { - 1}&1&{}&{}&{}\\ {}&{ - 1}&1&{}&{}\\ {}&{}& \ddots & \ddots &{}\\ {}&{}&{}&{ - 1}&1 \end{array}} \right) $ | (7) |
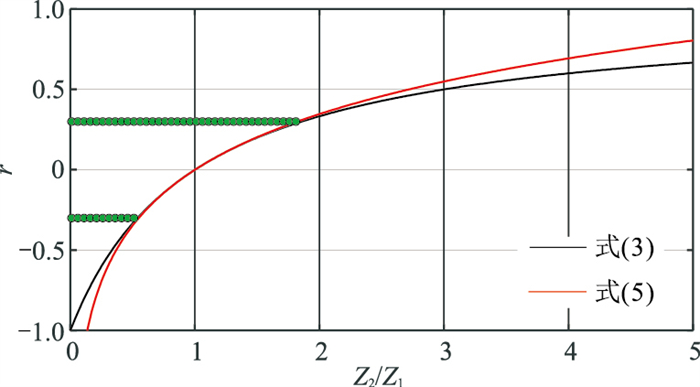
由式(3)得到式(5)的过程由于使用了等价无穷小代换,因此有必要分析、对比线性化的波阻抗正演近似公式(式(5))和精确公式(式(3))的正演结果。图 1为由式(3)和式(5)获得的反射系数。由图可见:当反射系数r的绝对值在一定范围(|r|≤0.3)时,式(5)与式(3)的结果几乎完全吻合;当|r|较大时二者的结果才有所差异。因此,当地下反射界面为弱反射界面,即|r|≤0.3时,利用式(5)计算地层的反射系数在理论上不会产生较大误差[20]。
|
图 1 由式(3)与式(5)获得的反射系数 Z1和Z2分别为反射界面上、下地层的波阻抗 |
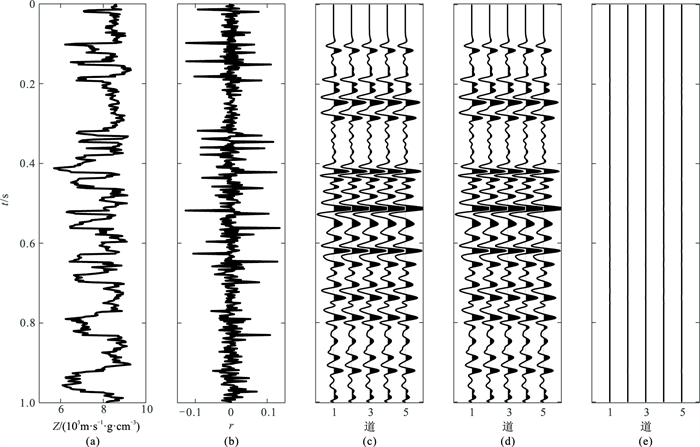
为了进一步了解式(5)的精度,给出了一个基于实际测井资料(图 2a)的正演结果(图 2)。可见,当反射系数的绝对值|r|≤0.3时(图 2b),式(5)(图 2d)与式(3)(图 2c)的正演结果几乎没有差异(图 2e),进一步证明式(5)作为线性化的波阻抗正演近似公式具有较高精度。
|
图 2 分别利用式(3)和式(5)对实际测井资料正演得到的地震记录 (a)实际地层波阻抗;(b)由式(3)获得的真实反射系数;(c)由式(3)得到的地震记录;(d)由式(5)得到的地震记录;(e)图c与图d的数据差 |
根据贝叶斯理论,已知观测数据d时,模型m的后验概率分布P(m|d)等于模型参数的先验概率分布P(m)与似然函数P(d|m)的乘积再除以边缘概率密度P(d),即
| $ P(\mathit{\boldsymbol{m}}\mid \mathit{\boldsymbol{d}}) = \frac{{P(\mathit{\boldsymbol{d}}\mid \mathit{\boldsymbol{m}})P(\mathit{\boldsymbol{m}})}}{{P(\mathit{\boldsymbol{d}})}} $ | (8) |
式中P(d)为一个常数,其作用是使后验概率分布的总和等于1。对于波阻抗反演,假设噪声服从高斯分布,则似然函数可以表示为
| $ \begin{array}{l} P(\mathit{\boldsymbol{D}}\mid \mathit{\boldsymbol{Z}}) = \\ \;\;\;\;{P_0}\exp \left[ { - \frac{1}{2}{{(\mathit{\boldsymbol{D}} - \mathit{\boldsymbol{WSZ}})}^{\rm{T}}}\mathit{\boldsymbol{C}}_e^{ - 1}(\mathit{\boldsymbol{D}} - \mathit{\boldsymbol{WSZ}})} \right] \end{array} $ | (9) |
式中:Ce为噪声的协方差。阻抗模型Z的先验分布可表示为
| $ P(\mathit{\boldsymbol{Z}}) = {P_{0z}}\exp [ - R(\mathit{\boldsymbol{Z}})] $ | (10) |
式中:R(Z)为Z的函数,不同的先验分布对应不同的R(Z);P0和P0Z分别为两个常数,其作用是使概率分布的总和为1。联立式(9)和式(10)并假设噪声独立分布(即Ce=σe2I,σe为噪声的标准差,I为单位矩阵),即可得到波阻抗的后验概率分布
| $ \begin{array}{l} P(\mathit{\boldsymbol{Z}}\mid \mathit{\boldsymbol{D}}) \propto \\ \exp \left[ { - \frac{1}{{2\sigma _e^2}}{{(\mathit{\boldsymbol{D}} - \mathit{\boldsymbol{WSZ}})}^{\rm{T}}}(\mathit{\boldsymbol{D}} - \mathit{\boldsymbol{WSZ}}) - \lambda R(\mathit{\boldsymbol{Z}})} \right] \end{array} $ | (11) |
其中λ为超参数。式(11)忽略了边缘概率密度P(D)。使式(11)中指数项最大的解就是最大后验概率解,因此可以建立反演目标函数
| $ J(\mathit{\boldsymbol{Z}}) = \frac{1}{{2\sigma _e^2}}{(\mathit{\boldsymbol{D}} - \mathit{\boldsymbol{WSZ}})^{\rm{T}}}(\mathit{\boldsymbol{D}} - \mathit{\boldsymbol{WSZ}}) + \lambda R(\mathit{\boldsymbol{Z}}) $ | (12) |
引入高斯先验分布,则R(Z)可表示为
| $ R(\mathit{\boldsymbol{Z}}) = \frac{1}{2}\left\| {\mathit{\boldsymbol{Z}} - {\mathit{\boldsymbol{Z}}_0}} \right\|_2^2 $ | (13) |
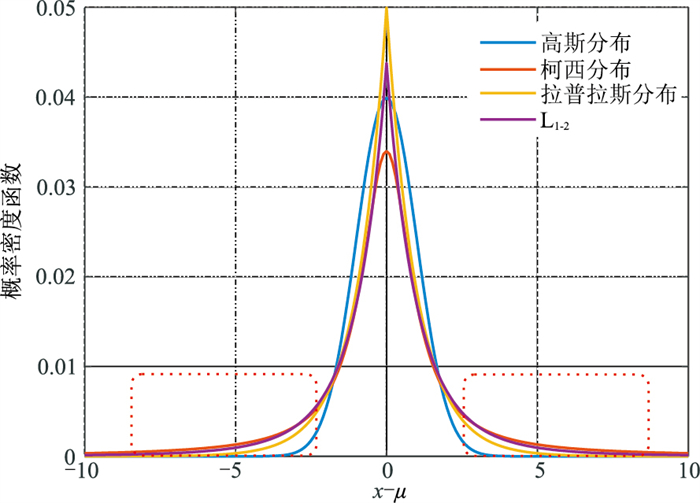
式中Z0为初始模型。在反演合成数据时,通过平滑真实波阻抗得到初始模型;在反演实际数据时,一般通过插值、外推测井数据得到初始模型。基于高斯先验分布的反演结果一般较光滑,为此前人利用其他分布提高反演分辨率,如柯西分布、拉普拉斯分布(L1范数)以及L1-2范数。图 3为不同分布的一维概率密度函数对比。由图可见:①高斯分布的峰值最宽,且没有“长尾”分布(“长尾”保证了反演结果中允许存在某些“大”值,即保证“稀疏”,如图中红色框位置),所以基于高斯分布的反演结果较光滑且抗噪性差。②柯西分布和拉普拉斯分布在提升反演结果稀疏度方面明显优于高斯分布,二者的概率密度函数的峰值更尖锐且有明显的“长尾”。③L1-2范数的概率密度函数的峰值更尖锐,且“长尾”更明显,因此在理论上可以获得更稀疏的反演结果。
|
图 3 不同分布的一维概率密度函数对比 横坐标为一维变量x的值减去均值μ (这里均值为0) |
为了更直观地对比几种不同的分布,绘制了L0范数、L1范数(对应拉普拉斯分布)、L2范数(对应高斯分布)以及L1-2范数的二维图像(图 4)。可见,相比于L2范数(图 4c)和L1范数(图 4b),L1-2范数(图 4d)与L0范数(图 4a)更相似,因此理论上基于L1-2范数约束可以获得比L2范数和L1范数约束更稀疏、分辨率更高的反演结果。

|
图 4 L0范数(a)、L1范数(b)、L2范数(c)以及L1-2范数(d)的二维图像 |
以二维向量(x,y)为例,几种范数的定义为
| $ \left\{ {\begin{array}{*{20}{l}} {{L_0} = \left\{ {\begin{array}{*{20}{c}} 0&{(x, y) = 0}\\ 2&{x \ne 0, y \ne 0}\\ 1&{{\rm{其他}}} \end{array}} \right.}\\ {{L_2} = \sqrt {|x{|^2} + |y{|^2}} }\\ {{L_1} = |x| + |y|}\\ {{L_{1 - 2}} = |x| + |y| - \sqrt {|x{|^2} + |y{|^2}} } \end{array}} \right. $ | (14) |
式中x、y为二维向量的分量。L0范数定义为计算模型中非零项的个数,也被认为是最稀疏的度量。因此可通过对比其他范数图像与L0范数图像的相似程度判断范数的稀疏性。
当引入L1-2正则化时,在式(13)的基础上,R(Z)可以表示为
| $ R(\mathit{\boldsymbol{Z}}) = \frac{\eta }{2}{\left\| {\mathit{\boldsymbol{Z}} - \mathit{\boldsymbol{Z}}} \right\|_0}_2^2 + \beta \left( {{{\left\| \mathit{\boldsymbol{Z}} \right\|}_1} - \alpha {{\left\| \mathit{\boldsymbol{Z}} \right\|}_2}} \right) $ | (15) |
式中:α≥0为权重参数,该值越大,L1-2范数越稀疏;η和β则分别控制高斯项和L1-2正则化项在目标函数中的比例。由于L1-2范数是一种稀疏范数,而波阻抗并不满足稀疏性假设,因此将式(15)代入式(12)进行反演必定会导致错误的反演结果。虽然波阻抗不满足稀疏假设,但波阻抗的空间导数满足稀疏条件,因此类似于TV正则化,本文通过对波阻抗的空间导数施加稀疏约束,从而获得高分辨率的反演结果。这样,基于L1-2正则化的波阻抗反演的目标函数可定义为
| $ \begin{array}{l} J(\mathit{\boldsymbol{Z}}) = \frac{1}{2}\left\| {\mathit{\boldsymbol{D}} - \mathit{\boldsymbol{WSZ}}} \right\|_2^2 + \frac{\eta }{2}\mathit{\boldsymbol{Z}} - {\mathit{\boldsymbol{Z}}_0}_2^2 + \\ \;\;\;\;\;\;\;\;\;\beta \left( {{{\left\| {\mathit{\boldsymbol{SZ}}} \right\|}_1} - \alpha {{\left\| {\mathit{\boldsymbol{SZ}}} \right\|}_2}} \right) \end{array} $ | (16) |
在反演过程中,通常需要多次试验获得参数η和β,以保证最终获得较满意的反演结果。利用IRLS算法求解式(16),将式(16)对Z求导可得
| $ \begin{array}{l} J(\mathit{\boldsymbol{Z}}) = \frac{1}{2}\left\| {\mathit{\boldsymbol{D}} - \mathit{\boldsymbol{WSZ}}} \right\|_2^2 + \frac{\eta }{2}\mathit{\boldsymbol{Z}} - {\mathit{\boldsymbol{Z}}_0}_2^2 + \\ \;\;\;\;\;\;\;\;\;\beta \left( {{{\left\| {\mathit{\boldsymbol{SZ}}} \right\|}_1} - \alpha {{\left\| {\mathit{\boldsymbol{SZ}}} \right\|}_2}} \right) \end{array} $ | (17) |
令
| $ \begin{array}{l} {\mathit{\boldsymbol{Z}}^{n + 1}} = {\left[ {{{(\mathit{\boldsymbol{WS}})}^{\rm{T}}}(\mathit{\boldsymbol{WS}}) + \eta \mathit{\boldsymbol{I}} + \mathit{\boldsymbol{w}}} \right]^{ - 1}} \times \\ \;\;\;\;\;\;\;\;\;\;\left[ {{{(\mathit{\boldsymbol{WS}})}^{\rm{T}}}\mathit{\boldsymbol{D}} + \eta {\mathit{\boldsymbol{Z}}^n}} \right] \end{array} $ | (18) |
式中:Zn为第n次迭代的解;w为重加权矩阵,可表示为
| $ w = \beta {\mathit{\boldsymbol{S}}^{\rm{T}}}\left[ {\frac{I}{{{\rm{diag}}\left( {\left| {\mathit{\boldsymbol{S}}{\mathit{\boldsymbol{Z}}^{n - 1}}} \right|} \right)}} - \alpha \frac{I}{{\mathit{\boldsymbol{S}}{\mathit{\boldsymbol{Z}}^{n - 1}}_2}}} \right]\mathit{\boldsymbol{S}} $ | (19) |
利用IRLS算法求解式(16)的算法流程为:
(1) 设定超参数η和β、权重参数α以及最大迭代次数K;
(2) 设定初始模型Z0;
(3) 给定子波矩阵W及差分矩阵S;
(4) 令n=1,根据式(19)计算w;
(5) 根据式(18)进行求解,并令n=n+1;
(6) 重复步骤(4)和步骤(5),直至达到最大迭代次数。
值得注意的是,K的选择对于反演结果的收敛以及算法的效率极为重要。一般来说,迭代10次左右即可获得满意的反演结果,但K的选择还与模型的复杂度以及数据的信噪比有关。在反演实际地震数据时,可通过对比井旁道的反演结果与实际测井资料设定较合适的K。
3 模型数据测试利用单道块状模型和二维SEG/EAGE推覆体模型,分别对比、分析基于L2范数、L1范数以及L1-2范数约束的波阻抗反演结果,以验证所提方法的效果。在反演推覆体模型时,对反演结果执行f-x域空间预测滤波以提高反演结果的横向连续性。文中信噪比定义为
| $ {\rm{SNR}} = 10\lg \frac{{\left\| {{\mathit{\boldsymbol{s}}^ * }} \right\|_2^2}}{{\left\| {\mathit{\boldsymbol{s}} - {\mathit{\boldsymbol{s}}^ * }} \right\|_2^2}} $ | (20) |
式中:s*为无噪地震数据;s为含噪地震数据。
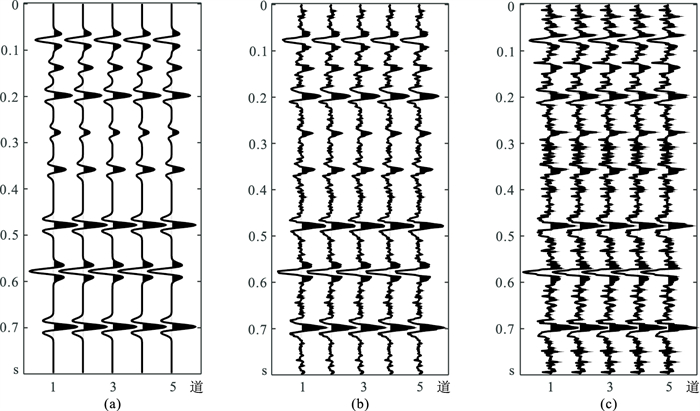
利用式(3)得到单道块状模型反射系数,与主频为30Hz的雷克子波褶积得到合成地震记录(图 5),然后利用合成地震记录反演得到波阻抗(图 6)。从结果来看:①由于没有施加稀疏约束,且数据含噪,对于块状模型,基于L2范数约束的反演效果明显较差(图 6a、图 6d)。②基于L1范数(图 6b、图 6e)和L1-2范数(图 6c、图 6f)约束的反演结果均呈明显的“块状”特征,反演效果优于L2范数,其中L1-2范数约束的反演结果与真实模型吻合度更高(图 6b、图 6c、图 6e、图 6f的红色箭头处)。③随着噪声能量增强,反演质量均下降。如基于L2范数约束的反演结果仍然无法精确刻画地层的“块状”特征(图 6d);基于L1范数约束的反演结果与真实值也存在偏差(图 6e);基于L1-2范数约束的反演结果虽然在某些层位与真实值稍有差别,但总体上吻合较好,且很好地刻画了波阻抗的“块状”特征(图 6f),证明了所提方法的有效性。
|
图 5 基于单道块状模型的合成地震数据 (a)无噪;(b)SNR=10dB;(c)SNR=4dB |
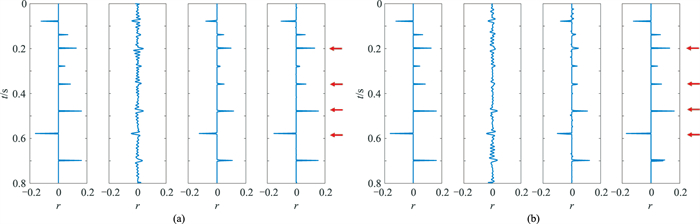
图 7为基于图 6数据计算的反射系数。由图可见:①无论信噪比为10dB还是4dB,基于L2范数约束的反演效果均较差,反演结果与真实的反射系数相差很大。这是由于L2范数为平滑约束,其概率分布函数在均值μ附近的峰值较宽(图 3),因此反演结果不能很好地压制一些“小值”,即抗噪性较差,而且概率密度函数“长尾”不明显,从而使某些离散点被压制,因此不能反演幅值较大的反射系数。②L1范数和L1-2范数约束的反演效果明显变好,其中L1-2范数由于更好地压制了“小值”,同时也保护了“大值”,因此基于L1-2范数约束的反演效果优于基于L1范数约束,尤其是当信噪比为4dB时(图 7b红色箭头处)。
|
图 7 基于图 6数据计算的反射系数
(a)SNR=10dB;(b)SNR=4dB 自左至右依次为真实反射系数、基于L2范数的反射系数、基于L1范数的反射系数以及基于L1-2范数的反射系数 |
利用式(3)得到SEG/EAGE推覆体模型(图 8b)反射系数,与主频为40Hz的雷克子波褶积并加入信噪比为4dB的随机噪声得到合成地震记录(图 8a)。图 8为基于SEG/EAGE推覆体模型的反演结果。从反演结果可见:①L1-2范数约束的反演结果的分辨率与精度最高(图 8f),与真实模型(图 8b)吻合很好;基于L1范数约束的反演效果略差(图 8e),但仍然好于基于L2范数约束(图 8d)。②由于单道算法的限制,反演结果中存在明显的横向不连续现象,尤其是当加入稀疏约束时,这种现象更明显(图 8e、图 8f)。因此,有必要改善反演结果的横向连续性。③三种范数约束的波阻抗反演结果(图 8d~图 8f)经过f-x域空间预测滤波后,横向连续性均有提升(图 8g~图 8i),尤其是图 8h和图 8i。该结果进一步证明了本文所提方法的有效性和可行性。

|
图 8 基于SEG/EAGE推覆体模型的反演结果 (a)合成地震记录;(b)推覆体模型;(c)反演输入的波阻抗初始模型;(d)基于L2范数的反演结果;(e)基于L1范数的反演结果;(f)基于L1-2范数的反演结果;(g)图d的f-x域滤波结果;(h)图e的f-x域滤波结果;(i)图f的f-x域滤波结果 |
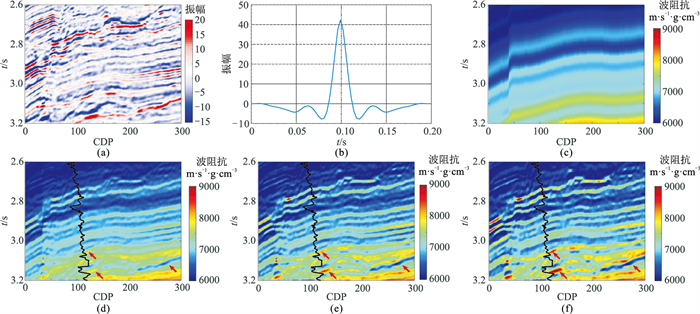
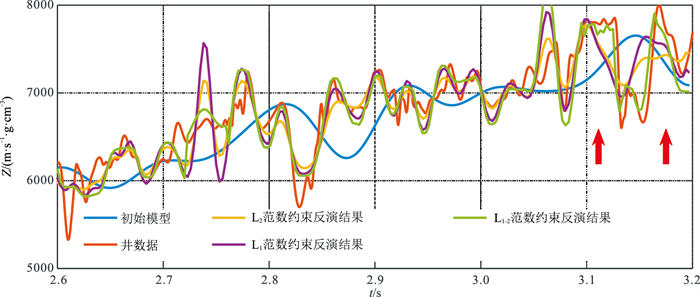
基于M区实际地震资料测试本文方法。图 9为M区叠后地震资料反演结果。可见:①基于L2范数约束的反演结果分辨率较低(图 9d)。②基于L1范数(图 9e)和L1-2范数约束(图 9f)的反演效果得到明显改善,反演分辨率更高,对地层的刻画更清晰,且后者优于前者(红色箭头处)。图 10为井旁道反演结果与经过Backus平均的实际测井资料对比结果。可见,基于L1-2范数约束的井旁道反演结果与测井曲线更吻合,尤其表现在对“块状”特征的反演(红色箭头处)。此外,通过求取目的层段(3.0~3.2s)反演结果与真实测井数据的相关系数,可以定量对比不同范数约束的反演结果差异。向量X与Y的相关系数定义为
| $ C = \frac{{c(\mathit{\boldsymbol{X}}, \mathit{\boldsymbol{Y}})}}{{\sqrt {c(\mathit{\boldsymbol{X}}, \mathit{\boldsymbol{X}}) \times c(\mathit{\boldsymbol{Y}}, \mathit{\boldsymbol{Y}})} }} $ | (21) |
|
图 9 M区叠后地震资料反演结果
(a)输入的叠后地震数据;(b)基于统计法提取的地震子波;(c)反演输入的初始波阻抗模型;(d)L2范数反演结果的f-x域空间预测滤波;(e)L1范数反演结果的f-x域空间预测滤波;(f)L1-2范数反演结果的f-x域空间预测滤波 时间采样间隔为3ms,空间总道数为300道。黑色曲线为测井波阻抗曲线 |
|
图 10 井旁道反演结果与经过Backus平均的实际测井资料对比结果 |
式中:c(X,Y)为X与Y的协方差;c(X,X)和c(Y,Y)分别为X和Y的方差。
基于L2范数、L1范数及L1-2范数的反演结果与真实测井数据的相关系数分别为0.6529、0.5197、0.7264,表明:基于L1-2范数的反演结果与真实测井数据更吻合,这是由于L1-2范数约束为稀疏约束(图 10的红色箭头处),可很好地反演地层的“块状”信息;基于L2范数和L1范数约束的反演效果则相对较差,其中基于L1范数约束的反演结果的相关系数小于基于L2范数约束,可能原因是前者的反演结果尽管在稀疏性方面要优于后者,但前者的反演结果在大约3.14s处存在一个明显的层位漂移,从而导致反演结果与真实测井数据的相关系数较低。
5 结论尽管波阻抗反演技术已经相当成熟,但仍然存在一定问题,如反问题的不适定性、反演的分辨率低以及对地层边界刻画不清晰等。针对这些问题,本文提出了基于L1-2正则化的地震波阻抗“块”反演方法。首先推导线性化的波阻抗正演近似公式并进行精度分析,证明近似式的精度较高。然后介绍了基于L1-2范数约束的波阻抗反演方法,与传统的基于L2范数和L1范数约束的反演方法相比,基于L1-2范数约束的反演结果明显提高了分辨率,反演结果更具“块状”特征。相关系数的定量对比也证明了基于L1-2范数的反演结果优于基于L1范数和L2范数。此外,文中引入f-x域空间预测滤波改善单道反演算法带来的横向不连续现象。显而易见的是,通过对反演结果执行f-x域空间预测滤波,明显提高了反演结果的横向连续性。合成和实际地震数据反演证明了所提方法的可行性和有效性。
| [1] |
渥·伊尔马滋著; 刘怀山, 王克斌, 童思友, 等译. 地震资料分析: 地震资料处理、反演和解释(下册)[M]. 北京: 石油工业出版社, 2006.
|
| [2] |
MAURYA S P, SARKAR P. Comparison of post stack seismic inversion methods: A case study from Blackfoot Field, Canada[J]. International Journal of Scientific and Engineering Research, 2016, 7(8): 1091-1101. |
| [3] |
张凌远, 张宏兵, 尚作萍, 等. 基于Zoeppritz方程的叠前和叠后混合多参数非线性地震反演[J]. 石油地球物理勘探, 2021, 56(1): 164-171. ZHANG Lingyuan, ZHANG Hongbing, SHANG Zuoping, et al. Nonlinear multi-parameter hybrid inversion of pre-stack and post-stack seismic data based on Zoeppritz equation[J]. Oil Geophysical Prospecting, 2021, 56(1): 164-171. |
| [4] |
周东红, 李景叶, 陈莉. 基于弹性波动方程的叠后地震反演方法[J]. 石油地球物理勘探, 2018, 53(2): 395-402. ZHOU Donghong, LI Jingye, CHEN Li. Poststack inversion based on the elastic wave equation[J]. Oil Geophysical Prospecting, 2018, 53(2): 395-402. DOI:10.13810/j.cnki.issn.1000-7210.2018.02.022 |
| [5] |
LINDSETH R O. Synthetic sonic logs: A process for stratigraphic interpretation[J]. Geophysics, 1979, 44(1): 3-26. |
| [6] |
邹振桓, 杨文采. 地震道的广义线性反演[J]. 石油地球物理勘探, 1987, 22(4): 363-375. ZOU Zhenhuan, YANG Wencai. Generalized linear inversion of seismic traces[J]. Oil Geophysical Prospecting, 1987, 22(4): 363-375. DOI:10.13810/j.cnki.issn.1000-7210.1987.04.001 |
| [7] |
LI S, PENG Z P. Seismic acoustic impedance inversion with multi-parameter regularization[J]. Journal of Geophysics and Engineering, 2017, 14(3): 520-532. |
| [8] |
冉喜阳, 周怀来, 张益明, 等. 一种基于稀疏窗S变换的分频-重构波阻抗反演方法[J]. 中国海上油气, 2019, 31(4): 75-84. RAN Xiyang, ZHOU Huailai, ZHANG Yiming, et al. A frequency division-reconstruction wave impedance inversion method based on sparse window S transform[J]. China Offshore Oil and Gas, 2019, 31(4): 75-84. |
| [9] |
郭朝斌, 杨小波, 陈红岳, 等. 约束稀疏脉冲反演在储层预测中的应用[J]. 石油物探, 2006, 45(4): 397-400. GUO Chaobin, YANG Xiaobo, CHEN Hongyue, et al. Constrained sparse pulse inversion research in north of Haitongji depression[J]. Geophysical Prospecting for Petroleum, 2006, 45(4): 397-400. DOI:10.3969/j.issn.1000-1441.2006.04.011 |
| [10] |
HAMID H, PIDLISECKY A. Multitrace impedance inversion with lateral constraints[J]. Geophysics, 2015, 80(6): M101-M111. |
| [11] |
WANG L Q, ZHOU H, WANG Y F, et al. Three-parameter prestack seismic inversion based on L1-2 minimization[J]. Geophysics, 2019, 84(5): R753-R766. DOI:10.1190/geo2018-0730.1 |
| [12] |
DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. |
| [13] |
ZHANG R, CASTAGNA J. Seismic sparse-layer reflectivity inversion using basis pursuit decomposition[J]. Geophysics, 2011, 76(6): R147-R158. |
| [14] |
刘国昌, 蔡加铭, 闫海洋, 等. 利用稀疏约束非平稳多项式回归去除地震噪声及拾取初至[J]. 石油地球物理勘探, 2020, 55(3): 548-556. LIU Guochang, CAI Jiaming, YAN Haiyang, et al. Using sparse-constrained nonstationary polynomial regression to remove seismic noises and picking up first arrival[J]. Oil Geophysical Prospecting, 2020, 55(3): 548-556. |
| [15] |
程三, 张志勇, 周峰, 等. 非结构化网格渐进自适应正则化反演算法[J]. 石油地球物理勘探, 2022, 57(2): 467-477. CHENG San, ZHANG Zhiyong, ZHOU Feng, et al. Study on step-by-step regularization inversion based on adaptive unstructured mesh[J]. Oil Geophysical Prospecting, 2022, 57(2): 467-477. |
| [16] |
CLAERBOUT J F, MUIR F. Robust modeling with erratic data[J]. Geophysics, 1973, 38(5): 826-844. |
| [17] |
TIKHONOV A N, GONCHARSKY A V, STEPANOV V V, et al. Numerical Methods for the Solution of Ill-Posed Problems[M]. Nether-lands: Springer, 1995.
|
| [18] |
BULAND A, OMRE H. Bayesian linearized AVO inversion[J]. Geophysics, 2003, 68(1): 185-198. |
| [19] |
TARANTOLA A. Inverse Problem Theory and Methods for Model Parameter Estimation[M]. Society for Industrial and Applied Mathematics, 2005.
|
| [20] |
ZHANG F C, DAI R H, LIU H Q. Seismic inversion based on L1-norm misfit function and total variation regularization[J]. Journal of Applied Geophysics, 2014, 109(10): 111-118. |
| [21] |
SUN J J, LI Y G. Adaptive Lp inversion for simultaneous recovery of both blocky and smooth features in a geophysical model[J]. Geophysical Journal International, 2014, 197(2): 882-899. |
| [22] |
WANG Y F, MA X, ZHOU H, et al. L1-2 minimization for exact and stable seismic attenuation compensation[J]. Geophysical Journal International, 2018, 213(3): 1629-1646. |
| [23] |
CANALES L L. Random noise reduction[C]. SEG Technical Program Expanded Abstracts, 1984, 3: 525-527.
|
| [24] |
SPITZ S. Seismic trace interpolation in the F-X domain[J]. Geophysics, 1991, 56(6): 785-794. |
| [25] |
姚建阳. 用地震道积分法提高地层的识别能力[J]. 石油物探, 1990, 29(1): 40-49. YAO Jianyang. Enhancement of the discernibility on formation by seismic trace integration[J]. Geophysical Prospecting for Petroleum, 1990, 29(1): 40-49. |



 陈小宏, 北京市昌平区府学路18号中国石油大学(北京)地球物理学院, 102249。Email:
陈小宏, 北京市昌平区府学路18号中国石油大学(北京)地球物理学院, 102249。Email: 
