地球物理学家希望通过观测数据反推得到地下介质模型参数,即建立观测数据与地下介质参数之间的关系。地震勘探中,地震记录可表示为地震子波与反射系数的褶积,也可表述为子波矩阵与反射系数向量的乘积。地震反演在无噪情况下可利用简单的矩阵求逆获得目标泛函的解。然而,地震记录通常是包含噪声的,这便需要利用最小二乘等方法获得最优解[1-2]。地震反演技术自提出以来便被广泛应用于烃类检测、储层预测等领域[3-6]。随着地震勘探技术的发展与进步,对反演精度与分辨率提出了更高要求[7-8]。稀疏地震反演除了可获得稀疏反射系数及“块化”阻抗之外,还可有效提高分辨率、横向连续性及层位边界保真度[9-10]。
匹配追踪(Matching Pursuit,MP)算法最早是由Mallat等[11]提出,用以进行信号分解及高精度时频分析的一种方法。近年来,MP被广泛应用于信号稀疏表示、高精度时频分析、地震信号分解与重构[12]、噪声与强反射压制[13-16]、储层预测[17]、薄层顶底反射系数提取[18]及砂体尖灭点刻画[19]等众多领域。此外,MP是求解L0范数的经典算法,可有效获取目标泛函的稀疏解[20]。然而,MP是一种贪婪的迭代算法,因此如何提高MP算法的计算效率一直是业内的热点问题。针对MP算法计算效率低等问题,众多MP的发展算法被提出,三参数快速MP可以通过缩减冗余字典的规模提高计算效率[21];动态MP通过改变时频原子局部瞬时属性提高信号分解速度[22-23];正则化正交MP可在字典不完备的情况下实现有效的稀疏信号恢复,且该算法具备良好的鲁棒性[24]。虽然在信号分析领域MP的发展算法层出不穷,但在地震反演领域,如何提高MP反演算法计算效率与稳定性仍是热点问题。
时间域地震反演具有稳定性高、方法简单可行的特点[25-28],但其分辨率较低。频率域反演通过构建频率域褶积模型,可以进行地震信号频带内的频率解耦,从而获得高分辨率反演结果,但其稳定性不足[20]。此外,地震反演是病态、多解的,反演多解性主要表现为多个地下参数模型都可产生相同的地震响应[29-30]。在反演框架中添加如高斯分布等先验信息是缓解反演多解性的有效方法之一,然而这种方式无法获得反射系数稀疏解,也就无法获得“块化”阻抗信息[10]。
本文首先从MP冗余字典的构建出发,结合时间域反演稳定性好、频率域反演分辨率高的特性,构建时频域冗余字典。对于MP算法,本文提出全域正则化快速MP算法,每次迭代同时选择所有可能的匹配原子,并通过正则化方法依据能量筛选出最优原子作为最终的匹配原子库。在此基础上,将初始模型约束引入反演框架,构建初始模型约束的时频域地震反演目标泛函,并通过最小二乘求解。最后,利用模型及实际地震资料测试了本文方法的有效性及实用性。模型及实际资料测试结果表明:本文方法可以有效获取反射系数的稀疏解。此外,相较于常规MP反演方法,本文方法的计算效率、反演结果的分辨率及边界保真度均得到了有效提升。
1 理论与方法 1.1 初始模型约束的时频域地震反演在地震反演领域,经典正演模型可表示为
| $ \mathit{\boldsymbol{S}}(t) = \mathit{\boldsymbol{W}} \cdot \mathit{\boldsymbol{R}} + \mathit{\boldsymbol{N}} $ | (1) |
式中S(t)、W、R、N、t分别表示时间域地震信号、地震子波矩阵、反射稀疏序列、噪声序列及时间。针对时间域稳定性高、但分辨率有限的问题,联合域褶积模型被提出[31]
| $ \mathit{\boldsymbol{S}}(f) = \mathit{\boldsymbol{F}}(f) \cdot \mathit{\boldsymbol{R}} + \mathit{\boldsymbol{N}}(f) $ | (2) |
式中S(f)、F(f)、N(f)分别为地震信号频谱、频率域核矩阵及噪声频谱,f表示频率。具体地,式(2)中时频域核矩阵的公式为
| $ \begin{array}{l} {{\mathit{\boldsymbol{F}}}}(f) = \\ {\left[ {\begin{array}{*{20}{c}} {W\left( {2\pi {f_1}} \right){{\rm{e}}^{ - {\rm{i}}2\pi {t_1}{f_1}}}}& \cdots &{W\left( {2\pi {f_1}} \right){{\rm{e}}^{ - {\rm{i}}2\pi {t_m}{f_1}}}}\\ {W\left( {2\pi {f_2}} \right){{\rm{e}}^{ - i2\pi {\pi _1}{f_2}}}}& \cdots &{W\left( {2\pi {f_2}} \right){{\rm{e}}^{ - i2\pi {t_m}{f_2}}}}\\ {}& \vdots &{}\\ {W\left( {2\pi {f_n}} \right){{\rm{e}}^{ - i2\pi {\pi _1}{f_n}}}}& \cdots &{W\left( {2\pi {f_n}} \right){{\rm{e}}^{ - {\rm{i}}2\pi {t_m}{f_n}}}} \end{array}} \right]_{n \times m}} \end{array} $ | (3) |
式中:fi为所选频率, i=1, 2, …, n;地震信号S(t)的采样点数为m; W(2πfi)为子波频率域形式。一般地,地震信号的有效频带为10~60Hz,而对于宽频地震信号,该范围的上、下限应该由地震信号分析获得。本文所用为常规地震信号,因此频带设定为10~60Hz。由于信号频谱是由虚部及实部两部分组成,因此可将时频域联合褶积模型改写为
| $ \left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{S}}{{(f)}_{\rm{r}}}}\\ {\mathit{\boldsymbol{S}}{{(f)}_{\rm{i}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{F}}{{(f)}_{\rm{r}}}}\\ {\mathit{\boldsymbol{F}}{{(f)}_{\rm{i}}}} \end{array}} \right]\mathit{\boldsymbol{R}}(t) + \left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{N}}{{(f)}_{\rm{r}}}}\\ {\mathit{\boldsymbol{N}}{{(f)}_{\rm{i}}}} \end{array}} \right] $ | (4) |
式中:下标r代表信号实部;下标i表示信号虚部。将式(4)改写为简单的矩阵形式
| $ \mathit{\boldsymbol{O}} = \mathit{\boldsymbol{DR}}(t) + \mathit{\boldsymbol{n}} $ | (5) |
式中:
为了提高反演结果的横向连续性,降低反演多解性,纵波阻抗初始模型约束被引入至反演目标泛函。需要注意的是,初始模型并非低频模型。纵波阻抗低频模型为
| $ {\mathit{\boldsymbol{P}}_{{\rm{low }}}} = {\left[ {{P_{{\rm{low1 }}}}, {P_{{\rm{low }}2}}, \cdots , {P_{{\rm{low }}m}}} \right]^{\rm{T}}} $ | (6) |
式中Plow为m×1阶向量。纵波阻抗初始模型为
| $ {\mathit{\boldsymbol{P}}_{{\rm{ini }}}} = \frac{1}{2}{\mathop{\rm In}\nolimits} {\left[ {{P_{{\rm{lowl }}}}/{P_{{\rm{lowl }}}}, {P_{{\rm{low }}2}}/{P_{{\rm{lowl }}}}, \cdots , {P_{{\rm{low }}m}}/{P_{{\rm{lowl }}}}} \right]^{\rm{T}}} $ | (7) |
联合时频域褶积模型与初始模型约束,可得
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{O}} = \mathit{\boldsymbol{DR}}(t)}\\ {\mathit{\boldsymbol{P}} = \mathit{\boldsymbol{CR}}(t)} \end{array}} \right. $ | (8) |
式中:C为m×m阶下三角阵,也即积分矩阵;Pini为m×1阶向量。
1.2 全域正则化快速匹配追踪MP是一种贪婪的迭代寻优方法,通过遍历冗余字典逐次寻找最优解[32]。MP主要包含以下几个步骤:①依据信号本身构建相应的冗余字典;②求取信号与冗余字典的内积,也即投影;③寻找内积最大值的位置并在字典中搜索对应的最佳匹配原子;④利用原信号减去最佳匹配原子获得残差;⑤将残差作为新信号重复①~④,直至残差小于设定阈值。对于地震信号,经过次迭代后的地震信号可表示为
| $ \mathit{\boldsymbol{S}}(t) = \sum\limits_{{\rm{Ite}} = 1}^k {{A_{{\rm{Itc}}}}} {\mathit{\boldsymbol{\chi }}_{{\rm{ttc}}}} + \mathit{\boldsymbol{d}} $ | (9) |
式中:AIte、χIte、d分别为经第Ite次迭代所得最佳匹配原子的振幅、最佳匹配原子及残差;k为迭代次数。
以下将着重介绍全域正则化快速匹配追踪算法。首先,计算信号与冗余字典的内积
| $ {\bf{Pro}} = \left\langle {{\bf{Sig}},\mathit{\boldsymbol{H}}} \right\rangle $ | (10) |
式中Sig与H分别表示时频域与纵波阻抗初始模型计算的对应信号与冗余字典,相应表达式为
| $ {\bf{Sig}} = \left[ {\begin{array}{*{20}{c}} {{\alpha _1}\mathit{\boldsymbol{O}}}\\ {_{\alpha 2}{\mathit{\boldsymbol{P}}_{{\rm{ini}}}}} \end{array}} \right]\quad \mathit{\boldsymbol{H}} = \left[ {\begin{array}{*{20}{c}} {{\alpha _1}\mathit{\boldsymbol{D}}}\\ {{\alpha _2}\mathit{\boldsymbol{C}}} \end{array}} \right] $ | (11) |
式中:Sig为(2n+m)×1阶向量;H为(2n+m)×m阶矩阵;Pro为m×1阶向量;α1与α2分别为时频域地震反演与初始模型约束的权重。α1一般取1即可;α2越大,反演结果越向初始模型靠拢。与常规多原子匹配追踪不同,本文方法在每次迭代中同时选取所有极大值位置点χ作为匹配原子备选库
| $ \mathit{\boldsymbol{\chi }} = {\rm{ localmax }}[{\rm{ }}{\bf{Pro }}] $ | (12) |
在此基础上,需要对备选原子库进行正则化筛选,在所有子集中依据能量筛选出能量最大的匹配原子库
| $ {\mathit{\boldsymbol{J}}_0} \in \mathit{\boldsymbol{\chi }}\quad {\rm{ s}}{\rm{. t}}{\rm{. }}\quad \left| {{\mathit{\boldsymbol{u}}_i}} \right| \le 2\left| {{\mathit{\boldsymbol{u}}_j}} \right|\quad i, j \in {\mathit{\boldsymbol{J}}_0} $ | (13) |
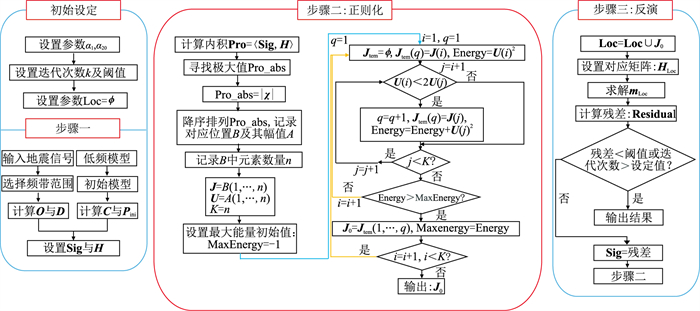
式中u、i和j的设定及具体正则化过程如图 1所示。式(13)所筛选出的原子库即为在原子库χ的所有子集中具有最大能量的子集J0,因此在某次迭代后最终的原子库为Loc=Loc∪J0(Loc在初次迭代前可设置为空集ϕ,详情可参考流程图中步骤二)。相较于常规快速匹配追踪反演中人为采用最大内积点的百分比函数进行计算,基于正则化的全域快速匹配追踪算法可更好地筛选出全域字典中所有的符合条件的原子,在提高计算效率的同时有效提高了反演的准确性。在获得匹配原子库后,可以利用最小二乘来获取对应振幅
| $ \mathit{\boldsymbol{m}} = {\left( {{\mathit{\boldsymbol{H}}_{{\rm{Loc}}}}^{\rm{T}} \cdot {\mathit{\boldsymbol{H}}_{{\rm{Loc}}}}} \right)^{ - 1}} \cdot \mathit{\boldsymbol{H}}_{{\rm{Loc}}}^{\rm{T}} \cdot \left[ {\begin{array}{*{20}{c}} {{\alpha _1}\mathit{\boldsymbol{O}}}\\ {{\alpha _2}{\mathit{\boldsymbol{P}}_{{\rm{ini }}}}} \end{array}} \right] $ | (14) |
|
图 1 全域正则化快速匹配追踪稀疏地震反演方法流程图 |
此时,残差信号可表示为
| $ {\rm{ }}{\bf{Residual }} = \left[ {\begin{array}{*{20}{c}} {{\alpha _1}\mathit{\boldsymbol{O}}}\\ {{\alpha _2}{\mathit{\boldsymbol{P}}_{{\rm{ini}}}}} \end{array}} \right] - {\mathit{\boldsymbol{H}}_{{\rm{Loc}}}}{\mathit{\boldsymbol{m}}_{{\rm{Loc}}}} $ | (15) |
得到残差后,令Sig=Residual,并重新进行正则化筛选与反演,直至迭代次数达到设定值或残差小于阈值。图 1给出了本文方法的详细流程。
1.3 一维模型试算为了验证本文方法的可行性,本文从测井资料中抽取了纵波速度与密度来合成纵波阻抗,并利用纵波阻抗计算得到反射系数。采用主频为30Hz的雷克子波与反射系数褶积得到了如图 2a所示的合成地震记录,其采样间隔为2ms,采样点数为250。若要获得稀疏解,需要降低迭代次数。
|
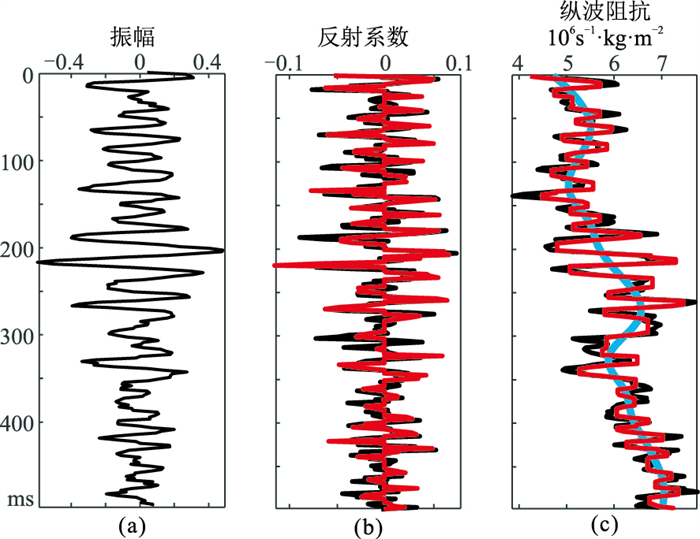
图 2 无噪地震记录稀疏反演结果
(a)合成地震记录;(b)反射系数;(c)纵波阻抗 迭代次数:9;α1=1.0,α2=0.5。黑色、红色及蓝色曲线分别代表模型值、反演值和初始模型值。下同 |
图 2为利用本文方法获得的稀疏解,由图可知,本方法可以很好地进行稀疏反射系数反演,且稀疏度与反射系数稀疏度较为一致,块化纵波阻抗的反演结果也与模型值高度相似。需说明的是本文中所有一维测试结果中的黑色、红色及蓝色曲线均分别代表模型值、反演值和初始模型值。
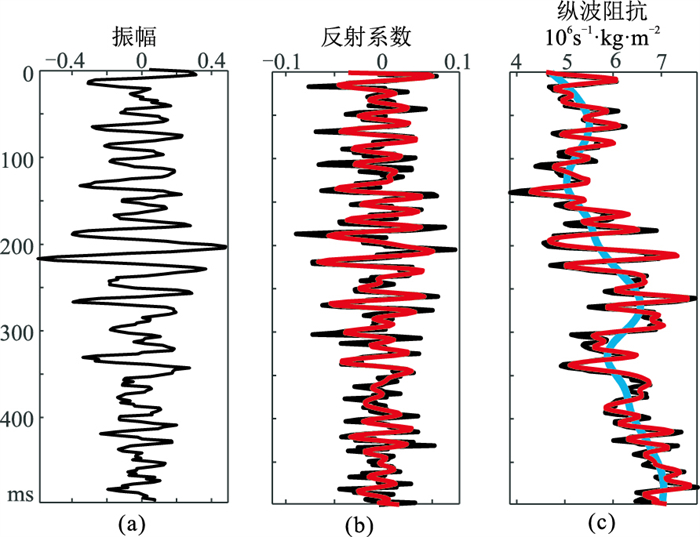
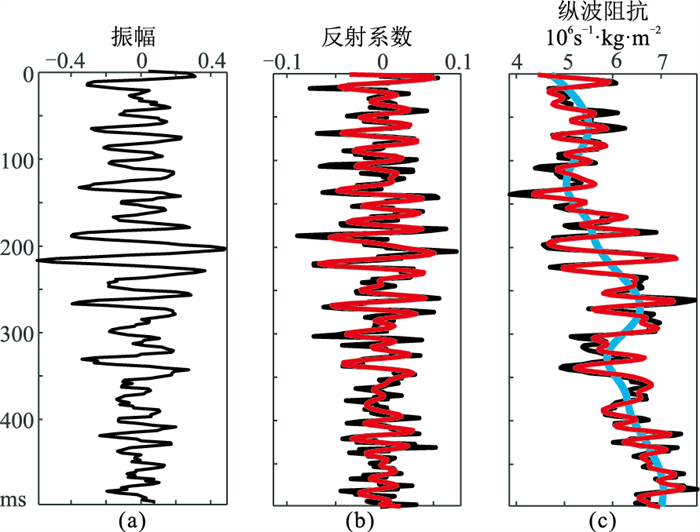
为了验证本文方法的有效性与实用性,分别利用本文方法与常规方法(快速匹配追踪地震反演方法)计算得到了如图 3、图 4所示的非稀疏反演结果。除迭代次数外,其余参数设置相同。其中,本文方法仅需15次迭代即可得到非稀疏反演结果(图 3c),而常规方法则需要50次迭代得到图 4c所示的非稀疏反演结果。此外,本文方法与传统方法用时分别为0.428s和1.265s。图 3、图 4中纵波阻抗反演结果与真实纵波阻抗相关系数分别为0.98和0.96。因此,本文方法反演所得结果在细节处与模型的匹配度稍高于常规方法所得反演结果。由对比结果可知,本文方法在有效提高计算效率的同时还可获得更准确的反演结果。
|
图 3 本文方法无噪地震记录非稀疏反演结果
(a)合成地震记录;(b)反射系数;(c)纵波阻抗 迭代次数:15;α1=1.0,α2=0.5 |
|
图 4 常规方法无噪地震记录非稀疏反演结果
(a)合成地震记录;(b)反射系数;(c)纵波阻抗 迭代次数:50;α1=1.0,α2=0.5 |
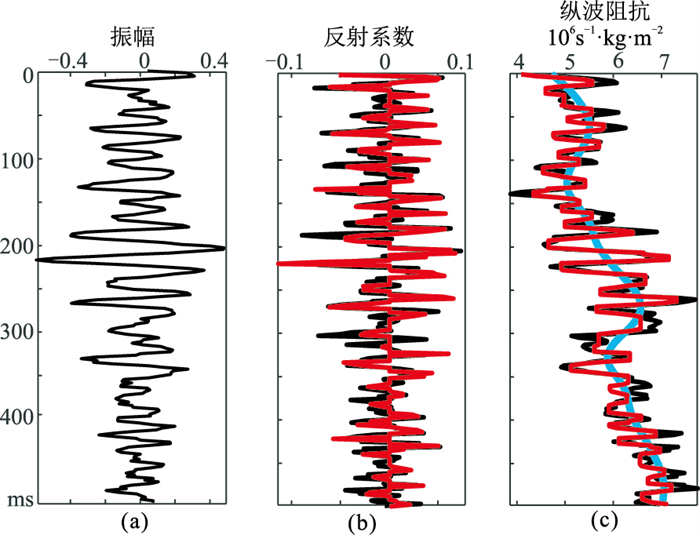
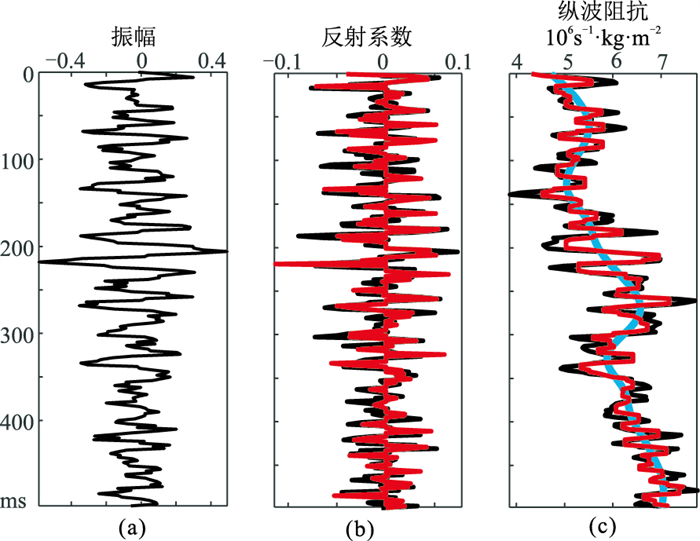
为测试本文方法的鲁棒性,在合成地震记录中加入了不同的随机高斯噪声,图 5a、图 6a、图 7a分别展示了信噪比(SNR)分别为5、2、1的含噪地震记录。由图可知,虽然随着信噪比的降低,反演值与模型值有所差异,但即使在信噪比为1的情况下,反演结果与模型值的相对变化吻合度依然较高。
|
图 5 SNR=5的反演结果
(a)合成地震记录;(b)反射系数;(c)纵波阻抗 迭代次数:9;α1=1.0,α2=0.8 |
|
图 6 SNR=2的反演结果
(a)合成地震记录;(b)反射系数;(c)纵波阻抗 迭代次数:8;α1=1.00,α2=1.05 |

|
图 7 SNR=1的反演结果
(a)合成地震记录;(b)反射系数;(c)纵波阻抗 迭代次数:8;α1=1.00,α2=1.11 |
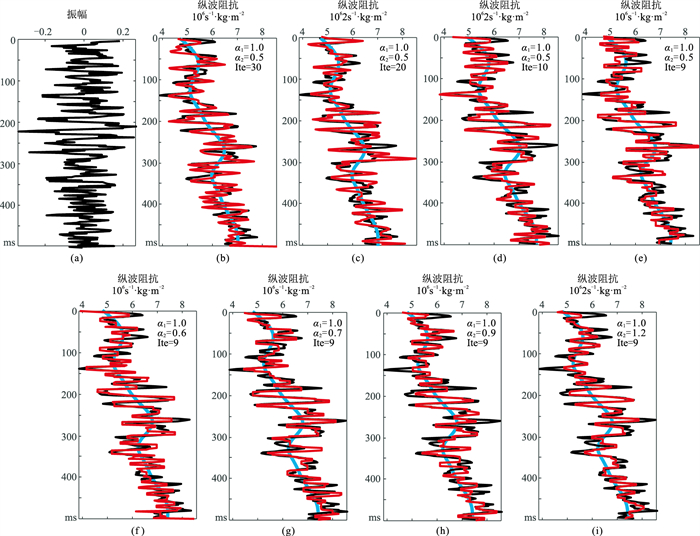
此外,笔者还对本文所提方法进行了质控测试(图 8)。所谓质控,即固定某些参数,只改变某个或部分参数来测试该参数对反演结果的影响。图 8a为信噪比为1的地震记录,后续质控测试都是在此地震记录之上进行的。首先,固定α1与α2,改变迭代次数来测试迭代次数(同图 1“初始设定”中的迭代次数)对反演结果的影响。图 8b~图 8e分别展示了迭代次数为30、20、10、9次的纵波阻抗反演结果。由图可知:对于含有较强噪声的地震记录,随着迭代次数的降低,反演结果逐渐趋于稳定。在此基础上,固定迭代次数(9次)不变,通过改变初始模型权重参数(α2)来测试初始模型约束对于反演结果的影响。图 8f~图 8i的迭代次数都为9次,而初始模型权重参数分别为0.6、0.7、0.9、1.2。由图 8可知,当减小迭代次数后,增加初始模型权重可以令反演结果靠近初始模型,从而进一步稳定反演结果。因此,当地震信号中含有过强噪声(SNR < 2)时,需要减小迭代次数同时提高初始模型约束项的权重(α2)获取稳定反演结果。综上,无噪及含噪地震信号的测试都说明了本文方法的可行性和有效性。
|
图 8 质控测试 (a)地震信号(SNR=1);(b)~(j)不同Ite或α2时纵波阻抗反演结果 |
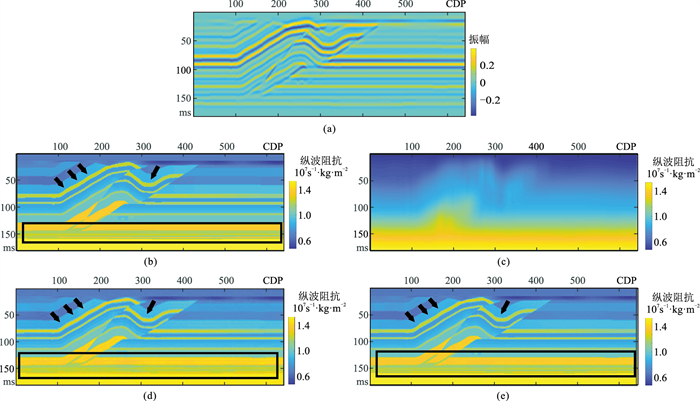
逆掩断层模型是测试稀疏反演方法边界保真度的有效模型。因此,为了进一步验证方法有效性,本文利用Marmousi逆掩断层二维模型对全域正则化快速匹配追踪算法进行测试。针对合成地震记录图 9a及原始纵波阻抗(图 9b),利用式(7)可获得对应的初始模型图 9c。分别采用常规快速匹配追踪算法及本文方法对该逆掩断层模型进行有效性测试。图 9d与图 9e分别为常规方法与本文方法的测试结果。由对比可知,利用全域正则化快速匹配追踪方法得到的纵波阻抗反演结果相较于常规方法得到的纵波阻抗反演结果具有更好的层位边界保真度。尤其在黑色箭头与黑色方框所示区域,可见本文方法所得结果具有清晰的边界与更好的横向连续性。
|
图 9 二维模型测试结果
(a)合成地震记录;(b)纵波阻抗;(c)纵波阻抗初始模型;(d)常规方法纵波阻抗反演结果;(e)本方法纵波阻抗反演结果 迭代次数:11;α1=1.0,α2=0.8 |
本文还针对二维模型进行了抗噪性测试,图 10a与图 10b分别展示了SNR=1的地震剖面与反演结果。由图可知,反演结果的横向连续性有些下降(图 10b中箭头所示),但其边界仍然较为清晰,且反演结果依然与模型保持了高度一致。

|
图 10 抗噪性测试结果
(a)含噪地震记录(SNR=1);(b)纵波阻抗反演结果 迭代次数:8;α1=1.0,α2=1.1 |
此外,仍然对二维模型反演的用时进行了记录。常规方法与本文方法用时分别为118s和35s。因此,本文方法的计算效率要高于传统快速匹配追踪算法,该测试同样验证了全域正则化快速匹配追踪稀疏地震反演方法的有效性。
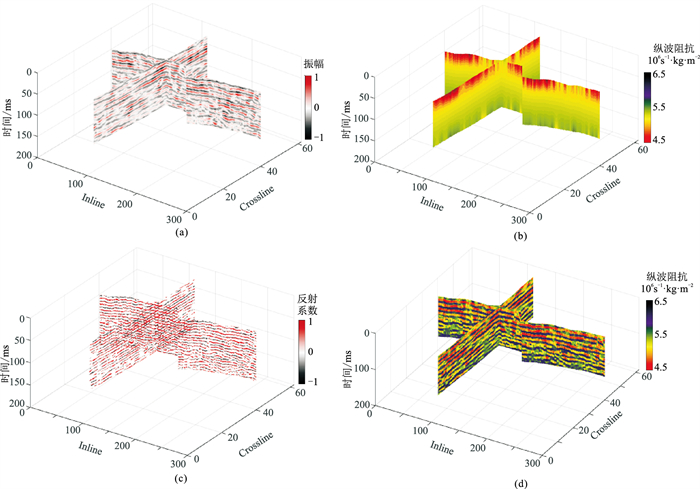
3 实际资料应用在模型测试的基础上,还需要利用实际资料来对本文方法的实用性进行测试。从中国东部M工区抽取了一个由18600道组成的三维地震数据体,测试本文方法的效果,并抽出两个剖面进行测试结果展示。从图 11a所示的地震剖面可知,该工区地层横向连续性较差,且存在多处弱反射区域。此外,快速的纵向变化及断层的发育都给地震反演方法带来了一定的困难与挑战。
|
图 11 三维地震数据反演结果
(a)地震剖面;(b)纵波阻抗低频模型;(c)稀疏反射系数反演结果;(d)块化纵波阻抗反演结果 迭代次数:9;α1=1.0,α2=0.8 |
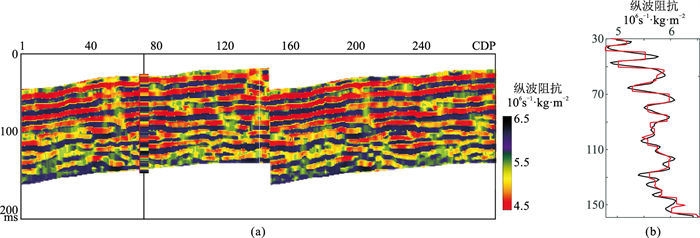
为了进行更加精确的反演,需利用高频滤波后的井数据建立纵波阻抗低频模型。图 11b为纵波阻抗低频模型,利用式(7)即可获得相应的纵波阻抗初始模型。图 11c与图 11d为采用全域正则化快速匹配追踪稀疏地震反演方法获得的稀疏反射系数反演结果与块化纵波阻抗反演结果。由图 11c可以看出,稀疏反射系数反演结果具有良好的横向连续性及稀疏度,其分辨率相对较高。由图 11d可知,块化纵波阻抗反演结果的层位边界较为清晰,可以有效对地层边界进行解释与刻画。为了说明方法的准确性,从三维反演结果中抽取一个剖面与井进行对比(图 12)。由于井数据频率较高,对实际井数据进行高频滤波,滤掉60Hz以上的频率成分,以与地震数据保持一致。由图 12可知,利用本文方法所得的纵波阻抗反演结果与井保持了高度一致,也说明了本文方法的有效性与实用性。
|
图 12 井震对比 (a)反演剖面,黑色竖线为井位置,柱状体为井数据;(b)反演结果(红)与井数据(黑)对比 |
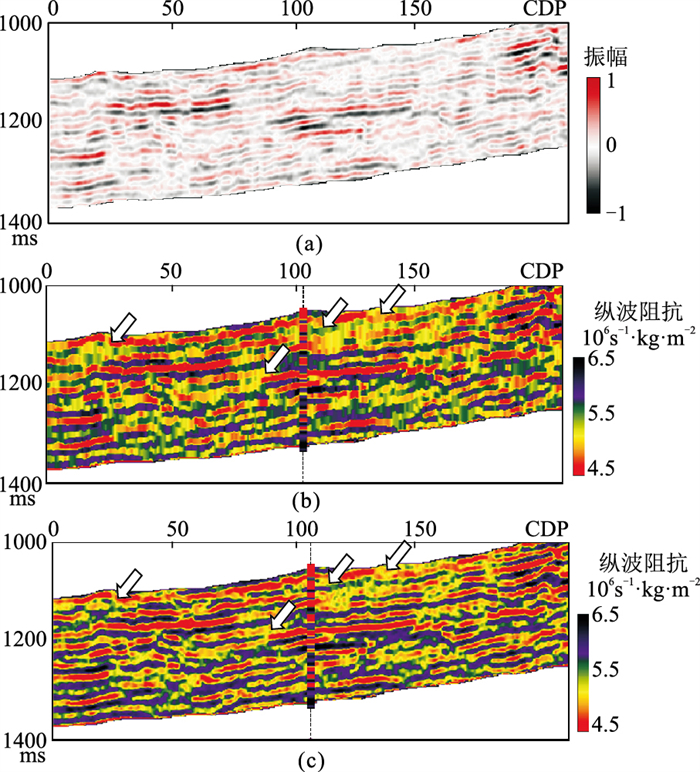
此外,为了进一步验证方法有效性,分别利用本文方法与常规方法对该工区另一剖面(图 13a)进行测试。图 13b与图 13c分别为本文方法及常规方法(快速匹配追踪地震反演方法)纵波阻抗反演结果。由图可知,本文方法反演结果横向连续性更高(白色箭头所指区域)。本文方法与常规方法的迭代次数分别为8次(用时3.8s)与30次(用时10.2s)。因此,相较于常规方法,本文方法可在更少的迭代次数及耗时的情况下获得更稳定精确的反演结果。
|
图 13 不同方法纵波阻抗反演结果对比
(a)地震剖面;(b)常规方法;(c)本文方法 迭代次数:8;α1=1.0,α2=0.85 |
(1) 全域正则化快速匹配追踪稀疏地震反演方法首先通过时频域褶积模型与纵波阻抗约束构建匹配追踪冗余字典。在此基础上利用对全域信号进行整体分析得出所有可能的匹配原子构建备选原子库,最后利用正则化方法筛选出能量最大子集构成最终的匹配原子库进行反演。
(2) 在利用全域正则化快速匹配追踪稀疏地震反演方法时,需要控制迭代次数。当地震资料包含较强噪声时,需要降低迭代次数、提高初始模型约束权重来获得稳定解。相反,若地震资料信噪比较高,则可以提高迭代次数获得较为精确的反演结果。
(3) 模型与实际资料测试表明,本文方法在保证反演准确性与鲁棒性的基础上有效地提高了匹配追踪稀疏反演方法的计算效率。通过对比由本文方法与常规方法获得的纵波阻抗反演结果可知:相较于常规方法,本文方法反演结果的横向连续性及边界保真度均有所提高。
| [1] |
ASTER R C, THURBER C H, BORCHERS B. Parameter Estimation and Inverse Problems[M]. International Geophysics, 2012.
|
| [2] |
TARANTOLA A. Inverse Problem Theory and Methods for Model Parameter Estimation[M]. Beijing: Science Press, 2009.
|
| [3] |
印兴耀, 张世鑫, 张繁昌, 等. 利用基于Russell近似的弹性波阻抗反演进行储层描述和流体识别[J]. 石油地球物理勘探, 2010, 45(3): 373-380. YIN Xingyao, ZHANG Shixin, ZHANG Fanchang, et al. Utilizing Russell approximation-based elastic wave impedance inversion to conduct reservoir description and fluid identification[J]. Oil Geophysical Prospecting, 2010, 45(3): 373-380. DOI:10.13810/j.cnki.issn.1000-7210.2010.03.011 |
| [4] |
印兴耀, 曹丹平, 王保丽, 等. 基于叠前地震反演的流体识别方法研究进展[J]. 石油地球物理勘探, 2014, 49(1): 22-34, 46. YIN Xingyao, CAO Danping, WANG Baoli, et al. Research progress of fluid identification method based on prestack seismic inversion[J]. Oil Geophysical Prospecting, 2014, 49(1): 22-34, 46. DOI:10.13810/j.cnki.issn.1000-7210.2014.01.002 |
| [5] |
印兴耀, 宗兆云, 吴国忱. 岩石物理驱动下地震流体识别研究[J]. 中国科学: 地球科学, 2015, 45(1): 8-21. YIN Xingyao, ZONG Zhaoyun, WU Guochen. Research on seismic fluid identification driven by rock physics[J]. Scientia Sinica(Terrae), 2015, 45(1): 8-21. |
| [6] |
LI K, YIN X Y, LIU J, et al. An improved stochastic inversion for joint estimation of seismic impedance and lithofacies[J]. Journal of Geophysics and Engineering, 2019, 16(1): 62-76. DOI:10.1093/jge/gxy005 |
| [7] |
LI K, YIN X Y, ZONG Z Y. Resolution enhancement of robust Bayesian pre-stack inversion in the frequency domain[C]. Exteneled Abstracts of 78th EAGE Conference & Exhibition, 2016, 1-5.
|
| [8] |
高君, 毕建军, 赵海山, 等. 地震波形指示反演薄储层预测技术及其应用[J]. 地球物理学进展, 2017, 32(1): 142-145. GAO Jun, BI Jianjun, ZHAO Haishan, et al. Seismic waveform inversion technology and application of thinner reservoir prediction[J]. Progress in Geophy-sics, 2017, 32(1): 142-145. |
| [9] |
DAI R H, ZHANG F C, LIU H. Seismic inversion based on proximal objective function optimization algorithm[J]. Geophysics, 2016, 81(5): R237-R246. DOI:10.1190/geo2014-0590.1 |
| [10] |
DAI R H, YIN C, ZAMAN N, et al. Seismic inversion with adaptive edge-preserving smoothing preconditioning on impedance model[J]. Geophysics, 2018, 84(1): R11-R19. |
| [11] |
MALLAT S, ZHANG Z F. Matching pursuits with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3397-3415. DOI:10.1109/78.258082 |
| [12] |
DO T T, GAN L, NGUYEN N, et al. Sparsity adaptive matching pursuit algorithm for practical compressed sensing[C]. 2008 42nd Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 2008, 581-587.
|
| [13] |
许璐, 吴笑荷, 张明振, 等. 基于局部频率约束的动态匹配追踪强反射识别与分离方法[J]. 石油地球物理勘探, 2019, 54(3): 587-593. XU Lu, WU Xiaohe, ZHANG Mingzhen, et al. Strong reflection identification and separation based on the local-frequency-constrained dynamic matching pursuit[J]. Oil Geophysical Prospecting, 2019, 54(3): 587-593. |
| [14] |
杨子鹏, 宋维琪, 刘军, 等. 多道联合约束的匹配追踪强反射轴压制方法[J]. 石油地球物理勘探, 2021, 56(1): 77-85. YANG Zipeng, SONG Weiqi, LIU Jun, et al. A me-thod of combining multi-channel signals to suppress the strong reflection through matching pursuit[J]. Oil Geophysical Prospecting, 2021, 56(1): 77-85. |
| [15] |
李晋, 燕欢, 汤井田, 等. 基于匹配追踪和遗传算法的大地电磁噪声压制[J]. 地球物理学报, 2018, 61(7): 3086-3101. LI Jin, YAN Huan, TANG Jingtian, et al. Magnetotelluric noise suppression based on matching pursuit and genetic algorithm[J]. Chinese Journal of Geophysics, 2018, 61(7): 3086-3101. |
| [16] |
李晋, 张贤, 蔡锦. 利用变分模态分解(VMD)和匹配追踪(MP)联合压制音频大地电磁(AMT)强干扰[J]. 地球物理学报, 2019, 62(10): 3866-3884. LI Jin, ZHANG Xian, CAI Jin. Suppression of strong interference for AMT using VMD and MP[J]. Chinese Journal of Geophysics, 2019, 62(10): 3866-3884. DOI:10.6038/cjg2019M0407 |
| [17] |
宋维琪, 朱卫星, 孙英杰. 复数子波匹配追踪算法识别薄层砂体[J]. 地球物理学进展, 2007, 22(6): 1796-1801. SONG Weiqi, ZHU Weixing, SUN Yingjie. Identify bed layer sandbody by complex wavelet matching algorithm[J]. Progress in Geophysics, 2007, 22(6): 1796-1801. |
| [18] |
杨昊, 郑晓东, 李劲松, 等. 基于匹配追踪的薄层自动解释方法[J]. 石油地球物理勘探, 2013, 48(3): 429-435. YANG Hao, ZHENG Xiaodong, LI Jinsong, et al. Thin-bed automatic interpretation based on matching pursuit[J]. Oil Geophysical Prospecting, 2013, 48(3): 429-435. |
| [19] |
张繁昌, 李传辉, 印兴耀. 三角洲砂岩尖灭线的地震匹配追踪瞬时谱识别方法[J]. 石油地球物理勘探, 2012, 47(1): 82-88. ZHANG Fanchang, LI Chuanhui, YIN Xingyao. Delta fringe line recognition based on seismic matching pursuit instantaneous spectral characteristics[J]. Oil Geophysical Prospecting, 2012, 47(1): 82-88. |
| [20] |
李坤, 印兴耀, 宗兆云, 等. 基于快速匹配追踪的混合域地震稀疏反演方法[J]. 中国石油大学学报(自然科学版), 2018, 42(1): 50-59. LI Kun, YIN Xingyao, ZONG Zhaoyun. Seismic-sparse inversion in mixed domain utilizing fast ma-tching pursuit algorithm[J]. Journal of China University of Petroleum (Edition of Natural Science), 2018, 42(1): 50-59. |
| [21] |
张繁昌, 刘汉卿, 张立强, 等. 复数道动态匹配追踪算法的改进[J]. 石油地球物理勘探, 2016, 51(1): 183-189. ZHANG Fanchang, LIU Hanqing, ZHANG Liqiang, et al. Improved complex-trace dynamic matching pursuit algorithm[J]. Oil Geophysical Prospecting, 2016, 51(1): 183-189. |
| [22] |
LIU J L, WU Y F, HAN D H, et al. Time-frequency decomposition based on Ricker wavelet[C]. SEG Technical Program Expanded Abstracts, 2004, 23: 1937-1940.
|
| [23] |
LIU J L, MARFURT K J. Matching pursuit decomposition using Morlet wavelets[C]. SEG Technical Program Expanded Abstracts, 2005, 24: 786-789.
|
| [24] |
NEEDELL D, Vershynin R. Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit[J]. Foundations of Computational Mathematics, 2009, 9(3): 317-334. |
| [25] |
LI K, YIN X Y, ZONG Z Y. Bayesian seismic multi-scale inversion in complex Laplace mixed domains[J]. Petroleum Science, 2017, 14(4): 694-710. |
| [26] |
LIU X X, YIN X Y, LI H S. Optimal variable-grid finite-difference modeling for porous media[J]. Journal of Geophysics and Engineering, 2014, 11(6): 065011. |
| [27] |
王宇, 韩立国, 周家雄, 等. L1-L2范数联合约束稀疏脉冲反演的应用[J]. 地球科学, 2009, 34(5): 835-840. WANG Yu, HAN Liguo, ZHOU Jiaxiong, et al. App-lication of L1-L2 norm joint constrained sparse pulse inversion[J]. Earth Sciences, 2009, 34(5): 835-840. |
| [28] |
郭朝斌, 杨小波, 陈红岳, 等. 约束稀疏脉冲反演在储层预测中的应用[J]. 石油物探, 2006, 45(4): 397-400. GUO Chaobin, YANG Xiaobo, CHEN Hongyue, et al. Constrained sparse pulse inversion research in north of Haitongji depression[J]. Geophysical Prospecting for Petroleum, 2006, 45(4): 397-400. |
| [29] |
YIN X Y, ZHANG S X. Bayesian inversion for effective pore-fluid bulk modulus based on fluid-matrix decoupled amplitude variation with offset approximation[J]. Geophysics, 2014, 79(5): R221-R232. |
| [30] |
GRANA D. Bayesian petroelastic inversion with multiple prior models[J]. Geophysics, 2020, 85(5): M57-M71. |
| [31] |
MARGRAVE G F. Theory of nonstationary linear filtering in the Fourier domain with application to time-variant filtering[J]. Geophysics, 1998, 63(1): 244-259. |
| [32] |
潘辉, 印兴耀, 李坤, 等. 基于经验模态分解字典的自适应匹配追踪谱分解方法及其在油气检测中的应用[J]. 石油地球物理勘探, 2021, 56(5): 1117-1129. PAN Hui, YIN Xingyao, LI Kun, et al. Spectral decomposition method of adaptive matching pursuit based on empirical mode decomposition dictionary and its application in oil and gas detection[J]. Oil Geophysical Prospecting, 2021, 56(5): 1117-1129. |



 印兴耀, 山东省青岛市经济技术开发区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
印兴耀, 山东省青岛市经济技术开发区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: 