渤海湾盆地南堡凹陷海陆过渡带的地下构造复杂,由于地表及地下黏弹介质吸收,导致地震波能量衰减严重,造成地震信号强度和频带宽度的损失,因此需要研究有效的地震成像方法[1-2]。深部地震数据通常具有能量弱、频率低、子波形状畸变等特点[3-5],信噪比和分辨率较低,进而影响地震勘探精度。在对此类地区的地震数据成像时,需要考虑由非弹性介质造成的振幅衰减、频率下降和相位畸变等因素[6-7]。为此,需要补偿地震波能量在地层中的衰减。总体而言,地震波能量衰减补偿主要有两大类方法。
一是直接作用在地震记录上的补偿方法,在时间域或频率域提高地震记录的分辨率,在处理过程中不考虑地震波的传播路径,反Q滤波[6, 8-9]和时频分析是常用的处理方法。反Q滤波是一种补偿大地衰减效应的方法,是均匀时变的,其算法不受噪声影响。一般求反Q滤波中的大地品质因子Q值采用Q扫描和谱分析两种方法。前者类似于速度扫描或频率扫描,属于一种定性分析方法;后者是一种定量估算方法,采用最小二乘法将谱的衰减趋势拟合为一条直线,振幅衰减的变化量和频率的变化量的比值恰为该直线的斜率,此斜率与Q的倒数成正比。时频分析方法是通过分析地震数据的频率、能量进行能量补偿,其基本思想是:地震波的高频部分要比低频部分衰减更严重,将原始地震数据进行时频分析,依据不同时间、不同频率信号的能量关系,对不同的频率成分乘以对应的时变补偿系数,以补偿不同时间、不同频率成分地震波的能量[8-9]。上述方法并没有考虑地震波的传播路径,然而实际地震波的能量衰减是与传播路径密切相关的。
二是考虑了地震波传播路径的Q偏移补偿方法,主要包括单程波补偿偏移[10-12]、衰减补偿逆时偏移[13-16]和衰减补偿高斯束偏移[13, 17]等。然而Q偏移补偿方法的实际应用较少,尤其在海陆过渡带。Q偏移补偿方法在理论上严格按照地震波的传播路径补偿和校正地震波传播过程中介质的非弹性吸收频散效应,可以有效提高深层地震信号的分辨率,从而更好地提高地震成像精度[18-19]。
通常Q偏移补偿方法的步骤主要分两步。第一步是估计Q模型。品质因子Q是量化地震波衰减和频散的重要参数,在非完全弹性介质中Q值越小,地震波在传播过程中的衰减越严重。提取Q值的方法较多,总体上分为时间域与频率域两类。第一类包括子波模拟法、上升时间法和振幅衰减法等[20]。第二类包括谱比法[6, 21-22]、质心偏移法[23]和频域属性组合等方法,基于提取的有效Q值,利用反演优化算法计算精确的Q模型,其中谱比法应用最广泛。第二步是基于得到的Q模型进行Q偏移成像。
本文利用Q层析建立渤海湾盆地南堡凹陷海陆过渡带的衰减模型,利用Q偏移补偿方法同时提高深部数据的能量及主频,以有效提高偏移剖面的成像分辨率、信噪比和保真度,并校正相位畸变,最终提高构造解释精度。
1 方法原理 1.1 Q初始速度场建模利用VSP资料计算目标区域地层的Q值,选择最终的叠前偏移速度场并进行插值处理,然后将插值处理后的叠前偏移速度场转换为地震道;以对应位置井的速度为标准值,以其他道的速度与标准值的比值为速度模型比例因子,建立目标区域地层的速度模型比例因子三维模型;利用上述模型的比例因子变化与目标区域地层的Q值变化的一致性,水平外推目标区域地层的Q值,从而建立三维初始Q体模型。
1.2 Q层析反演品质因子Q是度量地层衰减的重要参数,目前理论和实验均表明,岩石类型、孔隙度和流体饱和度是影响Q值的关键因素[24]。Q层析成像反演(衰减旅行时间层析反演)是一种基于衰减旅行时的反演方法,被定义为由有效Q值的一定权重表示的运动行波时间反演。首先获取地震反射波信号;然后再进行Q层析反演,主要是基于反射波的传播时间和衰减信息获得地下Q值的分布,其思想是不断更新迭代Q模型,进而使反演结果最优(即最接近地下真实地层情况)。在连续模型中,衰减旅行时被定义为[7]
| $ t_r^* = \int_{{\rm{ray }}} {\frac{1}{{\upsilon (\mathit{\boldsymbol{x}})}}} Q{(\mathit{\boldsymbol{x}})^{ - 1}}{\rm{d}}s $ | (1) |
式中:tr*第r条射线的衰减旅行时,一条射线即表示一项等式约束条件;ray表示射线路径;υ(x)和Q(x)分别为位置x处的速度和模型Q值;s为弧长。将υ(x)和Q(x)离散化,则式(1)变为
| $ t_r^* = \sum\limits_r {\frac{{{l_{r:i, j, k}}}}{{{u_{i, j, k}}}}} Q_{i, j, k}^{ - 1} = \sum\limits_r {{t_{r:i, j, k}}} Q_{i, j, k}^{ - 1} $ | (2) |
式中:υi, j, k为离散模型在(i, j, k)处的速度,i, j, k分别为笛卡尔坐标系中x, y, z方向的离散模型的编号;lr: i, j, k为第r条射线经过(i, j, k)处离散模型的长度; tr: i, j, k为第r条射线经过(i, j, k)处离散模型所需的时间;Qi, j, k为(i, j, k)处的Q值。将所有参与计算的方程联立为方程组,可以得到
| $ \mathit{\boldsymbol{TQ}} = t_{{\rm{obs}}}^* $ | (3) |
式中:T∈Rr×m为基于射线追踪得到的每一条射线经过每一个离散网格需要的时间,R为实数域空间,m=i×j×k为离散模型的参数总量;Q=[1/Q1, 1/Q2, …,1/Qm]T∈Rm×1;tobs*∈Rr×1为参与计算的观测衰减旅行时向量。由于式(3)通常是一个混定问题,且包含了较强的噪声信息,直接求解可能会导致反演失败,因此常用迭代法计算。定义初始Q模型Q0和真实Q模型之间的差值为ΔQ,则模型更新量Δt*和tobs*之间的关系为
| $ \Delta {\mathit{\boldsymbol{t}}^*} = \mathit{\boldsymbol{t}}_{{\rm{obs }}}^* - \mathit{\boldsymbol{t}}_{{\rm{cal}}}^* = \mathit{\boldsymbol{T}}\Delta \mathit{\boldsymbol{Q}} $ | (4) |
在实际计算中,只需要通过实际观测地震反射数据计算真实tobs*和基于模型计算的衰减旅行时向量tcal*。在实际应用中,基于对数谱比法可知,衰减旅行时在两个不同频段的频谱呈线性关系,利用最小二乘法拟合不同频率的对数谱比,在求得最佳线性方程的斜率之后,可以估算有效Q值Qeff
| $ \left\{ {\begin{array}{*{20}{l}} {{Q_{{\rm{eff }}}}\left( {{t_{{q_1}}}} \right) = {Q_{{\rm{interval }}}}\left( {{t_{{q_1}}}} \right)}\\ {{Q_{{\rm{interval }}}}\left( {{t_{{q_l}}}} \right) = \frac{{{t_{{q_l}}}}}{{\frac{{{Q_{{\rm{star}}{{\rm{t}}_{\rm{t}}}{\rm{ime}}}}}}{{{Q_{{\rm{interval }}}}}} + \sum\limits_{l = 2}^p {\frac{{{Q_{{\rm{tim}}{{\rm{e}}_{\rm{s}}}{\rm{amp}}}}}}{{{Q_{{\rm{interval }}}}}}} }}} \end{array}} \right. $ | (5) |
式中:l=2, …,p为分析的Q场采样数;tql=Qstart_time+(p-1)Qtime_samp为分析时窗的中心时间,Qstart_time为输出Q场的起始时间,Qtime_samp为输出Q场的采样率。根据衰减旅行时层析反演求取Q值流程,得到每条射线的衰减旅行时tobs*
| $ t_{{\rm{obs}}}^* = \sum\limits_r {\frac{t}{{Q_{{\rm{eff}}}^{{\rm{obs}}}(t)}}} $ | (6) |
式中:t为当前数据的总旅行时;Qeffobs(t)为关联炮点和检波点对在时间t的有效Q值。通过计算得到有效Q值,再通过插值、重采样获得初始Q模型;根据式(3)、式(4)得到tcal*,通过式(4)得到更新Q模型,由
| $ {\mathit{\boldsymbol{Q}}^{n + 1}} = {\mathit{\boldsymbol{Q}}^n} + \Delta \mathit{\boldsymbol{Q}} $ | (7) |
迭代更新Q模型。式中n为层析成像的迭代次数。设初始模型为Q0,通过不断重复式(4)~式(7)进行迭代,直至层析结果达到精度要求为止。
1.3 Q叠前深度偏移由层析反演得到Q场,结合叠前深度偏移得到速度场用于Q叠前深度偏移,以减少由偏移引起的振幅、频率和相位变化的影响[7, 12, 25]。由声波速度场c0(x)和Q场构造的复波速为
| $ c(\mathit{\boldsymbol{x}}, \omega ) = {c_0}(\mathit{\boldsymbol{x}})\left[ {1 - \frac{1}{2}{\rm{i}}{Q^{ - 1}}(\mathit{\boldsymbol{x}}) + \frac{1}{\pi }{Q^{ - 1}}(\mathit{\boldsymbol{x}})\ln \frac{\omega }{{{\omega _0}}}} \right] $ | (8) |
式中:ω为角频率;ω0为参考角频率。由
| $ {T_{\rm{c}}}(\mathit{\boldsymbol{x}}, \omega ) = T(\mathit{\boldsymbol{x}}) - \frac{1}{2}{\rm{i}}{T^\prime }(\mathit{\boldsymbol{x}}) - \frac{1}{\pi }{T^\prime }(\mathit{\boldsymbol{x}})\ln \frac{\omega }{{{\omega _0}}} $ | (9) |
计算复旅行时。式中:T(x)为旅行时;T′(x)为振幅补偿项,即
| $ {T^\prime }(\mathit{\boldsymbol{x}}) = \int_{{\rm{ray }}} {\frac{1}{{{c_0}(\mathit{\boldsymbol{x}})}}} Q{(\mathit{\boldsymbol{x}})^{ - 1}}{\rm{d}}s $ | (10) |
式(9)中第一项为偏移的运动学信息(由射线追踪或求解程函方程获得),可以通过常规声波介质旅行时计算方法求取;第二项为地震波振幅补偿项;第三项为频散相位畸变校正项。基于Q场的Kirchhoff叠前深度偏移积分公式为
| $ u(\mathit{\boldsymbol{x}}) = \int A \left( {\mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{S}}}} \right){\rm{d}}{\mathit{\boldsymbol{x}}_{\rm{S}}}\int F (\omega ){{\rm{e}}^{{\rm{i}}\omega \sigma \left( {x, {x_{\rm{S}}}} \right)}}D\left( {{\mathit{\boldsymbol{x}}_{\rm{S}}}, \omega } \right){\rm{d}}\omega $ | (11) |
式中:u(x)表示偏移剖面;A(x, xS)为振幅权重因子,xS为地表检波器位置;D(xS, ω)为频率域地震数据;F(ω)为频率域的相移因子;τ(x, xS)为从成像点到检波点的双程旅行时间。在弹性介质中τ(x, xS)为实数形式,在非完全弹性介质中,其表达为复数形式(式(9))[25]。
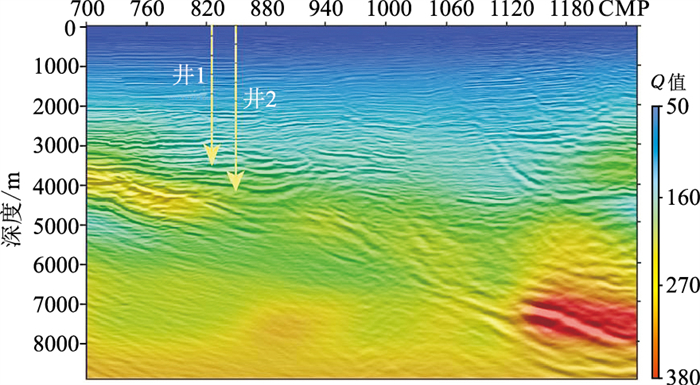
2 实际资料应用Q叠前深度偏移实现过程分两步。首先,由层析反演得到Q场。其次,开展Q叠前深度偏移计算。Q叠前深度偏移采用基于保幅Kirchhoff叠前深度偏移的地震成像方法,在偏移过程中考虑了沿不同路径传播的地震波衰减,从能量归位和衰减补偿两方面提高偏移成像质量,进而提高地震资料处理精度,满足属性反演和储层预测的需要,为岩性识别和油气检测提供可靠的数据基础。图 1为A区M测线基于衰减旅行时的Q值层析剖面和偏移成像剖面叠合。由图可见,剖面内Q值分布范围为50~380,浅部Q值较小,对地震波的衰减较严重,深部的Q值较大,符合Q值分布规律。
|
图 1 A区M测线基于衰减旅行时的Q值层析剖面和偏移成像剖面叠合 |
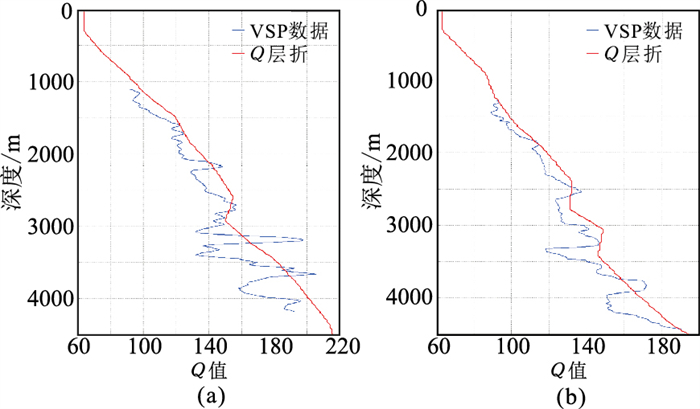
图 2为由井1、井2的VSP数据获得的Q值与对反射数据进行Q层析获得的Q值对比。由图可见,由VSP数据和反射数据Q层析得到的Q值的变化趋势一致,但由于前者的空间采样密度较高,其中包含较多高频信息,后者的Q值分布细节不如前者丰富。
|
图 2 由井1(a)、井2(b)的VSP数据获得的Q值与对反射数据进行Q层析获得的Q值对比 |
利用Q值层析获得A区的Q场分布后,再利用Q-Kirchhoff叠前深度偏移方法进行Q叠前深度偏移成像(图 3)。可见,Q叠前深度偏移剖面(图 3b)较常规叠前深度偏移剖面(图 3a)的成像效果更好(尤其是在红色箭头处),表现为:①明显提高了中深层的信噪比,波组特征清楚,构造形态清晰(图 3b);②恢复了中深层同相轴的频率和振幅,部分由于衰减引起的频率降低而混叠的同相轴得到分离。

|
图 3 N测线常规叠前深度偏移剖面(a)和Q叠前深度偏移剖面(b)对比 |
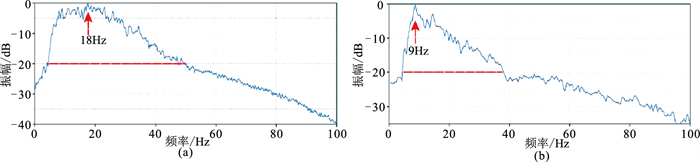
在非完全弹性介质中,能量吸收不仅导致深层反射波的能量衰减和相位偏移,而且会降低反射波的频率。图 4为图 3a和图 3b的频谱。由图可见,Q偏移不仅可以补偿偏移结果的深部振幅,同时也可以提升偏移结果的数据主频,并提高了叠前深度偏移结果的分辨率(图 4b)。
|
图 4 图 3a(a)和图 3b(b)的频谱 频谱分析的时间窗口为2000~3500ms。图a的数据体主频为18Hz,能量较强的数据频带范围为5~50Hz(加粗红色虚线的范围)。图b数据体的主频约为9Hz,能量较强的数据频带范围为4~38Hz(加粗红色虚线的范围) |
图 5为L测线Q-Kirchhoff叠前深度偏移结果和常规Kirchhoff叠前深度偏移结果对比。由图可见:①在时间域基于Q-Kirchhoff叠前深度偏移结果(图 5a)和常规Kirchhoff叠前深度偏移结果(图 5b)的主频存在较大差异。如,图 5a的主频、分辨率更高,图 5b的部分相邻反射同相轴相互混叠,分辨率较低。②在图 5a中存在强烈反射层位置的伽马曲线也呈剧烈变化,说明Q偏移结果与测井数据匹配较好;图 5b的偏移结果与测井数据匹配略差。

|
图 5 L测线Q-Kirchhoff叠前深度偏移结果(a)和常规Kirchhoff叠前深度偏移结果(b)对比 红线表示井位置,蓝色曲线为伽马曲线 |
渤海湾盆地海陆过渡带的地下构造复杂,由于地表及地下黏弹介质吸收,导致地震波能量衰减严重。本文应用Q叠前深度偏移,利用Q层析方法获得了Q模型,基于Q模型进行Kirchohoff叠前深度偏移成像,有效补偿了振幅、校正了相位畸变,提高了深部数据的信噪比、保真度及构造解释精度。
| [1] |
赵邦六, 王喜双, 董世泰, 等. 渤海湾盆地物探技术需求及发展方向[J]. 石油地球物理勘探, 2014, 49(2): 394-409. ZHAO Bangliu, WANG Xishuang, DONG Shitai, et al. Geophysical prospecting requirements and deve-lopment direction in Bohai Bay Basin[J]. Oil Geophysical Prospecting, 2014, 49(2): 394-409. DOI:10.13810/j.cnki.issn.1000-7210.2014.02.027 |
| [2] |
撒利明, 杨午阳, 杜启振, 等. 地震偏移成像技术回顾与展望[J]. 石油地球物理勘探, 2015, 50(5): 1016-1035. SA Liming, YANG Wuyang, DU Qizhen, et al. Past, present and future of seismic migration imaging[J]. Oil Geophysical Prospecting, 2015, 50(5): 1016-1035. |
| [3] |
KJARTANSSON E. Constant Q-wave propagation and attenuation[J]. Journal of Geophysical Research, 1979, 84(B9): 4737-4748. DOI:10.1029/JB084iB09p04737 |
| [4] |
FUTTERMAN W I. Dispersive body waves[J]. Journal of Geophysical Research, 1962, 67(13): 5279-5291. DOI:10.1029/JZ067i013p05279 |
| [5] |
GANLEY D C, KANASEWICH E R. Measurement of absorption and dispersion from check shot surveys[J]. Journal of Geophysical Research, 1980, 85(B10): 5219-5226. DOI:10.1029/JB085iB10p05219 |
| [6] |
CAVALCA M, Fletcher R, Riedel M. Q-compensation in complex media: ray-based and wavefield extrapolation approaches[C]. SEG Technical Program Expanded Abstracts, 2013, 32: 3831-3835.
|
| [7] |
CAVALCA M, MOOREL I, ZHANg L, et al. Ray-based tomography for Q estimation and Q compensation in complex media[C]. SEG Technical Program Expanded Abstracts, 30: 3989-3993.
|
| [8] |
BRAGA I, MORAES F S. High-resolution gathers by inverse Q filtering in the wavelet domain[J]. Geophysics, 2013, 78(2): V53-V61. DOI:10.1190/geo2011-0508.1 |
| [9] |
WANG Y H. A stable and efficient approach of inverse Q filtering[J]. Geophysics, 2002, 67(2): 657-663. DOI:10.1190/1.1468627 |
| [10] |
MITTET R, SOLLIE R, HOKSTAD K. Prestack depth migration with compensation for absorption and dispersion[J]. Geophysics, 1995, 60(5): 1485-1494. DOI:10.1190/1.1443882 |
| [11] |
WANG Y H, GUO J. Seismic migration with inverse Q filtering[J]. Geophysical Research Letters, 2004. DOI:10.1029/2004GL020525 |
| [12] |
ZHANG J F, WU J Z, LI X Y. Compensation for absorption and dispersion in prestack migration: An effective Q approach[J]. Geophysics, 2013, 78(1): S1-S14. DOI:10.1190/geo2012-0128.1 |
| [13] |
BAI M, CHEN X H, WU J, et al. Multiple-component Gaussian beam reverse-time migration based on attenu-ation compensation[J]. Chinese Journal of Geophysics, 2016, 59(9): 3379-3393. |
| [14] |
SONG M P, ZHANG J F, ZHANG J J. Viscoacoustic least-squares migration with a blockwise Hessian matrix: An effective Q approach[J]. Journal of Geophysics and Engineering, 2020, 17(4): 618-634. |
| [15] |
WANG Y F, ZHOU H, CHEN H M, et al. Adaptive stabilization for Q-compensated reverse time migration[J]. Geophysics, 2018, 83(1): S15-S32. DOI:10.1190/geo2017-0244.1 |
| [16] |
WANG Y F, ZHOU H, ZHAO X B, et al. CuQ-RTM: A CUDA-based code package for stable and efficient Q-compensated reverse time migration[J]. Geophysics, 2019, 84(1): F1-F15. DOI:10.1190/geo2017-0624.1 |
| [17] |
BAI M, CHEN X H, WU J, et al. Q-compensated migration by Gaussian beam summation method[J]. Journal of Geophysics and Engineering, 2016, 13(1): 35-48. DOI:10.1088/1742-2132/13/1/35 |
| [18] |
陈见伟, 范国章, 叶月明, 等. Q叠前深度偏移处理技术在深海资料处理中的应用[J]. 海洋工程装备与技术, 2019, 6(增刊): 242-244. CHEN Jianwei, FAN Guozhang, YE Yueming, et al. Application of Q prestack depth migration technology in deep marine data[J]. Ocean Engineering Equipment and Technology, 2019, 6(S): 242-244. |
| [19] |
高雪, 黄建平, 李振春, 等. 时间域黏声VTI介质自适应聚焦束偏移[J]. 石油地球物理勘探, 2021, 56(4): 771-781. GAO Xue, HUANG Jianping, LI Zhenchun, et al. Time-domain adaptive focused beam migration for vi-scous and VTI media[J]. Oil Geophysical Prospecting, 2021, 56(4): 771-781. |
| [20] |
TONN R. The determination of the seismic quality factor Q from VSP data: A comparison of different computational methods[J]. Geophysical Prospecting, 1991, 39(1): 1-27. DOI:10.1111/j.1365-2478.1991.tb00298.x |
| [21] |
BLIAS E. Accurate interval Q-factor estimation from VSP data[J]. Geophysics, 2012, 77(3): WA149-WA156. DOI:10.1190/geo2011-0270.1 |
| [22] |
ZHANG C J, ULRYCH T J. Estimation of quality factors from CMP records[J]. Geophysics, 2002, 67(5): 1542-1547. DOI:10.1190/1.1512799 |
| [23] |
QUAN Y, HARRIS J M. Seismic attenuation tomography using the frequency shift method[J]. Geophysics, 1997, 62(3): 895-905. DOI:10.1190/1.1444197 |
| [24] |
FRISILLO A L, STEWART T J. Effect of partial gas/brine saturation on ultrasonic absorption in sandstone[J]. Journal of Geophysical Research, 1980, 85(B10): 5209-5211. DOI:10.1029/JB085iB10p05209 |
| [25] |
TRAYNIN P, LIU J, REILLY J M. Amplitude and bandwidth recovery beneath gas zones using Kirchhoff prestack depth Q-migration[C]. SEG Technical Program Expanded Abstracts, 2008, 27: 2412-2416.
|



 陈见伟, 浙江省杭州市西溪路920号中国石油杭州地质研究院计算机应用研究所, 310023。Email:
陈见伟, 浙江省杭州市西溪路920号中国石油杭州地质研究院计算机应用研究所, 310023。Email: 