② 海洋油气勘探国家工程研究中心, 北京 100028;
③ 东方地球物理公司, 河北涿州 072750
② National Engineering Research Center of Offshore Oil and Gas Exploration, Beijing 100028, China;
③ BGP Inc., CNPC, Zhuozhou, Hebei 072750, China
伴随状态法[1]通过两次正演运算获取模型参数的梯度,可避免对所有震源和接收点格林函数的直接计算和存储,已广泛应用于地震波动方程偏移和反演,如逆时偏移(RTM)[2-5]、全波形反演(FWI)[6-10]、最小二乘逆时偏移(LSRTM)[11-13]、波动方程旅行时反演(WETI)[14-16]等。
伴随状态法通过震源波场和伴随波场间的相互运算(如相关)计算参数梯度/敏感核。但震源波场和伴随波场分别沿时间正向和逆向传播。为同时访问震源波场和伴随波场,震源波场需先保存在计算机内存中或在波场反向传播中进行重建。存储所有时刻、所有空间网格点的震源波场是不现实的,特别是三维情况。最优检测点方法(Optimal CheckPointing)在波场正向传播中仅需保存几个时刻(检测点)的震源波场,在波场反向传播中将存储的检测点波场作为初值重新计算相邻检测点之间的震源波场[17-19]。最优检测点方法可大幅减少计算机内存消耗,但需额外的正演运算。边界值方法采用位于边界区域几层(与差分精度有关)网格点的波场和最后两个时刻的快照重建震源波场[20-22]。常规边界值方法需要存储每个时刻M层网格点的边界波场(M为有限差分算子长度),存储量仍然较大。Feng等[23]采用变阶数有限差分算子重建震源波场,只需存储一层空间网格点的边界波场。但由于降阶处理,该方法的重建精度不高。Tan等[24]提出基于拉格朗日多项式或高阶波动方程外推法,该方法需保存一层或两层网格点的边界波场,内存需求约为常规方法的37.5%。Liu等[25]采用边界波场的线性组合重建震源波场,所需存储量仅为常规方法的1/M。段沛然等[26]将该方法推广到交错网格有限差分波场重建。Liu等[25]的方法存在如下问题:基于L2范数准则求取差分系数,有效波数范围/带宽较窄;重建系数的自由度较小(最小为2),很难精确逼近重建频散关系。为保证重建误差小于0.0025,每个波长需要的采样点数至少为5。Ren等[27]设计了新的差分模板,采用边界区域的N层波场和M-N层波场的线性组合来重建内部区域的震源波场(0 ≤ N ≤ M)。该方法通过调整N的大小实现重建精度和内存需求的折衷。当N=0时,退化为Liu等[25]的方法。Ren等[27]的方法每个波长只需3个采样点就可保证重建误差小于0.001。
Ren等[27]的方法是基于规则网格设计的,无法直接用于变密度声波或弹性波速度—应力方程RTM或FWI。本文发展了基于交错网格有限差分的震源波场重建方法,设计了新的交错网格差分模板,仍通过存储边界区域N层波场和M-N层波场的线性组合来重建震源波场;构建了无穷范数极小化目标函数,采用Remez交换算法[28-29]优化了重建系数。基于改进的差分模板和优化的重建系数,新方法可大幅提高震源波场的重建精度,且内存需求仅为常规方法的(N+1)/M。本文通过精度和稳定性分析、声波RTM和弹性波FWI算例验证了方法的有效性。
1 原理方法 1.1 交错网格有限差分震源波场重建方法交错网格有限差分离散格式为[30]
| $ {\left. {\frac{{\partial p}}{{\partial x}}} \right|_{x = 0}} = \frac{1}{h}\left[ {\sum\limits_{i = 1}^M {{a_i}} \left( {{p_{i - 0.5}} - {p_{ - i + 0.5}}} \right)} \right] $ | (1) |
式中:ai为差分系数;h为空间网格间隔;p为地震波场(压强或速度)。常规边界值方法采用边界区域的边界波场p-i+0.5(i=1, 2, …, M)重建内部区域的震源波场[20-22]。为减小内存需求,设计如图 1所示的差分模板。内部区域各层(x=jh,j=0, 1, …, M-1)的空间导数通过下式计算
| $ \left\{ {\begin{array}{*{20}{l}} {{{\left. {\frac{{\partial p}}{{\partial x}}} \right|}_{x = 0}} = \frac{1}{h}\left[ {\sum\limits_{i = 1}^M {{a_i}} \left( {{p_{i - 0.5}} - {p_{ - i + 0.5}}} \right)} \right]}\\ {{{\left. {\frac{{\partial p}}{{\partial x}}} \right|}_{x = h}} = \frac{1}{h}\left[ {{b_{1, 1}}\left( {{p_{1.5}} - {p_{0.5}}} \right) + \sum\limits_{i = 1}^N {{b_{1, 1 + i}}} \left( {{p_{2 + i - 0.5}} - {p_{ - i + 0.5}}} \right) + {b_{1, 1 + N + 1}}\sum\limits_{i = N + 1}^M {{a_i}} \left( {{p_{2 + i - 0.5}} - {p_{ - i + 0.5}}} \right)} \right]}\\ {{{\left. {\frac{{\partial p}}{{\partial x}}} \right|}_{x = 2h}} = \frac{1}{h}\left[ {\sum\limits_{i = 1}^2 {{b_{2, i}}} \left( {{p_{2 + i - 0.5}} - {p_{2 - i + 0.5}}} \right) + \sum\limits_{i = 1}^N {{b_{2, 2 + i}}} \left( {{p_{4 + i - 0.5}} - {p_{ - i + 0.5}}} \right) + {b_{2, 2 + N + 1}}\sum\limits_{i = N + 1}^M {{a_i}} \left( {{p_{4 + i - 0.5}} - {p_{ - i + 0.5}}} \right)} \right.}\\ {{{\left. {\frac{{\partial p}}{{\partial x}}} \right|}_{x = (M - 1)h}} = \frac{1}{h}\left[ {\sum\limits_{i = 1}^{M - 1} {{b_{M - 1, i}}} \left( {{p_{M - 1 + i - 0.5}} - {p_{M - 1 - i + 0.5}}} \right) + \sum\limits_{i = 1}^N {{b_{M - 1, M - 1 + i}}} \left( {{p_{2(M - 1) + i - 0.5}} - {p_{ - i + 0.5}}} \right) + } \right.}\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{b_{M - 1, M - 1 + N + 1}}\sum\limits_{i = N + 1}^M {{a_i}} \left( {{p_{2(M - 1) + i - 0.5}} - {p_{ - i + 0.5}}} \right)} \right]} \end{array}} \right. $ | (2) |

|
图 1 交错网络差分模板示意图 |
式中:ai(i=1, 2, …, M)和bj, i(j=1, 2, …, M-1, i=1, 2, …, N+j+1)统称为重建系数。式(2)可改写为
| $ \left\{ {\begin{array}{*{20}{l}} {{{\left| {\frac{{\partial p}}{{\partial x}}} \right|}_{x = 0}} = \frac{1}{h}\left[ {\sum\limits_{i = 1}^M {{a_i}} \left( {{p_{i - 0.5}} - {p_{ - i + 0.5}}} \right) + \sum\limits_{i = N + 1}^M {{a_i}} {p_{i - 0.5}} - A} \right]}\\ {{{\left. {\frac{{\partial p}}{{\partial x}}} \right|}_{x = jh}} = \frac{1}{h}\left[ {\sum\limits_{i = 1}^j {{b_j}} , i\left( {{p_{j + i - 0.5}} - {p_{j - i + 0.5}}} \right) + \sum\limits_{i = 1}^N {{b_{j, j + 1}}} \left( {{p_{2j + i - 0.5}} - {p_{ - i + 0.5}}} \right) + {b_{j, j + N + 1}}\sum\limits_{i = N + 1}^M {{a_i}} {p_{2j + i - 0.5}} - {b_{j, j + N + 1}}A} \right]}\\ {A = \sum\limits_{i = N + 1}^M {{a_i}} {p_{ - i + 0.5}}} \end{array}} \right. $ | (3) |
波场正向延拓中存储边界波场p-i+0.5 (i=1, 2, …, N)和波场的线性组合A,波场反向延拓中基于式(3)重建内部区域不同层(x=jh,j=0, 1, …, M-1)的空间偏导数。所提方法只需保存N层边界波场和波场线性组合A,内存需求为常规边界值方法的(N+1)/M。该方法可通过调节N控制重建精度和存储需求。随着N增大,重建系数的个数增加(自由度增大),精度提高,但存储量随之增加。当N=M或0时,本文方法退化为常规边界值方法[20-22]或Liu等[25]的方法。
基于平面波理论推导频散关系,将波场表示为
| $ {p_i} = {p_0}{{\rm{e}}^{i{k_x}^h}} $ | (4) |
式中kx为x方向的波数。将式(4)代入式(3),有
| $ \left\{ {\begin{array}{*{20}{l}} {{k_x}h \approx 2\sum\limits_{i = 1}^M {{a_i}} \sin \left[ {(i - 0.5){k_x}h} \right]}\\ {{k_x}h \approx 2\sum\limits_{i = 1}^j {{b_{j, i}}} \sin \left[ {(i - 0.5){k_x}h} \right] + }\\ {\;\;\;\;\;\;\;\;2\sum\limits_{i = 1}^N {{b_{j, j + i}}} \sin \left[ {(j + i - 0.5){k_x}h} \right] + }\\ {\;\;\;\;\;\;\;\;2{b_{j, j + N + 1}}\sum\limits_{i = N + 1}^M {{a_i}} \sin \left[ {(j + i - 0.5){k_x}h} \right]} \end{array}} \right. $ | (5) |
式中j=1, 2, …, M-1。式(5)为新重建方法的频散关系,定义如下的相对误差用于后续重建精度分析
| $ \left\{ {\begin{array}{*{20}{l}} {{\delta _0}\left( {{k_x}h} \right) = \sum\limits_{i = 1}^M {{a_i}} {\varphi _i}\left( {{k_x}h} \right) - 1}\\ {{\delta _j}\left( {{k_x}h} \right) = \sum\limits_{i = 1}^j {{b_{j, i}}} {\varphi _i}\left( {{k_x}h} \right) + }\\ {\;\;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^N {{b_{j, j + i}}} {\psi _{j, i}}\left( {{k_x}h} \right) + }\\ {\;\;\;\;\;\;\;\;\;\;{b_{j, j + N + 1}}\sum\limits_{i = N + 1}^M {{a_i}} {\psi _{j, i}}\left( {{k_x}h} \right) - 1} \end{array}} \right. $ | (6) |
| $ \left\{ {\begin{array}{*{20}{l}} {{\varphi _i}\left( {{k_x}h} \right) = \frac{{\sin \left[ {(i - 0.5){k_x}h} \right]}}{{0.5{k_x}h}}}\\ {{\psi _{j, i}}\left( {{k_x}h} \right) = \frac{{\sin \left[ {(j + i - 0.5){k_x}h} \right]}}{{0.5{k_x}h}}} \end{array}} \right. $ | (7) |
式(3)中涉及
| $ \left\{ {\begin{array}{*{20}{l}} {\sum\limits_{i = 1}^M {{a_i}} (2i - 1) = 1}\\ {\sum\limits_{i = 1}^j {{b_{j, i}}} (2i - 1) + \sum\limits_{i = 1}^N {{b_{j, j + i}}} (2j + 2i - 1) + }\\ {\;\;\;\;\;{b_{j, j + N + 1}}\sum\limits_{i = N + 1}^M {{a_i}} (2j + 2i - 1) = 1} \end{array}} \right. $ | (8) |
式(8)为约束方程,可保证低波数成分的重建精度。
将式(8)代入式(6),可得
| $ \begin{array}{l} {\delta _0}\left( {{k_x}h} \right) = {\varphi _1}\left( {{k_x}h} \right) + \\ \;\;\;\sum\limits_{i = 2}^M {{a_i}} \left[ {{\varphi _i}\left( {{k_x}h} \right) - (2i - 1){\varphi _1}\left( {{k_x}h} \right)} \right] - 1 \end{array} $ | (9) |
| $ \begin{array}{l} {\delta _j}\left( {{k_x}h} \right) = {\varphi _1}\left( {{k_x}h} \right) + \\ \;\;\;\;\sum\limits_{i = 2}^j {{b_{j, i}}} \left[ {{\varphi _i}\left( {{k_x}h} \right) - (2i - 1){\varphi _i}\left( {{k_x}h} \right)} \right] + \\ \;\;\;\;\sum\limits_{i = 1}^N {{b_{j, j + i}}} \left[ {{\psi _{j, i}}\left( {{k_x}h} \right) - (2j + 2i - 1){\psi _1}\left( {{k_x}h} \right)} \right] + \\ \;\;\;\;{b_{j, j + N + i}}\sum\limits_{i = N + 1}^M {{a_i}} \left[ {{\psi _{j, i}}\left( {{k_x}h} \right) - (2j + 2i - 1) \times } \right.\\ \;\;\;\;\left. {{\psi _1}\left( {{k_x}h} \right)} \right] - 1 \end{array} $ | (10) |
重建系数个数减少为
建立基于无穷范数的极小化目标函数
| $ \left\{ {\begin{array}{*{20}{l}} {{E_0} = \mathop {\max }\limits_{_{{k_x}h \in \left[ {0, {\beta _0}} \right]}} \left( {\left| {{\delta _0}\left( {{k_x}h} \right)} \right|} \right)}\\ {{E_j} = \mathop {\max }\limits_{_{{k_x}h \in \left[ {0, {\beta _j}} \right]}} \left( {\left| {{\delta _j}\left( {{k_x}h} \right)} \right|} \right)} \end{array}} \right. $ | (11) |
式中βj 为最大波数(j=0, 1, …, M-1)。利用式(11)无法直接求取导数,需采用Remez交换算法求解,详细步骤如下。
(1) 求解线性方程组
| $ {\delta _0}\left( {{k_{xl}}h} \right) = {( - 1)^l}{\lambda _0}\quad l = 1, 2, \cdots , M $ | (12) |
得到ai (i=2, 3, …, M)和λ0。式中:λ0为待求常数;kxl为kx的第l个采样点。M个初始采样点通过对波数范围[0, β0]均匀采样得到。
(2) 采用式(11)计算E0。当E0>η(η为最大允许误差),执行步骤(3);当E0≤η,执行步骤(6)。
(3) 式(12)中重建误差在采样点处正负交替,M个采样点之间存在M-1个根,M-1个根将[0, β0]分成M个区间,搜索得到M个区间的极值点。
(4) 将M个极值点作为新的采样点,重复步骤(1)~步骤(3),直到满足收敛条件E0≤η,输出优化的ai (i=2, 3, …, M)和β0。
(5) 若达到最大迭代次数,减小β0,重复步骤(1)~步骤(4)。
(6) 基于约束方程式(8)得到优化的a1。
(7) 求解下式得到bj, i(i=2, 3, …, N+j+1)和λj (j=1, 2, …, M-1)。
| $ \begin{array}{*{20}{c}} {{\delta _j}\left( {{k_{xl}}h} \right) = {{( - 1)}^l}{\lambda _j}}&{j = 1, 2, \cdots , M - 1;}\\ {}&{l = 1, 2, \cdots , N + j + 1} \end{array} $ | (13) |
式中λj为待求常数。初始采样点(N+j+1个)可通过对波数范围[0, βj]均匀采样得到。
(8) 采用式(11)计算Ej (j=1, 2, …, M-1)。当Ej>η,执行步骤(9);当Ej≤η,执行步骤(12)。
(9) 式(13)中重建误差在采样点处正负交替,N+j+1个采样点之间存在N+j个根,N+j个根将[0, βj] 分成N+j+1个区间,搜索得到N+j+1个区间的极值点。
(10) 将N+j+1个极值点作为新的采样点重复步骤(7)~步骤(9),直到满足收敛条件Ej≤η,输出优化的bj, i和βj。
(11) 若达到最大迭代次数,减小βj,重复步骤(7)~步骤(10)。
(12) 基于约束方程式(8)得到优化的bj, 1。
对于不同的层x=jh(j =0, 1, …, M-1),优化的最大波数βj是不同的。用于评价所提方法的重建精度的有效波数范围/带宽为
| $ {\beta _{\rm{f}}} = \mathop {\min {\beta _j}}\limits_{j = 0, 1, \cdots , M - 1} $ | (14) |
上述优化步骤可保证所提方法的重建误差在[0, βf] 范围内均小于最大允许误差η。表 1和表 2分别给出N=0和1时的重建系数。
|
|
表 1 本文方法的重建系数(N=0,M=6和η=0.001) |
|
|
表 2 本文方法的重建系数(N=1,M=6和η=0.001) |
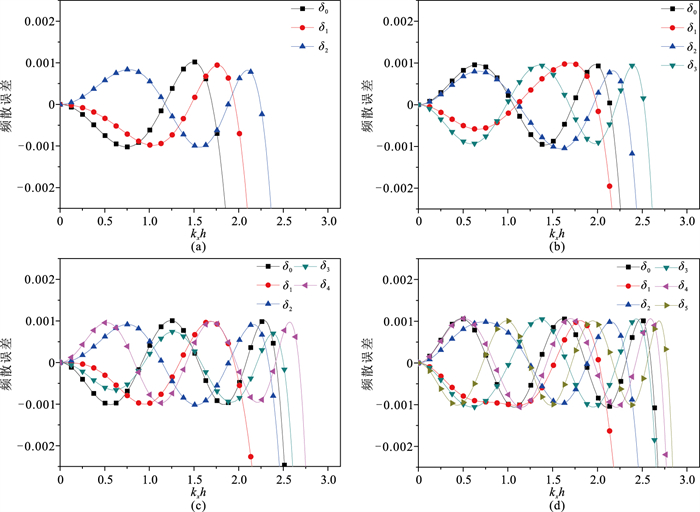
采用式(6)分析重建方法的精度。图 2和图 3分别为N=0和1时的频散曲线,可见本文方法的频散曲线呈波纹状分布。与δ0和δj (j=2, 3, …, M-1)相比,δ1 (x=h层的精度)的幅值最先超出最大允许误差(η= 0.001)。因此,δ1直接决定重建方法的精度。当M增大时,x=0和x=jh(j=2, 3, …, M-1)层的精度增加,但x=h层的精度几乎不变;当N增大时,x=h层的精度大幅改善。为了更好地比较,表 3给出不同方法的有效带宽βf。常规方法中采用优化差分系数[29]。随着N的增大,有效波数范围变大;当N=1时,本文方法的带宽与常规方法(存储M层)非常接近(约为2)。当一个波长采两个样点时,β=kxh达到尼奎斯特极限(等于π)。通过G=2π/βf将带宽βf转换为一个波长需要的采样点数G,表 4给出不同方法的G值。由表可知:本文方法的G值略大于常规方法。随着N增大,G逐渐减小,当N=1时,一个波长只需要3个采样点就可使重建误差小于0.001。

|
图 2 本文方法不同有限差分算子的频散曲线(N=0,η=0.001) (a)M=3;(b)M=4;(c)M=5;(d)M=6 |
|
图 3 本文方法不同有限差分算子的频散曲线(N=1和η=0.001) (a)M=3;(b)M=4;(c)M=5;(d)M=6 |
|
|
表 3 不同方法的有效带宽βf(η=0.001) |
|
|
表 4 不同方法一个波长需要的采样点数G(η=0.001) |
基于冯·诺依曼分析[27]可推导本文方法的稳定性条件。二维稳定性因子为
| $ \left\{ {\begin{array}{*{20}{l}} {s = \mathop {\min }\limits_{j = 0, 1, \cdots , M - 1} }\\ {{s_0} = \frac{{\sqrt 2 }}{2}{{\left[ {\sum\limits_{i = 1}^M {{a_i}} {{( - 1)}^{i + 1}}} \right]}^{ - 1}}}\\ {{s_j} = \frac{{\sqrt 2 }}{2}\left[ {\sum\limits_{i = 1}^j {{b_{j, i}}} {{( - 1)}^{i + 1}} + \sum\limits_{i = 1}^N {{b_{j, j + i}}} {{( - 1)}^{j + i + 1}} + } \right.}\\ {{{\left. {\;\;\;\;\;\;{b_{j, j + N + 1}}\sum\limits_{i = N + 1}^M {{a_i}} {{( - 1)}^{j + i + 1}}} \right]}^{ - 1}}} \end{array}} \right. $ | (15) |
式中:j=1, 2, …, M—1,s为允许的最大库朗数,稳定性随着s增大逐渐改善。表 3给出不同方法的稳定性因子。与常规方法相比,本文方法的稳定性条件更加严格。随着N的增加,稳定性略微变差。
|
|
表 5 不同方法的稳定性因子s |
将本文方法应用于声波逆时偏移和弹性波全波形反演进行检验。时间二阶、空间十二阶优化交错网格有限差分[29]用于波场正、反向延拓。常规边界值重建方法采用优化差分系数[29]。正向震源波场、常规方法得到的像和反演结果作为参考解,计算不同方法结果的最大绝对误差εMAV和均方根误差εRMS。
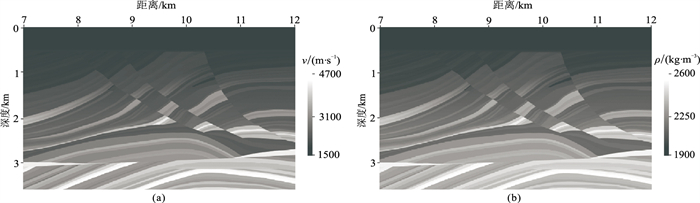
4.1 声波逆时偏移声波Marmousi模型如图 4, 时间步长为1.0ms,记录时间为4.0s,空间网格大小为10m×10m,网格点数为501×353,震源为20Hz主频的Ricker子波。51炮和501个检波点均匀分布于地表。图 5为不同方法重建的波场,炮点位于(9.5km, 0)。表 6给出不同方法重建波场的εMAV和εRMS。由表可知,常规方法的重建误差非常小,本文方法的εMAV和εRMS分别在10-2和10-4数量级。重建波场的误差随着N的增大有所减小。图 6为逆时偏移中采用不同重建方法得到的像,表 7为本文方法的εMAV和εRMS,可见,N=0或1都能保证成像结果的均方根误差小于10-3。当N=0或1时,本文方法的存储量为常规方法的16.6%或33.3%。为兼顾重建精度和内存需求,声波RTM建议采用N=0。
|
图 4 声波Marmousi模型 (a)速度;(b)密度 |
|
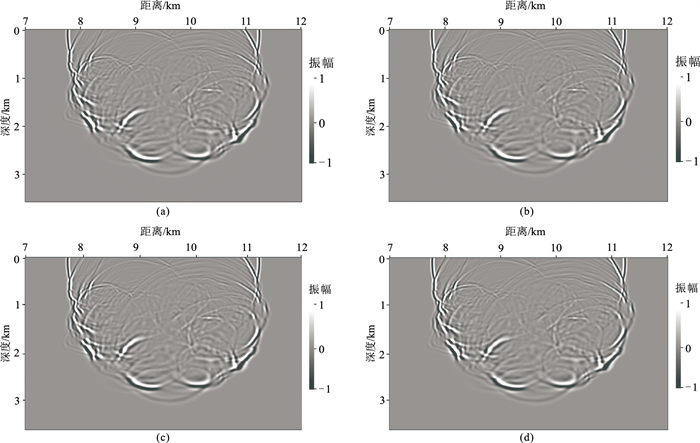
图 5 声波Marmousi模型不同方法重建的波场 (a)正传震源波场;(b)常规方法;(c)本文方法,N=0;(d)本文方法,N=1 |
|
|
表 6 声波Marmousi模型不同方法重建波场的εMAV和εRMS |

|
图 6 声波Marmousi模型不同方法的逆时偏移结果 (a)常规方法;(b)本文方法,N=0;(c)本文方法,N=1 |
|
|
表 7 声波Marmousi模型本文方法不同N的εMAV和εRMS |
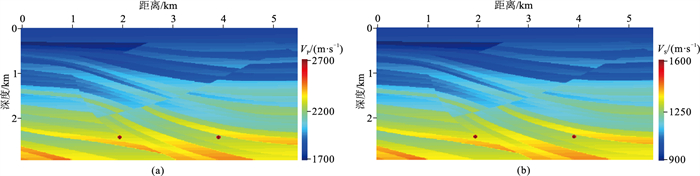
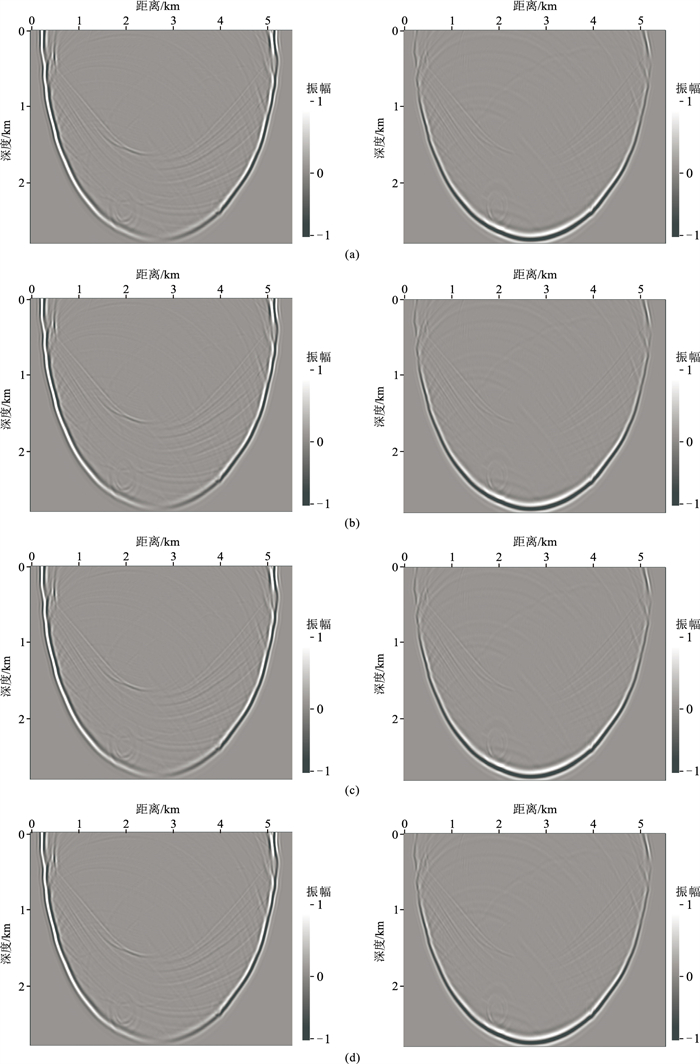
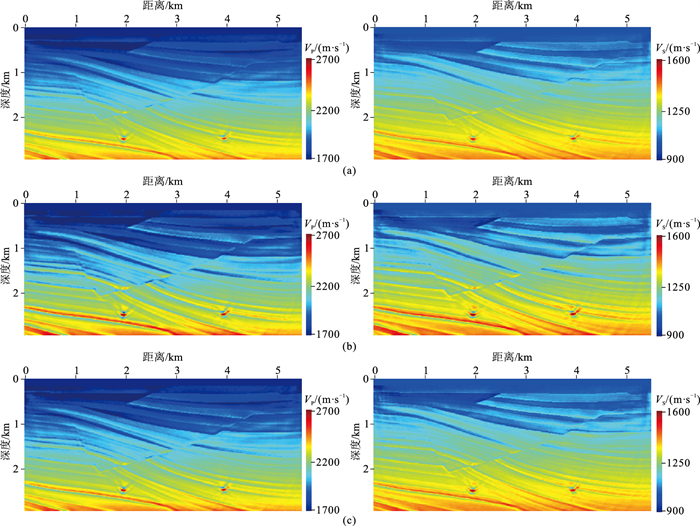
弹性波Sigsbee2A模型如图 7所示。空间网格尺寸为16m×16m,网格点数为351×186,时间步长为1.5ms,记录长度为4.5s。爆炸震源激发主频为15Hz的Ricker子波。36个震源和351个检波点均匀分布于地表。初始纵波和横波速度模型为随深度线性变化的一维模型(图 8)。采用多尺度反演(0~5Hz、0~10Hz和0~15Hz)策略,每个尺度上迭代10次。图 9给出不同方法得到的波场,炮点位于(2720m,0),表 8给出不同方法重建波场的εMAV和εRMS。常规方法(存储M层)的误差在10-6数量级,本文方法的误差随N的增大而减小。图 10为采用不同重建方法进行全波形反演得到的纵、横波速度模型。表 9为本文方法反演结果的εMAV和εRMS。当N=0时,反演结果的精度较差;当N=1时,反演精度得到大幅提高(εRMS<0.5 %)。本文方法的存储需求仅为常规方法的(N+1)/M。波场重建误差对模型参数梯度的精度有影响,为保证反演精度,全波形反演建议采用N=1。
|
图 7 弹性Sigsbee2A模型 (a)纵波速度VP;(b)横波速度VS |

|
图 8 弹性Sigsbee2A模型的初始模型 (a)纵波速度VP;(b)横波速度VS |
|
图 9 弹性Sigsbee2A模型不同方法重建的1.5s波场 (a)正传震源波场;(b)常规方法;(c)本文方法,N=0;(d)本文方法,N=1。左为水平分量,右为垂直分量 |
|
|
表 8 弹性Sigsbee2A模型不同方法重建波场的εMAV和εRMS |
|
图 10 弹性Sigsbee2A模型不同方法重建波场的全波形反演结果 (a)常规方法;(b)本文方法,N=0;(c)本文方法,N=1。左、右两侧分别为VP和VS反演结果 |
|
|
表 9 弹性Sigsbee2A模型本文方法不同N时反演结果的εMAV和εRMS |
与常规方法相比,本文方法可降低存储量,但重建波场的误差有所增加(详见精度分析和模型算例)。实际应用中,可通过调整N的大小进行重建精度和内存需求的折衷。由式(1)和式(3)可知,常规方法的计算复杂度为3M2,本文方法计算复杂度为(7M2+2MN+3M-4)/2。当N为0或1时,本文方法的计算量约为常规方法的7/6倍。与波场正、反向延拓相比,本文震源波场重建方法增加的计算量微不足道。
5 结论本文提出了一种交错网格有限差分震源波场重建方法。该方法通过存储N层边界波场和M—N层波场的线性组合重建震源波场。为提高重建精度,基于无穷范数准则和Remez交换算法优化了重建系数。详细分析了提出方法的精度和稳定性,并将其应用于声波逆时偏移和弹性波全波形反演。新方法可通过调整N的大小实现重建精度和存储需求的平衡。新方法能够获得较好的重建波场、像和反演结果,且内存需求仅为常规方法的(N+1)/M。
本文方法可直接应用于三维逆时偏移和全波形反演或其他基于伴随状态法的地球物理问题中,如最小二乘逆时偏移、波动方程旅行时反演或全球尺度波形层析等。但新方法无法用于基于黏声或黏弹波动方程的成像和反演中。如何避免衰减介质波场重建的不稳定性需要进一步考虑。
| [1] |
PLESSIX R E. A review of the adjoint-state method for computing the gradient of a functional with geophysical applications[J]. Geophysical Journal International, 2006, 167(2): 495-503. DOI:10.1111/j.1365-246X.2006.02978.x |
| [2] |
BAYSAL E, KOSLOFF D D, SHERWOOD J W C. Reverse time migration[J]. Geophysics, 1983, 48(11): 1514-1524. DOI:10.1190/1.1441434 |
| [3] |
ZHANG Y, SUN J. Practical issues in reverse time migration: true amplitude gathers, noise removal and harmonic source encoding[J]. First Break, 2009, 26: 29-35. |
| [4] |
LIU F, ZHANG G, MORTON S A, et al. An effective imaging condition for reverse-time migration using wavefield decomposition[J]. Geophysics, 2011, 76(1): S29-S39. DOI:10.1190/1.3533914 |
| [5] |
徐世刚, 包乾宗, 任志明, 等. 结合泊松算法和波场分解成像条件的各向异性优化纯声波方程逆时偏移[J]. 石油地球物理勘探, 2022, 57(3): 613-623. XU Shigang, BAO Qianzong, REN Zhiming, et al. Reverse-time migration of optimized pure acoustic equation in anisotropic media by combining Poisson algorithm and wavefield decomposition imaging condition[J]. Oil Geophysical Prospecting, 2022, 57(3): 613-623. |
| [6] |
TARANTOLA A. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics, 1984, 49(8): 1259-1266. DOI:10.1190/1.1441754 |
| [7] |
VIRIEUX J, OPERTO S. An overview of full-waveform inversion in exploration geophysics[J]. Geophysics, 2009, 74(6): WCC1-WCC26. DOI:10.1190/1.3238367 |
| [8] |
REN Z, LIU Y. A hierarchical elastic full-waveform inversion scheme based on wavefield separation and the multistep-length approach[J]. Geophysics, 2016, 81(3): R99-R123. DOI:10.1190/geo2015-0431.1 |
| [9] |
李昕洁, 王维红, 郭雪豹, 等. 全波形反演正则化方法对比[J]. 石油地球物理勘探, 2022, 57(1): 129-139. LI Xinjie, WANG Weihong, GUO Xuebao, et al. Comparison of regularization methods for full-waveform inversion[J]. Oil Geophysical Prospecting, 2022, 57(1): 129-139. |
| [10] |
何兵红. 基于声波方程转换的三参数递进式全波形反演[J]. 石油物探, 2020, 59(3): 325-335. HE Binghong. Three-parameter progressive full waveform inversion based on acoustic equation transformation[J]. Geophysical Prospecting for Petroleum, 2020, 59(3): 325-335. DOI:10.3969/j.issn.1000-1441.2020.03.001 |
| [11] |
DAI W, SCHUSTER G T. Plane-wave least-squares reverse-time migration[J]. Geophysics, 2013, 78(4): S165-S177. DOI:10.1190/geo2012-0377.1 |
| [12] |
ZHANG Y, DUAN L, XIE Y. A stable and practical implementation of least-squares reverse time migration[J]. Geophysics, 2015, 80(1): V23-V31. DOI:10.1190/geo2013-0461.1 |
| [13] |
陈汉明, 周辉, 田玉昆. 分数阶拉普拉斯算子黏滞声波方程的最小二乘逆时偏移[J]. 石油地球物理勘探, 2020, 55(3): 616-626. CHEN Hanming, ZHOU Hui, TIAN Yukun. Least-squares reverse-time migration based on a fractional Laplacian viscoacoustic wave equation[J]. Oil Geophysical Prospecting, 2020, 55(3): 616-626. |
| [14] |
LUO Y, SCHUSTER G T. Wave-equation traveltime inversion[J]. Geophysics, 1991, 56(5): 645-653. DOI:10.1190/1.1443081 |
| [15] |
MA Y, HALE D. Wave-equation reflection traveltime inversion with dynamic warping and full-waveform inversion[J]. Geophysics, 2013, 78(6): R223-R233. DOI:10.1190/geo2013-0004.1 |
| [16] |
REN Z, LI Z, GU B. Elastic reflection waveform inversion based on the decomposition of sensitivity kernels[J]. Geophysics, 2019, 84(2): R235-R250. DOI:10.1190/geo2018-0220.1 |
| [17] |
GRIEWANK A, WALTHER A. Algorithm 799:revolve: an implementation of checkpointing for the reverse or adjoint mode of computational differentiation[J]. ACM Transactions on Mathematical Software, 2000, 26(1): 19-45. DOI:10.1145/347837.347846 |
| [18] |
SYMES W W. Reverse time migration with optimal checkpointing[J]. Geophysics, 2007, 72(5): SM213-SM221. DOI:10.1190/1.2742686 |
| [19] |
ANDERSON J E, TAN L, WANG D. Time-reversal checkpointing methods for RTM and FWI[J]. Geophysics, 2012, 77(4): S93-S103. DOI:10.1190/geo2011-0114.1 |
| [20] |
GAUTHIER O, VIRIEUX J, TARANTOLA A. Two-dimensional nonlinear inversion of seismic waveforms: numerical results[J]. Geophysics, 1986, 51(7): 1387-1403. DOI:10.1190/1.1442188 |
| [21] |
DUSSAUD E, SYMES W W, WILLIAMSON P, et al. Computational strategies for reverse-time migration[C]. SEG Technical Program Expanded Abstracts, 2008, 27: 2267-2271.
|
| [22] |
王保利, 高静怀, 陈文超, 等. 地震叠前逆时偏移的有效边界存储策略[J]. 地球物理学报, 2012, 55(7): 2412-2421. WANG Baoli, GAO Jinghuai, CHEN Wenchao, et al. Efficient boundary storage strategies for seismic reverse time migration[J]. Chinese Journal of Geophysics, 2012, 55(7): 2412-2421. |
| [23] |
FENG B, WANG H. Reverse time migration with source wavefield econstruction strategy[J]. Journal of Geophysics and Engineering, 2012, 9(1): 69-74. DOI:10.1088/1742-2132/9/1/008 |
| [24] |
TAN S, HUANG L. Reducing the computer memory requirement for 3D reverse-time migration with a boundary-wavefield extrapolation method[J]. Geophysics, 2014, 79(5): S185-S194. DOI:10.1190/geo2014-0075.1 |
| [25] |
LIU S, LI X, WANG W, et al. Source wavefield reconstruction using a linear combination of the boundary wavefield in reverse time migration[J]. Geophy-sics, 2015, 80(6): S203-S212. |
| [26] |
段沛然, 谷丙洛, 李振春. 基于优化算子边界存储策略的高效逆时偏移方法[J]. 石油地球物理勘探, 2019, 54(1): 93-101. DUAN Peiran, GU Bingluo, LI Zhenchun. An efficient reverse time migration in the vertical time domain based on optimal operator boundary storage strategy[J]. Oil Geophysical Prospecting, 2019, 54(1): 93-101. |
| [27] |
REN Z, BAO Q, XU S. Memory-efficient source wavefield reconstruction and its application to 3D reverse time migration[J]. Geophysics, 2022, 87(1): S21-S34. |
| [28] |
HE Z, ZHANG J, YAO Z. Determining the optimal coefficients of the explicit finite-difference scheme using the Remez exchange algorithm[J]. Geophysics, 2019, 84(3): S137-S147. |
| [29] |
YANG L, YAN H, LIU H. Optimal staggered-grid finite-difference schemes based on the minimax approximation method with the Remez algorithm[J]. Geophysics, 2017, 82(1): T27-T42. |
| [30] |
KINDELAN M, KAMEL A, SGUAZZERO P. On the construction and efficiency of staggered numerical differentiators for the wave equation[J]. Geophysics, 1990, 55(1): 107-110. |



 包乾宗, 陕西省西安市雁塔区雁塔路126号长安大学地质工程与测绘学院地球物理系, 710054。Email:
包乾宗, 陕西省西安市雁塔区雁塔路126号长安大学地质工程与测绘学院地球物理系, 710054。Email: 