② 中国石油大学(华东)地球科学与技术学院, 山东青岛 266580
② School of Geosciences, China University of Petroleum (East China), Qingdao, Shandong 266580, China
陆地地震资料中的层间多次波是常见的干扰波,在东、西部复杂构造的中深层资料中尤为明显,通常由煤层、盐丘、火山岩等引起。随着勘探程度的不断深入,层间多次波对速度分析、地震成像和地震资料解释环节都造成了严重的困扰,成为困扰油气勘探的世界级难题。
在传统地震勘探数据处理中,成像前需要进行层间多次波压制。由于层间多次波与一次波的视速度差异较小且传播路径复杂,层间多次波的压制一直面临着精度低、成本高等一系列难题。目前层间多次波压制主要有两大类方法:一类是基于物理界面的共聚焦点方法[1]。该类方法依赖速度模型,且计算过程繁杂,不适合复杂介质中的层间多次波预测。另一类是基于点散射物理模型的逆散射级数方法[2]。该类方法基于散射理论[3]推导出一种多维直接反演方法,通过寻找特定的子级数实现对层间多次波的压制,精度较高但计算成本巨大。Carvalho等[4]、Araujo等[5]、Coates等[6]、Weglein等[7]、Malcolm等、刘华锋等[9-10]、金德刚等[11-12]、毕丽飞等[13]先后推动了该方法的发展。此外,Ikelle[14]提出通过构建虚同相轴的层间多次波预测方法,不需要速度等先验信息,在分层情况较好的情况下可以有效实现层间多次波的压制[15-16];Meles等[17]结合卷积型地震干涉法,将Marchenko自聚焦方法应用于层间多次波的预测、压制,在模型数据上取得了较好的效果,此后匡伟康等[18]、Santos等[19]、孙红日等[20]进一步推动了该方法的发展。目前已有的层间多次波压制方法的精度和计算成本严重制约了其实用化进程。
考虑到层间多次波是来自地下界面的真实反射,近年来,很多学者致力于层间多次波的有效利用,尝试对一次波和层间多次波分别或者同时成像。与自由表面多次波成像一样,由于层间多次波传播路径的复杂性而导致的成像串扰也会严重影响层间多次波成像的可靠性。Schuster等[21]、Malcolm等[22]、Fleury[23]、Zuberi等[24]、Behura等[25-26]、Berkhout[27]、Davydenko等[28]都在该领域开展了相关研究。刘伊克等[29-30]将层间多次波作为逆时偏移的反传数据实现了层间多次波成像,但层间多次波的提取精度直接影响了成像的质量,无法直接实现一次波和层间多次波的联合应用。王永强[31]发展了一种基于模型驱动的层间多次波成像方法,可以有效压制层间多次波成像引入的串扰噪声,但需预知速度场中的强反射层。目前发展的层间多次波成像方法不是无法实现一次反射波和层间多次波的联合成像,就是受计算成本影响而难以实用化。
综上所述,层间多次波分离技术目前还面临诸多挑战,分离的层间多次波精度较难保证。因此,单纯利用层间多次波进行成像极易导致错误的成像结果,而且较难实现与一次波成像结果的联合应用。因此,考虑如何在不分离层间多次波的前提下实现一次波和层间多次波的联合成像具有重要的理论研究价值。鉴于逆时偏移不仅可以对一次波成像还可以对多次波成像,本文基于逆时偏移算法对一次波和层间多次波联合成像方法开展了深入研究。首先,介绍了一次波和层间多次波联合成像原理,并引入基于上、下行波场分离的成像条件提高成像精度;然后,针对联合成像过程中引入的串扰假象,结合逆时反传过程分析了串扰产生的根源,提出了基于缺失边界匹配补偿的解决策略,实现了波场的保真逆时延拓,有效避免了串扰假象的产生;最后,通过数值试算验证了方法的可行性、有效性和适用性。
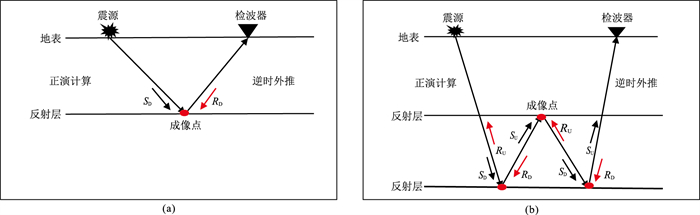
1 一次波和层间多次波联合成像方法原理与单程波偏移类似,逆时偏移也是先进行单炮偏移,然后通过多炮叠加实现最终成像。图 1a展示了一次波逆时偏移过程,具体可描述为如下三步:①正演计算,地表激发地震波后产生正向波场传播;②逆时延拓,将地震记录作为检波点波场进行逆时波场延拓;③成像,选择合适条件成像。
|
图 1 一次波(a)和层间多次波(b)逆时偏移过程示意图 S、R分别为震源和检波点波场,下标“U、D”分别表示上行和下行 |
由于互相关成像条件具有实现简单、稳定、方便并行,能够处理多波至以及不会损伤波场信息等优势,因此在常规一次波叠前逆时偏移中互相关成像条件得到了广泛的应用,可表示为
| $ I(\mathit{\boldsymbol{x}}) = \sum\limits_{t = 0}^T S (\mathit{\boldsymbol{x}}, t)R(\mathit{\boldsymbol{x}}, T - t) $ | (1) |
式中:I(x)为地下x处的成像结果;T是最大延拓时间。
图 1b为层间多次波逆时偏移过程示意图。对层间多次波的传播路径及成像过程进行分析,将常规逆时偏移成像条件作进一步整理可得
| $ \begin{array}{l} I(\mathit{\boldsymbol{x}}) = \sum\limits_{t = 0}^T S (\mathit{\boldsymbol{x}}, t)R(\mathit{\boldsymbol{x}}, T - t)\\ \;\;\;\;\;\;\; = \sum\limits_{t = 0}^T {\left[ {{S_{\rm{U}}}(\mathit{\boldsymbol{x}}, t) + {S_{\rm{D}}}(\mathit{\boldsymbol{x}}, t)} \right]} \left[ {{R_{\rm{U}}}(\mathit{\boldsymbol{x}}, T - t) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {{R_{\rm{D}}}(\mathit{\boldsymbol{x}}, T - t)} \right]\\ \;\;\;\;\;\;\; = {I_{{\rm{UU}}}}(\mathit{\boldsymbol{x}}) + {I_{{\rm{DD}}}}(\mathit{\boldsymbol{x}}) + {I_{{\rm{UD}}}}(\mathit{\boldsymbol{x}}) + {I_{{\rm{DU}}}}(\mathit{\boldsymbol{x}}) \end{array} $ | (2) |
通过对上行波和下行波分别应用成像条件,可以产生四部分成像结果。由图可见,其中成对的上行震源波场和上行检波波场以及成对的下行震源波场和下行检波点波场可以在界面处产生有效成像,对应式(2)中的成像项IDD(x)和IUU(x)。不成对的波场互相关则会产生噪声,即式(2)中IUD(x)和IDU(x)项。因此,为了获取高品质的一次波和层间多次波联合成像结果,需要对噪声产生项进行舍弃,即需要对上、下行波场进行分离,仅保留式(2)中前两项成像结果,成像条件可以进一步整理为
| $ \begin{array}{l} I(\mathit{\boldsymbol{x}}) = {I_{{\rm{UU}}}}(\mathit{\boldsymbol{x}}, t) + {I_{{\rm{DD}}}}(\mathit{\boldsymbol{x}}, t)\\ \;\;\;\;\;\;\; = \sum\limits_{t = 0}^T {\left[ {{S_U}(\mathit{\boldsymbol{x}}, t){R_{\rm{U}}}(\mathit{\boldsymbol{x}}, T - t) + } \right.} \\ \;\;\;\;\;\;\;\;\;\left. {{S_{\rm{D}}}(\mathit{\boldsymbol{x}}, t){R_{\rm{D}}}(\mathit{\boldsymbol{x}}, T - t)} \right] \end{array} $ | (3) |
通过上述分析可知,要去除成像中的串扰噪声,必须首先对延拓的波场进行上、下行波场分离[32-33],而常用的上、下行波场分离方法有F-K滤波法,该方法需要首先储存每个时刻的波场,然后对每个时刻波场进行F-K变换。根据波场速度的差异,在频率波数域上、下行波分布在不同的区域,并且以“能量线团”形式出现。分离上、下行波场滤波器为
| $ \left\{ {\begin{array}{*{20}{c}} {{S_{\rm{D}}}\left( {\omega , x, {k_z}} \right) = \left\{ {\begin{array}{*{20}{c}} {S\left( {\omega , x, {k_z}} \right)}&{{k_z} \ge 0}\\ 0&{{k_z} < 0} \end{array}} \right.}\\ {{S_{\rm{U}}}\left( {\omega , x, {k_z}} \right) = \left\{ {\begin{array}{*{20}{c}} {S\left( {\omega , x, {k_z}} \right)}&{{k_z} < 0}\\ 0&{{k_z} \ge 0} \end{array}} \right.} \end{array}} \right. $ | (4) |
| $ \left\{ {\begin{array}{*{20}{c}} {{R_{\rm{D}}}\left( {\omega , x, {k_z}} \right) = \left\{ {\begin{array}{*{20}{c}} {R\left( {\omega , x, {k_z}} \right)}&{{k_z} \ge 0}\\ 0&{{k_z} < 0} \end{array}} \right.}\\ {{R_{\rm{U}}}\left( {\omega , x, {k_z}} \right) = \left\{ {\begin{array}{*{20}{c}} {R\left( {\omega , x, {k_z}} \right)}&{{k_z} < 0}\\ 0&{{k_z} \ge 0} \end{array}} \right.} \end{array}} \right. $ | (5) |
式中kz为z方向的波数。再反变换回时空域,即可获得分离后的上行波和下行波。
由于地下传播的波场中同时含有一次波和层间多次波,因此,基于波场分离的一次波和层间多次波联合成像的条件可进一步表示为
| $ \begin{array}{l} I = {I_{{\rm{UU}}}} + {I_{{\rm{DD}}}} = \sum\limits_{t = 0}^T {\left( {{S_{\rm{U}}}{R_{\rm{U}}} + {S_{\rm{D}}}{R_{\rm{D}}}} \right)} \\ \;\; = \sum\limits_{t = 0}^T {\left[ {\left( {{S_{{\rm{PU}}}} + {S_{{\rm{IU}}}}} \right)\left( {{R_{{\rm{PU}}}} + {R_{{\rm{IU}}}}} \right) + } \right.} \\ \;\;\;\;\;\left. {\left( {{S_{{\rm{PD}}}} + {S_{{\rm{ID}}}}} \right)\left( {{R_{{\rm{PD}}}} + {R_{{\rm{ID}}}}} \right)} \right]\\ \;\; = \sum\limits_{t = 0}^T {\left( {{S_{{\rm{PU}}}}{R_{{\rm{PU}}}} + {S_{{\rm{IU}}}}{R_{{\rm{IU}}}} + {S_{{\rm{PD}}}}{R_{{\rm{PD}}}} + {S_{{\rm{ID}}}}{R_{{\rm{ID}}}}} \right)} + \\ \;\;\;\;\;\sum\limits_{t = 0}^T {\left( {{S_{{\rm{PU}}}}{R_{{\rm{IU}}}} + {S_{{\rm{IU}}}}{R_{{\rm{PU}}}} + {S_{{\rm{PD}}}}{R_{{\rm{ID}}}} + {S_{{\rm{ID}}}}{R_{{\rm{PD}}}}} \right)} \end{array} $ | (6) |
式中下标“P和I”分别表示表示一次波和层间多次波。
根据波场分离成像条件可知,式(6)倒数第二求和项对应一次波和层间多次波的正确成像结果,倒数第一求和项则为不相干波场的互相关。因此,在一次波和层间多次波联合成像过程中,尽管采用波场分离成像条件消除了一部分的串扰假象,但式(6)中倒数第一项所对应的串扰假象依然存在。考虑到层间多次波传播路径的复杂性,压制这种串扰噪声对高精度成像是极大挑战。
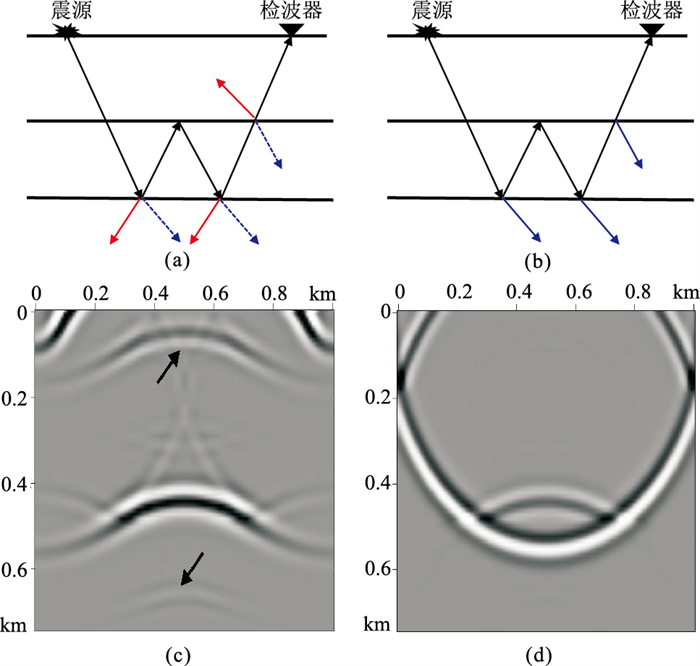
2 偏移假象产生机制及压制方法在逆时偏移波场反传过程中,由于地下左、右以及底边界处的波场无法记录,因此会导致地下界面位置处的波现象发生紊乱,引入非物理波路径现象。对于同时包含一次波和层间多次波的地震数据,层间多次波波场的复杂性使这一问题更为严重。图 2a展示了层间多次波非物理波路径产生的示意图。在第一个反射界面位置处反射波场(蓝色虚线箭头所示)的缺失将会导致反传时上行的非物理波路径假象(红色箭头所示);第二个反射界面位置处透射波场(蓝色虚线箭头)的缺失,则会在反传时产生下行的非物理波路径假象(红色箭头所示),反射波场或透射波场的缺失引入了严重的非物理波路径假象,这些非物理波路径与正传的震源波场互相关则会在成像结果中引入偏移假象。在理想情形下,如图 2b所示,若能补偿缺失的反射波场和透射波场则可以避免偏移假象的产生。图 2c展示了三层水平层状介质某时刻不保真逆时反传波场快照,可见,由于反射波和透射波的缺失,箭头处可见明显的非物理波路径假象。图 2d为理想情形下的保真逆时波场延拓快照,可见,波场延拓过程得到有效还原,无非物理波路径的影响。通过分析检波点波场的反传过程可得出如下结论,界面处的反射波场和透射波场只有同时被记录,入射波场才能够被保真重构。
|
图 2 层间多次波反传过程分析 (a)层间多次波非物理波路径的产生示意图;(b)层间多次波缺失波场补偿示意图;(c)不保真逆时延拓波场快照;(d)保真逆时延波场快照 |
由于实际地震勘探中只在地表布置检波器,无其他边界记录,这是造成非物理波路径的根本原因。由于震源波场正传时边界波场记录到了界面位置处对应层间多次波所缺失的透射波场或者反射波场,因此设想将震源波场正传时记录到的左、右以及下边界波场补偿为检波端波场反传时所缺失的左、右以及下边界波场,反传时也就能够避免非物理波路径的产生,进而避免了偏移假象的产生,即
| $ \left\{ {\begin{array}{*{20}{l}} {{D_{\rm{T}}}\left( {\mathit{\boldsymbol{s}}, {\mathit{\boldsymbol{r}}_{\rm{T}}}, t} \right) = D(\mathit{\boldsymbol{s}}, \mathit{\boldsymbol{r}}, t)}\\ {{D_{\rm{B}}}\left( {\mathit{\boldsymbol{s}}, {\mathit{\boldsymbol{r}}_{\rm{B}}}, t} \right) = {D_{\rm{S}}}\left( {\mathit{\boldsymbol{s}}, {\mathit{\boldsymbol{r}}_{\rm{B}}}, t} \right)}\\ {{D_{\rm{L}}}\left( {\mathit{\boldsymbol{s}}, {\mathit{\boldsymbol{r}}_{\rm{L}}}, t} \right) = {D_{\rm{S}}}\left( {\mathit{\boldsymbol{s}}, {\mathit{\boldsymbol{r}}_{\rm{L}}}, t} \right)}\\ {{D_{\rm{R}}}\left( {\mathit{\boldsymbol{s}}, {\mathit{\boldsymbol{r}}_{\rm{R}}}, t} \right) = {D_{\rm{S}}}\left( {\mathit{\boldsymbol{s}}, {\mathit{\boldsymbol{r}}_{\rm{R}}}, t} \right)} \end{array}} \right. $ | (7) |
式中:s为震源位置;r为检波器位置;D(s, r, t)为地表的地震记录;DS(s, rB, t)、DS(s, rL, t)和DS(s, rR, t)分别为正传震源波场对应的下、左和右边界波场;DT(s, rT, t)、DB(s, rB, t)、DL(s, rL, t)和DR(s, rR, t)分别为反传检波点波场对应的上、下、左和右边界波场值。基于检波点波场反传边界波场补偿的思想对缺失波场进行补偿,即可消除偏移假象。
然而,在实际资料处理时,由于子波是未知的,且精确的子波提取通常面临较大的挑战,而震源子波不准确将无法直接得到缺失的边界波场。为此,本文采用匹配波场的方式间接实现子波的匹配,即通过将震源正传所记录到的上边界波场与采集的实际地震记录进行匹配,在最小二乘反演框架下建立目标函数[34]
| $ E(f) = \left\| {D(\mathit{\boldsymbol{s}}, \mathit{\boldsymbol{r}}, t) - f{D_{\rm{S}}}\left( {\mathit{\boldsymbol{s}}, {\mathit{\boldsymbol{r}}_{\rm{T}}}, t} \right)} \right\|_2^2 $ | (8) |
式中:f为滤波因子;DS(s, rT, t)为在地表记录到的正演震源波场。通过求解上式目标函数即可得到滤波因子,将其作用于正演震源波场对应的左、右以及下边界即可消除子波的影响。因此式(7)可改写为
| $ \left\{ {\begin{array}{*{20}{l}} {{D_{\rm{T}}}\left( {\mathit{\boldsymbol{s}}, {\mathit{\boldsymbol{r}}_{\rm{T}}}, t} \right) = D(\mathit{\boldsymbol{s}}, \mathit{\boldsymbol{r}}, t)}\\ {{D_{\rm{B}}}\left( {\mathit{\boldsymbol{s}}, {\mathit{\boldsymbol{r}}_{\rm{B}}}, t} \right) = f{D_{\rm{S}}}\left( {\mathit{\boldsymbol{s}}, {\mathit{\boldsymbol{r}}_{\rm{B}}}, t} \right)}\\ {{D_{\rm{L}}}\left( {\mathit{\boldsymbol{s}}, {\mathit{\boldsymbol{r}}_{\rm{L}}}, t} \right) = f{D_{\rm{S}}}\left( {\mathit{\boldsymbol{s}}, {\mathit{\boldsymbol{r}}_{\rm{L}}}, t} \right)}\\ {{D_{\rm{R}}}\left( {\mathit{\boldsymbol{s}}, {\mathit{\boldsymbol{r}}_{\rm{R}}}, t} \right) = f{D_{\rm{S}}}\left( {\mathit{\boldsymbol{s}}, {\mathit{\boldsymbol{r}}_{\rm{R}}}, t} \right)} \end{array}} \right. $ | (9) |
通过波场匹配代替子波提取,理论上可以较好地恢复缺失的边界波场,实现逆时外推过程中的保真反传,进而避免非物理波路径假象的产生,最终获取高精度的一次波和层间多次波联合成像结果。
3 数值试算分别采用简单的三层模型和地下构造较为复杂的Sigsbee模型对本文的一次波和层间多次波联合成像方法的可行性、有效性和适用性进行验证。
首先采用如图 3a所示的简单三层模型验证本文方法的可行性。自上而下各层的速度分别为1500、3000、1000m/s,网格点数为151×201,网格间距为10m。采用中间放炮方式,101道接收,道间距为10m;共计101炮,炮间距为10m,记录长度为2.5s。图 3b为采用有限差分正演模拟得到的单炮记录。单炮记录中可以清晰地发现在1.0和1.3s附近存在能量较强的层间多次波。图 3c为对原始数据直接进行全波场逆时偏移得到的成像结果,图中可明显看到大量的成像假象(红色箭头所示)。为了获取高精度的成像结果,常规处理中通常需要对层间多次波进行叠前压制,这往往需要巨大的计算成本。为了去除部分一次波和层间多次波干涉形成的串扰噪声,首先采用上、下行波场分离的成像条件进行逆时偏移,得到如图 3d所示的成像结果。与图 3c对比可见,偏移假象都得到了部分的压制,但是依然可见较为清晰的串扰假象残留(红色箭头所示)。

|
图 3 三层模型及不同条件成像结果对比 (a)模型;(b)单炮记录;(c)全波场互相关条件成像结果;(d)波场分离互相关条件成像结果 |
为了进一步压制串扰假象,首先采用基于上述参数正演的炮记录模拟实际地震资料,然后选取与正演炮记录完全不同的震源子波进行逆时偏移的正向延拓。图 4a为直接将正演的左、右、下边界存放的震源波场作为逆时延拓过程中缺失的左、右、下边界接收波场,然后进行逆时外推所得到0.5s时刻反传波场的快照;图 4b则首先将上边界接收的震源波场与原始地震记录进行匹配,按照式(8)求取匹配因子,得到匹配因子后将其分别作用于正演左、右、下边界存放的震源波场,再进行逆时外推所得到的对应时刻的反传波场快照。图 4a中,由于偏移时选取的子波与模拟实际地震记录的子波不一致,虽然进行了边界波场的补偿,但是仍旧无法实现逆时偏移的保真反传,非物理波路径假象依然存在;而图 4b中,通过对逆时偏移中正向外推的上边界波场与模拟的实际地震记录进行匹配得到匹配因子,由于匹配因子中包含了子波信息,将其分别作用于正演的左、右、下边界波场后即可模拟真实缺失的边界波场,从而可以有效地消除地震子波的影响。波场快照中可以明显发现非物理波路径假象得到了有效消除,较好地实现了保真逆时延拓。

|
图 4 三层模型缺失边界波场直接补偿(a)与匹配后补偿(b)的反传快照(t=0.5s)对比 |
图 5为采用震源波场对缺失边界直接补偿与本文方法得到的偏移叠加结果对比。图 5a中仍然有串扰假象的残留,而图 5b中的串扰假象则得到了有效去除,得到了高精度的一次波和层间多次波联合成像结果,验证了本文方法的可行性和有效性。

|
图 5 三层模型缺失边界波场直接补偿(a)与匹配补偿(b)的一次波和层间多次波联合逆时偏移结果对比 |
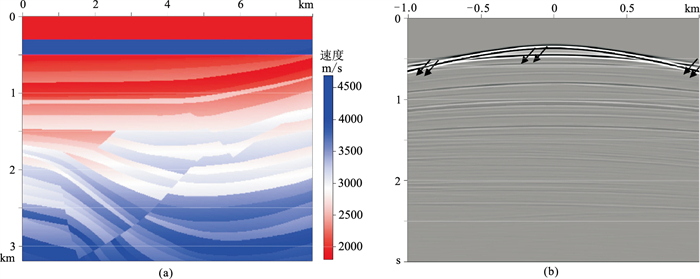
选取地下构造较为复杂的部分Sigsbee模型验证本文方法的适用性。为了突出层间多次波对成像的影响,在Sigsbee模型深度0.3~0.5km处添加了一高速层,其上、下界面产生强反射,是层间多次波形成的有利条件(图 6a)。模型网格数为320×800,网格间距为10m,采用中间放炮方式,200道接收,道间距为10m,共计300炮,炮间距为20m,记录长度为3s。图 6b为采用有限差分模拟的单炮记录,浅层可见明显的层间多次波(箭头所示)。
|
图 6 Sigsbee速度模型(a)及单炮记录(b) |
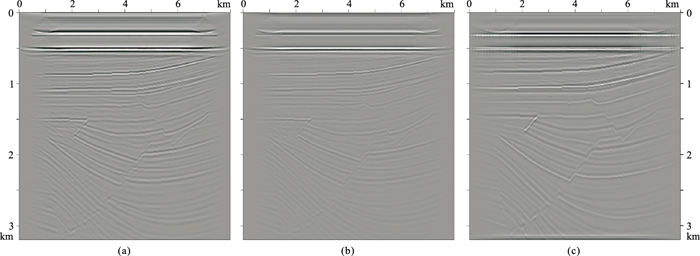
为了检验本文方法的优越性,在基于逆时偏移对正演炮记录进行成像的过程中选用了与正演炮记录完全不同的子波。图 7a为采用传统一次波逆时偏移方法对同时包含一次波和层间多次波的记录进行偏移得到的成像结果。由于未进行层间多次波压制,在成像过程中一次波与层间多次波能量互相干涉,在成像结果中引入了大量的串扰假象,对后续的的解释工作极为不利。根据串扰假象产生机制,采用缺失边界补偿的方法对串扰假象进行压制。图 7b为直接将左、右、下边界存放的震源波场作为逆时外推过程中缺失的左、右、下边界接收波场,然后进行逆时外推并运用上、下行波场分离成像条件得到的逆时偏移结果。由于未考虑子波的影响,即使进行了缺失边界波场补偿,仍无法实现保真逆时延拓,成像结果中的串扰假象依然清晰可见。图 7c为首先将上边界接收的震源波场与原始接收记录进行匹配,得到匹配因子后分别作用于左、右、下边界存放的震源波场,再进行逆时延拓并运用波场分离成像条件得到的逆时偏移结果。由图可见,成像界面清晰,串扰假象得到了有效消除。
|
图 7 Sigsbee模型不同方法成像结果对比 (a)传统一次波逆时偏移;(b)缺失边界直接补偿的联合逆时偏移;(c)缺失边界匹配补偿的联合逆时偏移 |
选取横向2~6 km、深度0.5~1.5 km区域的不同方法成像结果进行放大显示并与速度模型对比(图 8),可明显看出,图 8d的本文方法成像剖面中界面清晰,图 8b和8c中的串扰假象(箭头所示)都得到了有效消除,验证了本文方法的对复杂模型的适用性。
4 结论长期以来,层间多次波因其压制难度大且成本高,成为困扰地震勘探尤其是陆地地震勘探的棘手难题。考虑逆时偏移具有成像精度高且可以对多次波成像的优势,本文基于逆时偏移开展了同时对一次波和层间多次波进行成像的方法研究,旨在避免叠前层间多次波压制,在成像过程中消除层间多次波引入的串扰假象,实现高精度的一次波和层间多次波联合成像,数值试算结果验证了方法的可行性、有效性和对复杂模型适用性。结论如下:
(1) 通过一次波和层间多次波的传播路径分析发现,偏移成像过程中的有效成像只存在于成对的上、下行波中,因此,采用基于上、下行波场分离的成像条件可以消除部分相关串扰;
(2) 从波场逆时延拓角度分析了串扰假象的产生机制,发现其来自于边界处透射波场和反射波场的缺失;
(3) 考虑地震子波的影响,提出的基于缺失边界波场匹配补偿的解决策略,通过将正演上边界与实际地震资料进行匹配求取匹配因子,并将其作用于缺失边界正传波场从而实现保真逆时反传,可以有效避免串扰假象的产生。
需要指出,本文方法是对层间多次波成像的一种尝试,具有一定的理论研究价值,但考虑实际地震资料的复杂性,本文方法的实用性还需进一步研究。
| [1] |
BERKHOUT A J, VERSCHUUR D J. Removal of internal multiples with the common-focus-point (CFP) approach, Part 1:Explanation of the theory[J]. Geophysics, 2005, 70(3): V45-V60. DOI:10.1190/1.1925753 |
| [2] |
WEGLEIN A B, GASPAROTTO F A, CARVALHO P M, et al. An inverse scattering series method for attenuating multiples in seismic reflection data[J]. Geophysics, 1997, 62(6): 1975-1989. DOI:10.1190/1.1444298 |
| [3] |
NORTON S J. Iterative seismic inversion[J]. Geophysical Journal International, 1988, 94(3): 457-468. DOI:10.1111/j.1365-246X.1988.tb02268.x |
| [4] |
CARVALHO F M, WEGLEIN A B, STOLT R H. Examples of a nonlinear inversion method based on the T matrix of scattering theory: application to multiple suppression[C]. SEG Technical Program Expanded Abstracts, 1991, 10: 1319-1322.
|
| [5] |
ARAUJO F V, WEGLEIN A B, CARVALHO P M. Inverse scattering series for multiple attenuation: an example with surface and internal multiples[C]. SEG Technical Program Expanded Abstracts, 1994, 13: 1039-1041.
|
| [6] |
COATES R T, WEGLEIN A B. Internal multiple attenuation using inverse scattering: results from pre-stack 1 & 2D acoustic and elastic synthetics[C]. SEG Technical Program Expanded Abstracts, 1996, 15: 1522-1525.
|
| [7] |
WEGLEIN A B, ARAU'JO F V, CARVALHO P M, et al. Topical review: inverse scattering series and seismic exploration[J]. Inverse Problems, 2003, 19(6): R27-R83. DOI:10.1088/0266-5611/19/6/R01 |
| [8] |
MALCOLM A E, DE HOOP M V. Inverse multiple scattering in the downward continuation approach[C]. SEG Technical Program Expanded Abstracts, 2004, 23: 1293-1296.
|
| [9] |
刘华锋. 逆散射级数法衰减海上多次波[D]. 北京: 中国石油大学(北京), 2011.
|
| [10] |
刘华锋, 李庆春, 王立明. 利用改进的扩展多道匹配相减法压制多次波[J]. 石油地球物理勘探, 2009, 44(3): 270-275. LIU Huafeng, LI Qingchun, WANG Liming. Suppression of multiples by improved expanding multi-channel match minus method[J]. Oil Geophysical Prospecting, 2009, 44(3): 270-275. DOI:10.3321/j.issn:1000-7210.2009.03.005 |
| [11] |
金德刚. 基于波动方程的层间多次波预测方法研究[D]. 北京: 中国科学院地质与地球物理研究所, 2008.
|
| [12] |
金德刚, 常旭, 刘伊克. 逆散射级数法预测层间多次波的算法改进及其策略[J]. 地球物理学报, 2008, 51(4): 1209-1217. JIN Degang, CHANG Xu, LIU Yike. Algorithm improvement and strategy of internal multiples prediction based on inverse scattering series method[J]. Chinese Journal of Geophysics, 2008, 51(4): 1209-1217. DOI:10.3321/j.issn:0001-5733.2008.04.032 |
| [13] |
毕丽飞, 秦宁, 李钟晓, 等. 应用逆散射级数波场预测和2D卷积盲分离压制层间多次波[J]. 石油地球物理勘探, 2020, 55(3): 521-529. BI Lifei, QIN Ning, LI Zhongxiao, et al. Wavefield prediction with inverse scattering series and 2D blind separation of convolved mixtures for suppressing internal multiples[J]. Oil Geophysical Prospecting, 2020, 55(3): 521-529. |
| [14] |
IKELLE L T. A construct of internal multiples from surface data only: the concept of virtual seismic events[J]. Geophysical Journal International, 2006, 164(2): 383-393. DOI:10.1111/j.1365-246X.2006.02857.x |
| [15] |
崔永福, 刘嘉辉, 陈猛, 等. 虚同相轴方法及其在陆上地震层间多次波压制中的应用[J]. 石油地球物理勘探, 2019, 54(6): 1228-1236, 1245. CUI Yongfu, LIU Jiahui, CHEN Meng, et al. Land seismic peg-leg multiple attenuation with the virtual event method[J]. Oil Geophysical Prospecting, 2019, 54(6): 1228-1236, 1245. |
| [16] |
刘璐, 胡天跃, 安圣培, 等. 虚同相轴法预测地震层间多次波在实际应用中的可行性分析[J]. 北京大学学报(自然科学版), 2017, 53(1): 26-36. LIU Lu, HU Tianyue, AN Shengpei, et al. Feasibility analysis on practical application of virtual events method in predicting seismic interbed multiples[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2017, 53(1): 26-36. |
| [17] |
MELES G A, LÖER K, RAVASI M, et al. Internal multiple prediction and removal using Marchenko autofocusing and seismic interferometry[J]. Geophy-sics, 2015, 80(1): A7-A11. |
| [18] |
匡伟康, 胡天跃, 安圣培, 等. 基于Marchenko自聚焦的层间多次波压制[J]. 地球物理学进展, 2018, 33(6): 2347-2357. KUANG Weikang, HU Tianyue, AN Shengpei, et al. Internal multiples attenuation using Marchenko autofocusing[J]. Progress in Geophysics, 2018, 33(6): 2347-2357. |
| [19] |
SANTOS R S, REVELO D E, PESTANA R C, et al. A least-squares based approach for the Marchenko internal multiple elimination scheme[C]. SEG Technical Program Expanded Abstracts, 2020, 39: 3184-3188.
|
| [20] |
孙红日, 王维红, 石颖, 等. 基于Marchenko理论一步法压制层间多次波[J]. 地球物理学报, 2021, 64(9): 3295-3303. SUN Hongri, WANG Weihong, SHI Ying, et al. Suppression of internal multiples based on Marchenko theory by one step[J]. Chinese Journal of Geophy-sics, 2021, 64(9): 3295-3303. |
| [21] |
SCHUSTER G T, YU J, SHENG J, et al. Interferometric/daylight seismic imaging[J]. Geophysical Journal International, 2004, 157(2): 838-852. |
| [22] |
MALCOLM A E, URSIN B, DE HOOP M V. Seismic imaging and illumination with internal multiples[J]. Geophysical Journal International, 2009, 176(3): 847-864. |
| [23] |
FLEURY C. Increasing illumination and sensitivity of reverse-time migration with internal multiples[J]. Geophysical Prospecting, 2013, 61(5): 891-906. |
| [24] |
ZUBERI M A H, ALKHALIFAH T A. Generalized internal multiple imaging(GIMI)using Feynman-like diagrams[J]. Geophysical Journal International, 2014, 197(3): 1582-1592. |
| [25] |
BEHURA J, FORGHANI F. A practical approach to prediction of internal multiples and ghosts[C]. SEG Technical Program Expanded Abstracts, 2012, 31: 1-5.
|
| [26] |
BEHURA J, WAPENAAR K, SNIEDER R. Autofocus imaging: image reconstruction based on inverse scattering theory[J]. Geophysics, 2014, 79(3): A19-A26. |
| [27] |
BERKHOUT A J. Combining full wavefield migration and full waveform inversion, a glance into the future of seismic imaging[J]. Geophysics, 2012, 77(2): S43-S50. |
| [28] |
DAVYDENKO M, VERSCHUUR E. Including internal multiples from the estimated image in least-squares reverse-time migration[C]. SEG Technical Program Expanded Abstracts, 2020, 39: 2928-2932.
|
| [29] |
刘伊克, 朱伟林, 米立军, 等. 南海深水多次波成像[J]. 中国科学: 地球科学, 2015, 45(2): 152-160. LIU Yike, ZHU Weilin, MI Lijun, et al. Migration of multiples from the South China Sea[J]. Chinese Science: Earth Science, 2015, 45(2): 152-160. |
| [30] |
刘伊克, 刘学建, 张延保. 地震多次波成像[J]. 地球物理学报, 2018, 61(3): 1025-1037. LIU Yike, LIU Xuejian, ZHANG Yanbao. Migration of seismic multiple reflections[J]. Chinese Journal of Geophysics, 2018, 61(3): 1025-1037. |
| [31] |
王永强. 多次波成像方法研究[D]. 上海: 同济大学, 2016.
|
| [32] |
高少武, 孙鹏远, 方云峰, 等. 双检数据上下行波场分离技术研究进展[J]. 石油地球物理勘探, 2021, 56(6): 1419-1429. GAO Shaowu, SUN Pengyuan, FANG Yunfeng, et al. Research progress of up-going and down-going wavefield separation for dual-sensor data[J]. Oil Geophy-sical Prospecting, 2021, 56(6): 1419-1429. |
| [33] |
高少武, 钱忠平, 孙鹏远, 等. 水陆检数据上下行波场分离方法[J]. 石油地球物理勘探, 2020, 55(5): 991-996. GAO Shaowu, QIAN Zhongping, SUN Pengyuan, et al. A separation method of up-going and down-going wavefields for dual-sensor seismic data[J]. Oil Geophysical Prospecting, 2020, 55(5): 991-996. |
| [34] |
李钟晓, 高好天, 陈鑫泽, 等. 基于3D匹配滤波器和伪地震数据算法的多次波自适应相减方法[J]. 石油地球物理勘探, 2020, 55(3): 530-540. LI Zhongxiao, GAO Haotian, CHEN Xinze, et al. Adaptive multiple subtraction based on a 3D matching filter and pseudo seismic data algorithm[J]. Oil Geophysical Prospecting, 2020, 55(3): 530-540. |



 秦宁, 山东省东营市东营区北一路210号中国石化胜利油田分公司物探研究院, 257022。Email:
秦宁, 山东省东营市东营区北一路210号中国石化胜利油田分公司物探研究院, 257022。Email: 
