② 中国石化弹性波理论与探测技术重点实验室, 北京 10008;
③ 中国石油大学(北京)非常规油气科学技术研究院, 北京 102249;
④ 中国石化石油勘探开发研究院, 北京 100083
② SINOPEC Key Laboratory of Seismic Elastic Wave Technology, Beijing 100083, China;
③ Unconventional Petroleum Research Institute, China University of Petroleum (Beijing), Beijing 102249, China;
④ SINOPEC Petroleum Exploration and Production Research Institute, Beijing 100083 China
逆时偏移不受倾角和偏移孔径的限制,在复杂地层结构中,可比较精确地保存地震波振幅和相位等信息。随着三分量宽方位数据采集技术的不断发展,弹性逆时偏移成像技术也逐渐应用于实际数据。该方法考虑了转换波的特征,能够获得反映特殊结构(例如气藏)等更丰富的有效信息[1-4];通过求解弹性波方程,重建P波和S波波场,然后运用成像条件分别得到PP波、PS波、SP波和SS波成像结果[5-6]。但是,地震波在实际地层中传播时,耦合的P波和S波波场会产生串扰噪声,严重降低成像剖面的质量,所以在应用成像条件之前,需要准确分离P波和S波波场。
地面多分量地震记录可通过矢量合成法计算P波、S波的矢量方向[7],把地震波振幅旋转到真正的纵、横波矢量轴,实现P波、S波波场分离[8-10]。另外,也可以在逆时偏移波场延拓过程中进行波场分离,获得纯P波、纯S波波场。基于Helmholtz理论,通过散度和旋度算子得到标量和矢量势,然后计算P波、S波波场[11];也可以直接对散度和旋度算子计算的势进行成像[12]。另外,采用P波、S波解耦的弹性波方程,可以得到三维介质中分离的P波、S波波场[13]。通过Poynting矢量求取的质点振动方向并进行标量化,可得到标量PP波和PS波成像结果,但是该方法只适用于各向同性介质。
实际地下介质普遍呈现各向异性特征,通常由页岩层、定向排列的垂直裂缝以及具有周期性的薄互层引起[14],用横向各向同性即TI介质描述。若各向异性对称轴沿垂直方向,则称为VTI介质。当地层经受了强烈的构造运动,其对称轴与垂直方向形成一定夹角时,TTI介质是更精确的近似[15]。面对各向异性介质,以上分离方法不再适用,因为此时弹性波的偏振方向不再与传播方向平行或垂直,旋度和散度算子会造成不正确的投影,在弹性波场中产生不同波型能量残留[16],导致错误的成像结果。所以需要发展适合三维TTI介质的高效精确的弹性波场解耦方法,以提高弹性波逆时偏移的成像精度。
通过求解Christoffel方程,可以计算各向异性介质中波的偏振方向,进而对弹性波场进行分离[17]。很多学者都沿着这个思路对各向异性介质中的波场分离方法进行了研究,如利用非稳态滤波构建归一化的偏振方向,可以在非均匀VTI介质中实现P波和S波波场的分离[18]。考虑到地震波的矢量特征,可以在波数域实现VTI介质的弹性波场分解,且分解前后的波场具有相同的振幅、相位和量纲[19]。引入低秩近似思想后,矢量波场分解法的计算过程可以简化为混合域(空间波数域)的矩阵乘法形式[20]。另外,在波数域对VTI介质Christoffel方程进行特征分析,可以计算不同波模式的偏振方向,然后构建合适的矢量弹性波场分解算子[21]。但是,这些适用于VTI模型的分解算子无法考虑倾斜对称轴的情况,不能准确估计TTI介质中波的偏振方向。
直接求解TTI介质的Christoffel方程,可以计算与各向异性对称轴倾角有关的偏振方向,实现TTI介质的弹性波场分解[22]。但是,分解前、后的波场具有不同的振幅、相位和量纲。依据矢量弹性波场分解,有学者提出在波数域对二维Christoffel方程进行特征分析,通过构建VTI分解算子以及坐标旋转,得到TTI分解算子,最终实现二维TTI介质弹性波场分解[23]。该方法应用矩阵分解算法提高了计算效率,但是分解前、后的波场振幅不一致,当对称轴倾角以及各向异性参数都为零时,分解算子无法退化到各向同性的形式。
目前针对各向异性介质的弹性波场分解方法,主要都应用于二维介质,面对更复杂的三维TTI介质,分解方法主要还是基于散度和旋度算子,通过投影得到分离的标量P波场和矢量S波场。但是,在应用成像条件时,分离后的标量和矢量波场将产生三个PS波成像结果。而且在PS波成像界面中会出现极性反转的问题,如果不进行适当校正,会导致非相干叠加,产生假象。
为了解决三维TTI介质弹性波场分解面临的问题,本文首先从VTI弹性波动方程出发,对Christoffel方程进行特征分析,再推导出三维VTI分解算子;然后根据各向异性对称轴与观测坐标系之间的关系,利用坐标旋转导出了三维TTI介质波场分解算子;最后构建泊松方程,实现三维TTI介质弹性波场分解。为了避免直接求解泊松方程,引入了改进的快速算法计算辅助波场。该三维TTI波场分解算子考虑了随空间变化的弹性参数和对称轴倾角,适用于复杂的各向异性介质。对均匀和非均匀的三维TTI介质模型进行弹性波波场分解的数值模拟结果表明,该分解算子能够有效分离三维TTI介质中的弹性波场。
1 方法原理 1.1 三维各向异性弹性波动方程特征分析对各向异性介质的弹性波场进行特征分析,其特征值以及对应的特征向量分别表示不同的波模式。通过求解VTI介质Christoffel方程的特征向量,可以构建分解算子,实现VTI介质的弹性波场分解。针对TTI介质,将观测坐标系进行旋转,使垂向坐标轴沿着倾斜对称轴方向,此时可近似为VTI介质,于是适用于VTI介质的弹性波场分解方法就可以推广到TTI介质。
根据牛顿第二定理和广义胡克定律,三维VTI二阶弹性波动方程为
| $ \left\{ {\begin{array}{*{20}{l}} \begin{array}{l} \rho \frac{{{\partial ^2}{u_x}}}{{\partial {t^2}}} = \left( {{C_{11}}\frac{{{\partial ^2}}}{{\partial {x^2}}} + {C_{66}}\frac{{{\partial ^2}}}{{\partial {y^2}}} + {C_{44}}\frac{{{\partial ^2}}}{{\partial {z^2}}}} \right){u_x} + \\ \;\;\;\;\;\;\;\left( {{C_{11}} - {C_{66}}} \right)\frac{{{\partial ^2}}}{{\partial x\partial y}}{u_y} + \left( {{C_{13}} + {C_{44}}} \right)\frac{{{\partial ^2}}}{{\partial x\partial z}}{u_z} \end{array}\\ \begin{array}{l} \rho \frac{{{\partial ^2}{u_y}}}{{\partial {t^2}}} = \left( {{C_{11}} - {C_{66}}} \right)\frac{{{\partial ^2}}}{{\partial x\partial y}}{u_x} + \\ \;\;\;\;\;\;\;\left( {{C_{66}}\frac{{{\partial ^2}}}{{\partial {x^2}}} + {C_{11}}\frac{{{\partial ^2}}}{{\partial {y^2}}} + {C_{44}}\frac{{{\partial ^2}}}{{\partial {z^2}}}} \right){u_y} + \\ \;\;\;\;\;\;\;\left( {{C_{13}} + {C_{44}}} \right)\frac{{{\partial ^2}}}{{\partial y\partial z}}{u_z} \end{array}\\ \begin{array}{l} \rho \frac{{{\partial ^2}{u_z}}}{{\partial {t^2}}} = \left( {{C_{13}} + {C_{44}}} \right)\frac{{{\partial ^2}}}{{\partial x\partial z}}{u_x} + \\ \;\;\;\;\;\;\;\left( {{C_{13}} + {C_{44}}} \right)\frac{{{\partial ^2}}}{{\partial y\partial z}}{u_y} + \\ \;\;\;\;\;\;\;\left( {{C_{44}}\frac{{{\partial ^2}}}{{\partial {x^2}}} + {C_{44}}\frac{{{\partial ^2}}}{{\partial {y^2}}} + {C_{33}}\frac{{{\partial ^2}}}{{\partial {z^2}}}} \right){u_z} \end{array} \end{array}} \right. $ | (1) |
式中:ux、uy和uz表示位移三分量;C11、C13、C33、C44和C66为刚度矩阵中的独立元素;ρ为密度。在频率—波数域中,将式(1)写成矩阵形式
| $ \rho {\omega ^2}\left[ {\begin{array}{*{20}{l}} {{U_x}}\\ {{U_y}}\\ {{U_z}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{C_{11}}k_x^2 + {C_{66}}k_y^2 + {C_{44}}k_z^2}&{\left( {{C_{11}} - {C_{66}}} \right){k_x}{k_y}}&{\left( {{C_{13}} + {C_{44}}} \right){k_x}{k_z}}\\ {\left( {{C_{11}} - {C_{66}}} \right){k_x}{k_y}}&{{C_{66}}k_x^2 + {C_{11}}k_y^2 + {C_{44}}k_z^2}&{\left( {{C_{13}} + {C_{44}}} \right){k_y}{k_z}}\\ {\left( {{C_{13}} + {C_{44}}} \right){k_x}{k_z}}&{\left( {{C_{13}} + {C_{44}}} \right){k_y}{k_z}}&{{C_{44}}k_x^2 + {C_{44}}k_y^2 + {C_{33}}k_z^2} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{U_x}}\\ {{U_y}}\\ {{U_z}} \end{array}} \right] $ | (2) |
式中:Ux、Uy和Uz分别是ux、uy和uz的频率—波数域形式;ω是角频率;kx、ky和kz为观测坐标系下三个方向的波数。分别用A、U表示式(2)右侧的3×3矩阵和列向量,基于速度、频率和波数的频散关系v=ω/k,两边同时除以k2=kx2+ky2+kz2,式(2)可写为
| $ \frac{\mathit{\boldsymbol{A}}}{{{k^2}}}\mathit{\boldsymbol{U}} = \frac{{\rho {\omega ^2}}}{{{k^2}}}\mathit{\boldsymbol{U}} $ | (3) |
式中:ρω2是矩阵A的特征值,可以计算得到不同波型的相速度ω/k;U是矩阵A的特征向量,表示不同波的偏振方向。
通过特征分析,式(3)的特征值及对应的特征向量(详细推导见附录A)为
| $ \left\{ {\begin{array}{*{20}{l}} {{\lambda _1} = \rho v_{\rm{p}}^2\left[ {(1 + 2\varepsilon )\left( {k_x^2 + k_y^2} \right) + k_z^2} \right]}\\ {{\lambda _2} = \rho v_s^2\left[ {(1 + 2\gamma )\left( {k_x^2 + k_y^2} \right) + k_z^2} \right]}\\ {{\lambda _3} = \rho v_s^2\left( {k_x^2 + k_y^2 + k_z^2} \right)} \end{array}} \right. $ | (4) |
| $ {\mathit{\boldsymbol{\hat a}}_1} = \left[ {\begin{array}{*{20}{c}} {{k_x}}\\ {{k_y}}\\ {\frac{{\sqrt {\left[ {(1 + 2\delta )v_{\rm{P}}^2 - v_{\rm{S}}^2} \right]\left( {v_{\rm{P}}^2 - v_{\rm{S}}^2} \right)} }}{{(1 + 2\varepsilon )v_{\rm{P}}^2 - v_{\rm{S}}^2}}{k_z}} \end{array}} \right] $ | (5) |
| $ {\mathit{\boldsymbol{\hat a}}_2} = \left[ {\begin{array}{*{20}{c}} { - {k_y}}\\ {{k_x}}\\ 0 \end{array}} \right] $ | (6) |
| $ {\mathit{\boldsymbol{\hat a}}_3} = \left[ {\begin{array}{*{20}{c}} { - \frac{{\sqrt {\left[ {(1 + 2\delta )v_{\rm{P}}^2 - v_{\rm{S}}^2} \right]\left( {v_{\rm{P}}^2 - v_{\rm{S}}^2} \right)} }}{{(1 + 2\varepsilon )v_{\rm{P}}^2 - v_{\rm{S}}^2}}{k_x}{k_z}}\\ { - \frac{{\sqrt {\left[ {(1 + 2\delta )v_{\rm{P}}^2 - v_{\rm{S}}^2} \right]\left( {v_{\rm{P}}^2 - v_{\rm{S}}^2} \right)} }}{{(1 + 2\varepsilon )v_{\rm{P}}^2 - v_{\rm{S}}^2}}{k_y}{k_z}}\\ {k_x^2 + k_y^2} \end{array}} \right] $ | (7) |
式中:
| $ \left\{ {\begin{array}{*{20}{l}} {{C_{11}} = (1 + 2\varepsilon )\rho v_{\rm{P}}^2}\\ {{C_{33}} = \rho v_{\rm{P}}^2}\\ {{C_{44}} = \rho v_{\rm{S}}^2}\\ {{C_{66}} = (1 + 2\gamma )\rho v_{\rm{S}}^2}\\ {{C_{13}} = \rho \sqrt {\left[ {(1 + 2\delta )v_{\rm{P}}^2 - v_{\rm{S}}^2} \right]\left( {v_{\rm{P}}^2 - v_{\rm{S}}^2} \right)} - \rho v_{\rm{S}}^2} \end{array}} \right. $ | (8) |
式中vP和vS分别是沿各向异性对称轴方向的P波和S波速度。
在三维VTI介质中,包含各向异性对称轴的平面都是对称面,所以对任意方向入射的地震波,P波和SV波的偏振方向都在对称面内,而SH波的偏振方向在各向同性面内,与弹性参数无关。
1.2 构建三维TTI分解算子根据傅里叶变换的性质,将式(5)~式(7)从波数域转换到空间域,有
| $ {\mathit{\boldsymbol{a}}_1} = \left[ {\begin{array}{*{20}{c}} {\frac{\partial }{{\partial x}}}\\ {\frac{\partial }{{\partial y}}}\\ {\frac{{\sqrt {\left[ {(1 + 2\delta )v_{\rm{P}}^2 - v_{\rm{S}}^2} \right]\left( {v_{\rm{P}}^2 - v_{\rm{S}}^2} \right)} }}{{(1 + 2\varepsilon )v_{\rm{P}}^2 - v_{\rm{S}}^2}}\frac{\partial }{{\partial z}}} \end{array}} \right] $ | (9) |
| $ {\mathit{\boldsymbol{a}}_2} = \left[ {\begin{array}{*{20}{c}} { - \frac{\partial }{{\partial y}}}\\ {\frac{\partial }{{\partial x}}}\\ 0 \end{array}} \right] $ | (10) |
| $ {\mathit{\boldsymbol{a}}_3} = \left[ {\begin{array}{*{20}{c}} { - \frac{{\sqrt {\left[ {(1 + 2\delta )v_{\rm{P}}^2 - v_{\rm{S}}^2} \right]\left( {v_{\rm{P}}^2 - v_{\rm{S}}^2} \right)} }}{{(1 + 2\varepsilon )v_{\rm{P}}^2 - v_{\rm{S}}^2}}\frac{{{\partial ^2}}}{{\partial x\partial z}}}\\ { - \frac{{\sqrt {\left[ {(1 + 2\delta )v_{\rm{P}}^2 - v_{\rm{S}}^2} \right]\left( {v_{\rm{P}}^2 - v_{\rm{S}}^2} \right)} }}{{(1 + 2\varepsilon )v_{\rm{P}}^2 - v_{\rm{S}}^2}}\frac{{{\partial ^2}}}{{\partial y\partial z}}}\\ {\frac{{{\partial ^2}}}{{\partial {x^2}}} + \frac{{{\partial ^2}}}{{\partial {y^2}}}} \end{array}} \right] $ | (11) |
根据计算的偏振方向,将对应的波模式投影到各自的偏振方向上,实现弹性波场分解。在三维VTI介质中,P波、SV波和SH波的偏振方向互相垂直,于是可以利用P波的偏振方向,构建空间域的分解算子为
| $ {\tilde \nabla _{{\rm{VTI}}}} = \left[ {\begin{array}{*{20}{l}} {\frac{\partial }{{\partial x}}}\\ {\frac{\partial }{{\partial y}}}\\ {r\frac{\partial }{{\partial z}}} \end{array}} \right] $ | (12) |
| $ r = \frac{{\sqrt {\left[ {(1 + 2\delta )v_{\rm{P}}^2 - v_{\rm{S}}^2} \right]\left( {v_{\rm{P}}^2 - v_{\rm{S}}^2} \right)} }}{{(1 + 2\varepsilon )v_{\rm{P}}^2 - v_{\rm{S}}^2}} $ | (13) |
在此基础上,根据三维TTI介质各向异性对称轴与观测坐标系之间的几何关系,构建一个旋转矩阵,使垂向坐标轴沿着倾斜各向异性对称轴方向。定义θ为三维TTI介质对称轴在yOz平面内沿z轴顺时针方向的夹角(图 1),三维坐标旋转公式为
| $ \left[ {\begin{array}{*{20}{l}} {{x^\prime }}\\ {{y^\prime }}\\ {{z^\prime }} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&{\cos \theta }&{\sin \theta }\\ 0&{ - \sin \theta }&{\cos \theta } \end{array}} \right]\left[ {\begin{array}{*{20}{l}} x\\ y\\ z \end{array}} \right] $ | (14) |

|
图 1 三维TTI介质对称轴与观测坐标系的关系示意图 |
新坐标系和观测坐标系之间空间偏导数的关系为
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{\partial }{{\partial {x^\prime }}} = \frac{\partial }{{\partial x}}}\\ {\frac{\partial }{{\partial {y^\prime }}} = \cos \theta \frac{\partial }{{\partial y}} + \sin \theta \frac{\partial }{{\partial z}}}\\ {\frac{\partial }{{\partial {z^\prime }}} = - \sin \theta \frac{\partial }{{\partial y}} + \cos \theta \frac{\partial }{{\partial z}}} \end{array}} \right. $ | (15) |
代入式(12),可得三维TTI分解算子
| $ {\tilde \nabla _{{\rm{TTI }}}} = \left[ {\begin{array}{*{20}{c}} {\frac{\partial }{{\partial {x^\prime }}}}\\ {\frac{\partial }{{\partial {y^\prime }}}}\\ {\frac{\partial }{{\partial {z^\prime }}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\frac{\partial }{{\partial x}}}\\ {\cos \theta \frac{\partial }{{\partial y}} + \sin \theta \frac{\partial }{{\partial z}}}\\ {r\left( { - \sin \theta \frac{\partial }{{\partial y}} + \cos \theta \frac{\partial }{{\partial z}}} \right)} \end{array}} \right] $ | (16) |
三维TTI分解算子在新坐标系下可以近似为三维VTI分解算子。当θ=0°时,三维TTI分解算子
根据Helmholtz定理,任何一个弹性波场u都可以分解为一个无旋场uP和一个无散场uS。矢量分解将弹性波场分别投影到各自的偏振方向上,实现波场分离。通过构建泊松方程u=▽2w,可以在空间域实现各向同性介质波场分离
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{u}}^{\rm{P}}} = \nabla (\nabla \cdot \mathit{\boldsymbol{w}})}\\ {{\mathit{\boldsymbol{u}}^{\rm{s}}} = \nabla \times (\nabla \times \mathit{\boldsymbol{w}})} \end{array}} \right. $ | (17) |
式中w是一个辅助波场[24]。
而对各向异性介质,若已知分解算子
| $ \mathit{\boldsymbol{u}} = \tilde \nabla _{{\rm{TTI}}}^2\mathit{\boldsymbol{w}} $ | (18) |
则P波和S波波场可表示为
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{u}}^{\rm{P}}} = {{\tilde \nabla }_{{\rm{TTI}}}}\left( {{{\tilde \nabla }_{{\rm{TTI}}}} \cdot \mathit{\boldsymbol{w}}} \right)}\\ {{\mathit{\boldsymbol{u}}^{\rm{S}}} = - {{\tilde \nabla }_{{\rm{TTI}}}} \times \left( {{{\tilde \nabla }_{{\rm{TTI}}}} \times \mathit{\boldsymbol{w}}} \right)} \end{array}} \right. $ | (19) |
将式(18)展开并整理,有
| $ \left( {\frac{{{\partial ^2}}}{{\partial {x^2}}} + {r_1}\frac{{{\partial ^2}}}{{\partial {y^2}}} + {r_2}\frac{{{\partial ^2}}}{{\partial z}} + {r_3}\frac{{{\partial ^2}}}{{\partial x\partial z}}} \right)\mathit{\boldsymbol{w}} = \mathit{\boldsymbol{u}} $ | (20) |
| $ \left\{ {\begin{array}{*{20}{l}} {{r_1} = {{\cos }^2}\theta + {r^2}{{\sin }^2}\theta }\\ {{r_2} = {{\sin }^2}\theta + {r^2}{{\cos }^2}\theta }\\ {{r_3} = 2\left( {1 - {r^2}} \right)\sin \theta } \end{array}} \right. $ | (21) |
式(20)在频率—波数域可表示为
| $ - \left( {k_x^2 + {r_1}k_y^2 + {r_2}k_z^2 + {r_3}{k_y}{k_z}} \right)\mathit{\boldsymbol{W}} = \mathit{\boldsymbol{U}} $ | (22) |
式中W分别为w的频率—波数域形式。
利用式(22),通过Gaussian消元法可以直接在频率域内计算辅助波场,但是系数r1、r2和r3包含了随空间变化的弹性参数,所以波场分解只适用于平滑的各向异性模型[21]。为了在复杂各向异性介质里实现弹性波场分解,Zhang等[25]提出一种在二维VTI介质中快速求解辅助波场的方法,可以在空间域计算系数r1、r2和r3,以及构建w,本文将该快速算法扩展到三维TTI介质。式(22)可写为
| $ \mathit{\boldsymbol{W}} = - f(\varepsilon , \delta )\mathit{\boldsymbol{U}} $ | (23) |
式中系数f(ε, δ)=(kx2+r1ky2+r2kz2+r3kykz)-1,是三维弹性参数和对称轴倾角的函数。
基于弱各向异性介质的假设,将f在ε=δ=0处做Taylor展开,有
| $ \begin{array}{l} f(\varepsilon , \delta ) \approx \frac{1}{{{k_x}^2 + {k_y}^2 + {k_z}^2}} + \frac{1}{{{{\left( {{k_x}^2 + {k_y}^2 + {k_z}^2} \right)}^2}}} \times \\ \;\;\;\;\;\;\;\;\;\;\;\;{r_4}\left[ {{k_z}^2{{\cos }^2}\theta + {k_y}^2{{\sin }^2}\theta - {k_y}{k_z}\sin 2\theta } \right] \end{array} $ | (24) |
式中
| $ \mathit{\boldsymbol{W}} = - {\mathit{\boldsymbol{U}}_1} - {r_4}{\mathit{\boldsymbol{U}}_2}{\cos ^2}\theta - {r_4}{\mathit{\boldsymbol{U}}_3}{\sin ^2}\theta + {r_4}{\mathit{\boldsymbol{U}}_4}\sin 2\theta $ | (25) |
| $ {\mathit{\boldsymbol{U}}_1} = \frac{\mathit{\boldsymbol{U}}}{{k_x^2 + k_y^2 + k_z^2}} $ | (26) |
| $ {\mathit{\boldsymbol{U}}_2} = \frac{{\mathit{\boldsymbol{U}}k_z^2}}{{{{\left( {k_x^2 + k_y^2 + k_z^2} \right)}^2}}} $ | (27) |
| $ {\mathit{\boldsymbol{U}}_3} = \frac{{\mathit{\boldsymbol{U}}k_y^2}}{{{{\left( {k_x^2 + k_y^2 + k_z^2} \right)}^2}}} $ | (28) |
| $ {\mathit{\boldsymbol{U}}_4} = \frac{{\mathit{\boldsymbol{U}}{k_y}{k_z}}}{{{{\left( {k_x^2 + k_y^2 + k_z^2} \right)}^2}}} $ | (29) |
对式(25)做反傅里叶变换,有
| $ \mathit{\boldsymbol{w}} = - {\mathit{\boldsymbol{u}}_1} - {r_4}{\mathit{\boldsymbol{u}}_2}{\cos ^2}\theta - {r_4}{\mathit{\boldsymbol{u}}_3}{\sin ^2}\theta + {r_4}{\mathit{\boldsymbol{u}}_4}\sin 2\theta $ | (30) |
式中u1、u2、u3和u4分别是U1、U2、U3和U4在时间—空间域的形式。式(30)即为空间域计算辅助波场的公式,适用于三维复杂TTI介质。
三维TTI介质中弹性波场分解的具体计算步骤为:
(1) 对三分量原始波场u求三维傅立叶变换得到U;
(2) 在频率波数域计算U1、U2、U3和U4;
(3) 做反傅立叶变换得到u1、u2、u3和u4;
(4) 在空间域计算含倾角θ的三角函数和参数r4,用式(30)计算空间域的三维辅助波场;
(5) 利用式(19)计算P波和S波波场。
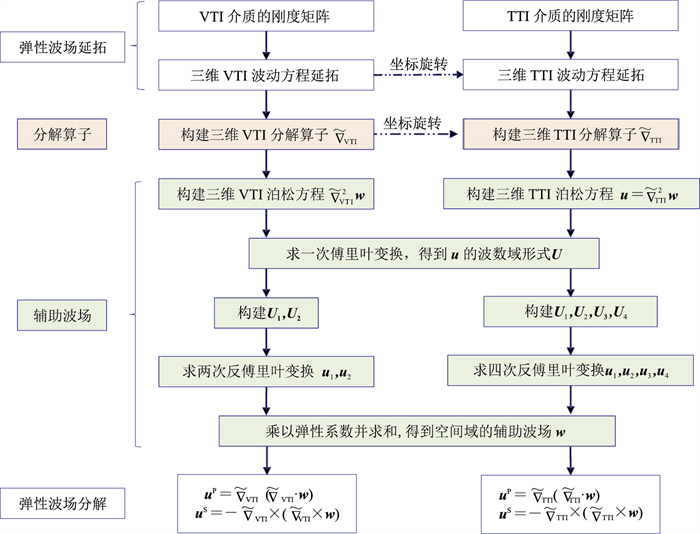
VTI介质是特殊的TTI介质,不用考虑对称轴倾角,辅助波场的求解过程大大简化(图 2)。
|
图 2 三维TTI与VTI介质弹性波场分解过程的对比 |
首先建立均匀TTI介质模型,对比各向同性和各向异性分解方法的结果,验证本文三维TTI弹性波场分解算子的有效性。模型的网格数为200×200×200,空间采样间隔均为10m。在模型中心设置一个主频为25Hz的Ricker子波作为爆炸源。为了满足弱各向异性介质的假设,设置三维TTI介质的弹性参数为:vP=3.25km/s,vS=1.90km/s,ρ=2.00g/cm3,ε=0.22,δ=0.22,γ=0,θ=30°。
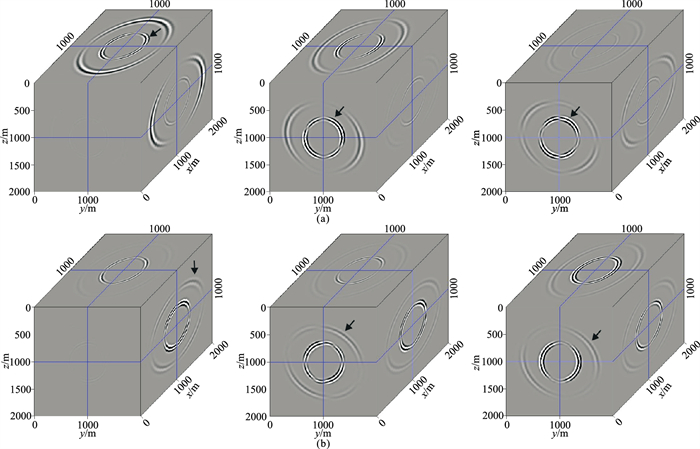
图 3为三维TTI介质均匀模型的正演三分量弹性波场,在延拓过程中,P波(白色箭头所示)和SV波(红色箭头所示)耦合在一起,波场不再沿坐标轴对称。图 4为利用各向同性分解算子(式(17))得到的弹性波场,由于该算子把地震波场投影到传播方向,而不是地震波的偏振方向,所以P波和SV波波场不能完全分离,无论是分解后的P波波场还是SV波波场,都存在串扰噪声(黑色箭头所示)。三维VTI介质分解算子

|
图 3 三维弱各向异性均匀模型正演弹性波场 (a)x分量;(b)y分量;(c)z分量。红色箭头所示为SV波波场,白色箭头所示为P波波场 |
|
图 4 三维弱各向异性均匀模型正演波场的各向同性算子分解结果 (a)P波场;(b)SV波场。左、中、右分别为x、y、z分量。黑色箭头所示为串扰噪声 |

|
图 5 三维弱各向异性均匀模型正演波场的VTI算子分解结果 (a)P波场;(b)SV波场。左、中、右分别为x、y、z分量。黑色箭头所示为串扰噪声 |
|
图 6 三维弱各向异性均匀模型正演波场的TTI算子分解结果 (a)P波场;(b)SV波场。左、中、右分别为x、y、z分量 |
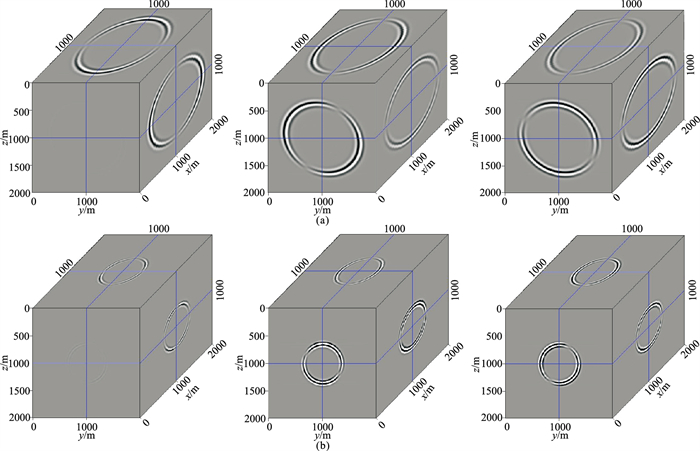
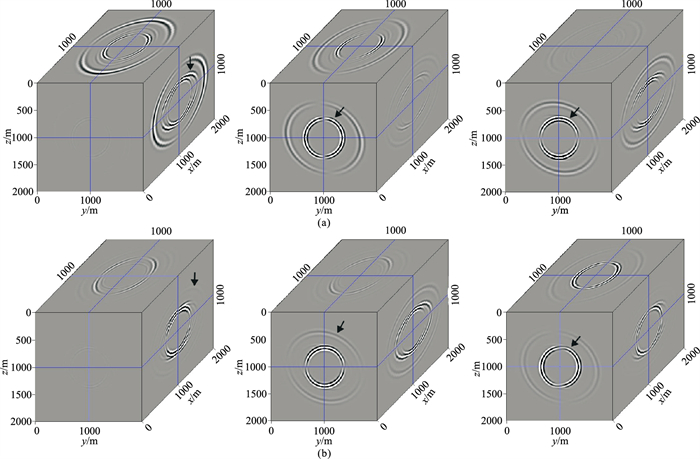
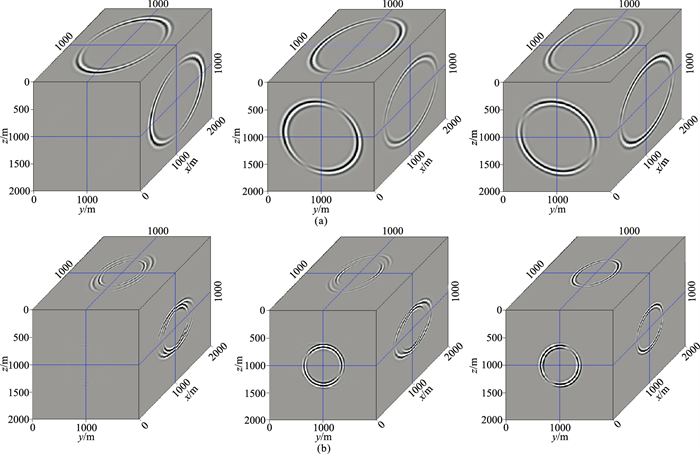
当地震波在实际三维各向异性介质中传播时,除了P波和SV波,还存在SH波。为了体现强横波各向异性特征,令上述三维TTI均匀介质的γ=0.5。在正演的三分量弹性波场中,蓝色箭头所示为SH波场(图 7)。VTI分解算子不能将弹性波场投影到实际的偏振方向(图 8),分解的P波和S波波场中都存在串扰噪声(黑色箭头所示)。只有同时考虑了各向异性和倾斜对称轴的影响,反映了真实弹性波偏振方向的分解算子才能压制串扰噪声(图 9)。比较不同算子的分解结果可见,对于三维TTI均匀介质的弹性波场,本文推导的三维TTI介质分解算子能更有效地分离P波和S波波场。
|
图 7 三维强各向异性均匀模型正演弹性波场 (a)x分量;(b)y分量;(c)z分量。红色箭头所示为SV波波场,白色箭头所示为P波波场,蓝色箭头所示为SH波波场 |
|
图 8 三维强各向异性均匀模型正演波场的VTI算子分解结果 (a)P波波场;(b)S波波场。左、中、右分别为x、y、z分量。黑色箭头所示为串扰噪声 |
|
图 9 三维强各向异性均匀模型正演波场的TTI算子分解结果 (a)P波波场;(b)S波波场。左、中、右分别为x、y、z分量 |
为了验证本文推导的三维TTI介质分解方法在层状介质中的有效性,建立三维两层TTI介质模型,对于反射波和透射波,采用两种分解算子,比较应用效果。第一层弹性参数为:vP=3.25km/s,vS=1.90km/s,ρ=2.00g/cm3,ε=0.22,δ=0.22,γ=0,θ=10°;第二层弹性参数为:vP=3.65km/s,vS=2.50km/s,ρ=2.35g/cm3,ε=0.24,δ=0.23,γ=0,θ=15°。界面深度为1000m,三分量位移震源的深度为200m。
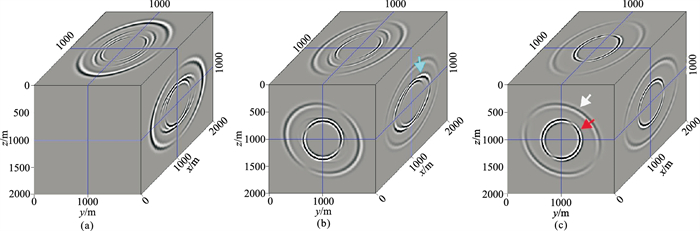
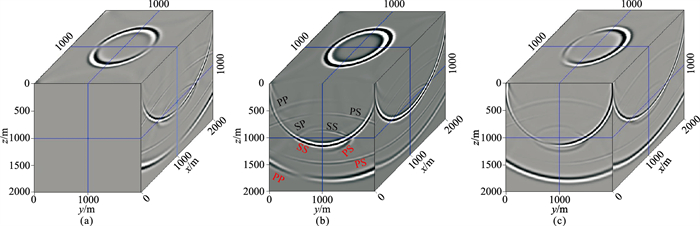
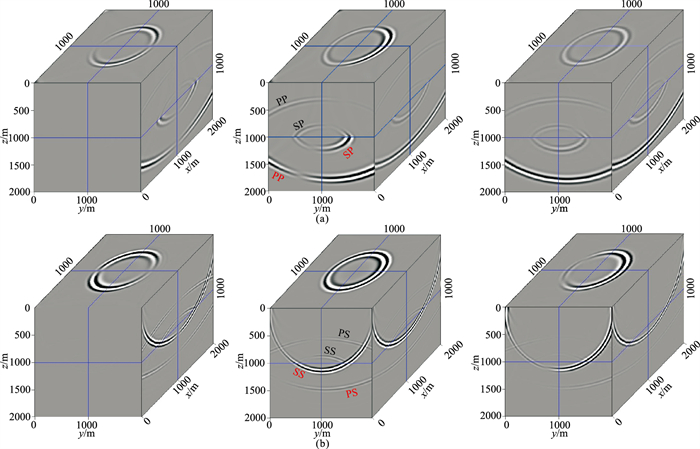
图 10为三维两层TTI模型的正演波场,既有反射PP、PS、SP和SS波(黑色字母所示),还有透射PP、PS、SP和SS波(红色字母所示)。由于各向异性对称轴并没有沿着垂直方向,而且第一层和第二层的对称轴倾角不同,所以反射和透射波场既不左右对称,也不沿界面上下对称。图 11为利用VTI分解算子得到的P波和S波波场,反射和透射弹性波场中,都存在能量较强的串扰噪声(黑色箭头所示)。图 12为三维TTI介质分解算子得到的分解结果,由于考虑了各向异性对称轴的倾角,P波波场只包含干净的反射和透射PP、SP波,S波波场仅有干净的反射和透射PS、SS波。通过以上的数值算例,说明本文推导的三维TTI分解算子可以有效应用于层状各向异性介质弹性波场。
|
图 10 三维两层TTI介质模型正演弹性波场 (a)x分量;(b)y分量;(c)z分量。黑色字母表示反射波场,红色字母表示透射波场 |

|
图 11 三维两层TTI介质模型正演波场的VTI算子分解结果 (a)P波波场;(b)SV波波场。左、中、右分别为x、y、z分量。黑色箭头所示为串扰噪声 |
|
图 12 三维两层TTI介质模型正演波场的TTI算子分解结果 (a)P波波场;(b)SV波波场。左、中、右分别为x、y、z分量。 |
为了解决三维TTI介质弹性波场的分解问题,本文利用三维VTI分解算子和倾斜对称轴与观测坐标系之间的几何关系,推导了适用于三维TTI介质的分解算子。相比于前人提出的波场分解方法,本文的方法在物理意义和数值稳定性方面均具有一定优势。
(1) 目前已实现的二维TTI各向异性波场分解方法中,已有研究学者通过求解Christoffel方程的特征向量计算各向异性分解算子[23]。但是当θ=0°和ε=δ=0时,无法退化为各向同性介质的形式。而本文推导的三维TTI分解算子,当介质退化为各向同性时,其表达式与弹性参数无关,只与传播方向有关,更符合实际地震波传播特征。
(2) 在适用于三维TTI介质的弹性波场分解方法中,所有基于散度和旋度的波场分离方法只能得到标量P波波场和矢量S波波场,这会导致PS波在成像界面出现极性反转[22],需要进一步对波场的振幅和相位进行校正。本文推导的三维TTI分解算子能同时计算矢量P波和S波波场,可以避免这一的问题。
本文的波场分离方法只针对波场传播过程中,三维各向异性介质P波、SV波和SH波极化方向垂直的情况,面对非正交快、慢横波的分离,还具有一定的局限性。可以将本文的分离方法引入到弹性波逆时偏移,但由于三维TTI介质分解算子包含了对称轴倾角参数,其波场分解的数值计算比VTI介质算子更复杂。在每一时刻求解辅助波场时,需要进行两次反傅里叶变换,导致基于三维TTI分解算子的弹性波逆时偏移需要更多的计算时间、计算量和内存。为解决这一问题,今后考虑将GPU并行引入三维TTI介质弹性波逆时偏移,可极大地提高计算效率,实现适用于复杂三维各向异性介质模型的、基于弹性波场分解的逆时偏移。
4 结束语本文通过对波数域的Christoffel方程进行特征分析,计算了不同波的偏振方向,构建适用于三维VTI介质的分解算子。在此基础上,根据倾斜对称轴与观测坐标系之间的几何关系,利用坐标旋转推导了适用于三维TTI介质的分解算子。为了提高计算效率,避免直接求解泊松方程,引入了快速算法计算辅助波场,最终实现三维TTI介质中矢量弹性波场的分解。数值算例的结果说明,本文推导的空间域三维TTI分解算子能有效实现三维复杂TTI介质中的弹性波场的纵、横波分离。
附录A 三维VTI介质特征值和特征向量的导出为了计算矩阵A的特征值λ,构建等式|λE-A|=0(其中E为单位矩阵),其三个解为
| $ {\lambda _2} = {C_{66}}\left( {k_x^2 + k_y^2} \right) + {C_{44}}k_z^2 $ | (A-1) |
| $ \begin{array}{l} {\lambda _{1, 3}} = \frac{{{D_1}\left( {k_x^2 + k_y^2} \right) + {D_2}k_z^2}}{2} \pm \frac{{{D_3}\left( {k_x^2 + k_y^2} \right) + {D_4}k_z^2}}{2} \times \\ \;\;\;\;\;\;\;\sqrt {1 + \frac{{{D_5}\left( {k_x^2 + k_y^2} \right)k_z^2}}{{{{\left[ {{D_3}\left( {k_x^2 + k_y^2} \right) + {D_4}k_z^2} \right]}^2}}}} \end{array} $ | (A-2) |
| $ \left\{ {\begin{array}{*{20}{l}} {{D_1} = {C_{44}} + {C_{11}}}\\ {{D_2} = {C_{33}} + {C_{44}}}\\ {{D_3} = {C_{11}} - {C_{44}}}\\ {{D_4} = {C_{33}} - {C_{44}}}\\ {{D_5} = 4\left( {{C_{44}}{C_{11}} - {C_{11}}{C_{33}} + C_{13}^2 + } \right.}\\ {\left. {\;\;\;\;\;\;\;{C_{33}}{C_{44}} + 2{C_{13}}{C_{44}}} \right)} \end{array}} \right. $ | (A-3) |
根据刚度矩阵和Thomsen参数之间的关系(式(8)),式(A-1)、式(A-2)可写为
| $ {\lambda _2} = \rho v_S^2\left[ {(1 + 2\gamma )\left( {k_x^2 + k_y^2} \right) + k_z^2} \right] $ | (A-4) |
| $ \begin{array}{l} {\lambda _{1, 3}} = \frac{{{T_1}\left( {k_x^2 + k_y^2} \right) + {T_2}k_z^2}}{2} \pm \rho \frac{{{T_3}\left( {k_x^2 + k_y^2} \right) + {T_4}k_z^2}}{2} \times \\ \;\;\;\;\;\;\sqrt {1 - \frac{{{T_5}\left( {k_x^2 + k_y^2} \right)k_z^2}}{{{{\left[ {{T_3}\left( {k_x^2 + k_y^2} \right) + {T_4}k_z^2} \right]}^2}}}} \end{array} $ | (A-5) |
| $ \left\{ {\begin{array}{*{20}{l}} {{T_1} = (1 + 2\varepsilon )v_{\rm{P}}^2 + v_{\rm{S}}^2}\\ {{T_2} = v_{\rm{P}}^2 + v_{\rm{S}}^2}\\ {{T_3} = (1 + 2\varepsilon )v_{\rm{P}}^2 - v_{\rm{S}}^2}\\ {{T_4} = v_{\rm{P}}^2 - v_{\rm{S}}^2}\\ {{T_5} = 8(\varepsilon - \delta )v_{\rm{P}}^2\left( {v_{\rm{P}}^2 - v_{\rm{S}}^2} \right)} \end{array}} \right. $ | (A-6) |
基于弱各向异性假设,将根号项用泰勒展开,可得式(4)的特征值。
为了求解特征值λ对应的特征向量,将等式|λE-A|=0展开,有
| $ \begin{array}{l} \lambda {U_x} = \left( {{C_{11}}k_x^2 + {C_{66}}k_y^2 + {C_{44}}k_z^2} \right){U_x} + \\ \;\;\;\;\;\;\;\left( {{C_{11}} - {C_{66}}} \right){k_x}{k_y}{U_y} + \left( {{C_{13}} + {C_{44}}} \right){k_x}{k_z}{U_z} \end{array} $ | (A-7) |
| $ \begin{array}{l} \lambda {U_y} = \left( {{C_{11}} - {C_{66}}} \right){k_x}{k_y}{U_x} + \left( {{C_{66}}k_x^2 + {C_{11}}k_y^2 + } \right.\\ \left. {\;\;\;\;\;\;\;\;{C_{44}}k_z^2} \right){U_y} + \left( {{C_{13}} + {C_{44}}} \right){k_y}{k_z}{U_z} \end{array} $ | (A-8) |
| $ \begin{array}{l} \lambda {U_z} = \left( {{C_{13}} + {C_{44}}} \right){k_x}{k_z}{U_x} + \left( {{C_{13}} + {C_{44}}} \right){k_y}{k_z}{U_y} + \\ \;\;\;\;\;\;\;\;\;\left[ {{C_{44}}\left( {k_x^2 + k_y^2} \right) + {C_{33}}k_z^2} \right]{U_z} \end{array} $ | (A-9) |
将λ1代入式(A-8)方程,且令Ux=Uy,可得
| $ {U_y} = \frac{{\left( {{C_{11}} - {C_{66}}} \right){k_x}{k_y} + \left( {{C_{13}} + {C_{44}}} \right){k_z}{k_y}{U_z}}}{{{\lambda _1} - \left( {{C_{66}}k_x^2 + {C_{11}}k_y^2 + {C_{44}}k_z^2} \right)}} $ | (A-10) |
将式(A-10)代入式(A-9),整理后有
| $ {U_z} = \frac{{{F_1} + \left( {{\lambda _1} - {F_2}} \right){F_3}}}{{\left( {{\lambda _1} - {F_2}} \right)\left( {{\lambda _1} - {F_4}} \right) - {F_5}}} $ | (A-11) |
| $ \left\{ {\begin{array}{*{20}{l}} {{F_1} = \left( {{C_{13}} + {C_{44}}} \right)\left( {{C_{11}} - {C_{66}}} \right)k_y^2{k_x}{k_z}}\\ {{F_2} = {C_{66}}k_x^2 + {C_{11}}k_y^2 + {C_{44}}k_z^2}\\ {{F_3} = \left( {{C_{13}} + {C_{44}}} \right){k_z}{k_x}}\\ {{F_4} = {C_{44}}k_x^2 + {C_{44}}k_y^2 + {C_{33}}k_z^2}\\ {{F_5} = {{\left( {{C_{13}} + {C_{44}}} \right)}^2}k_z^2k_y^2} \end{array}} \right. $ | (A-12) |
则对应于特征值λ1的特征向量为
| $ {\mathit{\boldsymbol{\hat a}}_1} = \left[ {\begin{array}{*{20}{l}} {{U_x}}\\ {{U_y}}\\ {{U_z}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{k_x}}\\ {{k_y}}\\ {\frac{{\sqrt {\left[ {(1 + 2\delta )v_{\rm{P}}^2 - v_{\rm{S}}^2} \right]\left( {v_{\rm{P}}^2 - v_{\rm{S}}^2} \right)} }}{{(1 + 2\varepsilon )v_{\rm{P}}^2 - v_{\rm{S}}^2}}{k_z}} \end{array}} \right] $ | (A-13) |
同理可以获得对应于特征值λ2和λ3的特征向量分别为
| $ {\mathit{\boldsymbol{\hat a}}_2} = \left[ {\begin{array}{*{20}{c}} { - {k_y}}\\ {{k_x}}\\ 0 \end{array}} \right] $ | (A-14) |
| $ {\mathit{\boldsymbol{\hat a}}_3} = \left[ {\begin{array}{*{20}{c}} { - \frac{{\sqrt {\left[ {(1 + 2\delta )v_{\rm{P}}^2 - v_{\rm{S}}^2} \right]\left( {v_{\rm{P}}^2 - v_{\rm{S}}^2} \right)} }}{{(1 + 2\varepsilon )v_{\rm{P}}^2 - v_{\rm{S}}^2}}{k_x}{k_z}}\\ { - \frac{{\sqrt {\left[ {(1 + 2\delta )v_{\rm{P}}^2 - v_{\rm{S}}^2} \right]\left( {v_{\rm{P}}^2 - v_{\rm{S}}^2} \right)} }}{{(1 + 2\varepsilon )v_{\rm{P}}^2 - v_{\rm{S}}^2}}{k_y}{k_z}}\\ {k_x^2 + k_y^2} \end{array}} \right] $ | (A-15) |
| [1] |
CALDWELL J. Marine multicomponent seismology[J]. The Leading Edge, 1999, 18(11): 1274-1282. DOI:10.1190/1.1438198 |
| [2] |
GRANLI J, ARNTSEN B, SOLLID A, et al. Imaging through gas-filled sediments using marine shear-wave data[J]. Geophysics, 1999, 64(3): 668-677. DOI:10.1190/1.1444576 |
| [3] |
ZHAO Y, ZHANG H Z, YANG J D, et al. Reducing artifacts of elastic reverse time migration by the de-primary technique[J]. Geophysics, 2018, 83(6): S569-S577. DOI:10.1190/geo2018-0260.1 |
| [4] |
于春玲, 王建民, 付雷, 等. 转换波各向异性速度分析与偏移成像[J]. 石油地球物理勘探, 2010, 45(增刊1): 44-47. YU Chunling, WANG Jianmin, FU Lei, et al. Anisotropic velocity analysis and migration imaging for converted wave[J]. Oil Geophysical Prospecting, 2010, 45(S1): 44-47. |
| [5] |
DENG F, MCMECHAN G A. Viscoelastic true-amplitude prestack reverse-time depth migration[J]. Geophysics, 2008, 73(4): S143-S155. DOI:10.1190/1.2938083 |
| [6] |
DU Q Z, GONG X F, ZHANG M Q, et al. 3D PS-wave imaging with elastic reverse-time migration[J]. Geophysics, 2014, 79(5): S173-S184. DOI:10.1190/geo2013-0253.1 |
| [7] |
张婧, 张文栋, 张铁强, 等. 应用τ-p域矢量旋转的地震数据波场分离[J]. 石油地球物理勘探, 2020, 55(1): 46-56. ZHANG Jing, ZHANG Wendong, ZHANG Tieqiang, et al. Seismic wave field decomposition method based on vector rotation in τ-p domain[J]. Oil Geophysical Prospecting, 2020, 55(1): 46-56. |
| [8] |
LU J, WANG Y, YAO C. Separating P-and S-waves in an affine coordinate system[J]. Journal of Geophysics and Engineering, 2012, 9(1): 12-18. DOI:10.1088/1742-2132/9/1/002 |
| [9] |
LU J, WANG Y, CHEN J Y, et al. P-and S-mode separation of three-component VSP data[J]. Exploration Geophysics, 2019, 50(4): 430-448. DOI:10.1080/08123985.2019.1606205 |
| [10] |
杜文波, 黄文凯, 朱红涛, 等. 台湾海峡西部海域沉积体系、地层架构与油气勘探前景[J]. 中国地质, 2020, 47(5): 1542-1553. DU Wenbo, HUANG Wenkai, ZHU Hongtao, et al. Sedimentary system, stratigraphic architecture and petroleum exploration prospect analysis in the western Taiwan Strait[J]. Geology in China, 2020, 47(5): 1542-1553. |
| [11] |
MORSE P M, FESHBACH H. Methods of Theoretical Physics[M]. New York: McGraw-Hill Book Co., 1953.
|
| [12] |
SUN R, CHOW J, CHEN K J. Phase correction in separating P-and S-waves in elastic data[J]. Geophysics, 2001, 66(5): 1515-1518. DOI:10.1190/1.1487097 |
| [13] |
周熙焱, 常旭, 王一博, 等. 基于纵横波解耦的三维弹性波逆时偏移[J]. 地球物理学报, 2018, 61(3): 1038-1052. ZHOU Xiyan, CHANG Xu, WANG Yibo, et al. 3D elastic reverse time migration based on P-and S-wave decoupling[J]. Chinese Journal of Geophysics, 2018, 61(3): 1038-1052. |
| [14] |
THOMSEN L. Weak elastic anisotropy[J]. Geophysics, 1986, 51(10): 1954-1966. DOI:10.1190/1.1442051 |
| [15] |
孙上饶, 梁锴, 印兴耀, 等. 三维TTI介质弹性波相、群速度的近似配方表征法[J]. 石油地球物理勘探, 2021, 56(3): 496-504, 518. SUN Shangrao, LIANG Kai, YIN Xingyao, et al. Approximate 3D phase and group velocities for elastic wave in TTI media based on an approximate match method[J]. Oil Geophysical Prospecting, 2021, 56(3): 496-504, 518. |
| [16] |
吴潇, 刘洋, 蔡晓慧. 弹性波波场分离方法对比及其在逆时偏移成像中的应用[J]. 石油地球物理勘探, 2018, 53(4): 710-721. WU Xiao, LIU Yang, CAI Xiaohui. Elastic wavefield separation methods and their applications in reverse time migration[J]. Oil Geophysical Prospecting, 2018, 53(4): 710-721. |
| [17] |
DELLINGER J, ETGEN J. Wave-field separation in two-dimensional anisotropic media[J]. Geophysics, 1990, 55(7): 914-919. |
| [18] |
YAN J, SAVA P. Elastic wave-mode separation for VTI media[J]. Geophysics, 2009, 74(5): WB19-WB32. |
| [19] |
ZHANG Q S, MCMECHAN G A. 2D and 3D elastic wavefield vector decomposition in the wavenumber domain for VTI media[J]. Geophysics, 2010, 75(3): D13-D26. |
| [20] |
CHENG J B, FOMEL S. Fast algorithms for elastic-wave-mode separation and vector decomposition using low-rank approximation for anisotropic media[C]. SEG Technical Program Expanded, Abstracts 2013, 32: 991-997.
|
| [21] |
ZUO J H, NIU F L, LIU L, et al. 3D anisotropic P-and S-mode wavefields separation in 3D elastic reverse-time migration[J]. Surveys in Geophysics, 2022, 43(3): 673-701. |
| [22] |
YAN J, SAVA P. Elastic wave mode separation for tilted transverse isotropic media[J]. Geophysical Prospecting, 2012, 60(1): 29-48. |
| [23] |
YANG J D, ZHANG H Z, ZHAO Y, et al. Elastic wavefield separation in anisotropic media based on eigenform analysis and its application in reverse-time migration[J]. Geophysical Journal International, 2019, 217(2): 1290-1313. |
| [24] |
ZHU H J. Elastic wavefield separation based on the Helmholtz decomposition[J]. Geophysics, 2017, 82(2): S173-S183. |
| [25] |
ZHANG L L, LIU L, NIU F L, et al. A novel and efficient engine for P/S wave-mode vector decomposition for VTI elastic reverse time migration[J]. Geophysics, 2022, 87(4): S185-S207. |



 赵杨, 北京市昌平区府学路18号中国石油大学(北京)非常规油气科学技术研究院, 102249。Email:
赵杨, 北京市昌平区府学路18号中国石油大学(北京)非常规油气科学技术研究院, 102249。Email: 