② 青岛海洋科学与技术国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266100;
③ 山东省烟台市自然资源和规划局, 山东烟台 264003
② Functional Laboratory of Marine Mineral Resources Evaluation and Exploration Technology, Qingdao National Laboratory of Marine Science and Technology, Qingdao, Shandong 266100, China;
③ Yantai Natural Resources and Planning Bureau, Yantai, Shandong 264003, China
弹性波正演是研究纵横波传播规律的重要工具之一,在多波地震的资料采集、处理、解释和反演等领域发挥着重要作用。弹性波方程及其模拟算法是多年来业界广泛关注的热点。
近年来,在弹性波方程的有限差分数值模拟领域开展了大量的研究工作,取得了许多成果,包括弹性波偏微分方程组中空间偏导数的高阶差分格式[1-5]、时间偏导数的高阶差分格式[6-9]、各种差分格式的稳定性条件[10-14]、数值频散的压制方法[15-19]、边界条件[20-23]以及计算效率提升方法[24-25]等。这些成果对于推动多波地震技术的发展具有重要意义。但总体而言,现有的弹性波正演技术仍存在诸多不足。①模拟精度与效率很难兼顾。小网格、高阶差分格式可以提高模拟精度,但意味着计算量的指数级增加,导致模拟效率降低。虽然近似解析离散[26-27]等方法可以适应大网格的差分计算,但其计算量仍远大于预期。②基于长方体网格的空间剖分方法无法准确拟合复杂界面的形态,导致模拟结果中出现大量绕射波。近年出现的不规则网格技术[4, 28-29]虽然缓解了这一问题,但距离根本解决还为时尚早;③现有算法能准确模拟弹性波的传播过程,模拟得到的三个分量均同时包含纵波和横波[30],必须借助额外的波场解耦算子[31-32]才能得到纯纵波和纯横波的模拟结果,即模拟的纵、横波记录和快照同时受制于差分算法的精度和解耦算子的精度,增加了误差来源[33-34]。
为解决上述第三个问题,本文通过对一阶速度—胀缩—旋转弹性波方程的差分离散实现弹性波的模拟。首先推导了一阶速度—胀缩—旋转弹性波方程在三维交错网格空间中的高阶有限差分格式,给出了相应的稳定性条件;然后导出了适应该方程的PML吸收边界条件,在此基础上实现了一阶速度—胀缩—旋转弹性波方程的正演模拟。本文的弹性波模拟方法的优势在于,不仅可以得到x、y、z三分量地震记录,而且无需显式地进行纵、横波解耦就可以得到横波振动速度矢量和纵波振动速度矢量,实现了纵、横波的保幅解耦。同时,数值求解该方程还可以直接得到各质点的体应变和旋转矢量,为分析不同速度模型条件下纵、横波的传播规律提供更详细的信息。
1 速度—胀缩—旋转弹性波方程各向同性介质中的三维一阶速度—胀缩—旋转弹性波方程[35]为
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial {\mathit{\boldsymbol{v}}_{\rm{P}}}}}{{\partial t}} = c_{\rm{P}}^2\nabla \theta }\\ {\frac{{\partial {\mathit{\boldsymbol{v}}_{\rm{S}}}}}{{\partial t}} = - c_{\rm{S}}^2\nabla \times \mathit{\boldsymbol{\omega }}}\\ {\mathit{\boldsymbol{v}} = {\mathit{\boldsymbol{v}}_{\rm{P}}} + {\mathit{\boldsymbol{v}}_{\rm{S}}}}\\ {\frac{{\partial \theta }}{{\partial t}} = \nabla \cdot \mathit{\boldsymbol{v}}}\\ {\frac{{\partial \mathit{\boldsymbol{\omega }}}}{{\partial t}} = \nabla \times \mathit{\boldsymbol{v}}} \end{array}} \right. $ | (1) |
式中:v=(vx,vy,vz)为质点振动速度矢量;vS=(vSx,vSy,vSz)为质点的横波振动速度矢量;vP=(vPx,vPy,vPz)为质点的纵波振动速度矢量;cP、cS分别为纵、横波传播速度;θ为体应变;ω=(ωx,ωy,ωz)为旋转矢量。
式(1)不仅显式地包含了常规弹性波方程中的质点总振动速度矢量,而且包含了由胀缩运动和剪切运动引起的质点振动速度矢量,同时还显式包含了θ和ω,因此利用该方程进行弹性波正演模拟不仅可以得到x、y、z三分量地震记录,而且无需显式地进行纵、横波解耦就可以得到纵波振动速度矢量和横波振动速度矢量。同时,数值求解该方程还可以直接得到各质点的体应变和旋转矢量,体应变一般只与纵波有关,旋转矢量一般只与横波有关,这为分析不同速度模型条件下纵、横波的传播规律提供了更详细的信息。
此外,由于目前的多波地震采集基本都采用纵波源激发,式(1)显然十分便于解决弹性波正演中的纵波源设置问题,模拟时只需将震源函数加载到体应变θ上即可实现纵波源激发。而采用传统的一阶速度—应力方程进行弹性波模拟时,纵波源必须加载到三个正应力分量上[9, 13],但纵波源的总能量按照什么样的比例分配到三个正应力分量上,目前并没有一个公认的结论。
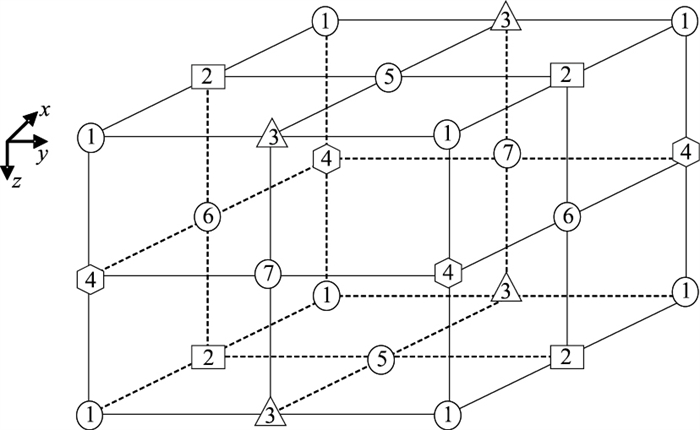
2 交错网格数值模拟方法 2.1 交错网格高阶差分格式三维情况下,在图 1所示的交错网格空间[3-4]中求解式(1),其中各波场分量在交错网格空间中的配置由表 1给出。
|
图 1 三维交错网格示意图 |
|
|
表 1 各波场分量在交错网格中的分布 |
采用高阶有限差分算法[6, 8-9]对式(1)进行差分离散,可得到三维一阶速度—胀缩—旋转弹性波方程正演模拟的时间2阶、空间2N阶有限差分格式。以θ分量为例,可表示为
| $ \begin{array}{c} \theta (i, j, k, n + 1) = \theta (i, j, k, n) + \frac{{\Delta t}}{{\Delta x}}\sum\limits_{m = 1}^N {{C_m}} \left[ {{v_x}\left( {i + m - \frac{1}{2}, j, k, n + \frac{1}{2}} \right) - {v_x}\left( {i - m + \frac{1}{2}, j, k, n + \frac{1}{2}} \right)} \right] + \\ \frac{{\Delta t}}{{\Delta y}}\sum\limits_{m = 1}^N {{C_m}} \left[ {{v_y}\left( {i, j + m - \frac{1}{2}, k, n + \frac{1}{2}} \right) - {v_y}\left( {i, j - m + \frac{1}{2}, k, n + \frac{1}{2}} \right)} \right] + \\ \frac{{\Delta t}}{{\Delta z}}\sum\limits_{m = 1}^N {{C_m}} \left[ {{v_z}\left( {i, j, k + m - \frac{1}{2}, n + \frac{1}{2}} \right) - {v_z}\left( {i, j, k - m + \frac{1}{2}, n + \frac{1}{2}} \right)} \right] \end{array} $ | (2) |
式中:Δt为时间延拓步长;Δx、Δy、Δz分别为直角坐标系中x、y、z方向上的网格剖分间距;n为时间离散序号;i、j、k分别代表x、y、z方向上的离散网格点序号;Cm为2N阶精度的交错网格差分系数,其计算公式为[4, 9, 13]
| $ {C_m} = \frac{{{{( - 1)}^{m + 1}}\prod\limits_{a = 1, a \ne m}^N {{{(2a - 1)}^2}} }}{{(2m - 1)\prod\limits_{a = 1}^{m - 1} {\left[ {{{(2m - 1)}^2} - {{(2a - 1)}^2}} \right]} \prod\limits_{a = m + 1}^N {\left[ {{{(2a - 1)}^2} - {{(2m - 1)}^2}} \right]} }} $ | (3) |
表 2为由式(3)得到的12阶以内各阶差分的系数,一般来说,差分阶数越高,模拟结果的精度越高。图 2为均匀介质模型的空间2阶和12阶有限差分模拟的vx分量快照,其中纵、横波速度分别为2800、1620m/s,空间三个方向的剖分间距均为5m,时间步长为0.5ms,纵波源是主频为30Hz的Ricker子波,位于(500m,500m,500m)处。显然,12阶精度的差分格式能获得更精确的模拟结果。虽然差分阶数越高模拟精度越高[5],但差分阶数的提高也意味着计算量的迅速增大。数值实验表明,当差分阶数增高到一定程度后,继续增高对模拟精度的提升十分有限。本文综合考虑模拟精度和计算效率两个因素后,采用12阶精度的差分格式实现式(1)的数值模拟。
|
|
表 2 交错网格不同阶次有限差分系数 |

|
图 2 均匀模型2阶(a)和12阶(b)有限差分模拟的波场快照 |
采用与文献[13, 36]相同的推导方法可得式(2)的稳定性条件为
| $ \sum\limits_{m = 1}^N {\left| {{C_m}} \right|} \cdot \Delta t \cdot {v_{\max }}\sqrt {\frac{1}{{\Delta {x^2}}} + \frac{1}{{\Delta {y^2}}} + \frac{1}{{\Delta {z^2}}}} \le 1 $ | (4) |
式中vmax为模型中的最大速度。
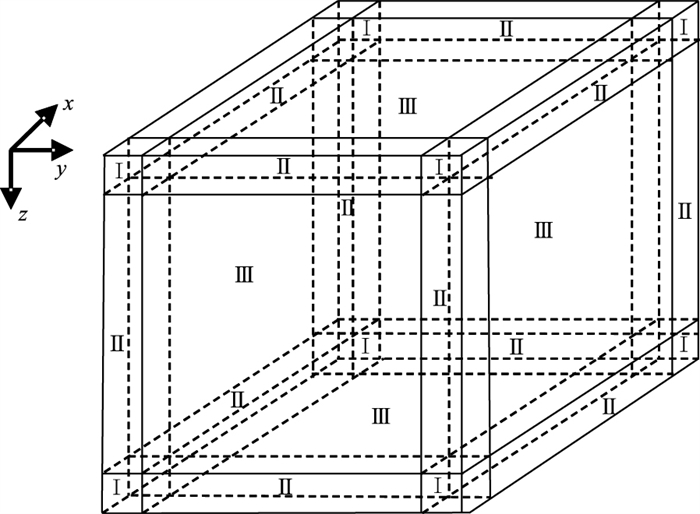
2.3 PML吸收边界条件本文引入地震波方程正演领域常用的PML边界条件[21-23]吸收入射到模型边界的外行波。采用图 3所示的镶边方案在模型周边镶嵌PML吸收层,图 3中区域Ⅰ为8个角点区,区域Ⅱ为12条棱边区,区域Ⅲ为剩余的6个面。
|
图 3 三维空间PML镶边方案示意图 |
以θ分量为例,在镶边区域将θ分量分解为θx、θy和θz三个分量,分别计算各分量,再求和得到镶边区域的θ分量,即
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial {\theta _x}}}{{\partial t}} + {d_x}{\theta _x} = \frac{{\partial {v_x}}}{{\partial x}}}\\ {\frac{{\partial {\theta _y}}}{{\partial t}} + {d_y}{\theta _y} = \frac{{\partial {v_y}}}{{\partial y}}}\\ {\frac{{\partial {\theta _z}}}{{\partial t}} + {d_z}{\theta _z} = \frac{{\partial {v_z}}}{{\partial z}}}\\ {\theta = {\theta _x} + {\theta _y} + {\theta _z}} \end{array}} \right. $ | (5) |
式中dx、dy、dz分别为x、y、z三个方向上的衰减因子,其计算公式为[9, 22]
| $ \left\{ {\begin{array}{*{20}{l}} {{d_x} = {{\left( {\frac{{{h_x}}}{\delta }} \right)}^4}\frac{{3V}}{{2\delta }}\lg \frac{1}{R}}\\ {{d_y} = {{\left( {\frac{{{h_y}}}{\delta }} \right)}^4}\frac{{3V}}{{2\delta }}\lg \frac{1}{R}}\\ {{d_z} = {{\left( {\frac{{{h_z}}}{\delta }} \right)}^4}\frac{{3V}}{{2\delta }}\lg \frac{1}{R}} \end{array}} \right. $ | (6) |
式中:V为波速,一般取纵波速度cP;R为理论边界反射系数,一般取经验值0.0001[9];δ为PML镶边层厚度;hx、hy、hz分别为镶边层中的各网格点与有效计算区域边界的最短距离。
同样在交错网格空间中对式(5)进行差分离散,可得到式(5)的高阶有限差分格式
| $ \left\{ {\begin{array}{*{20}{l}} \begin{array}{l} {\theta _x}(i, j, k, n + 1) = \frac{{1 - \frac{{\Delta t{d_x}}}{2}}}{{1 + \frac{{\Delta t{d_x}}}{2}}}{\theta _x}(i, j, k, n) + \frac{{\Delta t}}{{\Delta x\left( {1 + \frac{{\Delta t{d_x}}}{2}} \right)}}\sum\limits_{m = 1}^N {{C_m}} \left[ {{v_x}\left( {i + m - \frac{1}{2}, j, k, n + \frac{1}{2}} \right) - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{v_x}\left( {i - m + \frac{1}{2}, j, k, n + \frac{1}{2}} \right)} \right] \end{array}\\ \begin{array}{l} {\theta _y}(i, j, k, n + 1) = \frac{{1 - \frac{{\Delta t{d_y}}}{2}}}{{1 + \frac{{\Delta t{d_y}}}{2}}}{\theta _y}(i, j, k, n) + \frac{{\Delta t}}{{\Delta y\left( {1 + \frac{{\Delta t{d_y}}}{2}} \right)}}\sum\limits_{m = 1}^N {{C_m}} \left[ {{v_y}\left( {i, j + m - \frac{1}{2}, k, n + \frac{1}{2}} \right) - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{v_y}\left( {i, j - m + \frac{1}{2}, k, n + \frac{1}{2}} \right)} \right] \end{array}\\ \begin{array}{l} {\theta _z}(i, j, k, n + 1) = \frac{{1 - \frac{{\Delta t{d_z}}}{2}}}{{1 + \frac{{\Delta t{d_z}}}{2}}}{\theta _z}(i, j, k, n) + \frac{{\Delta t}}{{\Delta z\left( {1 + \frac{{\Delta t{d_z}}}{2}} \right)}}\sum\limits_{m = 1}^N {{C_m}} \left[ {{v_z}\left( {i, j, k + m - \frac{1}{2}, n + \frac{1}{2}} \right) - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{v_z}\left( {i, j, k - m + \frac{1}{2}, n + \frac{1}{2}} \right)} \right] \end{array} \end{array}} \right. $ | (7) |
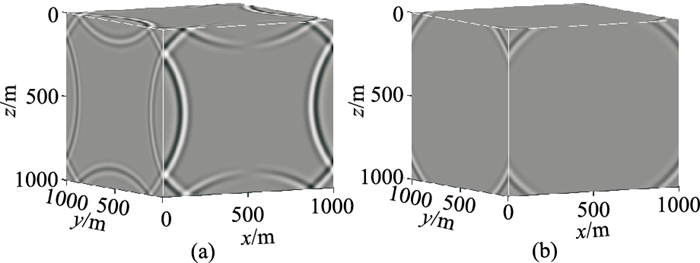
同理可得出其他波场分量的PML吸收边界及其高阶差分格式。对比均匀模型加与不加PML吸收边界的波场快照(图 4)可见,本文的PML边界条件几乎能完全吸收入射到截断边界的外行波。
|
图 4 不加(a)与加(b)PML吸收边界的vx分量快照对比 |
对一个简单的两层水平层状介质模型分别采用一阶速度—应力弹性波方程[9]和一阶速度—胀缩—旋转弹性波方程[32]进行数值模拟,利用模拟快照分析两个方程的联系和区别。模型尺寸为1000m×600m×1000m,上层纵、横波速度分别为2250、1300m/s,下层纵、横波速度分别为2900、1676m/s,界面埋深为350m,空间网格尺寸为5m×5m×5m,时间采样间隔为0.5ms。两个方程均采用空间12阶精度的有限差分算法进行模拟。经验证,以上模拟参数同时满足两个方程的稳定性条件。均采用主频为30Hz的Ricker子波作为纵波激发源,炮点位于(500m,300m,0)处。对一阶速度—应力方程模拟时,纵波源加载到三个正应力分量上,而对一阶速度—胀缩—旋转方程进行模拟时,由于该方程没有显式包含应力分量,故将纵波源加载到体应变θ上。两种算法模拟所需的计算量如表 3所示(一阶速度—应力方程的模拟过程包含了基于散度和旋度算子的纵横波分离运算),显然,相同精度条件下,本文算法的运算量低于一阶速度—应力弹性波方程数值模拟的运算量。
|
|
表 3 两种方法计算量对比 |
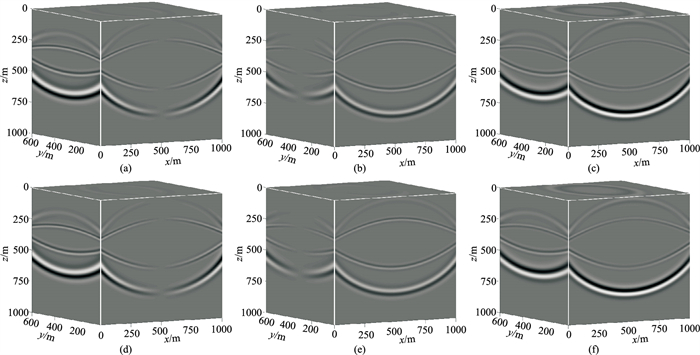
图 5为0.35s时刻两种方程模拟的vx、vy、vz分量快照,是野外采集中可以直接用速度检波器接收并记录的信息。由于波的传播方向并非与坐标轴完全平行,因此三个分量中均同时包含纵波与横波。显然,由两个方程得到的质点的振动速度是完全一致的(因为二者的物理意义本就是相同的)。这说明,如果以得到三分量炮记录为正演目标,则式(1)可以获得与一阶速度—应力方程完全相同的结果。
|
图 5 水平层状模型两种方程模拟的波前快照对比(一) (a)、(b)、(c)分别为速度—胀缩—旋转弹性波方程模拟的vx、vy、vz分量;(d)、(e)、(f)分别为速度—应力弹性波方程模拟的vx、vy、vz分量 |
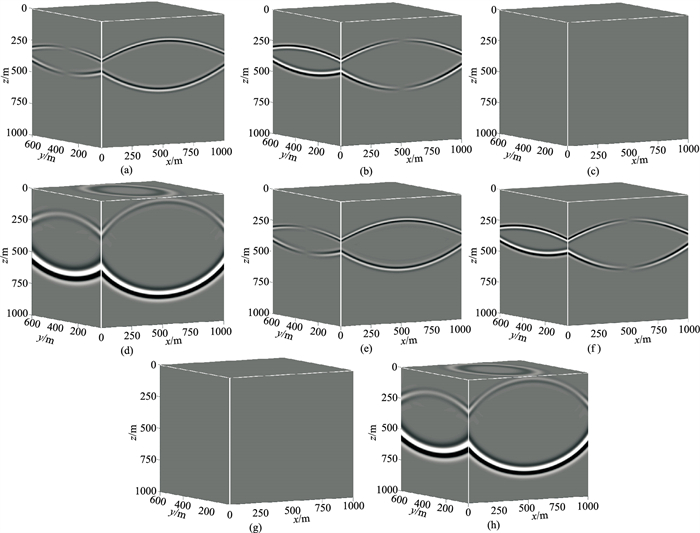
图 6a~图 6d为式(1)正演得到的ω的三分量快照和θ的快照。依据式(1),θ和ω对时间的偏导数分别对应v的散度和旋度,分别指示纵波和横波。图 6e~图 6g为直接对图 5d~图 5f求旋度和散度的结果,它们几乎与ω和θ的快照完全相同,表明θ和ω能代替一阶速度—应力弹性波方程中质点振动速度的散度和旋度。需要说明的是,虽然业界常通过直接求取v的散度和旋度分离纵、横波,但这种方法得到的结果只在波形上与真实的纵、横波相似,却没有明确的物理意义,因为只有当Helmholtz分解的对象是位移矢量时,分离结果才有明确的物理意义,因此图 6a~图 6d具有明确的物理意义,而图 6e~图 6g则不然。此外,对比图 6与图 5还可以看出,上述两种方法得到的横波的x分量和y分量与分离前混合波场中横波的x分量和y分量存在90°的相位差,其极性反转位置没有与分离前混合波场中的各分量对应。而分离后的横波z分量为零,这显然与实际情况不符。这说明基于散度和旋度算子的波场分离方法不能实现纵、横波的保幅分离。图 6c和图 6g为零的原因是:在进行旋度运算时,ωz是vy在x方向的偏导数与vx在y方向的偏导数之差,由于本算例所用的模型在z方向上水平分层,vy在x方向的偏导与vx在y方向的偏导相等,故旋度的z分量为零。
|
图 6 水平层状模型两种方程模拟的波前快照对比(二) (a)、(b)、(c)和(d)分别为速度—胀缩—旋转方程模拟的ωx、ωy、ωz和θ分量;(e)、(f)、(g)和(h)分别为对速度—应力方程模拟的质点振动速度矢量求旋度的x、y、z分量和求散度的结果 |
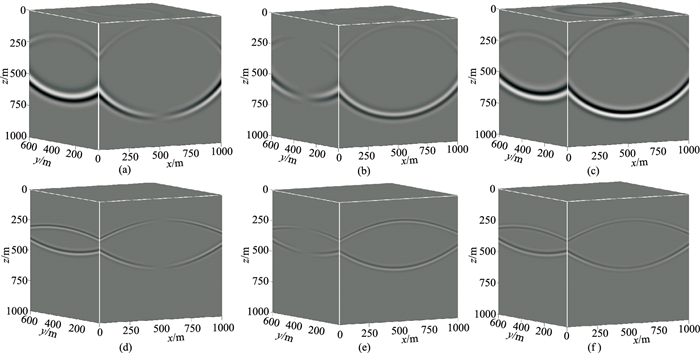
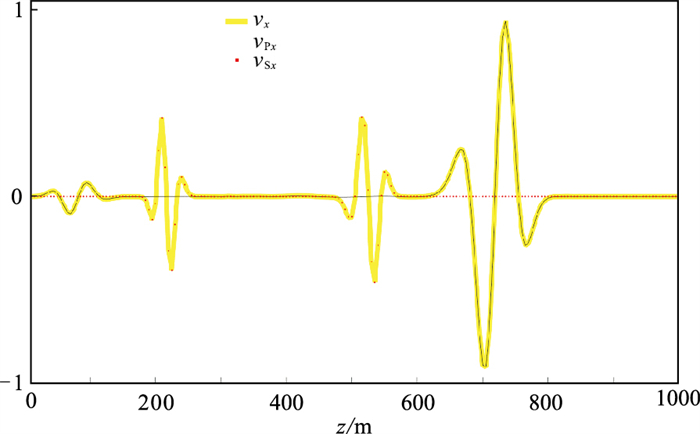
图 7为在式(1)方程的正演直接得到的纯vP和纯vS的三分量快照,与图 5对比可见,图 7不仅实现了纵、横波的完全分离,并且分离后各分量的纵、横波的极性与混合波场中的极性完全对应,相位也保持一致。同时,依据式(1),由于混合波场v是两个矢量波场vS和vP的简单相加,因此利用式(1)得到的纵、横波分离结果一定是保幅的。图 8为水平位置(250m,0)处vx、vPx、vSx分量垂向波形对比,证明了一阶速度—胀缩—旋转弹性波方程能够实现纵横波的保幅分离。与现有的纵、横波保幅分离算法相比,本文算法的优势在于:一阶速度—胀缩—旋转弹性波方程无需任何额外计算即可实现纵、横波的完全分离,分离精度只与模拟算法的精度有关,而现有的纵、横波保幅分离算法的精度同时受制于模拟算法的精度和解耦算子的精度。
|
图 7 水平层状模型速度—胀缩—旋转弹性波方程模拟的纯vP、纯vS各分量快照 (a)vPx;(b)vPy;(c)vPz;(d)vSx;(e)vSy;(f)vSz |
|
图 8 本文方法模拟的vx、vPx、vSx分量垂向波形对比 |
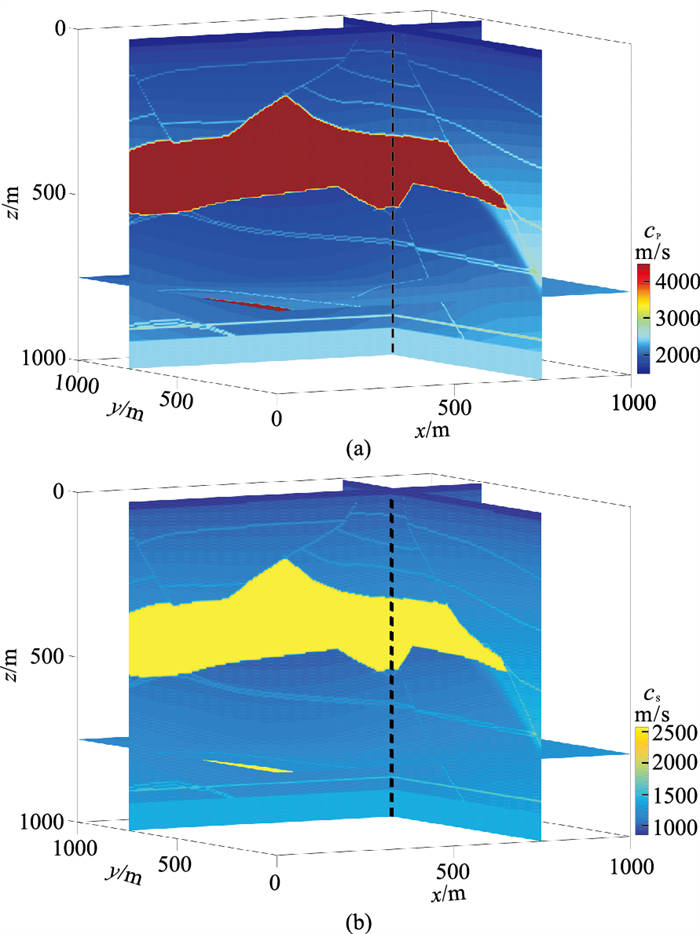
用SEG/EAGE盐丘模型检验本文模拟算法的正确性,并进一步分析一阶速度—胀缩—旋转方程在弹性波模拟与应用方面的优势。模型尺寸为1000m×1000m×1000m,纵、横波速度模型如图 9所示,空间网格尺寸为5m×5m×5m,时间步长为0.35ms,模拟参数满足稳定性条件。纵波震源是主频为30Hz的Ricker子波,炮点坐标为(500m,500m,0)。地震记录长度为1.05s,8条多分量接收线位于地表,间距为125m,第1、第8条分别位于y=0、y=875m处,每条线200道,道间距为5m,单炮共有1600道。
|
图 9 三维盐丘模型 (a)纵波速度;(b)横波速度 |
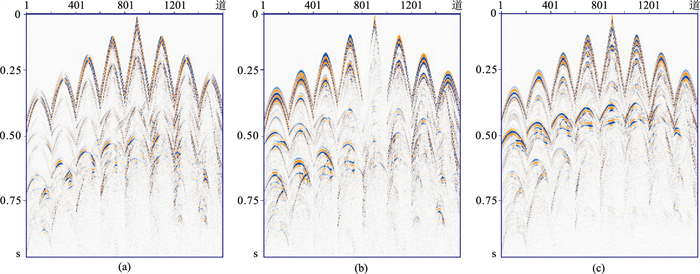
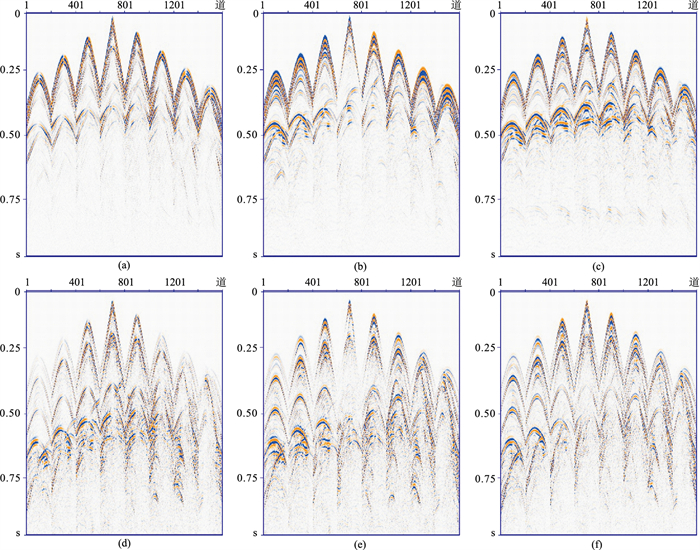
图 10、图 11为正演得到的各分量单炮记录。由于该模型包含了断层、凹陷、隆起、倾斜界面和水平界面,使得弹性波的传播过程极为复杂且混合波场中纵波与横波耦合在一起,难以区分,不便于分析纵、横波的传播过程,也不便于评价观测系统的合理性。而一阶速度—胀缩—旋转方程可以在波场延拓中直接获得vS和vP的各个分量,使混合在一起的波场得到分离,为分别研究反射纵波或转换横波的传播过程和机理提供了更准确的信息。同时,上述结果也说明一阶速度—胀缩—旋转弹性波方程还有利于在延拓过程中直接求取纯纵波或纯横波的某些属性,如纵波的传播方向、横波的传播方向及其极化方向等,而这些属性信息又往往是偏移和反演等环节的关键信息。
|
图 10 部分三维盐丘模型本文方法模拟的混合波场地震记录 (a)vx;(b)vy;(c)vz |
|
图 11 部分三维盐丘模型本文方法模拟的纯波地震记录 (a)vPx;(b)vPy;(c)vPz;(d)vSx;(e)vSy;(f)vSz |
本文给出了三维各向同性介质中一阶速度—胀缩—旋转弹性波方程的高阶有限差分格式及其稳定性条件,以此为基础实现了该方程的数值模拟,并利用模型模拟结果详细分析了该方程的优势,得出如下结论。
(1) 本文算法能实现一阶速度—胀缩—旋转弹性波方程的高精度数值模拟。
(2) 除能获得常规弹性波模拟中的三分量合成记录和波场快照外,一阶速度—胀缩—旋转弹性波方程还能够在不增加任何额外运算的前提下直接实现弹性波的保幅解耦。解耦结果是一个纵波速度矢量和一个横波速度矢量,除了便于分析纵、横波在各个方向的振动情况外,还特别有利于求取纯纵波或纯横波的传播方向和极化方向等属性信息。同时,由于解耦结果是两个矢量,避免了弹性波逆时偏移中进行互相关成像时矢量和标量无法相关的难题。
(3) 对一阶速度—胀缩—旋转弹性波方程进行数值模拟还可以直接得到一个体应变θ和旋转矢量ω,其物理意义与常规弹性波方程中位移矢量的散度和旋度算子的物理意义相同。θ与ω虽然与特定模型条件下的纵横波传播过程有关,但不能准确描述纵、横波传播过程。
(4) 本文模拟得到的vS和vP都是矢量,而事实上,各向同性介质中的纵波是标量,虽然vP可以准确描述由胀缩运动导致的质点振动在各个方向的投影情况,但由于业界习惯于将纵波当成一个独立标量处理和分析,因此将vP合成为一个标量更易为业界接受,现有的矢量波场的标量化处理技术完全可以解决这一问题。
| [1] |
ALTERMAN Z, KARAL F C. Propagation of elastic waves in layered media by finite difference methods[J]. Bulletin of the Seismological Society of America, 1968, 58(1): 367-398. |
| [2] |
BAYLISS A, JORDAN K E, LEMESURIER B J, et al. A fourth-order accurate finite difference scheme for the computation of elastic waves[J]. Bulletin of the Seismological Society of America, 1986, 76(4): 1115-1132. DOI:10.1785/BSSA0760041115 |
| [3] |
IGEL H, RIOLLET B, MORA P. Accuracy of staggered 3-D finite-difference grids for anisotropic wave propagation[C]. SEG Technical Program Expanded Abstracts, 1992, 11: 1244-1246.
|
| [4] |
董良国, 马在田, 曹景忠, 等. 一阶弹性波方程交错网格高阶差分解法[J]. 地球物理学报, 2000, 43(3): 411-419. DONG Liangguo, MA Zaitian, CAO Jingzhong, et al. A staggered-grid high-order difference method of one-order elastic wave equation[J]. Chinese Journal of Geophysics, 2000, 43(3): 411-419. DOI:10.3321/j.issn:0001-5733.2000.03.015 |
| [5] |
张会星, 何兵寿, 宁书年. 双相介质中纵波方程的高阶有限差分解法[J]. 物探与化探, 2004, 28(4): 307-309, 313. ZHANG Huixing, HE Bingshou, NING Shunian. High-order finite difference solution of dilatational wave equations in two-phase media[J]. Geophysical and Geochemical Exploration, 2004, 28(4): 307-309, 313. DOI:10.3969/j.issn.1000-8918.2004.04.008 |
| [6] |
CRASE E. High-order (space and time) finite-diffe-rence modeling of the elastic wave equation[C]. SEG Technical Program Expanded Abstracts, 1990, 9: 987-991.
|
| [7] |
HESTHOLM S, RUUD B O. 3-D finite-difference elastic wave modeling including surface topography[J]. Geophysics, 1998, 63(2): 613-622. DOI:10.1190/1.1444360 |
| [8] |
HE C, QIN G, WEI Z. High-order finite-difference modeling on reconfigurable computing platform[C]. SEG Technical Program Expanded Abstracts, 2005, 24: 1755-1758.
|
| [9] |
牟永光, 裴正林. 三维复杂介质地震数值模拟[M]. 北京: 石油工业出版社, 2005.
|
| [10] |
MADARIAGA R. Dynamics of an expanding circular fault[J]. Bulletin of the Seismological Society of America, 1976, 66(3): 639-666. DOI:10.1785/BSSA0660030639 |
| [11] |
VIRIEUX J. SH-wave propagation in heterogeneous media: Velocity-stress finite-difference method[J]. Geophysics, 1984, 49(11): 1933-1942. DOI:10.1190/1.1441605 |
| [12] |
LEVANDER A R. Fourth-order finite-difference P-SV seismograms[J]. Geophysics, 1988, 53(11): 1425-1436. DOI:10.1190/1.1442422 |
| [13] |
董良国, 马在田, 曹景忠. 一阶弹性波方程交错网格高阶差分解法稳定性研究[J]. 地球物理学报, 2000, 43(6): 856-864. DONG Liangguo, MA Zaitian, CAO Jingzhong. A study on stability of the staggered-grid high-order difference method of first-order elastic wave equation[J]. Chinese Journal of Geophysics, 2000, 43(6): 856-864. DOI:10.3321/j.issn:0001-5733.2000.06.015 |
| [14] |
孙耀充, 张延腾, 白超英. 二维弹性及粘弹性TTI介质中地震波场数值模拟: 四种不同网格高阶有限差分算法研究[J]. 地球物理学进展, 2013, 28(4): 1817-1827. SUN Yaochong, ZHANG Yanteng, BAI Chaoying. Seismic wavefield simulation in 2D elastic and visco-elastic media: comparison between four different kinds of finite-difference grids[J]. Progress in Geophysics, 2013, 28(4): 1817-1827. |
| [15] |
CHARI-HYUN J, SHIN C, SUH J H. An optimal 9-point, finite-difference, frequency-space, 2-D scalar wave extrapolator[J]. Geophysics, 1996, 61(2): 529-537. DOI:10.1190/1.1443979 |
| [16] |
MIN D J, SHINZ C, KWON B D, et al. Improved frequency-domain elastic wave modeling using weighted-averaging difference operators[J]. Geophysics, 2000, 65(3): 884-895. DOI:10.1190/1.1444785 |
| [17] |
FEI T, LARNER K. Elimination of numerical dispersion in finite-difference modeling and migration by flux-corrected transport[J]. Geophysics, 1995, 60(6): 1830-1842. DOI:10.1190/1.1443915 |
| [18] |
何兵寿, 魏修成, 刘洋. 三维波动方程的数值频散关系及其叠前和叠后数值模拟[J]. 石油大学学报(自然科学版), 2001, 25(1): 67-71. HE Bingshou, WEI Xiucheng, LIU Yang. Numerical dispersion relation of the three dimensional wave equation and numerical simulation of pre-stack and post-stack[J]. Journal of University of Petroleum (Edition of Natural Science), 2001, 25(1): 67-71. |
| [19] |
吴国忱, 王华忠. 波场模拟中的数值频散分析与校正策略[J]. 地球物理学进展, 2005, 20(1): 58-65. WU Guochen, WANG Huazhong. Analysis of nume-rical dispersion in wave-field simulation[J]. Progress in Geophysics, 2005, 20(1): 58-65. DOI:10.3969/j.issn.1004-2903.2005.01.012 |
| [20] |
CERJAN C, KOSLOFF D, KOSLOFF R, et al. A non-reflecting boundary condition for discrete acoustic and elastic wave equation[J]. Geophysics, 1985, 50(4): 705-708. DOI:10.1190/1.1441945 |
| [21] |
HIGDON R L. Absorbing boundary condition for elastic waves[J]. Geophysics, 1991, 56(2): 231-241. DOI:10.1190/1.1443035 |
| [22] |
BERENGER J P. A perfectly matched layer for the absorption of electromagnetic waves[J]. Journal of Computational Physics, 1994, 114(2): 185-200. DOI:10.1006/jcph.1994.1159 |
| [23] |
罗玉钦, 刘财. 近似完全匹配层边界条件吸收效果分析及衰减函数的改进[J]. 石油地球物理勘探, 2018, 53(5): 903-913. LUO Yuqin, LIU Cai. Analysis of absorption effect and improvement of attenuation function for boundary conditions of approximately perfect matching layer[J]. Oil Geophysical Prospecting, 2018, 53(5): 903-913. DOI:10.13810/j.cnki.issn.1000-7210.2018.05.003 |
| [24] |
何兵寿, 张会星, 韩令贺. 弹性波方程正演的粗粒度并行算法[J]. 地球物理学进展, 2010, 25(2): 650-656. HE Bingshou, ZHANG Huixing, HAN Linghe. Forward modelling of elastic wave equation with coarse-grained parallel algorithm[J]. Progress in Geophy-sics, 2010, 25(2): 650-656. DOI:10.3969/j.issn.1004-2903.2010.02.039 |
| [25] |
王绍文, 宋鹏, 谭军, 等. 弹性波数值模拟中的高斯型混合吸收边界条件及其GPU并行[J]. 石油地球物理勘探, 2021, 56(3): 485-495. WANG Shaowen, SONG Peng, TAN Jun, et al. Gaussian mixed absorption boundary conditions and GPU parallelism in elastic wave numerical simulation[J]. Oil Geophysical Prospecting, 2021, 56(3): 485-495. DOI:10.13810/j.cnki.issn.1000-7210.2021.03.007 |
| [26] |
KONDOH Y. On thoughts analysis of numerical schemes for simulation using a kernel optimum nearly-analytical discretization (KOND) method[J]. Journal of the Physical Society of Japan, 1991, 60(9): 2851-2861. DOI:10.1143/JPSJ.60.2851 |
| [27] |
YANG D H, TENG J W, ZHANG Z J, et al. A nearly analytic discrete method for acoustic and elastic wave equations in anisotropic media[J]. Bulletin of the Seismological Society of America, 2003, 93(2): 882-890. DOI:10.1785/0120020125 |
| [28] |
OPRSAL I, ZAHRDNIK J. Elastic finite-difference method for irregular grids[J]. Geophysics, 1999, 64(1): 240-250. DOI:10.1190/1.1444520 |
| [29] |
PITARKA A. 3D elastic finite-difference modeling of seismic motion using staggered grid with nonuniform spacing[J]. Bulletin of the Seismological Society of America, 1999, 89(1): 54-68. DOI:10.1785/BSSA0890010054 |
| [30] |
DELLINGER J, ETGEN J. Wave-field separation in two-dimensional anisotropic media[J]. Geophysics, 1990, 55(7): 914-919. DOI:10.1190/1.1442906 |
| [31] |
SUN R, CHOW J, CHEN K J. Phase correction in separating P- and S-waves in elastic data[J]. Geophysics, 2001, 66(5): 1515-1518. DOI:10.1190/1.1487097 |
| [32] |
李振春, 张华, 刘庆敏, 等. 弹性波交错网格高阶有限差分法波场分离数值模拟[J]. 石油地球物理勘探, 2007, 42(5): 510-515. LI Zhenchun, ZHANG Hua, LIU Qingmin, et al. Numeric simulation of elastic wavefield separation by staggering grid high-order finite-difference algorithm[J]. Oil Geophysical Prospecting, 2007, 42(5): 510-515. DOI:10.3321/j.issn:1000-7210.2007.05.006 |
| [33] |
张婧, 张文栋, 张铁强, 等. 应用τ-p域矢量旋转的地震数据波场分离[J]. 石油地球物理勘探, 2020, 55(1): 46-56. ZHANG Jing, ZHANG Wendong, ZHANG Tieqiang, et al. Wave field separation of seismic data using vector rotation in τ-p domain[J]. Oil Geophysical Prospecting, 2020, 55(1): 46-56. |
| [34] |
何兵寿, 高琨鹏, 徐国浩. 各向异性介质中弹性波逆时偏移技术的研究现状与展望[J]. 石油物探, 2021, 60(2): 210-223. HE Bingshou, GAO Kunpeng, XU Guohao. Elastic wave reverse time migration in anisotropic media: state of the art and perspectives[J]. Geophysical Prospecting for Petroleum, 2021, 60(2): 210-223. DOI:10.3969/j.issn.1000-1441.2021.02.003 |
| [35] |
TANG H G, HE B S, MOU H B. P-and S-wave ener-gy flux density vectors[J]. Geophysics, 2016, 81(6): T357-T368. DOI:10.1190/geo2016-0245.1 |
| [36] |
李凯瑞, 何兵寿, 胡楠. 基于一阶速度-胀缩-旋转方程的多分量联合逆时偏移[J]. 煤炭学报, 2018, 43(4): 1072-1082. LI Kairui, HE Bingshou, HU Nan. Multicomponent joint inverse time migration based on first order velo-city-dilatation-rotation equations[J]. Journal of China Coal Society, 2018, 43(4): 1072-1082. |



 何兵寿, 山东省青岛市松岭路238号中国海洋大学海洋地球科学学院地球探测与信息技术系, 266100。Email:
何兵寿, 山东省青岛市松岭路238号中国海洋大学海洋地球科学学院地球探测与信息技术系, 266100。Email: 