② 中国科学院大学, 北京 100049;
③ 中国科学院先进水下信息技术重点实验室, 北京 100190
② University of Chinese Academy of Sciences, Beijing 100049, China;
③ Key Laboratory of Science and Technology on Advanced Underwater Acoustic Signal Processing, Chinese Academy of Sciences, Beijing 100190, China
合成孔径成像声呐(Synthetic Aperture Sonar,SAS)作为海底成像和测绘的主要手段[1],在水下目标探查识别、海底资源开发、石油勘探、海难救助、海底地形地貌绘制等方面,具有广泛的应用前景[2],它提供的高分辨率水下图像能反映出丰富的水下信息。随着SAS成像算法、硬件设备、计算机技术的不断发展,声呐成像水平不断提高,使用场合也在不断扩大,结合声呐输出图像的综合分析和处理需求也在不断增加。
由于受复杂水文环境、声呐平台运动姿态的不稳定性、声传播损失、不同距离或不同地貌的散射/反射特性、声呐基阵指向性等各方面因素的影响[3],SAS图像相较于其他自然图像(尤其是光学图像),存在明显差异,通常表现为噪声干扰强、远近灰度不均衡、对比度不高等特点,增加了后续图像分割与拼接、目标检测、分类与识别等[4-7]任务的难度。SAS图像预处理是整个SAS图像处理的初始关键步骤,好的预处理图像将大大提高后续声呐图像处理的质量。本文基于图像预处理中重要的灰度不均衡问题进行了研究和分析。
目前,解决图像灰度不均衡的方法可分为两类:基于物理模型的硬件校正和基于图像处理的软件实现。基于物理模型的方法主要从声呐过程的物理和几何结构出发,直接从声呐数据估计距离、角度等相关校正因子,实现针对斜距、传播、指向性、载体速度、海底散射角等的校正。最常见的物理模型均衡如声呐电子系统接收电路中对远近回波差异补偿采用的时变增益(Time Varing Gain,TVG)[8],其增益参数由经验声学方程估计得到[9-10]。但由于海水复杂的空、时变特性,物理模型并不能完全适配[11];且声线弯曲、海底不平整等有别于实际情况的假设也会使基于物理模型的均衡增益存在偏差。实际上得到的声呐图像通常已经过TVG补偿,但大量数据仍具有灰度不均衡现象;由于噪声并不具备随距离衰减的特性,此类物理增益也会增强额外的噪声干扰,使声呐图像灰度的均衡更复杂。因此,基于物理模型的均衡方法常用于快速实时实现,得到声呐图像的初始粗均衡结果,但不能作为最终的均衡手段。
基于图像处理的图像均衡方法通常是一类不借助声呐数据而仅从图像本身出发去解决声呐图像灰度不均衡的手段。实际应用中,除了内部数据具有可知的声呐参数及姿态信息,外部获取的声呐图像并不具备相关声呐数据,也就无法根据物理参数的方法做均衡处理,此时需借助图像均衡方法实现均衡处理。图像域的均衡方法较多样化,如借鉴图像增强方法,主要包括灰度拉伸、直方图均衡、反锐化掩模、Retinex增强、傅里叶变换、离散余弦变换、小波变换、多尺度几何变换等[12-18];其他均衡方法包括模板匹配或函数拟合方法[10, 19-23]、噪声背景估计均衡方法[24-25]、比例改正方法[26]等。
声呐图像均衡的主要目的是抵消或减弱随距离、角度、指向性等因素造成的声能损失的差异性,而图像增强的目的是突出感兴趣区域特征,加强图像判读和识别效果,从而满足某些特殊分析需求。因此如Zhang等[15]提出的基于图像增强的诸多声呐图像均衡算法,虽然提高了图像对比度,扩大了图像中不同物体特征之间的差别,但均衡效果有所欠缺,未能很好地补偿声能损失的差异性。
从局部邻域出发的均衡算法(如中值滤波HM)具有良好的非线性滤波效果。Cervenka等[17]提出基于中值滤波的声呐图像均衡算法,其优点是简单高效,适用于实时处理,但只适用于部分背景简单的声呐图像,对于地貌复杂、细节较多的声呐图像效果较差,主要原因是中值滤波得到的曲线对于简单声呐图像能较好地拟合,但当地貌复杂时,中值滤波会受明显的奇异点(如高亮目标、阴影等)影响,只能做到大趋势上的拟合,对细节纹理等产生模糊,且存在横纹干扰时会加重其影响。
Celebi等[18]提出基于离散余弦变换(Discrete Cosine Transform,DCT)和马尔科夫随机场的声呐图像均衡算法,变换域方法在抑制噪声和保护边缘方面具有很大的改进,如DCT[27]、小波变换[28]、曲波变换[29]等,该方法是先对图像进行某种可逆的数学变换,然后在变换域对一些系数做减小或增大等处理,最后再通过逆变换获得已实现去噪、增强等功能的图像,变换域虽能通过频率系数、尺度系数等进行一定的去噪和边缘保护,但无法表征不均衡的机理,均衡效果不理想。
Galdran等[19]以构建的合适先验函数模型做背景灰度分布曲线模板匹配,取得了较好均衡效果,但最终效果与给定的函数模型和相关声呐数据有直接关系,当模型不合理或数据不匹配时,效果较差。
噪声背景估计方法最早应用于频域和波数域。Struzinski等[24]基于大量仿真和研究,通过噪声估计和背景均衡有效地滤除了随机起伏,改善了方位历程图像质量,并将其应用于声呐图像领域,同样取得了良好效果,但该类方法对于窗口参数选取要求较高,易滤除纹理细节及弱小目标。
基于物理模型的声呐图像均衡通常因实际环境的复杂性而具有不均衡残余,基于图像域的声呐图像均衡多从图像增强出发,但一味地增强处理并不能有效改善均衡问题。为此,本文通过分析声呐图像有别于其他图像的特点,建立时间演化的均衡模型,依据背景估计的思路,提出了一种基于图像局部背景迭代估计的SAS图像自适应均衡方法。
该方法首先利用图像背景、目标纹理的统计特性及均衡前、后图像的差分关系等对均衡函数、滤波分量(图像背景)进行自动迭代更新,当满足迭代终止条件时,得到原始图像的背景分量(的估计);然后通过背景均衡与动态范围调整得到最终均衡结果。一方面此方法涉及参数较少,除窗口大小外,其他参数具有自动更新能力,降低了对调参的依赖性;另一方面,算法参数和滤波函数的设计从实际声呐图像特点出发,在均衡同时对原图的纹理、边缘等特征也有较好保护作用,且对暗条纹干扰(由电源干扰、数据传输异常等引起)具有一定消除功能。
1 声呐图像自适应均衡方法 1.1 问题描述声信号的能量损失是水声信道最明显的传播特性。以扩展损失为例,声波在海水中传播时,其能量随作用距离的增大以指数函数形式衰减,远距离目标回波衰减严重,导致声呐图像近端较亮,远端较暗。其次,声呐基阵发射的脉冲具有很强的指向性,波束轴中心能量较强,两边较弱,也会导致图像灰度分布不均匀。另外,目标散射强度与掠射角有关,距离越远,掠射角越小,回波信号越弱,从而也造成了图像灰度的差异性。同时,海底的粗糙度也影响声波的散射性能,导致不同地貌成像的差异性。
实际SAS图像(图 1)与SAR (Synthetic Aperture Radar,合成孔径雷达)成像原理相似,但成像时条带沿距离向近端和远端回波强度差异较大,图像不均衡现象严重。另外声波为机械波,受水中环境噪声影响大,水声信道也远比光或电磁传输信道差,故SAS图像的信噪比较低、对比度较差、灰度畸变等特征表现得更严重。因此合适的声呐图像均衡处理尤为重要。

|
图 1 实际SAS图像 |
为了得到良好的均衡效果,本文算法模型基于以下声呐图像不均衡特点:
(1) 声呐图像背景在整个图像范围内根据地貌、底质不同,其起伏是变化的、任意的,但在局部范围内起伏是连续的、变化较小的。
(2) 目标被照射区域表现为高亮对应高灰度值,未被照射区域表现为阴影,对应低灰度值,其他区域为背景区,对应中灰度值。但由于声能损失、接收阵指向性等影响,声呐图像远端回波较弱,该区域目标、背景均表现为较低灰度值。
(3) 声呐图像均衡时,不应产生新的高亮与阴影,以免破坏了原图质地与结构。
(4) 声波随距离的损失、目标回波散射特性与掠射角关系、基阵发射波束指向性、混响、噪声干扰等对图像的灰度不均衡影响整体上呈现非线性和叠加性,是随时间演化累积的,任何一次性的处理方式均可能存在不均衡残余。
(5) 由于声速、波束辐射角度等在不同区域具有一定差异,声呐图像表现出的不均衡性是局部的而非全局的,因此均衡过程也是局部而非全局的,局部处理利用适当窗函数实现。
以上假设满足声呐图像灰度不均衡的基本特征,有别于SAR图像与光学图像。根据以上声图特征,本文将声呐图像灰度均衡处理划分为三个主要步骤,即背景估计、背景均衡和动态范围调整。
传统的图像均衡方法的思路较为简单,即认为观测到的非均衡图像由均衡图像与一系列线性或非线性核函数卷积得到,即
| $ I(x, y, t) = {I_0}(x, y) * G(x, y, t) $ | (1) |
式中:I(x,y,t)表示随时间演化得到的非均衡图,这里指已观测图像;I0(x,y)为理想海底声图,这里指待求均衡图;G(x,y,t)为卷积核;x,y分别表示方位向和距离向坐标;t为时间因子;“*”表示卷积算子。
不同核函数卷积产生不同的非均衡效果,通过不同局部区域的时间演化并累积,得到观测的非均衡声呐图像。而核函数的反推,一般可通过声学物理或数学模型获得,但实际非均衡更复杂,其演化方程变成
| $ I(x, y, t) = F\left[ {{I_0}(x, y), t} \right] $ | (2) |
式中F表示非均衡函数。
图像全局非均衡是局部非均衡的集合,则式(2)可进一步描述为
| $ I(x, y, t) = \sum\limits_{\mathit{\Omega } \in I} {{F_\mathit{\Omega }}} \left[ {{I_0}(x, y), t} \right] $ | (3) |
式中Ω表示局部区域。
因为函数FΩ通常无法用单一精确的表达式表述,所以一般性地将其视为一系列核函数的乘积,即随时间演化的非均衡过程,有
| $ {F_{\mathit{\Omega }, t}} = \prod\limits_{{t_j} \in t} {{G_{\mathit{\Omega }, {t_j}}}} $ | (4) |
式中GΩ,tj表示作用于局部区域Ω内tj时刻的非均衡函数。
因此非均衡声呐图像I(x,y,t)可看成由待求均衡图I0(x,y)随时间不断受局部非均衡函数GΩ,t累积作用的结果,即
| $ I(x, y, t) = \sum\limits_{\mathit{\Omega } \in I} {\prod\limits_{{t_j} \in t} {{G_{\mathit{\Omega }, {t_j}}}} } \left[ {{I_0}(x, y), {t_j}} \right] $ | (5) |
记GΩ, tj的反函数为ωΩ, tj=GΩ, tj-1,则求I0(x,y)的过程为非均衡的逆过程,逆过程的核心即均衡函数ωΩ,tj的求解。
由于目标信号的有效衰减系数大于无目标时背景的衰减系数[30],均衡(逆非均衡)过程可表述为
| $ \hat I\left( {{x_\mathit{\Omega }}, {y_\mathit{\Omega }}, {t_j}} \right) = {\omega _{\mathit{\Omega }, {t_j}}}*I\left( {{x_\mathit{\Omega }}, {y_\mathit{\Omega }}, {t_{j + 1}}} \right) $ | (6) |
式中
(1) 对于局部区域的背景部分,均衡滤波前、后应变化较小,尽可能地保留下来;
(2) 对于目标或边缘等奇异特征,受非均衡(及均衡)的影响程度远大于平整的背景部分,所以滤波前、后变化较大。
因此,均衡函数ωΩ,tj可建模为图像随时间变化的图像梯度的函数
| $ {\omega _{\mathit{\Omega }, {t_j}}} = f\left[ {\frac{{\partial I\left( {{x_\mathit{\Omega }}, {y_\mathit{\Omega }}, {t_{j + 1}}} \right)}}{{\partial {t_{j + 1}}}}} \right] $ | (7) |
式中:
假设tj时刻的非均衡图为I(xΩ,yΩ,tj),则有
| $ \frac{{\partial I\left( {{x_\mathit{\Omega }}, {y_\mathit{\Omega }}, {t_{j + 1}}} \right)}}{{\partial {t_{j + 1}}}} = \frac{{I\left( {{x_\mathit{\Omega }}, {y_\mathit{\Omega }}, {t_{j + 1}}} \right) - I\left( {{x_\mathit{\Omega }}, {y_\mathit{\Omega }}, {t_j}} \right)}}{{{t_{j + 1}} - {t_j}}} $ | (8) |
下面令
由均衡性质分析可知,此时f的选取通常具有下列三种形式。
(1) 平方反比环绕函数
| $ f(r) = \frac{1}{{{r^2}}} $ | (9) |
(2) 指数形式。进一步修改为依赖于空间常数的形式,即近似地模拟VLSI电阻网络空间的形式
| $ f(r) = {{\rm{e}}^{ - |r|/{c^2}}} $ | (10) |
式中c表示均衡控制因子。
(3) 高斯形式。这种形式更宽泛,在图像处理、机器视觉建模中应用最广
| $ f(r) = {{\rm{e}}^{ - {r^2}/{c^2}}} $ | (11) |
算法的关键是对背景分量的有效估计,背景分量的估计直接决定了最终的均衡效果,因此采用适用最广的高斯形式(式11)作为均衡函数的表征。此时滤波函数ωΩ,tj合理地利用了时间演化过程中图像的微分关系,且参数c是该算法的唯一参数,因此参数c的选取直接决定了对背景分量估计的准确性,也即决定了最终的均衡效果。
为满足自适应处理的需求,均衡参数c用局部图像均值表示,因此局部区域Ω内第tj时刻的均衡控制因子可表示为
| $ {c_{\mathit{\Omega }, {t_j}}} = \frac{1}{{{N_\mathit{\Omega }}}}\sum I \left( {{x_\mathit{\Omega }}, {y_\mathit{\Omega }}, {t_j}} \right) $ | (12) |
式中NΩ表示区域Ω像素总个数。
当图像局部区域包含较多目标区域时,此时均值较大,对应的均衡效果应该表现为小步迭代均衡,避免大步迭代过程中可能造成图像灰度畸变。当均衡效果越来越好时,此时估计得到的背景分量较多,cΩ,tj减小,可均衡尺度增大,均衡速率提高。
因此,tj时刻声呐图像均衡的整个滤波过程为
| $ \hat I\left( {x, y, {t_j}} \right) = \sum\limits_{\mathit{\Omega } \in I} {\frac{1}{{{A_{\mathit{\Omega }, {t_j}}}}}} {w_{\mathit{\Omega }, {t_j}}}*I\left( {{x_\mathit{\Omega }}, {y_\mathit{\Omega }}, {t_{j + 1}}} \right) $ | (13) |
式中
然后将tj时刻的均衡估计结果作为tj时刻的原始非均衡输入数据,即
| $ I(x, y, t) = \hat I(x, y, t) $ | (14) |
所以,第tj时刻的图像微分,即式(7)可表述为
| $ \begin{array}{l} {\omega _{\mathit{\Omega }, {t_j}}} = f\left[ {\frac{{\partial I\left( {{x_\mathit{\Omega }}, {y_\mathit{\Omega }}, {t_{j + 1}}} \right)}}{{\partial {t_{j + 1}}}}} \right]\\ \;\;\;\;\;\; = f\left[ {\frac{{I\left( {x, y, {t_{j + 1}}} \right) - \hat I\left( {x, y, {t_j}} \right)}}{{{t_{j + 1}} - {t_j}}}} \right] \end{array} $ | (15) |
一般默认tj+1-tj=1为单位时刻,默认操作由于后续的归一化处理不影响算法性能。
1.3 算法流程针对均衡处理中的背景估计、背景均衡和动态范围调整等三个主要步骤(图 2),为保证算法的有效实施,有如下几点事项说明:

|
图 2 图像均衡流程示意图 |
(1) 声呐图像的不均衡发生在斜距向,所以均衡过程为声呐图像逐行处理。
(2) 初始值设置:因为算法需经过迭代自适应处理,其初始的均衡图像可通过其他任意均衡算法得到,又考虑算法的快速实施与权重系数的初始化,故采用原始图像的局部均值滤波作为初始均衡结果,此时初始均衡函数ωΩ,tj由全1向量表示。
(3) 局部窗口选择:为了有效估计背景像素,窗口大小应尽量满足所选区域的背景像素占68%以上[19]。
(4) 算法终止条件:虽然不能预知非均衡的演化时间t或演化次数,也就无法得到逆解算回I0(x,y)所需的时间和次数,但我们知道该求解过程的第一步为背景分量估计,而背景通常是连续较平整的,因此可利用背景分量的特性,设置达到算法终止的约束条件。通常可采用两种方式,一是认为当相邻两次均衡图像的所有局部梯度方差小于一定阈值时,即达到最终均衡结果,由于非线性函数的均衡是一个持续振荡的过程,须避免阈值选取不合理导致无法收敛;二是当相邻两次均衡图像梯度方差与前一时刻相邻两次均衡图像梯度方差的比值小于某一阈值时停止迭代。也可直接给定最大均衡迭代次数。由门限阈值进行算法终止的两种方式的数学式为
| $ D\left[ {\frac{{\partial I\left( {x, y, {t_q}} \right)}}{{\partial {t_q}}}} \right] < {T_1} $ | (16) |
| $ \frac{{D\left[ {\frac{{\partial I\left( {x, y, {t_q}} \right)}}{{\partial {t_q}}}} \right]}}{{D\left[ {\frac{{\partial I\left( {x, y, {t_{q + 1}}} \right)}}{{\partial {t_{q + 1}}}}} \right]}} < {T_2} $ | (17) |
式中:T1对应绝对误差门限阈值;D[·]为序列方差;T2对应相对误差门限阈值。
1.3.1 背景估计声呐图像均衡第一步为背景估计,其流程为:
(1) 从图像左侧即近距端开始,根据滑动窗口,计算某时刻图像与其均衡结果的差分,通过式(11)、式(12)、式(15)得到均衡滤波函数ωΩ;
(2) 由式(13)、式(14)迭代更新均衡图像结果;
(3) 迭代终止:针对步骤(2)的均衡结果,通过式(16)、式(17)做均衡程度判别,当满足终止条件或达到迭代次数上限,算法终止; 否则,返回步骤(1)。
1.3.2 背景均衡上述过程得到的最终结果
| $ R = \frac{{I - \hat R}}{{\hat R + C}} $ | (18) |
式中:R为背景均衡结果,
对于背景均衡后的声呐图像,需进行对比度拉伸等处理,使最终结果的动态范围与原始声呐图像具有一致性。其过程如下
| $ {I_0} = \frac{{R - {\mu _R}}}{{{\sigma _R}}} \times {\sigma _I} + {\mu _I} $ | (19) |
其中
| $ \left\{ {\begin{array}{*{20}{l}} {{\mu _R} = \frac{1}{{MN}}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N R } (i, j)}\\ {{\mu _I} = \frac{1}{{MN}}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N I } (i, j)} \end{array}} \right. $ | (20) |
分别表示背景均衡图R和原始不均衡图I的均值;
| $ \left\{ {\begin{array}{*{20}{l}} {{\sigma _R} = \sqrt {\frac{1}{{MN - 1}}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{{\left[ {R(i, j) - {\mu _R}} \right]}^2}} } } }\\ {{\sigma _I} = \sqrt {\frac{1}{{MN - 1}}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{{\left[ {I(i, j) - {\mu _I}} \right]}^2}} } } } \end{array}} \right. $ | (21) |
分别为背景均衡图和原始不均衡图的标准差。
2 实际数据处理与分析本文给出三组具有不同地貌的典型湖试、海试合成孔径声呐图像数据进行均衡处理。若未特别说明,默认图像左侧为近距端,右侧为远距端。为了全面、客观评价本文算法,既比较了基于噪声背景的对照算法(OTA)[24],同时也比较了图像域其他较常用均衡算法,如中值滤波[17]、函数拟合(AM)[19]等,并给出了选定的图像评价的具体指标数值。
局部方差(SIG2)和峰值信噪比(PSNR)可评价图像算法的去噪质量,但忽略了对图像区域均衡效果及边缘、细节等信息的保持度的有效度量。而图像的异变信息(可用等效视数ENL评价)有效描述了区域的同质性即均衡效果,人眼视觉对图像质量好坏的感知则可从背景结构(可用结构相似性SSIM评价)中获取。因此,本文采用SIG2、PSNR、ENL、SSIM作为图像质量、均衡效果、细节保护的综合评价指标。其表达分别为
| $ \left\{ {\begin{array}{*{20}{l}} {{\rm{SIG}}2 = {\sigma ^2}}\\ {{\rm{PSNR}} = 10\lg \frac{{{L^2}}}{{\frac{1}{{MB}}\sum\limits_{x = 1}^M {\sum\limits_{y = 1}^N {{{\left[ {H\left( {x, y} \right) - K\left( {x, y} \right)} \right]}^2}} } }}}\\ {{\rm{ENL}} = \frac{{{\mu ^2}}}{{{\sigma ^2}}}}\\ {{\mathop{\rm SSIM}\nolimits} (x, y) = \frac{{\left( {2{\mu _x}{\mu _y} + {C_1}} \right)\left( {2{\sigma _x}{\sigma _y} + {C_2}} \right)}}{{\left( {\mu _x^2 + \mu _y^2 + {C_1}} \right)\left( {\sigma _x^2 + \sigma _y^2 + {C_2}} \right)}}} \end{array}} \right. $ | (22) |
式中:σ2表示方差;H表示处理图像,这里指均衡图像;K表示参考图像,这里指已观测图像;L表示像素灰度最大值,本文设定为255。
2.1 实际声呐图像均衡处理对比结果第一组SAS原始图像数据(图 3)为海底管道,成像使用高频合成孔径声呐。图像地貌简单、背景区域较大、目标明显。图像均衡处理结果如图 4所示。基于该组数据,对比四种算法均衡处理的效果(评判指标)。

|
图 3 第一组SAS数据原始图像 |

|
图 4 第一组SAS数据四种算法图像均衡结果 (a)HM;(b)AM;(c)OTA;(d)本文算法 |
第二组SAS图像数据的原始图像(图 5)为电缆图,成像使用高频SAS。该图像仍然具有地貌简单、背景区域较大、目标明显等特征。且存在一定的暗条纹干扰。图像均衡处理结果如图 6所示。将以该组数据说明几种均衡算法对目标的影响和对暗条纹的消除作用。

|
图 5 第二组SAS数据原始图像 |

|
图 6 第二组SAS数据四种算法图像均衡结果 (a)HM;(b)AM;(c)OTA;(d)本文算法 |
这两组数据处理结果主要体现简单背景下各均衡算法的性能,从直观视觉角度说明各均衡算法对图像细节、边缘等的保持作用。
第三组SAS图像数据的原始图像(图 7a)为地貌地形图,是典型的复杂地貌,也采用高频SAS成像。图像均衡处理结果如图 7所示。
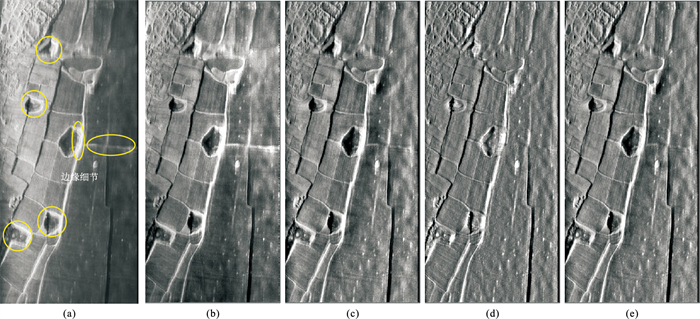
|
图 7 第三组SAS数据原始图像(a)、HM(b)、AM(c)、OTA(d)及本文算法(e)的图像均衡处理结果 |
从上述三组数据的处理结果可知,各算法均具有一定的均衡效果,声能损失造成的灰度差异得到有效补偿,背景变得更连续和平整。但从对图 3、图 4的指标定量分析(图 8)及图 7的直观定性分析等结果来看,相比于本文算法,其他均衡算法均存在一定局限性。

|
图 8 四种算法的局部区域SIG2(a)、ENL(b)、PSNR(c)和SSIM(d)等四项性能指标对比 |
HM算法处理结果(图 7b)虽然背景变得平整,但声能损失造成的低灰度值未得到有效补偿,仍存在较多暗区域。由图 6a可知,HM算法无法消除暗条纹干扰,且有进一步加重的现象。由图 4b和图 6b可知,AM算法存在一定的阴影扩展,破坏了原图结构,容易对后续基于高亮和阴影的分割、识别等处理造成干扰。由图 7d可知,OTA算法对边缘细节破坏严重,但对于简单背景图像(图 4c和图 6c),具有良好的均衡效果。
本文算法则较好地规避了上述算法存在的一些缺点,在实现图像亮度均衡的同时,有效地保护了原图边缘、细节等,也较好地消除了暗条纹干扰,图像质量和对比度有着明显提升。
2.3 声呐图像均衡性能评价指标比较分析为了更合理评估算法性能,对前两组数据进行了局部区域背景均衡性能评估(局部区域如蓝色矩形窗所示,分别记为R1~R4)。选取的区域应尽可能属于背景区,且满足:①局部区域选取不宜过大,以满足局部背景平整连续的假设;②局部区域尽可能不存在高亮、阴影、横纹干扰等,减小对均衡性能参数的影响。
图 8a给出SIG2的比较结果,经均衡处理后的局部背景区域,本文方法对应的SIG2值最小,说明背景更平整,更有利于突出高亮、阴影等特征。
图 8b显示ENL(等效视数/同质性)的比较结果,可看出评价区域中本文方法对应的ENL值最大,说明区域同质性更好,均衡效果更优。
图 8c的PSNR比较结果表明,本文方法具有比其他方法更高的峰值信噪比,仅区域4数值略小于HM算法,可见本文算法噪声抑制能力更强,均衡后图像质量更高。
从各算法的SSIM比较结果(图 8d)可见,本文方法与原始图像的结构相似性最大,说明了本文算法对图像结构(边缘、细节等)信息的保持度更好。
因此,综合来看,本文算法均衡效果最优,既有效消除了暗条纹干扰,也保护了图像细节与纹理,使得图像显示效果更优。
2.4 均衡算法在声呐图像分割中的应用为了进一步说明图像均衡的意义,分别对均衡前、后图像进行目标分割处理。针对原始图像(图 9a)存在近端亮、远端暗的灰度不均衡现象,进行均衡处理。可见处理结果(图 9b)的整个背景变得更均衡平整,黑色暗条纹干扰被滤除,远端的纹理细节变得清晰明了,整个图像的对比度得到较大提高,整体图像信息也更丰富。

|
图 9 SAS图像均衡前、后对比图及对应的阈值分割和线状目标提取对比 (a)原始图像;(b)均衡图像;(c)原始图像分割结果;(d)均衡图像分割结果 |
分别对图 9a、图 9b进行双阈值分割处理。从处理结果可看出,均衡后的图像分割结果(图 9d)背景分割完整、线状目标清晰明了,阴影与高亮更易识别;而原始图像的分割(图 9c)效果较差,无法有效区分高亮、背景和阴影。
3 结束语根据声呐图像的特点及不均衡问题,本文将图像均衡的问题转化为随时间演化的非线性滤波的累积问题,进而提出一种新的自适应均衡算法。该算法在实现声呐图像均衡的同时, 也能较充分地保护原始图像细节,并有效滤除暗条纹干扰,得到高质量的均衡声呐图像。需要指出的是,由于该算法采用迭代方式进行自适应均衡处理,耗时较长,不利于实时处理,这将在后续研究中进行优化。
针对各类图像的不同特点,通过构造不同的均衡函数或其他功能的滤波函数,以泛化算法的适用性,这也已列入后续深入研究的重要内容。
| [1] |
HAYES M P, GOUGH P T. Synthetic aperture sonar: a review of current status[J]. IEEE Journal of Oceanic Engineering, 2009, 34(3): 207-224. DOI:10.1109/JOE.2009.2020853 |
| [2] |
SHIPPEY G, BOLINDER A, FINNDIN R. Shade correction of side-scan sonar imagery by histogram transformation[C]. Proceedings of OCEANS'94, Brest, France, 1994: Ⅱ/439-Ⅱ/443.
|
| [3] |
CAPUS C G, BANKS A C, COIRAS E, et al. Data correction for visualisation and classification of side-scan SONAR imagery[J]. IET Radar, Sonar & Navigation, 2008, 2(3): 155-169. |
| [4] |
李宝奇, 黄海宁, 刘纪元, 等. 基于改进SSD的合成孔径声呐图像水下多尺度目标轻量化检测模型[J]. 电子与信息学报, 2021, 43(10): 2854-2862. LI Baoqi, HUANG Haining, LIU Jiyuan, et al. Synthetic aperture sonar underwater multi-scale target efficient detection model based on improved single shot detector[J]. Journal of Electronics and Information Technology, 2021, 43(10): 2854-2862. DOI:10.11999/JEIT201042 |
| [5] |
KURMI I, SCHEDL D C, BIMBER O. A statistical view on synthetic aperture imaging for occlusion removal[J]. IEEE Sensors Journal, 2019, 19(20): 9374-9383. DOI:10.1109/JSEN.2019.2922731 |
| [6] |
李宝奇, 黄海宁, 刘纪元, 等. 基于改进CycleGAN的光学图像迁移生成水下小目标合成孔径声呐图像算法研究[J]. 电子学报, 2021, 49(9): 1746-1753. LI Baoqi, HUANG Haining, LIU Jiyuan, et al. Optical image-to-underwater small target synthetic aperture sonar image translation algorithm based on improved CycleGAN[J]. Acta Electronica Sinica, 2021, 49(9): 1746-1753. |
| [7] |
KURMI I, SCHEDL D C, BIMBER O. Fast automa-tic visibility optimization for thermal synthetic aperture visualization[J]. IEEE Geoscience and Remote Sensing Letters, 2021, 18(5): 836-840. DOI:10.1109/LGRS.2020.2987471 |
| [8] |
ZHAO J H, YAN J, ZHANG H M, et al. A new radiometric correction method for Side-Scan sonar images in consideration of seabed sediment variation[J]. Remote Sensing, 2017, 9(6): 575. DOI:10.3390/rs9060575 |
| [9] |
FOLKESSON J, CHANG H S, BORE N. Lambert's cosine law and sidescan sonar modeling[C]. 2020 IEEE/OES Autonomous Underwater Vehicles Symposium (AUV), St. Johns, NL, Canada, 2020, 1-6.
|
| [10] |
刘维, 江泽林, 刘纪元, 等. 基于时变曲线模型的合成孔径声纳图像自动均衡方法研究[J]. 兵工学报, 2014, 35(3): 347-354. LIU Wei, JIANG Zelin, LIU Jiyuan, et al. A time-variant curve model-based automatic equalization method for synthetic aperture sonar images[J]. Acta Armamentarii, 2014, 35(3): 347-354. DOI:10.3969/j.issn.1000-1093.2014.03.009 |
| [11] |
滕惠忠, 严晓明, 李胜全, 等. 侧扫声纳图像增强技术[J]. 海洋测绘, 2004, 24(2): 47-49, 70. TENG Huizhong, YAN Xiaoming, LI Shengquan, et al. Processing techniques of enhancement for side scan sonar images[J]. Hydrographic Surveying and Charting, 2004, 24(2): 47-49, 70. |
| [12] |
严哲, 顾汉明, 蔡成国. 基于各向异性扩散滤波的地震图像增强处理[J]. 石油地球物理勘探, 2013, 48(3): 390-394. YAN Zhe, GU Hanming, CAI Chengguo. Seismic image enhancement based on anisotropic diffusion[J]. Oil Geophysical Prospecting, 2013, 48(3): 390-394. DOI:10.13810/j.cnki.issn.1000-7210.2013.03.009 |
| [13] |
夏平, 张光一, 雷帮军, 等. 复Contourlet域有向图与高斯混合模型的声纳图像增强[J]. 声学学报, 2021, 46(4): 529-539. XIA Ping, ZHANG Guangyi, LEI Bangjun, et al. Sonar image enhancement of digraph and Gaussian mixture model in complex contourlet domain[J]. Acta Acustica, 2021, 46(4): 529-539. |
| [14] |
武鹤龙, 邱政, 张维全. 侧扫声纳图像非下采样轮廓波变换域分区增强方法[J]. 兵工学报, 2021, 42(7): 1463-1470. WU Helong, QIU Zheng, ZHANG Weiquan. Partition enhancement method for NSCT domain of side-scan sonar image[J]. Acta Armamentarii, 2021, 42(7): 1463-1470. |
| [15] |
ZHANG T D, WAN L, XU Y R, et al. Sonar image enhancement based on particle swarm optimization[C]. 2008 3rd IEEE Conference on Industrial Electroni-cs and Applications, Singapore, 2008, 2216-2221.
|
| [16] |
史志晨, 曾庆军, 朱志宇, 等. 基于模糊增强算法的声呐图像目标增强研究[J]. 舰船科学技术, 2020, 42(15): 167-171. SHI Zhichen, ZENG Qingjun, ZHU Zhiyu, et al. Research on target enhancement of sonar image based on fuzzy enhancement[J]. Ship Science and Technology, 2020, 42(15): 167-171. |
| [17] |
CERVENKA P, DE MOUSTIER C D. Sidescan sonar image processing techniques[J]. IEEE Journal of Oceanic Engineering, 1993, 18(2): 108-122. |
| [18] |
CELEBI A T, GULLU M K, ERTURK S. Mine detection in side scan sonar images using Markov Random Fields with brightness compensation[C]. IEEE 19th Signal Processing and Communications Applications Conference (SIU), Antalya, Turkey, 2011, 916-919.
|
| [19] |
GALDRAN A, ISASI A, AL-RAWI M, et al. An efficient non-uniformity correction technique for side-scan sonar imagery[C]. OCEANS 2017-Aberdeen, Aberdeen, UK, 2017, 1-6.
|
| [20] |
AL-RAWI M S, GALDRAN A, YUAN X, et al. Intensity normalization of sidescan sonar imagery[C]. 2016 Sixth International Conference on Image Processing Theory, Tools and Applications (IPTA), Oulu, Finland, 2016, 1-6.
|
| [21] |
COBRA D T, OPPENHEIM A V, JAFFE J S. Geometric distortions in side-scan sonar images: a procedure for their estimation and correction[J]. IEEE Journal of Oceanic Engineering, 1992, 17(3): 252-268. |
| [22] |
SHEFFER T, GUTERMAN H. Geometrical correction of side-scan sonar images[C]. 2018 IEEE International Conference on the Science of Electrical Engineering in Israel (ICSEE), Eilat, Israel, 2018, 1-5.
|
| [23] |
YE X F, YANG H B, LI C L, et al. A gray scale correction method for side-scan sonar images based on retinex[J]. Remote Sensing, 2019, 11(11): 1281-1300. |
| [24] |
STRUZINSKI W A, LOWE E D. A performance comparison of four noise background normalization schemes proposed for signal detection systems[J]. Journal of the Acoustical Society of America, 1984, 76(6): 1738-1742. |
| [25] |
SUOJOKI T, TABUS I. A novel efficient normalization technique for sonar detection[C]. Proceedings of the 2002 International Symposium on Underwater Technology, Tokyo, Japan, 2002, 296-301.
|
| [26] |
张济博, 潘国富, 丁维凤. 侧扫声纳图像改正研究[C]. 2009年中国东西部声学学术交流会论文集, 陕西宝鸡, 2009, 48-51. ZHANG Jibo, PAN Guofu, DING Weifeng. Research on image correction of side scan sonar[C]. Procee-dings of the 2009 East West Acoustic Symposium, Baoji, Shaanxi, 2009, 48-51. |
| [27] |
SUN Q L, TANG J S. A new contrast measure based image enhancement algorithm in the DCT domain[C]. Proceedings of the IEEE International Confe-rence on Systems, Man & Cybernetics, Washington D C, USA, 2003, 2055-2058.
|
| [28] |
蔚立磊, 韩紫恒, 张剑. 小波变换域数字图像增强算法及实现[J]. 信息技术, 2009, 33(9): 132-135, 152. WEI Lilei, HAN Ziheng, ZHANG Jian. Algorithm of digital image enhancement based on wavelet transform domain and its realization[J]. Information Technology, 2009, 33(9): 132-135, 152. |
| [29] |
CANDÈS E J, DONOHO D L. Curvelets and curvili-near integrals[J]. Journal of Approximation Theory, 2001, 113(1): 59-90. |
| [30] |
杜竹峰, 黄铁侠, 卢益民, 等. 水下目标信号特性及其有效衰减系数分析[J]. 电子学报, 2003, 31(12): 1815-1819. DU Zhufeng, HUANG Tiexia, LU Yimin, et al. Analy-sis of underwater target signal characteristics and its effective attenuation coefficient[J]. Acta Electronica Sinica, 2003, 31(12): 1815-1819. |



 刘纪元, 北京市海淀区北四环西路19~21号中科院声学研究所, 100190。Email:
刘纪元, 北京市海淀区北四环西路19~21号中科院声学研究所, 100190。Email: 