② 油气藏地质及开发工程国家重点实验室(西南石油大学),四川成都 610500;
③ 电子科技大学信息与通信工程学院,四川成都 611731
② State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation (Southwest Petroleum University), Chengdu, Sichuan 610500, China;
③ School of Information and Communication Engineering, University of Electronic Science and Technology of China, Chengdu, Sichuan 611731, China
1917年,奥地利数学家Radon[1]首次提出Radon变换,经过众多学者的研究,将其引入各领域,并得到了广泛的使用。20世纪70年代,Claerbout等[2]首次将Radon变换引入地震数据处理,为Radon变换在地震勘探中的发展奠定了基础。
Radon变换将地震数据沿特定路径进行曲线积分,目的是将数据中的信号叠加为Radon域的稀疏信号,便于识别与分离。为了提高Radon变换压制多次波的精度,不少学者进行了相关的研究。Thorson等[3]提出了Radon变换最小二乘法和随机反演的理论,将Radon变换建模为一个稀疏逆问题,使Radon变换的分辨率得到一定程度的提高。李元钦等[4]结合平面映射,提出双曲Radon正、反变换,减少变换噪音和能量弥散,提高了地震资料的处理质量。Sacchi等[5-6]在频率域利用柯西稀疏约束提高了Radon变换的分辨率。牛滨华等[7]提出次数为“2”的多项式Radon变换。刘喜武等[8]采用最小二乘反演法实现高分辨率抛物线Radon变换和双曲线Radon变换,提高了精度和分辨率。Ethan等[9]提出加权最小二乘Radon变换,在压制多次波过程中能较好地保持振幅。刘保童等[10]提出一种频率域Radon变换方法,有效地提高了地震数据在Radon域的分辨率。Schonewille等[11]证明了Radon变换在时间域比在频率域更加稀疏,故Radon变换在时间域的分辨率比在频率域高,提高解复用效率。薛亚茹等[12]提出基于Radon变换和正交多项式变换的多方向正交多项式变换的方法,提高了对一次波与多次波的剩余时差的分辨率,在有效压制多次波的同时保留了一次波的AVO特性,增强了Radon变换的保幅特性。Lu[13]提出基于迭代二维模型收缩的混合时频域快速稀疏时不变Radon变换方法,利用混合时频域的优势,该算法既在时间域中提高了Radon模型的稀疏性,又在频率域得到更高的计算效率。薛亚茹等[14]提出高分辨率稀疏Radon变换和正交多项式变换结合的高阶稀疏Radon变换,能有效分离一次波和多次波。Sun等[15]提出基于光滑的L0范数的高阶、高分辨率频率-曲率域Radon变换,将正交多项式与Radon变换相结合,该算法具有更好的聚焦特性,并在压制多次波的同时能更好地保存一次波的AVO特性,且有更高的计算效率。薛亚茹等[16]提出应用加权迭代软阈值算法的高分辨率Radon变换,将迭代重加权最小二乘法的加权矩阵思想引入迭代软阈值算法中,提高了Radon变换分辨率。孙宁娜等[17]提出基于多窗口联合优化的多次波自适应相减方法,与传统的基于单窗口匹配的多次波自适应相减方法相比,该方法可更有效地压制残余多次波并保护一次波,且计算效率与基于小窗口匹配的传统多次波自适应相减方法相当。马继涛等[18]提出三维高精度保幅Radon变换多次波压制方法,该方法可获得高分辨率的模型域数据,能有效分离一次波与多次波,同时多项式拟合可保护有效波的振幅,高保真地实现多次波的压制。在Radon变换压制多次波的速度提升方面,很多学者也进行了相关的研究。Hampson[19]提出抛物线Radon变换压制多次波,进一步提升了计算效率。熊登等[20]提出一种新的混合域高分辨率抛物线Radon变换,对于多次波的压制既有很高的计算效率又有较高的分辨率。Brahim等[21]提出一种基于奇异值分解的改进的抛物线Radon变换,克服了频域Radon变换实现所需的繁重计算,具有更快的计算速度。张全等[22]提出CPU-GPU异构平台的抛物线Radon变换并行算法,大幅提高了Radon变换压制多次波的计算效率。随着深度学习的发展,不少学者将多次波压制与深度学习相结合。刘小舟等[23]提出数据增广的编解码卷积网络地震层间多次波压制方法,结合去噪卷积神经网络(DnCNN)和U形全卷积神经网络(U-Net)的优势,搭建了适合层间多次波压制的深层编、解码网络,并且利用数据增广提高网络的泛化能力,该网络能够很好地压制层间多次波、保护一次波,提高了多次波的压制效率。
本文在Lu[13]的研究基础上,将Liang等[24]提出的贪婪—快速迭代收缩阈值算法(Greedy Fast Ite-rative Shrinkage Thresholding Algorithm,Greedy FISTA)应用于混合域抛物线Radon变换,构建了一种快速稀疏时不变Radon变换进行地震多次波压制。实验结果表明,本文方法有效地提高了Radon变换压制多次波的精度和效率。
1 Radon变换多次波压制基本原理在地震数据处理中,常采用抛物线Radon变换实现一次波与多次波分离。动校正后,道集中的一次波被拉平,多次波呈“抛物线”形态,根据二者在Radon域的形态差异实现多次波压制。时域与Radon域地震数据可用数学模型表示为
| $ \boldsymbol{d}=\boldsymbol{L} \boldsymbol{m} $ | (1) |
式中:d为时空域地震数据;m为地震数据在Radon域的表示;L为Radon变换算子矩阵。通常情况下,d为已知数据,m为未知数据,L通常不可逆,常用共轭转置矩阵LH近似L的逆矩阵,故式(1)在数学上为一逆问题。求解逆问题的经典方法为最小二乘(LS)法
| $ \underset{m}{\arg \min }\|\boldsymbol{d}-\boldsymbol{L m}\|_2^2 $ | (2) |
L通常是病态的,且LS法不适用于求解病态方程,常添加正则化项解决此问题。基于L1范数的稀疏正则化是目前常用的提高Radon变换分辨率的方法
| $ \underset{\boldsymbol{m}}{\arg \min }\left(\lambda\|\boldsymbol{m}\|_1+\|\boldsymbol{d}-\boldsymbol{L} \boldsymbol{m}\|_2^2\right) $ | (3) |
式中λ>0为正则化系数。在时域和频域构成的混合域(简称混合域)实现Radon变换
| $ \boldsymbol{d}=\boldsymbol{F}^{-1}[\boldsymbol{L} \boldsymbol{F}(\boldsymbol{m})] $ | (4) |
式中:F(·)为傅里叶变换算子;F-1(·)为傅里叶逆变换算子。频率域的Radon变换算子为[26]
| $ L_{i j}=\exp \left(-\mathrm{j} 2 \pi f q_i x_j^2\right) $ | (5) |
式中:i=0,1,…,Nq,其中Nq为曲率q的个数;j=0,1,…,Nx,其中Nx为地震数据道数;f为频率;xj为第j道的炮检距。
Radon变换压制多次波在混合域的目标方程为
| $ \underset{\boldsymbol{m}}{\arg \min }\left\{\lambda\|\boldsymbol{m}\|_1+\left\|\boldsymbol{d}-\boldsymbol{F}^{-1}[\boldsymbol{L F}(\boldsymbol{m})]\right\|_2^2\right\} $ | (6) |
该目标方程的求解是影响多次波压制效率的重要因素。
2 Radon变换算法及其改进对式(6)的求解,传统的迭代重加权最小二乘(Iterative Reweighted Least Squares,IRLS)算法涉及大规模的求逆运算,耗时长。而基于梯度的迭代算法,计算复杂度小,且算法结构简单。本文主要将当前应用较广的迭代收缩阈值算法(Iterative Shrinkage-Thresholding Algorithm,ISTA)、快速迭代收缩阈值算法(Fast Iterative Shrinkage-Thresho-lding Algorithm,FISTA)以及Greety FISTA与抛物线Radon变换结合对多次波进行压制。
2.1 基于迭代收缩阈值的Radon变换算法ISTA是经典梯度算法的扩展,计算简单,是目前最常用的方法之一。Lu[13]将二维ISTA引入Radon变换,提出了基于迭代二维模型收缩的混合域快速稀疏时不变Radon变换(an accelerated sparse time-invariant Radon transform in the mixed frequency-time domain based on iterative 2D model shrinkage,SRTIS)。SRTIS算法流程如下。
(1) 输入时空域地震数据d,最大迭代次数K;
(2) 初始化模型m0,当前迭代次数k=0,迭代步长t>0;
(3) 若k≤K,迭代更新
| $ \begin{aligned} \boldsymbol{m}_{k+1}= & T_\alpha\left\{\boldsymbol{m}_k+2 t \boldsymbol{F}^{-1}\left\{\left(\boldsymbol{L}^{\mathrm{H}} \boldsymbol{L}\right)^{-1} \times\right.\right. \\ & \left.\left.\boldsymbol{L}^{\mathrm{H}}\left[\boldsymbol{F}(\boldsymbol{d})-\boldsymbol{L} \boldsymbol{F}\left(\boldsymbol{m}_k\right)\right]\right\}\right\} \\ & k+1 \rightarrow k \end{aligned} $ |
(4) 输出Radon域地震数据mk。
算法中,一般要求迭代步长
| $ T_\alpha\{\boldsymbol{m}, k\}_{i j}=\left(\left|m_{i j}\right|-\alpha \frac{K-k}{K} \widetilde{\boldsymbol{m}}_{i j}\right)_{+}+\operatorname{sgn}\left(m_{i j}\right) $ | (7) |
式中:
| $ (y)_{+}= \begin{cases}y & y \geqslant 0 \\ 0 & y<0\end{cases} $ | (8) |
相较于一些传统方法,SRTIS提高了Radon模型的稀疏性,从而提高了多次波的压制精度,同时还有更快的收敛速度。
2.2 基于快速迭代收缩阈值的Radon变换算法ISTA每次迭代只需考虑当前点的信息更新迭代起点,导致算法迭代速度较慢。FISTA在ISTA的基础上考虑当前点和前一点更新迭代起点,比ISTA具有更快的收敛速度。Li等[26]将该算法引入到Radon变换,提出了基于快速迭代收缩的混合域快速稀疏时不变Radon变换(an accelerated sparse time-invariant Radon transform in the mixed frequency-time domain based on fast iterative shrinkage-thresholding algorithm,SRTFIS)。SRTFIS算法流程如下。
(1) 输入时空域地震数据d,最大迭代次数K;
(2) 初始化模型m0,当前迭代次数k=0,迭代步长t>0,p0=1, y=m0;
(3) 若k≤K,迭代更新
| $ \begin{aligned} & p_k=\frac{1+\sqrt{1+4 p_{k-1}^2}}{2} \\ & a_k=\frac{p_{k-1}-1}{p_k} \\ & \boldsymbol{y}_k=\boldsymbol{m}_k+a_k\left(\boldsymbol{m}_k-\boldsymbol{m}_{k-1}\right) \\ & \boldsymbol{m}_{k+1}=T_\alpha\left\{\boldsymbol{y}_k+2 t \boldsymbol{F}^{-1}\left\{\left(\boldsymbol{L}^{\mathrm{H}} \boldsymbol{L}\right)^{-1} \times\right.\right. \\ & \left.\left.\boldsymbol{L}^{\mathrm{H}}\left[\boldsymbol{F}(\boldsymbol{d})-\boldsymbol{L} \boldsymbol{F}\left(\boldsymbol{y}_k\right)\right]\right\}\right\} \\ & k+1 \rightarrow k \end{aligned} $ |
(4) 输出Radon域地震数据mk。
算法中一般要求t=1/λmax(LHL)。
与SRTIS相比,SRTFIS使用yk代替mk,即在迭代步骤中,SRTFIS算法的迭代点mk不仅仅依赖于前一个迭代点mk-1,还在yk上使用了前两点{mk-1, mk-2}的线性组合,提高了收敛速度。惯性参数ak用于控制mk-mk-1的增长速度。
2.3 基于贪婪—快速迭代收缩阈值的Radon变换算法ISTA计算简单,但在收敛速度上较慢;FISTA的收敛速度虽然快于ISTA,但对于FISTA,当ak→1时,会引起振荡现象,对收敛速度造成一定的减缓。海量地震数据的处理,对算法的处理效率提出了更高的要求。Liang等[24]提出的Greedy FISTA在保持算法计算简单的同时,全局收敛速度比ISTA、FISTA更快,有更好的收敛性能,本文将该算法应用于稀疏Radon变换算法中,提出一种基于贪婪的快速迭代收缩的混合域快速稀疏时不变Radon变换(an accelerated sparse time-invariant Radon transform in the mixed frequency-time domain based on greedy fast iterative shrinkage-thresholding algorithm,SRTGFIS)。SRTGFIS算法流程如下。
(1) 输入时空域地震数据d,最大迭代次数K。
(2) 初始化模型m0,当前迭代次数k=0,迭代步长t>0, y1=m0, 步长t的收缩因子ξ<1, 算法收敛的控制因子S>1。
(3) 若k≤K,迭代更新
| $ \begin{aligned} & \boldsymbol{y}_k=\left(\boldsymbol{m}_k-\boldsymbol{m}_{k-1}\right) \\ & \boldsymbol{m}_{k+1}= T_\alpha\left\{\boldsymbol{y}_k+2 t \boldsymbol{F}^{-1}\left\{\left(\boldsymbol{L}^{\mathrm{H}} \boldsymbol{L}\right)^{-1} \times\right.\right. \\ &\left.\left.\boldsymbol{L}^{\mathrm{H}}\left[\boldsymbol{F}(\boldsymbol{d})-\boldsymbol{L} \boldsymbol{F}\left(\boldsymbol{y}_k\right)\right]\right\}\right\} \\ & k+1 \rightarrow k \end{aligned} $ |
重启条件:若(yk-mk+1)T(mk+1-mk)≥0,则
| $ \boldsymbol{y}_k=\boldsymbol{m}_k; $ |
收敛条件:若‖mk+1-mk‖≥S‖m1-m0‖,则
| $ \begin{aligned} & t=\max \{\xi t, t\} \\ & k+1 \rightarrow k \end{aligned} $ |
(4) 输出Radon域地震数据mk。
该算法中,一般要求t∈1/λmax(LHL), 2/λmax(LHL)。
为了解决FISTA中ak→1引起的振荡问题,Greedy FISTA对此引入了重启动方法,将pk重置为1,迫使ak从0开始增加,当ak→1引起下一次振荡时,进行重启,如此循环。为了缩短重启动的间隔,减小振荡周期,以此提高收敛速率,将ak取为常数1,但由于ak控制迭代步长t的大小,ak为常数将导致初始迭代步长过大,容易造成算法发散,因此Greedy FISTA算法还有一个保证收敛的条件。
整个重启动框架在保证收敛的情况下,缩短了重启间隔和振荡周期,相较于ISTA、FISTA算法,该算法提高了收敛速度。
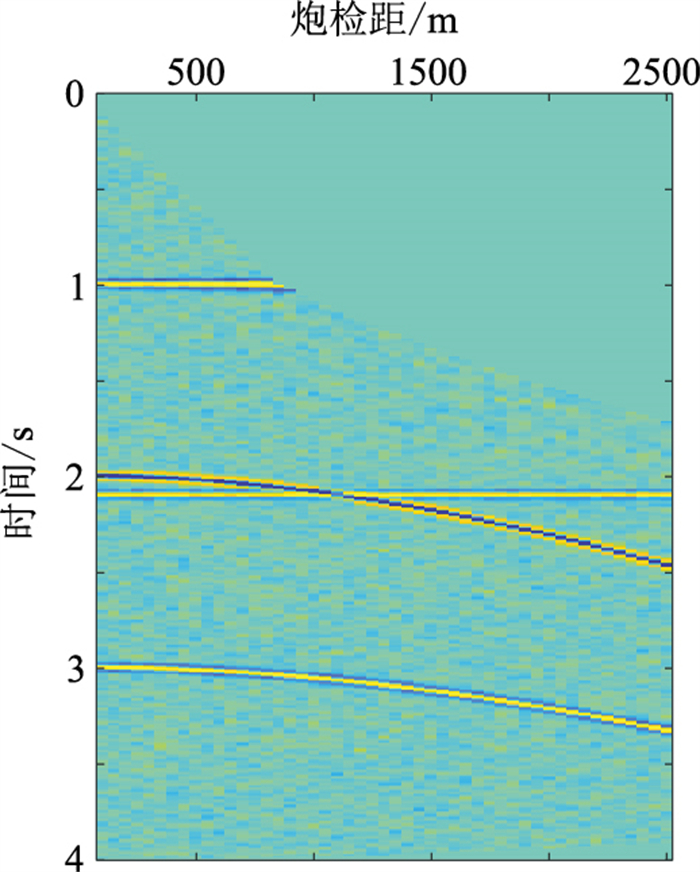
3 实验数据 3.1 模拟数据本文实验的模拟数据来自SeismicLab工具包合成的多次波模拟数据(图 1)。该模拟数据只有一个地震道集,共49道,每道有1001个样点,采样间隔为4ms。分别将频率域最小二乘法Radon变换(LSRT)、SRTIS、SRTFIS、SRTGFIS四种算法用于模拟数据进行比较(图 2)。
|
图 1 合成的多次波全波场模拟数据 |
|
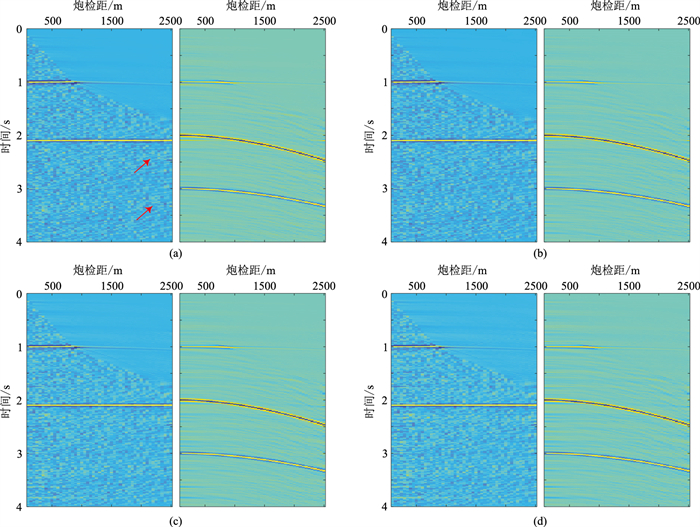
图 2 不同算法对模拟数据的多次波压制效果对比 (a)LSRT;(b)SRTIS;(c)SRTFIS;(d)SRTGFIS。左为多次波压制后的结果;右为压制的多次波 |
对于地震多次波压制的工程问题,不仅要考虑压制效果还要考虑计算速度,当多次波残留不可见时,即可停止迭代(此时算法可能并未完全收敛),工程上需要在精度和速度之间做出折中。数学上,SRTIS、SRTFIS和SRTGFIS三种算法推荐步长为
比较四种算法对模拟数据多次波的压制效果(图 2),其中SRTIS、SRTFIS和SRTGFIS算法的K均为20。由图可见,LSRT的压制效果一般,处理之后还有多次波的残余(图 2a红色箭头所指),而SRTIS(图 2b)、SRTFIS(图 2c)和SRTGFIS(图 2d)均能完全压制多次波。
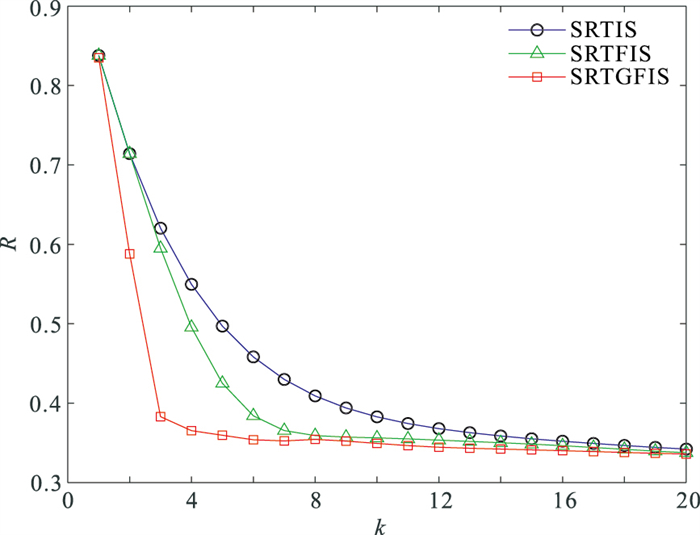
将SRTIS、SRTFIS和SRTGFIS算法Radon模型相关参数初始化为:m0=0,t=0.10,K=20,对比三种算法的收敛速度(图 3)。在迭代过程中,利用第k次迭代得到的数据dk模拟真实的地震数据d。为测量估计值与真实值的近似程度,使用归一化误差能量(Normalized Error Energy,NEE)
|
图 3 三种算法的收敛速度比较 |
在多次波压制精度相当的情况下,比较三种算法不同迭代次数的多次波压制结果(图 4),对比三种算法对模拟数据的计算速度(表 1)。图 4a为SRTIS在不同迭代次数下压制多次波的结果,当迭代到第7次时,多次波残余明显(红色箭头所示,下同),迭代到第16次时,多次波基本被压制,但依然有残余;图 4b为SRTFIS在不同迭代次数下压制多次波的结果,迭代到第7次时,多次波有少量残余,迭代到第8次,多次波基本被压制;图 4c为SRTGFIS在不同迭代次数下压制多次波的结果,迭代到第6次时,压制效果好于SRTFIS,迭代到第7次时,多次波已基本被压制。

|
图 4 不同算法不同迭代次数多次波压制结果对比 (a)SRTIS; (b)SRTFIS; (c)SRTGFIS |
|
|
表 1 模拟数据三种算法达到相同压制精度所需迭代次数和时间对比 |
同时,在相同的计算环境和实验数据下,对程序运行时间进行了测试。当达到相同的压制精度时,SRTIS、SRTFIS和SRTGFIS三种算法耗时(由各算法分别运行10次求得的平均值)见表 1,可见,SRTGFIS较其他两种算法计算效率更高。
3.2 实际数据实际数据来自SeismicLab工具包,只有1个地震道集,包含92道,每道401个样点,采样间隔为4ms。
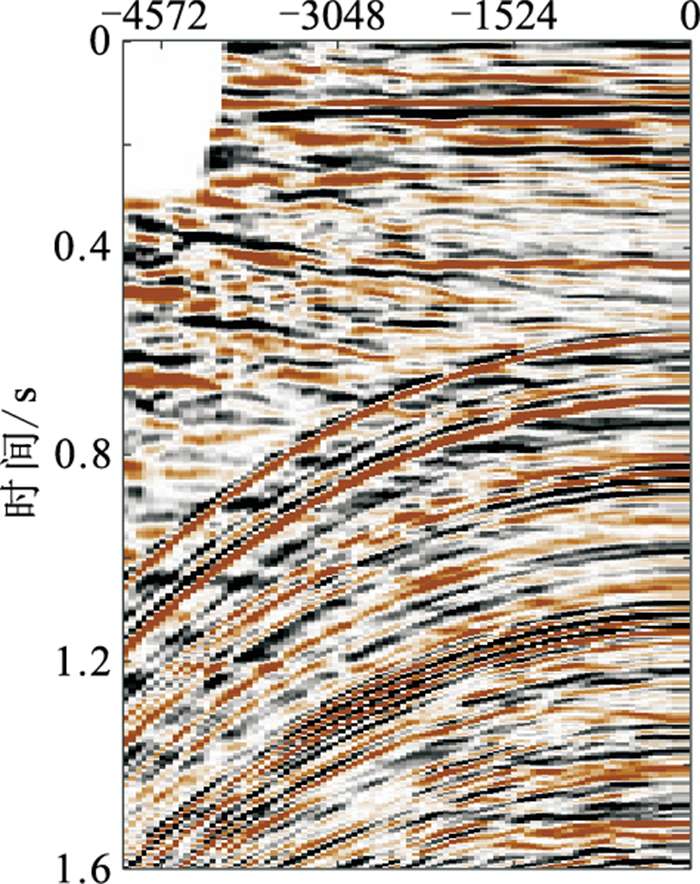
图 5为实际包含多次波与一次波的全波场数据。对于SRTIS、SRTFIS和SRTGFIS算法,当t=1/λmax(LHL)时,步长太小,多次波的压制效率均太低。考虑模拟数据的测试情况,对于实际数据,将步长设置为0.10时,SRTIS、SRTFIS和SRTGFIS三种算法分别需要迭代20、14、10次才能达到较好的多次波压制效果,故初始化Radon模型相关参数为:m0=0,t=0.10,K=20。LSRT、SRTIS、SRTFIS、SRTGFIS四种算法多次波的压制结果如图 6所示。LSRT算法的压制结果中还有残留的多次波(图 6a红色箭头所指);SRTIS(图 6b)、SRTFIS(图 6c)和SRTGFIS(图 4d)算法的多次波压制效果均优于LSRT算法。
|
图 5 实际数据 |

|
图 6 四种方法对实际数据的多次波压制结果对比 (a)LSRT;(b)SRTIS;(c)SRTFIS;(d)SRTGFIS。左为多次波压制后的结果;右为压制的多次波 |
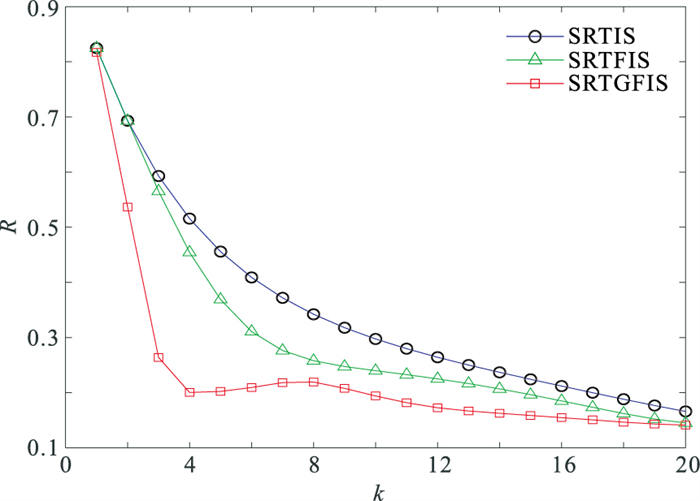
实际数据三种算法的收敛曲线(图 7)显示,SRTIS的收敛速度最慢,SRTGFIS算法的收敛速度最快,由于ak=1导致初始迭代步长过大,引起收敛曲线的波动。
|
图 7 三种算法的收敛速度比较 |
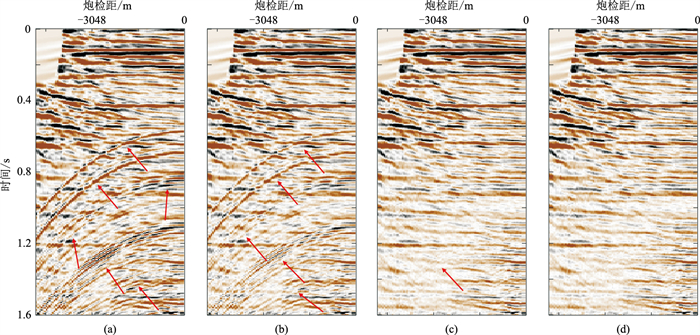
在多次波压制精度相当的情况下,分别比较三种算法不同迭代次数下的多次波压制效果(图 8~图 10)。SRTIS算法在迭代到第18次时,多次波有少量残余(图 8中红色箭头所指,下同),迭代到第20次时,多次波得到基本压制;SRTFIS算法在迭代到第12次时,多次波有少量残余,迭代到第14次时,多次波基本压制(图 9);SRTGFIS算法在迭代到第8次时,多次波有少量残余,迭代到第10次时,多次波得到很好压制(图 10)。
|
图 8 SRTIS法不同迭代次数下的多次波压制结果对比 (a)4次迭代;(b)6次迭代;(c)18次迭代;(d)20次迭代 |

|
图 9 SRTFIS法不同迭代次数下的多次波压制结果对比 (a)4次迭代;(b)6次迭代;(c)12次迭代;(d)14次迭代 |
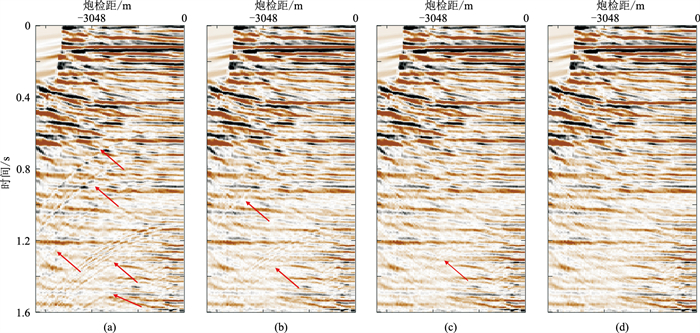
|
图 10 SRTGFIS法不同迭代次数下的多次波压制结果对比 (a)4次迭代;(b)6次迭代;(c)8次迭代;(d)10次迭代 |
在相同的计算环境和实验数据下,对程序运行所需时间进行了测试。当达到相同的压制精度时,SRTIS、SRTFIS及SRTGFIS算法耗时如表 2所示(各算法分别运行10次求得的平均值),SRTGFIS算法优于前两种,计算效率更高。
|
|
表 2 实际数据三种算法达到相同压制精度所需迭代次数和时间对比 |
本文将Greedy FISTA算法引入到Radon变换压制多次波的逆问题求解中,构建了SRTGFIS算法。模拟数据和实际数据的处理结果均表明:该算法对多次波的压制效果优于LSRT算法;与SRTIS和SRTFIS算法相比,当压制精度相同时,效率更高。
随着深度学习方法的不断发展,在其他学科领域均已展现出了巨大的优势,将其引入到多次波压制,避免传统多次波压制算法中逆问题求解的时间消耗,是下一步提高多次波压制效率的研究方向。
| [1] |
RADON J. On the determination of functions from their integrals along certain manifolds[J]. Mathematische Physikalische, 1917, 69: 262-267. |
| [2] |
CLAERBOUT J F, JOHNSON A G. Extrapolation of time-dependent waveforms along their path of propagation[J]. Geophysical Journal International, 1971, 26(1-4): 285-293. |
| [3] |
THORSON J R, CLAERBOUT J F. Velocity-stack and slant-stack stochastic inversion[J]. Geophysics, 1985, 50(12): 2727-2741. DOI:10.1190/1.1441893 |
| [4] |
李远钦, 杜友福. 双曲Radon变换及其在地震资料处理中的应用[J]. 江汉石油学院学报, 1990, 12(2): 16-20. LI Yuanqin, DU Youfu. Hyperbola Radon transform and its application in seismic data processing[J]. Journal of Jianghan Petroleum Institute, 1990, 12(2): 16-20. |
| [5] |
SACCHI M D, ULRYCH T J. High-resolution velo-city gathers and offset space reconstruction[J]. Geophysics, 1995, 60(4): 1169-1177. DOI:10.1190/1.1443845 |
| [6] |
SACCHI M D, PORSANI M. Fast high resolution parabolic Radon transform[C]. SEG Technical Program Expanded Abstracts, 1999, 18: 1477-1480.
|
| [7] |
牛滨华, 孙春岩, 张中杰, 等. 多项式Radon变换[J]. 地球物理学报, 2001, 44(2): 263-271. NIU Binhua, SUN Chunyan, ZHANG Zhongjie, et al. Polynomial Radon transform[J]. Chinese Journal of Geophysics, 2001, 44(2): 263-271. |
| [8] |
刘喜武, 刘洪, 李幼铭. 高分辨率Radon变换方法及其在地震信号处理中的应用[J]. 地球物理学进展, 2004, 19(1): 8-15. LIU Xiwu, LIU Hong, LI Youming. High resolution Radon transform and its application in seismic signal processing[J]. Progress in Geophysics, 2004, 19(1): 8-15. |
| [9] |
ETHAN J N, MATTHIAS G I. Amplitude preservation of Radon-based multiple-removal filter[J]. Geophysics, 2006, 71(5): 123-12. DOI:10.1190/1.2243711 |
| [10] |
刘保童, 朱光明. 一种频率域提高Radon变换分辨率的方法[J]. 西安科技大学学报, 2006, 26(1): 112-116, 129. LIU Baotong, ZHU Guangming. An approach to improve the resolution of Radon transform in frequency domain[J]. Journal of Xi'an University of Science and Technology, 2006, 26(1): 112-116, 129. |
| [11] |
SCHONEWILLE M, AARON P A. Applications of time-domain high-resolution Radon demultiple[J]. SEG Technical Program Expanded Abstracts, 2007, 26: 2565-2569. |
| [12] |
薛亚茹, 陈小宏, 马继涛. 多方向正交多项式变换压制多次波[J]. 地球物理学报, 2012, 55(10): 3450-3458. XUE Yaru, CHEN Xiaohong, MA Jitao. Multiples attenuation based on directional orthogonal polyno-mial transform[J]. Chinese Journal of Geophysics, 2012, 55(10): 3450-3458. |
| [13] |
LU Wenkai. An accelerated sparse time-invariant Radon transform in the mixed frequency-time domain based on iterative 2D model shrinkage[J]. Geophy-sics, 2013, 78(4): V147-V155. |
| [14] |
薛亚茹, 杨静, 钱步仁. 基于高阶稀疏Radon变换的预测多次波自适应相减方法[J]. 中国石油大学学报(自然科学版), 2015, 39(1): 43-49. XUE Yaru, YANG Jing, QIAN Buren. Multiples prediction and adaptive subtraction with high-order sparse Radon transform[J]. Journal of China University of Petroleum (Edition of Natural Sciences), 2015, 39(1): 43-49. |
| [15] |
SUN Wenzhi, LI Zhenchun, QU Yingming, et al. Multiple attenuation using λ-f domain high-order and high-resolution Radon transform based on SL0 norm[J]. Applied Geophysics, 2019, 16(4): 473-482. |
| [16] |
薛亚茹, 郭蒙军, 冯璐瑜, 等. 应用加权迭代软阈值算法的高分辨率Radon变换[J]. 石油地球物理勘探, 2021, 56(4): 736-744, 757. XUE Yaru, GUO Mengjun, FENG Luyu, et al. High resolution Radon transform based on the reweighted-iterative soft threshold algorithm[J]. Oil Geophysical Prospecting, 2021, 56(4): 736-744, 757. |
| [17] |
孙宁娜, 曾同生, 戴晓峰, 等. 基于多窗口联合优化的多次波自适应相减方法[J]. 石油物探, 2022, 61(3): 463-472. SUN Ningna, ZENG Tongsheng, DAI Xiaofeng, et al. Adaptive multiple subtraction based on multi-windows joint optimization[J]. Geophysical Prospecting for Petroleum, 2022, 61(3): 463-472. |
| [18] |
马继涛, 刘仕友, 廖震. 三维高精度保幅Radon变换多次波压制方法[J]. 石油地球物理勘探, 2022, 57(3): 582-592. MA Jitao, LIU Shiyou, LIAO Zhen. Research on multiple attenuation using 3D high-precision amplitude-preserving Radon transform[J]. Oil Geophysical Prospecting, 2022, 57(3): 582-592. |
| [19] |
HAMPSON D. Inverse velocity stacking for multiple elimination[C]. SEG Technical Program Expanded Abstracts, 1986, 5: 422-424.
|
| [20] |
熊登, 赵伟, 张剑锋. 混合域高分辨率抛物Radon变换及在衰减多次波中的应用[J]. 地球物理学报, 2009, 52(4): 1068-1077. XIONG Deng, ZHAO Wei, ZHANG Jianfeng. Hybrid-domain high-resolution parabolic Radon transform and its application to demultiple[J]. Chinese Journal of Geophysics, 2009, 52(4): 1068-1077. |
| [21] |
ABBAD B, URSIN B, PORSANI M J. A fast, modified parabolic Radon transform[J]. Geophysics, 2011, 76(1): V11-V24. |
| [22] |
张全, 林柏栎, 杨勃, 等. CPU-GPU异构平台的抛物线Radon变换并行算法[J]. 石油地球物理勘探, 2020, 55(6): 1263-1270. ZHANG Quan, LIN Baili, YANG Bo, et al. Parabolic Radon transform parallel algorithm for CPU-GPU heterogeneous platform[J]. Oil Geophysical Prospecting, 2020, 55(6): 1263-1270. |
| [23] |
刘小舟, 胡天跃, 刘韬, 等. 数据增广的编解码卷积网络地震层间多次波压制方法[J]. 石油地球物理勘探, 2022, 57(4): 757-767. LIU Xiaozhou, HU Tianyue, LIU Tao, et al. Seismic internal multiple suppression method with encoder-decoder convolutional network based on data augmentation[J]. Oil Geophysical Prospecting, 2022, 57(4): 757-767. |
| [24] |
LIANG J, SCHNLIEB C B. Improving FISTA: faster, smarter and greedier[DB/OL]. (2021-01-20). https://arxiv.org/abs/1811.01430v1.
|
| [25] |
曾华会, 王孝, 杨维, 等. 分级组合多次波压制技术——以玛湖地区为例[J]. 石油地球物理勘探, 2018, 53(增刊2): 13-19. ZENG Huahui, WANG Xiao, YANG Wei, et al. Stepped-combination multiples suppression: an exam-ple in Mahu Area[J]. Oil Geophysical Prospecting, 2018, 53(S2): 13-19. |
| [26] |
LI Z X, LI Z C. Accelerated parabolic Radon domain 2D adaptive multiple subtraction with fast iterative shrinkage thresholding algorithm and its application in parabolic Radon domain hybrid demultiple method[J]. Journal of Applied Geophysics, 2017, 143(1): 86-102. |



 彭博, 四川省成都市新都区新都大道8号西南石油大学(成都校区),610500。Email:
彭博, 四川省成都市新都区新都大道8号西南石油大学(成都校区),610500。Email: 