随着勘探精细化程度的深入,现有地震资料分辨率已远不能满足薄储层或小地质体等精细表征的要求[1-3],在地震资料处理及解释领域,时频分析、地震谱分解等处理技术[4-5]可从地震数据中发掘更丰富的地质信息,因此越来越受到人们的关注。目前地震资料处理中较常用的分频技术包括带通滤波、STFT[6]、Morlet小波变换[7-8]、S变换[9-10]等,但受限于窗函数或核函数的性质,常规方法对信号在时频平面的刻画存在窗口效应、时频分辨率低和能量聚焦性差等问题,难以满足精细化地震处理、解释的需求。而Mallat等[11]提出的匹配追踪(Matching Pursuit,MP)算法是一种信号稀疏表示方法,可自适应选择基函数进行信号分解[12-13],具有较高的局部自适应性和时频分辨率,避免了常规时频分析方法的弊端。基于MP算法的分频、高分辨率处理等技术也为储层的精细刻画提供了技术支持。
MP算法自提出以来,由其获得的瞬时谱高聚焦性相对于小波变换、S变换等得到进一步提高,具有更强的瞬时谱聚焦性和更高的时频分辨率,可更充分地挖掘信号的局部化信息,因此在储层预测和油气检测等方面得到了广泛应用。Zhang等[14]采用两步法MP算法,提取吸收系数等频变属性检测流体。冯磊等[15]利用MP寻找有利储层。黄捍东等[16]通过引入能量衰减因子和动态扫描方式提高了MP的准确性,并提取衰减梯度属性识别生物礁油气。宋维琪等[17]应用MP重构技术有效预测了薄层砂体。张繁昌等[18]基于楔形模型瞬时谱特征,提出砂岩尖灭线高精度识别方法;并依托MP算法,进一步提出振幅随频率变化的剖面构建方法,且完善了地震信号分频技术[19]。以上学者都为MP算法的应用及推广起到了积极推动作用。
由于MP算法可实现信号的自适应分解,并得到高分辨率的时频谱,则可尝试通过MP算法进一步提高地震资料分辨率,以利于薄层识别等。本文基于MP算法基本原理,详述了相对保幅AVF(振幅随频率变化)剖面的构建方法,有效避免了AVF剖面的同相轴弯曲现象,解决了MP分频重构难题;在此基础上,对MP算法做进一步分析和研究,提出了一种新的高分辨率处理方法。该方法在充分保留原始地震数据低频成分的基础上,对时频原子的时频谱进行能量的重新分配,提高原始数据本身存在的高频成分,有效提高了地震资料的分辨率,增强了对薄层等小地质体的分辨能力。
1 方法原理 1.1 匹配追踪基本原理MP算法的核心是利用基函数建立超完备原子库[20-21],将地震信号自适应分解并表示成有限个子波的线性组合。假设D={gγ(t)}为由一系列时频原子组成的超完备子波库,γ是子波库中各匹配子波的时移tn、主频fn和相位φn构成的集合,这里n表示对应序号。从子波库选取与待分解信号s(t)最匹配的子波gγ0(t),且满足
| $ \left|\boldsymbol{S}^{\mathrm{T}} \boldsymbol{G}_{\boldsymbol{\gamma}_0}\right|=\max \left|\boldsymbol{S}^{\mathrm{T}} \boldsymbol{G}_\boldsymbol{\gamma}\right| $ | (1) |
式中:S为s(t)构成的信号向量;Gγ0为匹配子波gγ0(t)构成的列向量。
经过一次迭代后,可将s(t)表示为
| $ s(t)=\left[\boldsymbol{S}^{\mathrm{T}} \boldsymbol{G}_{\gamma_0}\right] g_{\gamma_0}(t)+R^1[s(t)] $ | (2) |
式中R1为第一次迭代分解后的残差信号。对残差信号继续进行迭代分解,直至残差能量足够小。最终信号s(t)可表示为多个子波的线性组合
| $ s(t)=\sum\limits_n a_n g_{\gamma_n}(t) $ | (3) |
式中an为匹配子波的幅度。
1.2 基函数选取一般地,由于Ricker子波和Morlet小波具有良好的地震子波波形,通常被选作基函数构建超完备原子库。考虑到地震采集、地震正演、褶积模型和Ricker子波的特性,且Ricker子波作为地震信号中最常用子波[13],延续时间较短,收敛快。为此,选取Ricker子波构建原子库。该子波的时域表达式为
| $ w(t)=\left[1-2\left(\pi f_{\mathrm{p}} t\right)^2\right] \exp \left[-\left(\pi f_{\mathrm{p}} t\right)^2\right] $ | (4) |
式中fp为Ricker子波主频。
1.3 AVF剖面构建从时频原子定义可知,其能量分布具有有限支撑的特点,因此将时频原子的时域波形在频率方向按振幅谱大小扩展,可得时频分布函数为
| $ S_{\mathrm{AVF}, n}(t, f)=G_{\gamma_n}(f) \cdot g_{\gamma_n}(t) $ | (5) |
式中gγn(t)和Gγn(f)分别为时频原子及其频谱。若将所有时频原子gγ(t)的波形在频率方向按Gγ(f)进行加权,便可得到地震信号的AVF剖面
| $ S_{\mathrm{AVF}}(t, f)=\sum\limits_n a_n \cdot G_{\gamma_n}(f) \cdot g_{\gamma_n}(t) $ | (6) |
式(6)反映了地震信号随频率变化的规律,若沿频率方向积分,可得
| $ \begin{aligned} \int S_{\mathrm{AVF}}(t, f) \mathrm{d} f & =\int \sum\limits_n a_n \cdot G_{\gamma_n}(f) \cdot g_{\gamma_n}(t) \mathrm{d} f \\ & =\sum\limits_n a_n \cdot g_{\gamma_n}(t) \cdot \int G_{\gamma_n}(f) \mathrm{d} f \end{aligned} $ | (7) |
理论上,AVF剖面沿频率方向的积分结果应为原始地震信号,但式(7)与式(3)相比,二者并不一致,由此说明AVF剖面并不相对保幅,式(7)也无法实现地震信号的相对保幅重构。
在构建AVF剖面时,若要准确实现地震信号的相对保幅,首先对Gγn(f)做归一化处理,将式(6)更新为
| $ S_{\mathrm{AVF}}(t, f)=\sum\limits_n a_n \cdot g_{\gamma_n}(t) \cdot \frac{G_{\gamma_n}(f)}{\int G_{\gamma_n}(\lambda) \mathrm{d} \lambda} $ | (8) |
再对式(8)沿频率方向积分,可得
| $ \begin{aligned} \int S_{\mathrm{AVF}}(t, f) \mathrm{d} f & =\int \sum\limits_n a_n \cdot g_{\gamma_n}(t) \cdot \frac{G_{\gamma_n}(f)}{\int G_{\gamma_n}(\lambda) \mathrm{d} \lambda} \mathrm{d} f \\ & =\sum\limits_n a_n \cdot g_{\gamma_n}(t) \frac{\int G_{\gamma_n}(f) \mathrm{d} f}{\int G_{\gamma_n}(\lambda) \mathrm{d} \lambda} \\ & =\sum\limits_n a_n \cdot g_{\gamma_n}(t) \end{aligned} $ | (9) |
式(9)与原信号表征公式(3)完全一致,从而实现了原地震信号的相对保幅重构。
1.4 高分辨率处理利用MP算法得到单道地震记录的时频分布后,其每个采样点都有对应的频谱X(ti,f),具有较准确的时间和频率定位,可有效避免傅里叶变换中复杂的时窗问题。若对信号能量进行重新分配,其计算系数为
| $ \operatorname{coef}\left(t_i, f\right)=\left[\frac{\operatorname{Max}_i}{X\left(t_i, f\right)+\alpha \operatorname{Max}_i}\right]^\beta $ | (10) |
式中:Maxi为ti时刻振幅谱X(ti,f)的最大值;α为白噪占比,可用于调节信噪比和分辨率;β用于调节频谱的平滑度。
对所有ti时刻的点谱进行能量重新分配,便可得到高分辨率处理后的时频分布
| $ S_{\mathrm{AVF}}\left(t_i, f\right)=X\left(t_i, f\right) \cdot \operatorname{coef}\left(t_i, f\right) $ | (11) |
对该式的时频域数据沿频率方向积分,进行信号重构,便可得到高分辨率的地震数据。
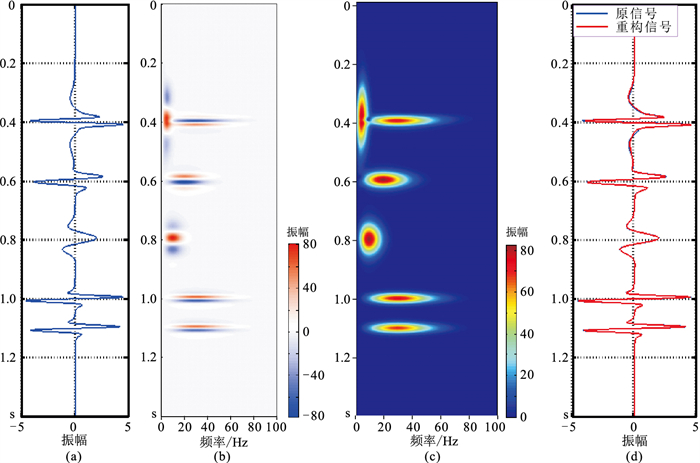
2 AVF剖面相对保幅性测试 2.1 AVF剖面相对保幅性验证为验证AVF剖面的构建是否具有相对保幅效应,制作图 1a所示由6个不同参数的Ricker子波叠加而成的合成地震记录,并得到相应改进后的AVF剖面(图 1b)、时频谱(图 1c)、原信号与重构信号的叠合(图 1d)。对比可见,改进后的AVF剖面重构的信号与原信号几乎完全重合,验证了AVF剖面的相对保幅性,且可进一步构建同频率剖面。
|
图 1 改进MP算法所得AVF剖面表现的相对保幅效果 (a)合成记录;(b)AVF剖面;(c)时频谱;(d)重构信号与原信号对比 |
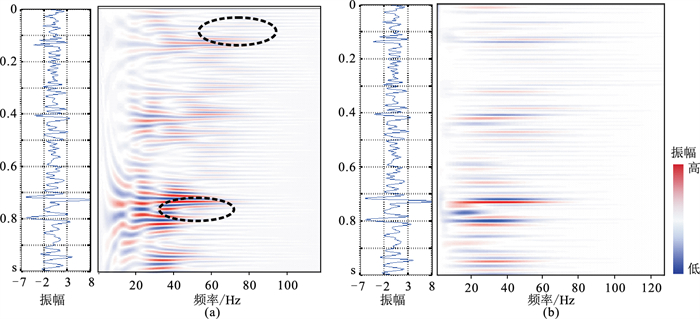
针对珠江口盆地惠州地区某道实际地震信号,分别应用小波变换法和MP算法得到AVF处理剖面(图 2)。对比可见:两者分频结果主要能量基本一致;但沿频率方向,由MP算法所得AVF剖面(图 2b)同相轴平直,不存在漂移现象,利于后续AVF分析;而小波变换法所得AVF剖面(图 2a)在高频部分出现明显同相轴弯曲、分叉现象(椭圆所示),从而有效验证了MP算法优于小波变换法。
|
图 2 两种方法获得的AVF剖面对比 (a)小波变换法;(b)MP算法 |
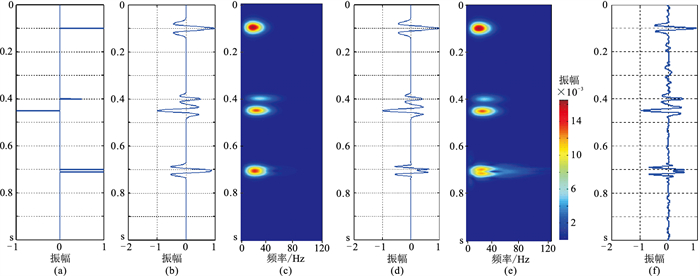
为验证基于MP算法的高分辨率处理方法的可靠性和实用性,构建图 3a所示反射系数序列,与主频为30Hz的Ricker子波褶积,得到合成地震记录(图 3b)及其时频谱(图 3c)。可见0.70s处相距较近的两个反射界面无法分辨。而经本文高分辨率方法处理后的地震数据(图 3d)和时频谱(图 3e),在0.10、0.40、0.45s等孤立界面处并未发生分裂和时移,表明了本文处理方法的可靠性;对于原始数据中0.70s附近无法分辨的反射系数,经本文方法处理后的数据及其时频谱在该处已清晰展示为两个信号,分辨率明显得到提高。
|
图 3 高分辨率处理前、后及与谱白化处理结果的对比 (a)反射系数;(b)合成地震记录;(c)原信号时频谱;(d)本文方法处理后数据;(e)本文方法处理后的时频谱;(f)谱白化处理后数据 |
此外,还进一步展示了本文高分辨率处理与谱白化处理方法的差异。从谱白化处理后结果(图 3f)可见,虽然在一定程度上提高了地震数据的分辨率,但却同时产生了抖动现象,相对于有效信号而言为无效信号,信噪比明显降低;而基于MP算法的高分辨率处理后地震数据(图 3d),不仅提高了分辨率,而且相对保幅,并未产生无效的抖动信号,在一定程度上压制了噪声。显然,谱白化处理需在分辨率与信噪比之间权衡,拓频效果有一定局限性。
3.2 实例分析图 4a为珠江口盆地惠州地区的实际地震剖面。该地区薄储层发育,且经过多年的勘探开发,常规地震资料已无法满足目标搜索、储层预测的需求。

|
图 4 高分辨率处理前(a)、后(b)地震剖面对比 |
为进一步挖潜该地区的勘探潜力,将本文基于MP的高分辨率处理方法应用于实际地震剖面,得到图 4b所示的地震剖面,以进一步验证该方法的实用性。
通过对比可知,经本文高分辨率方法处理后的剖面(图 4b)地震强弱波组关系更明显,复合波得到了有效分离(绿色圈),且弱信号能量也得到明显增强(红色和粉红色圈),使得反映薄层信息的细微特征得以凸显,薄层分辨能力得到增强。为检验高分辨率处理后,频带提高部分的信息是否可靠,对处理前、后的地震数据分别进行井震标定。其中原始地震资料目的层段(1.75~2.25s)主频为30Hz,因此原始地震数据采用对应30Hz主频的Ricker子波制作合成记录进行标定(图 5),而提高分辨率处理后资料的主频提高至约35Hz;再对高分辨率处理后地震数据采用35Hz主频Ricker子波制作合成记录进行标定(图 6),可见高分辨率处理后地震剖面与井的合成地震记录标定依然良好,处理后地震数据增加的信息可与合成地震记录相对应,说明拓频后多出来的地震同相轴对应的为真实地层分界面,并非虚假同相轴。同相轴变多、变细,体现了更多的地层变化细节,从而提高了分辨薄层的能力。

|
图 5 原始地震数据(左)及其合成记录(右) |

|
图 6 本文高分辨率方法处理后数据(左)及其合成记录(右) |
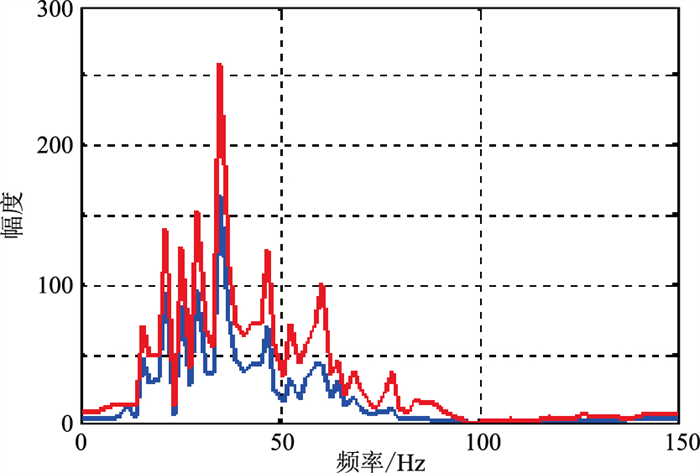
高分辨率处理前、后地震数据振幅谱对比(图 7)也证明,处理后的地震数据主频得到提高,有效频带拓宽,从而使弱信号得到明显增强,薄层等小地质体的纵向分辨能力也得到提高。
|
图 7 本文高分辨率方法处理前(蓝线)、后(红线)频谱对比 |
在分析MP算法的基本原理及相对保幅AVF剖面构建方法的基础上,本文提出了基于MP算法的高分辨率处理方法,显著提高了地震资料的分辨率。通过理论测试和实例分析,得出以下认识。
(1) MP相对保幅AVF剖面构建方法,有效避免了以滤波机制为基础的分频方法造成的平行同相轴假象,从而可有效追踪AVF剖面中同相轴振幅随频率的变化规律;
(2) 基于MP算法的高分辨率处理技术,可较好提高地震资料分辨率,处理后的地震资料频带得到拓宽,高频成分得到加强,从而使得反射特征更清晰,弱信号能量得到增强,在一定程度上有效改善了地震剖面质量;
(3) 该处理技术实现了对信号时频表征能量的重新分配,相对于业界常用的谱白化处理技术,不仅提高了地震资料的分辨率,同时也可抑制无效信号的产生,避免了常规处理方法中分辨率与信噪比相互制约的弊端。
基于MP算法的高分辨率处理方法可用于精细频率属性提取、薄互层和小尺度地质体的刻画,为后续储层识别和流体检测提供了强大支持。
| [1] |
凌云研究组. 地震分辨率极限问题的研究[J]. 石油地球物理勘探, 2004, 39(4): 435-442. LING Yun Research Group. Study of seismic re-solution limit[J]. Oil Geophysical Prospecting, 2004, 39(4): 435-442. DOI:10.3321/j.issn:1000-7210.2004.04.014 |
| [2] |
王延光, 李皓, 李国发, 等. 一种用于薄层和薄互层砂体厚度估算的复合地震属性[J]. 石油地球物理勘探, 2020, 55(1): 153-160. WANG Yanguang, LI Hao, LI Guofa, et al. A composite seismic attribute used to estimate the sand thickness for thin bed and thin interbed[J]. Oil Geophysical Prospecting, 2020, 55(1): 153-160. |
| [3] |
杨春生, 姜岩, 宋宝权, 等. 小河道薄砂层井震联合识别技术及应用——以大庆长垣西部AGL地区为例[J]. 石油地球物理勘探, 2022, 57(1): 159-167. YANG Chunsheng, JIANG Yan, SONG Baoquan, et al. Recognition technology integrating logging and seismic data for thin sand reservoir in narrow channel and its application: Taking the AGL area in western Daqing placanticline as an example[J]. Oil Geophysical Prospecting, 2022, 57(1): 159-167. |
| [4] |
周家雄, 张国栋. 地震谱分解方法在低阻油层储层预测中应用[J]. 地球物理学进展, 2017, 32(5): 2168-2175. ZHOU Jiaxiong, ZHANG Guodong. Application of spectral decomposition in low resistivity reservoir prediction[J]. Progress in Geophysics, 2017, 32(5): 2168-2175. |
| [5] |
PARTYKA G, GRIDLEY J, LOPEZ J. Interpretational applications of spectral decomposition in reservoir characterization[J]. The Leading Edge, 1999, 18(3): 353-360. DOI:10.1190/1.1438295 |
| [6] |
GABOR D. Theory of communication[J]. Journal on Institution of Electrical Engineering, 1946, 93(26): 429-457. |
| [7] |
CHAKRABORTY A, OKAYA D. Frequency-time decomposition of seismic data using wavelet-based methods[J]. Geophysics, 1995, 60(6): 1906-1916. DOI:10.1190/1.1443922 |
| [8] |
朱振宇, 高佳伦, 姜秀娣, 等. 基于三参数小波的频谱分解方法[J]. 石油地球物理勘探, 2018, 53(6): 1299-1306. ZHU Zhenyu, GAO Jialun, JIANG Xiudi, et al. Spectrum decomposition based on three-parameter wavelet[J]. Oil Geophysical Prospecting, 2018, 53(6): 1299-1306. |
| [9] |
STOCKWELL R G, MANSINHA L, LOWE R P. Localization of the complex spectrum: the S transform[J]. IEEE Transactions on Signal Processing, 1996, 44(4): 998-1001. DOI:10.1109/78.492555 |
| [10] |
MANSINHA L, STOCKWELL R G, LOWE R P. Pattern analysis with two-dimensional spectral localisation: Applications of two-dimensional S transforms[J]. Physica A: Statistical Mechanics and Its Applications, 1997, 239(1-3): 286-295. DOI:10.1016/S0378-4371(96)00487-6 |
| [11] |
MALLAT S G, ZHANG Z F. Matching pursuit with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3397-3415. DOI:10.1109/78.258082 |
| [12] |
张繁昌, 李传辉. 地震信号复数域高效匹配追踪分解[J]. 石油地球物理勘探, 2013, 48(2): 171-175. ZHANG Fanchang, LI Chuanhui. Complex domain efficient matching pursuit decomposition of seismic signals[J]. Oil Geophysical Prospecting, 2013, 48(2): 171-175. |
| [13] |
张繁昌, 刘汉卿, 代荣获. 基于Ricker子波的指数追踪地震信号分解算法[J]. 中国矿业大学学报, 2016, 45(1): 78-82. ZHANG Fanchang, LIU Hanqing, DAI Ronghuo. Exponential pursuit algorithm based on Ricker wavelet for seismic signal decomposition[J]. Journal of China University of Mining & Technology, 2016, 45(1): 80-82. |
| [14] |
ZHANG T Q, LI X Y, MARK C. Estimating frequencydependent seismic attributes by matching pursuit: a case study[C]. SEG Technical Program Expanded Abstracts, 2008, 27: 3023-3027.
|
| [15] |
冯磊, 姜在兴. 基于匹配追踪的谱分解方法及其应用[J]. 勘探地球物理进展, 2009, 32(1): 33-36. FENG Lei, JIANG Zaixing. Spectral decomposition based on matching pursuit and its application[J]. Progress in Exploration Geophysics, 2009, 32(1): 33-36. |
| [16] |
黄捍东, 郭飞, 王佳蓓, 等. 高精度地震时频谱分解方法及应用[J]. 石油地球物理勘探, 2012, 47(5): 773-780. HUANG Handong, GUO Fei, WANG Jiabei, et al. High precision seismic time-frequency spectrum decomposition method and its application[J]. Oil Geophysical Prospecting, 2012, 47(5): 773-780. |
| [17] |
宋维琪, 朱卫星, 孙英杰. 复数子波匹配追踪算法识别薄层砂体[J]. 地球物理学进展, 2007, 22(6): 1796-1801. SONG Weiqi, ZHU Weixing, SUN Yingjie. Identify bed layer sandbody by complex wavelet matching algorithm[J]. Progress in Geophysics, 2007, 22(6): 1796-1801. |
| [18] |
张繁昌, 李传辉, 印兴耀. 三角洲砂岩尖灭线的地震匹配追踪瞬时谱识别方法[J]. 石油地球物理勘探, 2012, 47(1): 82-88. ZHANG Fanchang, LI Chuanhui, YIN Xingyao. Delta fringe line recognition based on seismic matching pursuit instantaneous spectral characteristics[J]. Oil Geo-physical Prospecting, 2012, 47(1): 82-88. |
| [19] |
张繁昌, 李传辉. 匹配追踪保幅地震AVF剖面及同频率剖面的构建[J]. 石油物探, 2013, 52(3): 234-239. ZHANG Fanchang, LI Chuanhui. Amplitude-preserved AVF and isofrequency section construction based on seismic matching pursuit[J]. Geophysical Prospecting for Petroleum, 2013, 52(3): 234-239. |
| [20] |
张春梅, 尹忠科, 肖明霞. 基于冗余字典的信号超完备表示与稀疏分解[J]. 科学通报, 2006, 51(6): 628-633. ZHANG Chunmei, YIN Zhongke, XIAO Mingxia. Sparse decomposition of signal over-complete representation based on redundant dictionary[J]. Chinese Science Bulletin, 2006, 51(6): 628-633. |
| [21] |
许璐, 吴笑荷, 张明振, 等. 基于局部频率约束的动态匹配追踪强反射识别与分离方法[J]. 石油地球物理勘探, 2019, 54(3): 587-595. XU Lu, WU Xiaohe, ZHANG Mingzhen, et al. Strong reflection identification and separation based on the local-frequency-constrained dynamic matching pursuit[J]. Oil Geophysical Prospecting, 2019, 54(3): 587-595. |



 刘汉卿, 广东省深圳市南山区后海滨路(深圳湾段)中海石油(中国)有限公司深圳分公司南海东部石油研究院,518000。Email:
刘汉卿, 广东省深圳市南山区后海滨路(深圳湾段)中海石油(中国)有限公司深圳分公司南海东部石油研究院,518000。Email: