② 中海油田服务股份有限公司物探事业部,天津 300451;
③ 海洋油气勘探国家工程研究中心,北京 100028
② Geophysical Division of China Oilfield Services Limited, Tianjin 300451, China;
③ National Engineering Research Center of Offshore Oil and Gas Exploration, Beijing 100028, China
海上地震拖缆勘探是由勘探船拖拽枪阵与电缆沿测线航行,通过枪阵震源激发模拟地震波,并由拖缆上安装的检波器阵列接收海底反射的地震波信号以获得海底的构造地质信息,从而达到油气勘探的目的[1-4]。现阶段海上地震拖缆勘探一般采用多缆作业模式以提高施工效率。拖缆定位是海上地震勘探作业的关键步骤之一,其精度将直接影响地震数据的成像精度与可靠性[5-6]。
拖缆具有非刚体特性,一般长达数千米。水下环境复杂多变,如何对拖缆建立合理的数学模型并利用特定的算法对模型进行解算,是拖缆获得高精度缆形和位置的关键[7-8]。
国外较早开展拖缆建模和定位算法研究,Gilbert于1981年利用罗盘观测值对拖缆平面坐标之间的多项式系数进行估计,确定单缆的缆形和位置[9];又于1982年以拖缆里程为因变量,分别对单缆的三维坐标分量进行多项式拟合建模,并利用极大似然估计确定多项式系数[10];Zinn等[11]将拖缆视为若干段相连的圆弧,以罗盘节点确定每段圆弧的圆心、直径等参数,并按照圆弧的几何性质进行拖缆坐标推算;Combier[12]根据罗盘提供的方位对单缆的坐标进行推算,再通过尾标的精确位置对拖缆进行定位修正;Goutorbe等[13]利用罗盘观测值拟合整条拖缆的方位角,并沿曲线对坐标积分获得单缆上各点位置。中国于20世纪90年代开始对拖缆建模和定位方法进行了探讨[14],姚宜斌等[15]先通过近似曲线积分的方法对拖缆进行坐标推算,获得初始缆形,再通过声学测距网络的约束平差和拟稳平差确定声学节点的精确位置,然后通过分段旋转、缩放的方式使初始缆形与平差后的声学节点相吻合,该方法在多缆定位中取得了较好的效果;易昌华等[16]介绍了弧段模型与曲线积分模型,并对比分析了二者的适用场景和计算效率;易昌华[17]提出了利用近似曲线积分派生出前、中、后声学网络之间的虚拟距离观测值,并进行声学网络统一平差的方法。
上述拖缆定位算法大致分为两类:第一类是对拖缆建立特定的数学模型,并利用拖缆定位观测值对数学模型中的参数进行估计,拖缆的缆形和位置由模型直接导出。此类方法缺点是大部分拖缆模型只针对单缆定位,在多缆勘探场景下不能较好地利用距离观测值。第二类是先利用部分观测值进行近似曲线积分推算,得到一个近似的拖缆缆形,再通过声学测距网络平差的结果对拖缆进行调整。此类方法应用较为广泛,缺点是建立的拖缆模型不够严密,不能较好地利用罗盘观测值,且测距网络平差时通常需估计上百个声学节点的坐标,计算量较大。
针对以上存在的问题,本文建立了一种基于曲线积分的拖缆数学模型,通过模型参数描述拖缆的形状和位置,并基于模型充分利用拖缆定位网络中的观测值进行参数估计,从而实现多缆定位和精度评估,最后通过仿真与实测数据对算法进行验证。
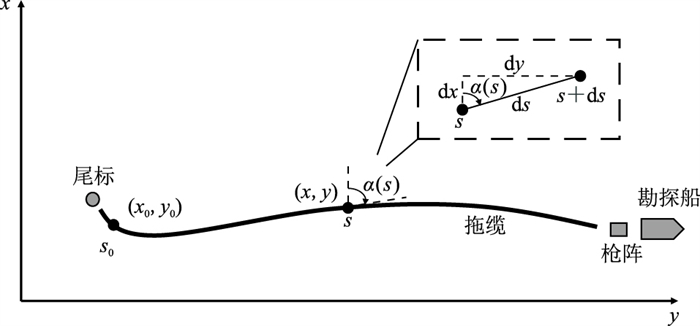
1 基于曲线积分的拖缆数学模型在进行海上地震勘探时,拖缆在水下呈现“光滑的曲线”形态,其上安装有深度控制传感器,用于控制拖缆的沉放深度,实际作业时拖缆各处检波器的深度差一般在1m之内。由于拖缆长度通常为3~10km,检波器深度差可忽略不计。以单条拖缆为例,其数学描述如图 1所示,其中α(s)为拖缆任意位置s处切线方位角的函数。
|
图 1 拖缆数学模型示意图 |
设拖缆位置s0处坐标为(x0, y0),以该点为基准点,则拖缆上任意点s的平面坐标(x, y)可表示为
| $ \left\{\begin{array}{l} x=x_0+\int_{x_0}^x \mathrm{~d} x \\ y=y_0+\int_{y_0}^y \mathrm{~d} y \end{array}\right. $ | (1) |
如图 1所示,拖缆上任意点的坐标(x, y)与其对应位置s之间存在如下微分关系
| $ \left\{\begin{array}{l} \mathrm{d} x=\cos \alpha(s) \mathrm{d} s \\ \mathrm{~d} y=\sin \alpha(s) \mathrm{d} s \end{array}\right. $ | (2) |
将式(2)代入式(1)可得拖缆上任意位置s处的坐标
| $ \left\{\begin{array}{l} x(s)=x_0+\int_{s_0}^s \cos \alpha(s) \mathrm{d} s \\ y(s)=y_0+\int_{s_0}^s \sin \alpha(s) \mathrm{d} s \end{array}\right. $ | (3) |
通过该模型,若能确定(x0, y0)和α(s),即可通过曲线积分导出拖缆上任意里程处点的坐标,确定整条拖缆的缆形。式(3)中x0、y0可看作拖缆的位置参数,函数α(s)中的参数可看作拖缆的形态参数。
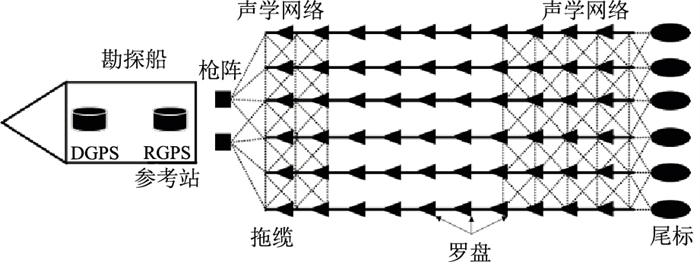
2 基于曲线积分模型的多缆定位算法 2.1 拖缆导航定位设备及定位模型海上地震拖缆勘探中使用的导航定位设备(图 2)有:①勘探船上安装的差分全球定位系统(Differential Global Positioning System,DGPS)和电罗经。其中,DGPS用于获取船的绝对位置,电罗经用于获取船的姿态。②枪阵与拖缆尾部挂载了GPS相对定位系统(Relative Global Positioning System,RGPS)浮标,用于测量其与拖船上RGPS参考站之间的基线向量,确定它们相对于拖缆的位置(有时拖缆头部也挂载RGPS)。③水下拖缆安装有声学设备和罗盘。其中,声学设备用于测定声学节点之间的距离,拖缆上的声学设备与枪阵、尾标上的声学设备一起组成声学测距网络,罗盘用于确定拖缆在各罗盘节点处的切线方位[18-22]。
|
图 2 拖缆导航定位系统示意图 |
海上地震勘探作业时,DGPS和RGPS的观测值精度较高,RGPS可将拖船的位置基准传递到枪阵与拖缆尾标,位于枪阵与拖缆尾标上的声学节点因此可获得较高的位置精度,可作为拖缆定位网络中的已知点。拖缆的α(s)是未知的,受勘探船修舵、海浪以及洋流的影响,拖缆在水下的缆形随之变化,因此,可以使用一个多项式对α(s)进行描述
| $ \alpha(s)=a_0+a_1 s+a_2 s^2+\cdots+a_n s^n $ | (4) |
式中:n为多项式阶数;α0,α1,…,αn为多项式系数,即待估计的拖缆形态参数。
多项式曲线具有良好的几何特性,可以较准确地拟合出不同的拖缆形状。拖缆基准点的选取对于最终的拖缆定位结果有直接影响,且基准点最好位于拖缆上。尽管拖缆尾标具有较高的位置精度,但由于其漂浮于水面之上,和拖缆之间有一定的高差,将其作为拖缆基准点进行积分计算会带来较大的系统误差。因此,可选取拖缆尾端的声学节点作为拖缆基准点,它与尾标之间存在声学距离观测值,将其坐标(x0, y0)作为待估计的拖缆位置参数,与拖缆形态参数一起参与平差,进行整体估计。这样既可使拖缆基准点获得较高的位置精度,又可避免积分过程中产生系统误差。
2.2 误差方程的建立拖缆上的定位传感器罗盘和声学测距安装位置已知。罗盘观测值和声学距离观测值的误差方程推导如下。
2.2.1 罗盘观测值误差方程罗盘的观测值为拖缆该节点处切线的磁方位角,拖缆上位于s处的罗盘方位观测值观测方程为
| $ A_s=\alpha(s)+m+\varepsilon_{\mathrm{a}} $ | (5) |
式中:As为s处的罗盘观测值;m为磁偏角改正量;εa为方位观测随机误差。该观测方程为线性,结合式(4)、式(5)可写为误差方程形式
| $ \left\{\begin{array}{l} v_{A_s}=\sum\limits_{k=0}^n s^k \delta \hat{a}_k-l_{A_s} \\ a_k=a_k^o+\delta \hat{a}_k \\ l_{A_s}=A_s-m-\sum\limits_{k=0}^n s^k a_k^o \end{array}\right. $ | (6) |
式中:vAs为残差项;ak为拖缆k阶形态参数;a°k为ak的近似值;
声学设备的距离观测值分为同缆观测值和异缆观测值。其中,同缆距离观测值两端对应的声学节点位于同一条拖缆,异缆观测值的声学节点则位于不同拖缆上。为不失一般性,先对异缆观测情况下的误差方程进行推导,同缆观测可看作异缆观测的一种特殊情况。设G缆与H缆为相邻的两条拖缆,i点位于G缆里程SG, i处,j点位于H缆里程SH, j处,i、j两点间的距离观测值为
| $ D_{i, j}=\sqrt{\left(x_{\mathrm{H}, j}-x_{\mathrm{G}, i}\right)^2+\left(y_{\mathrm{H}, j}-y_{\mathrm{G}, i}\right)^2}+\varepsilon_{\mathrm{d}} $ | (7) |
式中:xG, i与yG, i、xH, j与yH, j分别为i、j两点的平面坐标;εd为距离观测值随机误差。对式(7)进行线性化,得到
| $ \begin{aligned} v_{D_{i, j}}= & \frac{x_{\mathrm{H}, j}^{\circ}-x_{\mathrm{G}, i}^{\circ}\left(\delta \hat{x}_{\mathrm{H}, j}-\delta \hat{x}_{\mathrm{G}, i}\right)+}{D_{i, j}^{\circ}} \\ & \frac{y_{\mathrm{H}, j}^{\circ}-y_{\mathrm{G}, i}^{\circ}}{D_{i, j}^{\circ}}\left(\delta \hat{y}_{\mathrm{H}, j}-\delta \hat{y}_{\mathrm{G}, i}\right)-l_{D_{i, j}} \end{aligned} $ | (8) |
式中:vDi, j为残差项;
| $ \left\{\begin{array}{l} \frac{\partial x}{\partial x_0}=\frac{\partial y}{\partial y_0}=1 \\ \frac{\partial x}{\partial a_k}=-\int_{s_0}^s s^k \sin \alpha(s) \mathrm{d} s \\ \frac{\partial y}{\partial a_k}=\int_{s_0}^s s^k \cos \alpha(s) \mathrm{d} s \end{array}\right. $ | (9) |
将式(9)代入式(8),得
| $ v_{D_{i, j}}=-\sum\limits_{k=0}^{n_{\mathrm{G}}} \frac{-\Delta x_{i, j}^{\circ} \int_{s_{\mathrm{G}_0}}^{s_{\mathrm{G}, i}} s^k \sin \alpha_{\mathrm{G}}^{\circ}(s) \mathrm{d} s+\Delta y_{i, j}^{\circ} \int_{s_{\mathrm{G}_0}}^{s_{\mathrm{G}, i}} s^k \cos \alpha^{\circ}{ }_{\mathrm{G}}(s) \mathrm{d} s}{D_{i, j}^{\circ}} \delta \hat{a}_{\mathrm{G}, k}+ \\ \sum\limits_{k=0}^{n_{\mathrm{H}}} \frac{-\Delta x^{\circ}{ }_{i, j} \int_{s_{\mathrm{H}_0}}^{s_{\mathrm{H}, j}} s^k \sin \alpha_{\mathrm{H}}^{\circ}(s) \mathrm{d} s+\Delta y_{i, j}^{\circ} \int_{s_{\mathrm{H}_0}}^{s_{\mathrm{H}, j}} s^k \cos \alpha^{\circ}{ }_{\mathrm{H}}(s) \mathrm{d} s}{D_{i, j}^{\circ}} \delta \hat{a}_{\mathrm{H}, k}+ \\ \frac{\Delta x^{\circ}{ }_{i, j}}{D_{i, j}^{\circ}}\left(\delta \hat{x}_{\mathrm{H}_0}-\delta \hat{x}_{\mathrm{G}_0}\right)+\frac{\Delta y^{\circ}{ }_{i, j}}{D_{i, j}^{\circ}}\left(\delta \hat{y}_{\mathrm{H}_0}-\delta \hat{y}_{\mathrm{G}_0}\right)-l_{D_{i, j}} $ | (10) |
式中:nG、nH为G缆与H缆的方位角函数αG(s)、αH(s) 对应的多项式阶数;Δx°i, j=x°H, j-x°G, i; Δy°i, j=y°H, j-y°G, i; sG0、sH0为G缆与H缆基准点对应的里程值;α°G(s)、α°H(s)为αG(s)、αH(s)的近似;
式(10)即为距离观测误差方程的一般形式。对于同缆观测的情况,式(10)可简化为
| $ v_{D_{i, j}}=\sum\limits_{k=1}^n \frac{-\Delta x^{\circ}{ }_{i, j} \int_{s_i}^{s_j} s^k \sin \alpha^{\circ}(s) \mathrm{d} s+\Delta y_{i, j}^{\circ} \int_{s_i}^{s_j} s^k \cos \alpha^{\circ}(s) \mathrm{d} s}{D_{i, j}^{\circ}} \delta \hat{a}_k-l_{D_{i, j}} $ | (11) |
由式(11)可见,同缆距离观测的误差方程中不包含该拖缆的0阶形态参数
据式(6)、式(10)可确定设计矩阵A和闭合差向量L。随机模型P由观测值先验信息确定,目前一般采用经验定权的方法。根据最小二乘估计确定待估参数
| $ \hat{\boldsymbol{X}}=\left[\hat{a}_{1, 0} \cdots \hat{a}_{1, n_1}, \cdots, \hat{a}_{n, 0} \cdots \hat{a}_{n, n_n}, \hat{x}_{1_0}, \hat{y}_{1_0}, \cdots, \hat{x}_{n_0}, \hat{y}_{n_0}\right]^{\mathrm{T}} $ | (12) |
式中:n为拖缆数量,其中1, 2…,n为拖缆编号,n1,n2,…,nn为各拖缆对应的多项式阶数;
在确定了各拖缆的参数
| $ \boldsymbol{\varSigma}_{(\hat{x}, \hat{y})}=\hat{\sigma}_0^2 \boldsymbol{f} \boldsymbol{Q}_{\hat{\boldsymbol{X}} \hat{\boldsymbol{X}}} \boldsymbol{f}^{\mathrm{T}} $ | (13) |
式中:
为验证本文算法的应用效果,设计了如下的仿真实验与实测数据实验。
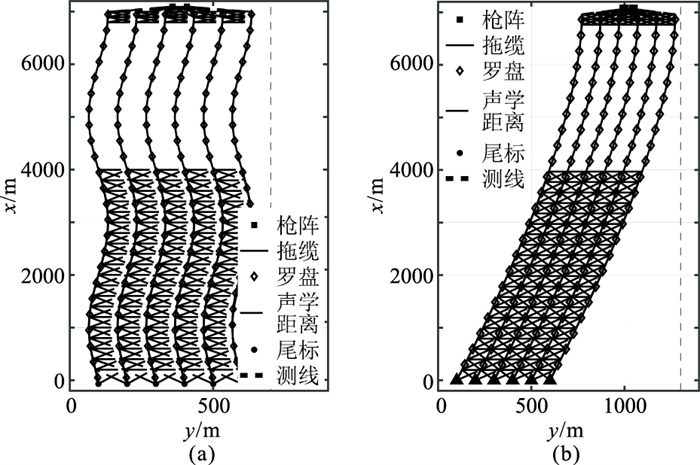
3.1 仿真实验分别选取正弦函数和对数函数作为拖缆方位角函数的真值,并据此生成了两套不同缆形的拖缆仿真数据(图 3)。每套仿真数据均为6缆配置,缆间距为100m,每条拖缆长为7km,且枪阵与拖缆尾标的位置已知。测线走向为正北。拖缆上包含有罗盘观测值和声学距离观测值,同一拖缆上的罗盘间距为300m,声学测距网络为前—后网络配置。其中,仿真数据1(图 3a)模拟拖缆多段弯曲的情况,仿真数据2(图 3b) 模拟拖缆整体弯曲的情况。
|
图 3 仿真数据拖缆配置示意图 (a)仿真数据1;(b)仿真数据2 |
仿真数据1和数据2采用的方位角函数分别为
| $ \widetilde{\alpha}_1(s)=3 \sin \left(\frac{s}{1000} \times \frac{\pi}{2}\right) $ | (14) |
| $ \tilde{\alpha}_2(s)=4 \operatorname{In}\left(1+\frac{s}{1000}\right) $ | (15) |
将式(14)、式(15)代入式(3),即可获得两组数据各条拖缆的真实坐标。罗盘观测值的真值可由式(14)和式(15)直接获得,声学距离观测值的真值可由各声学节点的真实坐标反算获得。罗盘观测值中加入随机误差εA~N(0, σA2), σA=0.5°; 声学距离观测值中加入随机误差εD~N(0, σD2), σD=2m。分别采用如下两种方案对两套仿真数据进行解算。
方案1:采用本文基于曲线积分的多缆定位算法对拖缆参数进行估计,并导出拖缆的缆形和位置信息。其中,拖缆方位角函数选用7阶多项式,这里的7阶为经验值。
方案2:采用传统的测边网平差算法进行计算,即先利用罗盘观测值对拖缆缆形进行近似曲线积分推算,再使用测边网平差的结果对拖缆缆形进行调整。
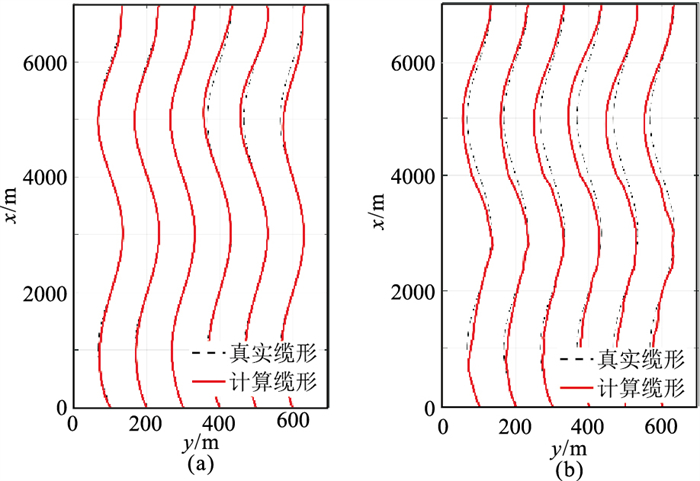
将仿真数据1和仿真数据2的解算结果与实际缆形进行对比,如图 4、图 5所示。由图可见,使用本文算法得到的拖缆缆形在整体上与实际缆形更加吻合,而使用测边网平差算法得到的拖缆在空间位置上存在更大的偏差,且其缆形多处不平滑。这是由于测边网平差算法是对拖缆上离散的声学节点进行较为精确的位置估计,位于声学节点之间的拖缆缆形只能通过罗盘观测值进行确定,而罗盘观测值没有参与平差,加入至其中的随机误差未能被较好地消除或减弱。其次,测边网平差算法中的拖缆需要通过分段调整以吻合平差后的声学节点位置,导致其各段的连接处出现缆形过渡不平滑的现象,不符合拖缆实际物理特性。本文算法使用一系列的拖缆参数描述拖缆的缆形和位置,并且将罗盘观测值和声学距离观测值共同纳入平差计算,直接对拖缆参数进行估计,再通过曲线积分导出拖缆任意里程处的坐标,更好地利用了拖缆上的不同类型的定位观测值,估计得到的缆形更加平滑,精度更高。
|
图 4 仿真数据1两种方案拖缆缆形对比 (a)方案1;(b)方案2 |
|
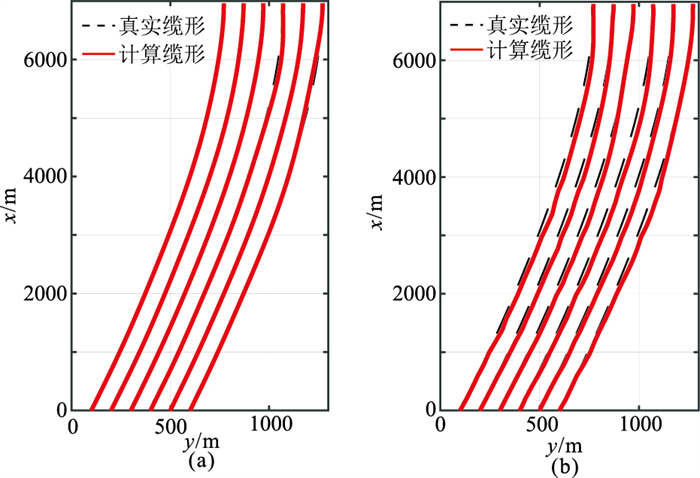
图 5 仿真数据2两种方案拖缆缆形对比 (a)方案1;(b)方案2 |
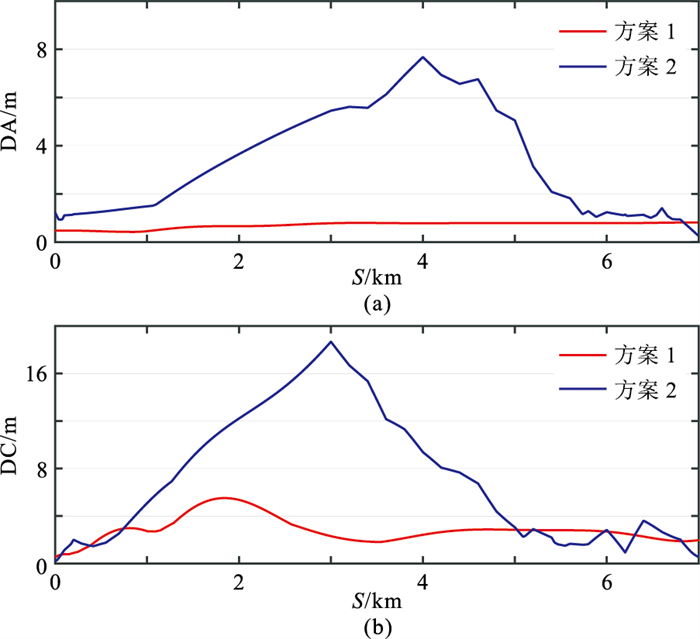
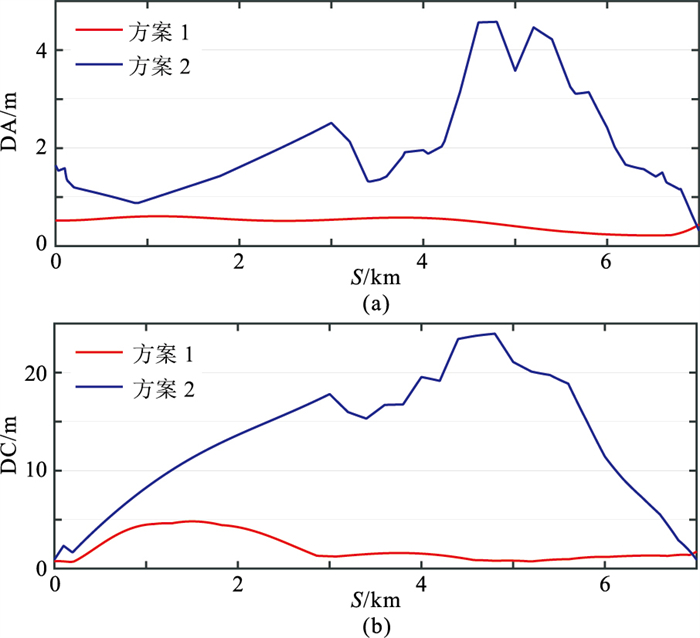
计算各拖缆位于任意里程处的位置偏差,并将其位置偏差投影到沿测线方向(Direction Along Line,DA)和垂直测线方向(Direction Cross Line,DC),这是因为勘探作业中更关心拖缆上检波器阵列在这两个方向上的位置偏差。由于拖缆数量较多,这里仅给出各拖缆在DA与DC方向上的平均偏差DA与DC对比。如图 6、图 7所示,由图可见,本文算法的拖缆定位精度整体上明显高于测边网平差算法。由于仿真数据均采用前—后声学网络配置(图 3),拖缆前中部缺少声学距离观测,测边网平差算法的定位误差在拖缆中部迅速增加,而本文算法在拖缆各处的定位精度均较为稳定。
|
图 6 仿真数据1两种方案拖缆位置偏差对比 (a)DA偏差;(b)DC偏差 |
|
图 7 仿真数据2两种方案拖缆位置偏差对比 (a)DA偏差;(b)DC偏差 |
表 1给出了两种方案计算结果与实际缆形之间的平均点位偏差、DA方向平均偏差以及DC方向平均偏差。结果表明,方案1的定位精度显著优于方案2。其中,方案1的DA方向平均偏差均小于1m,DC方向平均偏差均少于3m。针对仿真数据1,方案1相较于方案2,点位偏差减小了63.8%,DA方向偏差减小了79.5%,DC方向偏差减小了61.1%。针对仿真数据2,方案1相较于方案2点位偏差减小了84.1%,DA方向偏差减小了77.4%,DC方向偏差减小了84.5%。
|
|
表 1 不同方案偏差结果统计 |
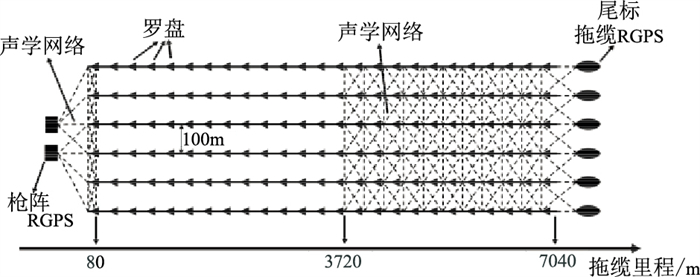
实测数据来自于2019年中国南海某测线拖缆定位数据,该测线为东南走向,方位角为149°,全长38km。如图 8所示,该次作业为6缆配置,拖缆长约7km,缆间距约为100m,每条拖缆挂载检波器564个,间距为12.5m;挂载罗盘25个,间距约300m;挂载声学设备15个,采用前—后声学网络配置。该套数据包含1600个响炮历元,响炮间隔为12~13s。使用本文算法对该套数据进行逐个历元解算,拖缆方位角函数根据经验选择为7阶多项式,并将解算结果与国外拖缆勘探导航定位数据处理软件SPRINT的解算结果进行对比分析。
|
图 8 实测数据拖缆配置示意图 |
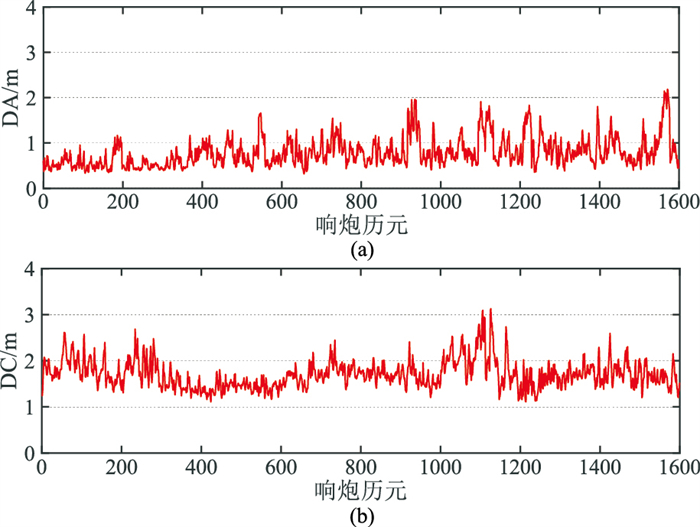
将SPRINT软件的解算结果作为参考值,计算本文算法得到的拖缆检波器坐标与SPRINT解算结果之间的差值,将坐标偏差投影到DA、DC方向,并统计每个历元6条电缆上共3384个检波器的平均DA、DC偏差。由表 2和图 9可以看出,本文算法的结果与SPRINT总体上非常接近,且各历元的检波器平均DA、DC偏差一直维持在一个较小的水平。这表明本文算法在应用于实测数据时可以获得较为正确、可靠的结果,且算法具有良好的稳定性。与SPRINT的解算结果相比,本文算法1600个响炮的历元平均DA偏差为0.79m,其中,99.6%的历元DA偏差小于2.00m,80.6%的历元DA偏差小于1m,标准差小于0.50m;平均DC偏差为1.73m,其中,99.8%的历元DC偏差小于3.00m,85.4%的历元DC偏差小于2.00m,标准差小于0.50m。
|
|
表 2 检波器位置偏差结果统计 |
|
图 9 检波器平均位置偏差随时间变化 (a)DA方向;(b)DC方向 |
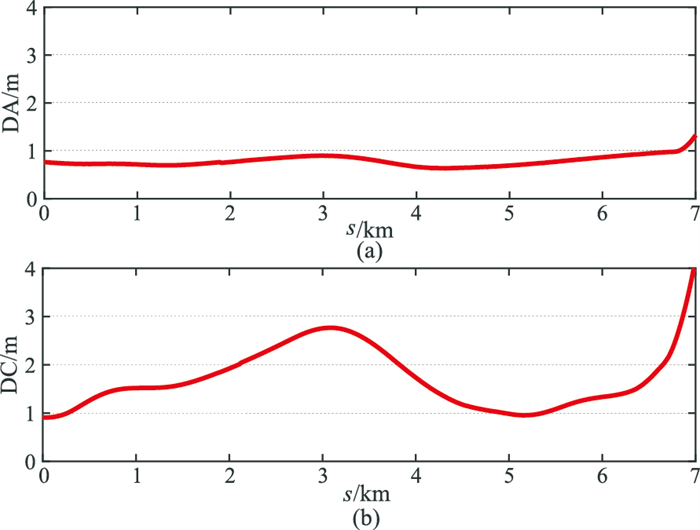
计算各拖缆上处于相同里程处检波器的平均DA、DC偏差,并统计1600个响炮历元的平均值,如图 10所示。可以看出,检波器平均DA偏差沿拖缆里程变化平缓,拖缆上99.1%的检波器平均DA偏差优于1.00m;检波器平均DC偏差在拖缆前中部与拖缆尾部都出现了峰值,拖缆上97.3%的检波器平均DC偏差优于3.00m,70.1%的检波器平均DC偏差优于2.00m。由于该条测线作业时采用了前—中后声学网络配置(图 8),拖缆前中部存在约3.7km长的部分没有声学距离观测,导致检波器DC偏差在拖缆前中部会出现一个峰值,仿真实验的结果也验证了这一点。而在拖缆尾部出现的DC偏差的快速增长,可能是由于SPRINT软件在定位解算时对拖缆尾部采取了某些不同的处理。
|
图 10 检波器平均位置偏差随拖缆里程变化 (a)DA方向;(b)DC方向 |
计算罗盘方位观测值与声学距离观测值各个历元的残差RMS值并进行统计,结果如表 3所示。其中,罗盘方位观测值残差RMS小于0.6°,声学距离观测值残差RMS小于1.3m,说明本文算法的建模效果较好,所建立的拖缆模型内符精度较高。
|
|
表 3 定位观测值残差RMS统计 |
高精度拖缆定位算法是海上地震勘探作业的重要保障,是后续地震波数据高精度成像的关键,且该技术长期以来受到国外的封锁。为解决现有定位算法数学模型不严密、定位观测值利用不充分的问题,本文针对水下拖缆光滑的物理特性,建立了一种基于严密曲线积分的拖缆数学模型,使用一系列位置参数与形态参数描述拖缆,并基于该模型提出了一种多缆定位严密平差算法,该算法能充分利用不同类型的定位观测值估计拖缆参数。
仿真实验表明了本文算法显著优于传统的测边网定位算法,验证了新算法在理论上的可行性、优越性。实测数据实验表明了本文算法的定位结果与国外成熟商业软件SPRINT的定位结果较为接近,验证了新算法在实际应用中的有效性、可靠性。综合各实验数值结果,本文提出的基于曲线积分的多缆定位算法在测线和垂直测线方向上的定位精度分别小于1m和3m,满足现代海上地震勘探对于拖缆定位精度的需求。
需要指出的是,文中拖缆方位角多项式阶数是一个经验值,并未考虑海洋流态环境的影响。阶数是否合理以及如何顾及海洋流态环境优化阶数,还需结合实际数据开展进一步的研究与验证。
| [1] |
杜向东. 中国海上地震勘探技术新进展[J]. 石油物探, 2018, 57(3): 321-331. DU Xiangdong. Progress of seismic exploration technology in offshore China[J]. Geophysical Prospecting for Petroleum, 2018, 57(3): 321-331. DOI:10.3969/j.issn.1000-1441.2018.03.001 |
| [2] |
魏峥嵘, 裴彦良, 刘保华. 深拖式多道高分辨率地震探测系统在南海首次应用[J]. 石油地球物理勘探, 2020, 55(5): 965-972. WEI Zhengrong, PEI Yanliang, LIU Baohua. A new deep-towed, multi-channel high-resolution seismic system and its preliminary application in the South China Sea[J]. Oil Geophysical Prospecting, 2020, 55(5): 965-972. |
| [3] |
王增波, 黄少卿, 尚民强, 等. 深海拖缆地震数据采集实时质量控制[J]. 石油地球物理勘探, 2020, 55(增刊1): 9-14. WANG Zengbo, HUANG Shaoqing, SHANG Minqiang, et al. Research and application of real-time QC on marine towed cable acquisition[J]. Oil Geophysical Prospecting, 2020, 55(S1): 9-14. |
| [4] |
魏继东, 曹国滨, 刘斌. 检波器性能参数现场测定方法[J]. 石油地球物理勘探, 2021, 56(3): 446-461. WEI Jidong, CAO Guobin, LIU Bin. An approach of sensor parameters measuring in field[J]. Oil Geophysical Prospecting, 2021, 56(3): 446-461. |
| [5] |
张振波, 王征, 董水利, 等. 海上多源多缆地震采集综合导航定位数据处理技术[J]. 石油物探, 2013, 52(6): 630-635. ZHANG Zhenbo, WANG Zheng, DONG Shuili, et al. Integrated navigation and positioning data processing in offshore multi-sources and multi-streamers seismic survey[J]. Geophysical Prospecting for Petroleum, 2013, 52(6): 630-635. |
| [6] |
张昊楠, 阮福明, 胡广浩, 等. 海上三维拖缆综合导航系统关键定位算法[J]. 测绘科学技术学报, 2019, 36(5): 441-446. ZHANG Haonan, RUAN Fuming, HU Guanghao, et al. Key positioning algorithm of marine 3D towed streamer integrated navigation system[J]. Journal of Geomatics Science and Technology, 2019, 36(5): 441-446. |
| [7] |
GIKAS V N. Least Squares Filtering and Testing for Positioning and Quality Control During 3D Marine Seismic Surveys[D]. Newcastle University, Newcastle Upon Tyne, 1996.
|
| [8] |
周波, 宋伟伟, 易文婷. 二维深海勘探导航定位数据处理系统的设计[J]. 武汉大学学报信息科学版, 2010, 35(6): 705-707. ZHOU Bo, SONG Weiwei, YI Wenting. Navigation data processing for deep-sea exploration[J]. Geoma-tics and Information Science of Wuhan University, 2010, 35(6): 705-707. |
| [9] |
GILBERT D. Seismic streamer position and shape estimation[C]. OCEANS 81, 1981, 1077-1081.
|
| [10] |
GILBERT D. Performance characteristics of a three-dimensional array shape estimator[C]. OCEANS 82, 1982, 140-145.
|
| [11] |
ZINN N D, RAPATZ P J V. Positioning networks in 3D marine seismic[C]. Offshore Technology Confe-rence, 1993, OTC-7078-MS.
|
| [12] |
COMBIER V. Single streamer positioning[J]. Lithos, 2006, 8: 113-118. |
| [13] |
GOUTORBE B, COMBIER V. On the reconstruction of the shape of a seismic streamer[J]. Geophysics, 2010, 75(1): H1-H6. |
| [14] |
李晓东. 海上石油地震勘探多缆定位[J]. 海洋测绘, 1997(1): 23-30. LI Xiaodong. Multi cable positioning for offshore oil seismic exploration[J]. Hydrographic Surveying and Charting, 1997(1): 23-30. |
| [15] |
姚宜斌, 易文婷, 宋伟伟. 深海拖缆导航勘探数据处理算法研究[J]. 武汉大学学报信息科学版, 2010, 35(6): 698-701. YAO Yibin, YI Wenting, SONG Weiwei. Processing methods for navigation data of offshore towed strea-mer exploration[J]. Geomatics and Information Science of Wuhan University, 2010, 35(6): 698-701. |
| [16] |
易昌华, 曹国发, 方守川, 等. 深海拖缆勘探电缆形状确定方法研究[J]. 武汉大学学报信息科学版, 2010, 35(6): 702-704. YI Changhua, CAO Guofa, FANG Shouchuan, et al. Fitting of offshore towed streamer shapes[J]. Geomatics and Information Science of Wuhan University, 2010, 35(6): 702-704. |
| [17] |
易昌华. 拖缆式石油勘探导航定位数据处理关键技术研究及系统实现[D]. 湖北武汉: 武汉大学, 2013. YI Changhua. Study on Key Techniques of Navigation & Positioning Data Processing and System Development in Marine Seismic Streamer Operation[D]. Wuhan University, Wuhan, Hubei, 2013. |
| [18] |
孔振兴, 赖祖龙. 地震导航定位算法研究[J]. 测绘通报, 2018(增刊1): 17-21. KONG Zhenxing, LAI Zulong. Research on seismic navigation and localization algorithm[J]. Bulletin of Surveying and Mapping, 2018(S1): 17-21. |
| [19] |
易昌华, 方守川, 曹国发. 基于卡尔曼滤波的海上地震勘探导航定位算法[J]. 石油地球物理勘探, 2011, 46(1): 17-21. YI Changhua, FANG Shouchuan, CAO Guofa. Off-shore seismic exploration navigation and positioning algorithm based on Kalman filtering[J]. Oil Geophysical Prospecting, 2011, 46(1): 17-21. |
| [20] |
张昊楠, 胡广浩, 樊贞, 等. 基于RT-PPP技术的船体及浮标定位系统[J]. 测绘科学技术学报, 2019, 36(3): 233-237. ZHANG Haonan, HU Guanghao, FAN Zhen, et al. Vessel and buoy positioning system based on RT-PPP[J]. Journal of Geomatics Science and Technology, 2019, 36(3): 233-237. |
| [21] |
邓元军, 乔秀海, 李江, 等. 声学定位网络在海上拖缆三维地震勘探的应用[J]. 中国石油勘探, 2016, 21(2): 84-91. DENG Yuanjun, QIAO Xiuhai, LI Jiang, et al. Application of acoustic positioning network in 3D seismic exploration of offshore streamer[J]. China Petroleum Exploration, 2016, 21(2): 84-91. |
| [22] |
易昌华, 韩华, 方守川, 等. 海上地震勘探罗经鸟数据对拖缆空间位置的影响[J]. 石油地球物理勘探, 2015, 50(5): 809-814. YI Changhua, HAN Hua, FANG Shouchuan, et al. Compass data influence on towed streamer positioning in marine seismic[J]. Oil Geophysical Prospecting, 2015, 50(5): 809-814. |
| [23] |
李庆扬, 王能超, 易大义. 数值分析[M]. 5版. 北京: 清华大学出版社, 2008. LI Qingyang, WANG Nengchao, YI Dayi. Numerical Analysis[M]. 5th ed. Beijing: Tsinghua University Press, 2008. |



 匡翠林, 湖南省长沙市岳麓区清水路中南大学新校区地球科学楼,410083。Email:
匡翠林, 湖南省长沙市岳麓区清水路中南大学新校区地球科学楼,410083。Email: