② 油气藏地质及开发工程国家重点实验室(西南石油大学),四川成都 610500;
③ 电子科技大学信息与通信工程学院,四川成都 611731
② State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation (Southwest Petroleum University), Chengdu, Sichuan 610500, China;
③ School of Information and Communication Engineering, University of Electronic Science and Technology of China, Chengdu, Sichuan 611731, China
随着油气勘探的不断发展,低分辨率的地震数据无法揭示复杂构造的细节信息,难以满足当今油气勘探需求。提高地震资料的分辨率是地球物理领域的研究热点之一。
众所周知,地震资料的低频成分可反映岩性变化,决定了基本的速度结构[1]。丰富的低频信息可使储层反演结果更清晰、可靠[2],有利于岩性油气藏的识别[3]。地震信号的频带宽度影响地震资料的分辨率[1],但在实际采集过程中,地震波受地层吸收衰减、检波器畸变等因素的影响,往往导致高、低频信息的缺失。低频信息的缺失会导致子波旁瓣增大,地震记录出现假同相轴等[4-5],此外,它会影响特殊构造的成像,造成深层构造不清晰[6];高频信息的缺失会导致资料分辨率下降,地层细节显示不清。针对这些问题,许多学者在频率补偿方面进行了研究。频率补偿传统方法有反褶积、反Q滤波和谱均衡等,但都有各自的局限性。反褶积法可以恢复低频成分,但同时会增强有效频段外的低频噪声[7]。反Q滤波法存在精确估计Q值较困难的问题,Tonn[8]对常见的7种Q值计算方法进行了比较,发现没有哪一种方法可适用于普遍情况,其效果依赖于地震资料的质量。近年来,一些学者运用压缩感知[9-11]稀疏重构的思想重构地震信号,再用重构的信号恢复原始信号的频率信息[12-13]。韩立国等[14]、张莹[15]根据压缩感知和稀疏约束的原理对地震信号进行全频带补偿,全面拓宽了地震频带。丁燕等[16]用改进的宽带俞氏低通滤波器,对地震信号进行了低频补偿,解决了频谱叠加信号的失真问题。
虽然对地震信号频率补偿算法进行了改进,但面对庞大的地震数据,该算法计算效率仍然不高。大规模的地震数据处理属于计算密集型任务,随着高性能计算的发展,运用多核CPU或者运用图形处理器(Graphics Prossessing Unit, GPU)进行地震资料处理已经成为时代的趋势。张军华等[17]分析了高性能计算在地震勘探行业的发展现状;赵虎等[18]运用OpenACC编程模型对逆时偏移算法进行并行加速;张全等[19]在CPU/GPU异构平台上对抛物线拉东变换与地震相干体算法进行并行加速;张全等[20]、吴吉忠等[21]将高性能计算运用在地球物理勘探领域,有效提高了地震资料处理的效率。
本文基于CUDA(Compute Unified Device Ar-chitecture)平台,对基于压缩感知的频率补偿方法进行了分析和并行化实现。
1 频率补偿算法原理根据地震褶积模型,地震信号s可描述为地震子波w和地下反射系数r的卷积与随机噪声n的和
| $ \boldsymbol{s}=\boldsymbol{w} * \boldsymbol{r}+\boldsymbol{n} $ | (1) |
式中“*”表示卷积。其频率域表示形式为
| $ \boldsymbol{S}=\boldsymbol{W} \boldsymbol{R}+\boldsymbol{N}=\boldsymbol{W} \text{F} \boldsymbol{r}+\bf{N} $ | (2) |
式中:S、W、R、N分别为地震信号、地震子波、反射系数、噪声的傅里叶变换;F为傅里叶变换算子[22]。
由于地震子波在传播途中受到大地滤波的作用,其频带是有限带宽的。地震子波在与反射系数卷积的过程中,必然使反射系数的频谱成分受到损失,最后得到的地震记录在频域也是有限带宽的,在时域表现为分辨率不高。为得到更高分辨率的记录,需估计出地震子波和反射系数,并对地震子波频带进行扩展。最后用宽频子波与地层反射系数卷积得到宽频的、高分辨率的地震记录。
该算法处理对象为动校正后的叠前道集数据,整个算法处理流程主要包括如下六个步骤。
(1) 统计子波。假设反射系数为白噪声,子波的自相关近似等于地震记录的自相关[23-24]。根据地震记录的自相关可估计叠加道子波和随炮检距变化的子波集SW。
(2) 计算叠加道。叠加道集中的所有道并求平均值,在一定程度上消除噪声的影响。
(3) 求解叠加道反射系数位置。为求解叠加道地层反射系数r,构建如下目标函数
| $ \boldsymbol{J}=\frac{1}{2}\|\boldsymbol{W} \text{F} \boldsymbol{r}-\boldsymbol{S}\|_2^2+\lambda\|\boldsymbol{r}\|_1^1 $ | (3) |
式中:‖·‖22为L2范数约束,目的是使求解的r与子波卷积后与s的误差在平方意义上最小;‖·‖11为L1范数约束,目的是保证r的稀疏性;λ为权重调节因子,其值越大,表示L1范数占的权重就越大。该优化问题可用快速迭代软阈值算法(Fast Iterative Shrinkage-Thresholding Algorithm,FISTA)[25]求解。根据上述步骤求解出叠加道反射系数后,可确定叠加道反射系数的位置序列P。
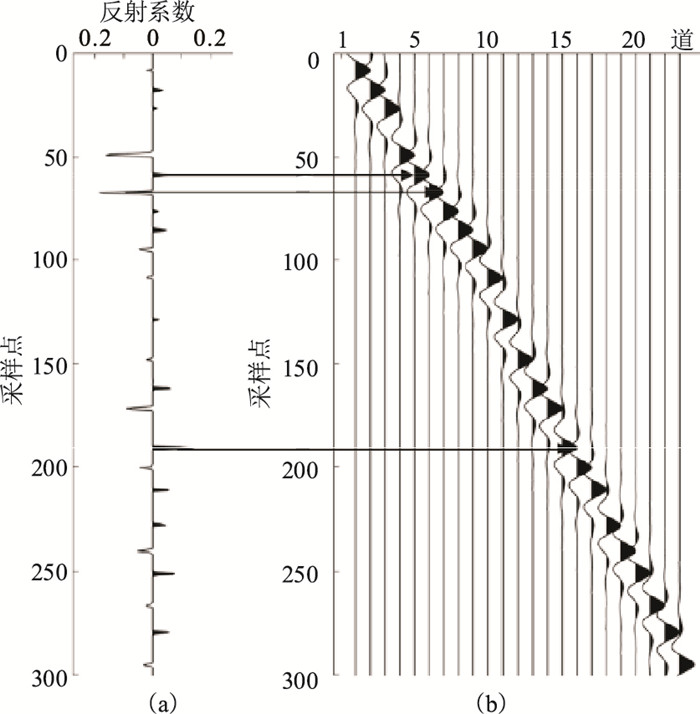
(4) 构建子波矩阵。根据反射系数位置可构建随炮检距变化的子波矩阵。每一道地震记录对应的子波应当从自相关统计的子波集SW中选取。假设一个地震道集第m道地震数据为dm,选取SW中第m个子波,根据步骤(3)获得的反射系数位置序列P,在强反射位置处为子波矩阵赋值,构建子波矩阵M(图 1)。
|
图 1 构造随炮检距变化子波矩阵示意图 (a)反射系数;(b)子波矩阵 |
(5) 计算每一道的反射系数。根据地震数据褶积模型,地震子波与反射系数卷积为线性变换过程,可以表示为子波矩阵与反射系数相乘的形式s=Mr(M可看作Toeplitz矩阵的特定列;r为反射系数除去零值后的序列,将卷积转化为矩阵相乘的形式便于计算,且利用反射系数的稀疏性节省了计算量),利用共轭梯度法[26-28]迭代求解可得到每一道的反射系数序列r,其步骤如下。
1) 任取r(0)∈Rn计算f(0)=s-Mr(0),取p(0)=f(0)。
2) 对于k=1, 2, …,计算
| $ \boldsymbol{\alpha}_k =\frac{\left\langle\boldsymbol{f}^{(k)}, \boldsymbol{f}^{(k)}\right\rangle}{\left\langle\boldsymbol{p}^{(k)}, \boldsymbol{M} \boldsymbol{p}^{(k)}\right\rangle} $ | (4) |
| $ \boldsymbol{r}^{(k+1)} =\boldsymbol{r}^{(k)}+\boldsymbol{\alpha}_k \boldsymbol{p}^{(k)} $ | (5) |
| $ \boldsymbol{f}^{(k+1)} =\boldsymbol{f}^{(k)}-\boldsymbol{\alpha}_k \boldsymbol{M} \boldsymbol{p}^{(k)} $ | (6) |
| $ \boldsymbol{\beta}_k =\frac{\left\langle\boldsymbol{f}^{(k+1)}, \boldsymbol{f}^{(k+1)}\right\rangle}{\left\langle\boldsymbol{f}^{(k)}, \boldsymbol{f}^{(k)}\right\rangle} $ | (7) |
| $ \boldsymbol{p}^{(k+1)} =\boldsymbol{f}^{(k+1)}+\boldsymbol{\beta}_k \boldsymbol{p}^{(k)} $ | (8) |
式中:k为迭代次数;f(k)为第k次迭代过程中的梯度向量;p(k)为第k次迭代过程中算法搜索方向;αk、βk分别为第k次迭代过程中的迭代梯度方向步长和搜索方向步长。
3) 当f(k)=0或小于误差限时停止计算,r(k)为反射系数的解。
(6) 将反射系数与宽频子波褶积得到拓频后的道集。
2 频率补偿算法的并行实现根据上述算法的计算过程,首先对算法的每一个步骤进行分段计时,分析算法的计算密集部分,然后针对该部分设计对应的并行方案。
2.1 计算瓶颈分析本文以道集为单位对CPU代码进行分段计时测试。测试环境:CPU为Intel Core(TM) i5900H;主频为2.40GHz;内存为8GB;操作系统为64位Windows10。测试数据为三维工区CRP道集,主测线范围为2201~2401,联络测线范围为1500~1700,每个道集有51道,每道有376个样点,采样间隔为4ms。测试结果为100次计时结果的平均值。主函数平均用时为183ms,步骤(1)~步骤(6)的用时和用时占比如表 1所示。
|
|
表 1 各步骤耗时及占比 |
由表 1可知,步骤(4)~步骤(5)为算法相对耗时的部分,为并行改进的重点。
2.2 并行算法流程步骤(4)、步骤(5)为算法最耗时的部分,也是本文算法改进的重点。在步骤(4)构造子波矩阵时,每一道的子波矩阵互相独立,涉及到大量赋值操作;在步骤(5)计算反射系数时,每一道反射系数的计算相互独立,运用共轭梯度法求解需要大量矩阵运算,矩阵运算天然地适用于并行。
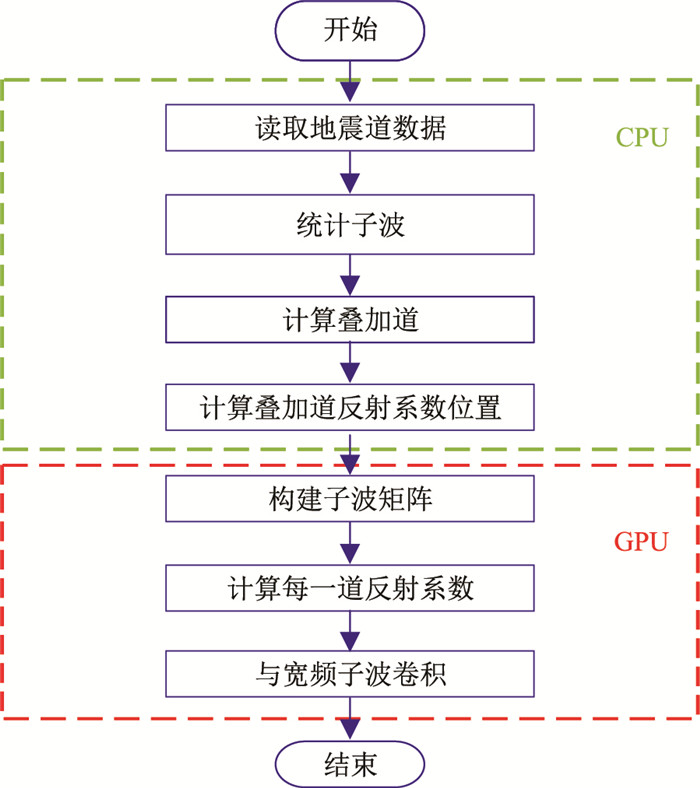
由于CPU和GPU不能直接互相访问各自的存储器,当GPU执行计算任务时,要将计算所需数据从CPU内存通过PCIE总线拷贝到GPU显存。这种数据拷贝目前无法避免,会增加额外的存取开销。为尽量减少额外开销,本文将关联性较强的子波矩阵和计算反射系数过程合并为一个处理模块,卷积操作为一个处理模块,两个模块在GPU端运行。将GPU端计算完成后的计算结果拷贝到CPU内存进行后续处理。根据分步骤的计时结果,统计子波、计算叠加道、确定反射系数位置这几个模块耗时较少,且不属于计算密集过程,需要在CPU端单独处理。并行改进后的算法流程如图 2所示。
|
图 2 低频补偿GPU并行算法流程 |
根据并行算法的计算过程,本文对算法最后三个步骤设计了不同的并行方案。在构造子波矩阵过程和求解反射系数过程中,首先分析了计算任务之间的独立性,然后将可并行的任务进行拆解,最后利用GPU大量轻量级的线程对任务进行细粒度的并行实现。两信号的卷积部分利用卷积定理,先将两个时域信号通过傅里叶变换转换到频域,再将两个频域信号点乘,再通过傅里叶逆变换将信号转换回时间域,并通过cufft库进行优化。此外,本文计算之前对地震信号数据进行了重新排列,并对数据访存进行优化。
2.3.1 构造子波矩阵CUDA的线程(thread)以计算网格(grid)的形式进行组织。一个grid可划分成多个块(block),一个block可包含多个thread,每一个block和thread都有自己的索引编号。当核函数(kernel)执行时,处于激活状态的thread将对kernel函数编译后的指令同时调用、执行,根据thread编号实现对不同显存区的操作。
对于每一个子波矩阵,需要对n个不同的位置赋值子波,彼此之间相互独立,因此分配n个block对应n个计算位置。block0对应0号采样点位置,block1对应1号采样点位置,依此类推。由于线程数一般以2的整数次幂进行分配,因此对每一个block分配256个thread,每一个thread对应一个子波的采样点。如此分配可以达到子波采样点数量级别的并行度。
如果子波长度超过256采样点,每一个block将进行多次计算,直到将子波的所有采样点被覆盖为止。对于计算能力强的GPU,可将每个block的线程数增加,比如分配512个thread。这些设置可根据计算任务的不同进行调整。
2.3.2 计算反射系数用共轭梯度法进行反射系数求解时用到大量矩阵相乘运算。子波矩阵在逻辑上可看作一个二维矩阵,多个子波矩阵数据排列可看作一个三维的数据体。地震记录可看作一维向量,多道地震记录排列可以看作一个二维数据体。因此,本文对道集数据进行处理时,先将地震道集数据拷贝到显存中统一以一维数组的形式进行存储。每一道数据紧接着上一道数据进行排列,访问数据时通过首地址加地址偏移量的方式寻址。道集对应的子波矩阵也采用同样的排列方式存储在一维数组中。这样的内存存放有利于适应thread的访存机制。对于同样大小的数据量,CUDA的thread连续寻址比跳跃寻址更快。在计算矩阵相乘的时候,相邻的thread访问相邻的内存区域,可大大提高存取效率。计算时,每一个子波矩阵与其对应的地震道进行迭代求解。在一个grid中分配多个block,每一个block负责一个子波矩阵和对应地震道的迭代求解。每一个block内,分配256个thread。
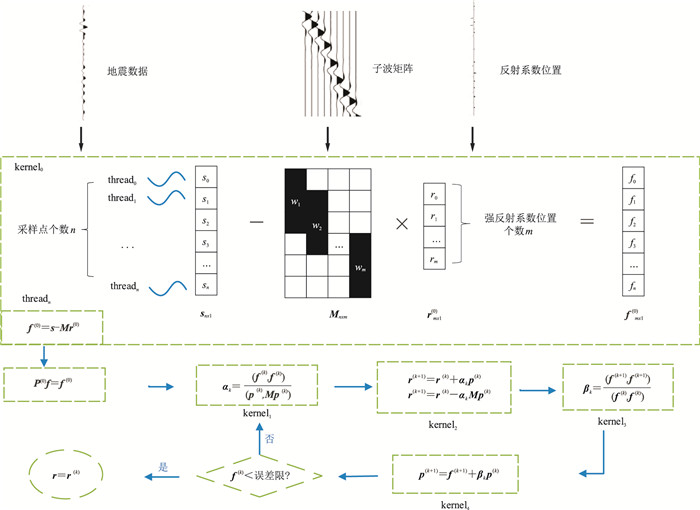
如图 3所示,以block0的计算为例:block0分配256个thread,每一个thread对应一个不同的采样点,如果采样点数n大于256则进行多轮计算。地震信号长度为n,反射系数位置个数为m,子波矩阵大小为n行、m列。将地震子波与反射系数卷积过程变为矩阵相乘的形式,r(0)为反射系数位置序列,计算矩阵与向量相乘时,线程编号与采样点编号对应,一个线程负责m次相乘累加操作。r初始值可选取步骤(3)叠加道反射系数位置的值。计算α、β、f、p变量可根据式(4)~式(8)拆分成n×m维矩阵与长度为m的向量乘法操作、长度为n的向量内积、长度为n的向量加法操作。首先,调用kernel0计算f(0)=s-Mr(0);其次,调用kernel1计算α;再次,调用kernel2更新r和f,调用kernel3再一次计算β;最后,调用kernel4更新变量p。由于kernel函数包含隐式同步,可以保证上一步向量更新完毕再进行下一步计算,符合该算法的数据依赖关系。经过多次迭代直到f小于误差限时跳出循环,得到反射系数序列r。在计算完成后,根据反射系数的位置索引,将r的值赋给初始化为零的长度为n的数组中,得到最终的反射系数序列。由于共轭梯度法具有二次终止性,理论上通过n次迭代可得到精确解。实际工程中可设置固定的迭代次数以满足精度要求。本文最终选定的迭代次数为5。
|
图 3 计算反射系数 |
在子波矩阵和地震道数据相乘时,地震道的数据是重复利用的,子波矩阵的每一行需与对应的反射系数相乘。因此,可将初始化反射系数事先存入共享内存进行加速。全局内存对所有的thread可见,共享内存只对同一个block的thread可见。但是共享内存带宽大约为1.5TB·s-1,远高于全局内存带宽190GB·s-1。在子波矩阵与地震数据进行乘法计算时,从共享内存中读取数据,大大提高了存取效率。
2.3.3 重构宽频地震记录原始版本的宽频地震记录重构方法是将反射系数与宽频子波卷积得到拓频的地震记录,假设反射系数与子波采样点数均为N,对于每一个采样点位置,需要进行N次相乘再相加的操作,时间复杂度为O(N2)。根据频率域卷积定理,两个函数卷积的傅里叶变换是函数傅里叶变换的乘积。
快速傅里叶变换时间复杂度为O(NlbN),向量点乘时间复杂度为O(N),改进后的算法需要两次傅里叶正变换,一次傅里叶逆变换,一次长度为N的向量点乘,总体时间复杂度为3O(NlbN)+O(N)。
可见将时间域卷积计算方式改为频率域点乘,再进行逆傅里叶变换,可有效降低算法的时间复杂度。在频率域点乘改进的基础上,将算法部署到GPU设备上进行,傅里叶变换部分采用cuFFT库进行。在本次计算任务中,傅里叶正变换为从实向量到复数向量的变换,该变换后的向量为共轭对称复向量。假设向量长度为J,运用cufftExecR2C句柄只用计算前J/2+1个值。向量点乘时由于共轭对称复向量点乘计算结果仍然共轭对称,所以只计算J/2+1长度的向量点乘结果。如此,相对于常规的复数形式的傅里叶变换可以节省约一半的计算量。计算后的向量仍然共轭对称,运用cufftExec-C2R句柄,将长度为J/2+1的复向量逆变换到时域,结果为长度为J的实向量。计算共轭复向量点乘时,由于每一个采样点的计算互相独立,具有良好的并行性。核函数进行计算时,每一个thread负责一个采样点的乘法计算并且互不影响,如此可达到采样点数量级别的并行度。
3 应用用实际地震数据对本文的GPU改进版进行精度和速度测试,计算环境与算法瓶颈分析平台相同。精度测试中,比较了GPU改进版本与CPU版本对单一道集处理结果的误差,展示了算法对单一道集的处理效果,以及该算法对叠加剖面成图效果的影响;速度测试中,比较了对单一道集和多道集数据两个版本的计算效率。
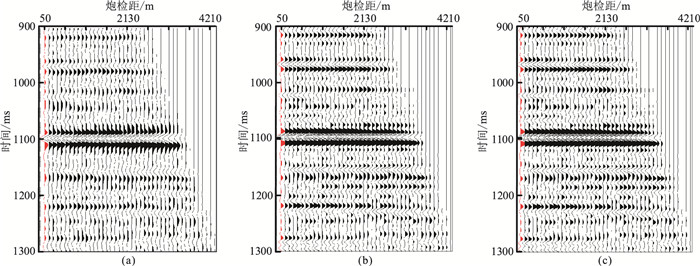
3.1 CPU与GPU算法精度比较测试数据为川西地区实际地震数据,Inline、Xline测线数均为1000,每一个道集包含51道,每一道包含2000个采样点。图 4a为算法处理前的共反射点道集;图 4b为CPU版本处理后的共反射点道集;图 4c为GPU版本算法处理后的共反射点道集。对比图 4a和图 4b可以看出,低频补偿之前同相轴不连续,低频补偿后,强轴反射位置更加突出,一些隐蔽的同相轴得以显现。比较CPU(图 4b)与GPU版本(图 4c)的计算结果,可见二者基本一致,相对误差在10-6数量级内,跟浮点数的存储形式和浮点数计算舍入误差有关,在单精度浮点数计算误差范围内。
|
图 4 CPU与GPU版本道集处理结果对比 (a)频率补偿前道集;(b)CPU版本处理结果;(c)GPU版本处理结果 |
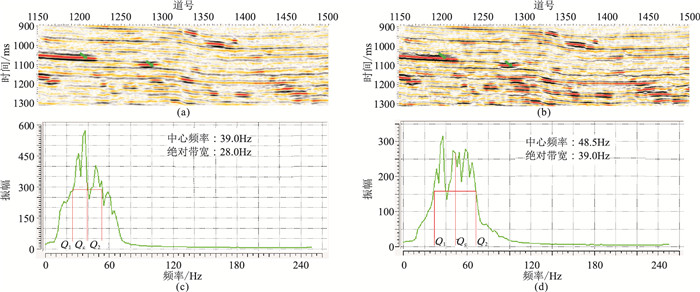
图 5a、图 5b分别为频率补偿前和本文的CPU版本处理后的叠加剖面。可见,频率补偿后叠加剖面层位特征更明显,绿色箭头处标志层位的细节更加丰富。对比频率补偿前、后的叠加剖面的频谱可以发现:补偿前中心频率Qc为39.0Hz,绝对带宽(Q2-Q1)为28.0Hz(图 5c);补偿后中心频率为48.5Hz,绝对带宽为39.0Hz(图 5d),主频提升了9.0Hz,有效带宽拓展了11.0Hz。
|
图 5 叠加剖面计算结果 (a)补偿前叠加剖面;(b)补偿后叠加剖面;(c)补偿前剖面频谱图;(d)补偿后剖面频谱图 |
以上实例说明本文的GPU改进版本的有效性。
3.2 CPU与GPU版本算法速度比较首先讨论了共轭梯度法求解反射系数过程中,迭代次数对于算法效率及精度的影响。然后比较了在相同迭代次数条件下CPU版本与GPU版本的计算效率。
3.2.1 迭代次数对算法耗时和精度的影响本文对不同精度的计算结果进行了测试。迭代次数为3时,相对误差较大不满足要求;迭代次数为5次时,前、后两次计算结果的相对误差在10-2数量级内;迭代次数为11时,计算结果相对误差在10-3数量级;迭代次数为21时,计算结果相对误差在10-5数量级。迭代次数越多,算法的精度越高,计算越耗时。但是,迭代次数对CPU版本算法的效率和GPU版本算法的影响并不相同。本文对工区中200个道集的数据进行了不同迭代次数的处理,测试结果如表 2所示。
|
|
表 2 迭代次数对算法性能的影响 |
可见,迭代次数的增加对CPU版本的影响较大,对GPU版本则影响较小。该结果间接验证了并行算法的有效性。如果实际工程要求更高精度的计算结果,需要人为增加迭代次数,GPU版本增加的时间成本远小于CPU版本,为更高精度的频率补偿提供了可能。由于相对误差在10-2数量级内已经满足精度要求,后续测试的迭代次数均设为5。
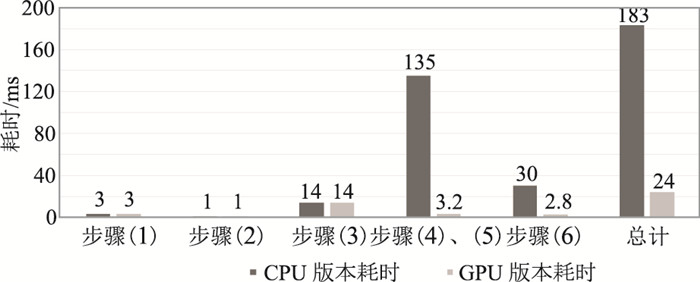
3.2.2 相同迭代次数CPU与GPU版本的计算速度首先对单一道集进行测试,用C++计时函数计时。由于改进后算法耗时较少,为保持测试结果相对准确,GPU版本计时采用1000次计算的平均值,CPU串行程序版本和GPU并行程序版本计时结果如图 6所示。
|
图 6 CPU与GPU版本各步骤耗时对比 |
为测试该算法模块的总体加速效果,选用该工区多道地震数据进行测试。测试软件为RevScope 3.5.4,计时工具为软件自带计时模块。在保证结果正确的前提下,计算GPU版本的加速比
| $ R=\frac{T_{\mathrm{c}}}{T_{\mathrm{g}}} $ | (9) |
式中:Tg为GPU改进版本总体运行时间;Tc为CPU版本总体运行时间。测试结果如表 3所示。
|
|
表 3 GPU版本算法性能测试结果 |
单一道集测试结果表明,算法计算时间由原来的183ms下降到24ms,加速比可达7.6倍,改进版本加速效果明显。步骤(4)+步骤(5)的计算时间由原来的135ms下降到3.2ms;步骤(6)计算时间由30ms下降到2.8ms。改进后算法瓶颈在于步骤(3),但是这一模块的求解算法为快速迭代收缩阈值算法,此迭代算法求解过程中,数据依赖非常强,不适合并行化,因此本文没有对该模块并行优化。
实际软件运行该处理模块时,工区测试结果加速比较道集测试结果加速比偏低。这是由于除了本文算法部分,测试软件端还有额外的开销,比如额外的函数调用。此外在处理规模较大工区数据时,会先将道集数据按批次从硬盘拷贝至内存。这些额外的开销会增加算法处理时间,导致加速比降低,属于正常现象。
4 结论与认识本文对频率补偿算法进行分析,发现耗时的主要步骤是计算反射系数、子波与反射系数的卷积。
(1) 本文对该算法耗时的部分进行重新设计,将求解反射系数部分设计成并行算法,通过CUDA将算法重写并部署在GPU上进行。将计算地震子波与地层反射系数卷积部分,从时间域计算改为频率域计算,并部署在GPU上进行。在PC端运算时,GPU版本相对于CPU版本算法加速比可达4倍以上,明显降低了地震数据处理的时间成本。
(2) 本文对比了CPU版本和GPU版本共轭梯度法求解反射系数过程中,迭代次数对计算精度与计算时间的影响。结果表明,迭代次数增加在提高计算精度的同时,也会增加计算时间,并且对CPU版本计算效率的影响较大。本文并行算法可有效降低迭代次数增加带来的时间成本。
成都晶石石油软件有限公司提供了GEO-SCOPE地质放大镜软件,在此深表感谢!
| [1] |
管路平, 唐权钧. 地震信号的高低频成分补偿[J]. 石油物探, 1990, 29(3): 35-45. GUAN Luping, TANG Quanjun. High/low frequency compensation of seismic signal[J]. Geophysical Prospecting for Petroleum, 1990, 29(3): 35-45. |
| [2] |
谷玉田, 魏继东, 张旭, 等. 陆上勘探低频信号的接收与恢复[J]. 石油物探, 2021, 60(4): 539-545. GU Yutian, WEI Jidong, ZHANG Xu, et al. Sensing and recovery of low-frequency signals in onshore surveys[J]. Geophysical Prospecting for Petroleum, 2021, 60(4): 539-545. DOI:10.3969/j.issn.1000-1441.2021.04.002 |
| [3] |
ZHI L X, CHEN S Q, LI X Y. Amplitude variation with angle inversion using the exact Zoeppritz equa-tions: Theory and methodology[J]. Geophysics, 2016, 81(2): N1-N15. DOI:10.1190/geo2014-0582.1 |
| [4] |
ZHANG Junhua, ZHANG Binbin, ZHANG Zaijin, et al. Low-frequency data analysis and expansion[J]. Applied Geophysics, 2015, 12(2): 212-220, 275. DOI:10.1007/s11770-015-0484-2 |
| [5] |
KROODE F T, BERGLER S, CORSTEN C, et al. Broadband seismic data: The importance of low fre-quencies[J]. Geophysics, 2013, 78(2): WA3-WA14. DOI:10.1190/geo2012-0294.1 |
| [6] |
张军华, 张在金, 张彬彬, 等. 地震低频信号对关键处理环节的影响分析[J]. 石油地球物理勘探, 2016, 51(1): 54-62. ZHANG Junhua, ZHANG Zaijin, ZHANG Binbin, et al. Low frequency signal influences on key seismic data processing procedures[J]. Oil Geophysical Prospecting, 2016, 51(1): 54-62. |
| [7] |
魏继东. 检波器反褶积对低频信息的补偿作用[J]. 石油地球物理勘探, 2016, 51(2): 224-231. WEI Jidong. Geophone deconvolution low-frequency compensation for seismic data[J]. Oil Geophysical Prospecting, 2016, 51(2): 224-231. |
| [8] |
TONN R. The determination of the seismic quality factor Q from VSP data: a comparison of different computational methods[J]. Geophysical Prospec-ting, 1991, 39(1): 1-27. DOI:10.1111/j.1365-2478.1991.tb00298.x |
| [9] |
段中钰, 李婷婷, 肖勇, 等. 基于压缩感知的SR-ADMM地震数据重建[J]. 石油地球物理勘探, 2021, 56(6): 1220-1228. DUAN Zhongyu, LI Tingting, XIAO Yong, et al. Seismic data Reconstruction by SR-ADMM algorithm based on compressed sensing[J]. Oil Geophysical Prospecting, 2021, 56(6): 1220-1228. |
| [10] |
张军华, 王静, 王延光, 等. 基于压缩感知的反射系数域沿层L2范数约束去强屏蔽方法[J]. 石油地球物理勘探, 2022, 57(2): 405-413. ZHANG Junhua, WANG Jing, WANG Yanguang, et al. A strong shielding removal of reflection coefficient domain based on compressed sensing with L2 norm constraint along layer[J]. Oil Geophysical Prospecting, 2022, 57(2): 405-413. |
| [11] |
闫海洋, 周辉, 刘海波, 等. FK和Shearlet域联合压缩感知数据重构技术[J]. 石油地球物理勘探, 2022, 57(3): 557-569, 491. YAN Haiyang, ZHOU Hui, LIU Haibo, et al. Com-pressed sensing data reconstruction technology in joint FK and Shearlet domain[J]. Oil Geophysical Prospecting, 2022, 57(3): 557-569, 491. |
| [12] |
CANDÈS E J. Compressive sampling[C]. Procee-dings on the International Congress of Mathemati-cians, 2006, 1433-1452.
|
| [13] |
韩红平. 压缩感知中信号重构算法的研究[D]. 江苏南京: 南京邮电大学, 2012. HAN Hongping. Research on Signal Reconstruction Algorithm of Compressive Sense[D]. Nanjing Uni-versity of Posts and Telecommunications, Nanjing, Jiangsu, 2012. |
| [14] |
韩立国, 张莹, 韩利, 等. 基于压缩感知和稀疏反演的地震数据低频补偿[J]. 吉林大学学报(地球科学版), 2012, 42(增刊3): 259-264. HAN Liguo, ZHANG Ying, HAN Li, et al. Com-pressed sensing and sparse inversion based low-frequency information compensation of seismic data[J]. Journal of Jilin University (Earth Science Edition), 2012, 42(S3): 259-264. |
| [15] |
张莹. 基于压缩感知和稀疏反演的低频补偿方法研究[D]. 吉林长春: 吉林大学, 2013. ZHANG Ying. A Study on Low-frequency Compen-sation Based on Compressed Sensing and Sparse In-version[D]. Jilin University, Changchun, Jilin, 2013. |
| [16] |
丁燕, 杜启振, 刘力辉, 等. 基于压缩感知和宽带俞式低通整形滤波器的地震低频信息特征分析与补偿[J]. 地球物理学报, 2019, 62(6): 2267-2275. DING Yan, DU Qizhen, LIU Lihui, et al. Feature analysis and compensation of seismic low-frequency based on compressed sensing and broad-band Yu-type low-passing shaping filter[J]. Chinese Journal of Geophysics, 2019, 62(6): 2267-2275. |
| [17] |
张军华, 臧胜涛, 单联瑜, 等. 高性能计算的发展现状及趋势[J]. 石油地球物理勘探, 2010, 45(6): 918-925. ZHANG Junhua, ZANG Shengtao, SHAN Lianyu, et al. Development status and trends for high per-formance computing[J]. Oil Geophysical Prospecting, 2010, 45(6): 918-925. |
| [18] |
赵虎, 武泗海, 尹成, 等. 基于OpenACC编程模型的逆时偏移多级并行的设计与优化[J]. 石油地球物理勘探, 2018, 53(6): 1307-1313, 1325. ZHAO Hu, WU Sihai, YIN Cheng, et al. Multi-level parallel design and optimization for reverse time mi-gration based on OpenACC programming model[J]. Oil Geophysical Prospecting, 2018, 53(6): 1307-1313, 1325. |
| [19] |
张全, 林柏栎, 杨勃, 等. CPU-GPU异构平台的抛物线Radon变换并行算法[J]. 石油地球物理勘探, 2020, 55(6): 1263-1270. ZHANG Quan, LIN Baiyue, YANG Bo, et al. Parabolic Radon transform parallel algorithm for CPU-GPU heterogeneous platform[J]. Oil Geophysical Prospecting, 2020, 55(6): 1263-1270. |
| [20] |
张全, 林柏栎, 彭博, 等. 基于CUDA的地震相干体并行算法[J]. 地质与勘探, 2020, 56(1): 147-153. ZHANG Quan, LIN Baiyue, PENG Bo, et al. Seismic coherence parallel algorithm based on CUDA[J]. Geology and Exploration, 2020, 56(1): 147-153. |
| [21] |
吴吉忠, 左虎. 叠前衰减补偿时间偏移及GPU实现[J]. 石油地球物理勘探, 2019, 54(1): 84-92. WU Jizhong, ZUO Hu. Attenuation compensation in prestack time migration and its GPU implementation[J]. Oil Geophysical Prospecting, 2019, 54(1): 84-92. |
| [22] |
陆基孟. 地震勘探原理[M]. 北京: 石油工业出版社, 1982. LU Jimeng. Principles of Seismic Exploration[M]. Beijing: Petroleum Industry Press, 1982. |
| [23] |
隋宇涵. 地震时变子波估计与盲稀疏脉冲反褶积[D]. 黑龙江哈尔滨: 哈尔滨工业大学, 2020. SUI Yuhan. Seismic Time-Varying Wavelet Estimation and Blind Sparse-Spike Deconvolution[D]. Harbin Institute of Technology, Harbin, Heilongjiang, 2020. |
| [24] |
戴永寿, 张彧豪, 张鹏, 等. 时变地震子波提取研究方法综述[J]. 石油物探, 2020, 59(2): 169-176. DAI Yongshou, ZHANG Yuhao, ZHANG Peng, et al. A review on time-varying seismic wavelet extraction[J]. Geophysical Prospecting for Petroleum, 2020, 59(2): 169-176. |
| [25] |
BECK A, TEBOULLE M. A fast iterative Shrinkage-Thresholding algorithm for linear inverse problems[J]. SIAM Journal on Imaging Sciences, 2009, 2(1): 183-202. |
| [26] |
李庆扬, 王能超, 易大义. 数值分析[M]. 第5版. 北京: 清华大学出版社, 2008. LI Qingyang, WANG Nengchao, YI Dayi. Numerical Analysis[M]. 5th Edition. Beijing: Tsinghua University Press, 2008. |
| [27] |
周竹生, 何继善, 赵荷晴. 利用广义共轭梯度算法求解地震道反演问题[J]. 石油地球物理勘探, 1998, 33(4): 439-447, 476-572. ZHOU Zhusheng, HE Jishan, ZHAO Heqing. Solving a seismic trace inversion problem by using gene-ralized conjugate gradient algorithm[J]. Oil Geophy-sical Prospecting, 1998, 33(4): 439-447, 476-572. |
| [28] |
刘宇航, 黄建平, 杨继东, 等. 弹性波全波形反演中的四种优化方法对比[J]. 石油地球物理勘探, 2022, 57(1): 118-128. LIU Yuhang, HUANG Jianping, YANG Jidong, et al. Comparison of four optimization methods in elastic full-waveform inversion[J]. Oil Geophysical Pro-specting, 2022, 57(1): 118-128. |



 彭博, 四川省成都市新都区新都大道8号西南石油大学(成都校区)计算机科学学院,610500。Email:
彭博, 四川省成都市新都区新都大道8号西南石油大学(成都校区)计算机科学学院,610500。Email: 