② 北京海洋声学装备工程技术研究中心,北京 100091;
③ 长安大学地质工程与测绘学院,陕西西安 710054;
④ 长安大学地球物理场多参数综合模拟实验室,陕西西安 710054
② Beijing Engineering Technology Research Center of Ocean Acoustic Equipment, Beijing 100091, China;
③ School of Geological Engineering and Geomatics, Chang'an University, Xi'an, Shaanxi 710054, China;
④ Integrated Geophysical Simulation Lab of Chang'an University (Key Laboratory of Chinese Geophysical Society), Xi'an, Shaanxi 710054, China
随着中国海洋强国战略的实施,海洋经济逐渐成为社会经济的重要组成部分,产业结构不断优化,海洋地质、海洋能源、海洋环境、海洋运输等领域快速发展[1-2]。瞬变电磁法(TEM)作为重要的地球物理探测手段,在海洋资源勘探、海洋地质探测及海洋工程与环境监测等方面显示出广阔的应用前景[3-8]。
海洋磁性源瞬变电磁法是一种时间域感应电磁方法,该方法采用磁性源作为发射源,具有体积效应小、与目标体耦合强等优点。为提高观测效率,海洋磁性源瞬变电磁法多采用船载拖曳式观测方式,在海水中进行发射和观测,具有快速、有效、便于实施的特点[9-11]。与陆域瞬变电磁探测相比,海洋瞬变电磁的探测目标受海水及海底沉积层的影响,电磁响应极易受水文、气象等环境因素影响,数据采集难度大,干扰强。在实际海洋TEM数据采集中,由于海底环境、洋流、航速不均等因素的影响,发射和接收回线装置在海水中的姿态难以保持稳定。常见的姿态变化包括横摇(Rolling)、纵摇(Pitching)、艏摇(Yawing)、拖体升沉变化(垂荡Heaving)、航行速度变化(线圈位置同向变化)。探测系统收、发回线姿态变化会导致其与目标体的耦合关系发生变化,带来观测误差,产生假异常,严重时可能造成水下重要小尺度目标体的漏检,同时也会对数据处理和资料解释造成较大影响。
对于移动平台瞬变电磁探测系统,海洋磁性源探测系统与航空探测系统在工作方式上有许多相似之处,不同的是前者的收、发线圈均置于海水中,导电性能良好的海水对电磁场的影响与空气对电磁场的影响差别较大。因此,需要结合海洋环境特点对海洋磁性源瞬变电磁探测系统进行研究,不能简单照搬航空系统的理论。
近年来,随着航空瞬变电磁系统的迅速发展,针对航空系统线圈姿态变化及校正的技术已相对成熟。Yin等[12]和Fitterman等[13]基于重叠偶极子理论给出三种常用线圈架构的航空频率域电磁系统的校正因子,对实测航空电磁数据进行姿态影响校正。在此基础上,嵇艳鞠等[14]研究了直升机瞬变电磁中心回线装置的单一姿态变化的影响,并对其进行了校正处理。王琦等[15]研究了发射、接收线圈姿态变化及吊舱横摇对固定翼时间域电磁响应的影响,并利用Occam反演对姿态变化的影响进行校正。贲放等[16]对Yin等[12]和Fitterman等[13]讨论的频率域航空电磁系统姿态变化的影响进行了分析,并改进其校正方法,同时考虑姿态角度变化及收、发线圈位置变化对航空瞬变电磁响应的影响,并基于重叠偶极子理论给出姿态校正因子。朱凯光等[17]针对固定翼航空电磁系统的姿态变化动态响应及静态响应进行分析,并基于BP神经网络进行姿态变化静态响应校正。
对海洋电磁探测系统中发射源姿态变化影响的研究始于二十世纪八十年代,主要集中在频率域可控源电磁勘探领域。Chave等[18]实现了海底为一维层状介质模型的电偶源电磁正演,指出在给定频率范围内,水平电偶源较垂直电偶源具有更强的信号振幅。Key[19]推导了水平层状介质中任意电偶极源场的频率域表达式,并通过正演计算分析了Inline、Broadside和Vertical三个方向发射源所产生的电磁场分布特征,并对海洋层状介质模型进行了一维反演,指出采用Inline方向的电偶极源能够得到地下介质更准确的电阻率分布。以上研究体现了海洋电磁方法电性源发射方向的任意性。刘云鹤等[20]利用欧拉旋转将发射源由源坐标系转换到大地坐标系,并研究了发射源姿态发生水平横摇、倾斜和水平旋转三种形式组合所产生的海洋电磁观测数据误差分布特征,最后指出,对于发射源水平横摇和倾斜造成的数据畸变,其分布规律取决于收发距大小。罗鸣等[21]针对海底为电阻率垂直各向异性的层状介质模型,对发射源与接收站在不同姿态、位置下的海洋可控源电磁响应进行模拟,分析了海洋可控源电磁观测系统发射源和接收站的姿态和位置变化引起电磁数据误差的机制。
上述文献研究表明,目前针对移动平台磁性源TEM系统姿态变化的影响研究主要集中在航空系统,相关研究思路和成果可为海洋磁性源TEM探测系统姿态影响分析提供参考。
目前海上油气勘探引领了海洋地球物理探测的主流技术发展方向,相关研究集中在深海频率域水平电性源探测系统[22-23]。相比磁性源,水平电性源姿态变化更简单。深海环境下可以忽略海水深度的影响,研究空间可等效为半空间模型;浅海环境下则需要考虑海水与空气界面的影响,计算相对复杂。目前针对有限水深条件下的时间域海洋磁性源系统的姿态影响研究还鲜见相关文献发表。
本文从电磁场麦克斯韦方程组出发,推导了有限水深条件下各向同性水平层状介质中任意磁偶极源的频率域电磁场表达式,在借鉴航空系统姿态相关研究成果的基础上,通过发射、接收双旋转矩阵及磁场格林张量的矩阵形式,建立了水下拖曳式磁性源姿态变化数学模型。基于模型算例,分析了磁性源瞬变电磁线圈姿态变化对电磁场的影响,进一步分析姿态变化下的电磁响应与衰减时间、海水深度、海底沉积层电性等参数之间的关系。
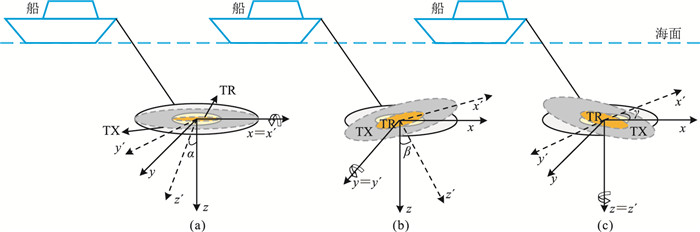
1 基本理论 1.1 磁性源瞬变电磁探测系统姿态变化为描述拖曳式磁性源瞬变电磁探测系统的工作原理,以海洋瞬变电磁收、发回线装置姿态变化为例,建立图 1所示的两个直角坐标系(以中心回线装置为例)。一个为系统坐标系P(x, y, z),该坐标系不随发射源姿态的变化而变化,x轴与航行方向一致,y轴与航行方向垂直,z轴垂直向下。另一个坐标系称为线圈坐标系P′(x′, y′, z′),它是描述发射与接收线圈姿态变化后的坐标系,该坐标系随发射线圈(TX)和接收线圈(TR)位置和方向的变化而改变。在理想航行状态(不存在姿态变化)时,这两个坐标系重合。
|
图 1 船载拖曳式磁性源瞬变电磁系统姿态变化示意图(以中心回线装置为例) (a)横摇变化;(b)纵摇变化;(c)艏摇变化 |
拖曳式磁性源水下瞬变电磁探测系统常见的姿态变化有:①横摇变化,即线圈绕x轴旋转;②纵摇变化,即线圈绕y轴旋转;③艏摇变化,即线圈绕z轴旋转;④航行速度变化,即线圈沿航迹或垂直航迹方向发生位置偏移;⑤拖体升沉变化,即线圈位置沿z方向变化。姿态变化①~③见图 1,姿态变化④、⑤简单、易于理解,本文不做详述。
系统坐标系与线圈坐标系的关系可表示为
| $ \boldsymbol{P}=\boldsymbol{R}_\alpha \boldsymbol{R}_\beta \boldsymbol{R}_\gamma \boldsymbol{P}^{\prime}=\boldsymbol{R}_{\alpha \beta \gamma} \boldsymbol{P}^{\prime} $ | (1) |
其中
| $ \left\{\begin{array}{l} \boldsymbol{R}_\alpha=\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha \\ 0 & \sin \alpha & \cos \alpha \end{array}\right] \\ \boldsymbol{R}_\beta=\left[\begin{array}{ccc} \cos \beta & 0 & -\sin \beta \\ 0 & 1 & 0 \\ \sin \beta & 0 & \cos \beta \end{array}\right] \\ \boldsymbol{R}_\gamma=\left[\begin{array}{ccc} \cos \gamma & -\sin \gamma & 0 \\ \sin \gamma & \cos \gamma & 0 \\ 0 & 0 & 1 \end{array}\right] \end{array}\right. $ | (2) |
| $ \boldsymbol{R}_{\alpha \beta \gamma}=\left[\begin{array}{lll} R_{11} & R_{12} & R_{13} \\ R_{21} & R_{22} & R_{23} \\ R_{31} & R_{32} & R_{33} \end{array}\right] $ | (3) |
式中:R11=cosβcosγ;R12=-cosαsinγ+sinαsinβ×cosγ;R13=sinαsinγ+cosαsinβcosγ;R21=cosβsinγ;R22=cosαcosγ+sinαsinβsinγ;R23=-sinαcosγ+cosαsinβsinγ;R31=-sinβ;R32=sinαcosβ;R33=cosαcosβ;α、β、γ和Rα、Rβ、Rγ分别表示横摇、纵摇和艏摇变化的角度(图 1)及对应的旋转矩阵。
海洋磁性源瞬变电磁探测系统的姿态变化可表示为发射回线和接收回线的坐标位置变化。假设发射线圈横摇、纵摇和艏摇的旋转角度分别为α1、β1、γ1,接收线圈的横摇、纵摇和艏摇的旋转角度分别为α2、β2、γ2。进一步地,令任意多边形发射回线各节点坐标为(x1i, y1i, z1i),其中i=1, 2, …, p,这里p为回线多边形的节点数,接收点坐标为(x2j, y2j, z2j),其中j=1, 2, …, q,q为接收回线多边形的节点数。假设探测系统发生姿态变化后发射回线多边形各节点的坐标变为(x1i′, y1i′, z1i′),相应的接收点坐标变为(x′2j, y′2j, z′2j)。通过旋转矩阵可得到姿态变化前、后坐标的转换关系
| $ \left\{\begin{array}{l} {\left[\begin{array}{c} x_{1 i}^{\prime} \\ y_{1 i}^{\prime} \\ z_{1 i}^{\prime} \end{array}\right]=\boldsymbol{R}_{\mathrm{TX}}\left[\begin{array}{l} x_{1 i} \\ y_{1 i} \\ z_{1 i} \end{array}\right]=\boldsymbol{R}_{a_1 \beta_1 \gamma_1}\left[\begin{array}{l} x_{1 i} \\ y_{1 i} \\ z_{1 i} \end{array}\right]} \\ {\left[\begin{array}{l} x_{2 i}^{\prime} \\ y_{2 i}^{\prime} \\ z_{2 i}^{\prime} \end{array}\right]=\boldsymbol{R}_{\mathrm{TR}}\left[\begin{array}{l} x_{2 i} \\ y_{2 i} \\ z_{2 i} \end{array}\right]=\boldsymbol{R}_{a_2 \beta_2 \gamma_2}\left[\begin{array}{l} x_{2 i} \\ y_{2 i} \\ z_{2 i} \end{array}\right]} \end{array}\right. $ | (4) |
式中RTX=Rα1β1γ1,RTR=Rα2β2γ2,分别表示发射线圈和接收线圈的旋转矩阵,其形式参照式(3)。姿态变化后系统坐标下的瞬变电磁响应,即接收线圈所记录的电磁响应为
| $ \begin{aligned} &\boldsymbol{f}^{\prime}\left(\alpha_1, \beta_1, \gamma_1, \alpha_2, \beta_2, \gamma_2\right)= \\ &\boldsymbol{R}_{\mathrm{TR}}^{\mathrm{T}} f\left(x_{1 i}^{\prime}, y_{1 i}^{\prime}, z_{1 i}^{\prime}, x_{2 j}^{\prime}, y_{2 j}^{\prime}, z_{2 j}^{\prime}\right) \end{aligned} $ | (5) |
式中f=[Ex, Ey, Ez, Hx, Hy, Hz]T为系统坐标系下接收线圈记录的电磁场响应,由电场E的三个分量(Ex, Ey, Ez)和磁场H的三个分量(Hx, Hy, Hz)组成。
1.2 磁性源瞬变电磁场响应建立图 2所示一维全空间海洋层状地质模型。模型从上至下包括空气层、海水层、海底沉积地层,编号分别为-1,0,1,2,…,n,n为海底地层总层数,图中D表示层厚度,σ表示电导率,h表示源与所在层底面的距离;发射磁矩为M的磁性源置于海水中,磁性源发射线圈的中心坐标为(0, 0, -h),通以电流I0。

|
图 2 一维层状海底地层TEM模型示意图 |
海水中,磁性源无论是水平放置还是垂直放置,由于电磁场满足叠加原理,电磁响应总场均可通过对磁偶极子的磁矢量位进行面积分获得。为求解方便,推导过程中引入矢量赫兹势F。取时谐因子为e-iωt,在谐变场中,F满足赫姆霍兹方程
| $ \nabla^2 \boldsymbol{F}-k^2 \boldsymbol{F}=0 $ | (6) |
式中k2=-(iωμσ+ω2με)表示波数,其中ω为角频率,μ=μ0μr为磁导率,这里μr为相对磁导率,μ0=4π×10-7H/m为自由空间磁导率,ε为介电常数。求得频率域电磁响应后,通过离散正/余弦变换可将其转换到时间域[24]。本文主要分析磁场强度分量,不对电场分量进行阐述。
1.2.1 垂直磁偶极源以全空间模型为例,推导任意形状场源在全空间中的一维电磁场响应,不局限于海洋模型。
在图 2所示模型的第j层中沿z轴放置磁矩M=M0e-iωt的垂直磁偶极子源,其中M0=I0S0g,S0表示发射线圈的面积,g表示发射线圈的匝数。根据边界条件及分离变量法[25]得到海底层状介质电磁场赫兹势为
| $ \begin{array}{*{20}{c}} {F_z(x, y, z)=\frac{\mathrm{i} \omega \mu M_0}{4 \pi} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \frac{1}{u_j}\left(\mathrm{e}^{-u_j|z+h|}+c_j \mathrm{e}^{u_j z}+\right.}\\ {\left.d_j \mathrm{e}^{-u_j z}\right) \mathrm{e}^{\mathrm{i}\left(k_x x+k_y y\right)} \mathrm{d} k_x \mathrm{~d} k_y} \end{array} $ | (7) |
式中:(x, y, z)表示接收点坐标;kx、ky分别为x、y方向的波数;uj2=λ2-kj2,其中λ表示波长,忽略位移电流则第j层波数为kj2=-iωμσj;cj、dj分别表示源在第j层的向上、向下衰减系数。本文暂不考虑各层的磁导率变化,假设各层磁导率均为μ0。进一步将式(7)中的双重傅里叶变换转换为Hankel变换形式[26]
| $ \begin{aligned} F_z(r, z)=& \frac{\mathrm{i} \omega \mu M_0}{4 \pi} \int_0^{\infty} \frac{\lambda}{u_j}\left(\mathrm{e}^{-u_j|z+h|}+c_j \mathrm{e}^{u_j z}+\right.\\ &\left.d_j \mathrm{e}^{-u_j z}\right) J_0(\lambda r) \mathrm{d} \lambda \end{aligned} $ | (8) |
其中
| $ \left\{\begin{array}{l} \hat{u}_j=u_j \frac{\hat{u}_{j+1}+u_j \operatorname{th}\left(u_j d_j\right)}{u_j+\hat{u}_{j+1} \operatorname{th}\left(u_j d_j\right)} \quad j=0, 1, \cdots, n-1 \\ \hat{u}_n=u_n=\sqrt{\lambda^2-k_n^2} \\ c_j=\frac{u_j-\hat{u}_{j+1}}{u_j+\hat{u}_{j+1}} \mathrm{e}^{-u_j h} \\ d_j=\frac{u_j-\hat{u}_{j-1}}{u_j+\hat{u}_{j-1}} \mathrm{e}^{-u_j H} \end{array}\right. $ | (9) |
式中:J0为0阶第一类贝塞尔函数;
| $ F_z(r, z)=\frac{\mathrm{i} \omega \mu M_0}{4 \pi} \int_0^{\infty} \frac{\lambda}{u_j}\left(\mathrm{e}^{-u_j|z+h|}+c_j \mathrm{e}^{u_j z}\right) J_0(\lambda r) \mathrm{d} \lambda $ | (10) |
根据式(9)可先求出底层系数
进一步可得到磁矩为M、沿z轴放置的垂直磁偶极子源的频率域二次磁场三分量为
| $ \left\{\begin{array}{l} H_{x z}=\frac{1}{i \mu \omega} \frac{\partial^2 F_z}{\partial x \partial z}=\frac{M_0}{4 \pi} \cos \varphi \times \\ \int_0^{\infty}\left(l \mathrm{e}^{-u_j|z+h|}+c_j \mathrm{e}^{u_j z}-d_j \mathrm{e}^{-u_j z}\right) \lambda^2 J_1(\lambda r) \mathrm{d} \lambda \\ H_{y z}=\frac{1}{i \mu \omega} \frac{\partial^2 F_z}{\partial y \partial z}=-\frac{M_0}{4 \pi} \sin \varphi \times \\ \quad \int_0^{\infty}\left(l \mathrm{e}^{-u_j|z+h|}+c_j \mathrm{e}^{u_j z}-d_j \mathrm{e}^{-u_j z}\right) \lambda^2 J_1(\lambda r) \mathrm{d} \lambda \\ H_{z z}=\frac{1}{i \mu \omega}\left(\frac{\partial^2}{\partial z^2}+k^2\right) F_z=\frac{M_0}{4 \pi} \times \\ \int_0^{\infty}\left(\mathrm{e}^{-u_j|z+h|}+c_j \mathrm{e}^{u_j z}+d_j \mathrm{e}^{-u_j z}\right) \frac{\lambda^3}{u_j} J_0(\lambda r) \mathrm{d} \lambda \end{array}\right. $ | (11) |
式中:x=rcosφ,y=rsinφ,φ表示接收点(x,y,z)和坐标原点之间的连线与x轴的夹角;当z≥-h时,l=-1,z<-h时,l=1;J1为1阶第一类贝塞尔函数。
对于图 2模型,发射源与接收点均位于海水中,并且有z≥-h,式(11)可进一步写为
| $ \left\{\begin{array}{l} &H_{x z} =\frac{M_0}{4 \pi} \cos \varphi \times \\ &\int_0^{\infty}\left(\mathrm{e}^{-u_0|z+h|}-c_0 \mathrm{e}^{u_0 z}+d_0 \mathrm{e}^{-u_0 z}\right) \lambda^2 J_1(\lambda r) \mathrm{d} \lambda \\ &H_{y z}= \frac{M_0}{4 \pi} \sin \varphi \times \\ &\int_0^{\infty}\left(e^{-u_0|z+h|}-c_0 \mathrm{e}^{u_0 z}+d_0 \mathrm{e}^{-u_0 z}\right) \lambda^2 J_1(\lambda r) \mathrm{d} \lambda \\ &H_{z z}= \frac{M_0}{4 \pi} \times \\ &\int_0^{\infty}\left(\mathrm{e}^{-u_0|z+h|}+c_0 \mathrm{e}^{u_0 z}+d_0 \mathrm{e}^{-u_0 z}\right) \frac{\lambda^3}{u_0} J_0(\lambda r) \mathrm{d} \lambda \end{array}\right. $ | (12) |
其中
| $ \left\{\begin{array}{l} c_0=\frac{u_0-\hat{u}_1}{u_0+\hat{u}_1} \mathrm{e}^{-u_0 h} \\ d_0=\frac{u_0-\lambda}{u_0+\lambda} \mathrm{e}^{-u_0 H} \end{array}\right. $ |
图 2所示模型中,磁矩为M、沿x轴放置于海底第j层的水平磁偶极子赫兹势Fx的Hankel形式表达式为[25, 27]
| $ \begin{aligned} &F_x(r, z)=\frac{-\mathrm{i} \omega \mu M_0}{4 \pi} \times \\ &\frac{\partial}{\partial x} \int_0^{\infty} \frac{1}{\lambda}\left(\mathrm{e}^{-u_j|z+h|}+c_j \mathrm{e}^{u_j z}+d_j \mathrm{e}^{-u_j z}\right) J_0(\lambda r) \mathrm{d} \lambda \end{aligned} $ | (13) |
由此可得水平磁偶极子的频率域二次磁场三分量响应为
| $ \left\{\begin{array}{l} H_{x x}=\frac{1}{\mathrm{i} \mu \omega} \frac{\partial^2 F_x}{\partial x \partial z}=\frac{M_0}{4 \pi} \times \\ \frac{\partial^2}{\partial x^2} \int_0^{\infty} \frac{u_j}{\lambda}\left(\mathrm{e}^{-u_j|z+h|}-c_j \mathrm{e}^{u_j z}+d_j \mathrm{e}^{-u_j z}\right) J_0(\lambda r) \mathrm{d} \lambda \\ H_{y x}=\frac{1}{i \mu \omega} \frac{\partial^2 F_x}{\partial y \partial z}=\frac{M_0}{4 \pi} \times \\ \frac{\partial^2}{\partial x \partial y} \int_0^{\infty} \frac{u_j}{\lambda}\left(\mathrm{e}^{-u_j|z+h|}-c_j \mathrm{e}^{u_j z}+d_j \mathrm{e}^{-u_j z}\right) J_0(\lambda r) \mathrm{d} \lambda \end{array}\right. $ | (14-1) |
| $ \begin{aligned} &H_{z x}=\frac{1}{\mathrm{i} \mu \omega}\left(\frac{\partial^2}{\partial z^2}+k^2\right) F_x=-\frac{M_0}{4 \pi} \times \\ &\frac{\partial}{\partial x} \int_0^{\infty}\left(\mathrm{e}^{-u_j|z+h|}+c_j \mathrm{e}^{u_j z}+d_j \mathrm{e}^{-u_j z}\right) \lambda J_0(\lambda r) \mathrm{d} \lambda \end{aligned} $ | (14-2) |
进一步,依据关系式
| $ {\begin{array}{*{20}{l}} {\left\{ {\begin{array}{*{20}{l}} \begin{array}{l} \frac{\partial }{{\partial x}} = \frac{x}{r}\frac{\partial }{{\partial r}}\\ \frac{{{\partial ^2}}}{{\partial {x^2}}} = \left( {\frac{1}{r} - \frac{{{x^2}}}{{{r^3}}}} \right)\frac{\partial }{{\partial r}} + \frac{{{x^2}}}{{{r^2}}}\frac{{{\partial ^2}}}{{\partial {r^2}}} \end{array}\\ {\frac{{{\partial ^2}}}{{\partial x\partial y}} = - \frac{{xy}}{{{r^3}}}\frac{\partial }{{\partial r}} + \frac{{xy}}{{{r^2}}}\frac{{{\partial ^2}}}{{\partial {r^2}}}} \end{array}} \right.}\\ {\left\{ {\begin{array}{*{20}{l}} {\frac{{\partial {J_0}(\lambda r)}}{{\partial r}} = - \lambda {J_1}(\lambda r)}\\ {\frac{{{\partial ^2}{J_0}(\lambda r)}}{{\partial {r^2}}} = \frac{\lambda }{r}{J_1}(\lambda r) - {\lambda ^2}{J_0}(\lambda r)} \end{array}} \right.} \end{array}} $ |
可将式(14)进一步改写为
| $ \left\{ \begin{array}{l} {H_{xx}} = \frac{{{M_0}}}{{4\pi }}\left[ {\left( {{{\cos }^2}\varphi - {{\sin }^2}\varphi } \right)\frac{1}{r} \times } \right.\\ \int_0^\infty {\left( {{{\rm{e}}^{ - {u_j}|z + h|}} - {c_j}{{\rm{e}}^{{u_j}z}} + {d_j}{{\rm{e}}^{ - {u_j}z}}} \right)} {u_j}{J_1}(\lambda r){\rm{d}}\lambda - \\ \left. {{{\cos }^2}\varphi \int_0^\infty {\left( {{{\rm{e}}^{ - {u_j}|z + h|}} - {c_j}{{\rm{e}}^{{u_j}z}} + {d_j}{{\rm{e}}^{ - {u_j}z}}} \right)} {u_j}\lambda {J_0}(\lambda r){\rm{d}}\lambda } \right]\\ {H_{yx}} = \frac{{{M_0}}}{{4\pi }}\cos \varphi \sin \varphi \left[ {\frac{2}{r} \times } \right.\\ \int_0^\infty {\left( {{{\rm{e}}^{ - {u_j}|z + h|}} - {c_j}{{\rm{e}}^{{u_j}z}} + {d_j}{{\rm{e}}^{ - {u_j}z}}} \right)} {u_j}{J_1}(\lambda r){\rm{d}}\lambda - \\ \left. {\int_0^\infty {\left( {{{\rm{e}}^{ - {u_j}|z + h|}} - {c_j}{{\rm{e}}^{{u_j}z}} + {d_j}{{\rm{e}}^{ - {u_j}z}}} \right)} {u_j}\lambda {J_0}(\lambda r){\rm{d}}\lambda } \right]\\ {H_{zx}} = \frac{{{M_0}}}{{4\pi }}\cos \varphi \times \\ \int_0^\infty {\left( {{{\rm{e}}^{ - {u_j}|z + h|}} + {c_j}{{\rm{e}}^{{u_j}z}} + {d_j}{{\rm{e}}^{ - {u_j}z}}} \right)} {\lambda ^2}{J_1}(\lambda r){\rm{d}}\lambda \end{array} \right. $ | (15) |
沿y轴放置的水平磁偶极子磁场响应的求解参照上式,通过简单的坐标变换即可求得,文中不再赘述。
综上可得置于海水层中的磁偶极源频率域二次场H的张量矩阵表达式为
| $ \mathit{\boldsymbol{H}} = \left[ {\begin{array}{*{20}{l}} {{H_{xx}}}&{{H_{xy}}}&{{H_{xz}}}\\ {{H_{yx}}}&{{H_{yy}}}&{{H_{yz}}}\\ {{H_{zx}}}&{{H_{zy}}}&{{H_{zz}}} \end{array}} \right] = \frac{{{M_0}}}{{4\pi }}\left[ {\begin{array}{*{20}{c}} {\left( {{{\cos }^2}\varphi - {{\sin }^2}\varphi } \right)\frac{{{u_0}{Y_0}}}{{\lambda r}} - {{\cos }^2}\varphi \frac{{{u_0}}}{\lambda }{Y_2}}&{ - \cos \varphi \sin \varphi \left( {\frac{2}{r}\frac{{{u_0}}}{\lambda }{Y_0} - \frac{{{u_0}}}{\lambda }{Y_2}} \right)}&{\cos \varphi {Y_1}}\\ {\cos \varphi \sin \varphi \left( {\frac{2}{r}\frac{{{u_0}}}{\lambda }{Y_0} - \frac{{{u_0}}}{\lambda }{Y_2}} \right)}&{\left( {{{\sin }^2}\varphi - {{\cos }^2}\varphi } \right)\frac{{{u_0}{Y_0}}}{{\lambda r}} - {{\sin }^2}\varphi \frac{{{u_0}}}{\lambda }{Y_2}}&{\sin \varphi {Y_1}}\\ {\cos \varphi {G_1}}&{\sin \varphi {G_1}}&{\frac{\lambda }{{{u_0}}}{G_0}} \end{array}} \right] $ | (16) |
其中
| $ \begin{aligned} &\left\{\begin{array}{l} Y_0=\int_0^{\infty}\left(\mathrm{e}^{-u_0|z+h|}-c_0 \mathrm{e}^{u_0 z}+d_0 \mathrm{e}^{-u_0 z}\right) \lambda J_1(\lambda r) \mathrm{d} \lambda \\ Y_1=\int_0^{\infty}\left(\mathrm{e}^{-u_0|z+h|}-c_0 \mathrm{e}^{u_0 z}+d_0 \mathrm{e}^{-u_0 z}\right) \lambda^2 J_1(\lambda r) \mathrm{d} \lambda \\ Y_2=\int_0^{\infty}\left(\mathrm{e}^{-u_0|z+h|}-c_0 \mathrm{e}^{u_0 z}+d_0 \mathrm{e}^{-u_0 z}\right) \lambda^2 J_0(\lambda r) \mathrm{d} \lambda \end{array}\right. \\ &\left\{\begin{array}{l} G_0=\int_0^{\infty}\left(\mathrm{e}^{-u_0|z+h|}+c_0 \mathrm{e}^{u_0 z}+d_0 \mathrm{e}^{-u_0 z}\right) \lambda^2 J_0(\lambda r) \mathrm{d} \lambda \\ G_1=\int_0^{\infty}\left(\mathrm{e}^{-u_0|z+h|}+c_0 \mathrm{e}^{u_0 z}+d_0 \mathrm{e}^{-u_0 z}\right) \lambda^2 J_1(\lambda r) \mathrm{d} \lambda \end{array}\right. \end{aligned} $ |
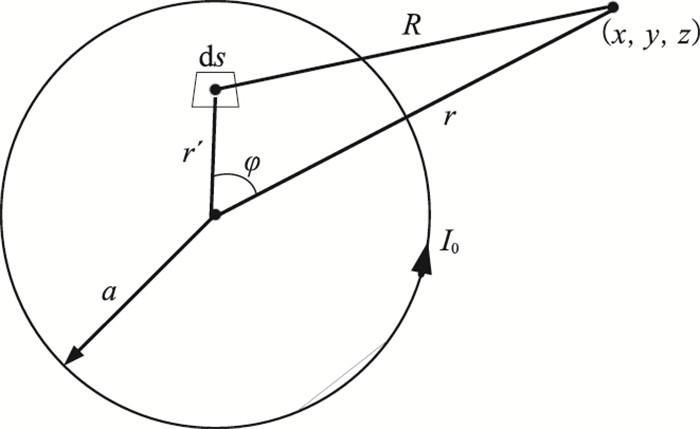
中心回线与偶极装置不同,发射线圈的面积不可忽略。依据电磁场叠加原理,有限大小的圆形发射线圈在某一点产生的磁场等于单位面积磁偶极子在该点的磁场沿发射线圈s的面积积分(图 3)
| $ \boldsymbol{F}^{\text {loop }}(\omega)=\int_0^s \boldsymbol{F}(\omega) \mathrm{d} s $ | (17) |
|
图 3 圆形发射回线源截面示意图 a、R分别表示回线线圈的半径和偶极矩元ds到观测点的距离,r′表示ds到回线中心的距离。 |
以水平回线源为例,根据式(8),式(17)进一步写作
| $ \begin{aligned} &F_z^{\text {loop }}(r, z)=\frac{\mathrm{i} \omega \mu M_0}{4 \pi} \int_0^{\infty} \frac{\lambda}{u_j}\left(\mathrm{e}^{-u_j|z+h|}+c_j \mathrm{e}^{u_j z}+\right. \\ &\left.d_j \mathrm{e}^{-u_j z}\right)\left[\int_0^a \int_0^{2 \pi} J_0(\lambda R) r^{\prime} \mathrm{d} \varphi \mathrm{d} r^{\prime}\right] \mathrm{d} \lambda \end{aligned} $ | (18) |
根据关系式
| $ \left\{ {\begin{array}{*{20}{l}} {{J_0}(\lambda R) = \sum\limits_{m = - \infty }^\infty {{J_m}} (\lambda r){J_m}\left( {\lambda {r^\prime }} \right)\cos m\varphi }\\ {\int {{x^n}} {J_{n - 1}}(x){\rm{d}}x = {x^n}{J_n}(x)} \end{array}} \right. $ |
可知,内层积分只有在m=0时才不为零,可进一步得到水平中心回线源的通解为
| $ \begin{gathered} F_z^{\text {loop }}(r, z)=\frac{\mathrm{i} \omega \mu I_0 a}{2} \int_0^{\infty} \frac{1}{u_j}\left(\mathrm{e}^{-u_j|z+h|}+c_j \mathrm{e}^{u_j z}+\right. \\ \left.d_j \mathrm{e}^{-u_j z}\right) J_0(\lambda r) J_1(\lambda a) \mathrm{d} \lambda \end{gathered} $ | (19) |
进一步得到磁场三分量响应为
| $ $ | (20) |
对于中心回线接收装置,r=0,J0(0)=1,J1(0)=0,仅磁场的垂直分量不为0,根据式(20)得到
| $ \left\{\begin{aligned} H_{x z}^{\text {loop }}=& \frac{1}{\mathrm{i} \mu \omega} \frac{\partial^2 F_z^{\text {loop }}}{\partial x \partial z}=-\frac{I_0 a}{2} \cos \varphi \int_0^{\infty}\left(l \mathrm{e}^{-u_j|z+h|}+\right.\\ &\left.c_j \mathrm{e}^{u_j z}-d_j \mathrm{e}^{-u_j z}\right) \lambda J_1(\lambda r) J_1(\lambda a) \mathrm{d} \lambda \\ H_{y z}^{\text {loop }}=& \frac{1}{\mathrm{i} \mu \omega} \frac{\partial^2 F_{z z}^{\text {loop }}}{\partial y \partial z}=-\frac{I_0 a}{2} \sin \varphi \int_0^{\infty}\left(l \mathrm{e}^{-u_j|z+h|}+\right.\\ &\left.c_j \mathrm{e}^{u_j z}-d_j \mathrm{e}^{-u_j z}\right) \lambda J_1(\lambda r) J_1(\lambda a) \mathrm{d} \lambda \\ H_{z z}^{\text {loop }}=& \frac{1}{\mathrm{i} \mu \omega}\left(\frac{\partial^2}{\partial^2 z}+k^2\right) F_z^{\text {loop }}=\frac{I_0 a}{2} \int_0^{\infty}\left(\mathrm{e}^{-u_j|z+h|}+\right.\\ &\left.c_j \mathrm{e}^{u_j z}+d_j \mathrm{e}^{-u_j z}\right) \frac{\lambda^2}{u_j} J_0(\lambda r) J_1(\lambda a) \mathrm{d} \lambda \end{aligned}\right. $ | (21) |
可进一步得到频率域二次磁场的张量矩阵表达式为
| $ \begin{array}{l} {\mathit{\boldsymbol{H}}^{{\rm{loop }}}} = \left[ {\begin{array}{*{20}{c}} {H_{xx}^{{\rm{loop }}}}&{H_{xy}^{{\rm{loop }}}}&{H_{xz}^{{\rm{loop }}}}\\ {H_{yx}^{{\rm{loop }}}}&{H_{yy}^{{\rm{loop }}}}&{H_{yz}^{{\rm{loop }}}}\\ {H_{zx}^{{\rm{loop }}}}&{H_{zy}^{{\rm{loop }}}}&{H_{zz}^{{\rm{loop }}}} \end{array}} \right]\\ = \frac{{{I_0}a}}{2}\left[ {\begin{array}{*{20}{c}} {\left( {{{\cos }^2}\varphi - {{\sin }^2}\varphi } \right)\frac{{{u_0}Y_0^\prime }}{{\lambda r}} - {{\cos }^2}\varphi \frac{{{u_0}}}{\lambda }Y_2^\prime }&{ - \cos \varphi \sin \varphi \left( {\frac{2}{r}\frac{{{u_0}}}{\lambda }Y_0^\prime - \frac{{{u_0}}}{\lambda }Y_2^\prime } \right)}&{\cos \varphi Y{{_1^\prime }_1}}\\ {\cos \varphi \sin \varphi \left( {\frac{2}{r}\frac{{{u_0}}}{\lambda }Y_0^\prime - \frac{{{u_0}}}{\lambda }Y_2^\prime } \right)}&{\left( {{{\sin }^2}\varphi - {{\cos }^2}\varphi } \right)\frac{{{u_0}Y_0^\prime }}{{\lambda r}} - {{\sin }^2}\varphi \frac{{{u_0}}}{\lambda }Y_2^\prime }&{\sin \varphi Y_1^\prime }\\ {\cos \varphi G_1^\prime }&{\sin \varphi G_1^\prime }&{\frac{\lambda }{{{u_0}}}G_0^\prime } \end{array}} \right] \end{array} $ | (22) |
其中
| $ \left\{\begin{aligned} Y_0^{\prime}=& \int_0^{\infty}\left(\mathrm{e}^{-u_0|z+h|}-c_0 \mathrm{e}^{u_0 z}+\right.\\ &\left.d_0 \mathrm{e}^{-u_0 z}\right) J_1(\lambda r) J_1(\lambda a) \mathrm{d} \lambda \\ Y_1^{\prime}=& \int_0^{\infty}\left(\mathrm{e}^{-u_0|z+h|}-c_0 \mathrm{e}^{u_0 z}+\right.\\ &\left.d_0 \mathrm{e}^{-u_0 z}\right) \lambda J_1(\lambda r) J_1(\lambda a) \mathrm{d} \lambda \\ Y_2^{\prime}=& \int_0^{\infty}\left(\mathrm{e}^{-u_0|z+h|}-c_0 \mathrm{e}^{u_0 z}+\right.\\ &\left.d_0 \mathrm{e}^{-u_0 z}\right) \lambda J_0(\lambda r) J_1(\lambda a) \mathrm{d} \lambda \end{aligned}\right. $ |
| $ \left\{\begin{aligned} G_0^{\prime}=& \int_0^{\infty}\left(\mathrm{e}^{-u_0|z+h|}+c_0 \mathrm{e}^{u_0 z}+\right.\\ &\left.d_0 \mathrm{e}^{-u_0 z}\right) \lambda J_0(\lambda r) J_1(\lambda a) \mathrm{d} \lambda \\ G_1^{\prime}=& \int_0^{\infty}\left(\mathrm{e}^{-u_0|z+h|}+c_0 \mathrm{e}^{u_0 z}+\right.\\ &\left.d_0 \mathrm{e}^{-u_0 z}\right) \lambda J_1(\lambda r) J_1(\lambda a) \mathrm{d} \lambda \end{aligned}\right. $ |
为了进一步验证本文磁偶源等效算法的正确性,以垂直磁偶源为例,将本文计算结果与前期基于开源软件Dipole 1D[19]改进的电偶源等效结果[28]进行对比。
模型参数如下:假设海底沉积层为均匀半空间,电导率σ1=1S·m-1;发射线框磁矩M=1A·m2,发射回线置于海水中,离海底高度h=5m;接收点坐标为(30m, 0, -5m),接收线圈面积为1m2;海水深度D0=50m。
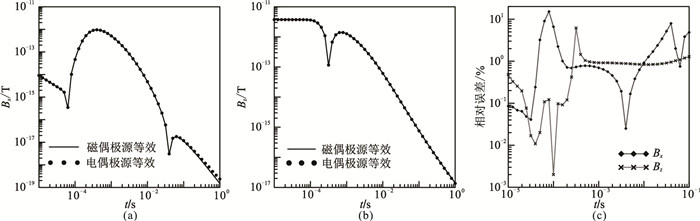
应用本文公式计算模型的三分量磁感应强度,并与文献[27]所示结果进行对比。由于By=0,这里不对此分量进行分析。本文方法计算结果与电性等效源计算结果对比见图 4a、图 4b,二者的相对误差见图 4c。可见磁偶极源的计算结果与电偶极等效源的计算结果吻合很好,整体误差小于2%,证明本文推导公式的正确性。
|
图 4 1D模型电偶极源磁场分量本文算法与电偶极源等效结果对比 (a)Bx;(b)Bz;(c)相对误差 |
姿态变化后接收线圈记录的电磁响应在两个坐标系下的转换关系为
| $ \begin{aligned} &H_{\mathrm{TR}}^{\prime}=\left(H_{x x}+H_{x y}+H_{x z}\right) R_{31}+ \\ &\quad\left(H_{y x}+H_{y y}+H_{y z}\right) R_{32}+\left(H_{z x}+H_{z y}+H_{z z}\right) R_{33} \end{aligned} $ | (23) |
实际测量的感应电动势εTR及磁感应强度BTR,可通过下式求得
| $ \left\{\begin{array}{l} B_{\mathrm{TR}}=\mu_0 H_{\mathrm{TR}} \\ \varepsilon_{\mathrm{TR}}=s_{\mathrm{TR}} \frac{\mathrm{d} B}{\mathrm{~d} t} \end{array}\right. $ | (24) |
式中sTR为接收线圈的有效接收面积。
为了衡量姿态变化对水下瞬变电磁数据的影响程度,定义姿态响应系数K用以描述姿态变化的影响情况,姿态响应系数K可以用姿态变化时瞬变电磁响应与理想状态下电磁响应的比值表示为
| $ \begin{aligned} K &=\frac{\varepsilon_{\mathrm{TR}}^{\prime}\left(\alpha_1, \beta_1, \gamma_1, \alpha_2, \beta_2, \gamma_2\right)}{\varepsilon_{\mathrm{TR}}(0, 0, 0, 0, 0, 0)} \\ &=\frac{H_{\mathrm{TR}}^{\prime}\left(\alpha_1, \beta_1, \gamma_1, \alpha_2, \beta_2, \gamma_2\right)}{H_{\mathrm{TR}}(0, 0, 0, 0, 0, 0)} \end{aligned} $ | (25) |
式中εTR(0, 0, 0, 0, 0, 0)和ε′TR(α1, β1, γ1, α2, β2, γ2)分别表示线圈发生姿态变化前、后接收线圈记录的感应电动势。
2 探测装置姿态变化对观测数据的影响分析为分析姿态变化对水下拖曳式磁性源瞬变电磁响应的影响特征及规律,参照图 2所示模型建立如下模型:空气层电导率σ-1=10-7S·m-1,空气层厚度d-1=105m,海水电导率σ0=3S·m-1,海水深度为d0,令沉积层为均匀介质,其电导率σ1=1S·m-1;发射线框半径为3m,发射电流为1A,接收面积为1m2,发射源离海底距离h=2m,z轴垂直向下为正。
以水平中心回线装置为例,首先对海底为均匀介质条件下的简单一维模型,通过姿态响应系数K分析水下瞬变电磁系统响应与姿态变化之间的关系。对于一维介质模型,艏摇变化对瞬变电磁系统响应的影响可忽略。进一步地,对于中心回线装置,式(23)可改写为
| $ \begin{aligned} H_{\mathrm{TR}}^{\prime}=& \cos \alpha_1 \sin \beta_1\left(\cos \alpha_2 \sin \beta_2 H_{x x}\right)+\sin \alpha_1 \sin \alpha_2 H_{y y}+\\ & \cos \alpha_1 \cos \alpha_2\left(\cos \beta_1 \cos \beta_2 H_{z z}\right) \end{aligned} $ | (26) |
将上式代入式(25),得到不同姿态变化时的响应系数K
| $ \left\{ \begin{array}{l} K(\alpha ) = \frac{{\varepsilon _{{\rm{TR}}}^\prime \left( {{\alpha _1}, 0, 0, {\alpha _2}, 0, 0} \right)}}{{{\varepsilon _{{\rm{TR}}}}(0, 0, 0, 0, 0, 0)}} = \frac{{\sin {\alpha _1}\sin {\alpha _2}{H_{yy}} + \cos {\alpha _1}\cos {\alpha _2}{H_{zz}}}}{{{H_{zz}}}} = \sin {\alpha _1}\sin {\alpha _2}\frac{{u_0^2}}{{{\lambda ^2}}}\left( { - \frac{{Y_0^\prime }}{{rG_0^\prime }}} \right) + \cos {\alpha _1}\cos {\alpha _2}\\ K(\beta ) = \frac{{\varepsilon _{{\rm{TR}}}^\prime \left( {0, {\beta _1}, 0, 0, {\beta _2}, 0} \right)}}{{{\varepsilon _{{\rm{TR}}}}(0, 0, 0, 0, 0, 0)}} = \frac{{\sin {\beta _1}\sin {\beta _2}{H_{xx}} + \cos {\beta _1}\cos {\beta _2}{H_{zz}}}}{{{H_{zz}}}} = \sin {\beta _1}\sin {\beta _2}\frac{{u_0^2}}{{{\lambda ^2}}}\left( {\frac{{Y_0^\prime }}{{rG_0^\prime }} - \frac{{Y_2^\prime }}{{G_0^\prime }}} \right) + \cos {\beta _1}\cos {\beta _2}\\ K(\alpha , \beta ) = \frac{{\varepsilon _{{\rm{TR}}}^\prime \left( {{\alpha _1}, {\beta _1}, 0, {\alpha _2}, {\beta _2}, 0} \right)}}{{{\varepsilon _{{\rm{TR}}}}(0, 0, 0, 0, 0, 0)}} = \frac{{\cos {\alpha _1}\sin {\beta _1}\left( {\cos {\alpha _2}\sin {\beta _2}{H_{xx}}} \right) + \sin {\alpha _1}\sin {\alpha _2}{H_{yy}} + \cos {\alpha _1}\cos {\alpha _2}\left( {\cos {\beta _1}\cos {\beta _2}{H_{zz}}} \right)}}{{{H_{zz}}}}\\ = \cos {\alpha _1}\sin {\beta _1}\left[ {\cos {\alpha _2}\sin {\beta _2}\frac{{u_0^2}}{{{\lambda ^2}}}\left( {\frac{{Y_0^\prime }}{{rG_0^\prime }} - \frac{{Y_2^\prime }}{{G_0^\prime }}} \right)} \right] + \sin {\alpha _1}\sin {\alpha _2}\frac{{u_0^2}}{{{\lambda ^2}}}\left( { - \frac{{Y_0^\prime }}{{rG_0^\prime }}} \right) + \cos {\alpha _1}\cos {\alpha _2}\cos {\beta _1}\cos {\beta _2} \end{array} \right. $ | (27) |
对于中心回线装置,接收线圈位于发射线圈的中心,即r→0,λr→0,φ=0,因而J0(λr→0)=1, J1(λr→0)=λr/2。当发射线圈与接收线圈刚性连接时,发射线圈与接收线圈的变化角度是一致的,即α1=α2,β1=β2,γ1=γ2。下面通过模型正演进一步分析姿态变化对浅海瞬变电磁场的影响特征。
2.1 不同衰减时间条件下姿态变化的影响分析首先,以中心回线装置为例,分析发射线圈与接收线圈为刚性连接的情况。海底为均匀介质,通过姿态响应系数K分析横摇(α1=α2, β=0, γ=0)、纵摇(α=0, β1=β2, γ=0)和艏摇(α=0, β=0, γ1=γ2)单个姿态变化对水下瞬变电磁响应的影响。考虑到浅海特别是极浅海域风浪影响明显,这里设海水深度d0=10m,姿态角度变化范围为[-40°, 40°],间隔为4°。
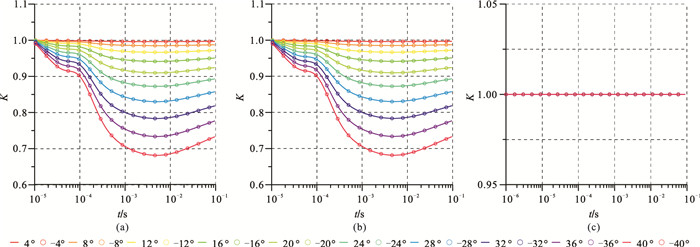
图 5为这三种单姿态变化时姿态响应系数K随衰减时间的变化曲线。由图可见,对于一维地质模型,艏摇对水下瞬变电磁响应的影响(图 5c)可以忽略。由于采用中心回线装置,发射源为圆形线框,横摇变化(图 5a)与纵摇变化(图 5b)对水下瞬变电磁响应的影响相同,故后文仅研究横摇姿态变化。
|
图 5 TR与TX刚性连接时不同姿态变化角度下系数K的衰减曲线 (a)横摇;(b)纵摇;(c)艏摇 |
从图 5b可知,横摇角度与响应系数K成反比例关系,即姿态角度越大,水下瞬变电磁响应影响越剧烈;姿态变化角度的正、负值具有对称性,即K值取决于姿态变化角度的绝对值。当姿态角度为±20°时,瞬变响应误差(即(1-K)×100%)在10%以内;而当姿态变化角度为±40°时,响应误差最大可达32%。随着时间的推移,响应系数K逐渐减小,即姿态变化对瞬变响应的影响逐渐增大,在5ms时达到峰值,之后K值又逐渐增大,表明姿态变化的影响逐渐降低。
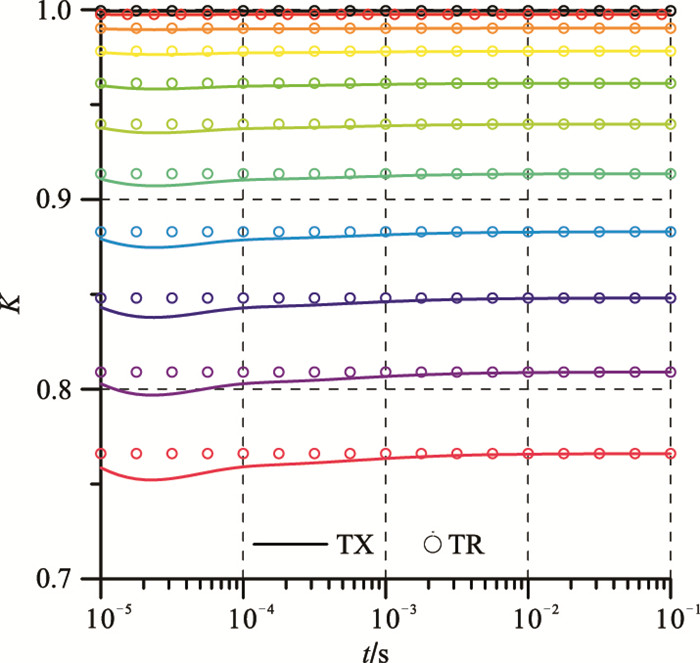
其次,仍以中心回线装置为例,进一步分析发射线圈与接收线圈为非刚性连接的情况,即单线圈(发射线圈或接收线圈)姿态变化时,通过K值分析姿态变化对磁响应的影响,结果见图 6(姿态变化角度同图 5)。
|
图 6 TR与TX非刚性连接时不同横摇角度下的K衰减曲线 不同角度对应线/圈颜色同图 5。 |
根据图 6,单线圈横摇姿态角度变化对观测数据的影响程度与图 5所示接收线圈TR和发射线圈TX同时变化的趋势一致,即同样呈现正比例关系。单TR横摇变化时,K值(K=cosα2cosβ2)基本不随衰减时间变化,主要受到接收面积变化的影响;单TX横摇变化时,由于海水深度较小,K值曲线的波动主要集中在早期时间段(t < 0.0005s),TX横摇的影响略大于TR。之后二者所对应的K值曲线逐渐趋于平缓并重合,说明在中晚期(t≥0.0005s)TX与TR单线圈横摇角度相同时二者对电磁场产生的影响是一致的,且都逐渐减小。
对比图 5与图 6可知,相同横摇角度时,与单线圈横摇姿态变化相比,TX、TR同时横摇姿态变化在早期对瞬变磁场数据的影响较小,但晚期的影响较大。
2.2 线圈升沉变化条件下姿态变化的影响分析水下探测系统在航行过程中由于受到外界环境及船体航速不均等因素影响会发生垂向升沉,即收发线圈距离海底的垂向高度发生变化。拖曳高度变化会对观测结果造成直接影响,相关影响分析参见文献[21]。本文以拖曳高度h=2m且不发生其他姿态变化时的瞬变电磁响应作为基准数据,对不同拖曳高度条件下、不同升沉高度的影响进行分析。
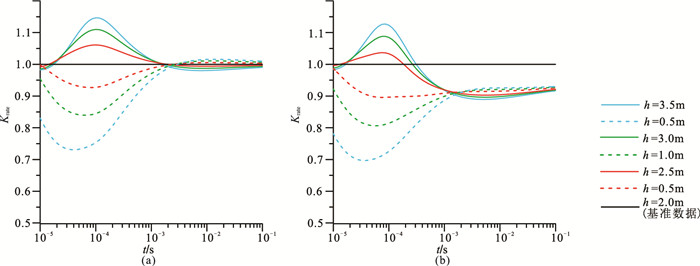
基本模型参数2.1节模型一致,海底为均匀介质,采用刚性连接中心回线探测装置,收、发线圈仅发生横摇变化,姿态角度α1=α2=20°。分别计算不同拖曳高度h时仅升沉变化(图 7a)和升沉与姿态同时变化时(图 7b)的K值与基准数据的比值Krate。
|
图 7 拖体升沉及姿态变化时的Krate曲线 (a)升沉变化(α=0°);(b)升沉及姿态变化(α=20°) |
由图 7a可知,水下拖体发生升沉变化时,Krate的变化主要集中在时间道早期,当拖体上升或下降同等距离时,Krate曲线具有一定的对称性,但拖体下沉时的比值偏离程度明显大于拖体上升相同高度时的情况。随着衰减时间的推移,拖体不同拖曳高度的Krate曲线逐渐趋于一致,这符合瞬变电磁场的传播规律。图 7b表明,当同时发生升沉与姿态变化时,Krate曲线偏离程度较单升沉情形更高,且整体偏离幅度与姿态角度有关,这与上文的研究结论是相符的。
2.3 不同海水深度下姿态变化影响分析与深海瞬变电磁探测系统相比,浅海瞬变电磁响应会更大程度地受到海水与空气层界面的影响,不同海水深度条件下的瞬变电磁响应特征不同。因此,本节进一步分析不同海水深度条件下姿态变化对瞬变响应的影响。
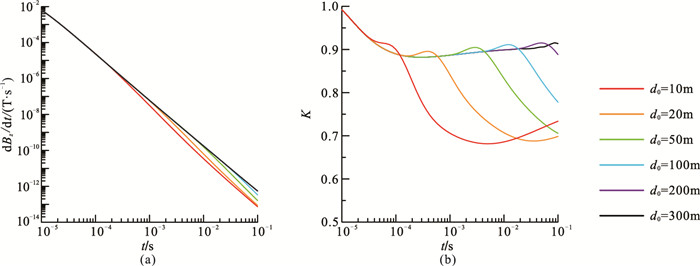
基本模型参数与2.1节模型一致,也采用中心回线探测装置,TX和TR刚性连接,仅发生横摇变化,姿态角度为α1=α2=40°,固定拖曳高度h=2m,分析不同海水深度D0情况下姿态变化对瞬变电磁响应的影响规律与特征。图 8a为不同海水深度条件下的dBz/dt衰减曲线,可见曲线形态变化主要集中在信号衰减的晚期;图 8b为对应的姿态响应系数K值曲线,可以看出不同海水深度条件下曲线形态基本一致,仅随着海水深度的变化K值曲线存在一定平移。这是由于海水较浅时,由于受到海水—空气界面的影响,响应系数K快速变化;随着海水深度的不断增加,感应电流向上穿透海水所需时间逐渐增加,响应系数K变化的时间亦逐渐后推;当海水深度增大到一定程度(本文模型参数条件下为300m)时,在探测时间道范围内涡流已无法穿透海水,响应系数K随时间变化平缓。图 8进一步说明,浅海特别是极浅海条件下线圈姿态变化对瞬变响应的影响是显著的。
|
图 8 不同海水深度条件下线圈横摇(α1=α2=40°)对瞬变电磁磁场的影响 (a)dBz/dt曲线; (b)K值曲线 |
通常探测目标是海底沉积层中的异常体,瞬变电磁法对不同电性介质的探测能力不同,为进一步研究不同海底沉积层电性情况下TX、TR姿态变化时的K值变化特征。
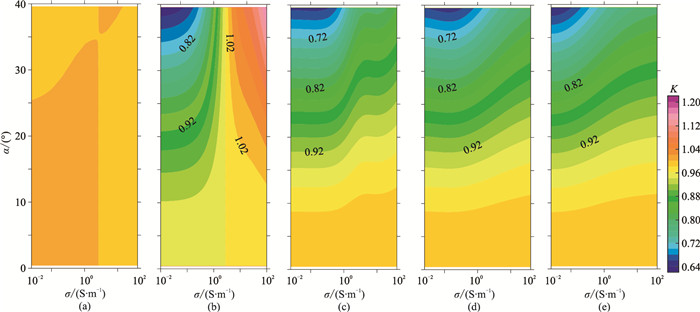
基本模型参数与2.1部分一致,沉积层为均匀半空间,以横摇姿态变化为例,分别计算海底沉积层不同电导率条件下不同时间道的K值分布(图 9)。由图可见,不同观测时间道上的K值随海底沉积层的电性变化特征是不同的,在时间道晚期的变化比早期更剧烈,这与2.3部分的结论是一致的。随着海底沉积层电导率的增加,K值曲线变化显著。
|
图 9 海底沉积层不同电导率、不同横摇角度下不同时间道的K值图 (a)t=1×10-5s; (b)t=1×10-4s; (c)t=1×10-3s; (d)t=1×10-2s; (e)t=1×10-1s |
前述研究中的模型海底沉积层为均匀介质,分析收、发系统姿态变化对磁场响应的影响。这里以海底沉积层为层状介质为例,进一步分析收、发系统姿态变化对瞬变电磁磁场数据的影响。参照图 2模型,分别设计海底沉积层含低阻层(H型模型)和高阻层(K型模型)的各向同性水平三层模型。具体模型参数如下:上覆盖层与底层电导率σ1=σ3=1S·m-1,相对磁导率均为1,上覆盖层厚度d1=10m;H型中间层σ2=10S·m-1, d2=10m;K型模型中间层σ2=0.01S·m-1,d2=10m。仍然采用刚性连接中心回线装置,仅研究收、发线圈发生横摇变化的情况。该模型不同横摇姿态角度下的全域视电导率(σa)曲线计算结果见图 10。
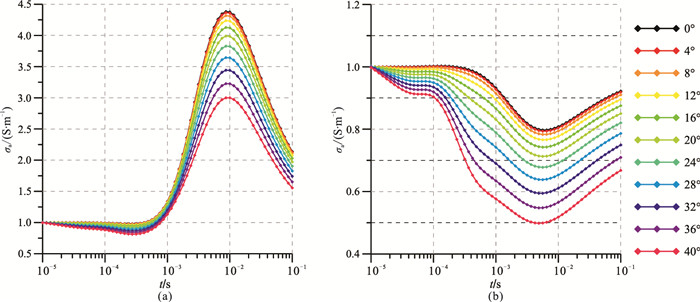
|
图 10 海底层状模型线圈横摇姿态变化时的全域σa曲线 (a)H型模型; (b)K型模型. |
由图 10可见,全域σa曲线随横摇角度的逐渐变化,曲线形态相应发生改变。不论是H型模型还是K型模型,横摇角度的变化直接影响海底异常层的响应,导致结果偏离正常异常响应值(图 10中0°曲线)。此外,随着横摇姿态角度的逐渐增大,全域σa幅值逐步降低,这可能会造成低导异常体的漏检,并出现假异常,严重影响探测结果的可靠性。
3 结论本文首先从电磁场理论出发,基于标量赫兹势,推导了有限水深条件下海底各向同性水平层状介质模型水平磁偶极子和垂直磁偶极子的频率域三分量电磁场表达式,并根据电磁场叠加原理推导出海洋瞬变电磁回线源电磁响应公式;其次,采用发射、接收双旋转矩阵及磁场格林张量矩阵的形式,建立了水下拖曳式磁性源姿态变化数学模型;最后,通过姿态响应系数K定性分析姿态变化对观测磁场数据的影响。通过浅海拖曳式磁性源电磁系统姿态变化模型正演及分析,获得以下结论。
(1) 对于移动平台拖曳式瞬变电磁系统,海洋系统与航空系统工作原理是不同的。对于海洋拖曳式磁性源瞬变电磁系统,姿态角度的变化对观测电磁数据影响较大,其影响程度随观测时间的推移不断发生变化。浅海特别是极浅海环境下,姿态变化的影响更显著,随着海水深度的增加,姿态响应系数K逐渐减小并趋近于常数。因此,深海条件下可直接根据姿态响应系数K进行数据校正。
(2) 海洋拖曳式磁性源瞬变电磁系统的姿态变化对磁场数据的影响程度不仅随观测时间变化,同时与海底沉积层电性参数有关,特别是海底地层为良导介质时,姿态响应系数K随海底电导率的变化显著;反之,当海底介质具弱导性时,K值曲线平缓,基本不随海底地层电导率的变化而变化。此外,拖曳系统在海水中的升沉变化也会影响观测数据,主要影响时间道早期数据。
(3) 通过模型正演结果分析可知,横摇姿态角度的增大会导致计算的全域视电导率降低,引起定性解释偏差,甚至造成弱导体的漏检,并出现假异常,严重影响探测结果。
海洋拖曳式磁性源瞬变电磁系统的姿态变化影响程度与姿态变化角度、衰减时间、海水深度、海底沉积层电性等参数有关,变化规律相对复杂,不能简单地通过响应系数K进行校正。本文通过多个模型算例定性分析了海洋磁性源瞬变电磁系统姿态变化对电磁响应的影响,以进一步了解电磁响应的特征及变化规律。因此,如何进行海洋磁性源瞬变电磁系统的定量姿态校正及反演解释是下一步的研究方向。
| [1] |
徐行. 我国海洋地球物理探测技术发展现状及展望[J]. 华南地震, 2021, 41(2): 1-12. XU Hang. Development status and prospect of marine geophysical exploration technology in China[J]. South China Journal of Seismology, 2021, 41(2): 1-12. |
| [2] |
何展翔, 孙卫斌, 孔繁恕, 等. 海洋电磁法[J]. 石油地球物理勘探, 2006, 41(4): 451-457. HE Zhanxiang, SUN Weibin, KONG Fanshu, et al. Marine electromagnetic approach[J]. Oil Geophysical Prospecting, 2006, 41(4): 451-457. DOI:10.3321/j.issn:1000-7210.2006.04.019 |
| [3] |
CHEESMAN S J, EDWARDS R N, CHAVE A D. On the theory of sea-floor conductivity mapping using transient electromagnetic systems[J]. Geophysics, 1987, 52(2): 204-217. DOI:10.1190/1.1442296 |
| [4] |
EVERETT M E, EDWARDS R N. Transient marine electromagnetics: the 2.5-D forward problem[J]. Geophysical Journal International, 1993, 113(3): 545-561. DOI:10.1111/j.1365-246X.1993.tb04651.x |
| [5] |
EDWARDS R N, CHAVE A D. A transient electric dipole-dipole method for mapping the conductivity of the sea floor[J]. Geophysics, 1986, 51(4): 984-987. DOI:10.1190/1.1442156 |
| [6] |
王一新, 王家林, 王家映, 等. 瞬变电磁系统探测海底电导率的研究[J]. 地球物理学报, 1998, 41(6): 841-847. WANG Yixin, WANG Jialin, WANG Jiaying, et al. The research of conductivity on sea-floor by transient electromagnetic system[J]. Chinese Journal of Geophysics, 1998, 41(6): 841-847. DOI:10.3321/j.issn:0001-5733.1998.06.015 |
| [7] |
BARSUKOV P O, FAINBERG E B. Transient marine electromagnetics in shallow water: a sensitivity and resolution study of the vertical electric field at short ranges[J]. Geophysics, 2014, 79(1): E39-E49. DOI:10.1190/geo2013-0125.1 |
| [8] |
REID J E, WORBY A P, VRBANCICH J, et al. Shipborne electromagnetic measurements of Antarctic sea-ice thickness[J]. Geophysics, 2003, 68(5): 1537-1546. DOI:10.1190/1.1620627 |
| [9] |
王艳, 刘长胜, 林君, 等. 浅海底瞬变电磁探测技术研究新进展[J]. 吉林大学学报(地球科学版), 2005, 35(增刊1): 23-26. WANG Yan, LIU Changsheng, LIN Jun, et al. Researching progress of shallow seafloor exploration using transient electromagnetic systems[J]. Journal of Jilin University(Earth Science Edition), 2005, 35(S1): 23-26. |
| [10] |
周胜, 席振铢, 宋刚, 等. 深海拖曳式瞬变电磁的响应规律[J]. 中南大学学报(自然科学版), 2012, 43(2): 605-610. ZHOU Sheng, XI Zhenzhu, SONG Gang, et al. Responses of the towed transient electromagnetic soun-ding on deep seafloor[J]. Journal of Central South University, 2012, 43(2): 605-610. |
| [11] |
SWIDINSKY A, HÖLZ S, JEGEN M. On mapping seafloor mineral deposits with central loop transient electromagnetics[J]. Geophysics, 2012, 77(3): E171-E184. DOI:10.1190/geo2011-0242.1 |
| [12] |
YIN C C, FRASER D C. Attitude corrections of helicopter EM data using a superposed dipole model[J]. Geophysics, 2004, 69(2): 431-439. DOI:10.1190/1.1707063 |
| [13] |
FITTERMAN D V, YIN C C. Effect of bird maneuver on frequency-domain helicopter EM response[J]. Geophysics, 2004, 69(5): 1203-1215. DOI:10.1190/1.1801937 |
| [14] |
嵇艳鞠, 林君, 关珊珊, 等. 直升机航空TEM中心回线线圈姿态校正的理论研究[J]. 地球物理学报, 2010, 53(1): 171-176. JI Yanju, LIN Jun, GUAN Shanshan, et al. Theoretical study of concentric loop coils attitude correction in helicopter-borne TEM[J]. Chinese Journal of Geophysics, 2010, 53(1): 171-176. |
| [15] |
王琦, 林君, 于生宝, 等. 固定翼航空电磁系统的线圈姿态及吊舱摆动影响研究与校正[J]. 地球物理学报, 2013, 56(11): 3741-3750. WANG Qi, LIN Jun, YU Shengbao, et al. Study on influence and correction of coil attitude and bird swing for the fixed wing time domain electromagnetic system[J]. Chinese Journal of Geophysics, 2013, 56(11): 3741-3750. |
| [16] |
贲放, 黄威, 吴珊, 等. 时间域航空电磁系统姿态变化影响研究[J]. 地球物理学报, 2018, 61(7): 3074-3085. BEN Fang, HUANG Wei, WU Shan, et al. Influence of attitude change for time domain airborne electromagnetic system[J]. Chinese Journal of Geophysics, 2018, 61(7): 3074-3085. |
| [17] |
朱凯光, 王昊, 彭聪, 等. 基于BP神经网络的固定翼航空电磁线圈姿态校正[J]. 吉林大学学报(地球科学版), 2020, 50(1): 252-260. ZHU Kaiguang, WANG Hao, PENG Cong, et al. Attitude correction of fixed-wing airborne electromagnetic coil based on BP neural network[J]. Journal of Jilin University(Earth Science Edition), 2020, 50(1): 252-260. |
| [18] |
CHAVE A D, COX C S. Controlled electromagnetic sources for measuring electrical conductivity beneath the oceans: 1. Forward problem and model study[J]. Journal of Geophysical Research: Solid Earth, 1982, 87(B7): 5327-5338. |
| [19] |
KEY K. 1D inversion of multicomponent, multifrequecy marine CSEM data: methodology and synthetic studies for resolving thin resistive layers[J]. Geophysics, 2009, 74(2): F9-F20. |
| [20] |
刘云鹤, 殷长春, 翁爱华, 等. 海洋可控源电磁法发射源姿态影响研究[J]. 地球物理学报, 2012, 55(8): 2757-2768. LIU Yunhe, YIN Changchun, WENG Aihua, et al. Attitude effect for marine CSEM system[J]. Chinese Journal of Geophysics, 2012, 55(8): 2757-2768. |
| [21] |
罗鸣, 裴建新, 徐震寰. 层状垂直各向异性介质海洋CSEM发射源及接收站姿态和位置对电磁响应影响研究[J]. 地球物理学报, 2017, 60(12): 4901-4915. LUO Ming, PEI Jianxin, XU Zhenhuan. Effects of uncertainties in the orientation and position of both the transmitter and receivers on marine CSEM responses in layered vertical anisotropic medium[J]. Chinese Journal of Geophysics, 2017, 60(12): 4901-4915. |
| [22] |
李肃义, 张熠, 张继昆, 等. 海洋可控源电磁信号噪声压制综述[J]. 石油地球物理勘探, 2020, 55(6): 1383-1394. LI Suyi, ZHANG Yi, ZHANG Jikun, et al. A review of noise suppression methods for marine controlled source[J]. Oil Geophysical Prospecting, 2020, 55(6): 1383-1394. |
| [23] |
刘勇, 李文彬, 邓方顺, 等. 海洋可控源电磁法深海油藏开采监测仿真[J]. 石油地球物理勘探, 2022, 57(1): 237-244. LIU Yong, LI Wenbin, DENG Fangshun, et al. Simulation of deep-sea reservoir development monitoring using marine controlled-source electromagnetic me-thod[J]. Oil Geophysical Prospecting, 2022, 57(1): 237-244. |
| [24] |
赵越, 许枫, 李貅, 等. 中心回线海底三维瞬变电磁响应规律分析[J]. 石油地球物理勘探, 2017, 52(5): 1093-1102. ZHAO Yue, XU Feng, LI Xiu, et al. Characteristics of 3D TEM response on seafloor with central loop configuration[J]. Oil Geophysical Prospecting, 2017, 52(5): 1093-1102. |
| [25] |
纳比吉安, 著; 赵经祥, 王艳军, 译. 勘查地球物理电磁法[M]. 北京: 地质出版社, 1992.
|
| [26] |
ALFREDO B. Dipole radiation in the presence of conducting half-space[J]. Ugeskrift for Laeger, 1966, 142(13): 827-828. |
| [27] |
SWIDINSKY A, NABIGHIAN M. Transient electromagnetic fields of a buried horizontal magnetic dipole[J]. Geophysics, 2016, 81(6): E481-E491. |
| [28] |
赵越, 许枫, 李貅, 等. 浅海瞬变电磁全波形响应特征及探测能力分析[J]. 地球物理学报, 2019, 62(4): 1526-1540. ZHAO Yue, XU Feng, LI Xiu, et al. Exploration capability of transmitter current waveform on shallow water TEM response[J]. Chinese Journal of Geophysics, 2019, 62(4): 1526-1540. |



 赵越, 北京市海淀区北四环西路21号中科院声学所,100091。Email:
赵越, 北京市海淀区北四环西路21号中科院声学所,100091。Email: 