大地电磁(MT)方法广泛应用于地壳研究[1-2]、岩石圈地幔调查[3-6]、资源勘探[7-11]和海洋调查[12]等领域。MT方法是一种典型的频域电磁测深方法[13],工作频率范围可达10-5~104Hz[14]。MT三维正演方法可以分为以下几类:积分方程法[15-17],有限差分方法[18-23],有限体积方法[24-25],有限元方法[26-32]以及无网格法[33]等。无论采用哪种正演方法,都需要求解多个频率的大型稀疏线性方程组[34]。MT响应频率范围通常很大,可能达到5个或更高数量级,每个数量级范围内通常包含5~10个采样频点[35]。此外,在每个频率上都需要针对x方向TE极化源和y方向TM极化源进行两次正演[27]。因此,一次MT正演一般需要求解几十个大型稀疏线性方程组,计算量很大。
学者们对此提出了多频电磁正演加速方法。Um等[36]引入了一种针对迭代法的预处理重复利用技术,只需求解最低频率的ILU预处理矩阵,并将该预处理矩阵重复应用于其他频率的正演计算,从而减少正演计算时间。但该算法对于较大频率间隔情况下(比如MT)的正演模拟的有效性还有待验证。另一种常用方法是并行计算技术[37],即采用多CPU计算设备并行计算多个频率的正演响应[38-39]。上述两种改进算法本质上都是基于不同发射频率正演响应的独立求解,当发射频点数增加时,方程求解次数或CPU数量也需要相应增加。
相对上述两种方法,Krylov子空间算法[40-43]更有效。随频率变化的电场响应可以表示为一个传递函数与源矢量的乘积[40],Krylov子空间算法可对其有效求解。Druskin等[40]基于多项式Krylov子空间近似的谱Lanczos方法(SLDM)求解上述电场响应表达式,但该算法的收敛速度依赖于频率范围和模型的电导率差异[41]。相对而言,有理Krylov子空间方法[41-44]的收敛性更好,且收敛性不依赖于模型电导率差异和空间网格分布。但是该算法需要求解多个极点的大型线性方程组。采用重复极点,结合直接求解器,可以显著提高求解速度。
尽管Krylov子空间算法可以求解人工源频率域多频电磁响应,但是该方法不能直接推广到MT正演求解。MT正演假设源是无限大的平面波源,通常采用边界条件隐式代替源的作用[18-19],相应的MT正演响应不能表示为一个传递函数与矢量的乘积形式。Kordy等[45]基于二次场方法,将MT响应表示为一个传递函数与二次场矢量的乘积形式,从而可以采用Krylov子空间算法进行求解,但是由于二次场是随频率变化的,因此求解每一个频率的正演响应时都需要重新构建一次Krylov子空间。为此,Kordy等[45]引入一种有理插值技术解决这一问题,但仍需要多次正演计算生成有理插值方法所需的训练集,因而相比常规的逐次求解各个频率正演响应的方法,该方法仅仅获得2~4倍的加速。
不同于Kordy等的处理方法,本文将MT的源显式表示为一个位于高空的平面电流的形式[46],该源对于所有频率都是一个常数。当平面电流位于模型上边界时,与Zhang等[47]直接在模型上边界赋值电场为1等效。在此基础上,可以将MT响应表示为一个传递函数与常数源矢量的乘积形式,从而可以采用有理Krylov方法求解MT响应[47]。
与可控源电磁法正演问题不同[42],模拟MT响应需对每一个频率计算TE和TM极化源的两次正演,这等价于一个多源正演问题。块状Krylov技术广泛应用于多源正演问题,可有效提高计算效率[48-50]。为进一步提高MT正演的计算速度,不同于Zhang等[47]直接采用有理Krylov方法进行求解,本文引入块状有理Krylov技术[51],将TE和TM极化源表示为块状源矢量,将求解两个极化源的正演响应简化为构建一个块状有理Krylov子空间。
极点是有理Krylov方法的一个重要参数,极点的选取会影响方法的计算速度和计算精度。Güttel[52]对极点的选取算法进行了总结,提出了一种最优化极点选取方法,即通过全局搜索得到多个最优化重复极点[50]。基于该方法,本文引入一种更简单、有效的方法获取最优化单个重复极点[42],结合直接法求解器[53],可实现MT三维模型的高效正演模拟。
本文首先介绍基于拟态有限体积的空间离散化方法[54],源项显式表示为面电流分布,从而将MT响应表示为传递函数与常数源矢量乘积的形式;然后,使用块状有理Krylov(BRK)算法获得传递函数的模型降阶近似解;最后,通过典型的一维半空间模型和3D都柏林测试模型1(DMT1)正演[34],验证本文算法的计算精度和计算速度。
1 正演算法 1.1 控制方程离散设电磁场随时间的变化关系为eiωt,忽略位移电流,则MT正演对应的控制方程为[14]
| $ \nabla \times \boldsymbol{E}+\mathrm{i} \omega \boldsymbol{B}=0 $ | (1) |
| $ \nabla \times \mu^{-1} \boldsymbol{B}-\sigma \boldsymbol{E}=\boldsymbol{S} $ | (2) |
式中:E和B分别表示电场强度矢量和磁场强度矢量;角频率ω=2πf,其中f是频率;μ是磁导率;σ是电导率;S是外加源项,显式表示为平面电流分布[46]。采用自然边界条件,利用基于交错网格的拟态有限体积方法[54],得到空间离散后的控制方程
| $ C e+\mathrm{i} \omega \boldsymbol{b}=0 $ | (3) |
| $ \boldsymbol{C}^{\mathrm{T}} \boldsymbol{M}_\mu \boldsymbol{b}-\boldsymbol{M}_\sigma \boldsymbol{e}=\boldsymbol{s} $ | (4) |
式中:C是离散形式的旋度算子;Mμ和Mσ分别是包含模型磁导率和电导率信息的离散矩阵,具体形式参见文献[42];e、b和s分别为离散形式的电场、磁场和发射源项。对于三维MT正演,同时考虑TE和TM极化源,采用如图 1所示的平面电流近似,平面电流位于空气层中一定高度,可得空间离散的源项为
| $ \begin{aligned} \boldsymbol{s}_1=& \hat{\boldsymbol{x}} \delta\left(y-y_j\right) \delta(z-h) \times \\ & {\left[\mathrm{H}\left(x-x_i\right)-\mathrm{H}\left(x-x_{i+1}\right)\right] } \\ & i=1, 2, \ldots, n_x-1 ; j=1, 2, \ldots, n_y \end{aligned} $ | (5) |
| $ \begin{aligned} \boldsymbol{s}_2=& \hat{\boldsymbol{y}} \delta\left(x-x_i\right) \delta(z-h) \times \\ & {\left[\mathrm{H}\left(y-y_j\right)-\mathrm{H}\left(y-y_{j+1}\right)\right] } \\ & i=1, 2, \ldots, n_x ; j=1, 2, \ldots, n_y-1 \end{aligned} $ | (6) |

|
图 1 TE极化模式(左图中蓝色箭头)和TM极化模式(右图中橙色箭头)的平面电流源分布示意图 |
式中:s1和s2分别为TE和TM极化源;
| $ \boldsymbol{s}=\left[\boldsymbol{s}_1, \boldsymbol{s}_2\right] $ | (7) |
消去式(4)中的磁场,得到关于电场的控制方程
| $ (\boldsymbol{A}+\mathrm{i} \omega \boldsymbol{I}) \boldsymbol{e}=-\mathrm{i} \omega \boldsymbol{X} $ | (8) |
式中:A=Mσ-1CTMμC;X=Mσ-1s;I是单位矩阵。式(8)的解可表示为
| $ \boldsymbol{e}(\omega)=g_\omega(\boldsymbol{A}) \boldsymbol{X} $ | (9) |
式中gω(A)=-iω(A+iωI)-1是一个关联源与场值的传递函数。
1.2 块状有理Krylov方法采用Krylov子空间方法近似求解gω(A)X,由于X是一个块状矩阵,因此可采用BRK方法一次性求解所有源的正演响应[51]。给定块状矩阵X和单个重复极点ξ,BRK方法采用Gram-Schmidt正交化方法求解得到有理Krylov子空间的基,由一系列的块状矢量v1, v2, …, vm+1构成,这里m表示子空间的维度。针对单个矢量和块状矩阵的有理Krylov方法(算法1)的程序实现见表 1[50]。
|
|
表 1 算法1——块状有理Krylov方法 |
对于单个矢量源的情况,算法1中的第7步vj+1=wjRj+1-1可简化为vj+1=wj/‖wj‖。采用算法1获得了有理Krylov子空间的基Vm+1,则式(9)的有理Krylov子空间近似解可以表示为
| $ \boldsymbol{e}_{\mathrm{rk}}(\omega)=\boldsymbol{V}_{m+1} g_\omega\left(\boldsymbol{A}_{m+1}\right) \boldsymbol{V}_{m+1}^{\mathrm{T}} \boldsymbol{X} $ | (10) |
式中Am+1=Vm+1TAVm+1为矩阵A在有理Krylov子空间中的投影矩阵。算法1中的迭代次数(即子空间维度)m很小(本文m < 200),因此Am+1是一个维度为(m+1)×2的小维度矩阵。相比求解有理Krylov子空间的基Vm+1,求解传递函数gω(Am+1)的计算量可忽略。只需要求解一次基Vm+1,后面所有频率的电场响应都可基于式(10)快速求解。算法1中求解基Vm+1最耗时的是多次求解第3步中关于大型稀疏系数矩阵A-ξI的线性方程组。由于采用单个重复极点,系数矩阵是固定不变的,因此可以采用直接求解器实现其快速求解。
为了实现算法1,还需要预先给出极点ξ和迭代次数m。本文采用单个重复极点ξ,其值可通过近似收敛率公式快速得到[42]。对于频率范围T=[ωmin, ωmax],最优化极点为
| $ \xi=-\sqrt{\omega_{\min } \omega_{\max }} $ | (11) |
得到最优化极点ξ后,可以采用替代算法[42]快速得到最优化迭代次数mopt。根据周建美等[42]的分析,频率为ωmin和ωmax时,收敛率最差(模型降阶解满足给定残差阈值所需迭代次数最大),但是最低频率ωmin对应的相对误差最大,因此可以简单地选择最低频率ωmin对应的模型降阶解的相对误差不再降低时的m作为mopt。由于已知最优化的单个重复极点ξ,本文求解mopt的替代算法较Börner等[41]提出的方法更加简化,算法的具体计算机实现过程算法2如表 2所示,其中:L0=diag(λ1, λ2…, λN)为替代对角矩阵,λ1, λ2,…, λN是[λmin=10-8, λmax=108]范围内N=500个对数等间隔分布的值;mmax为一个足够大的数,本文取mmax=200;R(m)表示Rm的集合; arg min R(m)表示寻找R(m)中最小Rm所对应的m。
|
|
表 2 算法2——求解mopt的替代算法 |
采用算法2,可以分析不同求解频率范围对有理Krylov方法的子空间维度m的影响。对于求解频率范围[fmin, fmax],设fmax/fmin=1000,仅改变频率范围,计算fmin的有理Krylov解的相对误差error=‖e-erk‖2/‖e‖2随m的变化,结果见图 2。由图可见,由于fmax/fmin固定,因此fmin的有理Krylov解的收敛率固定[38],因而fmin越大,有理Krylov解的最小相对误差越小。因此,如果以相对误差基本恒定作为mopt的选取标准,则fmax/fmin固定时,fmin越大,对应的mopt越大。进一步考虑最大求解频率fmax固定的情况,计算不同fmin时有理Krylov解的相对误差随m的变化,结果见图 3。由图可见,fmin越小,求解的频率范围越大,收敛率越小,有理Krylov解相对误差基本不变时所对应的m越大,即mopt越大。

|
图 2 fmax/fmin固定时不同fmin条件下有理Krylov解的相对误差error随m的变化曲线 |

|
图 3 求解频率范围的fmax固定时不同fmin的有理Krylov解的相对误差error随m的变化曲线 |
张量MT勘探典型的测量参数是地表水平电场Ex、Ey及全磁场分量Hx、Hy、Hz。假定有两个正交极化源,阻抗张量为
| $ \boldsymbol{Z}=\left[\begin{array}{ll} Z_{x x} & Z_{x y} \\ Z_{y x} & Z_{y y} \end{array}\right]=\left[\begin{array}{ll} E_{x 1} & E_{x 2} \\ E_{y 1} & E_{y 2} \end{array}\right]^{-1}\left[\begin{array}{ll} H_{x 1} & H_{x 2} \\ H_{y 1} & H_{y 2} \end{array}\right] $ | (12) |
其中下标“1”和“2”分别代表TE和TM极化模式。基于阻抗张量Z定义视电阻率和相位[13]分别为
| $ \rho_{q p}=\frac{1}{\omega \mu_0}\left|Z_{q p}\right|^2 $ | (13) |
| $ \phi_{q p}=\arctan \frac{\operatorname{Im}\left(Z_{q p}\right)}{\operatorname{Re}\left(Z_{q p}\right)} $ | (14) |
式中:下标“q”和“p”代表x或y;Re(·)和Im(·)分别表示取实部和虚部。
2 数值实例通过两个典型模型的正演验证BRK方法对MT正演计算的速度和精度。数值实例中空气层电阻率均为1×106Ω·m。本文计算设备为32G内存、四核主频3.6GHz的Intel i7CPU的台式电脑。
2.1 均匀半空间模型首先对均匀半空间模型进行模拟,通过与理论结果[15, 19]对比,验证本文算法的计算精度。假设模型均匀半空间电阻率为100Ω·m,fmin=0.001Hz,fmax=1Hz,频率范围内对数等间隔取31个频点。正演计算区域在x、y和z三个方向外扩边界距离源均为16δ,这里
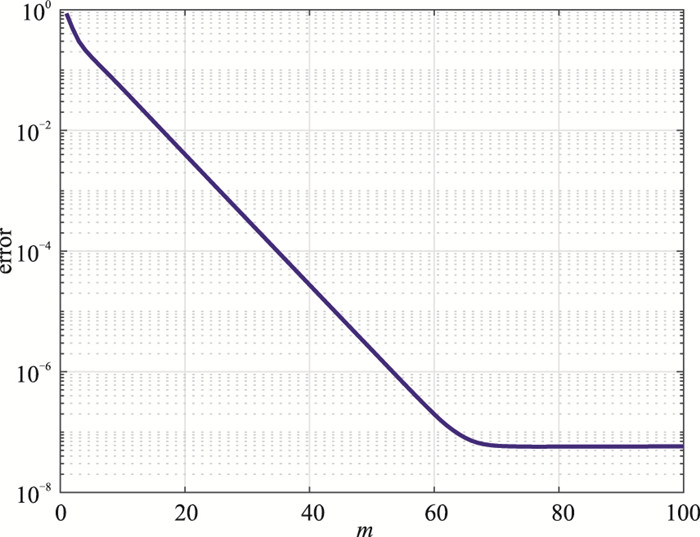
采用BRK方法计算MT响应。根据式(11)得到最优化极点ξ=-0.1987。采用替代算法求解mopt。图 4为频率fmin为0.001Hz时的有理Krylov子空间解的相对误差error随m的变化曲线。由图可见,m>70时,error小于1×10-6且基本恒定,满足计算精度要求,因此选取mopt=70。
|
图 4 均匀半空间模型fmin=0.001Hz的有理Krylov解的error曲线 |
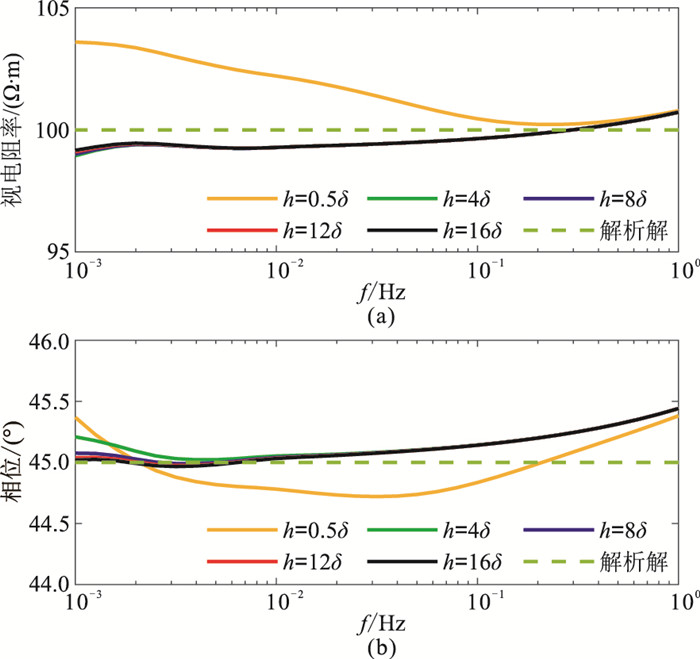
图 5为不同h时计算的视电阻率和相位正演结果与解析解的对比。对于均匀半空间模型,TE和TM模式的响应是相同的,因此图 5仅给出了TE模式的正演结果。
|
图 5 半空间模型不同h的MT视电阻率(a)和相位(b)响应与解析解对比 |
由图 5可见,在低频时,靠近地表(h=0.5δ)时,平面电流源不能较好地近似为平面波源,因此正演响应存在较大误差;当平面电流源逐渐远离地表(h=4δ,8δ,12δ)时,正演误差逐渐减小;当平面电流源位于空气层边界(h=16δ)时,所有频点视电阻率相对误差均小于1%,相位误差均小于0.5°。
均匀半空间模型计算结果表明,将平面电流源置于空气层边界时,本文BRK方法能够精确地模拟MT三维正演响应。
为了分析BRK方法的计算效率,对比本文BRK方法、非块状有理Krylov方法[42](RK)和逐次采用直接求解器PARDISO[53]求解各个频率的正演响应的直接求解法(Direct)的计算结果。虽然一维模型的TE模式和TM模式的响应是相同的,但是为了通用性考虑,在比较算法计算效率时,本文依然以计算TE和TM模式响应的总计算时间为依据。上述三种算法计算的MT响应基本相同,因此本文仅对计算时间进行比较,结果如表 3所示。可见,本文BRK方法只需1次系数矩阵分解及70次矩阵回代;RK方法分别求解TE和TM模式的响应,因此需要1次系数矩阵分解和140次矩阵回代;直接求解法(Direct)需对每个频率进行1次系数矩阵分解,因此共计需要31次系数矩阵分解和31次矩阵回代。因此,本文BRK方法相比直接求解法,能够显著提高计算速度,加速比高达22.5;相比RK方法,由于减小了1次子空间构建的运算次数,也能实现一定的加速效果。
|
|
表 3 均匀半空间模型MT响应模拟不同算法计算量及耗时对比 |
为了进一步分析BRK方法的精度和速度,利用三维都柏林测试模型1(DTM1)[30]进行正演响应计算,并与有限元法和积分方程方法的正演结果进行对比。
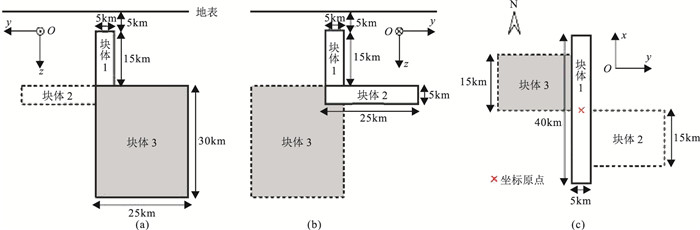
DTM1模型的均匀半空间包含3个块状电性异常体,具体参数见表 4和图 6。坐标原点位于块体1中心点的正上方地表,观测点位于坐标原点,fmin=10-4Hz,fmax=10Hz,在计算频率范围内对数等间隔取21个频点。计算区域离散为72×74×72个网格,最小网格长度为20m,网格放大系数为1.5。
|
|
表 4 DTM1模型块体空间坐标和电阻率 |
|
图 6 DTM1模型示意图 (a)x轴负方向yOz平面;(b)x轴正方向yOz平面;(c)xOy平面(俯视图) |
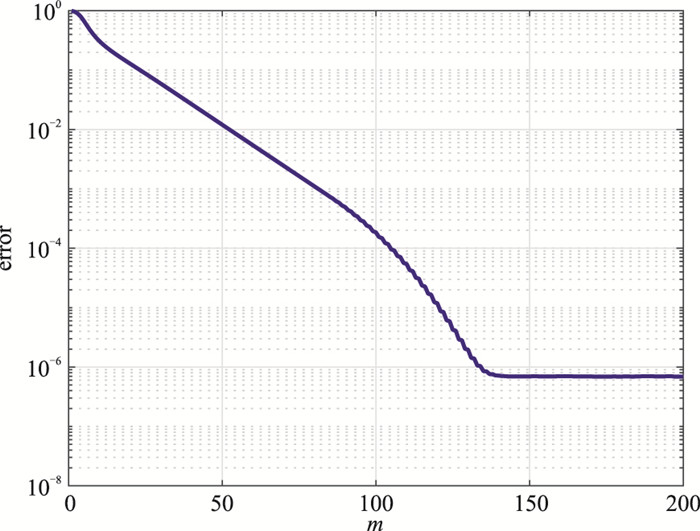
根据式(11)得到最优化极点ξ=-0.1987,与一维模型的最优化极点值相同,因为极点取决于最低频率和最高频率的乘积。采用替代算法求解mopt。图 7为fmin=1×10-4Hz的有理Krylov子空间解的相对误差error随m的变化曲线。相比一维模型,三维DTM1模型的求解频率范围更大,因此最小频率fmin对应的误差收敛率更小,从而相对误差稳定时所对应的m更大。由图 7可知,m>150时,相对误差基本恒定,因此选取mopt=150。
|
图 7 fmin=1×10-4Hz时有理Krylov子空间解的error随m的变化曲线 |
采用本文BRK方法得到的DTM1模型正演结果见图 8。文献[32]给出了多种方法的DTM1模型正演响应,其中积分方程法(IE)[55]和有限元法(FE)[27]的结果基本重合,因此本文以这两种算法的正演结果作为参考,验证本文算法的精度。由图 8可知,BRK方法正演得到的xy和yx分量的视电阻率(ρxy,ρyx)和相位曲线(ϕxy,ϕyx),与积分方程法[55]和有限元法[27]的结果基本重合;BRK方法正演得到的xx和yy分量的视电阻率(ρxx,ρyy)和相位(ϕxx,ϕyy),在高频段(>1Hz)由于视电阻率值太小没有显示,相位分布也相对杂乱;但是在低频段(<1Hz),本文计算结果与积分方程法和有限元法的结果基本一致。因此,本文BRK方法能够较精确地正演MT三维复杂模型的电磁响应。

|
图 8 DTM1模型不同方法的正演视电阻率(上)和相位(下)对比 (a)xx分量;(b)xy分量;(c)yx分量;(d)yy分量 |
统计本文BRK法、RK[42]法和Direct法[53]开展DTM1模型正演的耗时如表 5所示。相比Direct法,BRK法加速比达到11.8;相比RK方法,也能实现一定的加速效果。相比一维半空间模型,三维DTM1模型的正演加速比有所降低,主要原因在于三维DTM1模型求解的频率数量仅为21,每个数量级范围内仅选取4个频率,相比一维半空间模型(频率数量为31)有所减少,因而直接求解法所需的计算时间相对减少,导致BRK方法的加速效果相对下降。
|
|
表 5 DTM1模型MT响应正演耗时统计 |
MT正反演中如何选取频点一直是一个开放的问题[56],一般采用对数等间隔选取方法,每个数量级范围内选取3~4个频率[57]或者更少[58],少数情况下选取5~6个频率[59]甚至8个频率[60]。由于采用直接求解方法,每个频率都需要求解2次大型线性方程组,因此应选取尽量少的频率[56]。
采用本文BRK子空间方法则可以很好地避免上述问题。对于BRK子空间方法,增加求解频率数量,只是增加了求解模型降阶解方程(式(10))的次数。由于式(10)是小维度矩阵的传递函数求解,计算速度很快,因此相应增加的计算时间可以忽略。如果按照一维均匀半空间模型的频率分布密度采样,即在1×10-4~1×10Hz频率范围内计算51个对数等间隔分布的频率,对这些频点计算MT响应,BRK方法耗时仅为2988.5s,相比21个频率的MT响应计算时间2894.2s,增加了30个计算频率,但求解时间仅增加94.3s,即增加1个频率所需计算时间仅为3.1s。而采用直接求解法计算51个频率的正演响应,所需时间高达83504.2s,相比计算21个频率的计算时间34391.1s,意味着增加30个频率所需求解时间增加49113.1s,即增加1个频率的正演响应所需要的时间高达1637.1s,为BRK方法所需时间的528倍。计算51个频率的正演响应,BRK方法相比直接求解法的加速比高达27.9。显然,求解频点数越多,BRK方法的计算速度优势越明显。
图 9为采用BRK方法计算的51个频率和21个频率的MT响应结果,这里仅给出通常基于xy和yx分量计算的视电阻率和相位。如图 9所示,51个频率的MT视电阻率和相位曲线,相比21个频率的MT曲线,更能够体现曲线变化的细节特征。因此,在计算时间允许的条件下,建议选取尽可能多的频点数,可得到更精细的响应曲线特征。

|
图 9 DTM1模型采用BRK方法计算的不同频点的视电阻率(上)和相位(下) (a)xy分量;(b)yx分量 |
本文基于拟态有限体积离散和块状有理Krylov方法实现了一种求解MT三维正演响应的快速算法。通过将源显式表示为高空中的平面电流源,可将任意频率的MT正演响应表示为一个传递函数与源矢量的乘积。采用块状有理Krylov方法,只需要构建一次块状有理Krylov子空间即可实现TE和TM极化源在给定频率范围内所有频点的MT正演响应。采用渐近收敛公式得到块状有理Krylov方法的最优化单个重复极点,利用替代算法可快速得到最优化的Krylov子空间维度,结合直接求解器,将MT三维正演的计算量减小为一次系数矩阵分解和多次矩阵回代。相对常规的直接求解方法,本文方法极大地提高了计算速度。
均匀半空间模型的数值实例结果表明,将平面电流源设置在空间离散网格中空气层的最外边界区域,能够最大限度地近似为平面波源,降低正演近似误差。计算31个频率的半空间模型正演响应,相比直接求解方法,块状有理Krylov方法在保证计算结果精度的同时,实现了22.5倍的加速;计算21个频率的三维DTM1模型的正演响应,相比直接求解方法,块状有理Krylov方法实现了11.8倍的加速。求解频率数越多,块状有理Krylov方法的计算速度优势越明显。
本文块状有理Krylov方法的主要计算量为1次系数矩阵分解和mopt次回代,因此对于中小尺度模型,当求解频率数量较多时,本文算法在计算速度上优势显著。当模型的空间离散网格数量较大、需要求解的频率数量较少时,直接分解算法的计算时间和占用内存都会显著增加,此时基于迭代算法逐次求解各个频率响应的传统方法在计算速度上更具有优势。因此,实际工作中要根据模型规模和频率数量选择合适的正演求解方法。
| [1] |
UNSWORTH M. Magnetotelluric studies of active continent-continent collisions[J]. Surveys in Geophysics, 2010, 31(2): 137-161. DOI:10.1007/s10712-009-9086-y |
| [2] |
李大虎, 詹艳, 丁志峰, 等. 四川长宁Ms6.0地震震区上地壳速度结构特征与孕震环境[J]. 地球物理学报, 2021, 64(1): 18-35. LI Dahu, ZHAN Yan, DING Zhifeng, et al. Upper crustal velocity and seismogenic environment of the Changning Ms6.0 earthquake region in Sichuan, China[J]. Chinese Journal of Geophysics, 2021, 64(1): 18-35. |
| [3] |
JONES A G, FERGUSON I J. The electric Moho[J]. Nature, 2001, 409(6818): 331-333. DOI:10.1038/35053053 |
| [4] |
李宝春, 张乐天, 叶高峰, 等. 基于电性结构模型的青藏高原东缘上地幔热结构研究[J]. 地球物理学报, 2020, 63(3): 1043-1055. LI Baochun, ZHANG Letian, YE Gaofeng, et al. Upper mantle thermal structure beneath the eastern margin of the Tibetan Plateau inferred from electrical structure model[J]. Chinese Journal of Geophysics, 2020, 63(3): 1043-1055. |
| [5] |
杨文采, 金胜, 张罗磊, 等. 青藏高原岩石圈三维电性结构[J]. 地球物理学报, 2020, 63(3): 817-827. YANG Wencai, JIN Sheng, ZHANG Luolei, et al. The three-dimensional resistivity structures of the lithosphere beneath the Qinghai-Tibet Plateau[J]. Chinese Journal of Geophysics, 2020, 63(3): 817-827. |
| [6] |
李永博, 吴琼, 王刚, 等. 海岸效应对大地电磁响应的影响及校正方法[J]. 石油地球物理勘探, 2021, 56(3): 631-644. LI Yongbo, WU Qiong, WANG Gang, et al. Study on the influence and correction method of coast effect on magnetotelluric responses[J]. Oil Geophysical Prospecting, 2021, 56(3): 631-644. |
| [7] |
闵刚, 王绪本, 张兵, 等. AMT法在黔东北岑巩地区的页岩气勘探试验[J]. 石油地球物理勘探, 2014, 49(4): 815-824. MIN Gang, WANG Xuben, ZHANG Bing, et al. A shale gas exploration test with AMT method in Cengong area, Northeast Guizhou[J]. Oil Geophysical Prospecting, 2014, 49(4): 815-824. |
| [8] |
MEJU M A. Geoelectromagnetic exploration for na-tural resources: models, case studies and challenges[J]. Surveys in Geophysics, 2002, 23(2): 133-206. |
| [9] |
CAI H Z, ZHDANOV M S. Three-dimensional inversion of magnetotelluric data for the sediment-basement interface[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(3): 349-353. |
| [10] |
CAI H Z, ZHDANOV M S. Joint inversion of gravity and magnetotelluric data for the depth-to-basement estimation[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(8): 1228-1232. DOI:10.1109/LGRS.2017.2703845 |
| [11] |
吴懿豪, 韩江涛, 刘云鹤, 等. 内蒙古双尖子山矿集区三维电性结构及成矿意义[J]. 地球物理学报, 2021, 64(4): 1291-1304. WU Yihao, HAN Jiangtao, LIU Yunhe, et al. Three-dimensional electrical structures and mineralization significance in the Shuangjianzishan ore-concentrated area, Inner Mongolia[J]. Chinese Journal of Geophysics, 2021, 64(4): 1291-1304. |
| [12] |
JOHANSEN S E, PANZNER M, MITTET R, et al. Deep electrical imaging of the ultraslow-spreading Mohns Ridge[J]. Nature, 2019, 567(7748): 379-383. DOI:10.1038/s41586-019-1010-0 |
| [13] |
NABIGHIAN M N. Electromagnetic Methods in Applied Geophysics: Volume 2, Application, Parts A and B[M]. McLean: Society of Exploration Geophysicists, 1991: 641-712.
|
| [14] |
CHAVE A D, JONES A G. The Magnetotelluric Method: Theory and Practice[M]. New York: Cambridge University Press, 2012.
|
| [15] |
ZHDANOV M S, LEE S K, YOSHIOKA K. Integral equation method for 3D modeling of electromagnetic fields in complex structures with inhomogeneous background conductivity[J]. Geophysics, 2006, 71(6): G333-G345. DOI:10.1190/1.2358403 |
| [16] |
REN Z Y, KALSCHEUER T, GREENHALGH S, et al. Boundary element solutions for broad-band 3-D geo-electromagnetic problems accelerated by an adaptive multilevel fast multipole method[J]. Geophysical Journal International, 2013, 192(2): 473-499. DOI:10.1093/gji/ggs043 |
| [17] |
KRUGLYAKOV M, BLOSHANSKAYA L. High-performance parallel solver for integral equations of electromagnetics based on Galerkin method[J]. Mathe-matical Geosciences, 2017, 49(6): 751-776. DOI:10.1007/s11004-017-9677-y |
| [18] |
MACKIE L R, SMITH T, MADDEN T R. Three-dimensional electromagnetic modeling using finite difference equations: the magnetotelluric example[J]. Radio Science, 1994, 29(4): 923-935. DOI:10.1029/94RS00326 |
| [19] |
SIRIPUNVARAPORN W, EGBERT G, LENBURY Y. Numerical accuracy of magnetotelluric modeling: a comparison of finite difference approximations[J]. Earth Planets and Space, 2002, 54(6): 721-725. DOI:10.1186/BF03351724 |
| [20] |
LI G, ZHANG L L, HAN B. Stable electromagnetic modeling using a multigrid solver on stretching grids: the magnetotelluric example[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(3): 334-338. |
| [21] |
彭荣华, 胡祥云, 韩波, 等. 基于拟态有限体积法的频率域可控源三维正演计算[J]. 地球物理学报, 2016, 59(10): 3927-3939. PENG Ronghua, HU Xiangyun, HAN Bo, et al. 3D frequency-domain CSEM forward modeling based on the mimetic finite-volume method[J]. Chinese Journal of Geophysics, 2016, 59(10): 3927-3939. |
| [22] |
VARILSUHA D and CANDANSAYAR M E. 3D magnetotelluric modeling by using finite-difference method: comparison study of different forward mode-ling approaches[J]. Geophysics, 2018, 83(2): WB51-WB60. DOI:10.1190/geo2017-0406.1 |
| [23] |
LI J, LIU J X, EGBERT G D, et al. An efficient preconditioner for 3-D finite difference modeling of the electromagnetic diffusion process in the frequency domain[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(1): 500-509. |
| [24] |
HABER E, ASCHER U M, ARULIAH D A, et al. Fast simulation of 3D electromagnetic problems using potentials[J]. Journal of Computational Physics, 2000, 163(1): 150-171. |
| [25] |
JAHANDARI H, FARQUHARSON C G. Finite-volume modelling of geophysical electromagnetic data on unstructured grids using potentials[J]. Geophysical Journal International, 2015, 202(3): 1859-1876. |
| [26] |
MOGI T. Three-dimensional modeling of magnetotelluric data using finite element method[J]. Journal of Applied Geophysics, 1996, 35(2-3): 185-189. |
| [27] |
NAM M J, KIM H J, SONG Y, et al. 3D magnetotelluric modelling including surface topography[J]. Geo-physical Prospecting, 2007, 55(2): 277-287. |
| [28] |
FARQUHARSON C G, MIENSOPUST M P. Three-dimensional finite-element modelling of magnetotelluric data with a divergence correction[J]. Journal of Applied Geophysics, 2011, 75(4): 699-710. |
| [29] |
REN Z Y, KALSCHEUER T, GREENHALGH S, et al. A finite-element-based domain-decomposition approach for plane wave 3D electromagnetic modeling[J]. Geophysics, 2014, 79(6): E255-E268. |
| [30] |
秦策, 王绪本, 赵宁, 等. 频率域电磁法三维有限元正演线性方程组迭代算法[J]. 地球物理学报, 2020, 63(8): 3180-3191. QIN Ce, WANG Xuben, ZHAO Ning, et al. Research on the iterative solver of linear equations in three-dimensional finite element forward modeling for frequency domain electromagnetic method[J]. Chinese Journal of Geophysics, 2020, 63(8): 3180-3191. |
| [31] |
顾观文, 李桐林. 基于矢量有限元的带地形大地电磁三维反演研究[J]. 地球物理学报, 2020, 63(6): 2449-2465. GU Guanwen, LI Tonglin. Three-dimensional magnetotelluric inversion with surface topography based on the vector finite element method[J]. Chinese Journal of Geophysics, 2020, 63(6): 2449-2465. |
| [32] |
梁生贤, 张胜业, 吾守艾力, 等. 复杂三维介质的大地电磁正演模拟[J]. 地球物理学进展, 2012, 27(5): 1981-1988. LIANG Shengxian, ZHANG Shengye, WUSHOU Aili, et al. Magnetotelluric forward modeling in complex three-dimensional media[J]. Progress in Geophysics, 2012, 27(5): 1981-1988. |
| [33] |
JI Y J, HUANG T Z, HUANG W Y, et al. Meshfree method in geophysical electromagnetic prospecting: the 2D magnetotelluric example[J]. International Journal of Computational Methods, 2018, 15(2): 1750084. |
| [34] |
MIENSOPUST M P, QUERALT P, JONES A G, et al. Magnetotelluric 3-D inversion: a review of two successful workshops on forward and inversion code testing and comparison[J]. Geophysical Journal International, 2013, 193(3): 1216-1238. |
| [35] |
周聪, 汤井田, 原源, 等. 大地电磁多参考站阵列数据处理方法[J]. 石油地球物理勘探, 2020, 55(6): 1373-1382. ZHOU Cong, TANG Jingtian, YUAN Yuan, et al. Multi-reference array MT data processing method[J]. Oil Geophysical Prospecting, 2020, 55(6): 1373-1382. |
| [36] |
UM E S, COMMER M, NEWMAN G A. Efficient pre-conditioned iterative solution strategies for the electromagnetic diffusion in the Earth: finite-element frequency-domain approach[J]. Geophysical Journal International, 2013, 193(3): 1460-1473. |
| [37] |
PLESSIX R E, DARNET M, Mulder W A. An approach for 3D multisource, multifrequency CSEM modeling[J]. Geophysics, 2007, 72(5): SM177-SM184. |
| [38] |
CAI H Z, HU X Y, LI J H, et al. Parallelized 3D CSEM modeling using edge-based finite element with total field formulation and unstructured mesh[J]. Computers & Geosciences, 2017, 99: 125-134. |
| [39] |
白宁波, 周君君, 胡祥云. 优化策略的二维大地电磁光滑聚焦反演研究[J]. 石油地球物理勘探, 2021, 56(4): 902-909. BAI Ningbo, ZHOU Junjun, HU Xiangyun. Two-dimensional magnetotelluric smooth focusing inversion based on optimization strategy[J]. Oil Geophysical Prospecting, 2021, 56(4): 902-909. |
| [40] |
DRUSKIN V, KNIZHERMAN L. Spectral approach to solving three-dimensional Maxwell's diffusion equations in the time and frequency domains[J]. Radio Science, 1994, 29(4): 937-953. |
| [41] |
BÖRNER R U, ERNST O G, GVTTEL S. Three-dimensional transient electromagnetic modelling using Rational Krylov methods[J]. Geophysical Journal International, 2015, 202(3): 2025-2043. |
| [42] |
周建美, 刘文韬, 刘航, 等. 多频可控源电磁法三维有理函数Krylov子空间模型降阶正演算法研究[J]. 地球物理学报, 2018, 61(6): 2525-2536. ZHOU Jianmei, LIU Wentao, LIU Hang, et al. Research on rational Krylov subspace model order reduction algorithm for three-dimensional multi-frequency CSEM modelling[J]. Chinese Journal of Geophysics, 2018, 61(6): 2525-2536. |
| [43] |
ZHOU J M, LIU W T, LI X, et al. 3-D full-time TEM modeling using shift-and-invert Krylov subspace method[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(10): 7096-7104. |
| [44] |
谷宇, 殷长春, 邱长凯, 等. 基于有理Krylov子空间法的可控源海洋电磁三维各向异性正演研究[J]. 地球物理学进展, 2020, 35(6): 2332-2350. GU Yu, YIN Changchun, QIU Changkai, et al. Three-dimensional anisotropic forward modeling for marine CSEM method in time-domain based on rational Krylov subspace method[J]. Progress in Geophysics, 2020, 35(6): 2332-2350. |
| [45] |
KORDY M, CHERKAEV E, WANNAMAKER P. Null space correction and adaptive model order reduction in multi-frequency Maxwell's problem[J]. Advances in Computational Mathematics, 2017, 43(1): 171-193. |
| [46] |
WEISS J C. Project APhiD: A lorenz-gauged A-decomposition for parallelized computation of ultra-broadband electromagnetic induction in a fully hetero-geneous Earth[J]. Computers & Geosciences, 2013, 58: 40-52. |
| [47] |
ZHANG J F, LIU J R, FENG B, et al. Three-dimensional magnetotelluric modeling using the finite element model reduction algorithm[J]. Computers & Geosciences, 2021, 151: 104750. |
| [48] |
CALANDRA H, GRATTON S, LANGOU J, et al. Flexible variants of block restarted gmres methods with application to geophysics[J]. SIAM Journal on Scientific Computing, 2012, 34(2): A714-A736. |
| [49] |
PUZYREV V, CELA J M. A review of block Krylov subspace methods for multisource electromagnetic modelling[J]. Geophysical Journal International, 2015, 202(2): 1241-1252. |
| [50] |
QIU C K, GVTTEL S, REN X Y, et al. A block rational Krylov method for 3-D time-domain marine controlled-source electromagnetic modelling[J]. Geophysical Journal International, 2019, 218(1): 100-114. |
| [51] |
ELSWORTH S, GVTTEL S. The block rational arnoldi method[J]. SIAM Journal on Matrix Analysis and Applications, 2020, 41(2): 365-388. |
| [52] |
GVTTEL S. Rational Krylov Methods for Operator Functions[D]. Technische Universität Bergakademie Freiberg, Freiberg, 2010.
|
| [53] |
SCHENK O, GÄRTNER K. Solving unsymmetric sparse systems of linear equations with PARDISO[J]. Future Generation Computer Systems, 2004, 20(3): 475-487. |
| [54] |
HABER E. Computational Methods in Geophysical Electromagnetics[M]. Philadelphia: Society for Industrial and Applied Mathematics, 2014.
|
| [55] |
AVDEEV B D, KUVSHINOV A V, PANKRATOV O V, et al. Three-dimensional induction logging problems, Part I: an integral equation solution and model comparisons[J]. Geophysics, 2002, 67(2): 413-426. |
| [56] |
MIENSOPUST M P. Application of 3-D electromagnetic inversion in practice: challenges, pitfalls and solution approaches[J]. Surveys in Geophysics, 2017, 38(9): 869-933. |
| [57] |
MEQBEL N, WECKMANN U, MUÑOZ G, et al. Crustal metamorphic fluid flux beneath the Dead Sea Basin: constraints from 2D and 3D magnetotelluric modelling[J]. Geophysical Journal International, 2016, 207(3): 1609-1629. |
| [58] |
PATRO P K, EGBERT G D. Application of 3D inversion to magnetotelluric profile data from the Deccan Volcanic Province of Western India[J]. Physics of the Earth and Planetary Interiors, 2011, 187(1-2): 33-46. |
| [59] |
ROBERTSON K, HEINSON G, THIEL S. Litho-spheric reworking at the Proterozoic-Phanerozoic transition of Australia imaged using AusLAMP magnetotelluric data[J]. Earth and Planetary Science Letters, 2016, 452: 27-35. |
| [60] |
YANG B, EGBERT G D, KELBERT A, et al. Three-dimensional electrical resistivity of the north-central USA from EarthScope long period magnetotelluric data[J]. Earth and Planetary Science Letters, 2015, 422: 87-93. |



 周建美, 陕西省西安市雁塔路126号长安大学地质工程与测绘学院,710054。Email:
周建美, 陕西省西安市雁塔路126号长安大学地质工程与测绘学院,710054。Email: