② 中国自然资源航空物探遥感中心,北京 100083;
③ 中国地质大学(北京)地球物理与信息技术学院,北京 100083;
④ 中国地质科学院地球物理地球化学勘查研究所,河北廊坊 065000;
⑤ 自然资源部地球物理电磁法探测技术重点实验室,河北廊坊 065000
② China Aero Geophysical Survey and Remote Sensing Center for Natural Resources, Beijing 100083, China;
③ School of Geophysics and Information Techno-logy, China University of Geosciences (Beijing), Beijing 100083, China;
④ Institute of Geophysical and Geochemical Exploration, Chinese Academy of Geological Science, Langfang, Hebei 065000, China;
⑤ Key Laboratory of Geophysical Electromagnetic Probing Technologies of Ministry of Natural Resources, Langfang, Hebei 065000, China
重力场分离是重力数据反演、地质解释与推断的前提[1-3],是业内公认的重点研究课题和技术难题。早在1952年,Dobrin等[4]就提出重力解释中两个最重要的问题:一个是区域场与局部场的分离;另一个是基于分离得到的异常获取目标地质体的空间位置和密度信息。程方道等[5]指出,与磁异常相比,重力异常普遍存在强大的区域背景场,往往会造成局部异常发生畸变,甚至难于辨识,要对重力资料进行有效的地质解释,首先必须分离重力区域场与局部场;管志宁等[6]强调,正确划分不同规模的区域场与局部场是面积性测量资料解释能否获得良好地质效果的一个重要因素;曾华霖[7]认为,在密度界面反演中,只要平均深度取值合理,界面之间的密度差异比较接近实际情况,无论采用何种反演方法,都能得到达到一定的精度及相似的结果,但前提是用于反演的异常必须单纯由目标体引起;徐世浙等[8]认为重力场三维反演是个难度极大的课题,提出异于常规解决方案的开拓性思路,主要包括三个方面:对平面上的重力场进行不同深度的分离;用大深度位场向下延拓的迭代法将各个切割层在地面的重力场下延至相应深度;将顶面的重力场反演为视密度。现今,位场大深度的向下延拓技术和层源异常的反演技术已经得到了很好发展,位场分离方法是目前影响反演方法效果的关键技术,继续加强对异常分离方法的研究具有重要意义。
重力场分离方法大致可分为空间域方法和频率域(波数域)方法。频率域方法主要包括维纳滤波法[9]、匹配滤波法[10-12]、小波多尺度分析法[13-17]、优选滤波法[18-19]和优化滤波法[20]等,这些方法各有特点和优势,但同时又有不同的局限性。维纳滤波法是维纳滤波器在信号与干扰不相关条件下的一个特例,适用于白噪声的去除,不适合于场的分离,目前相关研究与应用不多;匹配滤波法对于埋深和尺寸相差较大的场源分离效果较好,但是若异常的功率谱不具明显的线性特征时,如何更加有效地确定深、浅源场的频段分布,是该方法在实际资料处理过程中的一个难点;小波多尺度分析法是一种新兴的位场分离方法,在区域性深部地壳结构研究方面取得了一些成果,但是存在小波母函数选择和阶次选择较难等问题;优选滤波法实现了指定频段或尺度的局部异常的分离,但实际应用中延拓高度往往很难正确选择;优化滤波法异常分离不受延拓高度的困扰,但其前提是目标层与其他深度层场源信息互不相关。实践表明,空间域方法有一定的技术优势。管志宁等[6]基于多年的重磁数据处理经验认为,由于受测区范围有限、数据离散化,以及不同埋深、不同位置场源体的重磁异常频谱特征部分重叠等诸多因素的影响,在波数域变换过程中会产生明显的误差和畸变,只能用作初步的定性估计;Spector[21]也认为,波数域方法只能对深源(区域场)和浅源(局部场)异常作定性的划分,不能用于定量研究,无法取代空间域中异常曲线拟合类方法。因而,本文以空间域方法为研究对象。
空间域方法主要包括趋势面拟合法[22-24]、经验模态分解法[25]、最小曲率法[26-28]、曲率滤波法[29-30]、有限单元法[31-37]、卡尔曼滤波法[38-39]、矩阵底秩分解法[40-41]和插值切割法[42-53]等。目前,空间域方法中较为前沿且应用较广的重力场分离方法是插值切割法,该方法基于多次切割法发展而来。程方道等[5]首次提出多次切割法,其基本原理是以四点圆周平均值为切割算子,通过连续切割得到切割区域场,并将其从总异常中减去,便得到切割局部场。为了压制多次切割法中的切割发散效应,文百红等[42]基于新型算子首次提出了插值切割法;之后,秦葆瑚[43]、段本春等[44]、徐世浙等[45]、邢怡等[46]、刘东甲[47]、葛粲等[48-49]围绕优化切割算子、探寻切割半径与异常埋深的关系展开了系统的研究工作,形成了以插值切割法为核心技术的方法系列,汪炳柱等[50]、杨金玉等[51]、万胜荣等[52]和赵文举等[53]将该方法广泛应用于油气勘探、矿产勘查、基础地学研究等诸多领域。
以上提及的插值切割法及其改进算法很少涉及重力异常产生的物理属性,多针对异常曲线本身进行插值切割计算。如果忽视异常产生的地质属性,往往会造成分析问题不够全面,甚至产生一定的计算误差。故本文在分析插值切割法基本原理基础上,证明了插值切割法的切割算子仅考虑了局部异常与区域异常弯曲方向相同的叠合情况,不能完全体现实际复杂的地下地质情况。因此,本文结合重力局部异常与区域异常的四种叠合关系,提出了一种基于异常约束条件的插值切割法,并将其命名为约束插值切割法。通过典型理论模型对比试算和实际测量数据应用,验证了约束插值切割法的准确性和优越性,可为大区域的基础地学研究提供技术支撑,在具备局部高精度重力资料的情况下,也可为油气远景区的预测提供一定技术参考。
1 插值切割法插值切割法是一种简单、有效的空间域非线性滤波方法,以当前计算点场值与周围多点平均值的插值运算为切割算子,通过连续切割得到切割区域场,并将其从位场异常中减去,便得到切割局部场[42]。根据插值切割算子的不同,形成了基于四点圆周插值切割算子[42]、八点窗口插值切割算子[46]和动态改进型插值切割算子[49]的插值切割方法。
1.1 计算思路插值切割法虽衍生出不同的切割算子,但其计算原理是一致的。下面以经典的四点圆周插值切割算子为例介绍插值切割法的计算思路。
设重力异常Z(x, y)由区域场R(x, y)和局部场L(x, y)组成,即
| $ Z(x, y)=R(x, y)+L(x, y) $ | (1) |
令M(x, y)表示与点(x, y)距离为r的4个点的重力异常平均值,即
| $ \begin{gathered} M(x, y)=\frac{1}{4}[Z(x+r, y)+Z(x-r, y)+ \\ Z(x, y+r)+Z(x, y-r)] \end{gathered} $ | (2) |
式中r也称为切割半径。区域场R(x, y)是Z(x, y)与M(x, y)的加权平均,即
| $ R(x, y)=a M(x, y)+b Z(x, y) $ | (3) |
式中a和b是加权系数,且a+b=1。令
| $ \overline{\Delta H_x}=Z(x, y)-\frac{1}{2}[Z(x+r, y)+Z(x-r, y)] $ | (4) |
| $ \overline{\Delta H_y}=Z(x, y)-\frac{1}{2}[Z(x, y+r)+Z(x, y-r)] $ | (5) |
| $ \Delta H_x=Z(x+r, y)+Z(x-r, y) $ | (6) |
| $ \Delta H_y=Z(x, y+r)+Z(x, y-r) $ | (7) |
| $ \begin{array}{*{20}{c}} {c=\frac{\left(\Delta H_x\right)^2}{\left(\overline{\Delta H_x}\right)^2+\left(\Delta H_x\right)^2}}\\ {\left(0 \leqslant c \leqslant 1\right., 且当 \Delta H_x=\overline{\Delta H_x}=0 时, \left.c=1\right)} \end{array} $ | (8) |
| $ \begin{array}{*{20}{c}} {d=\frac{\left(\Delta H_y\right)^2}{\left(\overline{\Delta H_y}\right)^2+\left(\Delta H_y\right)^2}}\\ {\left(0 \leqslant d \leqslant 1\right., 且当 \Delta H_y=\overline{\Delta H_y}=0 时, \left.d=1\right)} \end{array} $ | (9) |
| $ e=c+d \quad(0 \leqslant e \leqslant 2) $ | (10) |
取
| $ R(x, y)=\frac{1}{2} e Z(x, y)+\left(1-\frac{1}{2} e\right) M(x, y) $ | (11) |
用上述方法得到的区域场称为第1次切割的区域场,用R1(x, y)表示;对R1(x, y)重复使用以上方法,得到第2次切割的区域场R2(x, y);依次迭代,当
| $ \mathop {\lim }\limits_{n \to \infty } \left| {{R_n}(x,y) - {R_{n - 1}}(x,y)} \right| \to 0 $ | (12) |
有
| $ R(x, y) = \mathop {\lim }\limits_{n \to \infty } {R_n}(x, y) $ | (13) |
上式得到的区域场即为切割半径的区域场,将其与重力异常Z(x, y)相减,得到局部场
| $ L(x, y)=Z(x, y)-R(x, y) $ | (14) |
一般地,切割半径r越大,得到的局部场所反映的密度体的深度和规模就越大。根据前人大量模拟实验和实测资料[42-53]分析,以切割半径r得到的局部场可近似代表深度r以上地层的重力效应,但尚未得出切割半径r与密度体埋深的确切计算公式。由于切割算子中的加权系数引入了半二阶差分量,它们与负二阶水平导数即曲率成正比,因此插值切割对不同非线性异常有不同的作用,可提高对不同特征异常场的分离效果。
1.2 误差传递分析插值切割法采用当前计算点值与四点圆周平均值之间的插值关系作为切割算子G,将切割算子G作用于重力场Z(x, y),即可得到区域场
| $ \begin{aligned} R(x, y)=& G[Z(x, y)]=\frac{1}{2} e Z(x, y)+\\ &\left(1-\frac{1}{2} e\right) M(x, y) \end{aligned} $ | (15) |
设原始观测数据各点的均方误差δZ(x, y)=ε0,根据误差传递公式[54]得到区域场的误差传递关系为
| $ \begin{aligned} \varepsilon^2=&\left(\frac{1}{2} e\right)^2[\delta Z(x, y)]^2+\left(1-\frac{1}{2} e\right)^2 \times \\ & {[\delta M(x, y)]^2 } \\ =&\left(\frac{5}{16} e^2-4 e+\frac{1}{4}\right) \varepsilon_0^2 \end{aligned} $ | (16) |
令误差传递系数
那么,第1次切割后区域场的误差传递系数k1有
| $ \frac{\sqrt{5}}{5} \leqslant k_1 \leqslant 1 $ | (17) |
第i次切割后区域场的误差传递系数ki有
| $ \left(\frac{\sqrt{5}}{5}\right)^i \leqslant k_i \leqslant 1 $ | (18) |
由上式可见,多次切割后区域场的传递误差不会放大。
2 改进的插值切割法分析插值切割法基本理论公式,该方法主要对异常曲线本身进行插值切割计算,而对重力异常产生的地质属性考虑不足。忽略产生异常的地质属性得到的计算结果难免产生一定的误差。下面首先在理论层面分析插值切割法的不足之处,再从实际地质属性出发,结合重力场局部异常与区域异常的四种叠合关系,对插值切割法加以改进,提出一种基于异常约束条件的插值切割法,即约束插值切割法。
2.1 插值切割法不足的理论分析根据插值切割法的基本理论可知,切割区域场计算公式(式(15))中,0≤e≤2,不难证明R(x, y)介于Z(x, y)与M(x, y)之间,这就意味着经插值切割法计算得到的区域场值不能超出总场异常值与周围点平均值的取值区间。这种情形仅代表局部异常与区域异常弯曲方向相同的叠合情况,并不能完全代表复杂多变的实际地下地质情况,下面进一步分析局部异常与区域异常不同叠合关系的情形。
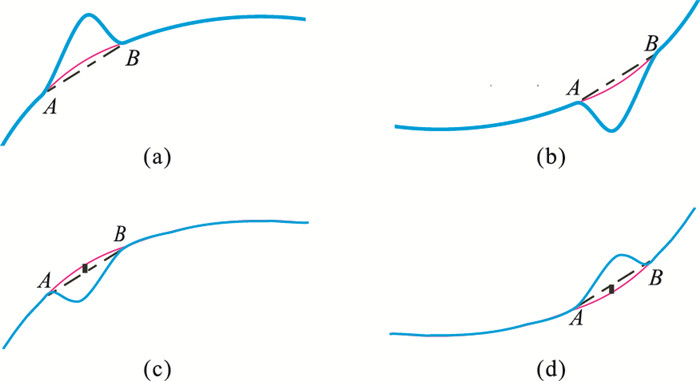
2.2 局部异常与区域异常叠合关系分类在勘探地球物理领域,一般认为区域异常是由埋藏较深、水平延伸范围较大的地质体或构造所产生的,在异常图中表现出形态宽缓、幅值较大、范围较广的特征;局部异常则是由埋藏较浅、水平延伸范围较小的地质体所产生的,在异常图中表现出形态陡窄、幅值较小、异常范围小的特征。在遵循这一基本原则的前提下,本文针对四种实际地质情形,总结了相应的局部异常与区域异常的四种叠合关系分类情形,详见表 1和图 1。不难发现,式(11)仅适用于分类情形1和2,即区域异常介于总场异常值与周围点平均值的取值区间。然而,对于区域异常与局部异常曲线弯曲方向相反的情形,即分类情形3和4,如仍使用式(11)计算切割区域场,计算结果虽可无限向周围点平均值逼近,但依然忽略了图 1c和图 1d中黑色竖线所示部分的异常,这部分异常代表计算得到切割区域场与理论区域场的差异。
|
|
表 1 局部异常与区域异常叠合关系分类表 |
|
图 1 对应表 1中分类情形1~4(a~d)的局部异常与区域异常叠合关系分类 A、B表示局部异常边界;蓝色实线表示总异常场,红色实线表示区域异常,黑色虚线表示局部异常两端点连线,黑色实线表示计算得到的切割区域场与理论区域场的差异。图 2同 |
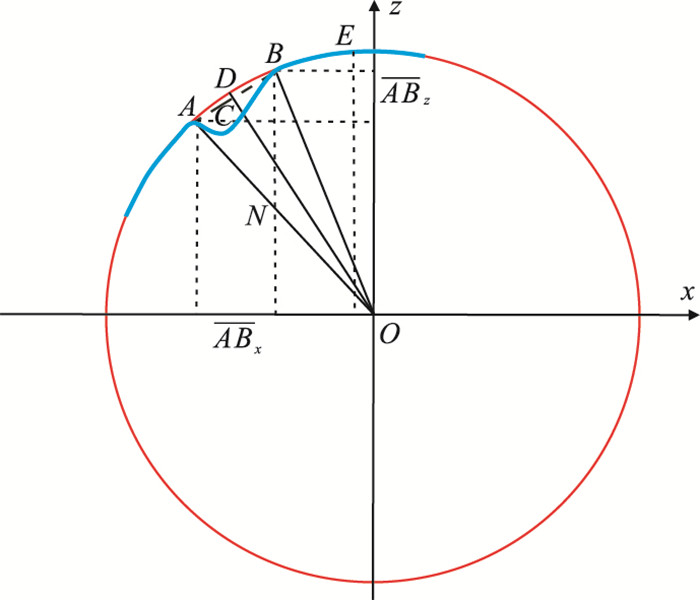
为弥补传统插值切割法的不足,本文提出了一种基于异常约束条件的改进方案,其基本思路是:首先,给定切割半径r,分析区域异常和局部异常曲线弯曲方向;其次,对区域异常与局部异常曲线弯曲方向相同的情形(即分类情形1和2),采用式(11)计算切割区域场,对弯曲方向相反的情形(即分类情形3和4),在式(11)基础上,增加切割区域异常修正量ΔZ(x, y)(图 2),即
| $ \begin{aligned} R(x, y)=& \frac{1}{2} e Z(x, y)+\\ &\left(1-\frac{1}{2} e\right) M(x, y)+\Delta Z(x, y) \end{aligned} $ | (19) |
|
图 2 切割区域异常修正量示意图 |
首先考虑x方向异常剖面,假设局部异常附近的区域异常是曲率半径为N、曲率中心为O的曲率圆的部分弧段(图 2中红色曲线与蓝色曲线重合部分),则x方向切割区域的异常修正量为
| $ \Delta Z(x)=N-\overline{O C}=N-\sqrt{N^2-\overline{A C^2}} $ | (20) |
式中OC、AC分别为线段OC和AC的长度,其中AC可根据勾股定理求得
| $ \overline{A C}=\frac{1}{2} \sqrt{\overline{A B}_x{ }^2+{\overline{A B_z}}^2} $ | (21) |
其中ABx、ABz分别为线段AB在x轴和z轴的投影长度。曲率半径N可根据曲率圆的曲率K求得
| $ N=\frac{1}{K}=\frac{\left(1+Z_{D, x}^{\prime 2}\right)^{\frac{3}{2}}}{Z_{D, x}^{\prime \prime}} $ | (22) |
式中Z′D,x、Z″D,x分别为Z(x, y)在D点对x的一阶导数和二阶导数。用一阶差分替代一阶导数,并忽略一阶余量,得到
| $ Z_{D, x}^{\prime} \approx \frac{Z(B)-Z(A)}{\overline{A B}} $ | (23) |
式中:Z(A)、Z(B)分别为Z(x, y)在A点和B点的值;AB表示线段AB的长度。用二阶差分替代二阶导数,并忽略二阶余量,则
| $ Z_{D, x}^{\prime \prime} \approx \frac{Z(A)+Z(E)-2 Z(B)}{\overline{A B}_x} $ | (24) |
同理,可得到y方向切割区域的异常修正量ΔZ(y),并取ΔZ(x, y)=[ΔZ(x)+ΔZ(y)]/2。
约束插值切割法详细计算步骤见附录A。以上算法基于MATLAB(R2008a)编程平台实现程序和界面编制。
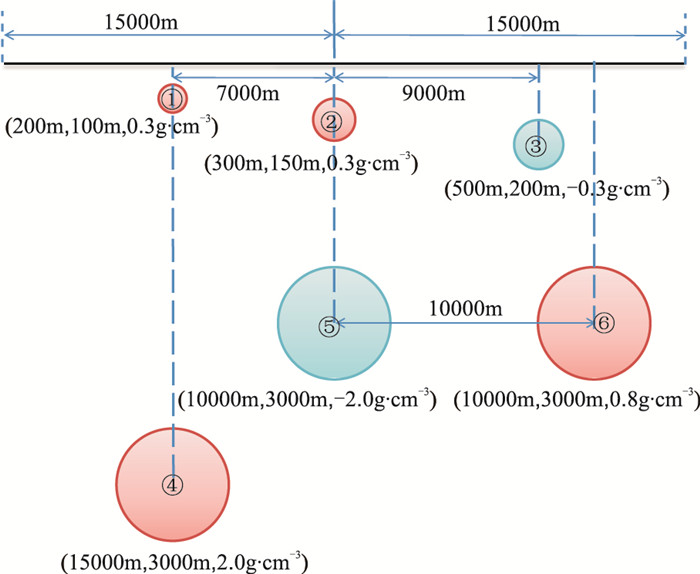
3 理论模型试算 3.1 理论模型设计本文理论模型设计参考了程方道等[5]、Kaftan等[31]、Zhu等[40]及刘东甲[47]的设计思路,即深部大尺度密度体产生的异常视为区域异常,浅部小尺度密度体产生的异常视为局部异常,不同之处是在同一个理论模型中综合考虑了局部异常与区域异常的四种叠合关系。鉴于2.2部分中分类情形1、3分别与2、4呈镜像对称关系,可合并处理,故本文设计了图 3所示的理论模型。三个不同深度的浅部球体(编号①、②、③)产生的是局部重力异常,其中浅部球体①、②产生局部重力高,浅部球体③产生局部重力低;三个不同深度的深部球体(编号④、⑤、⑥)产生的是区域重力异常,其中球体④、⑥引起的是区域重力高异常,球体⑤引起的是重力低异常。
|
图 3 理论模型 球体旁边标注的数值分别表示球心深度、球体半径和剩余密度 |
理论模型的重力异常为各球体剩余质量的引力位沿重力方向(定义为z方向)的导数之和[55],即
| $ \Delta g(x, y, z) = \sum\limits_{i = 1}^n {\frac{{\partial {V_i}}}{{\partial z}}} = \sum\limits_{i = 1}^n {\frac{{f{m_i}\left( {{z_{i0}} - z} \right)}}{{{r_i}}}} $ | (25) |
式中:Vi为球体i产生的引力位;n表示异常体数量,此例n=6;f=6.672×10-11m3·kg-1·s-2为万有引力常数;mi=43πRi3σi为球体i的剩余质量,这里Ri和σi分别为球体i的半径和剩余密度;ri=
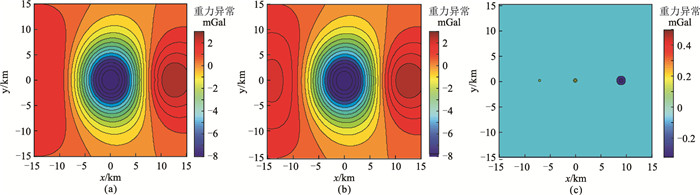
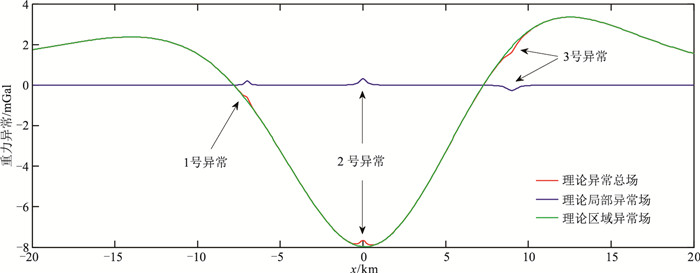
基于式(25),通过正演计算可得模型3的正演重力异常(图 4、图 5)。由图 4可见,局部异常基本淹没在区域异常之中。由图 5可见,1、2、3号异常分别对应2.2部分中分类情形1、4、3。
|
图 4 图 3模型重力异常正演结果 (a)理论异常总场; (b)理论区域异常场; (c)理论局部异常场 |
|
图 5 图 3模型重力异常正演剖面(y=0) |
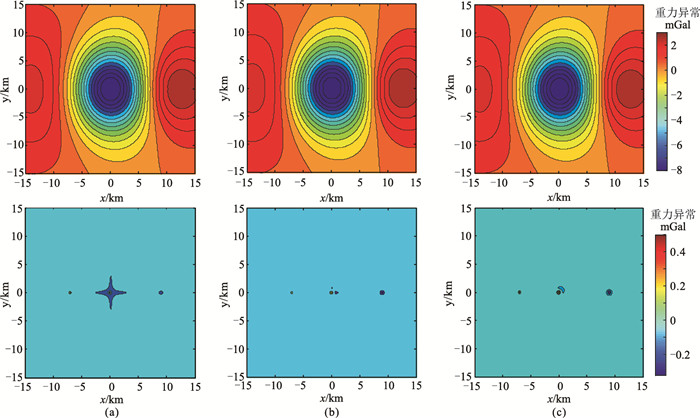
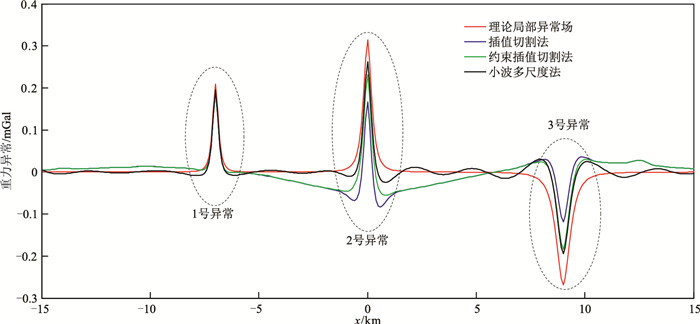
分别采用插值切割法、约束插值切割法、小波多尺度分解法[13]对理论模型正演结果进行重力场分离,分离得到的区域场和局部异常见图 6。基于切割半径与密度体埋深近似相等的对应关系,计算过程中以r=400m为初始值,以100m为增减量,采用多个切割半径r,经对比筛选,确定取r=500m。根据小波多尺度分解的尺度场源深度转换公式[14],因网格间距为100m,故采用1~4阶小波细节代表浅部球体产生的局部重力异常,用4阶小波逼近代表深部球体产生的区域重力异常。对比约束插值切割法和小波多尺度分解法得到的局部异常,可见前者更接近于理论局部异常(图 4c)。由于区域异常幅值较大,基本淹没了局部异常,故通过三种方法分离出的区域异常(图 6上)与理论区域异常(图 4b)基本一致。为了更直观地分析本文方法的优越性,绘制了沿y=0剖面的三种方法分离得到的局部异常曲线(图 7)。由图可见,由于1号异常为区域重力高叠加局部重力高(分类情形1),三种方法的结果基本一致,都能较准确地体现分类情形1所产生的局部重力异常;关于2号和3号异常,本文方法得到的分离结果明显改善了插值切割法的计算结果,且与小波多尺度分解的结果吻合。三种方法均在局部异常两翼附近产生了小幅度假异常,这是因为方法本身存在一定的计算误差。以上分析证明了本文提出的约束插值切割法基本理论的正确性和分离效果的正确性。
|
图 6 图 3模型重力场不同方法分离得到的区域异常场(上)和局部异常场(下) (a)插值切割法;(b)约束插值切割法;(c)小波多尺度分解法 |
|
图 7 不同方法分离的局部重力异常场(y=0) |
为了定量对比分析插值切割法、约束插值切割法和小波多尺度分解法的重力场分离效果,用下式计算局部异常ΔgⅠ与理论局部异常ΔgⅡ的相关系数
| $ {\mathop{\rm Re}\nolimits} \left( {\Delta {g_{\rm{I}}}, \Delta {g_{{\rm{II}}}}} \right) = \frac{{{\mathop{\rm Cor}\nolimits} \left( {\Delta {g_{\rm{I}}}, \Delta {g_{{\rm{II}}}}} \right)}}{{\sqrt {{\mathop{\rm Var}\nolimits} \left( {\Delta {g_{\rm{I}}}} \right){\mathop{\rm Var}\nolimits} \left( {\Delta {g_{{\rm{II}}}}} \right)} }} $ | (26) |
式中:Cor(·)表示协方差;Var(·)表示均方差。经计算,插值切割法、约束插值切割法和小波多尺度分解法得到的局部异常与理论局部异常的相关系数分别为0.42、0.75、0.70,可见本文提出的约束插值切割法得到的局部异常与理论局部异常具有最强的相关性。
另外,为了评价约束插值切割法对插值切割法的改善效果,引入评价航磁动态补偿效果的“改善率”(Improvement Ratio,IR)[56]评价改善效果,其计算公式为
| $ \mathrm{IR}=\frac{\operatorname{Std}\left(\Delta g_{\mathrm{cz}}-\Delta g_{\mathrm{II}}\right)}{\operatorname{Std}\left(\Delta g_{\mathrm{ys}}-\Delta g_{\mathrm{II}}\right)} $ | (27) |
式中:Δgcz表示插值切割法得到的局部异常;Δgys表示约束插值切割法得到的局部异常;Std(·)表示求标准差。
因为本文提出的新方法仅对2号、3号异常进行了优化,故仅对2号、3号局部异常的改善率进行评估。经计算,约束插值切割法对插值切割法的改善率IR为1.48,可见相比于插值切割法,新方法计算的局部异常效果改善了48%,优化效果明显。
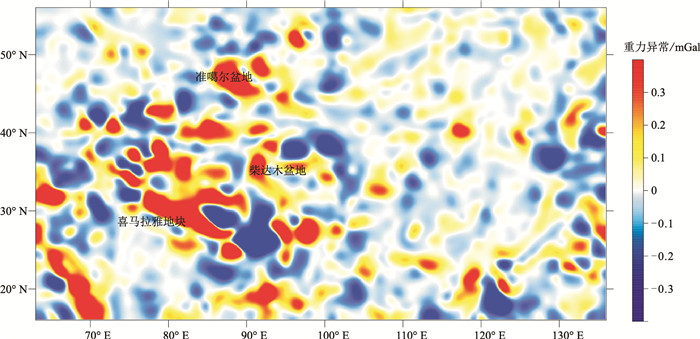
4 应用实例 4.1 中国大陆及周边区域重力数据分离本文以中国大陆及周边区域的重力数据为试验对象,范围为东经63°~136°,北纬15°~58°。重力数据来自美国国家地理空间情报局地球重力场研发小组发布的超高阶地球重力场模型EGM2008(Earth Gravitational Model 2008),该模型的阶次完全至2159次,空间分辨率约为5′,可用于小比例尺重力编图和构造研究[57]。本实例使用的布格重力异常的网格间距为4km。
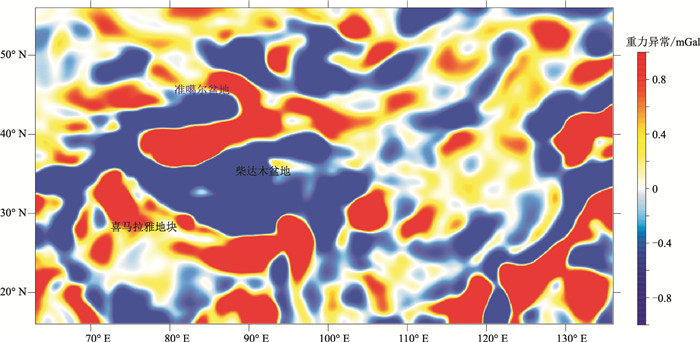
分别利用插值切割法和本文提出的约束插值切割法对布格重力异常进行分离。为了展示新方法的正确性和改进效果,以葛粲等[48]的研究结果为参照。根据徐世浙等[8]、葛粲等[48]提出的“切割半径应近似等于异常体埋深”的层切割思想,本例的切割半径r以网格间距4km为基准,并以其整数倍的形式逐步递增,每次切割得到的区域场作为下次切割的输入,并结合前人经验总结的“切割半径r得到的局部场可以近似代表深度r以上的地层重力效应”,当切割半径为19倍网格间距(r=76km)时,计算得到的局部异常可视为72~76km参考深度层的重力异常值,并将其视为上地幔顶部附近介质产生的重力异常。插值切割法和约束插值切割法计算得到的上地幔顶部附近重力异常分别见图 8和图 9。
|
图 8 插值切割法得到的中国大陆及周边地区上地幔顶部附近重力异常场 |
|
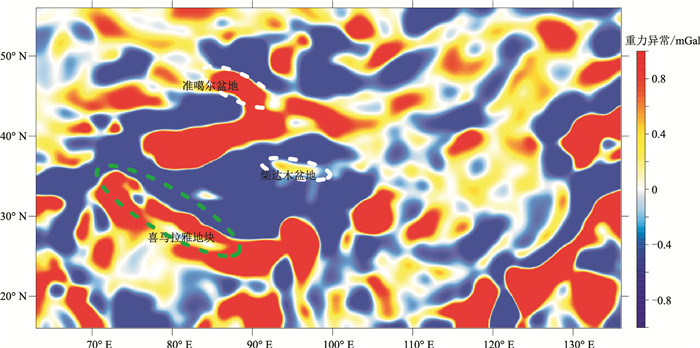
图 9 约束插值切割法得到的中国大陆及周边地区上地幔顶部附近重力异常场 |
对比图 8与葛粲等[48]的计算结果,可见重力异常分布特征基本一致,验证了本文编程实现的插值切割法的正确性。对比插值切割法(图 8)与约束插值切割法(图 9)得到的上地幔顶部附近重力异常,可见整体上重力异常形态相似,但约束插值切割法得到的正值重力异常幅度和范围相对更大,说明在负值背景下叠加正异常的情况下,约束插值切割法对异常分布进行了合理调整,这与约束插值切割法的基本原理和理论模型结论相一致。
为了定量对比约束插值切割法和插值切割法得到的重力异常,计算了两者的差值(图 10),即前文所述的修正量。由图可见,在准噶尔盆地、喜马拉雅地块等局部地区,本文方法的修正达50%以上。
根据图 9可得到初步的地质认识,即在喜马拉雅地块边界局部地区(图中绿色虚线椭圆区域),深部高密度支撑物质强烈北移侵入,而柴达木盆地和准噶尔盆地正高值范围的扩大(图中白色虚线所示),则意味着稳定盆地下方可能存在高密度物质。
杨文采等[58]利用小波多尺度分解法对中国陆域及周边布格重力异常进行了分离,获取了包括上地幔顶部异常(D7+D8)在内的4个深度界面所产生的重力异常。对比约束插值切割法与小波多尺度分解法对上地幔顶部异常的分离结果,可见在青藏高原等区域的异常分布特征与杨文采等[58]的研究成果相近,但约束插值切割法得到的异常细节更加丰富,主要是因为小波多尺度分解法仅将布格重力异常分离为4层,而约束插值切割法可分离为20层,对异常的分辨率更高[48]。
由于篇幅限制,结合地震、地质等资料的综合地质解释将另文详细阐述。据本例分析可见,约束插值切割法在实际应用中实现了对插值切割法计算结果的修正,可得到更准确的重力异常、更明确的重力异常梯度带。
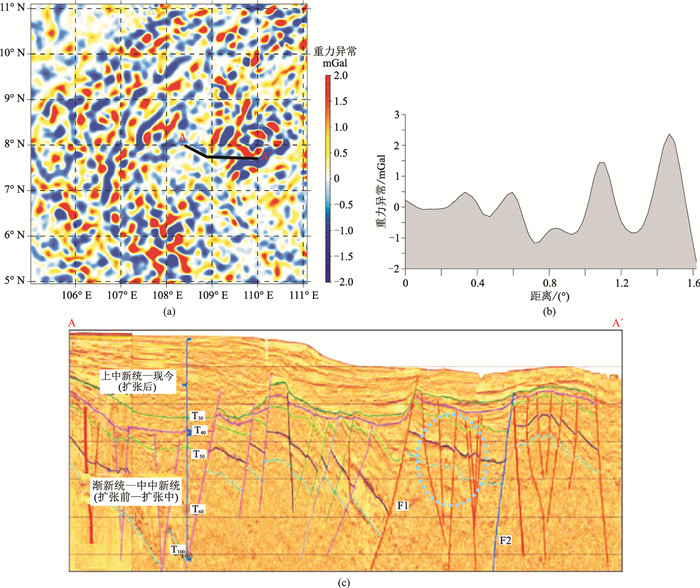
4.2 中国南海万安盆地及周边区域重力数据分离为了进一步验证约束插值切割法的实际应用效果,选取中国南海万安盆地及周边区域布格重力异常数据为研究对象,范围为东经104°~111°,北纬5°~11°,数据来源同4.1部分重力数据。陈玲等[59]认为南海万安盆地新生界沉积层厚度最大为12.5km,冯旭亮等[60]的研究结果显示该区域最大厚度大于10km,故本例约束插值切割法中选取切割半径为3倍网格间距(12km),经计算得到万安盆地及周边区域新生界沉积层的重力异常(图 11a)。图 11b为选取的一条地震剖面所对应的新生界沉积层重力异常,图 11c为该地震剖面构造解释剖面[60]。
|
图 11 中国南海万安盆地及周边地区重力数据及地震剖面 (a)约束插值切割法分离得到的新生界沉积层重力异常;(b)地震剖面(图a中黑色折线所示)对应的新生界沉积层重力异常;(c)地震剖面叠加构造解释。F1、F2表示断层。 |
为了说明本文方法计算结果的可靠性,与冯旭亮等[60]采用最小曲率位场分离方法得到的计算结果(文献[60]中的图 7、图 8)进行了对比,可以发现,图 11a中重力异常的整体分布特征与文献[60]中的图 7较吻合,图 11b中的重力异常曲线走势与文献[60]中的图 8a大致相同,但本文的计算结果更能反映沉积基底的起伏变化细节,特别是更加直观地显示了F1断层右侧沉积基底的局部凸起(图 11c中的虚线圈所示)。因此,基于本文方法分离得到的局部重力异常,可更清晰地解释新生界沉积层底界面的深度变化,为该区域新生界深度反演研究提供了较可靠的数据基础,同时也验证了约束插值切割法的实用性。
5 结论本文通过基本理论推导,并结合实际重力异常的叠合分类情形,实现了对插值切割法的优化和改进,提出了基于异常约束条件的插值切割法(约束插值切割法),并开展了理论模型试验和卫星重力数据处理、分析。得出以下几点认识。
(1) 通过对插值切割法切割算子的公式推导,结合四种情形的异常叠合关系,证明了插值切割法的切割算子仅考虑了局部异常与区域异常弯曲方向相同的叠合情况。基于此,给出了插值切割算子的补偿方法,提出了基于异常约束的插值切割法,制定了新方法的计算流程,并基于Matlab平台编程实现。
(2) 理论模型试算结果显示,插值切割法、约束插值切割法、小波多尺度分解法中约束插值切割法得到的局部异常与理论局部异常具有最强的相关性(相关系数为0.75),与插值切割法相比,对局部异常效果的改善达48%,优化效果明显。
(3) 对中国陆域及周边区域的布格重力异常进行了分离,获取了72~76km参考深度层产生的重力异常,约束插值切割法获取了该层位更真实可靠的重力异常值信息,在准噶尔盆地、喜马拉雅地块等局部地区的修正达50%以上,可为上地幔顶部构造特征研究提供参考。
(4) 利用约束插值切割法分离得到了万安盆地及周边区域新生界沉积层重力异常,与地震剖面显示的基底起伏特征基本一致,说明该方法可用于基底深度变化的反演研究。
总之,通过理论模型数据和实际重力数据分析,约束插值切割法计算结果均明显优化了插值切割法的计算结果,验证了前者理论的正确性及实用性,可为实际重力数据的地质解释提供更准确、可靠的重力异常信息。本文提出的新方法也可用于磁场数据的异常分离。
附录A 约束插值切割法计算步骤(1) 根据目标层位深度信息,对重力异常Z(x, y)设置切割半径r;
(2) 利用式(2)计算与点(x, y)相距r的某4个点重力异常的平均值M(x, y);
(3) 利用式(10)计算加权参数e;
(4) 比较区域异常与局部异常曲线弯曲方向,具体可细分为2步:
① 计算下列参数
| $ \begin{aligned} &I_{x 1}=Z(x+r, y+r)-\frac{Z(x+2 r, y+r)+Z(x, y+r)}{2} \\ &I_{y 1}=Z(x+r, y+r)-\frac{Z(x+r, y+2 r)+Z(x, y+r)}{2} \\ &I_{x 2}=Z(x+2 r, y+r)-\frac{Z(x+4 r, y+r)+Z(x, y+r)}{2} \\ &I_{y 2}=Z(x+r, y+2 r)-\frac{Z(x+r, y+4 r)+Z(x+r, y)}{2} \end{aligned} $ |
② 当比较参数不能同时满足下列条件时,表明区域异常和局部异常弯曲方向相同(即分类情形1和2)
| $ \begin{aligned} &I_{x 1} I_{y 1}>0 \\ &I_{y 1} I_{y 2}<0 \\ &I_{x 1} I_{x 2}<0 \\ &I_{y 2} I_{x 2}>0: \end{aligned} $ |
当比较参数同时满足下列条件时,表明区域异常和局部异常弯曲方向相反(即分类情形3和4)
| $ \begin{aligned} &I_{x 1} I_{y 1}>0 \\ &I_{y 1} I_{y 2}<0 \\ &I_{x 1} I_{x 2}<0 \\ &I_{y 2} I_{x 2}>0: \end{aligned} $ |
(5) 对于弯曲方向相同的情形,区域场等于Z(x, y)与M(x, y)的加权平均,采用式(11)计算切割区域场;
(6) 对于弯曲方向相反的情形,区域场为Z(x, y)与M(x, y)的加权平均的基础上增加切割区域异常修正量ΔZ(x, y),此种情况可细分为以下4步:
① 首先考虑x方向异常剖面,假设局部异常附近的区域异常为曲率半径为N、曲率中心为O的曲率圆的部分弧段,利用式(20)计算x方向切割区域异常修正量ΔZ(x)。
② 同理可得y方向切割区域异常修正量ΔZ(y);
③ 取ΔZ(x, y)=[ΔZ(x)+ΔZ(y)]/2;
④ 计算修正量ΔZ(x, y)后,采用式(19)计算切割区域场;
(7) 用上述方法得到第1次切割的区域场R1(x, y),对R1(x, y)重复使用步骤(1)~(6),得到第2次切割的区域场R2(x, y),依次迭代,直到满足式(12),迭代终止,得到切割区域场;
(8) 利用式(14)计算最终的局部场R(x,y)。
在构思本文的初期,与插值切割法的原创者——中国石油勘探开发研究院文百红老师进行了有益探讨,特别是在插值切割法的细节上得到了文百红老师的悉心指导,在此深表谢意;感谢中国自然资源航空物探遥感中心骆遥教授为文章的修改提出了建设性的意见!
| [1] |
徐世浙, 王华军, 余海龙, 等. 普光气田重力异常的视密度反演[J]. 地球物理学报, 2009, 52(9): 2357-2363. XU Shizhe, WANG Huajun, YU Hailong, et al. Apparent density inversion of gravity anomalies of Puguang gas field[J]. Chinese Journal of Geophysics, 2009, 52(9): 2357-2363. |
| [2] |
相鹏, 谭绍泉, 陈学国, 等. 利用高斯径向基函数的拟神经网络重力反演方法[J]. 石油地球物理勘探, 2021, 56(6): 1409-1418. XIANG Peng, TAN Shaoquan, CHEN Xueguo, et al. Gravity inversion method based on quasi-neural network featuring Gaussian radial basis function[J]. Oil Geophysical Prospecting, 2021, 56(6): 1409-1418. |
| [3] |
王彦国, 黄远生, 张瑾. 基于重力异常增强的改进小子域滤波方法[J]. 石油地球物理勘探, 2020, 55(1): 206-216. WANG Yanguo, HUANG Yuansheng, ZHANG Jin. Gravity interpretation using improved small sub-domain filtering of enhanced anomaly[J]. Oil Geophysical Prospecting, 2020, 55(1): 206-216. |
| [4] |
DOBRIN M B. Introduction to Geophysical Prospecting[M]. New York: McGraw Hill, 1952.
|
| [5] |
程方道, 刘东甲, 姚汝信. 划分重力区域场与局部场的研究[J]. 物化探计算技术, 1987(1): 1-9. CHENG Fangdao, LIU Dongjia, YAO Ruxin. A study of the identification of regional and local gravity fields[J]. Computing Techniques for Geophysical and Geochemical Exploration, 1987(1): 1-9. |
| [6] |
管志宁, 张昌达, 程方道, 等. 磁法勘探重要问题理论分析与应用[M]. 北京: 地质出版社, 1993.
|
| [7] |
曾华霖. 重力场与重力勘探[M]. 北京: 地质出版社, 2005.
|
| [8] |
徐世浙, 余海龙, 李海侠, 等. 基于位场分离与延拓的视密度反演[J]. 地球物理学报, 2009, 52(6): 1592-1598. XU Shizhe, YU Hailong, LI Haixia, et al. The inversion of apparent density based on the separation and continuation of potential field[J]. Chinese Journal of Geophysics, 2009, 52(6): 1592-1598. DOI:10.3969/j.issn.0001-5733.2009.06.021 |
| [9] |
PAWLOWSKI R S, HANSEN R O. Gravity anomaly separation by Wiener filtering[J]. Geophysics, 1990, 55(5): 539-548. DOI:10.1190/1.1442865 |
| [10] |
SYBERG F J R. A Fourier method for the regional-residual problem of potential fields[J]. Geophysical Prospecting, 1972, 20(1): 47-75. DOI:10.1111/j.1365-2478.1972.tb00619.x |
| [11] |
CHARABORTY K, AGARWAL B N P. Mapping of crustal discontinuities by wavelength filtering of gra-vity field[J]. Geophysical Prospecting, 1992, 40(7): 801-822. DOI:10.1111/j.1365-2478.1992.tb00553.x |
| [12] |
王明, 王林飞, 何辉. 匹配滤波技术分离重力场源[J]. 物探与化探, 2015, 39(增刊1): 126-132. WANG Ming, WANG Linfei, HE Hui. The application of the matched filtering technology to the separation of gravity field sources[J]. Geophysical and Geo-chemical Exploration, 2015, 39(S1): 126-132. |
| [13] |
侯遵泽, 杨文采. 中国重力异常的小波变换与多尺度分析[J]. 地球物理学报, 1997, 40(1): 85-95. HOU Zunze, YANG Wencai. Wavelet transform and multi-scale analysis on gravity anomalies of China[J]. Chinese Journal of Geophysics, 1997, 40(1): 85-95. DOI:10.3321/j.issn:0001-5733.1997.01.010 |
| [14] |
杨文采, 施志群, 侯遵泽, 等. 离散小波变换与重力异常多重分解[J]. 地球物理学报, 2001, 44(4): 534-541. YANG Wencai, SHI Zhiqun, HOU Zunze, et al. Discrete wavelet transform for multiple decomposition of gravity anomalies[J]. Chinese Journal of Geophysics, 2001, 44(4): 534-541. |
| [15] |
高德章, 侯遵泽, 唐建. 东海及邻区重力异常多尺度分解[J]. 地球物理学报, 2000, 43(6): 842-849. GAO Dezhang, HOU Zunze, TANG Jian. Multiscale analysis of gravity anomalies on East China Sea and adjacent regions[J]. Chinese Journal of Geophysics, 2000, 43(6): 842-849. DOI:10.3321/j.issn:0001-5733.2000.06.013 |
| [16] |
侯遵泽, 杨文采. 塔里木盆地多尺度重力场反演与密度结构[J]. 中国科学, 2011, 41(1): 29-39. HOU Zunze, YANG Wencai. Multi-scale gravity field inversion and density structure in Tarim basin[J]. Science China, 2011, 41(1): 29-39. |
| [17] |
杨文采, 孙艳云, 侯遵泽, 等. 用于区域重力场定量解释的多尺度刻痕分析方法[J]. 地球物理学报, 2015, 58(2): 520-531. YANG Wencai, SUN Yanyun, HOU Zunze, et al. An multi-scale scratch analysis method for quantitative interpretation of regional gravity fields[J]. Chinese Journal of Geophysics, 2015, 58(2): 520-531. |
| [18] |
PWALOWSKI R S. Preferential continuation for potential-field anomaly enhancement[J]. Geophysics, 1995, 60(2): 390-398. DOI:10.1190/1.1443775 |
| [19] |
MENG X H, GUO L H, CHEN Z X, et al. A method for gravity anomaly separation based on preferential continuation and its application[J]. Applied Geophysics, 2009, 6(3): 217-225. DOI:10.1007/s11770-009-0025-y |
| [20] |
郭良辉, 孟小红, 石磊, 等. 优化滤波方法及其在中国大陆布格重力异常数据处理中的应用[J]. 地球物理学报, 2012, 55(12): 4078-4088. GUO Lianghui, MENG Xiaohong, SHI Lei, et al. Preferential filtering method and its application to Bouguer gravity anomaly of Chinese continent[J]. Chinese Journal of Geophysics, 2012, 55(12): 4078-4088. DOI:10.6038/j.issn.0001-5733.2012.12.020 |
| [21] |
SPECTOR A. Comments and errata to classic papers[J]. Geophysics, 1985, 50(11): 2378. |
| [22] |
AGOCS W B. Least-squares residual anomaly determiration[J]. Geoghysics, 1951, 16(4): 686-696. |
| [23] |
OLDHAM C H G, SUTHERLAND D B. Orthogonal polynomials: their use in estimating the regional effect[J]. Geophysics, 1955, 20(2): 295-306. DOI:10.1190/1.1438143 |
| [24] |
刘金钊, 朱绿涛, 张双喜, 等. 基于改进的2D多项式拟合及加权迭代算法的重力异常垂向分离[J]. 大地测量与地球动力学, 2018, 38(9): 897-902, 907. LIU Jinzhao, ZHU Lutao, ZHANG Shuangxi, et al. Gravity anomalies vertical separation at different depths by an improved 2D polynomial fitting and weighting iterative algorithm[J]. Journal of Geodesy and Geodynamics, 2018, 38(9): 897-902, 907. |
| [25] |
HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society A: Mathematical Physical and Engineering Sciences, 1998, 454(1971): 903-995. |
| [26] |
MICKUS K L, AIKEN C L V, KENNEDY W D. Regional-residual gravity anomaly separation using the minimum-curvature technique[J]. Geophysics, 1991, 56(2): 279-283. |
| [27] |
纪晓琳, 王万银, 邱之云. 最小曲率位场分离方法研究[J]. 地球物理学报, 2015, 58(3): 1042-1058. JI Xiaolin, WANG Wanyin, QIU Zhiyun. The research to the minimum curvature technique for potential field data separation[J]. Chinese Journal of Geophysics, 2015, 58(3): 1042-1058. |
| [28] |
纪晓琳, 王万银, 邱之云. 最小曲率位场分离方法参数选择试验研究[J]. 地球物理学进展, 2019, 34(4): 1141-1452. JI Xiaolin, WANG Wanyin, QIU Zhiyun. Parameter choose experimental research to the minimum curvature technique potential field data separation method[J]. Progress in Geophysics, 2019, 34(4): 1141-1452. |
| [29] |
于长春, 熊盛青, 郭志红, 等. 改进的非线性滤波方法在中高山地区的应用[J]. 物探与化探, 2003, 27(1): 39-42, 62. YU Changchun, XIONG Shengqing, GUO Zhihong, et al. The improved nonlinear filtering method and its application in middle and high mountain areas[J]. Geophysical and Geochemical Exploration, 2003, 27(1): 39-42, 62. |
| [30] |
郭志宏, 刘浩军, 熊盛青. 平面网格位场数据的空间域非线性曲率滤波方法[J]. 地球物理学进展, 2003, 18(1): 134-137. GUO Zhihong, LIU Haojun, XIONG Shengqing. The nonlinear curvature filtering technique of plane potential grid data in space domain[J]. Progress in Geophysics, 2003, 18(1): 134-137. |
| [31] |
KAFTAN I, SALK M, SARI C. Application of the finite element method to gravity data case study: Wes-tern Turkey[J]. Journal of Geodynamics, 2005, 39(5): 431-443. |
| [32] |
KANNAN S, MALLICK K. Accurate regional-resi-dual separation by finite element approach, Bouguer gravity of Precambrian mineral prospect in north-western Ontario[J]. First Break, 2003, 21(4): 39-42. |
| [33] |
MALLICK K, SHARMA K K. A finite element method for computation of the regional gravity ano-maly[J]. Geophysics, 1999, 64(2): 461-469. |
| [34] |
MALLICK K, SARMA G S. Finite element formulation for seismicwave propagation in oil-bearing geological formations[C]. IMACS International Symposium on Mathematical Modelling and Scientific Computation, 1992, 1-12.
|
| [35] |
SARMA G, GADHINGLAJKAR V R, MALLICK K. Finite element simulation of bright-spot structures[J]. Journal of Association of Exploration Geophysicists, 1993, 14: 43-47. |
| [36] |
AGARWAL B N P, SRIVASTAVA S. A FORTRAN program to implement the method of finite elements to compute regional and residual anomalies from gravity data[J]. Computers & Geosciences, 2010, 36(7): 848-852. |
| [37] |
肖锋, 孟令顺. 用有限元插值法计算区域重力异常[J]. 吉林大学学报(地球科学版), 2006, 36(增刊2): 5-8. XIAO Feng, MENG Lingshun. Use finite element method for computation of the regional gravity ano-maly[J]. Journal of Jilin University(Earth Science Edition), 2006, 36(S2): 5-8. |
| [38] |
余运洋, 黄国祥. 卡尔曼滤波在重磁异常划分中的应用[J]. 物探化探计算技术, 1991(3): 220-228. YU Yunyang, HUANG Guoxiang. Application of Kalman filtering theory to regional-residual separation of gravity or magnetic anomalies[J]. Computing Techniques for Geophysical and Geochemical Exploration, 1991(3): 220-228. |
| [39] |
许家姝, 孟令顺, 刘银萍. 卡尔曼滤波在位场分离中的应用[J]. 科学技术与工程, 2010, 10(2): 394-399. XU Jiashu, MENG Lingshun, LIU Yinping. Application of Kalman filtering in the separation of potential field[J]. Science Technology and Engineering, 2010, 10(2): 394-399. |
| [40] |
ZHU D, LI H W, LIU T Y, et al. Low-rank matrix decomposition method for potential field data separation[J]. Geophysics, 2020, 85(1): G1-G16. |
| [41] |
朱丹, 刘天佑, 李宏伟. 利用数据低秩性和稀疏性的位场分离[J]. 石油地球物理勘探, 2019, 54(4): 925-936. ZHU Dan, LIU Tianyou, LI Hongwei. Potential field separation based on the low rank and sparse characteristics[J]. Oil Geophysical Prospecting, 2019, 54(4): 925-936. |
| [42] |
文百红, 程方道. 用于划分磁异常的新方法——插值切割法[J]. 中南矿冶学院学报, 1990(3): 229-235. WEN Baihong, CHENG Fangdao. A new interpolating cut method for identifying regional and local fields of magnetic anomaly[J]. Journal of Central South Institute of Mining and Metallurgy, 1990(3): 229-235. |
| [43] |
秦葆瑚. 用分层切割法研究复杂磁异常[J]. 物探化探计算技术, 1994(2): 96-101. QIN Baohu. Divisions of complex magnetic anomaly by layered dividing method[J]. Computing Techniques for Geophysical and Geochemical Exploration, 1994(2): 96-101. |
| [44] |
段本春, 徐世浙, 阎汉杰, 等. 划分磁异常场的插值切割法在研究火成岩体分布中的应用[J]. 石油地球物理勘探, 1998, 33(1): 125-131. DUAN Benchun, XU Shizhe, YAN Hanjie, et al. Application of interpolation-cut method for magnetic anomaly division to igneous mass investigation[J]. Oil Geophysical Prospecting, 1998, 33(1): 125-131. |
| [45] |
徐世浙, 张研, 文百红, 等. 切割法在陆东地区磁异常解释中的应用[J]. 石油物探, 2006, 45(3): 316-318. XU Shizhe, ZHANG Yan, WEN Baihong, et al. The application of cutting method to interpretation of magnetic anomaly in region of Ludong[J]. Geophysical Prospecting for Petroleum, 2006, 45(3): 316-318. |
| [46] |
邢怡, 滕菲, 张国利. 利用插值切割法研究重力区域场与局部场的分离[J]. 地质调查与研究, 2014, 37(3): 193-196. XING Yi, TENG Fei, ZHANG Guoli. An interpolating cut method for separation of regional and local gravity field[J]. Geological Survey and Research, 2014, 37(3): 193-196. |
| [47] |
刘东甲. 位场异常分离的递减半径迭代法[J]. 地球物理学报, 2017, 60(8): 3215-3228. LIU Dongjia. Decreasing radius iterative method for regional-residual separation of potential field data[J]. Chinese Journal of Geophysics, 2017, 60(8): 3215-3228. |
| [48] |
葛粲, 李修钰, 李晓晖, 等. 基于重力大数据的中国大陆区域地质构造解析[J]. 地质科学, 2017, 52(3): 714-726. GE Can, LI Xiuyu, LI Xiaohui, et al. Analysis of regional geological structure in China based on gravity big data[J]. Chinese Journal of Geology, 2017, 52(3): 714-726. |
| [49] |
葛粲, 任升莲, 李永东, 等. 重力异常分层分离方法改进及应用: 以安徽五河地区为例[J]. 地球物理学报, 2017, 60(12): 4826-4839. GE Can, REN Shenglian, LI Yongdong, et al. Improvement and application of the layered separation method for gravity anomalies: an example of the Wuhe area, Anhui Province[J]. Chinese Journal of Geophysics, 2017, 60(12): 4826-4839. |
| [50] |
汪炳柱, 徐世浙, 刘保华, 等. 多次插值切割法分场的一个实例[J]. 石油地球物理勘探, 1997, 37(3): 431-438. WANG Bingzhu, XU Shizhe, LIU Baohua, et al. An example of aeromagnetic anomaly separation using multi-interpolation division[J]. Oil Geophysical Prospecting, 1997, 37(3): 431-438. |
| [51] |
杨金玉, 徐世浙, 余海龙, 等. 视密度反演在东海及邻区重力异常解释中的应用[J]. 地球物理学报, 2008, 51(6): 1909-1916. YANG Jinyu, XU Shizhe, YU Hailong, et al. Application of apparent density inversion method in the East China Sea and its adjacent area[J]. Chinese Journal of Geophysics, 2008, 51(6): 1909-1916. |
| [52] |
万胜荣, 张伙带, 陈洁. 插值切割法在南海重力数据处理中的应用[J]. 海洋地质与第四纪地质, 2019, 39(1): 175-183. WAN Shengrong, ZHANG Huodai, CHEN Jie. Application of interpolation cut method to gravity data processing in South China Sea[J]. Marine Geology & Quaternary Geology, 2019, 39(1): 175-183. |
| [53] |
赵文举, 赵荔, 杨战军, 等. 插值切割位场分离方法改进及其在资料处理中的应用[J]. 物探与化探, 2020, 44(4): 886-893. ZHAO Wenju, ZHAO Li, YANG Zhanjun, et al. The improvement of the interpolation cutting potential field separation method and its application to data processing[J]. Geophysical and Geochemical Exploration, 2020, 44(4): 886-893. |
| [54] |
费业泰. 误差理论与数据处理[M]. 北京: 机械工业出版社, 1981.
|
| [55] |
候重初, 刘奎俊. 重磁异常场及其高阶导数的正演公式与程序[M]. 北京: 地质出版社, 1990.
|
| [56] |
孟庆奎, 周德文, 高维, 等. 国内外航磁补偿技术历史与展望[J]. 物探与化探, 2017, 41(4): 694-699. MENG Qingkui, ZHOU Dewen, GAO Wei, et al. History and prospects of aeromagnetic compensation technologies used in China and abroad[J]. Geophysical and Geochemical Exploration, 2017, 41(4): 694-699. |
| [57] |
杨金玉, 张训华, 张菲菲, 等. EGM2008地球重力模型数据在中国大陆地区的精度分析[J]. 地球物理学进展, 2012, 27(4): 1298-1306. YANG Jinyu, ZHANG Xunhua, ZHANG Feifei, et al. On the accuracy of EGM2008 earth gravitational mo-del in Chinese Mainland[J]. Progress in Geophysics, 2012, 27(4): 1298-1306. |
| [58] |
杨文采, 陈召曦, 侯遵泽, 等. 从卫星重力资料看中国及邻区地壳密度结构[J]. 地质学报, 2016, 90(9): 2167-2175. YANG Wencai, CHEN Zhaoxi, HOU Zunze, et al. Crustal density structures around Chinese continent by inversion of satellite gravity data[J]. Acta Geolo-gica Sinica, 2016, 90(9): 2167-2175. |
| [59] |
陈玲, 彭学超. 南沙海域万安盆地地震地层初步分析[J]. 石油物探, 1995, 34(2): 57-70. CHEN Ling, PENG Xuechao. Preliminary study of seismic stratigraphy of Wanan basin in Nansha waters[J]. Geophysical Prospecting for Petroleum, 1995, 34(2): 57-70. |
| [60] |
冯旭亮, 张功成, 王万银, 等. 基于重磁震资料的南海新生代盆地分布综合研究[J]. 地球物理学报, 2018, 61(10): 4242-4254. FENG Xuliang, ZHANG Gongcheng, WANG Wan-yin, et al. An integrated study on distribution of Ceno-zoic basins in the South China Sea based on gravity, magnetic and seismic data[J]. Chinese Journal of Geophysics, 2018, 61(10): 4242-4254. |



 高维, 北京市海淀区学院路31号自然资源部航空地球物理与遥感地质重点实验室,100083。Email:
高维, 北京市海淀区学院路31号自然资源部航空地球物理与遥感地质重点实验室,100083。Email: