② 成都理工大学“油气藏地质及开发工程”国家重点实验室,四川成都 610059
② State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Chengdu University of Technology, Chengdu, Sichuan 610059, China
准确预测渗透率是碳酸盐岩储层常规测井评价的重点内容。碳酸盐岩储层通常具有原生孔隙、次生孔隙及各种裂缝共同发育的特点,因受沉积环境、成岩作用及含气水饱和度等多种因素的影响,非均质性较强,常规地球物理测井解释存在多解性,需借助成像测井作为参照[1-3]。目前常规测井解释渗透率主要利用物理模型[4]和拟合模型[5],常用的物理模型有Kozeny-Carman[6-7]、指数型和幂律型[8]等,常用的拟合模型有多元线性回归和逐步回归等模型。在实际应用中,物理模型和拟合模型互为补充,其间的耦合程度还需进一步探索,如物理模型与机器学习模型对渗透率预测精度的影响程度以及离散岩石类型(Discrete Rock Type, DRT)[9]的划分原则等,都是影响碳酸盐岩非均质储层渗透率解释精度的因素。
为更科学地利用常规测井数据建立储层参数的拟合模型,人们应用机器学习模型替代储层参数与常规测井数据间的非线性表达式。目前性能较好的机器学习模型主要有支持向量机(Support Vector Machine, SVM)[10-11]、随机森林(Random Forest, RF)[12-14]和XGBoost[15-17]等。Zhang等[11]采用6种模型对碳酸盐岩储层流动单元指数(Flow Zone Indicator, FZI)进行预测并间接地计算渗透率,认为粒子群优化算法(Particle Swarm Optimization, PSO)-SVM模型性能最佳,测试集决定系数高达0.869;郭建宏等[13]利用RF模型预测煤层气含量;孙予舒等[15]利用XGBoost模型对复杂碳酸盐岩岩性进行识别。XGBoost[18]在众多机器学习模型中脱颖而出,得益于其算法和运行方式上的一些改进:在计算过程中加入正则化项,能有效防止过拟合;在运行方式上开辟多个线程并行处理,能在大规模计算时提高CPU利用率。
面对传统机器学习模型错综复杂的参数调试问题,人们引入遗传算法(Genetic Algorithm, GA)[19]、粒子群优化算法[20]、模拟退火(Simulated Annealing, SA)算法[21]等替代繁琐的人工调试手段,同时提高模型的预测精度。谷宇峰等[17]利用PSO算法改进XGBoost并得到了可靠的渗透率解释模型,但在求解复杂的碳酸盐岩储层渗透率非线性问题时效果却不理想,当渗透率数量级超过10-2~10mD时,孔隙结构更复杂,仅依靠机器学习模型直接预测渗透率难以取得较好的效果。为此,本文从优化模型参数的角度出发,利用改进的粒子群优化算法(IPSO)[22]同时优化物理模型参数及机器学习模型参数,进而提出渗透率预测的自适应模型,并阐述该算法原理及其在非均质碳酸盐岩储层渗透率预测中的应用。
1 方法原理Kozeny[6]和Carman[7]在前人研究的基础上根据渗流力学原理建立了Kozeny-Carman方程,定量地描述孔隙度与渗透率的复杂关系
| $ K = \frac{{{\varphi ^3}}}{{{{(1 - \varphi )}^2}}}\left[ {\frac{1}{{F{\tau ^2}{S^2}}}} \right] $ | (1) |
式中:K为渗透率;F为形状系数,圆柱形管时取2;τ为孔隙介质迂曲度,通常取1.5~3.0;φ是有效总孔隙度;S是单位体积颗粒比表面积,与φ值共同由气测实验确定。令
| $ H = F{\tau ^2} $ | (2) |
式中:H为卡兹尼常数,在实际应用中通常取值范围是5~100。
为实现对孔隙结构的定量评定,引入流动单元指数(FZI),其计算公式为
| $ \mathrm{FZI}=\frac{1}{\sqrt{F} \tau S} $ | (3) |
Amaefule等[23]根据FZI对Kozeny-Carman方程进行变形,得到
| $ K=1014.24(\mathrm{FZI})^2 \frac{\varphi^3}{(1-\varphi)^2} $ | (4) |
Mirzaei-Paiaman等[24-26]提出一种修正的流动单元指数(FZI*),并得到
| $ K=1014.24\left(\mathrm{FZI}^*\right)^2 \varphi $ | (5) |
Kharrat等[9]提出离散岩石类型(DRT)聚类算法,通过FZI或FZI*值划分DRT,表达式为
| $ \mathrm{DRT}=\mathrm{ROUND}(2 \operatorname{lnFZI}+C) $ | (6) |
式中:C为经验系数,由FZI或FZI*值的正态分布特性确定,初始值取10.6;ROUND(·)表示取整。
在建立储层参数模型时需要设定许多经验参数,如机器学习模型中SVM的惩罚系数、RF的决策树个数和XGBoost的最大回归树深度,物理模型中DRT聚类算法中的经验系数C等。采用IPSO优化算法能有效地处理多参数极值求取问题,同时解决线性下降(Linear Decreasing Inertia Weight,LDIW)-PSO算法在迭代过程中全局搜索和局部搜索比例不变问题,通过该算法优化可以加强渗透率预测模型中拟合模型和物理模型的耦合程度。
设定IPSO算法中粒子和种群为
| $ \boldsymbol{X}=\left(\boldsymbol{x}_1, \boldsymbol{x}_2, \cdots, \boldsymbol{x}_{\mathrm{N}}\right)^{\mathrm{T}} \in \boldsymbol{R}^{\mathrm{N} \times D} $ | (7) |
式中:X为种群,xN为第N个粒子,N为种群中粒子个数;D为优化参数个数,包含机器学习模型中的参数及式(6)中的C。在种群迭代寻优过程中,每个粒子xN通过个体极值和群体极值调整自身的速度和位置
| $ v_{i d}^{(k+1)}=\omega v_{i d}^{(k)}+c_1 r_1\left[p_{i d}^{(k)}-x_{i d}^{(k)}\right]+c_2 r_2\left[g_d^{(k)}-x_{i d}^{(k)}\right] $ | (8) |
| $ x_{i d}^{(k+1)}=x_{i d}^{(k)}+v_{i d}^{(k)} $ | (9) |
式中:ω为重力系数,本文采用高斯下降法(Gaussian Decreasing Inertia Weight,GDIW)[22]确定其值;c1、c2为加速系数;r1、r2为弹性系数;i=1, 2, …, N;d=1, 2, …, D;k为当前迭代次数;pid(k)、vid(k)、xid(k)分别为第i个粒子的第d个优化参数在第k次迭代的个体极值、速度和位置;gdk为第d个优化参数在第k次迭代的群体极值。通过采用动态递减重力系数ω并线性改变加速系数c1、c2的策略,平衡算法的全局搜索和局部搜索能力,在提高收敛速度的同时获得较好的优化结果。
综合前述原理,基于Python语言编译了孔、渗关系计算方程自动拟合算法。图 1为该自适应模型的计算流程,图中MSE为均方误差(Mean Squared Error),根据测试集所有DRT聚类算法优化预测模型得出的渗透率与实测渗透率计算获得,计算时对渗透率数据取对数。
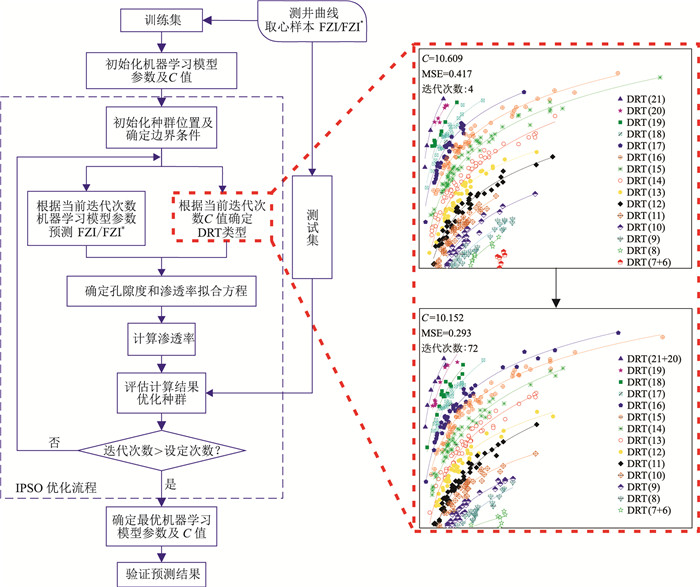
|
图 1 自适应模型的计算流程 全局最优MSE由IPSO-XGBoost模型基于FZI计算的渗透率获得;DRT括号内数字代表划分的岩石类型数量,下同 |
研究区目的层为川中北部高石梯—磨溪地区震旦系灯影组灯二段,该沉积期主要发育台地、台缘、斜坡及陆棚等沉积相带,是目前四川盆地发现的最古老的碳酸盐岩含气层段[27-28]。根据分析取心及成像测井资料,将储层分为孔隙型(图 2a)、裂缝—孔隙型(图 2b)、孔洞型(图 2c)及裂缝—孔洞型(图 2d),裂缝-孔洞型储层以斜交缝和水平缝为主,发育少量高角度缝,为该区气藏提供了优质的渗流通道。在同一孔隙结构中,不同产状裂缝的发育使渗透率呈幂级数增长,因此,得到准确碳酸盐岩储层渗透率解释值的关键在于科学合理划分孔渗等级进而确定储层的DRT。

|
图 2 实验目的层段储层类型 (a)孔隙型(M11井),深灰色粉—泥晶白云岩;(b)裂缝—孔隙型(M10井),浅灰色白云岩;(c)孔洞型(P1井),灰黑色白云岩;(d)裂缝—孔洞型(P1井),灰黑色白云岩 |
通过收集整理现有资料,共计获取研究区6口井目的层段425个岩心样本的孔隙度、渗透率及常规测井数据。孔隙度和渗透率数据均由气测实验获得,其中孔隙度分布范围为0.30%~12.39%,渗透率分布范围为0.001~216.236mD。
由式(4)和式(5)分别计算FZI和FZI*。每个样本包含5种常规测井曲线,分别是声波时差(AC)、补偿中子曲线(CNL)、密度曲线(DEN)、自然伽马曲线(GR)和原状地层电阻率曲线(RT)。部分样本数据见表 1。
|
|
表 1 样本数据(部分) |
对目的层实测孔隙度和渗透率数据进行交会分析,并建立指数模型进行拟合,其拟合度R2仅为0.483(图 3a),可见单一回归方程不满足解释精度。
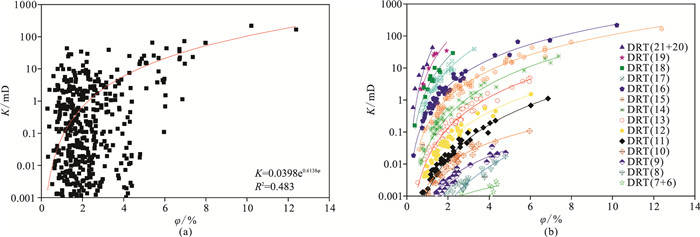
|
图 3 实验目的层段取心分析孔隙度与渗透率关系 (a)划分DRT前;(b)划分DRT后 |
根据式(4)和式(7)对复杂的孔渗关系进行划分得到16种DRT划分结果,将首尾样本数量小于4的DRT合并入相邻集合(图 3b),对划分后的样本建立回归方程进行拟合,部分计算结果见表 2。
|
|
表 2 孔隙度渗透率计算公式(部分) |
需要注意的是,式(7)中C值取动态调试后的最优值10.151,该常数会直接影响DRT的划分数量及回归方程的拟合度R2,间接地影响最终计算结果。
C值的确定与实测样本FZI值的正态分布特性密切相关,图 4展示了目的层段取心样本DRT划分后5种常规测井曲线参数的概率密度函数分布情况。由图可见,划分后各DRT类型对不同常规测井曲线参数的敏感程度也近似服从高斯正态分布[9]。
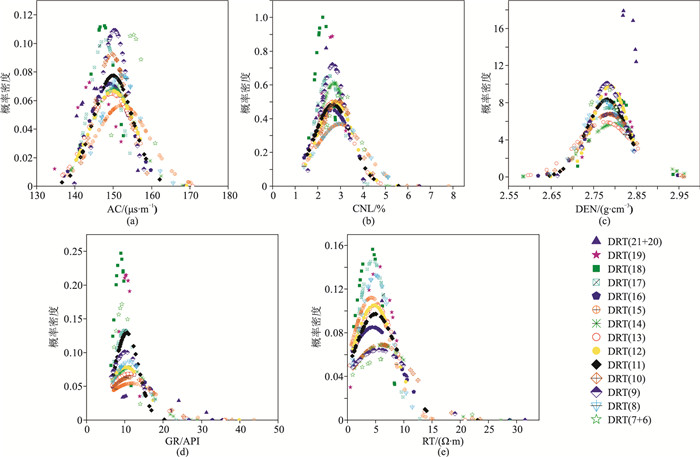
|
图 4 实验目的层段取心样本DRT划分后不同测井曲线参数概率密度函数分布 (a)AC;(b)CNL;(c)DEN;(d)GR;(e)RT |
AC曲线主要反映的是原生孔隙,对次生孔隙不敏感,具体表现为少部分DRT划分类型具有相似的AC概率密度函数(图 4a),各DRT划分后AC概率密度函数的均值不同。当孔隙结构中发育低角度裂缝或斜交缝时,AC曲线具有周波跳跃特征,造成其概率密度函数的方差变大。DRT聚类划分的序列越高表明孔隙结构中裂缝越发育、渗流能力越好。图 4c中划分后大部分DRT具有相似的DEN概率密度函数,均值和方差变化幅度小,表明不同DRT类型反映的是同一孔隙体积中原始孔隙、次生孔隙和裂缝的不同组合。图 4c和图 4d中DRT(21+20)对应的概率密度函数均明显异于其他类型,通过完井报告、薄片鉴定等手段核实,为溶蚀孔洞中充填泥质所致。影响CNL和RT曲线的地质因素较多,如地层水矿化度、含气水饱和度等,DRT划分结果对CNL和RT概率密度函数不敏感(图 4b、图 4e)。
针对Kozeny-Carman物理模型因基础资料不足而无法应用的问题,本文采用机器学习模型替代并建立常规测井曲线参数与FZI或FZI*值的非线性表达式,通过IPSO算法迭代寻优并自适应地获取机器学习模型参数和C值的最优解。文中采用SVM、RF和XGBoost等3种机器学习模型对FZI进行了预测,设计了2个实验验证该自适应模型的预测能力:实验1为基于FZI间接预测渗透率;实验2为基于FZI*间接预测渗透率。预测模型的主要参数设置见表 3。
|
|
表 3 预测模型主要参数设置 |
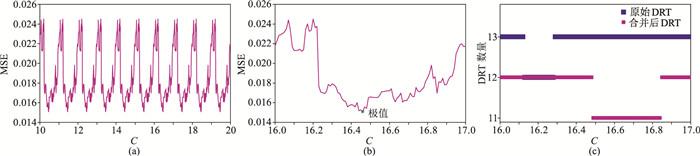
将425个样本实验数据按照7∶3的比例随机划分为2个集合,得到128个样本的测试集和297个样本的训练集。根据式(4)计算全部样本的FZI值,进而确定C值,再由式(6)根据不同C值计算DRT划分数量,在静态模式下探究C值对DRT划分数量及渗透率MSE的影响(图 5)。需要说明的是,静态模式不涉及机器学习模型及常规测井曲线参数。

|
图 5 实验1静态模式下由FZI确定的C值与DRT划分数量及MSE的关系 (a)C与MSE(全局); (b)C与MSE(局部); (c)C与DRT数量 |
由图 5a可知,不同C值对应的MSE呈现周期为1的性规律变化,表明C值仅在长度为1的闭区间内对MSE有较大的影响,并在C近似取10.82时获得MSE极值0.033(图 5b)。图 5c分别展示了不同C值对应的合并前、后DRT划分数量,合并前最大16类、最小15类,合并后最大为15类、最小为14类,表明不同C值会影响DRT划分的数量。图 5b和图 5c对比表明,采取合并离散样本建立物理模型的方式会增加MSE。另外,由于实验时C值的步长为0.01,图 5b中的极值近似等于该组样本测试集渗透率计算精度的“物理上限”。
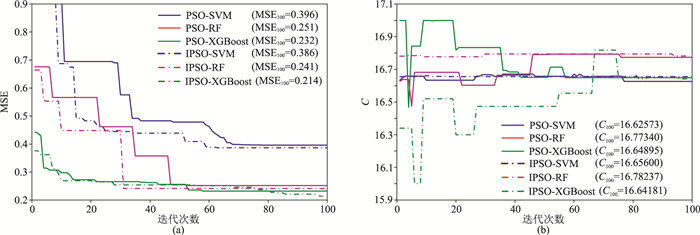
因建模过程中测试集样本的FZI值由机器学习模型与常规测井曲线建模预测获得,故预测值和实测值必然存在偏差。样本测试集渗透率MSE受多个参数的影响,需采用IPSO算法动态确定这些参数。因周期外的C值只影响DRT序列值的变化而不影响其他参数,为方便数据展示,C参数值取10~11(表 3),并将测试集预测渗透率与实测渗透率计算得到的MSE设定为适应度值并迭代寻优。图 6为3种机器学习模型与物理模型的自适应动态优化过程及最终优化结果。
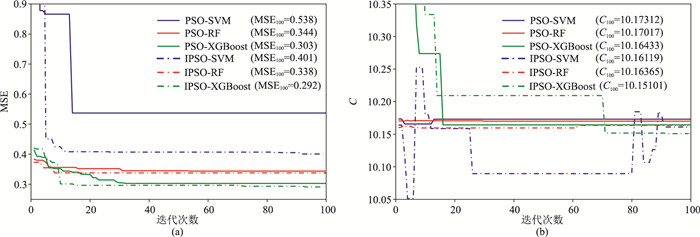
|
图 6 实验1机器学习模型与物理模型自适应动态优化过程及优化结果 (a)MSE与迭代次数; (b)C与迭代次数 |
相对于传统的PSO算法,IPSO算法在迭代次数和寻优精度方面明显处于优势,3种自适应模型在迭代次数20以内的优化结果均超越PSO算法,甚至还有更大的寻优潜力(图 6a)。在拟合精度方面,XGBoost模型性能最佳,MSE仅为0.292,表明XGBoost模型耦合能力最强,能较敏感地响应物理模型。图 6b显示3种自适应模型在迭代100次后C值存在多解性,表明不同机器学习模型与物理模型的耦合程度不同,仅依靠单一经验参数C较难推广。
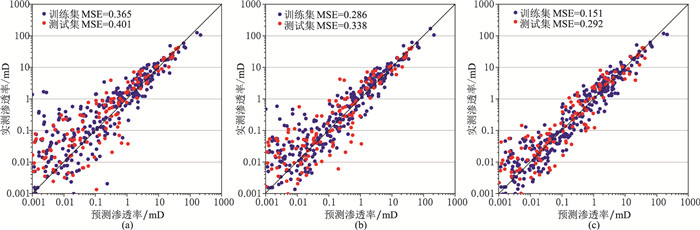
需要说明的是,IPSO算法在迭代次数超过100后仍有上升空间,但已经能有效完成渗透率预测,从侧面说明了IPSO迭代寻优算法的优越性。图 7为3种机器学习模型与物理模型最终自适应建模结果,不同机器学习模型的预测性能主要体现在其对10-3~1mD数量级范围内渗透率样本的拟合度效果。
|
图 7 实验1动态优化后机器学习模型预测结果对比 (a)IPSO-SVM; (b)IPSO-RF; (c)IPSO-XGBoost |
IPSO-SVM的自适应建模结果(图 7a)显示,该模型对10-3~1mD数量级范围的渗透率拟合效果较差,这是由于物理模型在该数量级区间分布最紧密,且为碳酸盐岩原生孔隙和溶蚀孔隙共同发育区域,非均质性极强,表明SVM模型与其耦合能力不足。IPSO-RF的自适应建模结果(图 7b)显示,该模型提升了对渗透率10-3~1mD数量级的拟合度,MSE由0.401降至0.338。图 7c中建模结果显示在该范围内样本点的拟合度最高,MSE进一步降至0.292。
2.3 实验2同样,将425个样本实验数据划分为2个集合,样本构成要素同实验1。由式(5)计算全部样本的FZI*值,进而确定C值,并根据式(6)基于不同C值计算DRT类型,图 8为静态模式下C值对DRT划分数量及渗透率MSE的影响。
|
图 8 实验2静态模式下由FZI*确定的C值与DRT划分数量及MSE的关系 (a)C与MSE(全局); (b)C与MSE(局部); (c)C与DRT类型数量 |
由图 8a可知,不同C值对应的MSE仍呈周期性规律变化,周期为1,并在C约为16.46时获得MSE极值0.015(图 8b)。图 8c展示了不同C值计算的原始DRT划分数量及合并后DRT数量,合并后最大为12类、最小为11类。对比实验1静态调试结果(图 5),实验2的DRT划分数量和MSE均有所下降,且相对于MSE,DRT划分数量下降幅度更大。在保证精度的情况下减少了计算工作量,表明FZI*计算方式更简洁,在实际应用中更容易被推广[24-26]。实验2中最小MSE由原始DRT划分数量13类合并至12类计算得到,而实验1中最小MSE是根据原始DRT划分数量15类计算得到,表明合并离散样本的方式在DRT划分数量较多的情况下会增加MSE,但在DRT数量较少的情况下相反,说明DRT划分数量与近似“物理上限”没有直接的联系。为方便数据展示,C值取值范围设定为16~17。图 9为3种机器学习模型与物理模型的自适应过程及最终优化结果。
|
图 9 实验2机器学习模型与物理模型动态自适应优化过程及优化结果 (a)MSE与迭代次数; (b)C与迭代次数 |
对比图 6实验1的优化过程及优化结果,图 9a中3种自适应模型的MSE均有所下降,单从MSE曲线看,基于FZI*的物理模型与机器学习模型耦合程度更高。图 9b显示3种自适应模型在迭代100次后C值仍存在多解性,再一次验证了采用IPSO算法优化C值的必要性。
图 10为本实验3种机器学习模型与物理模型自适应优化后的最终建模预测结果。相比实验1动态建模结果(图 7),实验2动态建模结果拟合效果均有提升,模型中的样本都更靠近45°线。仔细对比可见,IPSO-SVM模型中虽然大于0.1mD的样本都基本靠近45°线,但对10-3~10-1mD范围内的渗透率预测能力仍然不足,表明该模型在与物理模型的耦合方面难以推广应用(图 10a)。对于IPSO-RF,有少部分10-3~10-1mD范围的渗透率预测值与实测值不相符,样本点散落在45°线外侧,表明该模型能有效地适应不同的物理模型,且预测能力较稳定(图 10b)。对于IPSO-XGBoost,该范围内的渗透率预测值与实测值均为同一数量级,样本点更靠近45°线,表明该模型不仅稳定且预测能力最强(图 10c)。

|
图 10 实验2动态优化机器学习模型预测结果对比 (a)IPSO-SVM; (b)IPSO-RF; (c)IPSO-XGBoost |
综合分析实验1、实验2静态调试结果,表明实际取心过程受多种非地质因素的影响,FZI及FZI*值难以呈现理论上的正态分布特征,故单依靠固定的经验参数C值难以准确计算渗透率。综合分析实验1、实验2动态调试结果,表明IPSO算法可结合样本自身特性动态优化各种参数,自适应地耦合物理模型和拟合模型,最大程度地逼近“物理上限”。实验1、实验2综合结果分析表明,物理模型决定预测精度上限,拟合模型决定预测精度下限,3种机器学习模型中,XGBoost模型预测性能最佳。
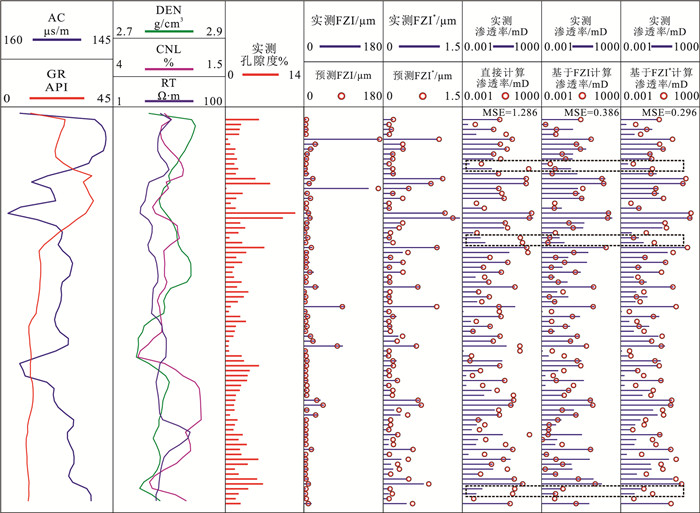
将建模以外的P1井79个取心样本作为验证集,验证本文自适应模型的外推能力。图 11展示了IPSO-XGBoost算法基于不同预测方式对验证集的计算结果,同样以MSE评价预测精度。由图可知,基于FZI和FZI*计算方式得到的结果均优于直接预测方式,经测算MSE由1.286分别降至0.386和0.296。从预测效果看,直接计算方式得到的结果数值跳跃误差更大(黑色虚线框内),表明自适应模型中DRT聚类算法有效地卡控了渗透率预测的数量级。基于2种不同流动单元指数计算方法得到的结果均能为后续准确识别有效储层提供合理支撑。
|
图 11 P1井目的层段取心样本IPSD-XGBoost模型渗透率计算结果 |
为验证本文自适应模型在实际井中的应用情况,利用IPSO-XGBoost算法单独对研究区M9井目的层段孔隙度进行了连续预测,并对M9井目的层段储层进行了常规测井综合评价(图 12)。基于孔隙度及渗透率预测结果,根据有效储层下限判断原则在5420~5510m分析得到13个小层。常规测井解释结果与射孔区段实际产气量对比分析表明,本文建立的自适应模型能够满足目的层段储层评价的要求。
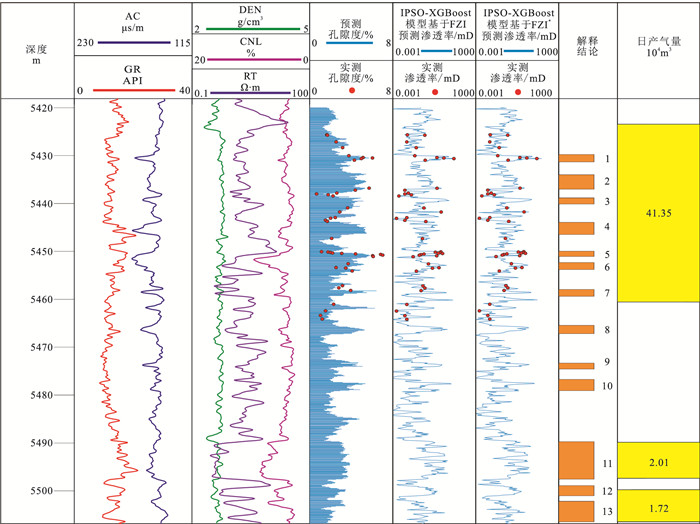
|
图 12 M9井目的层段5420~5510m测井解释结果与产剖面对比 |
本文从优化拟合模型、物理模型参数出发,利用IPSO算法同时优化物理模型参数及机器学习模型参数,得到碳酸盐岩储层渗透率预测的自适应模型,并基于流动单元指数的2种不同计算方式分别进行了实验,得到以下认识:
(1) 针对建模时物理模型基础资料不充足问题,采用拟合模型作为补充,两者耦合提高了模型的预测能力及适用性;
(2) DRT聚类算法中经验系数C值在应用过程中存在多解性,依靠单一经验值适用性差;
(3) IPSO算法在应对多参数求极值问题方面明显优于传统PSO算法,迭代次数更少,寻优精度更高,具有很强的推广性;
(4) 物理模型决定渗透率预测精度上限,拟合模型决定渗透率预测精度下限。
| [1] |
刘冬冬, 杨东旭, 张子亚, 等. 基于常规测井和成像测井的致密储层裂缝识别方法——以准噶尔盆地吉木萨尔凹陷芦草沟组为例[J]. 岩性油气藏, 2019, 31(3): 76-85. LIU Dongdong, YANG Dongxu, ZHANG Ziya, et al. Fracture identification for tight reservoirs by conventional and imaging logging: a case study of Permian Lucaogou Formation in Jimsar Sag, Junggar Basin[J]. Lithologic Reservoirs, 2019, 31(3): 76-85. |
| [2] |
任杰. 碳酸盐岩裂缝性储层常规测井评价方法[J]. 岩性油气藏, 2020, 32(6): 129-137. REN Jie. Conventional logging evaluation method for carbonate fractured reservoir[J]. Lithologic Reservoirs, 2020, 32(6): 129-137. |
| [3] |
张宸嘉, 樊太亮, 孟苗苗, 等. 塔河油田奥陶系碳酸盐岩储集层成像测井地质解释[J]. 新疆石油地质, 2018, 39(3): 352-360. ZHANG Chenjia, FAN Tailiang, MENG Miaomiao, et al. Geological interpretation of Ordovician carbonate reservoir in Tahe oilfield: application of imaging logging technology[J]. Xinjiang Petroleum Geology, 2018, 39(3): 352-360. |
| [4] |
张冲, 张占松, 张超谟. 基于等效岩石组分理论的渗透率解释模型[J]. 测井技术, 2014, 38(6): 690-694. ZHANG Chong, ZHANG Zhansong, ZHANG Chaomo. A permeability interpretation model based on equivalent rock elements theory[J]. Well Logging Technology, 2014, 38(6): 690-694. DOI:10.3969/j.issn.1004-1338.2014.06.010 |
| [5] |
陈俊, 谢润成, 刘成川, 等. 中江气田侏罗系致密砂岩气藏测井流体识别及定量评价[J]. 天然气工业, 2019, 39(增刊1): 136-141. CHEN Jun, XIE Runcheng, LIU Chengchuan, et al. Flow characterization and quantitative evaluation of the tight gas-bearing sandstone reservoirs in the Jurassic member of Zhongjiang gas field[J]. Natural Gas Industry, 2019, 39(S1): 136-141. |
| [6] |
KOZENY J. Ueber kapillare leitung des Wassers in Boden[J]. Royal Academy of Science Vienna Proc, 1927, 136(2a): 271-306. |
| [7] |
CARMAN P C. Permeability of saturated sands, soils and clays[J]. The Journal of Agricultural Science, 1939, 29(2): 262-273. DOI:10.1017/S0021859600051789 |
| [8] |
李凯, 张浩, 冉超, 等. 考虑应力敏感的页岩气产能预测模型研究——以川东南龙马溪组页岩气储层为例[J]. 西安石油大学学报(自然科学版), 2016, 31(3): 57-61. LI Kai, ZHANG Hao, RAN Chao, et al. Productivity model of shale gas well with consideration of stress sensitivity: taking Longmaxi formation shale gas re-servoir in southeastern Sichuan basin as an example[J]. Journal of Xi'an Shiyou University (Natural Science), 2016, 31(3): 57-61. |
| [9] |
KHARRAT R, MAHDAVI R, BAGHERPOUR M H, et al. Rock type and permeability prediction of a heterogeneous carbonate reservoir using artificial neural networks based on flow zone index approach[C]. SPE Middle East Oil and Gas Show and Conference, 2009, SPE-120166-MS.
|
| [10] |
邓浩阳. 高孔低渗碳酸盐岩储层孔隙结构及物性表征方法研究[D]. 四川成都: 西南石油大学, 2018. DENG Haoyang. The Evaluation Method of Pore Structure and Physical Property in Carbonate Rock Reservoir with High Porosity and Low Permeability[D]. Southwest Petroleum University, Chengdu, Sichuan, 2018. |
| [11] |
ZHANG Z, ZHANG H, LI J, et al. Permeability and porosity prediction using logging data in a heterogeneous dolomite reservoir: An integrated approach[J]. Journal of Natural Gas Science and Engineering, 2021, 86: 103743. |
| [12] |
周雪晴, 张占松, 张超谟, 等. 基于粗糙集—随机森林算法的复杂岩性识别[J]. 大庆石油地质与开发, 2017, 36(6): 127-133. ZHOU Xueqing, ZHANG Zhansong, ZHANG Chaomo, et al. Complex lithologic identification based on rough set-random forest algorism[J]. Petroleum Geo-logy & Oilfield Development in Daqing, 2017, 36(6): 127-133. |
| [13] |
郭建宏, 张占松, 张超谟, 等. 用地球物理测井资料预测煤层气含量——基于斜率关联度随机森林方法的工作案例[J]. 物探与化探, 2021, 45(1): 18-28. GUO Jianhong, ZHANG Zhansong, ZHANG Chaomo, et al. The exploration of predicting CBM content by geophysical logging data: a case study based on slope correlation random forest method[J]. Geophysi-cal and Geochemical Exploration, 2021, 45(1): 18-28. |
| [14] |
ZHANG Z, CAI Z X. Permeability prediction of carbonate rocks based on digital image analysis and rock typing using random forest algorithm[J]. Energy & Fuels, 2021, 35(14): 11271-11284. |
| [15] |
孙予舒, 黄芸, 梁婷, 等. 基于XGBoost算法的复杂碳酸盐岩岩性测井识别[J]. 岩性油气藏, 2020, 32(4): 98-106. SUN Yushu, HUANG Yun, LIANG Ting, et al. Identification of complex carbonate lithology by logging based on XGBoost algorithm[J]. Lithologic Re-servoirs, 2020, 32(4): 98-106. |
| [16] |
闫星宇, 顾汉明, 肖逸飞, 等. XGBoost算法在致密砂岩气储层测井解释中的应用[J]. 石油地球物理勘探, 2019, 54(2): 447-455. YAN Xingyu, GU Hanming, XIAO Yifei, et al. XGBoost algorithm applied in the interpretation of tight-sand gas reservoir on well logging data[J]. Oil Geophysical Prospecting, 2019, 54(2): 447-455. |
| [17] |
谷宇峰, 张道勇, 鲍志东. 测井资料PSO-XGBoost渗透率预测[J]. 石油地球物理勘探, 2021, 56(1): 26-37. GU Yufeng, ZHANG Daoyong, BAO Zhidong. Permeability prediction using PSO-XGBoost based on logging data[J]. Oil Geophysical Prospecting, 2021, 56(1): 26-37. |
| [18] |
CHEN T Q, GUESTRIN C. XGBoost: a scalable tree boosting system[C]. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2016, 785-794.
|
| [19] |
蔡恒雨, 郑启龙. 深度学习节点分配的遗传算法设计[J]. 小型微型计算机系统, 2021, 42(6): 1158-1164. CAI Hengyu, ZHENG Qilong. Design of genetic algorithm for node assignment in deep learning[J]. Journal of Chinese Computer Systems, 2021, 42(6): 1158-1164. |
| [20] |
陈愿愿, 邓小江, 王小兰, 等. 粒子群优化支持向量机算法在页岩储层总有机碳含量预测中的应用——以渝西地区Z井区为例[J]. 石油物探, 2021, 60(4): 652-663. CHEN Yuanyuan, DENG Xiaojiang, WANG Xiaolan, et al. Application of a PSO-SVM algorithm for predicting the TOC content of a shale gas reservoir: a case study in well Z in the Yuxi area[J]. Geophysical Prospecting for Petroleum, 2021, 60(4): 652-663. |
| [21] |
郭彩杏, 郭晓金, 柏林江. 改进遗传模拟退火算法优化BP算法研究[J]. 小型微型计算机系统, 2019, 40(10): 2063-2067. GUO Caixing, GUO Xiaojin, BAI Linjiang. Research on improved BP algorithm for genetic simulated annealing algorithm[J]. Journal of Chinese Computer Systems, 2019, 40(10): 2063-2067. |
| [22] |
盛晓晨, 史旭东, 熊伟丽. 改进粒子群优化的极限学习机软测量建模方法[J]. 计算机应用研究, 2020, 37(6): 1683-1687. SHENG Xiaochen, SHI Xudong, XIONG Weili. Soft sensor modeling of extreme learning machine based on improved particle swarm optimization[J]. Application Research of Computers, 2020, 37(6): 1683-1687. |
| [23] |
AMAEFULE J O, ALTUNBAY M, TIAB D, et al. Enhanced reservoir description: using core and log data to identify hydraulic (flow) units and predict permeability in uncored intervals/wells[C]. Proceedings of the SPE Annual Technical Conference and Exhibition, 1993, SPE-26436-MS.
|
| [24] |
MIRZAEI-PAIAMAN A, SABOORIAN-JOOYBARI H, POURAFSHARY P. Improved method to identify hydraulic flow units for reservoir characterization[J]. Energy Technology, 2015, 3(7): 726-733. |
| [25] |
MIRZAEI-PAIAMAN A, SABBAGH F, OSTAD-HASSAN M, et al. A further verification of FZI* and PSRTI: newly developed petrophysical rock typing indices[J]. Journal of Petroleum Science and Engineering, 2019, 175: 693-705. |
| [26] |
MIRZAEI-PAIAMAN A, ASADOLAHPOUR S R, SABOORIAN-JOOYBARI H, et al. A new framework for selection of representative samples for special core analysis[J]. Petroleum Research, 2020, 5(3): 210-226. |
| [27] |
谷明峰, 朱茂, 梁锋, 等. 四川盆地磨溪地区灯四段前积体产状定量解释及其应用[J]. 石油地球物理勘探, 2021, 56(4): 853-868. GU Mingfeng, ZHU Mao, LIANG Feng, et al. Quantitative interpretation and application of progradatio-nal reflection in the fourth member of Dengying Formation in the Moxi area, Sichuan Basin[J]. Oil Geophysical Prospecting, 2021, 56(4): 853-868. |
| [28] |
戴晓峰, 徐右平, 甘利灯, 等. 川中深层—超深层多次波识别和压制技术——以高石梯—磨溪连片三维区为例[J]. 石油地球物理勘探, 2019, 54(1): 54-64. DAI Xiaofeng, XU Youping, GAN Lideng, et al. Deep & ultra-deep multiple suppression in central Sichuan: an example of Gaoshiti-Moxi[J]. Oil Geophysical Prospecting, 2019, 54(1): 54-64. |



 徐鹏宇, 四川省成都市成华区二仙桥东三路1号成都理工大学“油气藏地质及开发工程”国家重点实验室,610059。Email:
徐鹏宇, 四川省成都市成华区二仙桥东三路1号成都理工大学“油气藏地质及开发工程”国家重点实验室,610059。Email: