② 海洋石油高效开发国家重点实验室,北京 100020
② State Key Laboratory of Offshore Oil Exploitation, Beijing 100020, China
小于地震极限分辨率(1/4波长)的薄层单砂体厚度与薄互层累积砂体厚度预测是油藏地球物理领域重点研究的内容之一[1-5]。现有薄(互)层砂体厚度预测方法大致可以分为以下四类。
① 利用振幅[1, 6]或频率类[7-10]地震属性,基于一次或二次函数式拟合地震属性与薄(互)层砂岩厚度之间的映射关系,这也是当前薄(互)层砂岩厚度预测的主流做法。Widess[1]和Kallweit等[6]最早研究了地震振幅与薄层厚度之间的关系;Robertson等[10]率先将频率类属性引入薄层厚度的预测中。尔后,学者们不断完善基于地震振幅类和频率类属性的薄层砂岩厚度预测方法。②基于薄层反射的陷频特性,应用谱分解与谱反演[11-13]技术的薄(互)层砂岩厚度估算方法。杨林[12]基于薄层时间厚度等同于陷频周期倒数这一理论基础,实现了对实际资料的薄层厚度预测。Puryear等[13]结合先验信息与谱分解技术,应用频谱反演方法实现了薄层厚度预测。③基于非线性反演框架的薄(互)层砂岩厚度反演与基于神经网络的多属性回归薄(互)层砂岩厚度预测。柏冠军等[14]根据地震属性与薄层砂岩厚度的非线性关系,利用非线性反演框架预测了薄层厚度;黄真萍等[15]、邵治龙等[16]利用人工神经网络预测了薄互层累积砂岩厚度。④构建新的地震复合属性,并以此提升薄(互)层砂岩厚度预测精度。王延光等[2]利用振幅和频率两种对薄层厚度最为敏感的地震属性构建了一种新的复合地震属性,有效提升了薄层单砂体厚度的估算精度和薄互层砂岩累积厚度的预测精度。
然而,上述利用地震属性预测薄(互)层砂岩厚度方法的理论基础都源自Widess单砂体楔形模型实验[1]。而理论上该模型适用于无限均匀介质中仅含一套薄储层的情况,这与实际情况中常见的砂、泥岩薄(互)层广泛发育不同,导致应用上述方法预测薄(互)层砂岩厚度时,不可避免地引入较大预测误差,造成实际应用时很难从地震属性与薄(互)层厚度的交会图中拟合出理想的楔形模型实验映射关系。
为提升利用地震属性预测砂、泥岩薄(互)层砂岩厚度的预测精度,本文提出基于测井正演量板与高斯概率场的薄(互)层砂岩厚度预测方法,提供了最大概率薄(互)层砂岩厚度与砂岩厚度置信度两种平面属性估计,前者保留砂岩厚度预测结果的不确定性、多解性,后者在提升薄(互)层砂岩厚度预测精度的同时,相对量化地表征预测结果的不确定性,有助于指导后续井位设计。
1 基于测井曲线的楔形模型正演楔形模型正演是研究薄层调谐厚度效应的经典方法。然而,实际薄(互)层砂体内部弹性参数(密度、纵/横波速度等)变化复杂,导致按照常速、常密度或速度、密度按照简单变化规律建立的楔形模型与真实薄(互)层模型存在差异,并将误差引入提取的地震属性预测结果中。消除上述误差的最佳方式是直接利用储层段测井的弹性参数进行楔形模型正演,从而有效逼近地下薄(互)层真实地质条件。
渤海湾W油田的明化镇组主力储层属于浅水三角洲相沉积,枝蔓状窄河道薄(互)层砂体叠置、连片发育,且均有探井钻遇,可根据测井储层段真实弹性参数建立更加逼近薄(互)层实际地质条件的楔形模型。
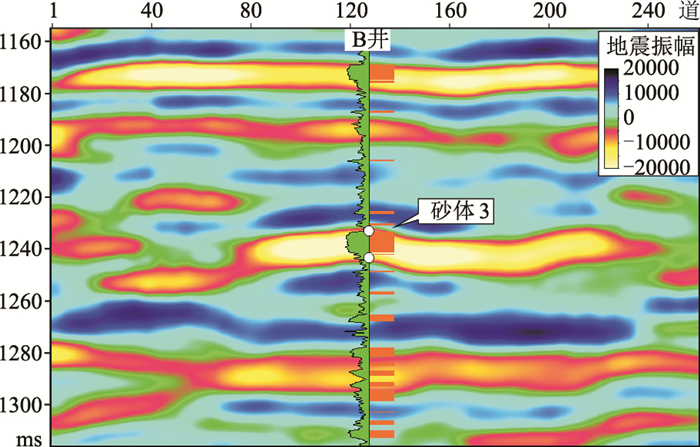
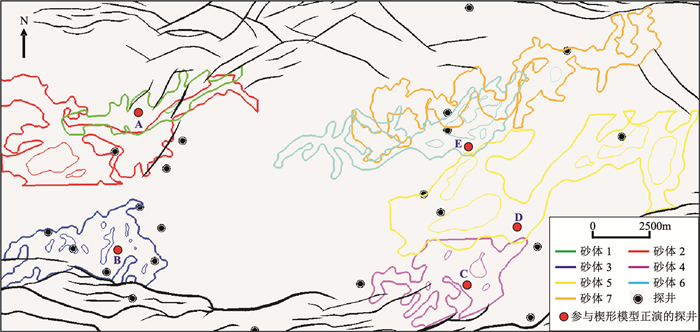
选取油田内5个典型砂体(砂体1、3、4、5、6)及钻遇对应砂体的探井A~E(图 1),提取储层段测井密度、速度参数建立楔形模型。经统计,5个典型砂体的速度变化范围为2100~2350m/s,密度变化范围为2.06~2.24g/cm3。井点位置地震道弹性参数取自测井速度、密度数据,其他地震道弹性参数由井点处沿楔状层位外推得到。泥岩弹性参数分别根据研究区多口探井统计的泥岩速度(2258m/s)和密度(2.32g/cm3)设定。
|
图 1 W油田典型砂体与钻遇探井平面分布 |
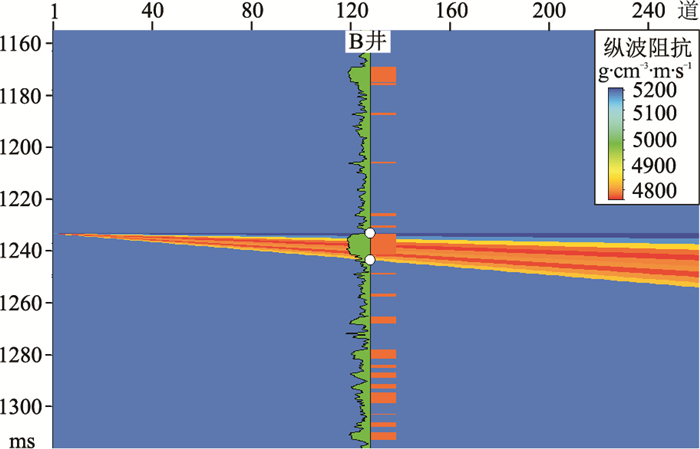
以B井钻遇的砂体3为例(图 2),对该套6.5m的相对厚储层进行模拟,根据测井曲线建立的楔形纵波阻抗模型(图 3)较好地体现了砂体内部弹性参数变化。
|
图 3 根据B井钻遇的砂体3弹性参数建立的纵波阻抗楔形模型 |
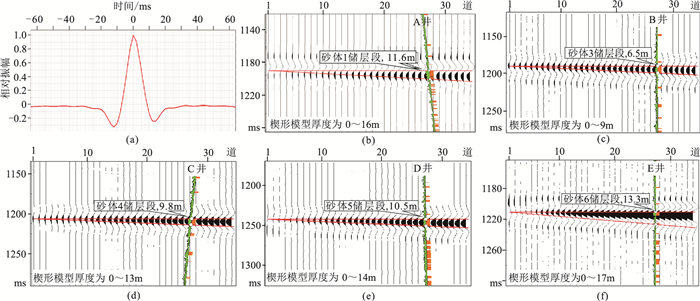
按照同样方式,利用探井A、C、D、E的测井曲线分别建立砂体1、4、5、6对应的楔形模型,从原始地震数据800~1600ms时窗中提取统计性子波(图 4a),子波主频为35Hz,结合该区域砂、泥岩速度信息,可知地震可分辨砂体厚度极限约为14m。统计性子波与模型褶积得到零炮检距地震剖面,进一步采用-90°相移处理得到5个典型砂体的楔形模型波阻抗剖面(图 4b~图 4f),其反射波谷振幅强弱能够近似反映砂体储层发育情况(井上钻遇砂岩厚度及楔形模型厚度见图 4标注)。
|
图 4 统计性子波和典型砂体对应的相对波阻抗剖面(红色直线代表楔形模型顶、底) (a)原始地震数据提取的统计性子波;(b)砂体1;(c)砂体3;(d)砂体4;(e)砂体5;(f)砂体6 |
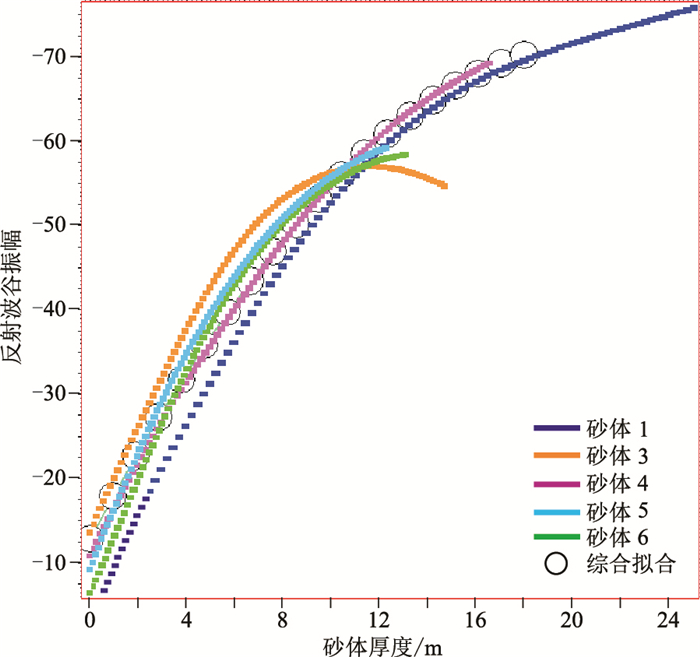
以-90°相移数据为基础,研究地震反射波谷振幅随砂层厚度变化关系,统计规律如图 5所示。由图可见,砂体3振幅—砂岩厚度曲线在11m厚度附近出现拐点,推测可能是受该砂体调谐厚度的影响;其余曲线形态较一致。综合平均5个楔形模型正演结果,得到能够代表W油田地震振幅属性随砂体厚度变化的综合拟合曲线。
|
图 5 砂体楔形模型地震振幅随砂体厚度变化关系统计 |
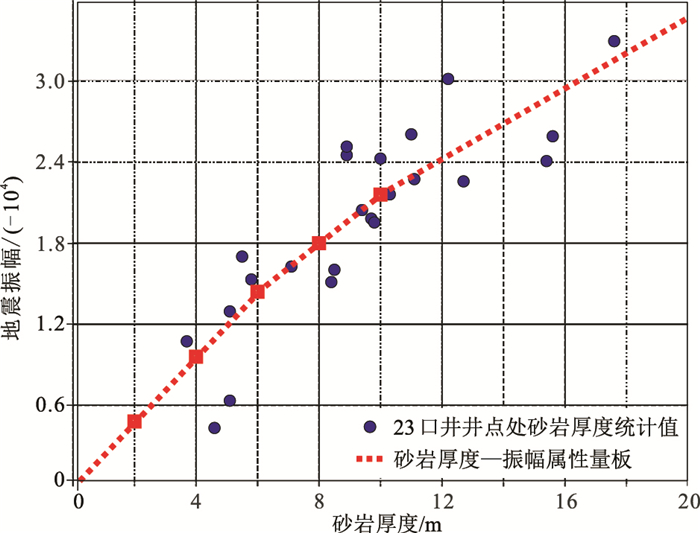
利用分段线性函数逼近图 5中的综合拟合曲线,得到W油田砂岩厚度—振幅属性量板(图 6中红色点线所示)。与油田内其他井点钻遇砂体的对比统计结果表明:基于5个典型砂体弹性参数建立的砂体厚度—振幅属性量板与W油田砂体整体吻合度较好,与23口井统计结果的均方根误差约为2.3m。据此形成一套能够定性表征砂岩厚度的振幅属性显示色标(图 7)。以砂体7为例,利用该显示色标对应显示反射波谷振幅属性,能够定性刻画砂体累积厚度的平面展布(图 8),其结果与钻遇该砂体的2口井所揭示的砂岩厚度吻合度较高。
|
图 6 W油田砂岩厚度—振幅属性量板 |

|
图 7 振幅属性显示色标 |

|
图 8 依据显示色标对砂体7累积砂岩厚度的定性刻画结果 |
砂岩厚度—振幅属性量板是在现有楔形模型实验的主流砂岩厚度预测方法基础上进行了改进,考虑了储层段弹性参数的垂向变化,但仍是基于单一砂体假设,未考虑储层结构对地震振幅的影响,因此在利用楔形模型实验得到的理想曲线拟合实际累积砂岩厚度—振幅属性交会时,常表现为欠拟合。另一方面,累积砂岩厚度—振幅属性交会通常呈现椭圆型数据分布形态,存在明显的长轴、短轴方向,因此本文利用考虑了协方差估计的二维高斯分布进行椭圆拟合,以此表征砂岩累积厚度—振幅属性复杂的内在关联。
二维高斯分布可表达为
| $ f(\boldsymbol{x})=\frac{1}{2 \pi|\mathit{\pmb{\Sigma}}|^{\frac{1}{2}}} \exp \left[-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{\mathrm{T}} \mathit{\pmb{\Sigma}}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\right] $ | (1) |
式中:x=[xthick, xattr]T为由砂体累积厚度xthick与地震振幅属性xattr组成的列向量;μ=[μthick, μattr]T为由xthick的平均值μthick与xattr的平均值μattr组成的列向量;Σ为协方差矩阵,表征xthick与xattr之间的线性相关程度,有
| $ \mathit{\pmb{\Sigma}}=\left[\begin{array}{cc} \operatorname{cov}\left(x_{\text {thick }}, x_{\text {thick }}\right) & \operatorname{cov}\left(x_{\text {thick }}, x_{\text {attr }}\right) \\ \operatorname{cov}\left(x_{\text {attr }}, x_{\text {thick }}\right) & \operatorname{cov}\left(x_{\text {attr }}, x_{\text {attr }}\right) \end{array}\right] $ | (2) |
其中cov(·)为协方差计算函数
| $ \operatorname{cov}\left(x_i, x_j\right)=\mathrm{E}\left[\left(x_i-\mathrm{E}\left|x_i\right|\right)\left(x_j-\mathrm{E}\left|x_j\right|\right)\right] $ | (3) |
式中xi, xj代表xthick或xattr,E|·|表示求取期望值函数。
基于二维高斯分布建立累积砂岩厚度—振幅属性高斯概率场,进一步求解得到给定振幅属性的具有最大概率的累积砂岩厚度估计,以此作为累积砂岩厚度定量预测结果。具体步骤如下。
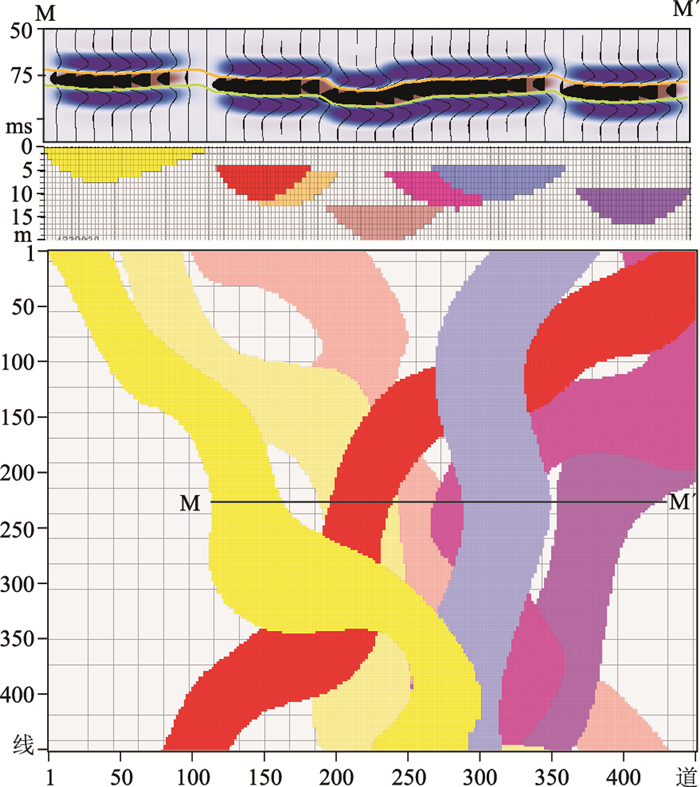
首先,利用Petrel软件建立河道型薄互层模型(图 9),模型中7条薄层河道砂体叠置发育,河道砂体宽度为300~500m、单条河道厚度为6~8m,河道砂岩速度为2340m/s、密度为2.0g/cm3,泥岩速度为2420m/s、密度为2.2g/cm3。采用35Hz的Ricker子波与模型褶积得到正演地震数据(垂向分辨率约为17m),之后对正演结果进行-90°相移处理,得到刻画薄互层河道砂的基础数据,基于相移数据剖面解释了复合河道储层反射顶、底层位(图 9上)。图 9下显示了7条河道的平面展布。
|
图 9 河道砂薄互层模型 上:-90°相移剖面,黄色、绿色层位分别为复合河道储层顶、底面;中:河道砂体地质模型剖面;下:7条河道的平面展布,MM′为剖面所在平面位置 |
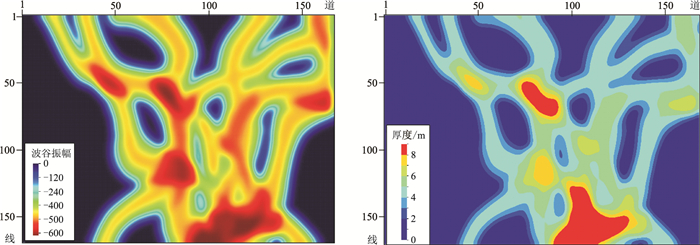
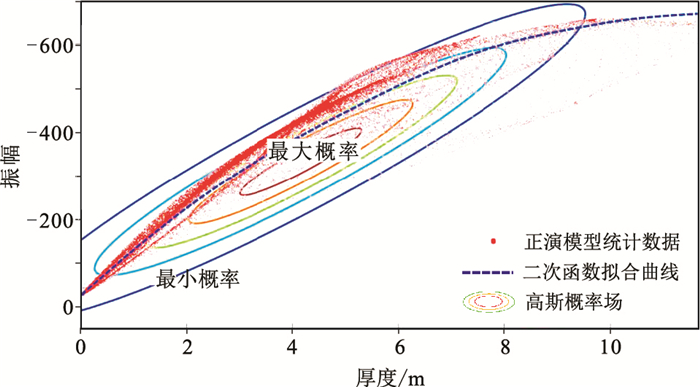
其次,提取复合河道储层反射波谷振幅属性,并统计模型累积砂岩厚度(图 10),根据式(2)和式(3)得到累积砂岩厚度与复合河道储层反射波谷振幅值的协方差信息,根据式(1)建立考虑协方差估计的二维高斯分布函数,绘制等值线,以此建立累积砂岩厚度—振幅属性高斯概率场(图 11),图中显示了高斯概率场中的5条椭圆型等值线。然后分别采用传统二次函数关系式拟合方法和基于高斯概率场的预测方法,利用反射波谷振幅属性预测储层累积砂岩厚度。应用基于高斯概率场预测累积砂岩厚度时,先固定输入的振幅属性值,之后分别以较大网格间距和较小网格间距遍历可能的累积砂岩厚度取值,从中筛选出当前振幅属性值下具有最大概率的累积砂岩厚度作为预测结果。
|
图 10 河道型薄互层模型储层反射波谷振幅属性(左)与累积砂岩厚度平面分布(右) |
|
图 11 累积砂岩厚度—振幅属性高斯概率场 |
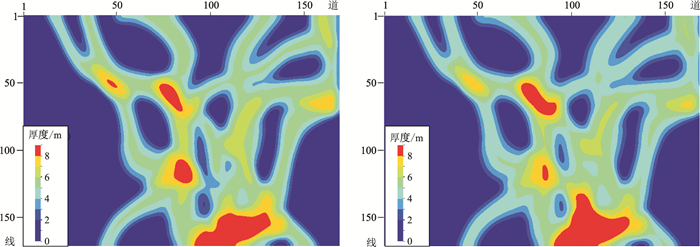
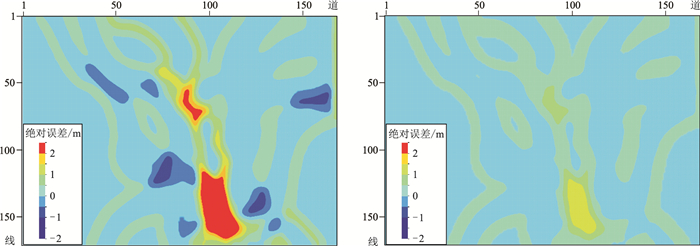
两种方法得到的累积砂岩厚度预测结果(图 12)和预测绝对误差(图 13)表明:基于高斯概率场的累积砂岩厚度预测结果与真实砂岩厚度更为接近,优于传统二次函数关系拟合预测结果。
|
图 12 两种方法的累积砂岩厚度预测结果 左:基于传统二次函数拟合;右:基于累积砂岩厚度—振幅属性高斯概率场 |
|
图 13 两种方法的累积砂岩厚度预测绝对误差 左:基于传统二次函数拟合;右:基于累积砂岩厚度—振幅属性高斯概率场 |
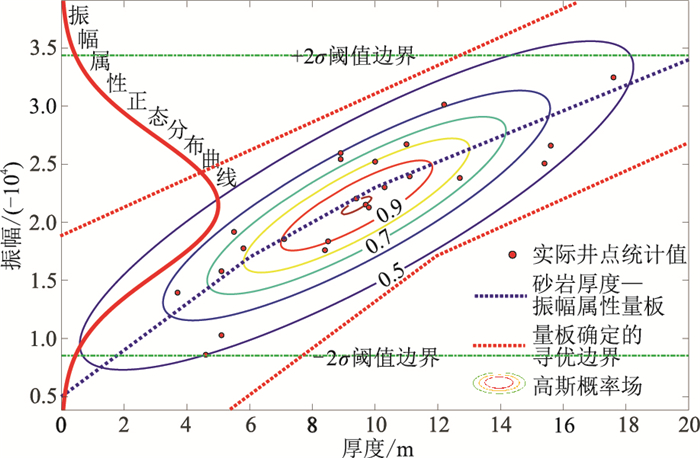
应用累积砂岩厚度—振幅属性高斯概率场预测W油田砂体累积砂岩厚度。根据测井资料统计砂体1~砂体7累积砂岩厚度及其对应反射波谷振幅属性值,建立W油田累积砂岩厚度—振幅属性高斯概率场(图 14)。由于实际钻井信息有限,建立的高斯概率场存在因数据量不足引入的误差。基于此,一方面结合前述形成的砂体厚度—振幅属性量板,在量板两侧一定范围内寻找高斯概率场中具有最大概率的累积砂岩厚度以及砂岩厚度置信度,即由厚度—振幅属性量板确定左、右寻优边界;另一方面,根据正态分布2倍标准差原则,在利用振幅属性预测累积砂岩厚度时,对偏大和偏小的振幅属性值采取阈值处理,即
| $ H= \begin{cases}\operatorname{arc}\left[G_{\max }(K)\right] \quad K \in\left[\mu_{\mathrm{attr}}-2 \sigma, \mu_{\mathrm{attr}}+2 \sigma\right] \\ \operatorname{arc}\left[G_{\max }\left(\mu_{\mathrm{attr}}+2 \sigma\right)\right] K>\left(\mu_{\mathrm{attr}}+2 \sigma\right) \\ \operatorname{arc}\left[G_{\max }\left(\mu_{\mathrm{attr}}-2 \sigma\right)\right] K<\left(\mu_{\mathrm{attr}}-2 \sigma\right)\end{cases} $ | (4) |
|
图 14 W油田累积砂岩厚度—振幅属性高斯概率场 |
式中:H为预测累积砂岩厚度;arc[Gmax(K)]代表振幅属性值为K时,高斯概率场中最大概率对应的累积砂岩厚度;σ为振幅属性值的标准差。当振幅属性值落在(μattr-2σ, μattr+2σ)区间外(根据正态分布2σ原则,在此区间外概率不足5%)时,被认为是小概率事件,对应累积砂岩厚度取边界值K=μattr±2σ时的砂岩厚度。
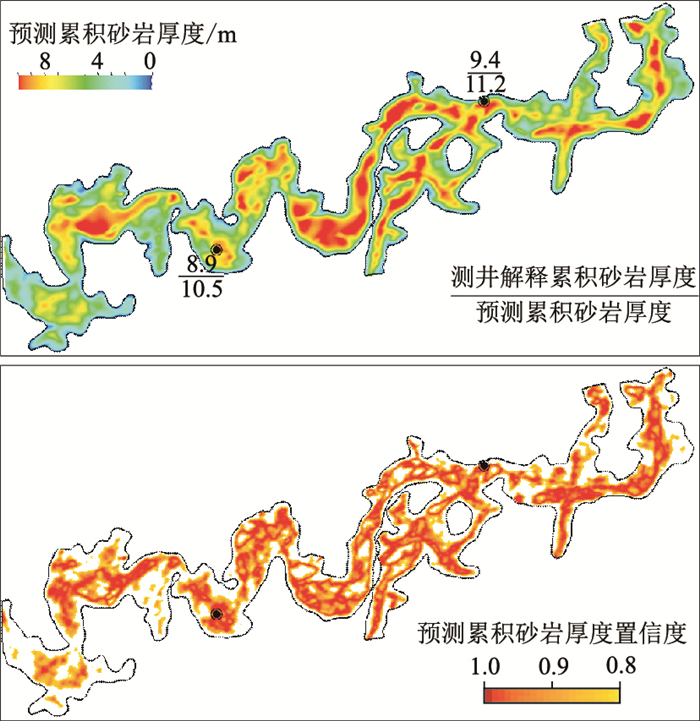
以砂体7为例,利用累积砂岩厚度—振幅属性高斯概率场(图 14)预测得到最大概率累积砂岩厚度和砂岩厚度置信度平面属性结果(图 15)。其中,砂岩厚度置信度属性图上任意样点的取值表示:该样点反射波谷振幅属性值与最大概率累积砂岩厚度值组成的二维变量在高斯概率场中对应的概率值,反映了累积砂岩厚度预测结果的可靠程度。
|
图 15 最大概率累积砂岩厚度(上)与砂岩厚度置信度属性(下) |
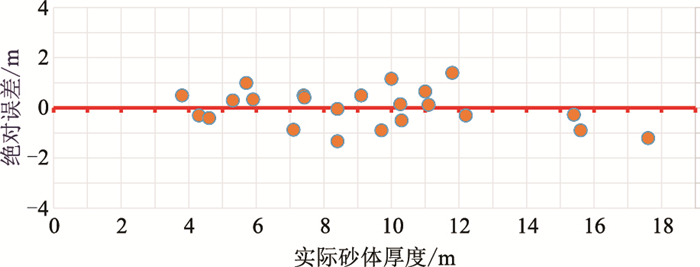
此外,由图 15上井标注数据可知,累积砂岩厚度预测绝对误差在钻遇该砂体的两口井位置均小于2m。统计W油田内22个井样点,砂体累积厚度范围集中在4~16m,基于高斯概率场方法的累积砂岩厚度预测绝对误差随实际砂岩厚度的变化关系如图 16所示,可见误差整体控制在2m以内,进一步验证了本文方法预测结果较为可靠。同时,设置砂岩厚度置信度属性门槛阈值为80%,即可保留累积砂岩厚度预测结果较可靠区域。砂岩厚度置信度属性保留了地球物理预测的多解性,相对量化地表征了预测结果的不确定性,为后续开发井位设计、优化提供了指导与参考。
|
图 16 高斯概率场累积砂岩厚度预测绝对误差随实际累积砂岩厚度变化关系 |
砂岩厚度预测是地震储层预测工作的重要环节之一,预测结果对后续地质建模、井位部署均具有重要影响。当前业界的主流做法是利用振幅、频率等地震属性,基于拟合关系式预测累积砂岩厚度,方法易操作也具有一定的稳定性。但该方法是基于单一薄层假设,与薄互层发育的实际情况相矛盾,导致预测精度存在局限。
为提升累积砂岩厚度预测精度,本文提出两种预测方法,主要针对具有2~3层砂体结构的储层。一是基于油田实际测井曲线进行楔形模型正演并形成砂体厚度—振幅属性量板,与油田实际地质背景更为吻合,能够根据振幅属性色标相对定性地反映砂体累积厚度平面分布,同时可以质控后续砂岩厚度定量预测结果的合理性。二是基于二维高斯函数形成的累积砂岩厚度—振幅属性高斯概率场,根据反射波谷振幅—砂岩厚度交会结果(往往呈现具有明显长、短轴方向的椭圆形态),利用高斯概率场表征任一属性值条件下不同累积砂岩厚度的概率分布,该方法能够定量预测最大概率累积砂岩厚度和砂岩厚度置信度,在进一步提升预测精度的同时,砂岩厚度置信度属性保留了地球物理储层预测的多解性,为后续地质建模与油藏布井中砂岩厚度预测结果的不确定性提供度量。上述两种方法为薄(互)层砂岩厚度预测提供了新的思路。
| [1] |
WIDESS M B. Quantifying resolving power of seismic systems[J]. Geophysics, 1982, 47(8): 1160-1173. DOI:10.1190/1.1441379 |
| [2] |
王延光, 李皓, 李国发, 等. 一种用于薄层和薄互层砂体厚度估算的复合地震属性[J]. 石油地球物理勘探, 2020, 55(1): 153-160. WANG Yanguang, LI Hao, LI Guofa, et al. A composite seismic attribute used to estimate the sand thickness for thin bed and thin interbed[J]. Oil Geophysical Prospecting, 2020, 55(1): 153-160. |
| [3] |
杜昕, 范廷恩, 董建华, 等. 基于多层感知机网络的薄储层预测[J]. 石油地球物理勘探, 2020, 55(6): 1178-1187. DU Xin, FAN Ting'en, DONG Jianhua, et al. Characterization of thin sand-shale reservoirs based on multi-layer perceptron deep neural network[J]. Oil Geophysical Prospecting, 2020, 55(6): 1178-1187. |
| [4] |
DU X, LI G F, ZHANG M, et al. Multichannel band-controlled deconvolution based on a data-driven structural regularization[J]. Geophysics, 2018, 83(5): R401-R411. DOI:10.1190/geo2017-0516.1 |
| [5] |
杜昕, 范廷恩, 范洪军, 等. 少井背景下基于稀疏层反射系数反演的薄层预测[J]. 石油地球物理勘探, 2021, 56(2): 356-363. DU Xin, FAN Ting'en, FAN Hongjun, et al. Prediction of thin reservoirs with less well data based on sparse-layer reflectivity inversion[J]. Oil Geophysical Prospecting, 2021, 56(2): 356-363. |
| [6] |
KALLWEIT R S, WOOD L C. The limits of resolution of zero-phase wavelet[J]. Geophysics, 1982, 47(7): 1035-1046. DOI:10.1190/1.1441367 |
| [7] |
PARTYKA G, GRIDLEY J, LOPEZ J. Interpretational applications of spectral decomposition in reservoir characterization[J]. The Leading Edge, 1999, 18(3): 353-360. DOI:10.1190/1.1438295 |
| [8] |
姚建阳. 在频率域中求取薄地层的厚度[J]. 石油地球物理勘探, 1991, 26(5): 594-599. YAO Jianyang. Calculating thin-bed thickness in frequency domain[J]. Oil Geophysical Prospecting, 1991, 26(5): 594-599. |
| [9] |
高君, 曹思远, 吕雪雁, 等. 峰值频率法估算薄层厚度[J]. 地球物理学进展, 2018, 33(1): 204-210. GAO Jun, CAO Siyuan, LYU Xueyan, et al. Estimation of the thickness of thin layers using peak frequency method[J]. Progress in Geophysics, 2018, 33(1): 204-210. |
| [10] |
ROBERTSON J D, NOGAMI H H. Complex seismic trace analysis of thin beds[J]. Geophysics, 1984, 49(4): 344-352. |
| [11] |
孙鲁平, 郑晓东, 首皓, 等. 薄层地震峰值频率与厚度关系研究[J]. 石油地球物理勘探, 2010, 45(2): 254-259, 271. SUN Luping, ZHENG Xiaodong, SHOU Hao, et al. The studies on relationship between thin layer seismic peak frequency and its thickness[J]. Oil Geophysical Prospecting, 2010, 45(2): 254-259, 271. |
| [12] |
杨林. 地震频谱分解技术应用中有关问题的讨论[J]. 石油物探, 2008, 47(4): 405-409. YANG Lin. Discussion on the problems in using the technology of seismic spectral decomposition[J]. Geo-physical Prospecting for Petroleum, 2008, 47(4): 405-409. |
| [13] |
PURYEAR C I, CASTAGNA J P. Layer-thickness determination and stratigraphic interpretation using spectral inversion: theory and application[J]. Geophysics, 2008, 73(2): R37-R48. |
| [14] |
柏冠军, 吴汉宁, 赵希刚, 等. 地震资料预测薄层厚度方法研究与应用[J]. 地球物理学进展, 2006, 21(2): 554-558. BAI Guanjun, WU Hanning, ZHAO Xigang, et al. Research on prediction of thin bed thickness using seismic data and its application[J]. Progress in Geophysics, 2006, 21(2): 554-558. |
| [15] |
黄真萍, 王晓华, 王云专. 薄层地震属性参数分析和厚度预测[J]. 石油物探, 1997, 36(3): 28-38. HUANG Zhenping, WANG Xiaohua, WANG Yunzhuan. Parameter analysis of seismic attributes and thickness prediction for thin bed[J]. Geophysical Prospecting for Petroleum, 1997, 36(3): 28-38. |
| [16] |
邵治龙, 尹成, 黄德济, 等. 用多参量法计算薄层和薄互层厚度[J]. 石油物探, 1997, 36(4): 92-98. SHAO Zhilong, YIN Cheng, HUANG Deji, et al. The calculation of thin bed and thin interbed thicknesses using the multiparameter method[J]. Geophysical Prospecting for Petroleum, 1997, 36(4): 92-98. |



 杜昕, 北京市朝阳区太阳宫南街6号院中海油研究总院有限责任公司,100020。Email:
杜昕, 北京市朝阳区太阳宫南街6号院中海油研究总院有限责任公司,100020。Email: