地下介质中应力不仅是控制油气运移[1]、压实成岩作用[2]、构造演化[3]等的关键因素,同时也对储层压裂[4]、注水开发[5]、钻井井壁稳定性[6]、钻井安全[7]等工程作业影响较大。因此,地应力分析受到业界的关注。Fillippone[8]基于地层速度与地层有效应力的关系,综合不同实际资料给出了地层速度与地层压力之间的经验关系式,提出了一种利用地震资料预测地层压力的有效方法,该方法在油气勘探中得到进一步发展和应用[9-10];Dillen[11]建立了反射系数与应力的关系,直接利用地震资料预测地应力,并逐渐形成技术体系[12-13]。
地层异常压力预测一般基于以下认识:当地层中孔隙流体在特定地质条件下承担了部分上覆地层重力时,流体压力增大,同时地层有效应力相对降低,导致地层压实作用减弱,速度减小。另外,根据岩石力学相关认识可知,在地层中存在构造变化(起伏或断裂)时,上覆介质重力会不均匀作用于地层[14],此时地层有效应力发生横向变化,必然影响地层速度。文献[15]初步探讨了上述问题,指出断层下降盘的滚动背斜的速度急剧变化可能部分源于应力变化引起的差异压实作用,实例分析证明这种速度变化严重影响同类构造的勘探、开发。截至目前,未见地应力横向变化对地层速度及构造解释影响的定量分析文献。为此,本文基于测井数据,参考了土木工程、固体矿产、钻井工程等领域的研究成果[16-19],采用有限差分法模拟应力场,分析局部地应力对地层速度的影响机理,以提高构造解释精度。
1 地应力与地层速度的关系 1.1 测井数据统计在沉积环境相对简单、构造平缓、无断裂影响的情况下,同一位置、不同深度的垂向地应力差ΔPz主要来源于重力,其与地层密度ρ的关系为
| $ \Delta P_z=\int_{z_1}^{z_2} \rho(z) g \mathrm{~d} z $ | (1) |
式中:z为深度,z1、z2分别为数据统计层段的起、止深度;g为重力加速度,取9.81m/s2。实际应用中,可基于测井密度数据估算ΔPz,其离散表达式为
| $ \Delta P_z \cong \sum\limits_{i=1}^m \rho_{z_i} g \Delta z $ | (2) |
式中:Δz为样点的深度间隔;m为样点数;ρzi为深度zi处的地层密度。
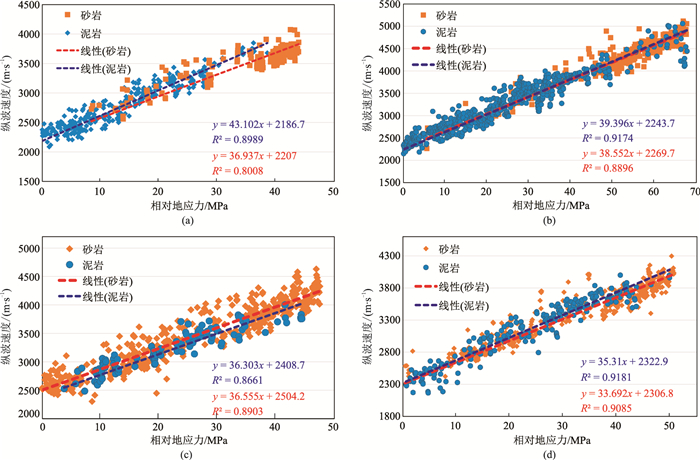
若以特定深度为基准点,可利用式(2)及测井数据统计速度随垂向地应力的变化。针对地应力与地层速度之间的关系,选取A区典型钻井数据进行分析。以HZ-A1井为例,该井在深度大于1200m后井径变化较小,对应数据较可靠,因此将1200m深度作为该井数据的参考点。为便于进一步统计、分析,对测井数据进行整理,包括:①通过重采样将不同数据深度对齐(采样率为2m),并且剔除异常点;②利用密度数据求取任意深度点相对参考点的垂向地应力差,将时差数据转换为速度数据;③利用泥质含量区分砂(泥质含量小于25%的碎屑岩)、泥(泥质含量大于75%的碎屑岩)岩;④绘制地层纵波速度随相对地应力变化曲线(图 1a),可见,地层速度近似与垂向地应力呈线性正相关关系,而且砂、泥岩差别较小,斜率(应力对地层速度的影响系数,以下简称影响系数)约为40m·s-1·MPa-1。
|
图 1 A区HZ-A1井(a)、HZ-B1井(b)、PY-A1井(c)、XJ-A1井(d)砂、泥岩纵波速度随相对地应力的变化曲线 x、y分别代表横、纵坐标变量,R2为拟合系数,下同 |
A区其他井的砂、泥岩纵波速度随相对地应力的变化与HZ-A1井类似,如HZ-B1井(图 1b)、PY-A1井(图 1c)、XJ-A1井(图 1d)。表 1为A区影响系数统计表,可见:①同一井点,地应力变化对砂、泥岩速度的影响接近;②不同井点,地应力变化对地层速度的影响略有差异;③影响系数分布于30~40m·s-1·MPa-1。
|
|
表 1 A区影响系数统计表 |
对于埋深较小、范围较小的靶区,可忽略沉积环境、胶结作用等其他因素的影响,上述认识也适用于横向地层。速度与垂向地应力之间的线性正相关关系可简述为:速度增量Δv与应力差ΔPz之间呈正比例关系,即
| $ \Delta v=\alpha \Delta P_z $ | (3) |
式中α为影响系数,本文取分析井点的平均值(约为37m·s-1·MPa-1)。对于地质情况复杂或大尺度区域,可以认为α值随空间位置变化,但式(3)仍然成立。
1.2 地应力与速度换算基于式(3),假设未压实碎屑岩对应的平均纵波速度为v0,可估算地下任意点介质的速度期望值
| $ v=v_0+\alpha P_z $ | (4) |
式中:v为层速度;Pz为垂向地应力。进一步通过
| $ \frac{Z}{v_{\mathrm{a}}}=\frac{T_Z}{2}=\int_0^z \frac{1}{v_0+\alpha P_z} \mathrm{~d} z $ | (5) |
获得平均速度。式中:TZ为深度Z处的地震波双程旅行时;va为0~Z深度段的平均速度。式(5)的离散形式为
| $ \frac{N_Z}{v_{\mathrm{a}}}=\sum\limits_{i=1}^{N_Z} \frac{1}{v_0+\alpha P_{z, i}} $ | (6) |
式中:NZ为地面至深度Z处的样点数;Pz, i为第i个样点处的垂向地应力。
基于式(6)将地应力场转化为平均速度场,可以指导精细构造解释。
2 地应力模拟采用连续介质条件下的有限差分法阐述二维介质地应力场模拟的基本原理及实现过程。
2.1 基本原理一般情况下地下介质同时具有弹性和塑性,在平衡状态下,介质的塑性无法恢复,其应力源于弹性形变,应力和应变之间服从胡克定律。假设介质为各向同性介质,在二维情况下存在以下关系
| $ \left\{\begin{array}{l} \sigma_x=(\lambda+2 \mu) \varepsilon_x+\lambda \varepsilon_z \\ \sigma_z=(\lambda+2 \mu) \varepsilon_z+\lambda \varepsilon_x \\ \tau_{x z}=\mu \varepsilon_{x z} \\ \lambda=K-\frac{4}{3} G \\ \mu=G \end{array}\right. $ | (7) |
式中:λ、μ为拉梅常数;K、G分别为介质的体积模量、剪切模量;σx、σz分别为x、z方向的正应力;τxz为切应力;εx、εz分别为x、z方向的正应变;εxz为切应变。弹性介质在外力作用下会发生位移,其在x、z方向的位移分量分别为u(x, z)和w(x, z)(下文简写为u和w),应变与位移之间有如下关系
| $ \left\{\begin{array}{l} \varepsilon_x=\frac{\partial u}{\partial x} \\ \varepsilon_z=\frac{\partial w}{\partial z} \\ \varepsilon_{x z}=\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x} \end{array}\right. $ | (8) |
另外,在平衡状态下,地下介质受应力、重力共同作用,应力分量满足运动平衡方程
| $ \left\{\begin{array}{l} \frac{\partial \sigma_x}{\partial x}+\frac{\partial \tau_{x z}}{\partial z}=0 \\ \frac{\partial \tau_{x z}}{\partial x}+\frac{\partial \sigma_z}{\partial z}=-\rho g \mathrm{~d} z \end{array}\right. $ | (9) |
根据式(7)~式(9),得到以下二阶偏微分方程组
| $ \left\{\begin{array}{l} (\lambda+2 \mu) \frac{\partial^2 u}{\partial x^2}+\mu \frac{\partial^2 u}{\partial z^2}+(\lambda+\mu) \frac{\partial^2 w}{\partial x \partial z}+ \\ \frac{\partial(\lambda+2 \mu)}{\partial x} \frac{\partial u}{\partial x}+\frac{\partial \lambda}{\partial x} \frac{\partial w}{\partial z}+\frac{\partial \mu}{\partial z}\left(\frac{\partial w}{\partial x}+\frac{\partial u}{\partial z}\right)=0 \\ (\lambda+2 \mu) \frac{\partial^2 w}{\partial z^2}+\mu \frac{\partial^2 w}{\partial x^2}+(\lambda+\mu) \frac{\partial^2 u}{\partial x \partial z}+ \\ \frac{\partial(\lambda+2 \mu)}{\partial z} \frac{\partial w}{\partial z}+\frac{\partial \lambda}{\partial z} \frac{\partial u}{\partial x}+\frac{\partial \mu}{\partial x}\left(\frac{\partial w}{\partial x}+\frac{\partial u}{\partial z}\right)=-\rho g \mathrm{~d} z \end{array}\right. $ | (10) |
求解式(10)得到u和w,依次代入式(8)和式(7)得到地应力场。在地应力场尺度下地下岩石一般为非均质介质,弹性常数的偏导数不为0,因此需要保留式(10)的一阶微分项。
2.2 边界条件基于应力仅受重力和构造影响且处于平衡状态的假设条件,给定模型边界条件如下:
(1) 上边界设定为自由边界,即横向位移、垂向位移的法向导数均赋0,为第二类边界条件;
(2) 左、右边界设定为横向固定边界,即横向位移赋0,垂向位移的法向导数赋0,为混合边界条件;
(3) 下边界设定为垂向固定边界,即垂向位移赋0,横向位移的法向导数赋0,为混合边界条件。
2.3 模型参数建立二维地质模型需要ρ、K、G共3个参数模型,各参数取值参考A区HZ-B1井测井数据(井筒长度接近4km),参数模型建立过程如下。
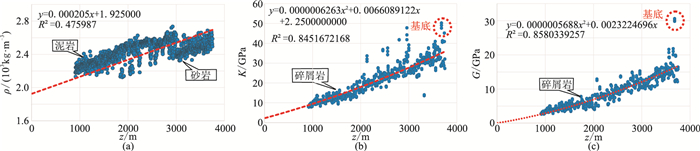
(1) 绘制ρ、K、G随深度变化曲线,并拟合趋势线(图 2)。数据中存在个别异常点,部分可能与特殊岩性有关,但对趋势线影响较小,这里不详细讨论。
|
图 2 HZ-B1井ρ(a)、K(b)、G(c)随深度变化曲线 散点为测井实测点,红色虚线为拟合趋势线 |
(2) 利用拟合趋势线对应关系,给定模型中每个深度点的参数值作为基础参数值。
(3) 基于基础参数设计构造格架,对每套地层在一定范围内给定增量(变化量为幅值的10%)。
(4) 基底为致密岩石,ρ赋常值,K、G分别为50、30GPa。
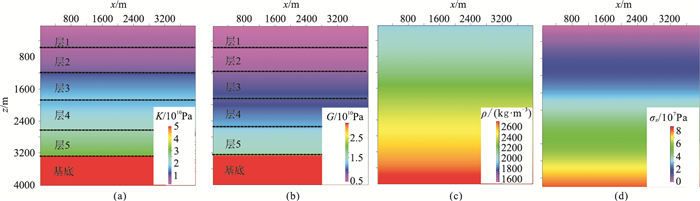
为消除重力变化的影响,所有模型的ρ均采用基础参数值。以水平层状介质为例,建立水平层状地质模型(图 3)。可见,该模型中每一质点上覆地层重力随深度逐渐增加而增大,当埋深为4000m时,重力场最大(约87MPa,图 3d)。
|
图 3 岩石物理参数趋势模型(模型1) (a)K;(b)G;(c)ρ;(d)σz |
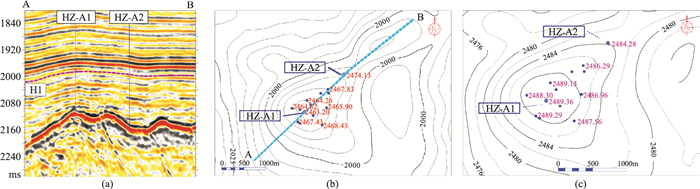
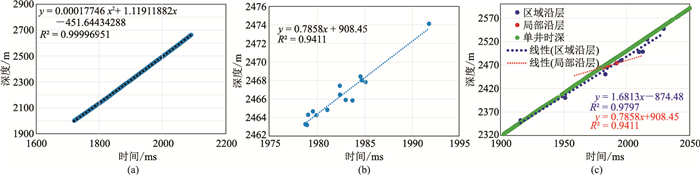
披覆背斜是在古隆起上沉积的地层经压实作用形成的背斜构造,一般由深至浅构造幅度逐渐减小,且倾角与基底相差较大,但走向、倾向基本一致。实钻结果表明,该类构造翼部的地层速度通常小于高点。如HZ-A油田已进入开发后期,井控程度较高,基于井点等T0值(图 4b)与顶面实钻深度(图 4b的蓝色实心点的红色数值)获得各井点位置va(图 4c的紫色数值),可见翼部的井点va显然小于高部位井点,这种速度变化由不同时深关系[20]体现。利用单井时深关系(图 5a,方法1)及H1油藏局部沿层时深关系(图 5b,方法2)预测的构造含油面积分别为1.22(图 6a)、3.95km2(图 6b),对应的预测储量分别为X万m3、2.72X万m3,而根据该油藏实际生产动态反推H1油藏储量约为2.85X万m3,因此方法2的结果与实际更吻合。显然,对于少井油田,由方法1预测的构造含油范围更小、深度预测误差更大,会明显低估油田规模(图 6a、图 6b)。将平面上距油田5km范围内的探井数据纳入方法2统计结果(图 5c,区域时深关系——方法3),预测储量为1.04X万m3(图 6c),与方法1的结果接近,也低估了油田规模。
|
图 4 HZ-A油田过井地震剖面(a)、H1油藏等T0(ms)图(b)及H1油藏沿层va(m·s-1)图(c) |
|
图 5 HZ-A油田时深关系 (a)HZ-AHZ-A1井时深关系(方法1);(b)H1油藏局部沿层时深关系(方法2);(c)H1油藏区域沿层时深关系(方法3) |

|
图 6 不同方法得到的H1油藏深度构造图及深度预测绝对误差 单位:m (a)方法1;(b)方法2;(c)方法3 |
方法1的结果反映了正常压实情况下地层速度与深度的关系,即速度随埋深增加而增大。方法2时深关系斜率更小,反映了局部范围内速度变化较快,构造翼部速度减小。方法3与方法1的时深关系斜率接近,表明较大区域范围内沿层地层速度变化受正常压实规律控制。本文认为局部范围内的速度变化主要受局部应力场变化的影响,且对勘探初期的油气田(特别是海上油气田,常用方法1或方法3计算储量)储量评估影响较大。
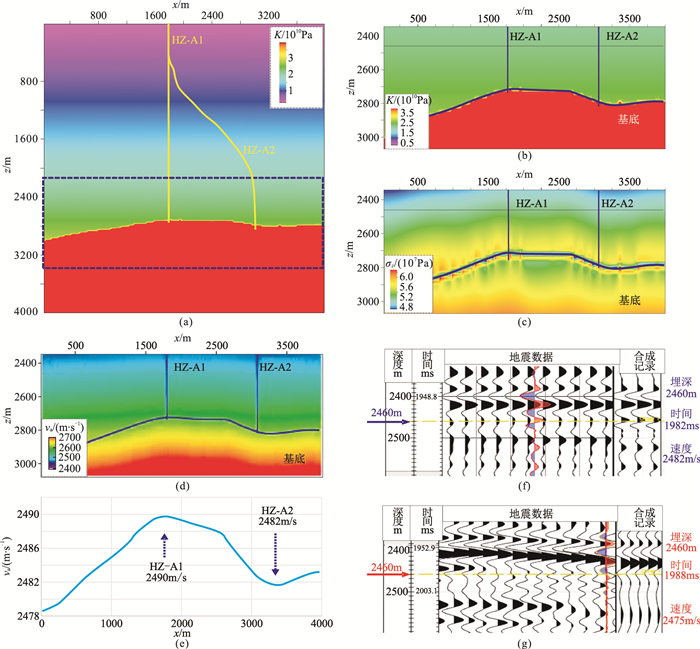
3.1.2 应力模拟分析参考图 4a建立地质模型模拟应力,弹性参数按前文方法给定。图 7为HZ-A油田地应力模拟及速度预测结果。可见:HZ-A1井至HZ-A2井之间基底介质的起伏幅度约为80m(图 7a、图 7b),根据σz局部剖面(图 7c),采用式(4)~式(6)获得va局部剖面(图 7d)及z=2460m的va切片(图 7e),其中HZ-A2井的va较HZ-A1井约小8m/s,与HZ-A1井(图 7f)和HZ-A2井(图 7g)层位标定结果估算的速度差(约7m/s)接近,误差较小。因此,基于应力模拟预测的速度变化与实钻数据基本吻合。
|
图 7 HZ-A油田地应力模拟及速度预测结果 (a)K;(b)K局部(图a蓝色虚线框范围,下同)剖面;(c)σz局部剖面;(d)va局部剖面;(e)图d之z=2460m切片;(f)HZ-A1井层位标定;(g)HZ-A2井层位标定 |
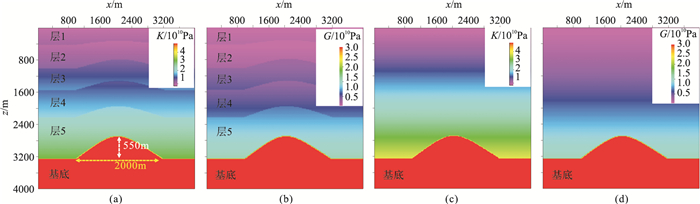
为了解披覆背斜的应力变化特征、控制因素,设计了模型2(图 8a、图 8b)、模型3(图 8c、图 8d)进行地应力模拟。
|
图 8 披覆背斜弹性参数模型 (a)模型2的K;(b)模型2的G;(c)模型3的K;(d)模型3的G 模型2基底存在一个宽度约2000m、高度约550m的古潜山,其上存在5套沉积地层,构造幅度小于潜山,且由深至浅起伏逐渐变缓,弹性参数按前文方法给定。模型3不考虑沉积地层构造变化,即除基底之外,弹性参数均取基础值 |
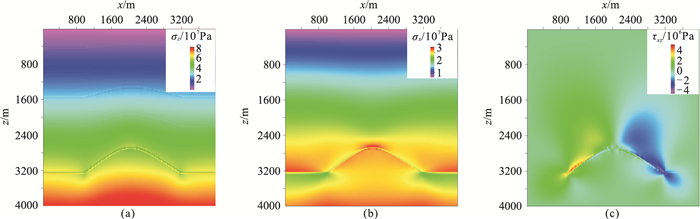
模型2地应力模拟结果(图 9)表明:①σz在构造高点集中且数值较大,在翼部减小且变化较快(图 9a);σz在浅层变化较缓、深层变化较快,在古构造附近较集中。②σx在基底附近集中,在古潜山的高点较大,向翼部快速减小,在外围逐渐增大(图 9b)。③τxz在古潜山翼部集中,最大约为5MPa(图 9c)。
|
图 9 模型2地应力模拟结果 (a)σz;(b)σx;(c)τxz |
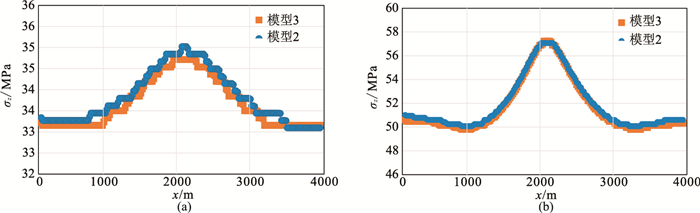
模型3地应力模拟结果与模型2类似,文中不再赘述。图 10为z=1700m、z=2500m的σz切片。由图可见,模型2、模型3的σz横向变化基本一致,说明该类构造局部应力变化主要受古构造控制。综合模型2、模型3的地应力模拟结果可知:古构造高点上覆地层在τxz作用下分担了较多的重力,造成σz较高;古构造翼部上覆地层重力被其他位置地层分担,导致σz降低。
|
图 10 z=1700m(a)、z=2500m(b)的σz切片 |
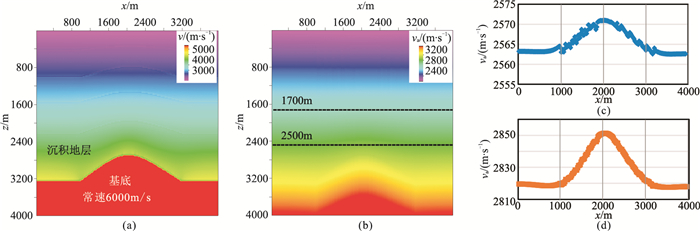
分别利用式(4)和式(6)将σz(图 9a)转化为v(图 11a)和va(图 11b)(v0=2000m/s),并提取z=1700m(图 11c)、z=2500m(图 11d)的va切片。可见,该类构造在地应力影响下导致构造高部位v及va较翼部大,且埋深越大变化越快。
|
图 11 基于图 9a的速度预测 (a)v;(b)va;(c)z=1700m的va切片;(d)z=2500m的va切片 |
除披覆背斜外,发育在正断层上盘的小型背斜构造(滚动背斜或逆牵引背斜)也可能受压实作用影响,文献[15]分析了南海东部该类构造局部范围的速度变化规律,得到如下经验关系式
| $ V_{x, y} \approx V_0-k H D_{\mathrm{F}} \ln \frac{L_{x, y}}{L_0} $ | (11) |
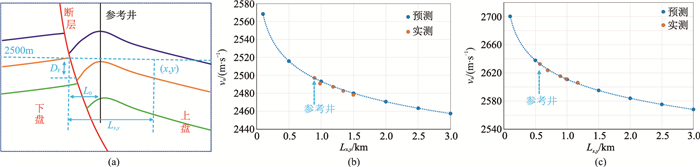
式中:Vx, y为水平方向平均速度;H为深度;V0为参考井平均速度;L0为参考井距断层垂直距离;Lx, y为(x, y)点距断层垂直距离;DF为断层最大断距;k为经验常数(63.38m·s-1·km-2)。参考A区滚动背斜油田HZ-D实钻数据(图 12a),设定H、V0、L0、DF分别为2510m、2497.12m/s、890m、205m以及2990m、2632.62m/s、572m、205m预测Vx, y变化,统计井点位置Vx,y变化并叠合显示(图 12b、图 12c),预测与实钻结果基本一致。可见,在A区断层上盘的Vx, y具有向断层方向增大、埋深越大且越靠近断层变化越快的特点。
|
图 12 HZ-D油田滚动背斜速度变化特征 (a)构造示意图;(b)z=2510m的速度分布;(c)z=2990m的速度分布 |
断层影响致使应力场特征复杂,难以准确获取应力场分布。受技术水平限制,本文基于理想假设条件,采用数值模拟方法分析应力场机理:①剩余应力、区域应力在研究范围对地层的影响是均匀的,故模拟中不予考虑;②正断层引起断层两盘地层之间的剪切应力释放,相互作用减小;③将断层等效为弹性模量小于围岩且具有一定宽度的弹性介质(传递介质);④将整个下盘作传递介质,以突出(滚动背斜发育的)上盘的应力分布特征。
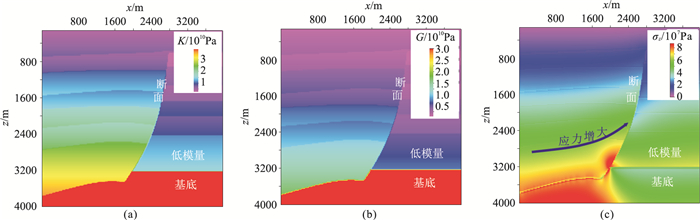
基于上述假设条件建立滚动背斜地质模型(图 13a、图 13b),加载重力后模拟地应力得到σz(图 13c)。结合式(10)、式(12)得到v(图 14a)和va(图 14b),并提取z=2500m(图 14c)和z=3000m(图 14d)的va切片,可读取同样1000m距离内的速度变化量分别约为70m/s(图 14c)和101m/s(图 14d)。可见,正断层上盘断面附近σz快速增大,导致va具有向断层方向增大、埋深越大且越靠近断层变化越快的特点。模拟的速度场特征与实钻数据吻合,表明地应力场可能是滚动背斜速度变化的主要因素之一。
|
图 13 滚动背斜地质模型应力场模拟 (a)K;(b)G;(c)σz 断层由深度500m处断至基底,下盘弹性模量为上盘的0.5倍 |

|
图 14 基于图 13c的速度预测 (a)v;(b)va;(c)z=2500m的va切片;(d)z=3000m的va切片 |
在沉积盆地中应力场与构造运动、压力场、温度场相互作用[21],无论在区域尺度还是局部尺度上准确获取应力场分布均是难点问题[16-18],本文结合地震数据研究地应力,基于以下较理想的假设条件:①不考虑地层异常压力等复杂情况;②针对研究区的拉张应力背景[22],将区域应力场或古应力场视为均匀分布,不影响速度横向变化,因此在构造圈闭尺度上重力可能是局部构造应力变化的主要因素。实例分析表明:在没有异常地层压力情况下,区域沿层时深关系(图 5c)与单井时深关系一致(图 5a);局部沿层时深关系斜率更小(图 5b),即局部存在压实变化,间接说明研究区应力分布满足上述假设。
3.3.2 地层速度的应力影响因素实例分析表明,局部地层速度变化主要取决于应力变化,且是由地层压实作用间接形成的。因此,当地层应力减小时,压实作用减弱,在地层速度减小的同时,储层物性变好(孔隙度增大),反之亦然。HZ-A油田HZ-A2井的地层速度较小,储层有效孔隙度整体较HZ-A1井高(图 15),佐证了上述观点。
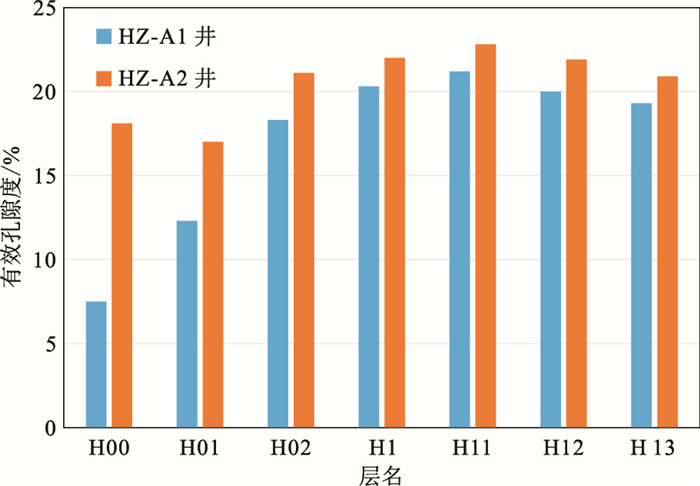
|
图 15 HZ-A油田测井解释有效孔隙度 |
目前人们认为,影响纵波速度横向变化的应力因素主要为地层异常流体压力。本文综合地应力模拟、速度预测及其实例分析认为,在圈闭或局部构造尺度上,应力变化引起的速度变化可能会严重干扰地震资料解释。因此,有必要将与构造有关的应力变化作为一种影响地层速度的因素予以关注。
4 结束语文中利用多口钻井数据,统计、分析了研究区碎屑岩地层在压实作用下速度与垂向地应力之间的关系,获得统计学意义上速度随应力变化的趋势,进一步结合地应力模拟讨论了两种典型局部构造的速度分布特征及成因机理,形成以下认识:
(1) 地应力通过压实作用直接影响地层速度,地应力受局部构造影响而变化较快,进一步影响局部速度分布规律及地震资料的构造解释,应予以关注;
(2) 在古构造影响下,披覆背斜构造翼部地应力相对较小,导致翼部速度较低,实际构造幅度可能小于常见构造预测方法的预测结果;
(3) 在断层影响下,正断层下降盘的构造应力向断层方向增大,导致远离断层速度减小,真实构造高形态与常规方法预测结果出现差异。
尚需指出,本文基于二维模型研究局部地应力对地层速度的影响机理,仅可定性或半定量分析圈闭或局部构造尺度的速度变化,若要获得准确的应力—速度关系,还需考虑三维区域应力、应力变化史等因素。
| [1] |
王生奥, 韩复兴, 孙章庆, 等. 地应力测量及其对油气运移和断层封堵性影响的发展现状与趋势[J]. 地球物理学进展, 2021, 36(2): 675-688. WANG Shengao, HAN Fuxing, SUN Zhangqing, et al. Present situation and the development trend of in-situ stress measurement and its effect on hydrocarbon migration and fault block[J]. Progress in Geophysics, 2021, 36(2): 675-688. |
| [2] |
刘震, 孙迪, 李潍莲, 等. 沉积盆地地层孔隙动力学研究进展[J]. 石油学报, 2016, 37(10): 1193-1215. LIU Zhen, SUN Di, LI Weilian, et al. Advances in research on stratigraphic porodynamics of sedimentary basins[J]. Acta Petrolei Sinica, 2016, 37(10): 1193-1215. DOI:10.7623/syxb201610001 |
| [3] |
王冰, 刘成林, 李宗星, 等. 柴达木盆地东部中生代以来构造应力场及构造演化[J]. 地球科学与环境学报, 2017, 39(1): 83-94. WANG Bing, LIU Chenglin, LI Zongxing, et al. Tectonic-stress field and tectonic evolution in the Eastern Qaidam Basin since Mesozoic[J]. Journal of Earth Sciences and Environment, 2017, 39(1): 83-94. DOI:10.3969/j.issn.1672-6561.2017.01.006 |
| [4] |
张洪, 孟选刚, 邵长金, 等. 水平压裂裂缝形成机理及监测——以七里村油田为例[J]. 岩性油气藏, 2018, 30(5): 138-145. ZHANG Hong, MENG Xuangang, SHAO Changjin, et al. Forming mechanism and monitoring of horizontal hydraulic fracture: A case from Qilicun Oilfield[J]. Lithologic Reservoirs, 2018, 30(5): 138-145. |
| [5] |
张志强, 师永民, 卜向前, 等. 低渗透油藏注水开发中地应力方向变化的研究分析[J]. 北京大学学报(自然科学版), 2016, 52(5): 861-870. ZHANG Zhiqiang, SHI Yongmin, BU Xiangqian, et al. A Study of in-situ stress direction change during waterflooding in the low permeability reservoirs[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2016, 52(5): 861-870. |
| [6] |
DARVISHPOUR A, SEIFABAD M C, WOOD D A, et al. Wellbore stability analysis to determine the safe mud weight window for sandstone layers[J]. Petrole-um Exploration and Development, 2019, 46(5): 1031-1038. DOI:10.1016/S1876-3804(19)60260-0 |
| [7] |
宋杰. 砂岩油藏地应力及岩石力学参数与套管损坏相关性[J]. 地质力学学报, 2014, 20(3): 324-330. SONG Jie. The correlations between geological stress and casing damage and between rock mechanics parameters and casing damage in sandstone reservoir[J]. Journal of Geomechanics, 2014, 20(3): 324-330. DOI:10.3969/j.issn.1006-6616.2014.03.012 |
| [8] |
FILLIPPONE W R. Estimation of formation parameters and the prediction of overpressures from seismic data[C]. SEG Technical Program Expanded Abstracts, 1982, 1: 502-503.
|
| [9] |
SAYERS C M. An introduction to velocity based pore pressure estimation[J]. The Leading Edge, 2006, 25(12): 1496-1500. DOI:10.1190/1.2405335 |
| [10] |
周东红, 熊晓军. 一种高精度地层压力预测方法[J]. 石油地球物理勘探, 2014, 49(2): 344-348. ZHOU Donghong, XIONG Xiaojun. A method for high-precision prediction of formation pressure[J]. Oil Geophysical Prospecting, 2014, 49(2): 344-348. |
| [11] |
DILLEN M W P. Time-Lapse Seismic Monitoring of Subsurface Dynamics[D]. Delft University of Technology, Delft, the Netherlands, 2000.
|
| [12] |
SARKAR D, BAKULIN A, KRANZ R L. An isotropic inversion of seismic data for stressed media: theory and a physical modeling study on Berea sandstone[J]. Geophysics, 2003, 68(2): 690-704. DOI:10.1190/1.1567240 |
| [13] |
马妮, 印兴耀, 孙成禹, 等. 基于方位地震数据的地应力反演方法[J]. 地球物理学报, 2018, 61(2): 697-706. MA Ni, YIN Xingyao, SUN Chengyu, et al. Inversion for crustal stress based on azimuthal seismic data[J]. Chinese Journal of Geophysics, 2018, 61(2): 697-706. |
| [14] |
席道瑛, 徐松林. 岩石物理学基础[M]. 安徽合肥: 中国科学技术大学出版社, 2012.
|
| [15] |
刘振, 李黎, 李伟, 等. 南海东部滚动背斜速度变化特征及勘探、开发启示[J]. 石油地球物理勘探, 2021, 56(5): 1105-1116. LIU Zhen, LI Li, LI Wei, et al. Velocity variation characteristic of rollover anticline and its enlightenment for exploration and development in the eastern South China Sea[J]. Oil Geophysical Prospecting, 2021, 56(5): 1105-1116. |
| [16] |
沈海超, 程远方, 赵益忠, 等. 基于实测数据及数值模拟断层对地应力的影响[J]. 岩石力学与工程学报, 2008, 27(增刊2): 3985-3990. SHEN Haichao, CHENG Yuanfang, ZHAO Yizhong, et al. Study on influence of faults on geostress by measurement data and numerical simulation[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(S2): 3985-3990. |
| [17] |
王学滨, 郭长升, 邓超群. 三种应力的断层阻隔效应的数值模拟研究——以正断层下盘开采为例[J]. 地球物理学进展, 2020, 35(4): 1605-1611. WANG Xuebin, GUO Changsheng, DENG Chaoqun. Numerical modeling of fault barrier effects on three kinds of stresses: A case of footwall mining on the normal fault[J]. Progress in Geophysics, 2020, 35(4): 1605-1611. |
| [18] |
陈洋宏, 万晓燕, 刘志强. 高地应力缓倾软硬互层岩体中隧道底鼓影响因素模拟分析[J]. 铁道建筑, 2020, 60(2): 65-69. CHEN Yanghong, WAN Xiaoyan, LIU Zhiqiang. Simulation analysis of influencing factors of tunnel gloor heave in the gently inclined soft hard interbedded rock under high geostress[J]. Railway Engineering, 2020, 60(2): 65-69. |
| [19] |
陆基孟, 王永刚. 地震勘探原理[M]. 山东东营: 中国石油大学出版社, 2009.
|
| [20] |
彭军, 周家雄, 马光克, 等. 构造成图时深转换方法[J]. 地质与勘探, 2020, 56(2): 411-417. PENG Jun, ZHOU Jiaxiong, MA Guangke, et al. Time-depth conversion methods in preparation of structural maps[J]. Geology and Exploration, 2020, 56(2): 411-417. |
| [21] |
罗晓容. 构造应力超压机制的定量分析[J]. 地球物理学报, 2004, 47(6): 1086-1093. LUO Xiaorong. Quantitative analysis on overpressuring mechanism resulted from tectonic stress[J]. Chinese Journal of Geophysics, 2004, 47(6): 1086-1093. |
| [22] |
王平. 拉张型盆地内的压性剪切断裂: 渤海湾盆地第三系断层力学性质小议[J]. 石油勘探与开发, 1986, 13(3): 1-9. WANG Ping. Compressive shearing faults in tensile type basin: A discussion on the stress properties of the faults in Tertiary formationin Bohaiwan Basin area[J]. Petroleum Exploration and Development, 1986, 13(3): 1-9. |



 刘振, 广东省深圳市南山区后海滨路(深圳湾段)3168号中海油大厦A座南海东部石油研究院,518041。Email:
刘振, 广东省深圳市南山区后海滨路(深圳湾段)3168号中海油大厦A座南海东部石油研究院,518041。Email: 