② 山东省第一地质矿产勘查院, 山东济南 250100;
③ 中国石油塔里木油田分公司, 新疆库尔勒 841000
② Institute of Geology and Mineral Resources of Shandong Province, Jinan, Shandong 250100, China;
③ RIPED Tarim Oilfield Company PetroChina, Korla, Xinjiang 841000, China
随着地震勘探复杂程度的日益增加,对高精度速度建模提出了更高要求。20世纪80年代,Taran-tola[1]提出时间域全波形反演(Full Waveform Inversion,FWI)方法,即通过多次迭代更新,不断降低观测记录与预测记录的残差,实现对地下速度结构的精确反演。FWI充分利用丰富的波形信息,因此它相较于其他方法具有更高的速度建模精度。但FWI存在高度病态的非线性特性[2-3],当预测数据与观测数据对应的反射轴时差大于半个周期时,就会出现“周波跳跃”现象,此时直接求取残差会使反演陷入“局部极值”。精确的初始速度模型能有效缓解“周波跳跃”现象。因此,初始模型精度是FWI的关键。而实际应用中,初始模型往往无法达到较高精度。为了降低FWI对初始模型的依赖性,许多学者做了大量的研究工作。低频信号可反演宏观速度信息,高频信号刻画速度细节,从低频到高频的反演策略能降低FWI对初始速度信息的依赖性。Mora[4]研究表明,大炮检距地震记录中含有丰富的低频信息,有效缓解了“周波跳跃”,从而获得较高精度的反演结果。Bunks等[5]在研究中发现,当低频信息丰富时FWI目标函数的局部极值较少,由此提出多尺度FWI策略,即采用从低频逐渐反演到高频,或从大网格逐渐反演到小网格的多尺度反演方法,可降低FWI对初始速度模型的依赖性。Pratt等[6]提出频率域FWI方法,更易实现从低频到高频的反演策略,但该方法在低频成分不足时,无法恢复模型的长波长结构。Sirgue等[7]利用低通滤波器获得炮记录低频信息,进而构建初始速度场。Chen等[8]提出时间衰减的FWI方法,可降低每一步反演过程中的参数要求,从浅层向深层做反演,较好地缓解“周波跳跃”。黄建平等[9]将频率—波数滤波引入FWI,获得了较好反演效果。
由于地震有效频带宽度和去噪处理的影响,地震数据往往缺失低频信息。Shin等[10-11]提出Laplace域FWI方法,通过加入阻尼波场获得波场的零频分量,该方法能反演出模型的长波长特征,但反演的深度受阻尼系数制约。Wu等[12]认为地震数据本身虽低频成分不足,但其Hilbert包络面中含有丰富低频成分。据此采用包络残差的思想构建目标函数,并推导出对应的梯度公式,其反演结果能恢复地下速度的背景信息,再利用该速度作为常规FWI的初始模型,最终得到较理想反演结果。胡勇等[13]提出解调包络方法重构地震记录中缺失的低频信息,有效降低了FWI的非线性程度。包乾宗等[14]对炮记录做低通滤波,并对滤波结果利用对数包络提取地震数据中的低频成分,反演得到较好的初始模型。Zhang等[15]利用褶积和反褶积方法在重构炮记录低频数据的同时消除了震源函数的影响,一定程度上缓解了低频数据缺失和震源函数不准确导致的“周波跳跃”。Guo等[16]将参考点震源信息引入平面波多尺度反演,控制射线参数,逐步恢复低频数据,反演效果显著提升。
通量校正运输(Flux Corrected Transport,FCT)技术最早由Boris等[17]和Book等[18]提出,用于消除不连续点附近的梯度剧烈变化,后也被应用于地球物理领域。Fei等[19]将FCT思想引入逆时偏移,获得无数值频散的高分辨率逆时偏移结果。吴国忱等[20]用FCT技术做声波方程正演模拟,一定程度上压制了数值频散。陈可洋[21]提出一种优化的FCT正演技术,将对角元素引入波场校正,通过声波方程正演模拟,证明该方法能更好地压制数值频散,提高正演模拟精度。赵威等[22]推导了弹性波方程的FCT公式,将FCT引入弹性波方程正演模拟。Kalita等[23]在FWI中利用FCT对波场进行校正,增加波场的低频成分,降低了FWI对初始模型的依赖性,在模型测试和海上实际资料应用中都取得良好效果。
本文基于FCT理论,推导出基于双对角通量校正(Double Diagonal Flux Corrected Transport,DF)的二维声波方程格式,并进行二维声波方程正演模拟,讨论其重构低频信息的有效性;然后推导基于双对角FCT格式的FWI梯度更新公式,通过动态控制通量校正参数实现多尺度反演。为验证该方法的有效性,采用改进Marmousi模型分别进行不含噪和含噪炮记录的FWI测试。结果表明,该方法能在反演初期构建宏观速度场信息,最终获得高精度反演结果。对于含噪炮记录,也能得到较好反演结果,证实该方法具有一定抗噪性。与其他方法[24]不同,该方法不需修改目标函数,省去了繁冗运算,只需通过简单的波场校正和多尺度反演策略即可获得较好的反演效果。
1 基于双对角通量校正的多尺度全波形反演理论时间域FWI的强非线性,要求在反演初期取得较准确的初始速度信息[25]。该初始速度信息可视为FWI的先验信息。初始速度不准确,易导致“周波跳跃”现象,进而使反演陷入局部极值。为此,提出基于双对角通量校正的多尺度FWI方法,忽略波场的剧烈震荡,拓展波场的低频信息,使目标函数收敛,同时压制噪声和反演假象,恢复模型的大尺度成分。
1.1 FCT基础理论Boris等[17]和Book等[18]提出的FCT理论,在流体力学研究中用于减少数值模拟时产生的高频激荡现象;在地球物理领域主要用于解决波动方程正演模拟中产生的频散。其主要步骤有三:①计算x、z方向的扩散通量;②对所求扩散通量得到的波场进行平滑校正;③进行反扩散通量校正。
二维声波方程可表示为
| $ \left(\Delta^2-\frac{1}{\boldsymbol{v}^2} \frac{\partial^2}{\partial t^2}\right) \boldsymbol{u}=\boldsymbol{f} $ | (1) |
式中:u为时间域波场;v为地震波速度;f为震源项;t为时间。
令$\boldsymbol{S}=\Delta^2-\frac{1}{\boldsymbol{v}^2} \frac{\partial^2}{\partial t^2}$,则式(1)简化为
| $ \boldsymbol{Su}=\boldsymbol{f} $ | (2) |
对式(1)采用时间2阶、空间2N阶差分离散,可得
| $ \begin{aligned} &u_{m, n}^{k+1}=2 u_{m, n}^k-u_{m, n}^{k-1}+ \\ &\frac{v^2 \Delta t^2}{2 \Delta x^2}\left[a_0 u_{m, n}^k+\sum\limits_{i=1}^N a_i\left(u_{m+i, n}^k+u_{m-i, n}^k\right)\right]+ \\ &\frac{v^2 \Delta t^2}{2 \Delta z^2}\left[a_0 u_{m, n}^k+\sum\limits_{i=1}^N a_i\left(u_{m, n+i}^k+u_{m, n-i}^k\right)\right] \end{aligned} $ | (3) |
式中:ai为差分系数;k、m、n分别为t、x、z方向的序号;Δx、Δz为网格间距。
第一步,计算k时刻x、z方向波场的扩散通量
| $ \left\{\begin{array}{l} q_{x, i, j+1 / 2}^k=\xi\left[\left(u_{i+1, j}^k-u_{i, j}^k\right)-\left(u_{i+1, j}^{k-1}-u_{i, j}^{k-1}\right)\right] \\ q_{z, i, j+1 / 2}^k=\xi\left[\left(u_{i, j+1}^k-u_{i, j}^k\right)-\left(u_{i, j+1}^{k-1}-u_{i, j}^{k-1}\right)\right] \end{array}\right. $ | (4) |
式中ξ为扩散通量的校正参数,根据流体力学理论可知,其取值范围是0~1。
第二步,进行波场平滑校正
| $ \begin{aligned} \tilde{u}_{i, j}^{k+1}=& u_{i, j}^{k+1}+\left(q_{x, i+1 / 2, j}^k-q_{x, i-1 / 2, j}^k\right)+\\ &\left(q_{z, i, j+1 / 2}^k-q_{z, i, j-1 / 2}^k\right) \end{aligned} $ | (5) |
第三步,进行反扩散通量计算,求出k+1时刻的x、z方向波场扩散通量
| $ \left\{\begin{array}{l} q_{x, i, j+1 / 2}^{k+1}=\psi\left[\left(u_{i+1, j}^{k+1}-u_{i, j}^{k+1}\right)-\left(u_{i+1, j}^k-u_{i, j}^k\right)\right] \\ q_{z, i, j+1 / 2}^{k+1}=\psi\left[\left(u_{i, j+1}^{k+1}-u_{i, j}^{k+1}\right)-\left(u_{i, j+1}^k-u_{i, j}^k\right)\right] \end{array}\right. $ | (6) |
式中ψ为反扩散通量校正参数。其取值范围也是0~1。之后进行x、z方向的反扩散通量计算
| $ \left\{\begin{array}{l} X_{i+1 / 2, j}=\left(\tilde{u}_{i+1, j}^{k+1}-u_{i+1, j}^k\right)-\left(\tilde{u}_{i, j}^{k+1}-u_{i, j}^k\right) \\ Z_{i, j+1 / 2}=\left(\tilde{u}_{i, j+1}^{k+1}-u_{i, j+1}^k\right)-\left(\tilde{u}_{i, j}^{k+1}-u_{i, j}^k\right) \end{array}\right. $ | (7) |
得到最终的校正波场
| $ \begin{aligned} \hat{u}_{i, j}^{k+1}=& \tilde{u}_{i, j}^{k+1}+\left(X_{i+1 / 2, j}^{\mathrm{c}}-X_{i-1 / 2, j}^{\mathrm{c}}\right)+\\ &\left(Z_{i, j+1 / 2}^{\mathrm{c}}-Z_{i, j-1 / 2}^c\right) \end{aligned} $ | (8) |
式中
| $ \left\{\begin{aligned} X_{i+1 / 2, j}^{\mathrm{c}}=& S_x \max \left\{0, \min \left[S_x X_{i-1 / 2, j}, \right.\right.\\ &\left.\left.\operatorname{abs}\left(q_{x, i+1 / 2, j}^{k+1}\right), S_x X_{i+3 / 2, j}\right]\right\} \\ Z_{i, j+1 / 2}^{\mathrm{c}}=& S_z \max \left\{0, \min \left[S_z Z_{i, j-1 / 2}, \right.\right.\\ &\left.\left.\operatorname{abs}\left(q_{z, i, j+1 / 2}^{k+1}\right), S_z Z_{i, j+3 / 2}\right]\right\} \\ S_x=& \operatorname{sign}\left(q_{x, i+1 / 2, j}^{k+1}\right) \\ S_z=& \operatorname{sign}\left(q_{z, i, j+1 / 2}^{k+1}\right) \end{aligned}\right. $ | (9) |
如式(9)所示,在求取反扩散通量的过程中,需要求取最大值、最小值、绝对值、sign函数,这些函数均为不可微函数,而地震信号却为连续信号。因此,为了在FWI中获得有效的反演梯度,当将FCT引入FWI时,仅对波场进行扩散通量校正,不需考虑上述第三步。
1.2 双对角FCT理论在地震波场数值模拟中,相邻点波场间有很强的相互关系。因此,考虑对角线方向的波场对校正目标点波场的影响,获得最佳波场校正效果,在FCT过程中加入双对角方向波场值,计算各方向扩散通量,双对角通量校正的扩散通量可表示为
| $ \left\{\begin{array}{l} q_{x, i+1 / 2, j}^k=\xi\left[\left(u_{i+1, j}^k-u_{i, j}^k\right)-\left(u_{i+1, j}^{k-1}-u_{i, j}^{k-1}\right)\right] \\ q_{z, i, j+1 / 2}^k=\xi\left[\left(u_{i, j+1}^k-u_{i, j}^k\right)-\left(u_{i, j+1}^{k-1}-u_{i, j}^{k-1}\right)\right] \\ q_{x z 1, i+1 / 2, j+1 / 2}^k=\xi\left[\left(u_{i+1, j+1}^k-u_{i, j}^k\right)-\left(u_{i+1, j+1}^{k-1}-u_{i, j}^{k-1}\right)\right] \\ q_{x z 2, i+1 / 2, j+1 / 2}^k=\xi\left[\left(u_{i, j+1}^k-u_{i+1, j}^k\right)-\left(u_{i, j+1}^{k-1}-u_{i+1, j}^{k-1}\right)\right] \end{array}\right. $ | (10) |
利用式(10)求出不同方向扩散通量,对地震波场进行校正,双对角FCT对应的校正波场表示为
| $ \begin{aligned} \tilde{u}_{i, j}^{k+1 \mathrm{DF}}=& u_{i, j}^{k+1}+\left(q_{x, i+1 / 2, j}^k-q_{x, i-1 / 2, j}^k\right)+\\ &\left(q_{z, i, j+1 / 2}^k-q_{z, i, j-1 / 2}^k\right)+\\ &\left(q_{x z 1, i+1 / 2, j+1 / 2}^k-q_{x z 1, i-1 / 2, j-1 / 2}^k\right)+\\ &\left(q_{x z 2, i-1 / 2, j+1 / 2}^k-q_{x z 2, i+1 / 2, j-1 / 2}^k\right) \end{aligned} $ | (11) |
式中$\tilde{\boldsymbol{u}}^{\mathrm{DF}}$为经双对角通量校正后的波场。若校正参数为0,则不对波场做通量校正。扩散通量的校正参数ξ控制校正后波场的平滑程度。过大的校正参数会导致波场的不稳定,过小则达不到校正效果。
根据文献[23],为确定双对角通量校正参数ξ的取值范围,采用改进Marmousi模型进行二维声波正演模拟。如图 1所示,为便于区分直达波与反射波,在Marmousi模型上层添加速度为2400m/s的地层。改进Marmousi模型的网格横纵数目为596×180,网格间距Δx=Δz=8m,整个模型横向距离为4768m,纵向深度为1440m。震源加载20Hz雷克子波,震源坐标为(2320m,8m),沿地表均匀布设596个检波器,检波器间距为8m,采样间隔为0.5ms,采样时间为2.25s,采用30层PML边界条件对边界反射进行处理。

|
图 1 改进Marmousi模型 |
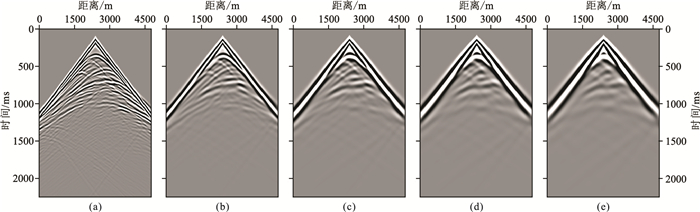
图 2分别表示常规正演与不同校正参数所对应的单炮记录。从图中可看出,随着ξ的逐渐增大单炮记录逐渐平滑。
|
图 2 常规正演与双对角FCT的单炮记录 (a)常规炮记录;(b)ξ=0.02的炮记录;(c)ξ=0.04的炮记录;(d)ξ=0.06的炮记录;(e)ξ=0.08的炮记录 |
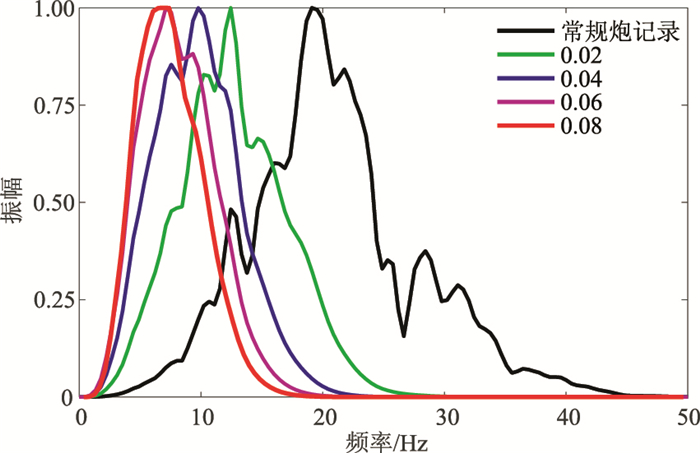
对图 2中各单炮记录抽取2000m处数据,进行频谱分析,频谱分析结果如图 3所示。从图 3可见,采用双对角通量校正技术获得的地震记录信号频率随ξ的增大而降低,而当ξ>0.08时,出现数值不稳定现象,无法获得有效的炮记录,因此,双对角通量校正取ξ=0.08能获得最佳信号拓展低频效果。对FWI而言,低频信息的增多能缓解“周波跳跃”现象,降低反演问题的非线性程度,从而有效地降低FWI对初始模型的依赖性[26]。
|
图 3 常规正演与双对角FCT(ξ=0.02、0.04、0.06、0.08)对应的频谱分析 |
FWI通过优化算法不断迭代降低观测数据与预测数据之间的残差,使反演结果不断逼近真实速度信息,其中求取反演梯度和步长是FWI的关键。
本文采用L2范数作为目标函数
| $ E(v)=\frac{1}{2} \sum\limits_{n_{\mathrm{r}}} \sum\limits_{n_{\mathrm{s}}}\left(\boldsymbol{d}_{\mathrm{cal}}-\boldsymbol{d}_{\mathrm{obs}}\right)^2 $ | (12) |
式中:dobs为观测数据;dcal为预测数据;ns为震源数量;nr为检波点数量。利用Plessix[27]给出的伴随状态法可知L2范数目标函数的反演梯度为
| $ \nabla_v E(v)=-\left(\frac{\partial \boldsymbol{S}}{\partial v} \boldsymbol{u}\right)^{\mathrm{T}}\left(\boldsymbol{S}^{-1}\right)^{\mathrm{T}} \boldsymbol{R}^{\mathrm{T}} \mathtt{δ} \boldsymbol{d} $ | (13) |
将式(2)代入式(13),可得
| $ \nabla_v E(v)=-\frac{2}{v^3}\left(\frac{\partial^2 \boldsymbol{u}}{\partial t^2}\right)^{\mathrm{T}}\left(\boldsymbol{S}^{-1}\right)^{\mathrm{T}} \boldsymbol{R}^{\mathrm{T}} \mathtt{δ} \boldsymbol{d} $ | (14) |
上两式中:S是波场延拓算子;S-1是波场反传算子;R是将波场限制到检波点位置的算子;δd=dcal-dobs为预测数据与观测数据之间的残差,即反演的伴随源。因此,反演梯度为正传波场关于时间上的二阶导数和伴随源的反传波场在时间上的内积。
基于双对角通量校正的多尺度FWI,对正传波场(u)及残差反传波场做双对角通量校正(结果为$\tilde{\boldsymbol{S}}^{-1}$),因此仅需在常规FWI基础上,引入校正后的波场$\tilde{\boldsymbol{u}}^{\mathrm{DF}}$,将式(11)代入式(14),则对应的梯度可表示为
| $ \nabla_v E(v)^{\mathrm{DF}}=-\frac{2}{v^3}\left(\frac{\partial^2 \tilde{\boldsymbol{u}}^{\mathrm{DF}}}{\partial t^2}\right)^{\mathrm{T}}\left(\tilde{\boldsymbol{S}}^{-1}\right)^{\mathrm{T}} \boldsymbol{R}^{\mathrm{T}} \mathtt{δ} \boldsymbol{d}^{\mathrm{DF}} $ | (15) |
本文利用三点抛物插值法求取反演步长,该方法需已知三个步长值α1、α2、α3和三个对应的目标函数值E(α1)、E(α2)、E(α3,一般设α1=0,且满足
| $ \alpha_1<\alpha_2<\alpha_3, E\left(\alpha_1\right)>E\left(\alpha_2\right), E\left(\alpha_2\right)<E\left(\alpha_3\right) $ | (16) |
假设目标函数E(α)与步长满足以下二次关系
| $ \left\{\begin{array}{l} E\left(\alpha_1\right)=a \alpha_1^2+b \alpha_1+c \\ E\left(\alpha_2\right)=a \alpha_2^2+b \alpha_2+c \\ E\left(\alpha_3\right)=a \alpha_3^2+b \alpha_3+c \end{array}\right. $ | (17) |
求取E(α)的极值:E′(α)=2aα+b=0
可知最佳步长为:αopt=-b/2a。根据之前给定的三个试探步长和对应的目标函数值可知最佳步长表达式为
| $ \alpha_{\mathrm{opt}}=\frac{\alpha_3^2\left[E\left(\alpha_2\right)-E\left(\alpha_1\right)\right]-\alpha_2^2\left[E\left(\alpha_3\right)-E\left(\alpha_1\right)\right]}{2 \alpha_3\left[E\left(\alpha_2\right)-E\left(\alpha_1\right)\right]-2 \alpha_2\left[E\left(\alpha_3\right)-E\left(\alpha_1\right)\right]} $ | (18) |
在求得反演梯度和最佳步长后,利用下式更新速度模型
| $ v_n=v_{n-1}+\alpha_{\mathrm{opt}} \nabla_v E(v)^{\mathrm{DF}} $ | (19) |
式中:vn为更新后的速度;vn-1为更新前的速度。
基于双对角通量校正的多尺度FWI过程中针对正传波场和残差的反传波场进行校正,求取梯度,修改过程较为简单,因此能够推广至其他目标函数的反演方法。
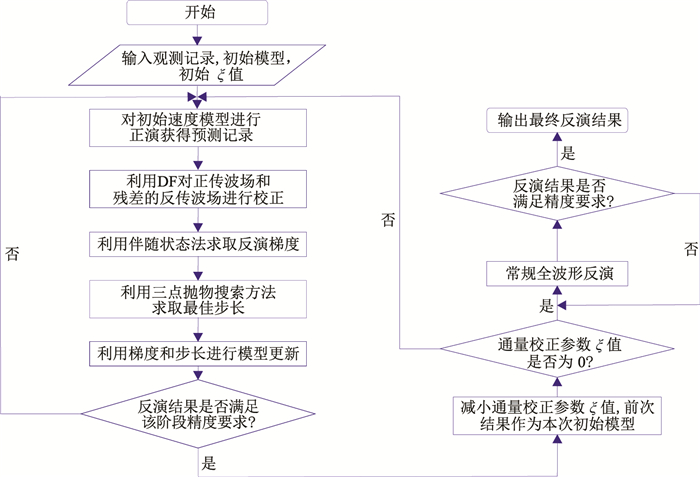
1.4 基于双对角通量校正的多尺度FWI流程本文提出基于双对角通量校正的多尺度FWI方法对现有FWI程序有很强的适应性。此方法不需改变现有FWI框架。在反演算法中仅加入校正后的波场,并且加入校正波场所产生的计算成本对于整个FWI程序而言可忽略不计。较大的ξ能增加波场中的低频成分,减少“周波跳跃”现象,为反演提供一个较平滑的梯度。通过控制通量校正参数ξ的值逐渐减小直至0,实现多尺度反演,上一个ξ值得到的反演结果作为下一个ξ值反演的初始模型,当ξ=0时,进行常规的FWI。在初始模型速度信息不准确的情况下,获得较好的反演结果。
2 模型测试 2.1 不精确初始速度模型条件下的FWI为了测试基于双对角通量校正的多尺度FWI方法的有效性,利用修改Marmousi模型(图 1)进行模型测试。在深度8m处均匀布设60个炮点,炮间距为80m。沿地表均匀布设596个检波器,检波器间距为8m。震源加载20Hz雷克子波,采样间隔为0.5ms,采样时长为2.25s。
|
图 4 基于双对角通量校正的多尺度FWI流程 |
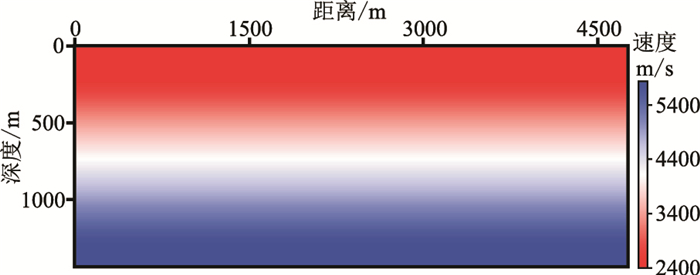
图 5为反演的初始速度模型。从地表到深度240m范围内速度恒为2400m/s,深度240m以下速度开始线性增加,范围是2400~5800m/s,初始模型中不含真实模型的构造信息。
|
图 5 初始速度模型 |
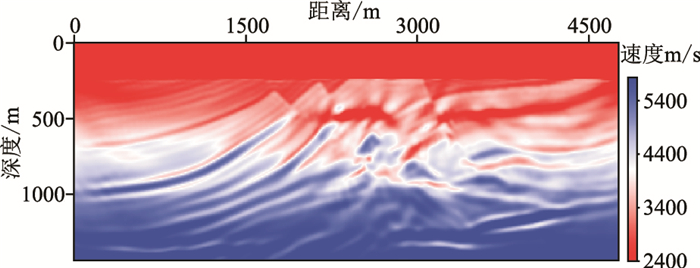
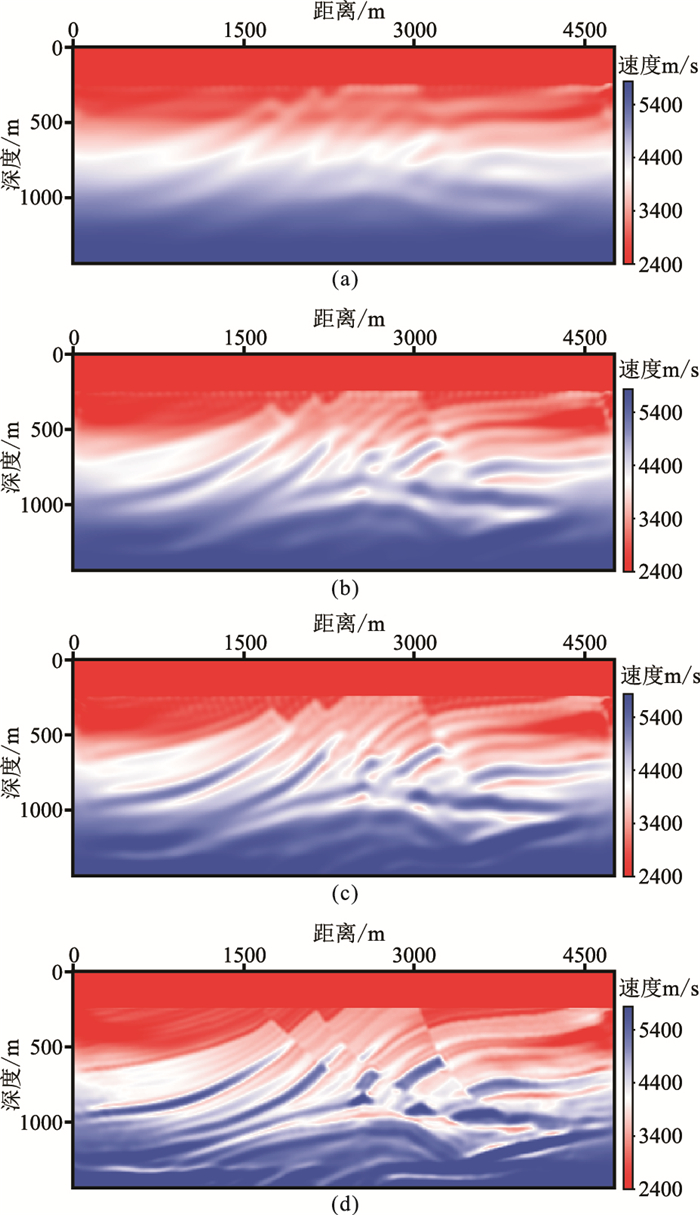
分别用常规FWI(图 6)和基于双对角通量校正的多尺度FWI(图 7)进行90次迭代,得到反演结果。基于双对角通量校正的多尺度FWI是通过逐渐降低ξ值实现多尺度反演。用该方法分别在ξ={0.08、0.06、0.04、0.03、0.02、0.01、0}时迭代{6、8、8、8、10、15、35}次,得到最终结果,其中ξ=0.08、0.04、0.02、0的反演结果如图 7所示。从图 7(基于本文方法反演结果)可看出,随着ξ值的逐渐降低,反演结果逐步向真实模型收敛,反演较好地恢复了模型的长波长速度信息,为ξ=0的常规FWI提供了较准确的初始速度模型。最终ξ=0的反演结果,恢复了真实模型的主要构造,包括三个断层和下部的背斜等细小的构造。而从图 6的常规反演结果可知,常规FWI能反演得到浅层信息,但因初始速度模型不准确,导致深层和细小构造信息的反演不精确。
|
图 6 常规FWI结果 |
|
图 7 不同通量校正参数的反演结果 (a)ξ=0.08;(b)ξ=0.04;(c)ξ=0.02;(d)ξ=0 |
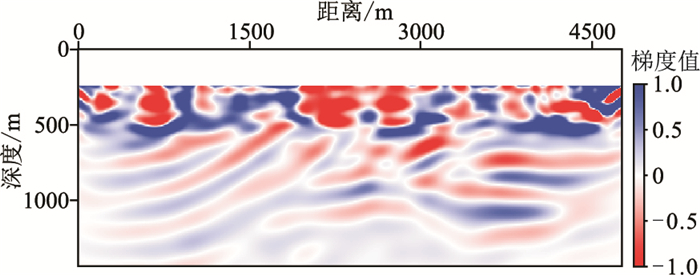
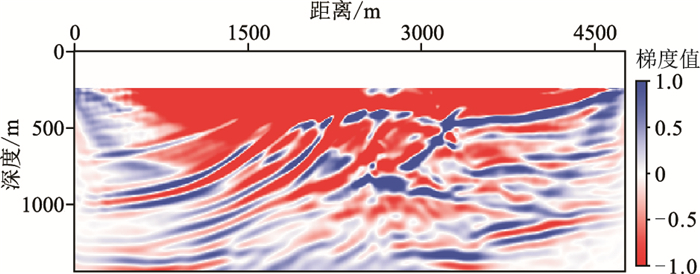
图 8和图 9分别为ξ=0.08和利用常规FWI进行第一次迭代所获得的梯度场,对比可看出本文方法能在反演初期提供一个较平滑的反演梯度,从而恢复了模型长波长信息。
|
图 8 ξ=0.08的第一次迭代梯度 |
|
图 9 常规FWI的第一次迭代梯度剖面 |
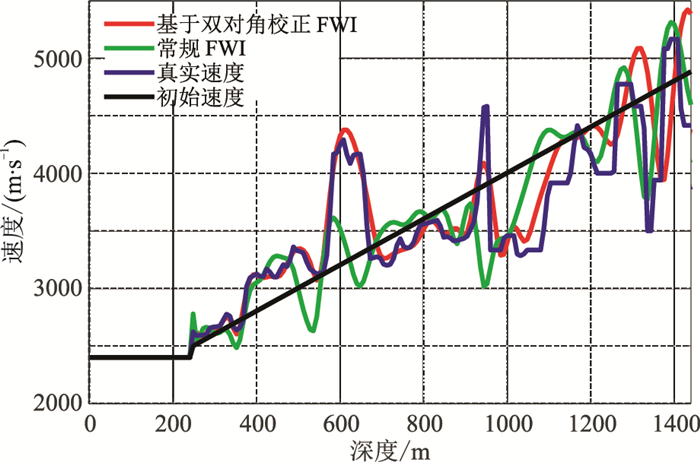
为了定量分析本文方法较常规FWI方法的准确程度,抽取初始模型、真实模型和两种反演方法在1200m和3200m两处最终结果的速度曲线(图 10、图 11)并进行对比。
|
图 10 1200m处的速度曲线对比 |
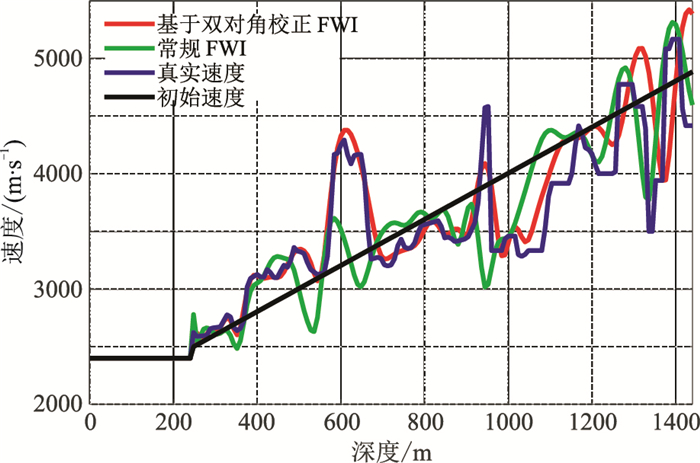
|
图 11 3200m处的速度曲线对比 |
从图 10和图 11可看出,基于本文方法所得到的曲线较常规FWI的更接近于真实速度模型,对速度突变更敏感。将从图 10和图 11两种方法得到的速度曲线分别与真实速度模型求取相关系数。图 10中常规FWI方法的相关系数为0.8216,基于本文方法的相关系数为0.8921。图 11中常规FWI方法的相关系数为0.8723,本文方法的相关系数为0.9365。因此,采用基于双对角通量校正方法进行反演能有效降低FWI问题的非线性程度,降低对初始模型的依赖性,提高反演结果的准确性。
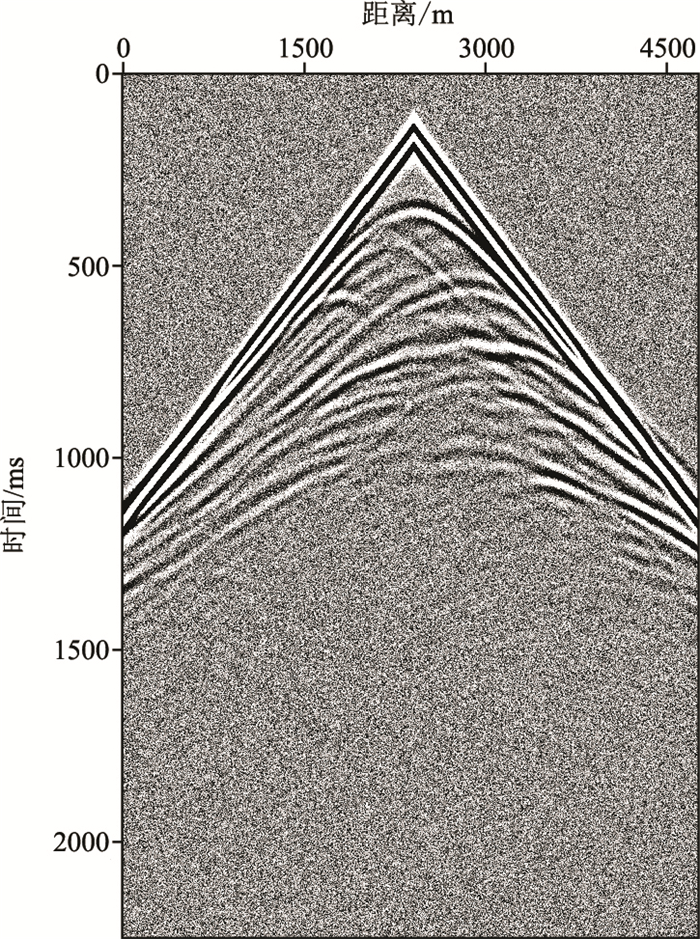
2.2 含噪观测记录的测试实际应用中,在采集原始地震数据时,往往会存在各种不确定干扰因素,使得采集的地震数据含有噪声[28-30]。为了验证基于本文方法的抗噪性,在利用真实模型得到观测炮记录后,再使用SU软件在观测记录中加入能量为原始信号最大振幅4%的高斯噪声,获得加入噪声后的观测记录(图 12)。
|
图 12 加入高斯噪声后的观测记录 |
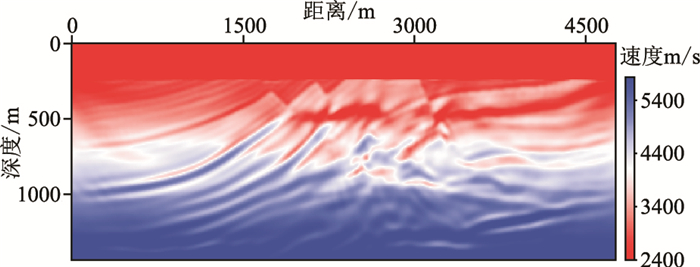
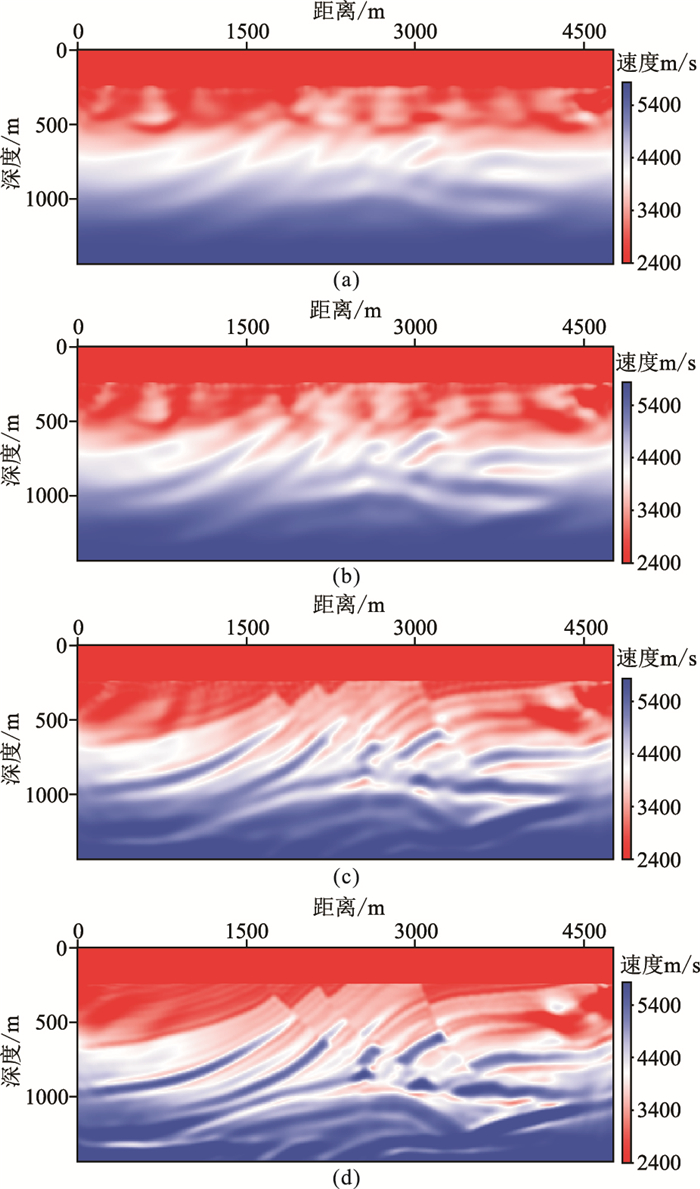
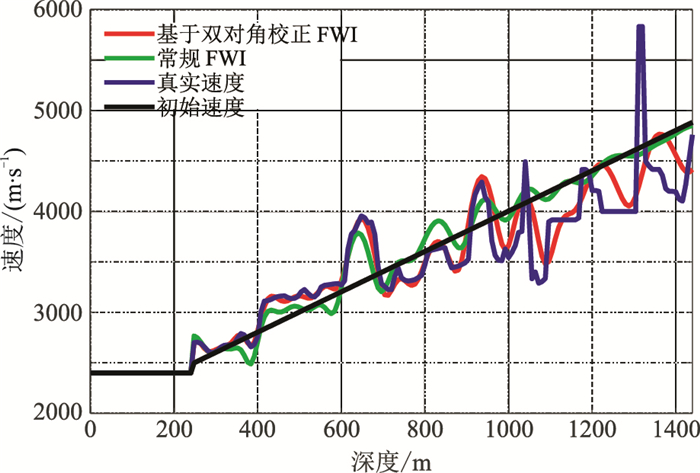
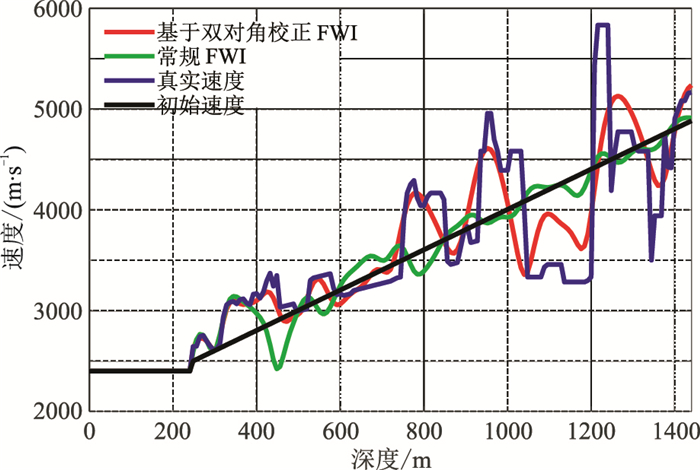
反演参数与无噪声反演相同。常规FWI结果如图 13所示,浅层有效信号较强区域有一定的反演效果,而在深层有效信号被噪声淹没,速度信息无法恢复。基于本文方法结果如图 14所示。对比图 14a~图 14d可看出,在反演初期ξ较大时,噪声对反演结果造成一定的干扰,浅层出现斑状速度异常,但恢复了模型的长波长信息。为下一阶段反演打下良好基础。随着ξ的不断减小,反演结果逐渐收敛于真实模型。为了对比反演结果的准确性,抽取两种方法1600m和3600m处的反演结果(图 15、图 16)进行对比。从图中能看出基于本文方法结果更逼近于真实速度曲线,分别对图 15和图 16两种方法结果与真实速度求取相关系数。图 15中本文方法的相关系数为0.9462,常规FWI的相关系数为0.9204。图 16中本文方法的相关系数为0.9199,常规FWI的相关系数为0.8197。从两种反演结果的相关系数看,当存在一定噪声干扰时,本文方法依旧能获得较好结果,表明它具有一定抗噪优势。
|
图 13 存在高斯噪声情况下的常规全波形反演结果 |
|
图 14 存在高斯噪声时不同通量校正参数的反演结果 Figure 14 (a)ξ=0.08; (b)ξ=0.04; (c)ξ=0.02; (d)ξ=0 |
|
图 15 1600m处的速度曲线对比 |
|
图 16 3600m处的速度曲线对比 |
基于双对角通量校正的多尺度FWI是对常规时间域FWI方法的一种改进。通过从大到小动态调整通量校正参数ξ的取值,实现多尺度的反演策略,获得准确的反演结果。应用该方法进行模型测试、抗噪性分析,得到如下认识和结论:
(1) 采用双对角通量校正方法对波场进行校正,拓展波场中的低频信息,低频信息可靠,能够缓解初始速度模型不精确所导致的“周波跳跃”现象。
(2) 基于双对角通量校正的多尺度FWI较常规FWI而言,在反演初期,能从高频主导的地震记录中提供较平滑的梯度场,恢复长波长速度信息,在初始模型较差时,也能得到高精度FWI结果。
(3) 当地震记录含有一定噪声时,该方法依旧能获得较好反演效果,说明该方法具有较好抗噪性。
(4) 基于本文方法,运用到FCT技术中的扩散和校正技术,对波场进行校正,并不需对目标函数做修改,对现有的FWI程序有较强可移植性。
| [1] |
TARANTOLA A. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics, 1984, 49(8): 1259-1266. DOI:10.1190/1.1441754 |
| [2] |
王庆, 张建中. 时间域地震全波形反演方法进展[J]. 地球物理学进展, 2015, 30(6): 2797-2806. WANG Qing, ZHANG Jianzhong. Progress in the time-domain full waveform inversion[J]. Progress in Geophysics, 2015, 30(6): 2797-2806. |
| [3] |
卞爱飞, 於文辉, 周华伟. 频率域全波形反演方法研究进展[J]. 地球物理学进展, 2010, 25(3): 982-993. BIAN Aifei, YU Wenhui, ZHOU Huawei. Progress in the frequency-domain full waveform inversion method[J]. Progress in Geophysics, 2010, 25(3): 982-993. DOI:10.3969/j.issn.1004-2903.2010.03.037 |
| [4] |
MORA P. Nonlinear two-dimensional elastic inversion of multi offset seismic data[J]. Geophysics, 1987, 52(9): 1211-1228. DOI:10.1190/1.1442384 |
| [5] |
BUNKS C, SALECK F M, ZALESKI S, et al. Multiscale seismic waveform inversion[J]. Geophysics, 1995, 60(5): 1457-1473. DOI:10.1190/1.1443880 |
| [6] |
PRATT R G, SHIN C, HICKS G J. Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion[J]. Geophysical Journal International, 1998, 133(2): 341-362. DOI:10.1046/j.1365-246X.1998.00498.x |
| [7] |
SIRGUE L, PRATT R G. Efficient waveform inversion and imaging: a strategy for selecting temporal frequencies[J]. Geophysics, 2004, 69(1): 231-248. DOI:10.1190/1.1649391 |
| [8] |
CHEN G X, CHEN S C, WU R S. Full waveform inversion in time domain using time-damping filters[C]. SEG Technical Program Expanded Abstracts, 2015, 34: 1451-1455.
|
| [9] |
黄建平, 崔超, 刘梦丽. 基于频率-波数滤波的联合多尺度全波形反演方法及其实现策略[J]. 中国石油大学学报(自然科学版), 2018, 42(2): 50-59. HUANG Jianping, CUI Chao, LIU Mengli. A hybrid multi-scale full waveform inversion method based on frequency-wavenumber filter and its implementation strategies[J]. Journal of China University of Petroleum (Edition of Natural Science), 2018, 42(2): 50-59. DOI:10.3969/j.issn.1673-5005.2018.02.006 |
| [10] |
SHIN C, CHA Y H. Waveform inversion in the Laplace domain[J]. Geophysical Journal International, 2008, 173(3): 922-931. DOI:10.1111/j.1365-246X.2008.03768.x |
| [11] |
SHIN C, HA W. A comparison between the behavior of objective function for waveform inversion in the frequency and Laplace domains[J]. Geophysics, 2008, 73(5): VE119-VE133. DOI:10.1190/1.2953978 |
| [12] |
WU R S, LUO J R, WU B Y. Ultra-low-frequency information in seismic data and envelope inversion[C]. SEG Technical Program Expanded Abstracts, 2013, 32: 3078-3082.
|
| [13] |
胡勇, 韩立国, 许卓, 等. 基于精确震源函数的解调包络多尺度全波形反演[J]. 地球物理学报, 2017, 60(3): 1088-1105. HU Yong, HAN Liguo, XU Zhuo, et al. Demodulation envelope multi-scale full waveform inversion based on precise seismic source function[J]. Chinese Journal of Geophysics, 2017, 60(3): 1088-1105. |
| [14] |
包乾宗, 陈俊霓, 吴浩. 基于地震数据包络的多尺度全波形反演方法[J]. 石油物探, 2018, 57(4): 584-591. BAO Qianzong, CHEN Junni, WU Hao. Multi-scale full waveform inversion based on logarithmic envelope of seismic data[J]. Geophysical Prospecting for Petroleum, 2018, 57(4): 584-591. DOI:10.3969/j.issn.1000-1441.2018.04.012 |
| [15] |
ZHANG Pan, HAN Liguo, ZHOU Yan, et al. Passive-source multitaper-spectral method based low-frequency data reconstruction for active seismic sources[J]. Applied Geophysics, 2015, 12(4): 585-597. DOI:10.1007/s11770-015-0520-2 |
| [16] |
GUO Y D, HUANG J P, CUI C, et al. Direct building background velocity field by plane-wave multi-source multi-scale full-waveform inversion[J]. Exploration Geophysics, 2020, 51(3): 327-340. DOI:10.1080/08123985.2019.1691442 |
| [17] |
BORIS J P, BOOK D L. Flux-corrected transport. Ⅰ: SHASTA, a fluid transport algorithm that works[J]. Journal of Computational Physics, 1973, 11(1): 38-69. DOI:10.1016/0021-9991(73)90147-2 |
| [18] |
BOOK D L, BORIS J P, HAIN K. Flux-corrected transport Ⅱ: Generalizations of the method[J]. Journal of Computational Physics, 1975, 18(3): 248-283. DOI:10.1016/0021-9991(75)90002-9 |
| [19] |
FEI T, LARNER K. Elimination of numerical dispersion in finite-difference modeling and migration by flux-corrected transport[J]. Geophysics, 1995, 60(6): 1830-1842. DOI:10.1190/1.1443915 |
| [20] |
吴国忱, 王华忠. 波场模拟中的数值频散分析与校正策略[J]. 地球物理学进展, 2005, 20(1): 58-65. WU Guochen, WANG Huazhong. Analysis of nume-rical dispersion in wave-field simulation[J]. Progress in Geophysics, 2005, 20(1): 58-65. DOI:10.3969/j.issn.1004-2903.2005.01.012 |
| [21] |
陈可洋. 地震波数值模拟中优化的通量校正传输方法[J]. 内陆地震, 2012, 26(2): 169-179. CHEN Keyang. An optimized flux-corrected transport method in the seismic wave numerical simulation[J]. Inland Earthquake, 2012, 26(2): 169-179. DOI:10.3969/j.issn.1001-8956.2012.02.008 |
| [22] |
赵威, 李伟波, 桂志先, 等. 基于波动方程有限差分数值模拟及FCT消频散分析[J]. 中国锰业, 2018, 36(2): 187-191. ZHAO Wei, LI Weibo, GUI Zhixian, et al. Finite difference numerical simulation of wave equation and its dispersion analysis of FCT elimination[J]. China's Manganese Industry, 2018, 36(2): 187-191. |
| [23] |
KALITA M, ALKHALIFAH T. Flux-corrected transport for full-waveform inversion[J]. Geophysical Journal International, 2019, 217(3): 2147-2164. DOI:10.1093/gji/ggz105 |
| [24] |
张彬彬, 张军华, 吴永亭. 地震数据低频信号保护与拓频方法研究[J]. 地球物理学进展, 2019, 34(3): 1139-1144. ZHANG Binbin, ZHANG Junhua, WU Yongting. Research on protection and extension for seismic low frequencies[J]. Progress in Geophysics, 2019, 34(3): 1139-1144. |
| [25] |
廖建平, 刘和秀, 郑桂娟, 等. 基于多尺度迭代求解三维频率-空间域声波方程的全波形速度反演研究——理论模型[J]. 地球物理学进展, 2014, 29(1): 204-208. LIAO Jianping, LIU Hexiu, ZHENG Guijuan, et al. Research on multiscale iterative three dimensional acoustic wave full waveform velocity inversion in frequency-space domain: theoretical model[J]. Progress in Geophysics, 2014, 29(1): 204-208. |
| [26] |
张军华, 张在金, 张彬彬, 等. 地震低频信号对关键处理环节的影响分析[J]. 石油地球物理勘探, 2016, 51(1): 54-62. ZHANG Junhua, ZHANG Zaijin, ZHANG Binbin, et al. Low frequency signal influences on key seismic data processing procedures[J]. Oil Geophysical Prospecting, 2016, 51(1): 54-62. |
| [27] |
PLESSIX R E. A review of the adjoint-state method for computing the gradient of a functional with geophysical applications[J]. Geophysical Journal International, 2006, 167(2): 495-503. |
| [28] |
邹志辉, 张翊孟, 卞爱飞, 等. 常规检波器低频数据的评价与恢复及其在地震成像中的应用[J]. 石油地球物理勘探, 2016, 51(5): 841-849. ZOU Zhihui, ZHANG Yimeng, BIAN Aifei, et al. Low-frequency evaluation and recovery of conventional geophone data and applications in seismic imaging[J]. Oil Geophysical Prospecting, 2016, 51(5): 841-849. |
| [29] |
芮拥军, 邹志辉, 王胜阁, 等. 基于高低频联测的常规检波器数据低频振幅和相位同时恢复方法[J]. 石油地球物理勘探, 2017, 52(4): 631-643. RUI Yongjun, ZOU Zhihui, WANG Shengge, et al. Low-frequency amplitude and phase simultaneous recovery of conventional geophones data based on joint deployment of high- and low-frequency geophones[J]. Oil Geophysical Prospecting, 2017, 52(4): 631-643. |
| [30] |
廖建平, 王华忠, 李伟波, 等. 三维微分方程滤波法及线性噪声压制[J]. 石油物探, 2007, 46(6): 550-556. LIAO Jianping, WANG Huazhong, LI Weibo, et al. 3D partial differential equation filtering and linear noise attenuation[J]. Geophysical Prospecting for Petroleum, 2007, 46(6): 550-556. |



 黄建平, 山东省青岛市经济技术开发区长江西路66号中国石油大学(华东)地球科学与技术学院,266580。Email:
黄建平, 山东省青岛市经济技术开发区长江西路66号中国石油大学(华东)地球科学与技术学院,266580。Email: