全波形反演(Full Waveform Inversion,FWI)充分利用地震记录中包含的丰富信息,可获得更精细的深度域速度模型,成为油气勘探领域的研究热点[1]。20世纪80年代,Lailly[2]和Tarantola[3]率先在时域引入基于广义最小二乘优化原理的FWI理论与方法,其开创性的工作对反演理论的发展产生了重要而深远的影响。随后,Pratt[4]将FWI推广到频率域,并提出由低频到高频的反演格式,只需要几个离散频率就能获得较高精度的反演结果。然而,由于观测数据中低频信息的缺失和实际观测中大量噪声的存在,FWI通常是严重不适定问题,主要表现为多解性和对噪声的敏感性[5-7]。为此,必须采用有效的正则化技术求取其稳定的近似解。
经典的Tikhonov正则化[8]选取L2范数作为罚项,其作用在于通过压制大的分量而产生光滑的近似解。全变差(Total Variation,TV)正则化[9]能在抑制噪声的同时保持尖锐边缘。近十几年来,该方法已广泛应用于求解地球物理反问题,实现了对层间尖锐界面的有效识别,以及高对比度盐体的有效成像[10-11]。但TV正则化在反演过程中会导致图像结构细节信息的丢失,并产生“阶梯伪影”[12-13]。
由于在复杂地质背景下,速度模型中可能同时包含平滑结构和锐利边界,单一的正则化技术很难提供较好的反演结果。为此,Lin等[14]建立了基于修正TV正则化的FWI模型,将FWI分解为两个交错的子问题:一是具有Tikhonov正则化项的传统FWI问题,二是基于一阶TV正则化去噪问题,得到较理想的反演结果,但阶梯状伪影依然存在。Peng等[15]将TV正则化与箱约束相结合,提升模型的物理可解释性,并提出改善反演精度的自适应原始对偶梯度法。Aghamiry等[16]将TV正则化项与Tikhonov正则化项加权耦合,并利用交替方向乘子法求解相应的目标泛函,数值试算结果表明所提耦合方法优于单一正则化方法。
本文将速度模型扰动量的L2范数与TV正则化相融合,构建能克服FWI的不适定性的优化目标泛函,针对目标泛函的不可微性,提出修正正交有限内存拟牛顿算法(modified Orthant-Wise Limited- Memory Quasi-Newton,mOWL-QN)进行迭代计算;该算法基于有限内存拟牛顿方法[17],在下降的过程中引入正交函数寻找下降方向以避免不可微项的求导。将mOWL-QN算法引入FWI,不仅提高了FWI的计算效率,而且可引导反演结果更贴近真实速度。基于具有复杂构造的修正Marmousi模型和BG Compass模型的数值试验,且与无正则化FWI及邻近有限内存拟牛顿(proximal Limited-memory Broyden-Fletcher-Goldfarb-Shanno,proxL-BFGS)方法[18]进行比较,验证了mOWL-QN算法求解混合正则化FWI的有效性。
1 原理方法 1.1 频域FWI的混合正则化模型从观测数据与计算数据相吻合的角度出发,FWI可归结为如下的非线性二次优化问题
| $ \underset{\mathit{\boldsymbol{m}}}{\arg \min }\left[\frac{1}{2}\left\|\boldsymbol{d}_{\mathrm{obs}}-\boldsymbol{d}_{\mathrm{cal}}(\boldsymbol{m})\right\|_2^2\right] $ | (1) |
式中:m∈Rn是离散网格上的速度模型向量;||·||2表示L2范数。对于频率ω,计算数据dcal=P×Aω(m)-1Q。其中:$A_\omega(\boldsymbol{m})=\frac{\omega^2}{\mathit{\boldsymbol{m}}^2}+\nabla^2$,是一个具有PML边界条件的离散Helmholtz算子;Q代表震源;P是将Helmholtz方程的解投影到观测位置的投影算子。
为了克服FWI的不适定性,获得一个既包含光滑内部结构,又具有锐利边缘的速度模型,将Tikho-nov与TV正则化项线性加权后添入式(1),得到
| $ \begin{aligned} \underset{\mathit{\boldsymbol{m}}}{\arg \min }\{& \frac{1}{2}\left\|\boldsymbol{d}_{\mathrm{obs}}-\boldsymbol{d}_{\mathrm{cal}}(\boldsymbol{m})\right\|_2^2 \\ &\left.+\frac{\lambda}{2}\|\mathtt{δ} \boldsymbol{m}\|_2^2+\beta\|\nabla(\mathtt{δ} \boldsymbol{m})\|_1\right\} \end{aligned} $ | (2) |
式中:λ和β均大于0,为正则化参数;δm=m-m0,其中m0是对真实解的预先猜测,也可作为优化算法的初值,||·||1表示L1范数。
求解式(2)的主要计算困难在于L1范数的不可微性。为了解决这一问题,Gong等[19]提出mOWL-QN算法。mOWL-QN方法先利用TV正则项内变量的每个坐标都不变号的特点计算正则项的导数;再使用当前正交对象所求得的导数构造一个搜索方向,并将其限制在该正交对象上[20]。mOWL-QN算法在高效计算不可微优化问题的同时继承了LBFGS方法求解大规模问题的优点,所以本文利用mOWL- QN算法求解式(2),以达到权衡计算效率与反演精度的目的。
1.2 mOWL-QN算法首先,给出mOWL-QN算法中必需的正交函数π(x,y)的定义[21]
| $ \pi(x, y)= \begin{cases}x & \operatorname{sign}(x)=\operatorname{sign}(y) \\ 0 & \text { 其他 }\end{cases} $ |
函数π(x,y)主要目的是限制x与y的象限相同;sign(·)为符号函数。
为了简化符号,令
| $ f(\boldsymbol{m})=\frac{1}{2}\left\|\boldsymbol{d}_{\mathrm{obs}}-\boldsymbol{d}_{\mathrm{cal}}(\boldsymbol{m})\right\|_2^2+\frac{\lambda}{2}\|\mathtt{δ} \boldsymbol{m}\|_2^2 $ |
将式(2)简写成
| $ \underset{\mathit{\boldsymbol{m}}}{\arg \min }\left\{f(\boldsymbol{m})+\beta\|\nabla(\mathtt{δ} \boldsymbol{m})\|_1\right\} $ | (3) |
利用伪梯度的定义[19],式(3)中目标函数Φ(m)=f(m)+β||▽(δm)||1在第i处的伪梯度
| $ ◇ \boldsymbol{g}\left(m_i\right)= \begin{cases}g_i(\boldsymbol{m})+\beta w_i & \mathtt{δ} m_i>0 \text { 或 } \mathtt{δ} m_i=0 \\ & \text { 且 } g_i(m)+\beta w_i<0 \\ g_i(\boldsymbol{m})-\beta w_i & \mathtt{δ} m_i<0 \text { 或 } \mathtt{δ} m_i=0 \\ & \text { 且 } g_i(m)-\beta w_i>0 \\ 0 & \text { 其他 }\end{cases} $ |
式中:g(m)为f(m)的梯度,即gi(m)=∂f/∂mi,mi表示参数m的第i个元素;wi表示δm向量化后的第i个元素。
对于大规模非线性优化问题,LBFGS方法常被用来计算近似的Hessian阵的逆。其主要思想是通过存储向量的方式避免存储大量的矩阵,提升计算效率。为此,式(3)的下降方向为
| $ \boldsymbol{d}^k=-\boldsymbol{H}^k \diamond \boldsymbol{g}\left(\boldsymbol{m}^k\right) $ | (4) |
式中:Hk是由LBFGS方法计算的目标泛函Φ(m)的Hessian阵的逆;◇g(mk)是目标函数的伪梯度;k为迭代次数。同时,将正交函数作用在下降方向dk上,得到新的下降方向
| $ \boldsymbol{p}^k=\pi\left[\boldsymbol{d}^k, -◇\boldsymbol{g}\left(\boldsymbol{m}^k\right)\right] $ |
并利用正交函数π(x,y)对m进行更新,得到
| $ \boldsymbol{m}^{k+1}=\pi\left(\boldsymbol{m}^k+\alpha_1 \boldsymbol{p}^k, \boldsymbol{\xi}^k\right) $ | (5) |
式中:mik≠0时,ξik=sign(mik);mik=0时,ξik=sign-◇g(mik);步长α1满足Wolfe条件。
但由于式(3)中的不可微项的存在,导致证明式(5)的收敛性存在一定困难。因此,Gong等[19]提出mOWL-QN算法,主要的修正体现在原算法中加入最速下降步。最速下降方向是将梯度的负方向作为模型下一步的迭代方向,并且利用线搜索方法寻找合适的步长。在最速下降法中,对mk+1进行迭代更新的表达式为
| $ \boldsymbol{m}^{k+1}=\boldsymbol{m}^k-\alpha_2 \diamond \boldsymbol{g}\left(\boldsymbol{m}^k\right) $ | (6) |
式中:步长α2利用如下线搜索准则进行更新:假设存在常数μ1, μ2∈(0, 1),α0>0以及i=0, 1, …,则找到最小的i,使得α2=α0μ1i且α2满足下式[21]
| $ f\left[\boldsymbol{m}^k\left(\alpha_2\right)\right] \leqslant f\left(\boldsymbol{m}^k\right)-\frac{\mu_2}{2 \alpha_2}\left\|\boldsymbol{m}^k\left(\alpha_2\right)-\boldsymbol{m}^k\right\| $ |
在迭代中,mk+1的更新策略是由集合Ik决定的。集合Ik定义如下
| $ \begin{aligned} \boldsymbol{I}^k &=\left\{i=(1, 2, \cdots, n): 0<\left|m_i^k\right|\right.\\ &\left.\leqslant \min \left(\left\|-\diamond \boldsymbol{g}\left(\boldsymbol{m}^k\right)\right\|, \varepsilon_1\right), -m_i^k \diamond \boldsymbol{g}\left(m_i^k\right)<0\right\} \end{aligned} $ |
式中ε1是足够小的正数。如果集合Ik是空集,那么mk+1=π(mk+αpk,ξk);否则,利用最速下降法式(6)进行更新。
综上,mOWL-QN算法的主要步骤是先给出初始值m0,α0,误差限ε1,最大迭代次数Mmax以及LBFGS算法的初始矩阵S0、Y0,计算伪梯度◇g(mi)以及集合Ik。其次,判断集合Ik是否为空集,若Ik=∅,则利用式(5)更新m;否则,mk+1=mk-α2◇g(mk);然后更新Sk、Yk,令k←k+1,此时判断是否满足迭代停止准则,若不满足,则继续进行循环;否则输出反演结果。其中迭代停止准则为:$\left\|\boldsymbol{m}^{k+1}-\boldsymbol{m}^k\right\|_2^2 /\left\|\boldsymbol{m}^k\right\|_2^2 \leqslant \varepsilon_1$或达到最大迭代次数时,迭代停止。mOWL-QN算法的伪代码归纳在表 1中。
|
|
表 1 mOWL-QN算法的伪代码 |
使用传统LBFGS算法求解式(3)具有挑战性,其主要原因在于TV正则化的不可微性。因此,本文选择proxL-BFGS作为对比算法求解式(3)。该算法将传统LBFGS与邻近算子结合,克服目标泛函的不可微性,得到反演模型参数的近似解。
凸泛函G(m)=β||▽(δm)||1的邻近算子定义为
| $ \operatorname{prox}_G(\boldsymbol{z})=\arg \min \left[G(\boldsymbol{m})+\frac{1}{2}\|\boldsymbol{z}-\boldsymbol{m}\|_2^2\right] $ | (7) |
根据凸优化的一阶条件可得式(7)的最优解
| $ \operatorname{prox}_G(\boldsymbol{z})=[\boldsymbol{I}+\partial G(\boldsymbol{m})]^{-1}(\boldsymbol{z}) $ | (8) |
式中:∂G(m)为凸泛函G(m)的次梯度;I为单位矩阵。
在LBFGS算法中,迭代更新公式为
| $ \boldsymbol{m}^{k+1}=\boldsymbol{m}^k-\alpha^k \boldsymbol{H}_{\mathrm{L}}^k \boldsymbol{g}\left(\boldsymbol{m}^k\right) $ | (9) |
式中步长α>0满足Wolfe条件,HLk是Hessian阵的逆。
下面给出利用邻近有限内存拟牛顿算法(表 2)的伪代码。
|
|
表 2 proxL-BFGS算法的伪代码 |
为了保证对比实验的公平性,上述算法步骤中的参数与本文所提算法mOWL-QN的参数设置保持一致。
2 数值算例数值试算基于具有复杂构造的修正Marmousi模型及BG Compass模型进行。考虑到算法的实用性,实验数据中添加了1%的高斯噪声。本文选择结构相似性指数(SSIM)、峰值信噪比(PSNR)及均方根误差(RMSE)三项指标对算法进行评估。其中:SSIM和PSNR越高表明反演结果越接近真实值;RMSE越低表明反演结果与真实值之间的误差越小。为了保证实验的公平性,所有实验均使用Matlab 2018a进行反演试算,并且在内存为64GB、八核处理器的计算机环境中运行。
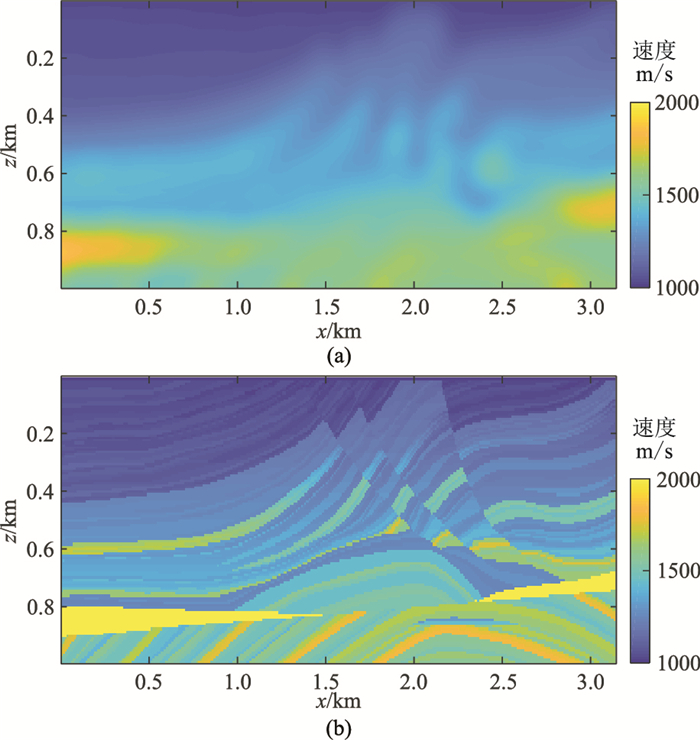
2.1 修正Marmousi模型首先,对修正Marmousi模型进行试算,其真实模型如图 1b所示,尺寸为Nz×Nx=260×891。本文选择平滑处理后的初始模型(图 1a),并将网格间距设置为3.8m。在模型的表层放置77个点源及231个接收器(接收点源发射的完整数据)。为了避免周期跳跃性,在[2Hz,26Hz]频率范围选取12个重复频段进行反演。实验中,最大迭代次数为60,正则化参数分别为λ=10-3、β=10-6,设置误差限ε1=ε2=10-7,选择α0=1作为初始步长。
|
图 1 修正Marmousi模型 (a)初始模型;(b)真实模型 |
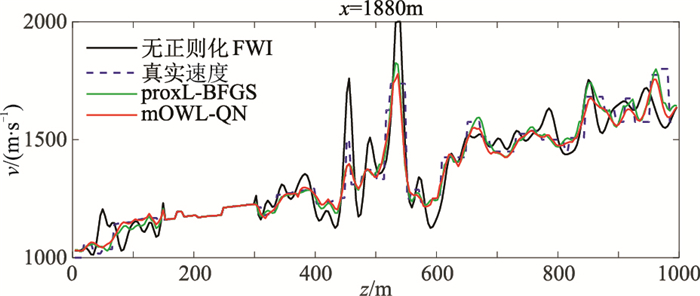
三种算法得到的反演结果如图 2所示。仔细观察对比这三种反演结果,无正则化FWI的反演结果(图 2a)存在较多伪影且无法恢复模型的精细结构;本文算法(图 2c)更好地保留了地质模型的细节;与proxL-BFGS算法(图 2b)相比,本文算法还可抑制噪声的影响,且只存在较少伪影。图 3展示的是三种算法得到的反演结果在x=1880m处的速度曲线。虽然proxL-BFGS算法与mOWL-QN算法的反演速度模型都很贴合真实速度,但mOWL-QN算法得到的反演速度(红色实线)与模型真实速度(蓝色虚线)拟合效果更好。算法的评估指标结果如表 3所示,本文mOWL-QN算法以少量的计算时间增加(比无正则化FWI多耗时约14%)在三种定量评估数值上表现最佳,且全方面完胜proxL-BFGS算法。

|
图 2 修正Marmousi模型的三种方法反演结果 (a)无正则化FWI;(b)proxL-BFGS;(c)mOWL-QN |
|
图 3 修正Marmousi模型的三种方法 反演的纵向速度曲线对比 |
|
|
表 3 修正Marmousi模型三种方法反演的指标及耗时统计 |
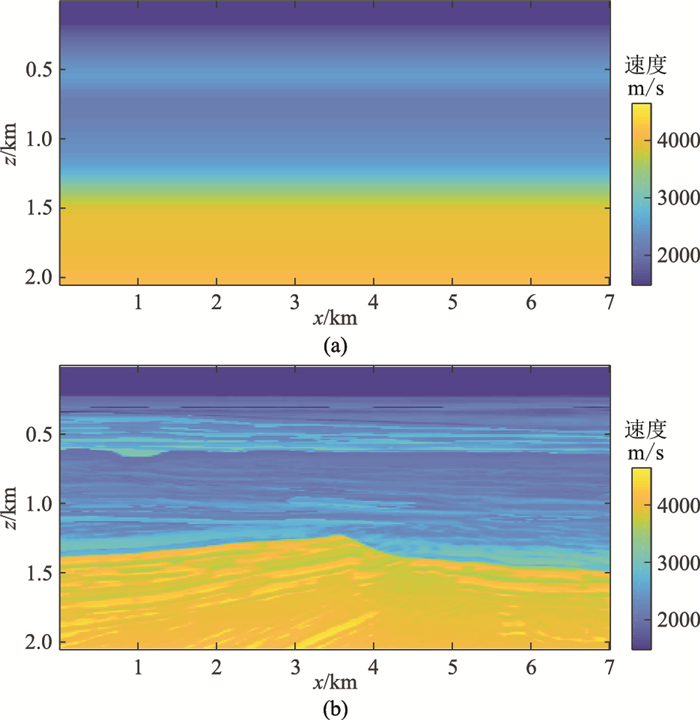
再对BG Compass模型进行试算。设定网格间隔为10m,真实模型网格点数为205×701(图 4b);无任何横向信息的初始模型如图 4a。在靠近地表的水平面上放置64个点源和192个接收器。同样选取12个重复频段进行反演,频率范围是2.6~28Hz。在实验中,设置正则化参数λ=10-2、β=10-5,其他参数同前述实验。
|
图 4 BG Compass模型 (a)初始模型;(b)真实模型 |
|
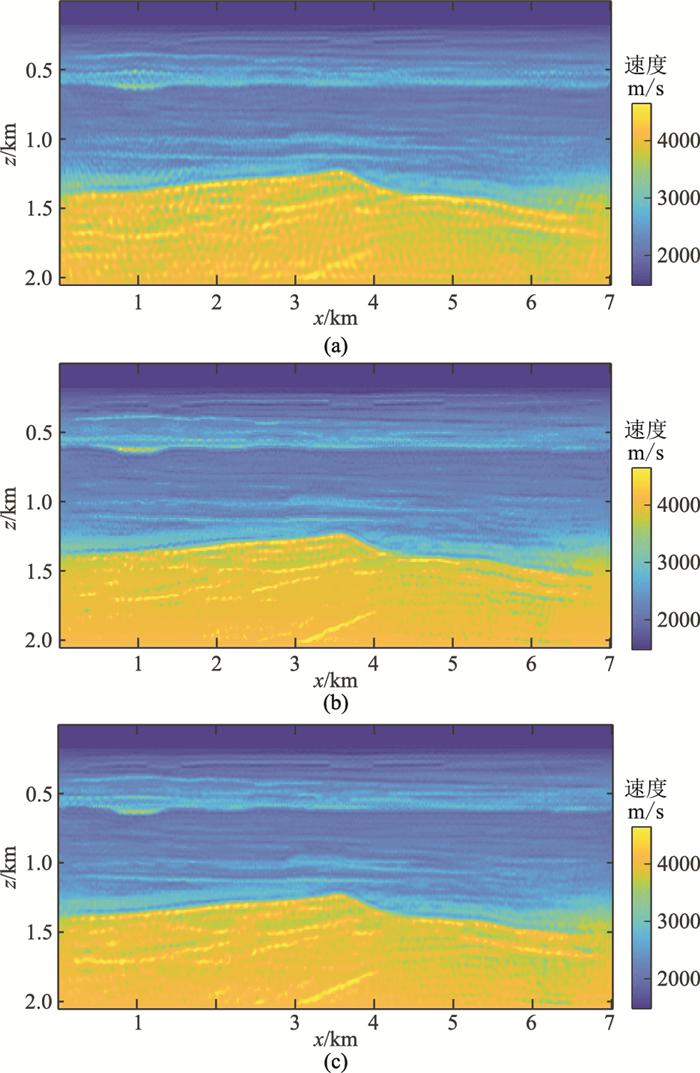
图 5 BG Compass模型的三种方法反演结果 (a)无正则化FWI;(b) proxL-BFGS;(c) mOWL-QN |
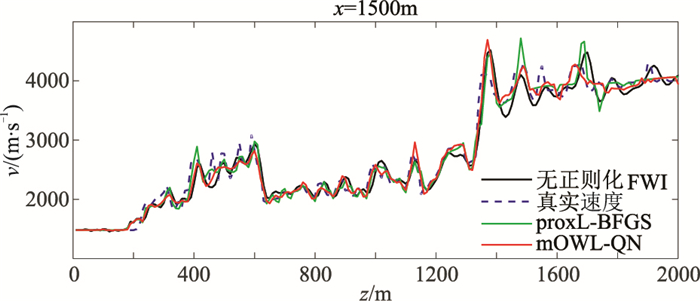
最终反演结果如图 5所示,三种算法都可得到较满意的反演效果。mOWL-QN算法(图 5c)能更多地保留地质结构细节,具有更好的视觉效果。图 6为三种算法所得反演结果在x=1500m处的速度曲线。可以看出,相对于无正则化FWI及proxL- BFGS算法,本文算法的拟合程度更高,尤其在模型的下半部分,mOWL-QN算法得到的反演速度(红色实线)更接近模型的真实速度(蓝色虚线)。表 4展示的评估指标统计结果表明本文算法在定量分析上具有优越性。该实验结论与前述算例保持一致,再次验证了mOWL-QN算法的有效性。
|
图 6 BG Compass模型三种方法反演的纵向速度曲线对比 |
|
|
表 4 BG Compass模型三种方法反演的评价指标及耗时统计 |
FWI是一种非线性的、不适定的优化问题,通常使用正则化技术缓解其不适定性。应用单一的Tikhonov正则化会产生过度光滑的解,将Tikhonov正则化与TV正则化相融合,能有效改进反演成像的效果。为了克服混合正则化目标泛函的不可微性,本文提出mOWL-QN反演优化迭代算法,该算法继承了拟牛顿方法优点,且在一定程度上提升了大规模反演问题的计算效率,得到高分辨率成像结果。基于修正Marmousi模型和BG Compass模型进行的数值仿真和对比试验,验证了所提方法的有效性。
| [1] |
VIRIEUX J, OPERTO S. An overview of full-waveform inversion in exploration geophysics[J]. Geophysics, 2009, 74(6): WCC1-WCC26. DOI:10.1190/1.3238367 |
| [2] |
LAILLY P. The seismic inverse problem as a sequence of before stack migrations[C]. Theory and Applications, Society for Industrial and Applied Mathematics, 1983, 206-220.
|
| [3] |
TARANTOLA A. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics, 1984, 49(8): 1259-1266. DOI:10.1190/1.1441754 |
| [4] |
PRATT R G. Seismic waveform inversion in the frequency domain: Part 1, theory and verification in a physical scale model[J]. Geophysics, 1999, 64(3): 888-901. DOI:10.1190/1.1444597 |
| [5] |
张子良, 李振春, 张凯, 等. 地质模型约束的全波形速度建模反演及在复杂断块区的应用[J]. 石油地球物理勘探, 2020, 55(3): 599-606. ZHANG Ziliang, LI Zhenchun, ZHANG Kai, et al. Research of geological model-constrained FWI and application in complex fault-block zones[J]. Oil Geophysical Prospecting, 2020, 55(3): 599-606. |
| [6] |
杜泽源, 吴国忱, 王玉梅. 基于测井约束的地震全波形反演方法[J]. 石油地球物理勘探, 2017, 52(6): 1184-1192. DU Zeyuan, WU Guochen, WANG Yumei. Full waveform inversion based on well logging data constraint[J]. Oil Geophysical Prospecting, 2017, 52(6): 1184-1192. |
| [7] |
王豆豆, 王守东, 邹少峰, 等. 基于混合快速共轭梯度法的有限差分对比源反演[J]. 石油地球物理勘探, 2020, 55(2): 351-359. WANG Doudou, WANG Shoudong, ZOU Shaofeng, et al. Finite difference comparison source inversion based on hybrid fast conjugate gradient method[J]. Oil Geophysical Prospecting, 2020, 55(2): 351-359. |
| [8] |
TIKHONOV A N, GONCHARSKY A V, STEPANOV V V, et al. Numerical Methods for the Solution of Ill-Posed Problems[M]. Kluwer Acade-mic Publishers, Boston, 1995.
|
| [9] |
RUDIN L I, OSHER S, FATEMI E. Nonlinear total variation based noise removal algorithms[J]. Physica D: Nonlinear Phenomena, 1992, 60(1-4): 259-268. DOI:10.1016/0167-2789(92)90242-F |
| [10] |
ESSER E, GUASCH L, VAN LEEUWEN T, et al. Total variation regularization strategies in full-waveform inversion[J]. SIAM Journal on Imaging Sciences, 2018, 11(1): 376-406. DOI:10.1137/17M111328X |
| [11] |
AGHAMIRY H S, GHOLAMI A, OPERTO S. ADMM-based multi-parameter wavefield reconstruction inversion in VTI acoustic media with TV regula-rization[J]. Geophysical Journal International, 2019, 219(2): 1316-1333. DOI:10.1093/gji/ggz369 |
| [12] |
DURAND S, FROMENT J. Reconstruction of wavelet coefficients using total variation minimization[J]. SIAM Journal on Scientific Computing, 2003, 24(5): 1754-1767. DOI:10.1137/S1064827501397792 |
| [13] |
BENNING M, BURGER M. Modern regularization methods for inverse problems[J]. Acta Numerica, 2018, 27: 1-111. DOI:10.1017/S0962492918000016 |
| [14] |
LIN Y Z, HUANG L J. Acoustic- and elastic-waveform inversion using a modified total-variation regularization scheme[J]. Geophysical Journal International, 2014, 200(1): 489-502. DOI:10.1093/gji/ggu393 |
| [15] |
PENG Y, LIAO W Y, HUANG J P, et al. Total vriation regularization for seismic waveform inversion using an adaptive primal dual hybrid gradient method[J]. Inverse Problems, 2018, 34(4): 045006. DOI:10.1088/1361-6420/aaaf8e |
| [16] |
AGHAMIRY H S, GHOLAMI A, OPERTO S. Compound regularization of full-waveform inversion for imaging piecewise media[J]. IEEE Transactions on Geoscience & Remote Sensing, 2019, 58(2): 1192-1204. |
| [17] |
苗永康. 基于L-BFGS算法的时间域全波形反演[J]. 石油地球物理勘探, 2015, 50(3): 469-474. MIAO Yongkang. Full waveform inversion in time domain based on limited-memory BFGS algorithm[J]. Oil Geophysical Prospecting, 2015, 50(3): 469-474. |
| [18] |
SCHEINBERG K, TANG X C. Practical inexact proximal quasi-Newton method with global complexity analysis[J]. Mathematical Programming, 2016, 160(1): 495-529. |
| [19] |
GONG P H, YE J P. A modified Orthant-Wise limited memory Quasi-Newton method with convergence analysis[C]. Proceedings of the 32nd International Conference on International Conference on Machine Learning, 2015, 276-284.
|
| [20] |
DAI M X, CHEN J B, CAO J. l1-Regularized full-waveform inversion with prior model information based on orthant-wise limited memory quasi-Newton method[J]. Journal of Applied Geophysics, 2017, 142: 49-57. |
| [21] |
ANDREW G, GAO J F. Scalable training of L1-regularized log-linear models[C]. Proceedings of the 24th International Conference on Machine Learning, 2007, 33-40.
|



 傅红笋, 辽宁省大连市甘井子区凌海路1号大连海事大学理学院,116026。Email:
傅红笋, 辽宁省大连市甘井子区凌海路1号大连海事大学理学院,116026。Email: