随着油气勘探开发目标由构造型油气藏转化为岩性油气藏、构造岩性复合型油气藏和非常规油气藏,对地震数据反演成像技术的要求越来越高,不仅对地震数据全波形反演技术实用化的呼声越来越强烈,而且要求以地下构造成像为目标的波动方程偏移方法应保幅、保真,还希望地震数据反演结果能直接反映地层的物性变化。
以获取地下波阻抗空间变化的地层物性反演成像技术自20世纪70年代以来得到了很大的发展,如叠后地震波阻抗反演[1-6]、基于Zoeppritz方程及其近似的弹性阻抗反演[7-13]和全波形反演[14-16]。叠后波阻抗反演虽然具有计算效率高的优势,也是当前生产中比较常用的技术,但由于地震数据水平叠加处理固有的不足,因此叠后波阻抗反演方法在复杂地区的应用受到限制。基于Zoeppritz方程及其近似的AVO和AVA反演方法直接在叠前数据道集上进行,可有效地利用地震振幅随炮检距或入射角变化的信息,能用于多种物性和岩性参数的反演。由于Zoeppritz方程是一种描述平面波入射到无穷大平界面的反射、透射和波型转换的理论[17],因此该方程对于实际地震勘探中常见的非平面波和非平界面可能会不适应。利用基于物性参数(如波阻抗)的波动方程全波形反演,数理严谨,可完整地利用地震波场的时空变化信息,但计算量大,对地震数据要求高(如要求数据有尽可能低的低频信息和大炮检距数据)[18],是油气地震勘探近30年的研究热点和亟待突破的技术。
给定一个具有地震波运动学特征准确的地下介质光滑模型,得到以地下反射率为模型参数的地震数据线性正演公式,地震偏移可视为一种有关地下反射率的线性反演[19-20]。Zhang等[21-22]基于真振幅逆时偏移提出了一种速度和波阻抗反演方法,并认为角度域共成像点道集的小角度成像结果主要反映波阻抗的变化,大角度成像结果主要反映速度的变化,为利用波动方程偏移实现地下波阻抗反演提供了思路。但是该方法所用的真振幅逆时偏移中的成像条件是源于Bleistein等[19, 23]利用Kirchhoff近似导出的成像公式。而Kirchhoff近似中反射波与入射波间的关系仅适合平面波小于临界角入射到无穷大平界面的特殊情况,而不适合实际地震勘探中常见的非平面波和非平界面。陈生昌等[24-26]曾利用推导出的反射波线性依赖于阻抗相对扰动的反射波方程,开展了有关波阻抗相对变化成像、波阻抗扰动的近似反演和最小二乘反演方法的初步研究,为利用反射地震数据进行地层成像打下了基础。
针对以上有关波阻抗或地层物性参数反演成像存在的问题和关于地震数据波动方程偏移成像的认识,以及对不同模型参数的地震数据正演公式会产生不同的反演目标和反演算法的认知[27],本文基于波动方程偏移的概念,利用用于地震数据偏移的光滑介质模型,根据地震波传播理论导出了基于地下反射体波阻抗相对扰动的地震数据线性正演公式;然后在此基础上结合线性反演理论,研究利用地震数据对地下反射体的波阻抗相对扰动的近似反演,构建以波阻抗变化为主要目标的地震数据地层成像方法。将提出的地震数据地层成像方法分别应用于标量波方程描述的地震数据和声波方程描述的地震数据,均取得了理想的成像结果。
1 基于波阻抗相对扰动的线性正演在常规油气地震勘探中,地表激发的地震波向地下传播,当地震波遇到非均匀体或地层分界面时会产生散射或反射等次生波,再向上传播到地表被检波器接收。地震波在地下的传播和散射(或反射)可用波动方程描述,如变密度声波方程
| $ \begin{gathered} \left\{\frac{1}{\rho(\boldsymbol{x}) v^2(\boldsymbol{x})} \frac{\partial^2}{\partial t^2}-\nabla \cdot\left[\frac{1}{\rho(\boldsymbol{x})} \nabla\right]\right\} u\left(\boldsymbol{x}, t ; \boldsymbol{x}_{\mathrm{s}}\right) \\ =s(t) \delta\left(\boldsymbol{x}-\boldsymbol{x}_{\mathrm{s}}\right) \end{gathered} $ | (1) |
式中:u(x, t; xs)为压力波场;ρ(x)为密度场;v(x)为速度场;s(t)为震源函数;x=(x, y, z), 为空间坐标;xs为震源位置。
式(1)中,波场u(x, t; xs)与右端震源项呈线性关系(震源项不包含波场u(x, t; xs)),与地下介质密度ρ(x)和速度v(x)呈非线性关系,这种非线性关系可表示为
| $ u=F(\rho, v) $ | (2) |
式中F是关于ρ和v的非线性函数。将随空间变化的密度ρ(x)和速度v(x)用背景模型和扰动模型表示,即
| $ \left\{\begin{array}{l} \rho(\boldsymbol{x})=\rho_{\mathrm{b}}(\boldsymbol{x})+\Delta \rho(\boldsymbol{x}) \\ v(\boldsymbol{x})=v_{\mathrm{b}}(\boldsymbol{x})+\Delta v(\boldsymbol{x}) \end{array}\right. $ | (3) |
式中:ρb(x)和vb(x)分别为介质的背景密度和背景速度;Δρ(x)和Δv(x)分别为相对于背景密度和背景速度的扰动。本文不仅要求ρb(x)和vb(x)光滑变化,还要求在背景密度和背景速度下地震波的运动学特征与真实介质中地震波一致。
如果取式(1)中的密度和速度为背景密度和背景速度,有
| $ \begin{gathered} \left\{\frac{1}{\rho_{\mathrm{b}}(\boldsymbol{x}) v_{\mathrm{b}}^2(\boldsymbol{x})} \frac{\partial^2}{\partial t^2}-\nabla \cdot\left[\frac{1}{\rho_{\mathrm{b}}(\boldsymbol{x})} \nabla\right]\right\} u_{\mathrm{b}}\left(\boldsymbol{x}, t ; \boldsymbol{x}_{\mathrm{s}}\right) \\ =s(t) \delta\left(\boldsymbol{x}-\boldsymbol{x}_{\mathrm{s}}\right) \end{gathered} $ | (4) |
式中ub(x, t; xs)为背景密度和背景速度下的压力波场,也称为背景波场。如果式(4)右端的震源函数s(t)为脉冲函数,则该方程对应的解即为背景密度和背景速度下的Green函数g(x, t; xs)。利用背景波场ub(x, t; xs)和Green函数g(x, t; xs),并根据Lippmann-Schwinger方程的级数展开式和一阶Born近似,式(2)可近似为
| $ u=u_{\mathrm{b}}+g p u_{\mathrm{b}} $ | (5) |
式中p为式(1)中的波动算子与式(4)中的波动算子之差,即
| $ \begin{aligned} p=&\left\{\left[\frac{1}{\left[\rho_{\mathrm{b}}(\boldsymbol{x})+\Delta \rho(\boldsymbol{x})\right]\left[v_{\mathrm{b}}(\boldsymbol{x})+\Delta v(\boldsymbol{x})\right]^2}-\right.\right.\\ &\left.\left.\frac{1}{\rho_{\mathrm{b}}(\boldsymbol{x}) v_{\mathrm{b}}^2(\boldsymbol{x})}\right] \frac{\partial^2}{\partial t^2}\right\}-\\ & \nabla \cdot\left\{\left[\frac{1}{\rho_{\mathrm{b}}(\boldsymbol{x})+\Delta \rho(\boldsymbol{x})}-\frac{1}{\rho_{\mathrm{b}}(\boldsymbol{x})}\right] \nabla\right\} \end{aligned} $ | (6) |
式(5)右端第二项称为由速度和密度扰动产生的一阶Born近似扰动波场,有
| $ u_{\mathrm{p}}=u-u_{\mathrm{b}}=g p u_{\mathrm{b}} $ | (7) |
与式(5)所对应的波动方程为
| $ \begin{gathered} \left\{\frac{1}{\rho_{\mathrm{b}}(\boldsymbol{x}) v_{\mathrm{b}}^2(\boldsymbol{x})} \frac{\partial^2}{\partial t^2}-\nabla \cdot\left[\frac{1}{\rho_{\mathrm{b}}(\boldsymbol{x})} \nabla\right]\right\} u_{\mathrm{p}}\left(\boldsymbol{x}, t ; \boldsymbol{x}_{\mathrm{s}}\right) \\ =\frac{\left(a_v+a_\rho\right)}{\rho_{\mathrm{b}}(\boldsymbol{x}) v_{\mathrm{b}}^2(\boldsymbol{x})} \frac{\partial^2 u_{\mathrm{b}}\left(\boldsymbol{x}, t ; \boldsymbol{x}_{\mathrm{s}}\right)}{\partial t^2}- \\ \nabla \cdot\left[\frac{a_\rho}{\rho_{\mathrm{b}}(\boldsymbol{x})} \nabla u_{\mathrm{b}}\left(\boldsymbol{x}, t ; \boldsymbol{x}_{\mathrm{s}}\right)\right] \end{gathered} $ | (8) |
式中av和aρ分别为速度和密度的相对扰动,即
| $ \left\{\begin{array}{l} a_v=1-\frac{v_{\mathrm{b}}^2(\boldsymbol{x})}{v^2(\boldsymbol{x})} \approx \frac{2 \Delta v(\boldsymbol{x})}{v_{\mathrm{b}}(\boldsymbol{x})} \\ a_\rho=1-\frac{\rho_{\mathrm{b}}(\boldsymbol{x})}{\rho(\boldsymbol{x})} \approx \frac{\Delta \rho(\boldsymbol{x})}{\rho_{\mathrm{b}}(\boldsymbol{x})} \end{array}\right. $ | (9) |
由于ρb(x)和vb(x)的光滑性,ub(x, t; xs)不包含散射波和反射波,因此在地表观测情况下,有ub(xr, t; xs)=0,其中xr为检波点坐标。对于式(7)中一阶Born近似的扰动波场,有
| $ \begin{aligned} &u_{\mathrm{p}}\left(\boldsymbol{x}_{\mathrm{r}}, t ; \boldsymbol{x}_{\mathrm{s}}\right)=u\left(\boldsymbol{x}_{\mathrm{r}}, t ; \boldsymbol{x}_{\mathrm{s}}\right)=\int_{\mathit{\Omega}} \mathrm{d} \boldsymbol{x} g\left(\boldsymbol{x}_{\mathrm{r}}, t ; \boldsymbol{x}\right) *{ }_t \\ &\quad\left\{\frac{a_v+a_\rho}{\rho_{\mathrm{b}}(\boldsymbol{x}) v_{\mathrm{b}}^2(\boldsymbol{x})} \frac{\partial^2 u_{\mathrm{b}}\left(\boldsymbol{x}, t ; \boldsymbol{x}_{\mathrm{s}}\right)}{\partial t^2}-\right. \\ &\left.\quad \nabla \cdot\left[\frac{a_\rho}{\rho_{\mathrm{b}}(\boldsymbol{x})} \nabla u_{\mathrm{b}}\left(\boldsymbol{x}, t ; \boldsymbol{x}_{\mathrm{s}}\right)\right]\right\} \end{aligned} $ | (10) |
式中:Ω表示av和aρ的空间分布范围;“*t”表示时间方向的褶积。利用分部积分法,式(10)可进一步化简为[11]
| $ \begin{aligned} &u_{\mathrm{p}}\left(\boldsymbol{x}_{\mathrm{r}}, t ; \boldsymbol{x _ { \mathrm { s } }}\right)=\int_{\mathit{\Omega}} \mathrm{d} \boldsymbol{x}\left[\frac{a_v+a_\rho}{\rho_{\mathrm{b}}(\boldsymbol{x}) v_{\mathrm{b}}^2(\boldsymbol{x})} \frac{\partial^2 u_{\mathrm{b}}\left(\boldsymbol{x}, t ; \boldsymbol{x}_{\mathrm{s}}\right)}{\partial t^2} *_t\right. \\ &\left.g\left(\boldsymbol{x}_{\mathrm{r}}, t ; \boldsymbol{x}\right)+\frac{a_\rho}{\rho_{\mathrm{b}}(\boldsymbol{x})} \nabla u_{\mathrm{b}}\left(\boldsymbol{x}, t ; \boldsymbol{x}_{\mathrm{s}}\right) *{ }_t \nabla g\left(\boldsymbol{x}_{\mathrm{r}}, t ; \boldsymbol{x}\right)\right] \end{aligned} $ | (11) |
对于非均匀体产生的扰动波场,陈生昌等[20]根据非均匀体分布范围Ω的尺寸与地震波长之间的相对大小关系,把相对于地震波长为小尺度的非均匀体产生的扰动波场称为散射波场,相应的非均匀体称为散射体;而把相对于地震波长为大尺度的非均匀体产生的扰动波场称为反射波场,相应的非均匀体称为反射体。为了得到基于反射体波阻抗扰动的反射波场,根据文献[26, 28],式(11)可表示为
| $ \begin{aligned} u_{\mathrm{R}}\left(\boldsymbol{x}_{\mathrm{r}}, t ; \boldsymbol{x}_{\mathrm{s}}\right)=& \int_{\mathit{\Omega}} \mathrm{d} \boldsymbol{x} g\left(\boldsymbol{x}_{\mathrm{r}}, t ; \boldsymbol{x}\right) *{ }_t \\ & \frac{I_{\mathrm{R}}(\boldsymbol{x}, \sigma)}{\rho_{\mathrm{b}}(\boldsymbol{x}) v_{\mathrm{b}}^2(\boldsymbol{x})} \frac{\partial^2 u_{\mathrm{b}}\left(\boldsymbol{x}, t ; \boldsymbol{x}_{\mathrm{s}}\right)}{\partial t^2} \end{aligned} $ | (12) |
式中:uR(xr, t; xs)为采集到的反射波场;σ为反射波传播方向与入射波传播方向间的反射开角;IR(x, σ)称为波阻抗相对扰动,有IR(x, σ)=av+aρ×(1+cosσ)。对于沿反射面法向的入射及其反射,有σ=0,则
| $ \begin{aligned} I_{\mathrm{R}}(\boldsymbol{x}, \sigma=0) &=a_v+2 a_\rho \\ &=\frac{2 \Delta v(\boldsymbol{x})}{v_{\mathrm{b}}(\boldsymbol{x})}+\frac{2 \Delta \rho(\boldsymbol{x})}{\rho_{\mathrm{b}}(\boldsymbol{x})} \approx \frac{2 \Delta I(\boldsymbol{x})}{I_{\mathrm{b}}(\boldsymbol{x})} \end{aligned} $ | (13) |
式中:Ib(x)=vb(x)ρb(x),为背景介质波阻抗;ΔI(x)=Δv(x)ρ(x)=ρ(x)Δv(x)+v(x)Δρ(x),为波阻抗扰动。式(12)即为基于波阻抗相对扰动的地震反射波场线性正演表示,对应的波动方程为
| $ \begin{gathered} \left\{\frac{1}{\rho_{\mathrm{b}}(\boldsymbol{x}) v_{\mathrm{b}}^2(\boldsymbol{x})} \frac{\partial^2}{\partial t^2}-\nabla \cdot\left[\frac{1}{\rho_{\mathrm{b}}(\boldsymbol{x})} \nabla\right]\right\} u_{\mathrm{R}}\left(\boldsymbol{x}, t ; \boldsymbol{x}_{\mathrm{s}}\right) \\ =\frac{I_{\mathrm{R}}(\boldsymbol{x}, \sigma)}{\rho_{\mathrm{b}}(\boldsymbol{x}) v_{\mathrm{b}}^2(\boldsymbol{x})} \frac{\partial^2 u_{\mathrm{b}}\left(\boldsymbol{x}, \mathrm{t} ; \boldsymbol{x}_{\mathrm{s}}\right)}{\partial t^2} \end{gathered} $ | (14) |
在式(14)中,波场uR(x, t; xs)与右端源项成线性关系。
上述线性关系依赖于反射体波阻抗相对扰动的地震反射波场表达式(式(12))和式(14),是本文利用反射地震数据获取地下波阻抗空间变化的地层成像方法的理论基础。
2 波动方程地层成像地震数据的正演是地震数据反演的基础。利用上述基于波阻抗相对扰动的地震数据线性正演公式,结合线性反演理论,可构建以波阻抗扰动为目标的地震数据地层成像方法。
式(12)两边对时间做Fourier变换,有
| $ \begin{aligned} \tilde{u}_{\mathrm{R}}\left(\boldsymbol{x}_{\mathrm{r}}, \mathit{\omega} ; \boldsymbol{x}_{\mathrm{s}}\right)=& \int_{\mathit{\Omega}} \mathrm{d} \boldsymbol{x} \tilde{g}\left(\boldsymbol{x} _{\mathrm{r}}, \mathit{\omega} ; \boldsymbol{x}\right) \times \\ & \frac{-\mathit{\omega}^2 \tilde{u}_{\mathrm{b}}\left(\boldsymbol{x}, \mathit{\omega} ; \boldsymbol{x}_{\mathrm{s}}\right)}{\rho_{\mathrm{b}}(\boldsymbol{x}) v_{\mathrm{b}}^2(\boldsymbol{x})} I_{\mathrm{R}}(\boldsymbol{x}, \sigma) \end{aligned} $ | (15) |
式中:上划“~”表示在频率域;ω表示圆频率。令
| $ \tilde{m}(\boldsymbol{x}, \mathit{\omega})=\frac{-\mathit{\omega}^2 \tilde{u}_{\mathrm{b}}\left(\boldsymbol{x}, \mathit{\omega} ; \boldsymbol{x}_{\mathrm{s}}\right)}{\rho_{\mathrm{b}}(\boldsymbol{x}) \nu_{\mathrm{b}}^2(\boldsymbol{x})} I_{\mathrm{R}}(\boldsymbol{x}, \sigma) $ | (16) |
则式(15)可写为
| $ \tilde{u}_{\mathrm{R}}\left(\boldsymbol{x}_{\mathrm{r}}, \mathit{\omega} ; \boldsymbol{x}_{\mathrm{s}}\right)=\int_{\mathit{\Omega}} \mathrm{d} \boldsymbol{x} \tilde{g}\left(\boldsymbol{x}_{\mathrm{r}}, \mathit{\omega} ; \boldsymbol{x}\right) \tilde{m}\left(\boldsymbol{x}, \mathit{\omega} ; \boldsymbol{x}_{\mathrm{s}}\right) $ | (17) |
上式可描述为已知左端项$\tilde{u}_{\mathrm{R}}$(xr, ω; xs)和右端积分项中的$\tilde{g}$(xr, ω; x),求积分项中的$\tilde{m}$(x, ω; xs),称为Fredholm第一类积分方程。
将式(17)写为矩阵形式,有
| $ \boldsymbol{d}=\mathit{\boldsymbol{{L m}}} $ | (18) |
式中:d为$\tilde{u}$R(xr, ω; xs)的离散形式;L为空间积分核函数$\tilde{g}$(xr, ω; x)的离散形式,即背景介质中的波场传播矩阵;m为$\tilde{m}$(x, ω; xs)组成的模型参数矩阵。
由式(18)中各个矩阵的数学物理性质可知,求解式(18)中的m相当于反演源(产生反射波场的虚源)[29]。根据线性最小二乘反演理论,式(18)的最小二乘解为
| $ \boldsymbol{m}=\boldsymbol{L}^{-1} \boldsymbol{d}=\left(\boldsymbol{L}^* \boldsymbol{L}\right)^{-1} \boldsymbol{L}^* \boldsymbol{d} $ | (19) |
式中L-1、L*分别为传播矩阵L的最小二乘逆和伴随矩阵。在地震数据的反演中,特别是三维地震数据的反演中,矩阵L的规模通常非常大,(L*L)-1的计算在当前的计算机条件下难以直接实现。因此,在地震数据的反演中通常把式(19)近似(即用L*代替L-1)为
| $ \mathit{\boldsymbol{m}}_{\mathrm{a}}=\boldsymbol{L}^* \boldsymbol{d} $ | (20) |
式中ma为m的近似结果。
式(20)相比于式(19),不仅计算量大为减少,而且计算更稳定。式(19)通常被称为对m的最小二乘反演,式(20)为对m的近似反演或成像。地震数据的逆时偏移就是采用类似式(20)的运算实现对地下反射率的成像。式(20)中L*对波场d的运算表示波场d的伴随传播。这种波场的伴随传播,在地震数据的反演成像中,是通过波场的逆时传播实现的[16]。
由于矩阵m中各个元素的组成不仅包含有x处待成像的波阻抗相对扰动,还含有频率域的二阶导数和x处已知的背景波场以及背景密度与背景速度,因此需要从ma中消除背景波场、背景密度和背景速度,并处理好频率域的二阶导数运算,才能得到x处波阻抗相对扰动的成像结果。
根据上述的推导和论述,关于IR(x, σ)成像的计算步骤归纳如下:
(1) 应用式(3)计算背景波场ub(x, t; xs);
(2) 利用伴随传播对式(14)右端虚源项成像,即地表波场uR(xr, t; xs)的逆时传播
| $ \left\{\begin{array}{l} \left\{\frac{1}{\rho_{\mathrm{b}}(\boldsymbol{x}) v_{\mathrm{b}}^2(\boldsymbol{x})} \frac{\partial^2}{\partial t^2}-\right. \\ \left.\nabla \cdot\left[\frac{1}{\rho_{\mathrm{b}}(\boldsymbol{x})} \nabla\right]\right\} u_{\mathrm{R}}\left(\boldsymbol{x}, t ; \boldsymbol{x}_{\mathrm{s}}\right)=0 \\ u_{\mathrm{R}}\left(\boldsymbol{x}_{\mathrm{r}}, t ; \boldsymbol{x}_{\mathrm{s}}\right)=u_{\mathrm{R}}\left(\boldsymbol{x}, t ; \boldsymbol{x}_{\mathrm{s}}\right) \delta\left(\boldsymbol{x}_{\mathrm{r}}-\boldsymbol{x}\right) \end{array}\right. $ | (21) |
(3) 消除虚源项成像结果中的频率域的二阶导数、背景波场、背景密度和背景速度,得到IR(x, σ)在角度σ域成像结果的平均值IR(x),该步骤类似于逆时偏移中的成像运算
| $ \bar{I}_{\mathrm{R}}(\boldsymbol{x})=\rho_{\mathrm{b}}(\boldsymbol{x}) v_{\mathrm{b}}^2(\boldsymbol{x}) \int_0^{T_{\max }} \frac{u_{\mathrm{R}}\left(\boldsymbol{x}, t ; \boldsymbol{x}_{\mathrm{s}}\right)}{\frac{\partial^2 u_{\mathrm{b}}\left(\boldsymbol{x}, t ; \boldsymbol{x}_{\mathrm{s}}\right)}{\partial t^2}} \mathrm{~d} t $ | (22) |
式中Tmax为地震数据的记录长度。
上述波阻抗相对扰动成像的计算步骤与地震数据逆时偏移基本相同,仅在第(3)步的成像公式存在差别。本文的成像公式(式(22))是根据本文的地震反射波场线性正演公式(式(12))和反射波动方程(式(14))得到的。
为了得到反射开角σ域的成像结果IR(x, σ),在应用成像公式(式(22))之前,需要先对x处的波场uR(x, t; xs)和ub(x, t; xs)进行角度分解[30-31],得到角度域的波场uR(x, t, θR; xs)和ub(x, t, θI; xs),其中θR为反射角(即z轴方向沿逆时针与反射波传播方向间的夹角),θI为入射角(即z轴方向沿逆时针与入射波传播方向间的夹角),有σ=π+θI-θR。IR(x, σ)可进一步表示为
| $ I_{\mathrm{R}}(\boldsymbol{x}, \sigma)=2 \frac{\Delta v(\boldsymbol{x})}{v_{\mathrm{b}}(\boldsymbol{x})} \sin ^2 \frac{\sigma}{2}+2 \frac{\Delta I(\boldsymbol{x})}{I_{\mathrm{b}}(\boldsymbol{x})} \cos ^2 \frac{\sigma}{2} $ | (23) |
因此式(22)的成像公式在角度域可写为
| $ I_{\mathrm{R}}(\boldsymbol{x}, \sigma)=\rho_{\mathrm{b}}(\boldsymbol{x}) v_{\mathrm{b}}^2(\boldsymbol{x}) \int_0^{T_{\max }} \frac{u_{\mathrm{R}}\left(\boldsymbol{x}, t, \theta_{\mathrm{R}} ; \boldsymbol{x}_{\mathrm{s}}\right)}{\frac{\partial^2 u_{\mathrm{b}}\left(\boldsymbol{x}, t, \theta_{\mathrm{I}} ; \boldsymbol{x}_{\mathrm{s}}\right)}{\partial t^2}} \mathrm{~d} t $ | (24) |
对于式(24),如果σ比较小,则成像结果主要反映波阻抗的相对扰动ΔI(x)/Ib(x);如果σ比较大,则成像结果主要反映速度的相对扰动Δv(x)/vb(x)。利用角度域成像公式(式(24))得到的角度域共成像道集是进一步物性和岩性分析、反演的基础。
虽然成像公式(式(24))可提供角度域共成像道集,得到不同角度的地层成像结果,但波场角度域分解的计算量比较大,尤其是三维波场的角度域分解。常规油气地震勘探数据采集中的炮检距一般都比较小,因此由成像公式(式(22))得到的IR(x)也可近似定义为波阻抗的相对扰动,是一种相对快捷的地层成像方式。
如果在成像过程中不考虑密度变化,仅考虑地下介质的速度变化,则可用标量波方程代替声波方程描述地震波,即
| $ \left[\frac{1}{v^2(\boldsymbol{x})} \frac{\partial^2}{\partial t^2}-\nabla^2\right] u\left(\boldsymbol{x}, t ; \boldsymbol{x}_{\mathrm{s}}\right)=s(t) \delta\left(\boldsymbol{x}-\boldsymbol{x}_{\mathrm{s}}\right) $ | (25) |
对应的地层性成像结果是地下介质的速度相对扰动av(x),相应的计算步骤为:
(1) 计算背景波场ub(x, t; xs)
| $ \left[\frac{1}{v_{\mathrm{b}}^2(\boldsymbol{x})} \frac{\partial^2}{\partial t^2}-\nabla^2\right] u_{\mathrm{b}}\left(\boldsymbol{x}, t ; \boldsymbol{x}_{\mathrm{s}}\right)=s(t) \delta\left(\boldsymbol{x}-\boldsymbol{x}_{\mathrm{s}}\right) $ | (26) |
(2) 地表反射波场uR(xr, t; xs)的逆时传播
| $ \left\{\begin{array}{l} {\left[\frac{1}{v_{\mathrm{b}}^2(\boldsymbol{x})} \frac{\partial^2}{\partial t^2}-\nabla^2\right] u_{\mathrm{R}}\left(\boldsymbol{x}, t ; \boldsymbol{x}_{\mathrm{s}}\right)=0} \\ u_{\mathrm{R}}\left(\boldsymbol{x}_{\mathrm{r}}, t ; \boldsymbol{x}_{\mathrm{s}}\right)=u_{\mathrm{R}}\left(\boldsymbol{x}, t ; \boldsymbol{x}_{\mathrm{s}}\right) \delta\left(\boldsymbol{x}_{\mathrm{r}}-\boldsymbol{x}\right) \end{array}\right. $ | (27) |
(3) 速度相对扰动av(x)的成像
| $ a_v(\boldsymbol{x})=v_{\mathrm{b}}^2(\boldsymbol{x}) \int_0^{T_{\max }} \frac{u_{\mathrm{R}}\left(\boldsymbol{x}, t ; \boldsymbol{x}_{\mathrm{s}}\right)}{\frac{\partial^2 u_{\mathrm{b}}\left(\boldsymbol{x}, t ; \boldsymbol{x}_{\mathrm{s}}\right)}{\partial t^2} \mathrm{~d} t} $ | (28) |
由于标量波方程中的波场是标量,不涉及方向,因此利用标量波波动方程的物性成像方法只能得到角度域平均的速度相对扰动,而不能得到类似于式(24)的角度域成像结果。
式(3)、式(21)、式(22)和式(24)表示以波阻抗相对扰动为目标的地震数据地层成像方法,式(26)~式(28)为以速度相对扰动为目标的地震数据地层成像方法。本文的地震数据地层成像方法虽然是以地震数据线性表示为基础,但实现过程与波动方程逆时偏移一致,都需波场外推和成像。如果不进行波场角度分解的角度域成像,则地层成像方法的计算量与逆时偏移基本相当。此外,本文的地层成像方法对背景模型的要求与逆时偏移也是相同的,即要求有一个空间光滑变化的背景模型,背景模型的地震波运动学特征与真实模型一致。
基于上述认识,将本文提出的方法称为基于波动方程偏移的地震数据地层成像方法。
3 数值试验为了验证本文的地层成像方法的正确性和有效性,对两个模型的合成数据进行试验。由于方法的计算步骤和计算公式以及对模型的要求与逆时偏移相同,因此主要验证方法的正确性。
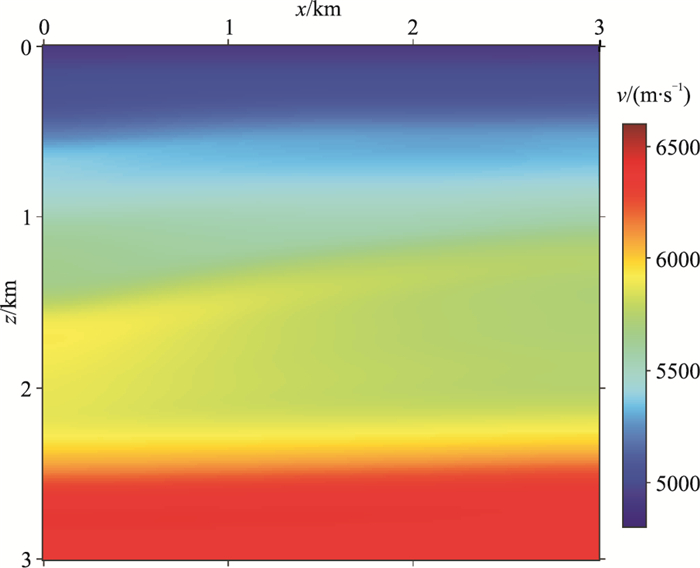
3.1 标量波动方程的速度相对扰动成像假定地下介质的密度为常数,仅考虑地下介质的速度变化,使用标量波动方程描述地震波的传播。图 1为用于合成地震数据的速度模型,是部分Sig-sbee2A模型。模型尺寸为3km×3km,网格间距为15m。应用波动方程有限差分方法合成地震数据,震源为主频20Hz的Ricker子波,炮间距为30m,共101炮;道间距为15m,每炮有201道。图 2为图 1经过平滑、用于速度相对扰动成像的背景速度模型,图 3为由图 1和图 2得到的速度相对扰动的理论模型。

|
图 1 Sigsbee2A部分速度模型 |
|
图 2 Sigsbee2A背景速度模型 |

|
图 3 Sigsbee2A模型理论速度相对扰动 |
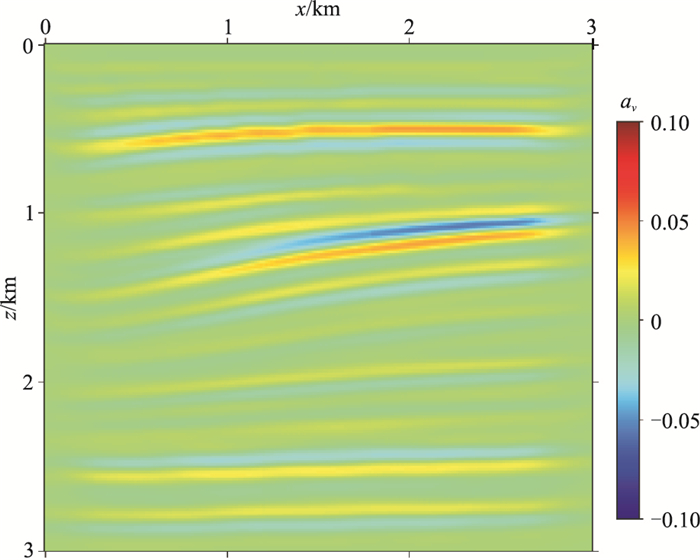
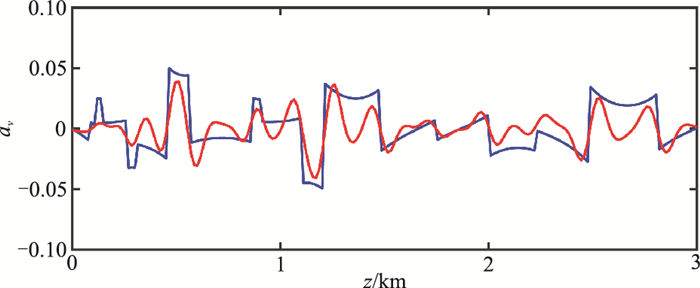
利用本文提出的标量波地震数据地层性成像方法,对合成地震数据进行速度相对扰动的地层成像(图 4)。对比图 4与图 3可见,图 4的地层成像结果准确地反映了图 3的速度相对扰动变化。由于模型边部的地震波照明能量不足,致使模型边部的成效果较差。为了与模型理论值进行仔细对比,提取图 3和图 4中x=1500m处的单道曲线,如图 5所示,可见,成像结果中的速度相对扰动与模型的理论速度相对扰动具有较高的一致性。由此可知,本文提出的速度相对扰动成像方法可以有效地实现对地层速度扰动的成像。
|
图 4 Sigsbee2A模型的速度相对扰动成像结果 |
|
图 5 Sigsbee2A模型速度扰动成像结果(红)与理论值(蓝)的单道对比 |
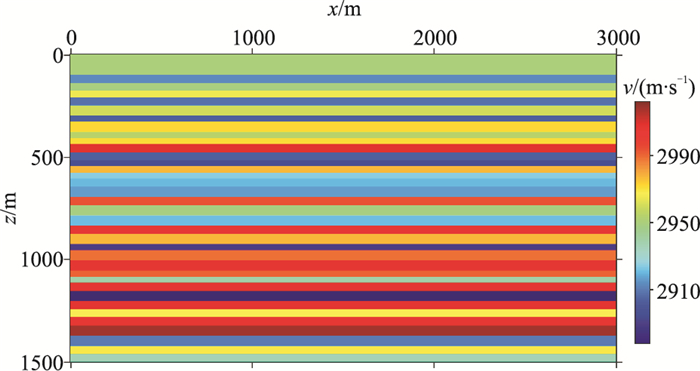
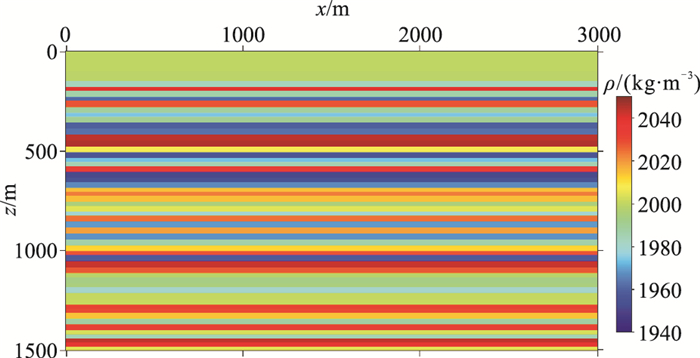
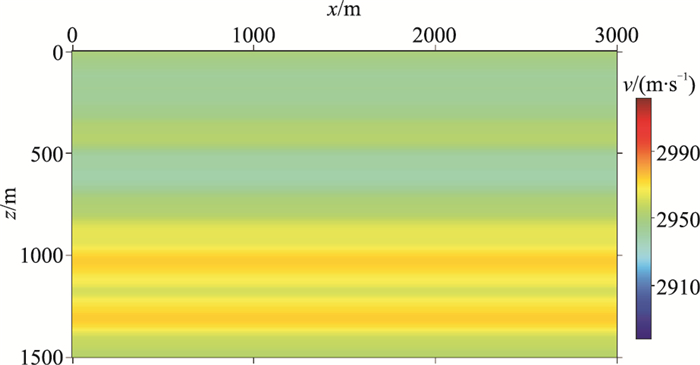
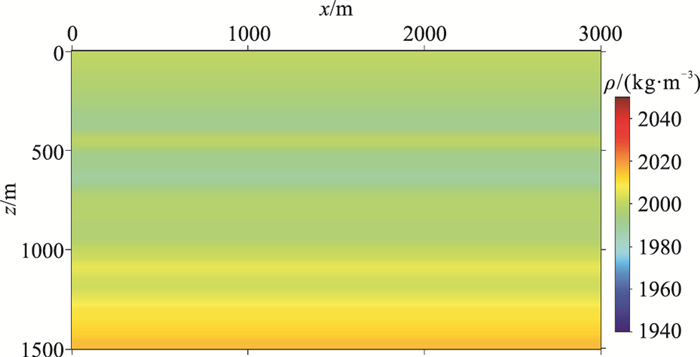
同时考虑地下介质的密度和速度变化,使用声波方程描述地震波的传播。图 6和图 7分别为用于合成地震数据的随机层状速度和密度模型,尺寸是3000m×1500m,两个方向的网格间距均为10m。应用波动方程有限差分方法合成地震数据,震源是主频为20Hz的Ricker子波,炮间距为20m,共151炮;道间距为10m,每炮有301道。图 8和图 9分别为用于地层成像的光滑背景速度模型和光滑背景密度模型。
|
图 6 随机层状速度模型 |
|
图 7 随机层状密度模型 |
|
图 8 随机层状模型的背景速度 |
|
图 9 随机层状模型的背景密度 |
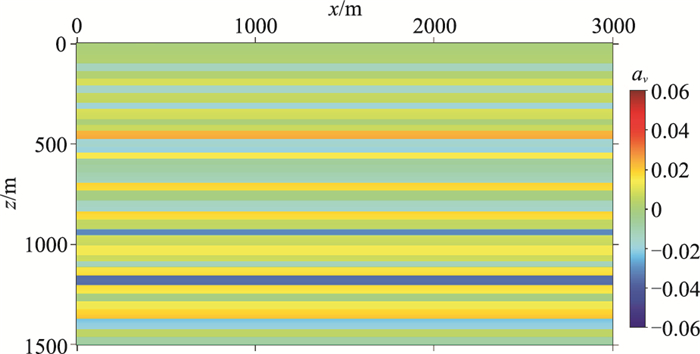
根据给定的速度、密度模型和背景模型可计算得到波阻抗相对扰动理论模型(图 10)和速度相对扰动理论模型(图 11)。
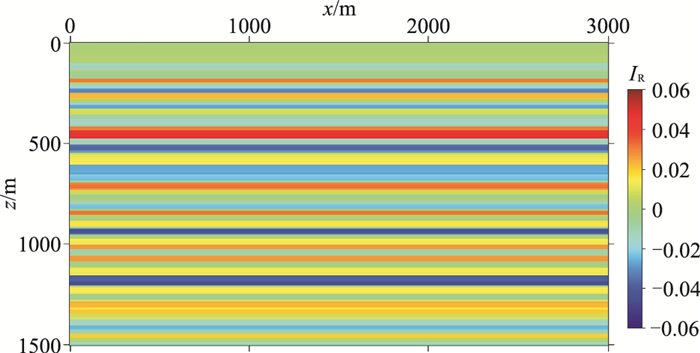
|
图 10 随机层状模型的理论波阻抗相对扰动 |
|
图 11 随机层状模型的理论速度相对扰动 |
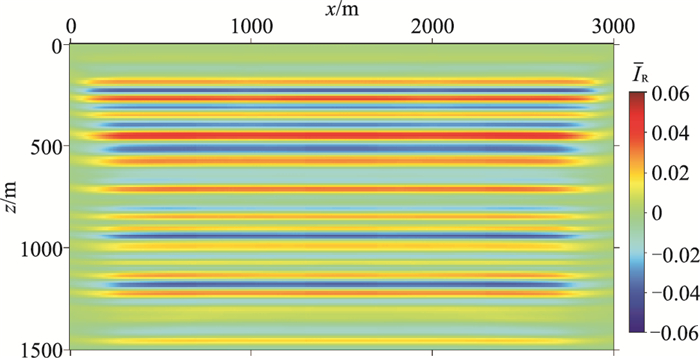
利用本文提出的声波地震数据地层成像方法,对合成地震数据进行波阻抗相对扰动成像。首先对波场不做角度分解,利用成像公式(式(22))得到角度平均的波阻抗相对扰动成像结果IR(x);然后再通过对波场做角度分解,利用式(24)可得到角度域波阻抗相对扰动的共成像道集IR(x, σ)和不同角度的波阻抗相对扰动成像结果。
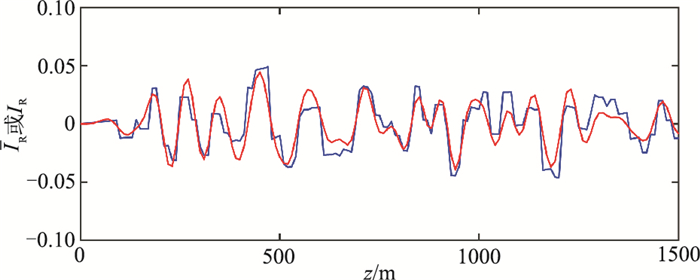
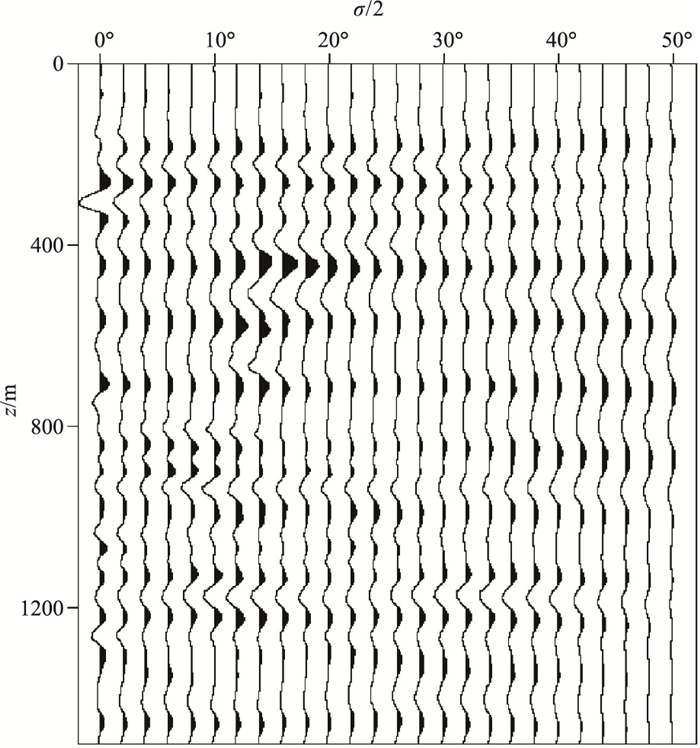
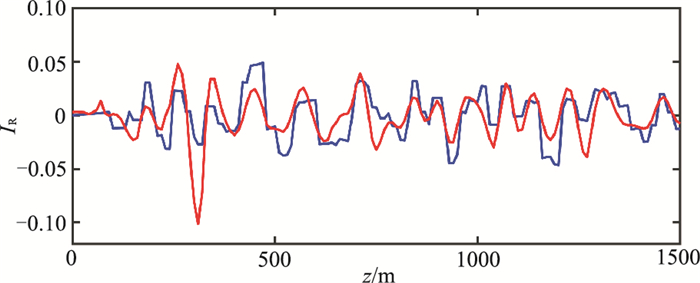
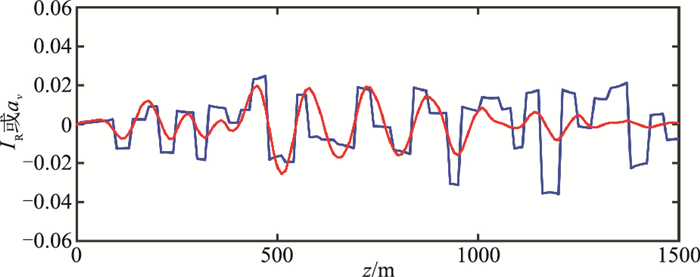
图 12为角度域平均的波阻抗相对扰动成像结果IR(x),是波阻抗相对扰动的近似。对比图 12与图 10可以看出,图 12的地层成像结果准确地反映了图 10所示的波阻抗相对扰动变化。为了仔细对比,提取图 10和图 12中位于x=1500m的单道曲线,如图 13所示。由图 13可以看出,成像结果与波阻抗相对扰动理论值具有很高的一致性。图 14为x=1500m处的角度σ/2域的波阻抗相对扰动共成像点道集,角度范围为[0°, 50°],间隔为2°。由式(23)可知,当σ/2=0°时,有IR(x, σ)=2ΔI(x)/Ib(x)。因此角度域共成像点道集上0°道的成像结果是该处波阻抗相对扰动ΔI(x)/Ib(x)的反映。图 15为图 14的0°道的成像结果与图 10在x=1500m处波阻抗相对扰动理论值的对比,可以看出,二者一致性较高。由IR(x, σ)的表达式可知,随着角度σ的增大,越来越接近速度相对扰动,当σ/2=90°时,IR(x, σ)=2Δv(x)/vb(x)。图 16为图 14的50°道的成像结果与图 11在x=1500m处速度相对扰动理论值的对比,可以看出,50°道的成像结果与速度相对扰动理论值在浅部具有比较高的一致性,而在深度大于1000m后一致性逐渐变低,这是由于随着深度的增加,实际的反射开角会逐渐减小,因此把大角度的IR(x, σ)近似为速度相对扰动,其误差会随着深度增大而逐渐增大。
|
图 12 随机层状模型角度域平均波阻抗相对扰动成像结果 |
|
图 13 随机层状模型角度域平均的波阻抗相对扰动成像结果(红色)与理论波阻抗相对扰动(蓝色)的单道对比 |
|
图 14 随机层状模型x=1500m处的角度域共成像点道集 |
|
图 15 随机层状模型x=1500m处σ/2=0°对应的波阻抗相对扰动成像结果(红色)与理论波阻抗相对扰动(蓝色)的单道对比 |
|
图 16 随机层状模型x=1500m处σ/2=50°对应的波阻抗相对扰动成像结果(红色)与理论速度相对扰动(蓝色)的单道对比 |
由上述数值实验结果可知,本文提出的波阻抗相对扰动成像方法可以有效地实现对地层波阻抗扰动的成像,得到的角度域平均成像结果和角度域共成像点道集不同角度的成像结果可作为地层波阻抗相对扰动或速度相对扰动的估计。本文的地层成像方法只需地震波运动学特征准确的地下介质光滑模型,就能具有与逆时偏移方法一样的实用性。
4 结论与讨论通过引入具有地震波运动学特征准确的地下介质光滑模型,波动方程偏移是一种基于地震波传播理论的地震数据线性反演,其目标是对地层分界面反射率的成像。本文根据地震数据波动方程偏移成像的思想,利用用于偏移的地下介质光滑模型,推导了基于地下地层波阻抗相对扰动的地震数据线性正演公式,结合线性反演理论,构建了面向地层波阻抗相对扰动的地震数据地层成像方法。如果在成像中不对波场进行角度分解,地层成像方法对于常规小炮检距观测系统的反射地震数据可以快捷地获取角度域平均的地层成像结果。如果在成像中对波场进行角度分解,地层成像方法虽然可以得到角度域共成像点道集和不同角度的地层成像结果,但计算量大增,尤其是三维地震数据的地层成像。波阻抗相对扰动的角度域共成像点道集可为发展精细的物性岩性分析、反演奠定基础。地层成像方法的数值试验结果表明,标量波方程对应的速度相对扰动成像和声波方程对应的波阻抗相对扰动成像均取得了理想的效果。
本文的地层成像具有与逆时偏移相同的计算步骤和相当的计算量,适用于逆时偏移的地震数据同样适用于本文提出的地层成像方法,因此本文的地层成像方法对于实际地震资料具有与逆时偏移一样的实用性。
| [1] |
LAVERGNE M. Pseudo-diagraphics de vitesse en offshore profound[J]. Geophysical Prospecting, 1975, 23(4): 695-711. DOI:10.1111/j.1365-2478.1975.tb01554.x |
| [2] |
LINDSETH R O. Synthetic sonic logs: a process for stratigraphic interpretation[J]. Geophysics, 1979, 44(1): 3-26. DOI:10.1190/1.1440922 |
| [3] |
COOKE D A, SCHNEIDER W A. Generalized linear inversion of reflection seismic data[J]. Geophysics, 1983, 48(6): 665-676. DOI:10.1190/1.1441497 |
| [4] |
OLDENBURG D W, SCHEUER T, LEVY S. Reco-very of the acoustic impedance from reflection seismograms[J]. Geophysics, 1983, 48(10): 1318-1337. DOI:10.1190/1.1441413 |
| [5] |
伊小蝶, 吴帮玉, 孟德林, 等. 数据增广和主动学习在波阻抗反演中的应用[J]. 石油地球物理勘探, 2021, 56(4): 707-715. YI Xiaodie, WU Bangyu, MENG Delin, et al. Application of data augmentation and active learning to seismic wave impedance inversion[J]. Oil Geophysical Prospecting, 2021, 56(4): 707-715. |
| [6] |
王泽峰, 许辉群, 杨梦琼, 等. 应用时域卷积神经网络的地震波阻抗反演方法[J]. 石油地球物理勘探, 2022, 57(2): 279-286, 296. WANG Zefeng, XU Huiqun, YANG Mengqiong, et al. Seismic impedance inversion method based on temporal convolutional neural network[J]. Oil Geophysical Prospecting, 2022, 57(2): 279-286, 296. |
| [7] |
CONNOLLY P. Elastic impedance[J]. The Leading Edge, 1999, 18(4): 438-452. DOI:10.1190/1.1438307 |
| [8] |
WHITECOMBE D N. Elastic impedance normalization[J]. Geophysics, 2002, 67(1): 60-62. DOI:10.1190/1.1451331 |
| [9] |
LU J, YANG Z, WANG Y, et al. Joint PP and PS AVA seismic inversion using exact Zoeppritz equations[J]. Geophysics, 2015, 80(5): R239-R250. DOI:10.1190/geo2014-0490.1 |
| [10] |
宗兆云, 印兴耀, 张峰, 等. 杨氏模量和泊松比反射系数近似方程及叠前地震反演[J]. 地球物理学报, 2012, 55(11): 3786-3794. ZONG Zhaoyun, YIN Xingyao, ZHANG Feng, et al. Reflection coefficient equation and pre-stack seismic inversion with Young's modulus and Poisson ratio[J]. Chinese Journal of Geophysics, 2012, 55(11): 3786-3794. DOI:10.6038/j.issn.0001-5733.2012.11.025 |
| [11] |
ZONG Z Y, YIN X Y, WU G C. Elastic impedance parameteriztion and inversion with Yong's modulus and Poisson's ratio[J]. Geophysics, 2013, 78(6): N35-N42. DOI:10.1190/geo2012-0529.1 |
| [12] |
周林, 廖建平, 李景叶, 等. 基于精确Zoeppritz方程的储层含油气性预测方法[J]. 地球物理学报, 2021, 64(10): 3788-3806. ZHOU Lin, LIAO Jianping, LI Jingye, et al. Prediction method of reservoir oil-gas potential based on exact Zoeppritz equations[J]. Chinese Journal of Geo-physics, 2021, 64(10): 3788-3806. DOI:10.6038/cjg2021P0099 |
| [13] |
宋磊, 印兴耀, 宗兆云, 等. 基于先验约束的深度学习地震波阻抗反演方法[J]. 石油地球物理勘探, 2021, 56(4): 716-727. SONG Lei, YIN Xingyao, ZONG Zhaoyun, et al. Deep learning seismic impedance inversion based on prior constraints[J]. Oil Geophysical Prospecting, 2021, 56(4): 716-727. |
| [14] |
TARANTOLA A. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics, 1984, 49(8): 1259-1266. DOI:10.1190/1.1441754 |
| [15] |
TARANTOLA A. A strategy for nonlinear inversion of seismic reflection data[J]. Geophysics, 1986, 51(4): 1893-1903. |
| [16] |
VIRIEUX J, OPERTO S. An overview of full-waveform inversion in exploration geophysics[J]. Geophysics, 2009, 74(6): WCC1-WCC26. DOI:10.1190/1.3238367 |
| [17] |
AKI K, RICHARDS P G. Quantitative Seismology(2nd Edition)[M]. University Science Books, Sau-salito, 2002.
|
| [18] |
SIRGUE L. The importance of low frequency and large offset in waveform inversion[C]. Extended Abstracts of 68th EAGE Conference & Exhibition, 2006, A037.
|
| [19] |
BLEISTEIN N, STOCKWELL J W, COHEN J K. Mathematics of Multidimensional Seismic Imaging, Migration, and Inversion[M]. Springer, New York, 2001.
|
| [20] |
陈生昌, 周华敏. 再论地震数据偏移成像[J]. 地球物理学报, 2016, 59(2): 643-654. CHEN Shengchang, ZHOU Huamin. Re-exploration to migration of seismic data[J]. Chinese Journal of Geophysics, 2016, 59(2): 643-654. |
| [21] |
ZHANG Y, RATCLIFFE A, DUAN L, et al. Velocity and impedance inversion based on true amplitude reverse time migration[C]. SEG Technical Program Expanded Abstracts, 2013, 32: 949-953.
|
| [22] |
DUAN L, PENG L Z, ZHANG Y. Band-limited impedance perturbation inversion using cross-correlative least-squares RTM[C]. SEG Technical Program Expanded Abstracts, 2014, 33: 3720-3725.
|
| [23] |
BLEISTEIN N, ZHANG Y, XU S, et al. Migration/inversion: think image point coordinates, process in acquisition surface coordinates[J]. Inverse Problem, 2005, 21(5): 1715-1744. DOI:10.1088/0266-5611/21/5/013 |
| [24] |
陈生昌, 周华敏. 基于反射波动方程的叠前地震反射数据波阻抗相对变化成像研究[J]. 石油物探, 2017, 56(5): 651-657. CHEN Shengchang, ZHOU Huamin. A relative impedance variation imaging of pre-stack seismic reflection data based on reflection wave equation[J]. Geophysical Prospecting for Petroleum, 2017, 56(5): 651-657. DOI:10.3969/j.issn.1000-1441.2017.05.005 |
| [25] |
陈生昌. 基于反射波动方程的地震反射数据波形成像[J]. 石油地球物理勘探, 2018, 53(3): 487-501. CHEN Shengchang. Waveform imaging of seismic reflection data based on reflection wave equation[J]. Oil Geophysical Prospecting, 2018, 53(3): 487-501. |
| [26] |
陈生昌. 用于地震反射数据偏移的反射波方程[J]. 石油物探, 2019, 58(3): 433-443. CHEN Shengchang. Reflection wave equations for the migration of seismic reflected data[J]. Geophysical Prospecting for Petroleum, 2019, 58(3): 433-443. |
| [27] |
TARANTOLA A. Inverse Problem Theory and Methods for Model Parameter Estimation[M]. Society for Industrial and Applied Mathematics, Philadelphia, 2004.
|
| [28] |
STOLT R H, WEGLEIN A B. Seismic Imaging and Inversion: Application of Linear Inverse Theory[M]. Cambridge University Press, New York, 2012.
|
| [29] |
DEVANEY J. Mathematical Foundations of Imaging, Tomography and Wavefield Inversion[M]. New York: Cambridge University Press, 2012.
|
| [30] |
SAVA P C, FOMEL S. Angle-domain common-image gathers by wavefield continuation methods[J]. Geophysics, 2003, 68(3): 1065-1074. |
| [31] |
YOON K, MARFURT K J. Reverse-time migration using the Poynting vector[J]. Exploration Geophy-sics, 2006, 37(1): 102-107. |



 陈生昌, 浙江省杭州市西湖区浙大路38号浙江大学地球科学学院,310027。Email:
陈生昌, 浙江省杭州市西湖区浙大路38号浙江大学地球科学学院,310027。Email: