在饱和流体介质中,地震波发生频散和衰减的机制有多种,如地震波诱导流体流动[1-4]、地震波散射[5-6]、热弹性效应及相变等。其中,对前两种机制的研究最广泛[7-9],而第一种机制与储层孔隙结构、流体性质以及渗流特征密切相关[10]。
近些年,关于各向异性介质地震波频散和衰减的研究越来越多,在理论[11-12]和实验[13-14]两方面都取得了极大进展。在裂缝性孔隙介质中,当地震波通过裂缝时会挤压裂缝,并产生局部的压力梯度[15-16],为了平衡该压力梯度,黏弹性流体发生流动——地震波诱导流体流动。流体流动并不是瞬时完成的,需要一定的时间(松弛时间)重新达到压力平衡,因此地震波传播具有频变特性。松弛时间的倒数(特征频率)决定了地震波随频率发生频散(或衰减)的频率范围,并将频变特性分为低频特性和高频特性。当地震波频率较低时,孔隙流体有足够多的时间发生流动而达到平衡,因此孔隙空间(孔隙和裂缝)呈柔性特征,称为“松弛”状态;当地震波频率较高时,孔隙流体没有时间发生流动,被“困在”孔隙空间内,称为“非松弛状态”,可将裂缝视为孔隙背景介质中的孤立裂缝。因此,在低频极限和高频极限时,地震波不发生频散和衰减,而在中间频带,压力得到部分平衡,地震波产生频散和衰减。当介质中只有孔隙时,特征频率与微观的松弛时间有关;当介质中存在中观尺度裂缝(远大于孔隙尺度,但远小于波长)时,存在两种尺度的流体流动,对应两个松弛时间(特征频率),即与孔隙有关的微观松弛时间和与裂缝相关的中观松弛时间。这两种尺度的流体流动共同导致地震波的频散和衰减。微观尺度的流体流动往往发生在超声波频带,而中观尺度的流体流动一般发生在地震频带[17]。
基于Biot黏弹性理论和喷射流理论,Chapman[3]讨论了孔隙和微裂缝之间的流体流动,并引入一组定向排列的中观尺度裂缝,将其扩展为横向各向同性(TI)介质中的喷射流模型。大多数各向异性介质地震波衰减的研究只针对TI介质,即包含一组垂向裂缝[18]。实际上,由于成岩作用和地层压力等因素,储层中往往存在多组正交或斜交裂缝[19],因此研究含多组裂缝储层的地震波频散和衰减非常必要。Chapman[20]建立了包含两组裂缝的中观尺度喷射流模型,但是没有讨论两组裂缝对特征频率、频散和衰减幅度的影响。Chapman模型本质上是基于叠加理论的一阶近似模型,因此启发人们利用黏弹性模型表征Chapman模型,并将其扩展为包含多组裂缝的情况。
本文首先对Chapman模型数值模拟,讨论裂缝参数对特征频率和频散、衰减幅度的作用,然后分析Chapman模型和标准线性固体模型之间的关系,最后建立利用广义标准线性固体模型计算包含多组裂缝储层的频变纵波模量的方法。该方法利用低频、高频极限模量和模量损失表征地震波的频散和衰减特性,其中模量损失可表征每组裂缝的贡献。同时给出了低频、高频极限模量的计算方法。本文旨在提出一种简便、可行的方法,分析含多组不同长度和方向裂缝储层的纵波频变特性,并为处理复杂裂缝储层提供一个实用的岩石物理模型。
1 Chapman模型Chapman模型的孔隙空间包括球状孔隙、硬币状微裂缝和硬币状中观尺度裂缝。其中:微裂缝的尺度与孔隙相同;中观尺度裂缝的尺度远大于孔隙,而小于地震波波长。孔隙及微裂缝呈随机分布,裂缝定向排列,实际应用时一般忽略微裂缝的作用。Chapman模型中最重要的参数是流体的松弛时间。流体流动发生在两个尺度上,因此存在两个松弛时间:微观尺度松弛时间τm,与孔隙结构等有关,一般由实验室测定;中观尺度松弛时间τf,不仅与孔隙结构相关,还与裂缝参数相关
| $ \tau_{\mathrm{f}}=\frac{r}{\zeta} \tau_{\mathrm{m}} $ | (1) |
式中:r为裂缝半径;ζ是颗粒尺度(孔隙尺度)。由式(1)可以看出,τf与r成正比。当r增加时(假设裂缝密度和裂缝纵横比保持不变),比表面积减小,必须有更多的流体通过单位表面积以平衡压力,因此需要更多的时间[21]。根据Chapman裂缝模型,包含两组定向排列裂缝的孔隙介质的频变刚度矩阵为
| $ \boldsymbol{C}=\boldsymbol{C}^0-\phi \boldsymbol{C}^1-\varepsilon_{\mathrm{f}}^1 \boldsymbol{C}^2-\varepsilon_{\mathrm{f}}^2 \boldsymbol{C}^3 $ | (2) |
式中:C0为不含孔隙的背景介质刚度张量;C1为孔隙修正项;C2和C3为两组裂缝的修正项;ϕ为孔隙度;εf1和εf2分别为两组裂缝的密度。C1、C2和C3均为复数形式,包含了衰减信息,是基质参数、流体参数、裂缝参数和频率的函数,其推导过程和具体形式见文献[20]。特征频率是地震波频散和衰减最大时的频率[22],因此本文定义特征频率为纵波逆品质因子QP-1(QP-1=Im(VP2)/Re(VP2),VP为纵波速度,Im(·)、Re(·)分别表示取虚部、实部)最大时的频率。通过式(2)得到C,利用Christoffel方程计算VP及QP-1随频率的变化关系。
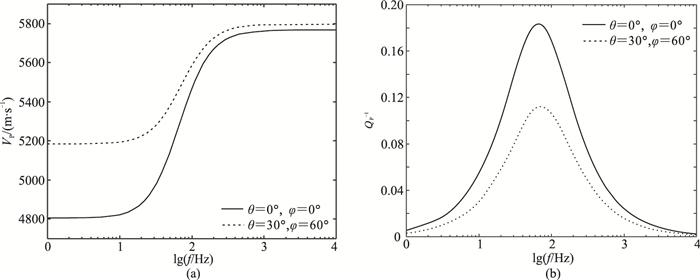
2 裂缝参数对纵波衰减的作用 2.1 裂缝方向对地震波的作用在笛卡尔坐标系中,假定P波垂直入射(沿z轴方向入射)。图 1为不同裂缝方向的VP和QP-1随频率f的变化曲线。由图可见:①在整个频带上,θ=0°、φ=0°的VP小于θ=30°、φ=60°(图 1a),但前者的高频、低频的速度差(纵波模量损耗)大于后者,这是由于当θ=0°、φ=0°时裂缝平面法线方向为z轴方向,地震波对裂缝的挤压作用最大所致。②QP-1随f的变化(图 1b)与VP的变化规律一致,即频散(高频、低频的速度差)越大,衰减(QP-1的极大值)也越大。
|
图 1 不同裂缝方向的VP(a)和QP-1 (b)随频率f的变化曲线 假定固体颗粒的拉梅系数分别为λ=51GPa、μ=29 GPa,密度为ρ=2710kg/m3,孔隙度ϕ=8%。微观尺度的松弛时间为4×10-7s,ζ=200×10-6m。裂缝法向方向失量n=(cosθsinφ, sinθsinφ, cosφ),θ为方位角,φ为倾角。模型中只有一组裂缝,r=1m,裂缝密度εf=0.04 |
图 2为不同入射方向的VP和QP-1随f的变化曲线。由图可见,VP(图 2a)和QP-1(图 2b)的幅度随着入射方向不同而变化,虽然存在两组裂缝,但只有一个特征频率。综上所述,裂缝方位(图 1)和地震波入射方向(图 2)只影响地震波挤压裂缝的强度,即只影响频散幅度和衰减幅度,而不影响特征频率,即不影响频散频带和衰减频带。

|
图 2 不同入射方向的VP (a)和QP-1(b)随f的变化曲线 地震波入射方向由入射角Θ和方位角Φ决定。模型中包含两组裂缝(θ=0°、φ=0°和θ=30°、φ=60°),r=1m,εf1=εf2=0.02 |
在笛卡尔坐标系中,设P波垂直入射(沿z轴方向入射)。图 3为不同r组合的VP和QP-1随f的变化曲线。由图可见,存在两个速度快速变化频带(图 3a),对应QP-1的两个极值点(图 3b),指示了与r对应的两个特征频率。由于两种r组合的总裂缝密度相同,因此两种情况的高频、低频速度相等。但是两种r组合的两组裂缝的r不一致,因此导致第二个特征频率的位置改变。

|
图 3 不同r组合的VP (a)和QP-1 (b)随f的变化曲线 模型中包含两组水平排列的裂缝(θ=0°、φ=0°),法线方向为(0, 0, 1)。εf1=εf2=0.02 |
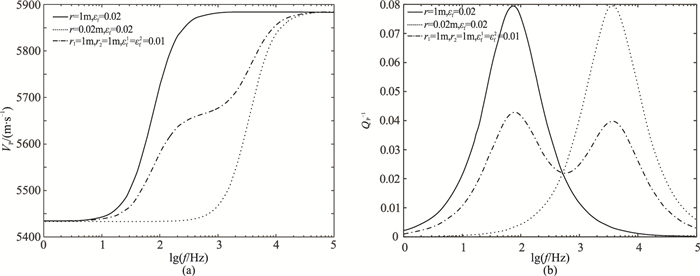
为了分离两组裂缝的作用,考察不同裂缝发育情况对纵波衰减的作用。图 4为不同裂缝发育情况的VP和QP-1随f的变化曲线。由图可见:①因为模型的总裂缝密度相同,所以不同裂缝发育情况的高、低频速度相同(图 4a)。②模型中只有一组裂缝时,VP (图 4a)和QP-1(图 4b)曲线形态完全相同,仅特征频率不同。③模型中包含两组不同r的裂缝时,存在两个转换频带(特征频率)。④不同裂缝发育情况的VP (或QP-1)曲线间存在某种代数关系,因此可以利用单组裂缝的VP (或QP-1)曲线表示两组甚至多组裂缝的VP (或QP-1)曲线。
|
图 4 不同裂缝发育情况的VP(a)和QP-1 (b)随f的变化曲线 |
黏弹性模型可以描述具有弛豫行为的黏弹性介质[23]。Picotti等[24]利用Cole-Cole模型研究了斑块饱和模型的地震波传播特性与频率变化规律,指出标准线性固体(SLS)模型适合模拟Biot理论模型和喷射流理论模型,而Cole-Cole模型可更好地近似斑块饱和模型。Chapman模型本质上是喷射流模型,因此可利用SLS模型对其模拟。弹性体和Kelvin-Voigt模型串联构成SLS模型,多个SLS模型并联构成广义标准线性固体(GSLS)模型。SLS模型的关键参数包括高频极限模量、低频极限模量和特征频率。通过上述数值模拟可知,裂缝半径控制特征频率,而裂缝方向、地震波入射方向和裂缝密度影响低频极限和高频极限模量(或最大逆品质因子),即控制频散和逆品质因子曲线形态。因此利用SLS模型近似Chapman模型的关键是寻找表征裂缝方向、地震波入射方向和裂缝密度共同作用的参数。
3.1 SLS模型模拟单裂缝模型当模型中只有一组裂缝时,复模量M可由高频极限纵波模量M∞、低频极限纵波模量M0和特征圆频率ωc表示为
| $ M(\omega)=\frac{M_{\infty}\left(M_0+\mathrm{i} \frac{\omega}{\omega_{\mathrm{c}}} \sqrt{M_0 M_{\infty}}\right)}{M_{\infty}+\mathrm{i} \frac{\omega}{\omega_{\mathrm{c}}} \sqrt{M_0 M_{\infty}}} $ | (3) |
式中M∞和M0为实数,与圆频率ω无关,即在低频极限和高频极限条件下介质呈弹性性质。QP-1也可通过复模量的虚部与实部的比值表示
| $ Q_{\mathrm{P}}^{-1}=\frac{\operatorname{Im}(M)}{\operatorname{Re}(M)}=\frac{M_{\infty}-M_0}{\sqrt{M_{\infty} M_0}} \frac{\frac{\omega}{\omega_{\mathrm{c}}}}{1+\left(\frac{\omega}{\omega_{\mathrm{c}}}\right)^2} $ | (4) |
最大逆品质因子为
| $ Q_{\mathrm{P}, \max }^{-1}=\frac{M_{\infty}-M_0}{2 \sqrt{M_{\infty} M_0}} $ | (5) |
式中
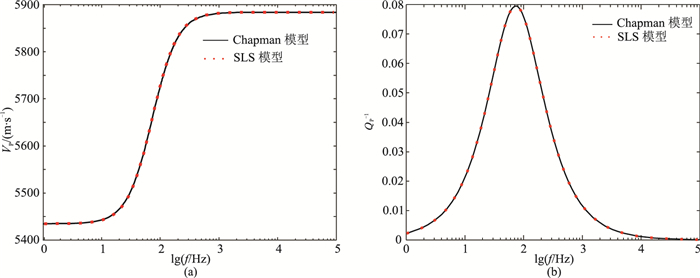
VP与M之间的关系为M=ρVP2(ρ为介质密度),因此通过此关系将低频极限地震波速度V0、高频极限地震波速度V∞转化为M0和M∞。图 5为SLS模型对Chapman单裂缝模型的模拟结果,可见拟合效果较好。
|
图 5 SLS模型对Chapman单裂缝模型的模拟结果 (a)VP;(b)QP-1 |
对于两组裂缝的情况,可以利用两组裂缝的模量损失代表两组裂缝的贡献。将式(3)拓展为包含两个特征频率的形式
| $ \begin{array}{r} M(\omega)=\frac{D^1}{D^1+D^2} \frac{M_{\infty}\left(M_0+\mathrm{i} \frac{\omega}{\omega_{\rm{c}}^1} \sqrt{M_0 M_{\infty}}\right)}{M_{\infty}+\mathrm{i} \frac{\omega}{\omega_{\rm{c}}^1} \sqrt{M_0 M_{\infty}}}+ \\ \frac{D^2}{D^1+D^2} \frac{M_{\infty}\left(M_0+\mathrm{i} \frac{\omega}{\omega_{\rm{c}}^2} \sqrt{M_0 M_{\infty}}\right)}{M_{\infty}+\mathrm{i} \frac{\omega}{\omega_{\rm{c}}^2} \sqrt{M_0 M_{\infty}}} \end{array} $ | (6) |
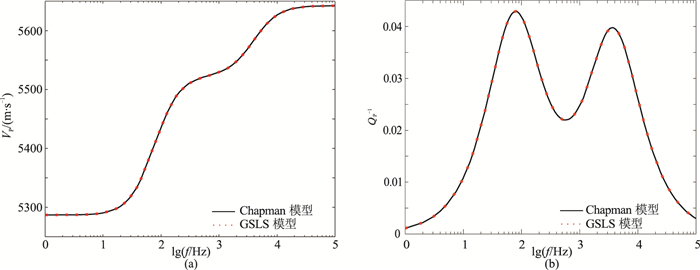
式中:ωc1和ωc2分别为两组裂缝的特征频率;D1和D2分别为两组裂缝的模量损失。当两组裂缝的产状、密度完全相同时,式(6)退化为式(3)。图 6为GSLS模型对Chapman双裂缝模型的模拟结果,可见拟合效果较理想。
|
图 6 GSLS模型对Chapman双裂缝模型的模拟结果 (a)VP;(b)QP-1 模型中包含两组裂缝,r1=0.02m,r2=1m,εf1=εf2=0.01 |
将式(6)拓展为包含n组裂缝的情况
| $ M(\omega)=\sum\limits_{k=1}^n \frac{D^k}{\sum\limits_{k=1}^n D^k} \frac{M_{\infty}\left(M_0+\mathrm{i} \frac{\omega}{\omega_{\mathrm{c}}^k} \sqrt{M_0 M_{\infty}}\right)}{M_{\infty}+\mathrm{i} \frac{\omega}{\omega_{\mathrm{c}}^k} \sqrt{M_0 M_{\infty}}} $ | (7) |
式中:ωck为第k组裂缝的特征圆频率,体现了裂缝半径的影响;Dk为第k组裂缝的模量损失,体现了裂缝密度、裂缝方位和地震波入射方向的共同作用。因此,利用式(7)可以研究包含多组裂缝模型的地震波频变特性。ωck和Dk可以通过Chapman模型计算。但是,包含多组裂缝模型的M∞和M0是未知的,由Chapman双裂缝模型并不能得到。
由于Chapman模型在低频时与Gassmann方程一致,在高频时与Hudson裂缝模型一致。因此,可以利用各向异性Gassmann方程计算M0,利用Hudson模型计算M∞,再通过Chapman模型得到ωck和Dk,进而通过式(7)得到M(ω),最终计算VP和QP-1。下文讨论存在多组裂缝时计算M∞和M0的方法。
在低频极限条件下,饱和流体的Chapman模型的孔隙校正项和裂缝校正项耦合在一起,无法直接分离纯裂缝校正项。但是对于干燥的Chapman模型,孔隙校正项和裂缝校正项是解耦的,因此首先令模型为干燥模型,即假定孔隙空间中的包含物密度及体积模量均为0,利用单裂缝Chapman模型得到低频极限条件的刚度矩阵,并分离孔隙校正项Cp、背景介质刚度矩阵Cb及裂缝修正项Cf,通过改变裂缝参数,可得到不同裂缝参数对应的修正项Cfk。由于Chapman单裂缝模型是VTI介质模型,因此通过矩阵旋转将Cfk变换到统一坐标系。由于低频极限条件的裂缝修正项是独立且线性可加的,故将Cfk相加可得到多组裂缝的总修正项,即CFlow=∑Cfk。因此,包含多组裂缝的干燥岩石在低频极限条件的有效刚度矩阵为
| $ \boldsymbol{C}^{\mathrm{dry}}=\boldsymbol{C}_{\mathrm{b}}-\boldsymbol{C}_{\mathrm{p}}-\boldsymbol{C}_{\mathrm{F}}^{\mathrm{low}} $ | (8) |
然后利用各向异性Gassmann方程将式(8)转换为饱和流体等效刚度矩阵Csat,其各分量为
| $ \boldsymbol{C}_{i j}^{\mathrm{sat}}=\boldsymbol{C}_{i j}^{\mathrm{dry}}+\alpha_i \alpha_j N \quad i, j=1,2, \cdots, 6 $ | (9) |
其中
| $ \left\{\begin{array}{l} \alpha_i=1-\frac{\sum\limits_{m=1}^3 \boldsymbol{C}_{i m}^{\mathrm{dry}}}{3 K_{\mathrm{g}}} \\ N=\frac{K_{\mathrm{g}}}{\left(1-\frac{K^*}{K_{\mathrm{g}}}\right)-\phi_{\mathrm{s}}\left(1-\frac{K^*}{K_1}\right)} \end{array}\right. $ | (10) |
而
| $ K^*=\frac{1}{9} \sum\limits_{i=1}^3 \sum\limits_{j=1}^3 \boldsymbol{C}_{i j}^{\mathrm{dry}} $ |
式中:Kg和Kl分别为基质和流体的体积模量;ϕs=ϕp+ϕf为总孔隙度, ϕp为孔隙孔隙度,ϕf为裂缝孔隙度。
在高频极限条件下,可以忽略孔隙和裂缝间的流体流动。因此,无论是干燥还是饱和状态,Cp和Cf都是解耦的,可以直接得到裂缝饱和流体时的校正项Cfhigh。通过矩阵旋转、将Cfhigh相加便得到高频条件的多组裂缝的总校正项CFhigh,则高频极限条件的等效刚度矩阵为
| $ C^{\text {high }}=C_{\mathrm{b}}-\boldsymbol{C}_{\mathrm{p}}-\boldsymbol{C}_{\mathrm{F}}^{\text {high }} $ | (11) |
在得到低频和高频极限条件的等效刚度矩阵后,通过求解Christoffel方程计算V0(或V∞),进而计算M0=ρV02(或M∞=ρV∞2)。然后由式(7)计算M(ω),进而得到VP和QP-1。
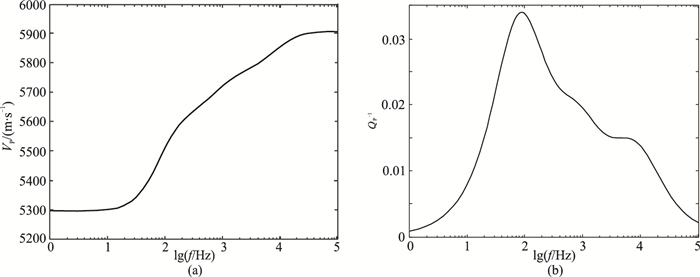
建立一个包含三组相互正交裂缝的模型,考察正交各向异性介质的VP和QP-1随f的变化规律。图 7为正交各向异性介质模型的VP和QP-1随f的变化曲线。由图可见,VP曲线存在三个单调上升的频带(图 7a),对应QP-1的三个极值点(图 7b),分别指示三组裂缝的不同特征频率,但其中两个特征频率不清晰。之所以产生上述曲线特征,是由于地震波垂直入射时,水平分布的裂缝(法线方向平行于z轴)受的挤压应力最大,而其裂缝半径最大,因此特征频率最低。而另两组裂缝的特征频率不明显。若存在更多组裂缝,QP-1在较宽的频带内近似为常数(常Q模型),则VP呈线性变化。
|
图 7 正交各向异性介质模型的VP(a)和QP-1(b)随f的变化曲线 模型包含三组裂缝,三组裂缝的法向方向分别与直角坐标系的三个坐标轴平行。固体颗粒的拉梅系数分别为λ=51GPa、μ=29GPa,ρ=2710kg/m3,ϕ=8%。三组裂缝的裂缝半径、裂缝密度分别为:r1=0.01m、εf1=0.02;r2=0.1m、εf2=0.02;r3=1m、εf3=0.02。流体参数分别为Kl=25MPa、ρl=65kg/m3 |
本文首先回顾了Chapman双裂缝模型的基本理论,分析了不同参数对纵波频散和衰减的影响,然后利用SLS模型模拟Chapman模型。通过GSLS模型可以计算包含多组裂缝的裂缝性孔隙介质中P波的频变特性。根据低频极限和高频极限情况下Chapman模型中孔隙校正项和裂缝校正项的解耦特征,提出了计算低频极限模量和高频极限模量的方法。在低频条件时,裂缝校正项与包含孔隙的背景项只有在干燥Chapman模型时才是解耦的。在高频条件时,裂缝校正项和包含孔隙的背景项无论在干燥还是饱和Chapman模型中都是解耦的,因此可利用Chapman模型和各向异性Gassmann方程得到低频模量,利用Chapman模型得到高频模量。
值得注意的是,当地震波传播方向与裂缝平行时,质点振动方向与裂缝方向平行,裂缝的挤压变形较小,特别是当裂缝中充斥着水、油等体积模量相对较大的流体时,裂缝的挤压变形较小。在这种情况下,裂缝表现出较强的刚度,裂缝的变形量较小。因此,P波速度随频率的变化很小,P波衰减达到最小。另外,本文没有考虑在裂缝互相连通的情况下流体在裂缝之间流动所产生的特征频率的现象。
虽然Chapman模型本身存在一些假设条件限制,如模型适应于孔隙度较低、裂缝形状最好为“硬币状”、孔隙空间中仅饱和单一流体等,影响了该模型的实际应用效果。但本文提出的基于Chapman模型和GSLS模型计算包含多组裂缝介质的P波频变特性的方法,对于研究各向异性介质的地震波场特征及地震响应机理具有一定实际意义。
| [1] |
BIOT M A. Theory of propagation of elastic waves in fluid-saturated porous solid.Ⅰ.Low-frequency range[J]. Journal of the Acoustical Society of America, 1956, 28(2): 168-178. DOI:10.1121/1.1908239 |
| [2] |
BIOT M A. Theory of propagation of elastic waves in a fluid-saturated porous solid.Ⅱ.Higher frequency range[J]. Journal of the Acoustical Society of America, 1956, 28(2): 179-191. DOI:10.1121/1.1908241 |
| [3] |
CHAPMAN M. Frequency dependent anisotropy due to meso-scale fractures in the presence of equant porosity[J]. Geophysical Prospecting, 2003, 51(5): 369-379. DOI:10.1046/j.1365-2478.2003.00384.x |
| [4] |
凌云, 杜向东, 曹思远. 基于Zener线性体的黏弹孔隙介质衰减频散特征分析[J]. 地球物理学进展, 2017, 32(1): 205-209. LING Yun, DU Xiangdong, CAO Siyuan. Attenuation and dispersion characteristics analysis in visco-poroelastic medium based on Zener linear solid[J]. Progress in Geophysics, 2017, 32(1): 205-209. |
| [5] |
李灿苹, 刘学伟. 随机均匀介质地震波振幅属性研究[J]. 石油物探, 2009, 48(5): 465-469. LI Canping, LIU Xuewei. Study on amplitude attribu-tes of seismic wave in random-uniform medium model[J]. Geophysical Prospecting for Petroleum, 2009, 48(5): 465-469. DOI:10.3969/j.issn.1000-1441.2009.05.006 |
| [6] |
YUAN S, WANG S, MA M, et al. Sparse Bayesian learning-based time-variant deconvolution[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(11): 6182-6194. DOI:10.1109/TGRS.2017.2722223 |
| [7] |
刘建华, 胥颐, 郝天珧. 地震波衰减的物理机制研究[J]. 地球物理学进展, 2004, 19(1): 1-7. LIU Jianhua, XU Yi, HAO Tianyao. Study on physical mechanism of the seismic wave attenuation[J]. Progress in Geophysics, 2004, 19(1): 1-7. DOI:10.3969/j.issn.1004-2903.2004.01.001 |
| [8] |
刘炯, 巴晶, 马坚伟, 等. 随机孔隙介质中地震波衰减分析[J]. 中国科学: 物理学力学天文学, 2010, 40(7): 858-868. |
| [9] |
BAIRD A F, KENDALL J M, ANGUS D A. Frequency-dependent seismic anisotropy due to fractures: Fluid flow versus scattering[J]. Geophysics, 2013, 78(2): WA111-WA122. DOI:10.1190/geo2012-0288.1 |
| [10] |
白旭明, 张以明, 杜启振, 等. 黏弹性裂缝诱导各向异性介质地震波场传播特征--以束鹿凹陷沙河街组三段下亚段泥灰岩储层为例[J]. 石油学报, 2015, 36(增刊1): 50-58. BAI Xuming, ZHANG Yiming, DU Qizhen, et al. Seismic wave field propagation characteristics of viscoelastic fracture-induced anisotropic medium: a case study of calcilutite reservoirs in the lower part of Member 3 of Shahejie Formation, Shulu sag[J]. Acta Petrolei Sinica, 2015, 36(Z1): 50-58. |
| [11] |
刘芸菲, 陈学华, 罗鑫, 等. 双相不混溶流体饱和裂缝-孔隙岩石依赖频率的地震响应数值分析[J]. 石油地球物理勘探, 2020, 55(4): 821-830. LIU Yunfei, CHEN Xuehua, LUO Xin, et al. Numerical analysis of frequency-dependent seismic responses from fractured-porous rock saturated with two-phase immiscible fluids[J]. Oil Geophysical Prospecting, 2020, 55(4): 821-830. |
| [12] |
尹志恒, 狄帮让, 魏建新, 等. 裂缝参数对纵波能量衰减影响的物理模型研究[J]. 石油地球物理勘探, 2012, 47(5): 728-734, 753. YIN Zhiheng, DI Bangrang, WEI Jianxin, et al. P-wave attenuation by fracture parameter on physical models[J]. Oil Geophysical Prospecting, 2012, 47(5): 728-734, 753. |
| [13] |
李民龙, 刘浩杰, 杨宏伟, 等. 跨频段岩石波速及频散的实验研究[J]. 石油地球物理勘探, 2020, 55(2): 373-378. LI Minlong, LIU Haojie, YANG Hongwei, et al. Experimental study on cross-frequency wave velocity and dispersion in rocks[J]. Oil Geophysical Prospecting, 2020, 55(2): 373-378. |
| [14] |
张繁昌, 桑凯恒, 路亚威. 硬币型裂缝介质的频散与衰减[J]. 石油地球物理勘探, 2019, 54(4): 836-843. ZHANG Fanchang, SANG Kaiheng, LU Yawei. Frequency dispersion and attenuation of porous rocks with penny shaped fractures[J]. Oil Geophysical Prospecting, 2019, 54(4): 836-843. |
| [15] |
GUREVICH B, BRAJANOVSKI M, GALVIN R, et al. P-wave dispersion and attenuation in fractured and porous reservoirs-poroelasticity approach[J]. Geophysical Prospecting, 2009, 57(2): 225-237. |
| [16] |
MULLER T M, GUREVICH B, LEBEDEV M. Seismic wave attenuation and dispersion resulting from wave-induced flow in porous rocks-A review[J]. Geo-physics, 2010, 75(5): 75A147-75A164. |
| [17] |
段茜, 刘向君, 梁利喜, 等. 裂缝参数对纵波各向异性影响的数值模拟[J]. 石油地球物理勘探, 2020, 55(3): 575-583, 590. DUAN Xi, LIU Xiangjun, LIANG Lixi, et al. Numeri-cal simulation to the influence of fracture parameters on P-wave anisotropy[J]. Oil Geophysical Prospecting, 2020, 55(3): 575-583, 590. |
| [18] |
SAROUT J. Impact of pore space topology on permea-bility, cut-off frequencies and validity of wave propagation theories[J]. Geophysical Journal International, 2012, 189(1): 481-492. |
| [19] |
SHI P D, YUAN S Y, WANG T Y, et al. Fracture identification in a tight sandstone reservoir: A seismic anisotropy and automatic multisensitive attribute fusion framework[J]. IEEE Geoscience Remote Sensi-ng Letter, 2018, 15(10): 1525-1529. |
| [20] |
CHAPMAN M. Modeling the effect of multiple sets of mesoscale fractures in porous rock on frequency-dependent anisotropy[J]. Geophysics, 2009, 74(6): D97-D103. |
| [21] |
MAULTZSCH S, CHAPMAN M, LIU E, et al. Modelling frequency-dependent seismic anisotropy in fluid-saturated rock with aligned fractures: implication of fracture size estimation from anisotropic measurements[J]. Geophysical Prospecting, 2003, 51(5): 381-392. |
| [22] |
YUAN S Y, LIU Y, ZHANG Z, et al. Prestack stochastic frequency-dependent velocity inversion with rock-physics constraints and statistical associated hydrocarbon attributes[J]. IEEE Geoscience Remote Sensing Letter, 2019, 16(1): 140-144. |
| [23] |
PICOTTI S, CARCIONE J M, RUBINO J G, et al. A viscoelastic representation of wave attenuation in poro-us media[J]. Computer & Geoscience, 2010, 36(1): 44-53. |
| [24] |
PICOTTI S, CARCIONE J M. Numerical simulation of wave-induced fluid flow seismic attenuation based on the Cole-Cole model[J]. Journal of the Acoustical Society of America, 2017, 142(1): 134-145. |



 张金伟, 山东省青岛市黄岛区前湾港路579号山东科技大学地球科学与工程学院,266590。Email:
张金伟, 山东省青岛市黄岛区前湾港路579号山东科技大学地球科学与工程学院,266590。Email: 