② 中国石油西南油气田分公司勘探开发研究院,四川成都 610000
② Exploration and Development Research Institute, PetroChina Southwest Oil & Gasfield Company, Chengdu, Sichuan 610000, China
地震全波形反演利用完整的波场信息估算地下介质的属性模型,与传统方法相比,精度更高。全波形反演可在时间域或频率域进行,但无论在哪个域,计算成本都很高,这限制了它在实际生产中的应用。地震数值模拟作为全波形反演的重要组成部分,在很大程度上影响着反演精度和效率。当前波形反演中所使用的数值模拟方法按计算域可分为时间域和频率域。频率域的优势在于频率分量选取灵活、计算成本低。在具体的正演方法实现上,有限差分方法具有实现简单、占用内存小等特点被广泛使用[1]。
1972年,Lysmer等[2]提出了频率—空间域正演模拟方法;随后Marfurt[3]定量对比了时间域与频率域的声波和弹性波数值模拟方法,指出频率—空间域正演模拟比较适合多炮激发,且容易解决计算的不稳定性问题。由于频率域方法相较于时间域方法,频散现象更严重,为了降低频散误差,研究人员做了许多尝试。Jo等[4]提出了频率域波动方程的最优化9点差分格式,频散现象得到了较好压制,即每一波长内分布有4个网格点就能使相速度误差限制在1% 以内;Shin等[5]在此基础上提出了25点优化差分算子,使每一波长内的网格点数可进一步降低到2.5;吴国忱等[6]在此基础上建立了25点优化差分算子,实现了VTI介质准P波的数值模拟;刘璐等[7]提出了优化15点差分格式,有较高的计算效率和较好的频散压制效果;范娜等[8]提出了一种三维声波方程有限差分系数优化算法,在给定有限差分模板情况下即可求解出优化系数,较传统的差分系数具有更低的数值频散。唐超等[9]基于L1范数建立目标函数,采用交替方向乘子法(ADMM)求解交错网格有限差分系数,提出了一种新的声波方程交错网格优化有限差分正演模拟方法,数值试验表明该方法能将频散控制得更低。
以上方法大都基于方形网格,而实际模型通常是矩形网格。为此,Tang等[10]构建了一种二维自适应17点有限差分格式,该方法不仅适用于正方形网格,也适应于矩形网格,且将每一波长内的网格点数降低到2.4;Xu等[11]提出了一种自适应的9点有限差分格式,不仅适用于矩形网格,而且还具有一般25点格式的精度和最优化9点差分格式的效率。
另一方面,为提高频率域正演的计算效率,也出现了一些较实用的技术策略,如:殷文[12]针对频率—空间域有限差分弹性波的数值模拟,采用了流水线技术和分治策略进行并行计算,提高了计算效率;有研究人员实现了基于多重网格预条件的迭代法正演,并在标准模型上得到了较精确的结果[13-14];Du等[15]基于双共轭梯度稳定(BiCGstab)算法进行二维声波方程的数值模拟,在保证一定精度的条件下,相较于LU直接分解法大大减少了内存消耗和计算时间;Belonosov等[16]同样基于BiCGstab算法,提出了适用于三维各向同性非均质弹性波模拟的迭代求解器,结合混合并行技术(MPI与OpenMP相结合),加快了收敛速度、提高了效率;熊治涛等[17]在大地电磁响应计算中采用不完全LU直接分解法预条件因子的BiCGstab算法求解有限元方程,也得到了可靠的结果;Jiang等[18]开发了一种频率域多尺度有限差分方法,能够以较小的内存和较短的时间求解Helmholtz方程,可在低频情况下得到精确的解;Jaysaval等[19]使用Schur补迭代方法(即广义极小残量法),降低了求解Helmholtz方程的复杂度,提高了频率域数值模拟的计算效率;颜红芹[20]在利用声波散射理论进行VSP波场模拟的过程中,引入预条件算子和最小二乘方法,在计算优化的同时使过程更加稳定。上述策略均是基于固定网格进行的优化,有学者受到时间域数值模拟变网格技术的启发,还提出了频率域的变网格模拟方法,为提高频率域地震正演效率提供了新的思路:韩利等[21]根据频率域正演中不同频率间相互独立的特点,在低频段采用大网格、高频段采用小网格计算,实现了变网格步长模拟,在保证模拟精度的同时,减少了计算量和内存消耗;郭振波等[22]进一步发展了变网格技术,构建了起伏地表条件下的频域正演算法,计算效率可提高5倍以上,同时内存占用大幅减少;吴悠等[23]结合交错网格和混合网格完成了频率—空间域非均质声波方程有限差分模拟,有效提高了计算效率。
在频率域正演迭代法中,基于Krylov子空间的方法应用较为广泛。基于Krylov子空间法的BiCGstab算法因内存消耗小、收敛速度快,成了许多学者的选择,但在实现时往往需要设计较为复杂的预处理器,且在处理复杂模型时容易出现迭代不收敛的情况。针对现有频率域地震正演方法在求解时谐波动方程所遇到的问题,同时考虑计算的效率和稳定性,本文在传统的共轭梯度(CG)算法基础上,采用合理、优化的最小二乘共轭梯度参数,发展了一种混合共轭梯度迭代(MLSCG) 算法。试验结果表明,本文算法在保证计算精度的同时可高效地实现数值模拟,并且克服了传统迭代方法计算不稳定的缺点。
1 方法原理 1.1 波动方程的有限差分离散首先,将二维时间域声波方程进行傅里叶变换,得到频率域波动方程
| $ \nabla^2 P+\frac{\omega^2}{v^2} P=S(\omega) \delta\left(x-x_{\mathrm{s}}\right) \delta\left(z-z_{\mathrm{s}}\right) $ | (1) |
式中:ω为角频率;P(x, z, ω)为压力场;v为介质速度;S(ω)表示频率域震源项;xs、zs分别为震源横、纵坐标。
本文使用最优化9点有限差分格式[4],其最终的差分方程为
| $ \begin{aligned} &a \frac{P_{m+1, n}+P_{m-1, n}-4 P_{m, n}+P_{m, n+1}+P_{m, n-1}}{h^2}+(1-a) \frac{P_{m+1, n+1}+P_{m-1, n+1}-4 P_{m, n}+P_{m+1, n-1}+P_{m-1, n-1}}{2 h^2}+ \\ &\frac{\omega^2}{\nu^2}\left[b P_{m, n}+c\left(P_{m+1, n}+P_{m-1, n}+P_{m, n+1}+P_{m, n-1}\right)+\frac{1-b-4 c}{4}\left(P_{m+1, n+1}+P_{m-1, n+1}+P_{m+1, n-1}+P_{m-1, n-1}\right)\right]=S_{m, n} \end{aligned} $ | (2) |
式中:h是空间网格间隔;Pm, n表示点(m, n)处的压力场;a=0.5461、b=0.6248、c=0.09381是最优化差分系数。
时谐、常密度声波方程也可用Helmholtz方程表示为
| $ \left\{\begin{array}{l} L P=S \\ L=-K^2-\Delta \end{array}\right. $ | (3) |
式中:L为波算子;K=ω/v为波数;Δ是拉普拉斯算子。
使用有限差分将式(3)离散,得到线性系统
| $ \mathit{\boldsymbol{Ap}}{\rm{ = }}\mathit{\boldsymbol{b}} $ | (4) |
式中:A是大型稀疏复值矩阵;待求单频波场向量p由P离散得到;向量b由S离散得到。设计算网格的离散点数为i,空间维数是D,则A的尺度是iD×iD。频率域声波方程转化为线性方程组之后,如何求解该方程系统十分关键。一般的直接法是使用LU分解法,该方法计算精度高但占用内存大,耗费时间长,且难以模拟高维度、高密度采集;Krylov子空间迭代法中使用较多的是BiCGstab算法,该方法计算效率高,收敛速度快,但对计算稳定性条件要求较高,且容易出现迭代不收敛。为此,本文引入最小二乘混合共轭梯度迭代求解方法,在保持计算效率的条件下有效提高了计算的稳定性。
1.2 混合共轭梯度迭代算法计算数学中对大型不定方程组的求解,一般采用Krylov子空间迭代法,这类算法实际上是共轭梯度算法的推广。算法从初始值p0开始,迭代计算更新pk(其中k为迭代次数),直到剩余误差|b-Apk|达到足够小时求得近似解。若没有预处理器,这种方法收敛缓慢或根本不收敛[24]。为了提高计算稳定性和收敛速度,往往需要构造合理的预处理器。
CG算法是由Hestenes等[25]提出,其共轭梯度参数(CG(HS))定义为
| $ \beta_k^{\mathrm{HS}}=\frac{\boldsymbol{g}_{k+1}^{\mathrm{T}} \boldsymbol{y}_k}{\boldsymbol{d}_k^{\mathrm{T}} \boldsymbol{y}_k} $ | (5) |
式中:βkHS是CG参数;gk+1是f(x)在xk+1处的梯度,即gk+1=▽f(xk+1); yk是f(x)在xk+1和xk处梯度之差,即yk=gk+1-gk; dk是搜索方向,且满足
| $ \left\{\begin{array}{l} \boldsymbol{d}_0=-\boldsymbol{g}_0 \\ \boldsymbol{d}_{k+1}=-\boldsymbol{g}_{k+1}+\beta_k^{\mathrm{HS}} \boldsymbol{d}_k \end{array} \quad k=0, 1, \cdots, M\right. $ | (6) |
式中M为终止迭代次数。
由于CG算法的收敛速度较慢,Dai等[26]提出了修正的共轭梯度参数(CG(DY))
| $ \beta_k^{\mathrm{DY}}=\frac{\left\|\boldsymbol{g}_{k+1}\right\|^2}{\boldsymbol{d}_k^{\mathrm{T}} \boldsymbol{y}_k} $ | (7) |
该算法在一定程度上可以提高收敛速度[27]。
为了优化计算性能,本文给出一种混合算法,即MLSCG,有效结合了式(5)和式(7)各自的特性,新的共轭梯度参数为
| $ \beta_k^{\mathrm{MCG}}=\left(1-\theta_k\right) \beta_k^{\mathrm{HS}}+\theta_k \beta_k^{\mathrm{DY}} $ | (8) |
式中θk为最小二乘系数,可以通过最小二乘问题求出
| $ \left\{\begin{array}{l} {\mathit{\Theta}}(x)=\min _\theta\left\|\boldsymbol{d}_{k+1}^{\mathrm{MCG}}-\boldsymbol{d}_{k+1}^{\mathrm{ZZL}}\right\|^2 \\ \boldsymbol{d}_{k+1}^{\mathrm{MCG}}=-\boldsymbol{g}_{k+1}+\beta_k^{\mathrm{HS}} \boldsymbol{d}_k+\theta_k \frac{\boldsymbol{g}_{k+1}^{\mathrm{T}} \boldsymbol{g}_k}{\boldsymbol{s}_k^{\mathrm{T}} \boldsymbol{y}_k} \boldsymbol{s}_k \\ \boldsymbol{d}_{k+1}^{\mathrm{ZZL}}=-\boldsymbol{g}_{k+1}+\beta_k^{\mathrm{HS}} \boldsymbol{d}_k-\frac{\boldsymbol{g}_{k+1}^{\mathrm{T}} \boldsymbol{s}_k}{\boldsymbol{s}_k^{\mathrm{T}} \boldsymbol{y}_k} \boldsymbol{y}_k \end{array}\right. $ | (9) |
式中:Θ(x)是目标函数;dk+1MCG是MLSCG算法的搜索方向;dk+1ZZL是一种CG拓展算法的搜索方向[28];sk=αkdk,其中αk是迭代步长。
dkZZL搜索方向参数具有更快地收敛速度和较高的计算稳定性。最小二乘系数θk的选取原则是通过寻找已知的搜索方向dk+1ZZL和新的搜索方向dk+1MCG的误差平方和的最小值,充分结合上面所述的两种CG参数的优点,在保证收敛速度的条件下,使算法更稳定。若最小二乘系数计算耗费大量的时间,则会影响算法的计算效率。因此为了研究最小二乘系数计算对整体计算效率的影响,设计了三种尺寸模型,离散样点数分别为100×100、200×200、400×400,对应的稀疏矩阵模型分别为10000×10000、40000×40000、160000×160000。分别记录迭代一次的平均计算总用时和系数计算用时,测试结果如表 1所示。数值试验表明系数计算占迭代计算时长的1.8%~3.0%,不会对计算全过程产生太大影响。
|
|
表 1 最小二乘系数计算时间对比统计 |
使用迭代算法求解线性系统Ap=b,需要设置迭代误差ε用于控制迭代过程。迭代误差定义为
| $ \varepsilon=\frac{|\mathit{\boldsymbol{Ap}}-\mathit{\boldsymbol{b}}|}{|\mathit{\boldsymbol{b}}|} $ | (12) |
由于矩阵A具有对角占优且高度稀疏的特点,所以本文使用雅各比预处理算子进行优化,以加速迭代收敛。
为了说明MLSCG算法的特性,设计了1000×1000的稀疏矩阵求解问题。准确解为单位向量,迭代初值为零向量,最大相对误差是1.0×10-7。使用混合算法、BiCGstab算法等四种方法进行计算,所得到的迭代收敛曲线如图 1所示。由图可见:CG(HS)算法收敛速度较慢,但迭代过程相对稳定;CG(DY)收敛速度快,但稳定性条件较为苛刻;BiCGstab算法从曲线上看并不是很稳定,有一定的锯齿现象(在后续的模型试验中会有说明);MLSCG算法在提高收敛速度的同时,保持了算法的稳定性,并且在处理复杂线性系统时能够正确地得到近似解。
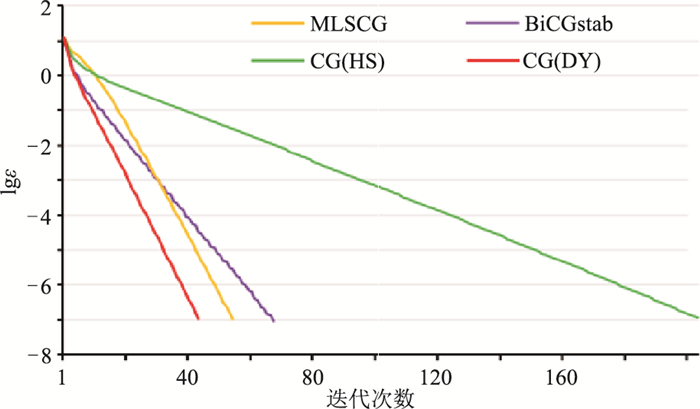
|
图 1 不同算法的迭代收敛曲线 |
时间复杂度是指执行算法所需要的计算工作量。设N是模型离散化后系数矩阵的阶数,M是总迭代次数。如果仅考虑单一炮记录的数值模拟,LU分解法和MLSCG算法的时间复杂度对比分析如表 2所示。可以看出,LU分解法的时间复杂度不管是在2D还是3D情况下都远大于MLSCG算法,这是因为MLSCG算法并不需要对线性系统进行分解,同时值得注意的是,在3D情况下,LU分解法的时间复杂度过高,导致其难以推广应用。
|
|
表 2 两种方法时间复杂度、内存需求对比 |
LU分解法和MLSCG算法的实际内存需求如表 2所示。两种方法的内存需求与N阶矩阵规模紧密相关,而MLSCG算法的内存需求和迭代次数无直接关系。在2D情况下,MLSCG算法的内存需求稍小于LU算法;但在3D情况下,MLSCG的内存优势较为明显。在模型实例中会有详细的两种方法的实际计算时间和内存消耗对比。
2 数值算例本文所有数值模拟的硬件参数为Intel(R)Xeon (R) Silver 4110 CPU @ 2.1GHz(8核16线程),RAM 32GB,模拟过程在单线程下进行。
2.1 层状介质模型为了验证频域数值方法的正确性和适用性,本文设计了层状声学介质模型(图 2)进行数值模拟。模型网格数为300×300;网格尺寸为5m×5m;震源为Ricker子波,主频为30Hz,位于(750m,750m);模型四周采用完全匹配层(Perfectly Matched Layer,PML)吸收边界条件,宽度为50个网格。通过数值模拟,可以得到不同方法的单频波场数据片(图 3)和合成波场快照(图 4)。
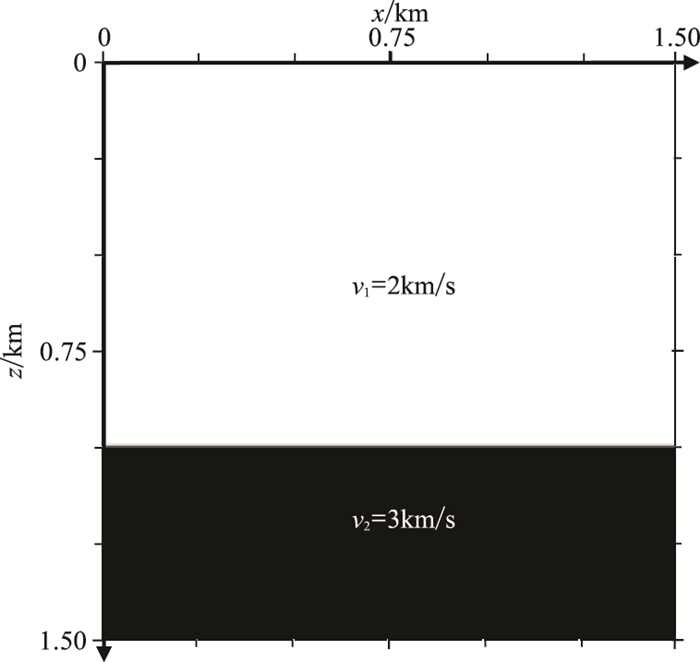
|
图 2 层状介质模型 |
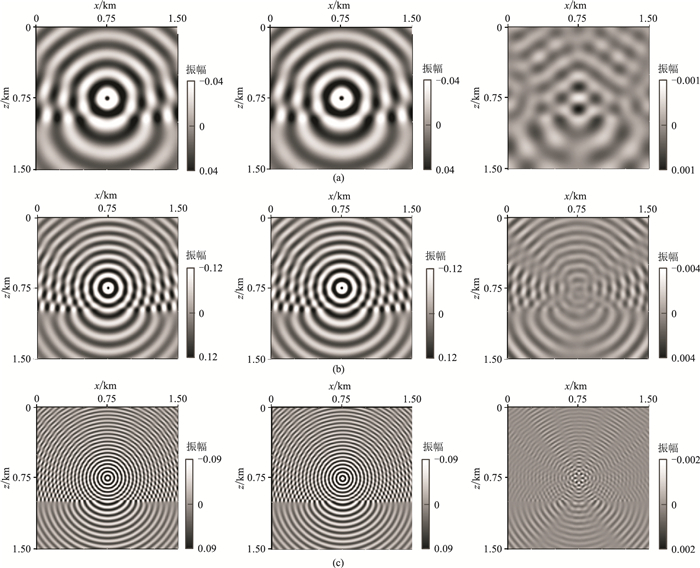
|
图 3 不同频率MLSCG法(左)、LU法(中)单频实部波场切片及其对应的残差对比(右) (a)10Hz;(b)30Hz;(c)50Hz |
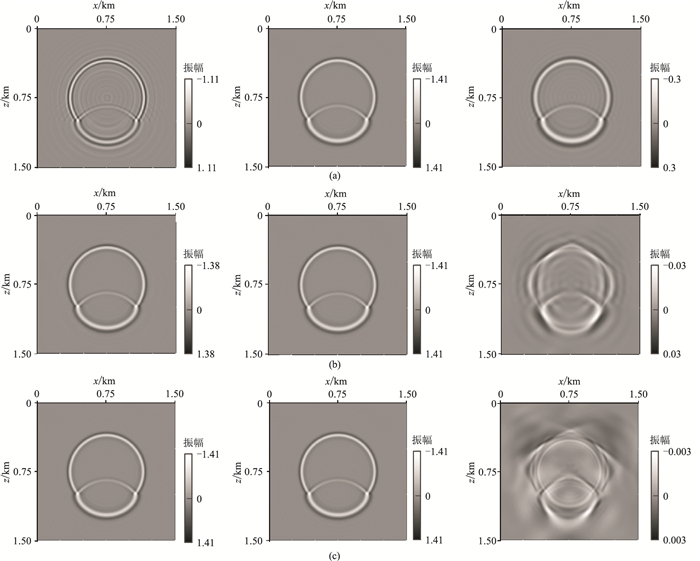
|
图 4 不同迭代误差条件下MLSCG法(左)、LU法(中)波场快照及其对应的残差对比(右) (a)ε=0.100%;(b)ε=0.010%;(c)ε=0.001% |
由图 3可见:①MLSCG迭代法在ε=0.01%条件下,得到的10、30、50Hz的波场切片与LU直接法的结果基本一致;②从波场残差来看,其振幅的相对变化范围在2%~4%,由此可证明本文算法具有较好的计算精度;③10、30、50Hz的波场幅值符合震源傅里叶变换后对应频率的振幅值;④在模型的速度分界面处波形出现相应的变化,上层波场受分界面处反射波的影响出现了局部的干涉现象;⑤30和50Hz单频波场残差变化具有一定的空间分布特征,以震源为中心在局部呈辐射状。
将不同的单频波场加权组合后可以得到时间域的合成波场快照(图 4)。图 4比较了3种迭代误差条件下MLSCG算法与LU分解法波场快照的差异性。需要说明的是,此处的波场记录是由60个单频波场分量(1~60Hz)叠加得到,波场快照时刻为200ms。由图 4可见:①当ε=0.100%时,与LU法结果相比,MLSCG迭代法波场快照出现了较为明显的频散现象;②当ε=0.010%时,两种方法的波场快照基本一致,相对偏差为2%;③当ε=0.001%时,两种方法的相对偏差仅为0.2%。
同时,为了进一步考察算法的计算效率,以及为MLSCG算法最大相对误差参数的设置提供参考,将MLSCG迭代法最大相对误差分别设置为0.1000%、0.0100%、0.0010%、0.0001%,与LU算法(相对误差为0)的计算时间对比如图 5所示。可以看出:ε=0.0100%时的计算时间是ε=0.1000%时的6倍;ε=0.0010%时的计算时间是ε=0.0100%时的1.6倍;ε=0.0001%计算时间仅是ε=0.0010%时的1.4倍;即使ε=0.0001%时所用时间也只是LU方法的48.72%。

|
图 5 不同精度的MLSCG法和LU法的计算时间对比 Ⅰ、Ⅱ、Ⅲ、Ⅳ分别对应ε=0.1000%、0.0100%、0.0010 %、0.0001%的MLSCG算法 |
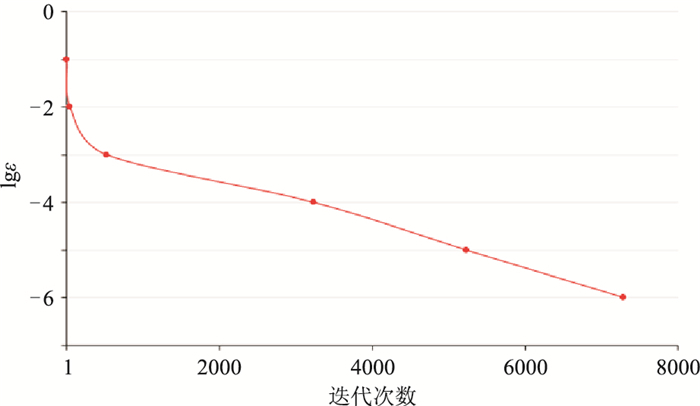
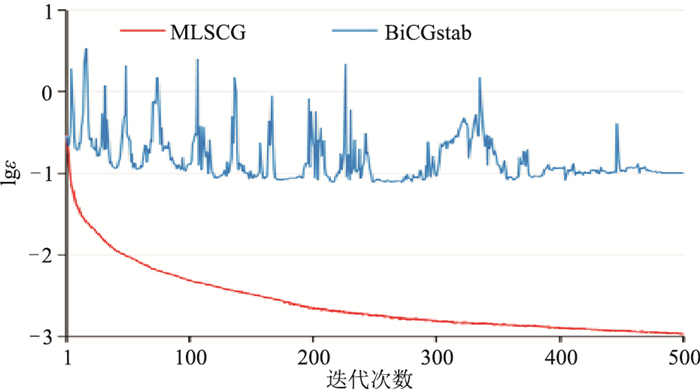
应用层状模型对算法的稳定性进行分析。当相对误差分别达到10%、1%、0.1%、0.01%、0.001%、0.0001%时,数值模拟所需迭代次数如图 6所示。由图可见,在经过530次迭代后,相对误差迅速地从10.0% 降到0.1%,之后收敛速度放缓,当相对误差达到0.0001%时,则需要近7500次迭代。图 7为BiCGstab法和本文算法相对误差随迭代次数变化曲线的对比,其中两种迭代方法初值均设为零,并采用雅各比预处理。可以看出:本文算法在前20次迭代收敛迅速,随后收敛速度逐渐变慢,在500次迭代过后相对误差接近0.1%,而且整体的曲线变化较为平稳,迭代误差基本随着迭代次数增加而减少;BiCGstab算法的收敛曲线波动很大,尤其是前300次迭代,基本不收敛,直到400~500次迭代相对误差才逐渐收敛到10%左右。值得注意的是,若将误差设置为0.0100%,本文算法需要进行3200次迭代,而BiCGstab算法只需2000次,因此BiCGstab算法的后续收敛速度较快,但稳定性难以保证,如在层状模型试验中有相当一部分的频率分量使用BiCGstab算法时并不能收敛。
|
图 6 相对误差随迭代次数的变化曲线 |
|
图 7 两种迭代算法收敛曲线对比 |
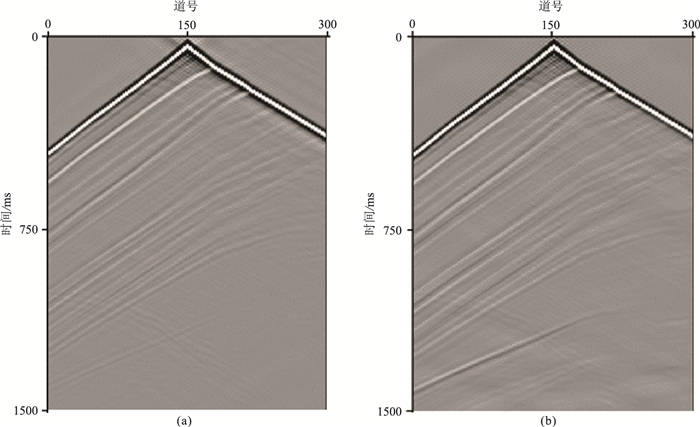
为进一步验证本文频域模拟方法的适用性,选取部分Marmousi-1模型(图 8)进行试算。模型网格数为300×300,网格尺寸为5m×5m;震源是主频为30Hz的Ricker子波位于(750m,5m);检波器均匀分布在模型表面,间隔为5m;四周同样采用PML边界,厚度为50层;记录长度为1.5s。图 9为本文算法和LU算法模拟的单炮记录,可以看出,本文算法的单炮记录与LU方法基本一致,说明本文算法对于复杂模型仍然有较高的精度。

|
图 8 Marmousi-1速度模型 内部黑色矩形框代表实际数值计算区域,下三角表示激发点位置,上三角表示检波点位置 |
|
图 9 部分Marmousi-1模型两种算法模拟的单炮记录对比 (a)MLSCG算法(ε=0.01%);(b)LU算法 |
为了分析模型的网格数对频域数值模拟的影响,对Marmousi-1模型进行重采样。原始模型网格数为737×751,记为模型1;对其横、纵向都进行1/4重采样,网格数变为184×187,记为模型2;横、纵向都进行1/2重采样,网格数变为368×375,记为模型3;网格尺寸都设置为10m×10m,PML边界厚度设置为20层,除正演时长根据模型大小等比例延长外,其余参数设置相同。设置ε=0.01%,针对30Hz单频波场,三个模型的模拟所占内存及计算时间如表 3所示。由表可见:①随着模型网格数的增大,LU算法和MLSCG迭代算法所占用内存均呈线性增长,但MLSCG法占用内存相较LU减少了15%~20%,且模型越大,内存减少越多;②模型网格数增大4倍,LU方法计算时间会增加接近15倍,而MLSCG迭代算法由于其良好的收敛性,增加的计算时间并不多,相比LU方法,对于模型3计算时间减少了70%以上,对于模型1甚至减少了87.98%。
|
|
表 3 三个模型、两种方法30Hz波场模拟内存占用和用时统计 |
本文提出了一种基于混合共轭梯度迭代(MLSCG)的频率域地震数值模拟方法。该方法使用最小二乘方法优化共轭梯度参数,提高了频率域正演的计算稳定性。相比传统直接求解算法,该方法内存占用更小、计算速度更快;相比常规迭代算法,只需要简单的预处理,不仅能保持较快的收敛速度,还有更高的计算稳定性。
| [1] |
刘文革, 贺振华. 地震波形反演[M]. 北京: 科学出版社, 2015. LIU Wenge, HE Zhenhua. Seismic Waveform Inversion[M]. Beijing: Science Press, 2015. |
| [2] |
LYSMER J, DRAKE L A. A finite element method for seismology[J]. Methods in Computational Physi-cs Advances in Research and Applications, 1972, 11(2): 181-216. |
| [3] |
MARFURT K J. Accuracy of finite-difference and finite-element modeling of the scalar and elastic wave equations[J]. Geophysics, 1984, 49(4): 533-549. |
| [4] |
JO C H, SHIN C, SUH J H. An optimal 9-point, finite difference, frequency-space, 2D scalar wave extrapolator[J]. Geophysics, 1996, 61(2): 529-537. DOI:10.1190/1.1443979 |
| [5] |
SHIN C, SOHN H. A frequency-space 2-D scalar wave extrapolator using extended 25-point finite-difference operator[J]. Geophysics, 1998, 63(1): 289-296. DOI:10.1190/1.1444323 |
| [6] |
吴国忱, 梁锴. VTI介质频率-空间域准P波正演模拟[J]. 石油地球物理勘探, 2005, 40(5): 535-545. WU Guochen, LIANG Kai. Quasi P-wave forward modeling in frequency-space domain in VTI media[J]. Oil Geophysical Prospecting, 2005, 40(5): 535-545. DOI:10.3321/j.issn:1000-7210.2005.05.010 |
| [7] |
刘璐, 刘洪, 刘红伟. 优化15点频率-空间域有限差分正演模拟[J]. 地球物理学报, 2013, 56(2): 644-652. LIU Lu, LIU Hong, LIU Hongwei. Optimal 15-point finite difference forward modeling in frequency-space domain[J]. Chinese Journal of Geophysics, 2013, 56(2): 644-652. |
| [8] |
范娜, 成景旺, 秦雷, 等. 一种优化的频率域三维声波有限差分模拟方法[J]. 地球物理学报, 2018, 61(3): 1095-1108. FAN Na, CHENG Jingwang, QIN Lei, et al. An optimal method for frequency-domain finite-difference solution of 3D scalar wave equation[J]. Chinese Journal of Geophysics, 2018, 61(3): 1095-1108. |
| [9] |
唐超, 文晓涛, 王文化. 基于最小范数优化交错网格有限差分系数的波动方程数值模拟[J]. 石油地球物理勘探, 2021, 56(5): 1039-1047. TANG Chao, WEN Xiaotao, WANG Wenhua. Numerical simulation of wave equations based on minimum-norm optimization of staggered-grid finite difference coefficients[J]. Oil Geophysical Prospecting, 2021, 56(5): 1039-1047. |
| [10] |
TANG X D, LIU H, ZHANG H, et al. An adaptable 17-point scheme for high-accuracy frequency-domain acoustic wave modeling in 2D constant density media[J]. Geophysics, 2015, 80(6): T211-T221. DOI:10.1190/geo2014-0124.1 |
| [11] |
XU W H, GAO J H. Adaptive 9-point frequency-domain finite difference scheme for wavefield modeling of 2D acoustic wave equation[J]. Journal of Geophy-sics and Engineering, 2018, 15(4): 1432-1445. DOI:10.1088/1742-2140/aab015 |
| [12] |
殷文. 基于频率域高阶有限差分法的正演模拟及并行算法[J]. 吉林大学学报(地球科学版), 2008, 38(1): 144-151. YIN Wen. Forward modeling and parallel algorithm based on high-order finite-difference method in frequency domain[J]. Journal of Jilin University (Earth Science Edition), 2008, 38(1): 144-151. |
| [13] |
马召贵, 王尚旭, 宋建勇. 频率域波动方程正演中的多网格迭代算法[J]. 石油地球物理勘探, 2010, 45(1): 1-5. MA Zhaogui, WANG Shangxu, SONG Jianyong. Multigrid iterative algorithm in frequency domain wave equation forward modeling[J]. Oil Geophysical Prospecting, 2010, 45(1): 1-5. |
| [14] |
曹健, 陈景波, 曹书红. 频率域波动方程正演基于多重网格预条件的迭代算法研究[J]. 地球物理学报, 2015, 58(3): 1002-1012. CAO Jian, CHEN Jingbo, CAO Shuhong. Studies on iterative algorithms for modeling of frequency-domain wave equation based on multi-grid precondition[J]. Chinese Journal of Geophysics, 2015, 58(3): 1002-1012. |
| [15] |
DU Z L, LIU J J, LIU W G, et al. Frequency-space domain acoustic wave simulation with the BiCGstab (1) iterative method[J]. Journal of Geophysics and Engineering, 2016, 13(1): 70-77. |
| [16] |
BELONOSOV M, KOSTIN B, NEKLYUDOV D, et al. 3D numerical simulation of elastic waves with a frequency-domain iterative solver[J]. Geophysics, 2018, 83(6): T333-T344. |
| [17] |
熊治涛, 唐新功, 李丹丹. 二维电性各向异性极化体的频率域响应[J]. 石油物探, 2020, 59(3): 481-490. XIONG Zhitao, TANG Xingong, LI Dandan. Frequency responses of a two-dimensional anisotropic polarization body[J]. Geophysical Prospecting for Petroleum, 2020, 59(3): 481-490. |
| [18] |
JIANG W, CHEN X H, JIANG S S, et al. Multiscale finite-difference method for frequency-domain acoustic wave modeling[J]. Geophysics, 2021, 86(4): T193-T210. |
| [19] |
JAYSAVAL P, DATTA D, SEN M, et al. A schur complement based fast 2D finite-difference multimodel modeling of acoustic wavefield in the frequency domain[C]. SEG Technical Program Expanded Abstracts, 2017, 36: 4086-4090.
|
| [20] |
颜红芹. 基于声波散射理论的零井源距VSP波场数值模拟方法[J]. 石油地球物理勘探, 2020, 55(3): 567-574. YAN Hongqin. Numerical simulation of zero-offset VSP wave field based on the acoustic scattering theory[J]. Oil Geophysical Prospecting, 2020, 55(3): 567-574. |
| [21] |
韩利, 韩立国, 李翔, 等. 二阶声波方程频域PML边界条件及频域变网格步长并行计算[J]. 吉林大学学报(地球科学版), 2011, 41(4): 1226-1232. HAN Li, HAN Liguo, LI Xiang, et al. PML boundary conditions for second-order acoustic wave equations and variable grid parallel computation in frequency-domain modeling[J]. Journal of Jilin University (Earth Science Edition), 2011, 41(4): 1226-1232. |
| [22] |
郭振波, 李振春. 起伏地表条件下频率空间域声波介质正演模拟[J]. 吉林大学学报(地球科学版), 2014, 44(2): 683-693. GUO Zhenbo, LI Zhenchun. Acoustic wave modeling in frequency-spatial domain with surface topography[J]. Journal of Jilin University (Earth Science Edition), 2014, 44(2): 683-693. |
| [23] |
吴悠, 吴国忱, 李青阳, 等. 频率-空间域非均质声波有限差分模拟[J]. 石油地球物理勘探, 2022, 57(2): 342-356. WU You, WU Guochen, LI Qingyang, et al. A finite difference scheme in frequency-space domain to solve heterogeneous acoustic wave equation[J]. Oil Geophysical Prospecting, 2022, 57(2): 342-356. |
| [24] |
PLESSIX R E, MULDER W A. Separation-of-variables as a preconditioner for an iterative Helmholtz solver[J]. Applied Numerical Mathematics, 2003, 44(3): 385-400. |
| [25] |
HESTENES M R, STIEFEL E. Methods of conjugate gradients for solving linear systems[J]. Journal of Research of the National Bureau of Standards, 1952, 49(6): 409-436. |
| [26] |
DAI Y H, YUAN Y. A nonlinear conjugate gradient method with a strong global convergence property[J]. SIAM Journal on Optimization, 1999, 10(1): 177-182. |
| [27] |
BABAIE-KAFAKI S, GHANBARI R. A hybridization of the Hestenes-Stiefel and Dai-Yuan conjugate gradient methods based on a least-squares approach[J]. Optimization Methods and Software, 2015, 30(4): 673-681. |
| [28] |
ZHANG L, ZHOU W J, LI D H. Some descent three-term conjugate gradient methods and their global convergence[J]. Optimization Methods and Software, 2007, 22(4): 697-711. |



 刘文革, 四川省成都市新都区新都大道8号西南石油大学地球科学与技术学院,610500。Email:
刘文革, 四川省成都市新都区新都大道8号西南石油大学地球科学与技术学院,610500。Email: