② 东方地球物理公司,河北涿州 072750;
③ 东方地球物理公司研究院处理中心,河北涿州 072751
② BGP Inc., CNPC, Zhuozhou, Hebei 072750, China;
③ Processing Center, GRI, BGP Inc., CNPC, Zhuozhou, Hebei 072751, China
自20世纪70年代起,Radon变换引入地球物理勘探,经过几十年的发展,已逐步用于地震资料处理的诸多方面,如地震道重建、VSP上、下波场分离及多次波压制等[1-6]。尤其在多次波压制方面,Radon变换因其应用简便、操作灵活,受到业界的广泛关注。Hampson[7]首次利用τ-p变换压制多次波,但由于变换域能量聚焦不足,存在严重的能量“拖尾”现象,多次波压制效果并不理想;随后,Kostov[8]、Sacchi[9]提出了高分辨率Radon变换,有效地解决了“剪刀状”能量发散问题,提高了多次波压制精度;Wood等[10]推出一种混合域高分辨率Radon变换,充分利用时间域的高分辨率和频率域可解耦的特点,进一步提高了Radon域内解的稀疏度和分辨率,但计算成本偏高;Abbad等[11]基于奇异值分解技术提出了频率域快速求解算法,即λ-f域Radon变换,通过引入变量λ消除变换算子与频率的关系,显著提高了计算效率。
中国学者也深入研究了Radon变换多次波压制方法。刘喜武等[12]利用稀疏约束共轭梯度算法实现高分辨率Radon变换,并成功用于多次波压制;王维红等[13]提出了一种加权抛物Radon变换,利用变化的权系数提高抗假频能力;熊登等[14]利用混合域Radon变换在时间域进行稀疏约束,提高了Radon域内能量团的分辨率;石颖等[15-18]基于二维λ-f域Radon变换优化和改进地震道重建、多次波压制和波场分离等方法。近年来,在Radon变换的保幅处理方面也取得一定突破。薛亚茹等[19-22]基于正交多项式变换和常规Radon变换的不同特征,将二者结合形成高阶Radon变换,通过构建多阶Radon子区间,使每个子区间保留不同的振幅变化信息,从而具有AVO特性;唐欢欢等[23]将高阶二维Radon变换成功拓展到三维,并取得很好的保幅效果。王亮亮等[24]实现了快速Radon变换算法;张全等[25]提出了CPU-GPU异构并行算法,加速比达到约30倍,提高了Radon变换计算效率。
在实际资料处理中,二维抛物Radon变换压制多次波的方法已经相当成熟,但是没有考虑地震子波的空间传播特性,忽略了波场随空间曲率的变化信息,在处理宽方位三维地震数据时,往往多次波压制效果不佳,存在一定的多次波残余。为此,本文基于二维抛物Radon变换,借鉴Abbad等[11]的方法,深入研究了常规三维抛物Radon变换,并首次提出了λ-f域三维抛物Radon变换多次波压制方法。结果表明:常规三维抛物Radon变换多次波压制方法的计算效率过低,不利于大规模实际应用;λ-f域三维抛物Radon变换多次波压制方法重新定义了变换算子的构建方式,消除了算子对地震数据频率的依赖,使整个变换过程仅需计算一次变换算子及其广义逆算子,大大减少了矩阵求逆运算的次数,明显提高了计算效率。同时,根据一次波和多次波映射到λ-f域的空间分布特征,设计了三维椎体滤波器,使一次波能量投影到保留区,多次波能量投影到切除区,避免了人工定义切除区域的过程,更便于实际应用。因此,针对海量三维地震数据处理,本文所提方法可以极大地节省人工成本。
1 方法原理 1.1 常规三维抛物Radon变换原理二维抛物Radon变换是沿着抛物线路径对地震数据积分、求和的过程。类似地,三维抛物Radon变换的物理意义是沿着抛物面对地震数据求和处理,其正、反变换的离散形式分别为
| $ \boldsymbol{m}\left(q_x, q_y, \tau\right)=\sum\limits_x \sum\limits_y \boldsymbol{d}\left(x, y, t=\tau+q_x x^2+q_y y^2\right) $ | (1) |
| $ \boldsymbol{d}(t, x, y)=\sum\limits_{q_x} \sum\limits_{q_y} \boldsymbol{m}\left(\tau=t-q_x x^2-q_y y^2, q_x, q_y\right) $ | (2) |
式中:d(t, x, y)为三维地震数据体,t为时间坐标,x、y分别为横、纵向炮检距;m(qx, qy, τ)为变换域的模型空间,qx和qy分别为横、纵向离散曲率参数,τ为变换域零炮检距截距时间。
对式(1)、式(2)两边进行傅里叶变换,分别得到频率域的正、反变换
| $ \boldsymbol{M}\left(q_x, q_y, f\right)=\sum\limits_x \sum\limits_y \mathrm{e}^{\mathrm{i} f q_x x^2} \boldsymbol{D}(x, y, f) \mathrm{e}^{\mathrm{i} f q_y y^2} $ | (3) |
| $ \widetilde{\boldsymbol{D}}(x, y, f)=\sum\limits_{q_x} \sum\limits_{q_y} \mathrm{e}^{-\mathrm{i} f q_x x^2} \boldsymbol{M}\left(q_x, q_y, f\right) \mathrm{e}^{-\mathrm{i} f q_y y^2} $ | (4) |
式中:f为频率;D为三维地震数据的频率域矩阵;
通常情况下,应用Radon变换压制多次波,多是对正变换的模型空间进行处理,再反变换回时空域,而Radon域能量团的收敛性直接影响多次波去除效果。因此,本文着重推导了三维抛物Radon正变换的实现过程。根据式(4)可知,在频率域内,不同频率切片的三维地震数据具有解耦性,对某个频率,其矩阵简化形式为
| $ \widetilde{\boldsymbol{D}}=\boldsymbol{L}_{q_x} \boldsymbol{M} \boldsymbol{L}_{q_y} $ | (5) |
式中:Lqx=e-ifqxx2为与x有关的算子;Lqy=e-ifqyy2为与y有关的算子。采用最小二乘方法,使式(5)的目标函数最小化,即
| $ J=\|\boldsymbol{D}-\widetilde{\boldsymbol{D}}\|_2^2 $ | (6) |
分别求取矩阵Lqx和Lqy的逆,可以得到Radon域数据M。因此在最小二乘意义下,式(5)的解为
| $ \boldsymbol{M}=\boldsymbol{L}_{q_x}^{\mathrm{H}}\left(\boldsymbol{L}_{q_x} \boldsymbol{L}_{q_x}^{\mathrm{H}}\right)^{-1} \boldsymbol{D}\left(\boldsymbol{L}_{q_y}^{\mathrm{H}} \boldsymbol{L}_{q_y}\right)^{-1} \boldsymbol{L}_{q_y}^{\mathrm{H}} $ | (7) |
上标“H”表示取共轭。为了防止奇异值对矩阵求逆过程产生异常影响,引入阻尼因子μ(通常取值为0.01~1.00),主要用于增强矩阵求逆的稳定性。最终解的表达式为
| $ \boldsymbol{M}=\boldsymbol{L}_{q_x}^{\mathrm{H}}\left(\boldsymbol{L}_{q_x} \boldsymbol{L}_{q_x}^{\mathrm{H}}+\mu \boldsymbol{I}\right)^{-1} \boldsymbol{D}\left(\boldsymbol{L}_{q_y}^{\mathrm{H}} \boldsymbol{L}_{q_y}+\mu \boldsymbol{I}\right)^{-1} \boldsymbol{L}_{q_y}^{\mathrm{H}} $ | (8) |
式中I为单位矩阵。由变换算子Lqx、Lqy定义可知,该算子的构建与频率f密切相关,对每一个频率切片计算时,变换算子Lqx、Lqy及其共轭LqxH、LqyH均发生变化,会产生大量的矩阵求逆运算,严重消耗计算机时,使常规三维抛物Radon变换的计算效率偏低,不利于海量三维地震数据处理。
1.2 λ-f域三维抛物Radon变换原理针对常规三维抛物Radon变换计算效率偏低的问题,本文借鉴Abbad等[11]提出的改进二维Radon变换方法,重新定义变换算子的构建方式,引入两个数学运算变量λx=qxf和λy=qyf(其物理意义为曲率与频率的乘积),可将常规三维抛物Radon变换的f-qx-qy域转换到一个全新的λx-λy-f域。该法继承了二维λ-f域Radon变换思路,创新实现了三维算法,故简称为λ-f域三维抛物Radon变换方法。
针对任意频率分量,将变量λx和λy引入变换公式,则改进三维抛物Radon正、反变换为
| $ \boldsymbol{M}\left(\lambda_x, \lambda_y, f\right)=\sum\limits_x \sum\limits_y \mathrm{e}^{\mathrm{i} \lambda_x x^2} \boldsymbol{D}(x, y, f) \mathrm{e}^{\mathrm{i} \lambda_y y^2} $ | (9) |
| $ \widetilde{\boldsymbol{D}}(x, y, f)=\sum\limits_{\lambda_x} \sum\limits_{\lambda_y} \mathrm{e}^{-\mathrm{i} \lambda_x x^2} \boldsymbol{M}\left(\lambda_x, \lambda_y, f\right) \mathrm{e}^{-\mathrm{i} \lambda_y y^2} $ | (10) |
类似于常规三维抛物Radon变换方法,针对某个频率切片,将式(10)的矩阵形式简化为
| $ \widetilde{\boldsymbol{D}}=\boldsymbol{L}_{\lambda_x} \boldsymbol{M} \boldsymbol{L}_{\lambda_y} $ | (11) |
式中Lλx、Lλy为重构的变换算子,具体形式为
| $ \boldsymbol{L}_{\lambda_x}=\left[\begin{array}{cccc} \mathrm{e}^{-\mathrm{i} \lambda_{x_1} x_1^2} & \mathrm{e}^{-\mathrm{i} \lambda_{x_2} x_1^2} & \cdots & \mathrm{e}^{-\mathrm{i} \lambda_{x_n} x_1^2} \\ \mathrm{e}^{-\mathrm{i} \lambda_{x_1} x_2^2} & \mathrm{e}^{-\mathrm{i} \lambda_{x_2} x_2^2} & \cdots & \mathrm{e}^{-\mathrm{i} \lambda_{x_n} x_2^2} \\ & & \vdots & \\ \mathrm{e}^{-\mathrm{i} \lambda_{x_1} x_m^2} & \mathrm{e}^{-\mathrm{i} \lambda_{x_2} x_m^2} & \cdots & \mathrm{e}^{-\mathrm{i} \lambda_{x_n} x_m^2} \end{array}\right] $ |
| $ \boldsymbol{L}_{\lambda_y}=\left[\begin{array}{cccc} \mathrm{e}^{-\mathrm{i} \lambda_{y_1}} y_1^2 & \mathrm{e}^{-\mathrm{i} \lambda_{y_2} y_1^2} & \cdots & \mathrm{e}^{-\mathrm{i} \lambda_{y_k} y_1^2} \\ \mathrm{e}^{-\mathrm{i} \lambda_{y_1} y_2^2} & \mathrm{e}^{-\mathrm{i} \lambda_{y_2} y_2^2} & \cdots & \mathrm{e}^{-\mathrm{i} \lambda_{y_k} y_2^2} \\ & & \vdots & \\ \mathrm{e}^{-\mathrm{i} \lambda_{y_1}} y_p^2 & \mathrm{e}^{-\mathrm{i} \lambda_{y_2} y_p^2} & \cdots & \mathrm{e}^{-\mathrm{i} \lambda_{y_k} y_p^2} \end{array}\right] $ |
式中:m和p分别为三维地震道集的纵测线和非纵测线的道数;n和k为λ-f域的三维模型空间的维度。通过对变换算子Lλx、Lλy重构,Lλx由炮检距xm和λxn(λx的离散值)计算获得,Lλy由炮检距yp和λyk(λy的离散值)计算获得,从而消除了对频率f的依赖。
采用最小二乘求解方式得到λ-f域三维抛物Radon变换的解
| $ \boldsymbol{M}=\boldsymbol{L}_{\lambda_x}^{\mathrm{H}}\left(\boldsymbol{L}_{\lambda_x} \boldsymbol{L}_{\lambda_x}^{\mathrm{H}}+\mu \boldsymbol{I}\right)^{-1} \boldsymbol{D}\left(\boldsymbol{L}_{\lambda_y}^{\mathrm{H}} \boldsymbol{L}_{\lambda_y}+\mu \boldsymbol{I}\right)^{-1} \boldsymbol{L}_{\lambda_y}^{\mathrm{H}} $ | (12) |
由于变换算子Lλx和Lλy与频率无关,对所有频率切片计算时,只需进行一次Lλx、Lλy、LλxH、LλyH及其广义逆运算,并存储到相应数组中,均可随时调用。相比于常规三维抛物Radon变换算法,λ-f域三维抛物Radon正变换能够大幅减少矩阵求逆次数,极大地提升了计算效率。
以模拟的三维地震记录为例,对比、分析常规三维抛物Radon正变换及λ-f域三维抛物Radon正变换的谱分布特征及聚焦性(图 1)。利用常规三维抛物Radon变换将合成数据(图 1a)变换到三维Radon域,并抽取四条同相轴对应最大能量团的垂向(图 1b)和横向(图 1c)切片。理论上,当截距时间和介质速度横向变化不大时,同相轴映射到变换域应呈“点”状分布,但受采集孔径限制,形成空间截断效应,能量团存在“拖尾”现象,能量泄露造成收敛不足(图 1b、图 1c)。对图 1a进行λ-f域三维抛物Radon正变换,抽取变换域内不同位置的纵向切片(图 1d),由于地震数据中每条同相轴的曲率qx、qy基本固定,因此λx和λy与频率f成正比,四条抛物同相轴映射到λ-f域呈以不同曲率为斜率的“窄直线”状分布,且当计算频率极低时,λx和λy趋于0,即所有直线近似过原点。抽取λ-f域内不同频率的横向切片(图 1e)发现,四条同相轴在λ-f域能量团较收敛,且随着频率增加,更容易区分能量团的相对位置关系,便于后续的多次波分离。
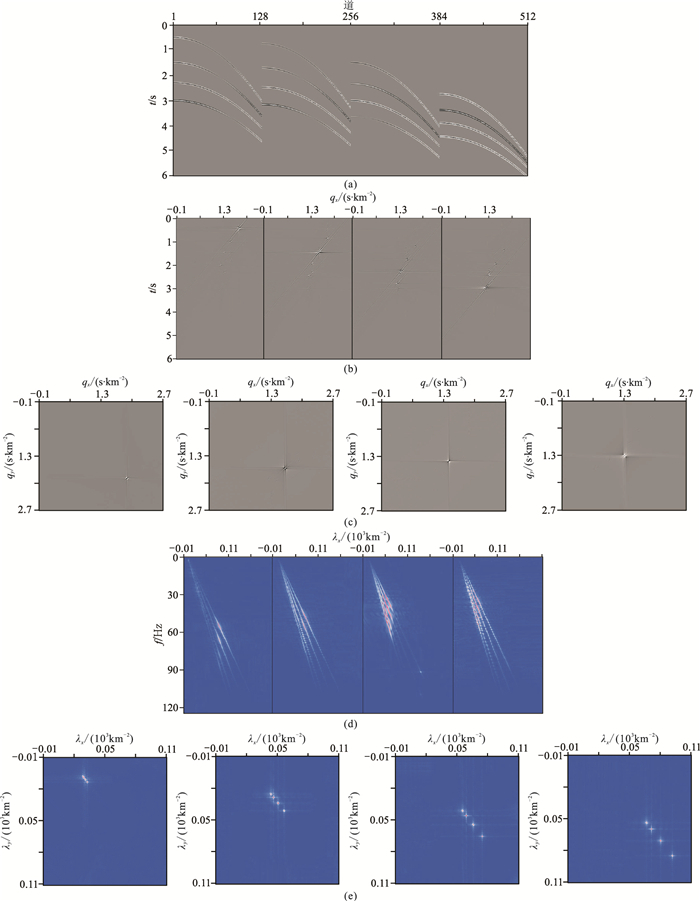
|
图 1 合成炮记录Radon正变换结果 (a)y方向的第1、第40、第80、第120排列合成数据;(b)qy=1.92,1.73,1.47,1.20s·km-2处的常规三维抛物Radon变换域垂向剖面;(c)τ=0.5,1.5,2.3,3.0s处的常规三维抛物Radon变换域水平等时切片;(d)λy=10,80,160,220km-2处的λ-f域三维抛物Radon变换域垂向剖面;(e)f=10,30,50,70Hz处的λ-f域三维抛物Radon变换域水平等频率切片观测系统在y和x方向均为128个网格点,网格间距为10m |
为了避免λ-f域三维抛物Radon变换出现假频而影响算法精度,需要将所有同相轴对应的Nλ(λx和λy的个数)值准确映射到变换域。若Nλ不足使同相轴能量映射不完整,造成能量泄露;若Nλ过大会引入一定的随机噪声,降低资料信噪比。选取合适的Nλ值是必要的,决定该值的两个重要参数是采样间隔和扫描范围。
根据常规三维抛物Radon变换的曲率选取准则,由λx=qxf、λy=qyf可知,λ-f域重采样间隔Δλx和Δλy应满足
| $ \Delta q_x<\frac{1}{f\left(x_{\max }^2-x_{\min }^2\right)} \Rightarrow \Delta \lambda_x=\Delta q_x f<\frac{1}{x_{\max }^2-x_{\min }^2} $ | (13) |
| $ \Delta q_y<\frac{1}{f\left(y_{\max }^2-y_{\min }^2\right)} \Rightarrow \Delta \lambda_y=\Delta q_y f<\frac{1}{y_{\max }^2-y_{\min }^2} $ | (14) |
式中:xmax、xmin和ymax、ymin分别为横向和纵向最大、最小炮检距;Δqx、Δqy分别为横、纵向曲率采样间隔。
根据式(11),重构的Radon算子Lλx、Lλy的相位误差必须满足
| $ 2 \pi \lambda_x x_{\max }^2-2 \pi \lambda_x\left[x_{\max }-\Delta x\right]^2<2 \pi $ | (15) |
| $ 2 \pi \lambda_y y_{\max }^2-2 \pi \lambda_y\left[y_{\max }-\Delta y\right]^2<2 \pi $ | (16) |
因此,根据qx、qy及地震数据最大频率fmax,可以确定参数λx和λy的扫描范围
| $ \left|\lambda_x\right|=q_x f_{\max }<\frac{1}{2 x_{\max } \Delta x} $ | (17) |
| $ \left|\lambda_y\right|=q_y f_{\max }<\frac{1}{2 y_{\max } \Delta y} $ | (18) |
由式(13)~式(18)可见,Δλx、Δλy及λx、λy的扫描范围仅与纵、横向最大、最小炮检距以及空间采样间隔Δx、Δy有关,而与频率无关。
三维抛物Radon变换采样间隔Δλx、Δλy和λx、λy的扫描范围类似于常规二维Radon变换(图 2)[11],即:在任意频率范围内,所有同相轴的曲率q的扫描范围相同(图 2a),对于低频同相轴而言,在有限的曲率范围内,频率过低可能造成采样不足,无法满足采样定理要求,出现低频同相轴能量泄露、聚焦不稳定的问题;基于λ-f域抛物Radon变换方法,参数λ的采样间隔和扫描范围仅与炮检距、道间距有关,在一定的λ取值范围内,曲率和频率呈反比,即频率越低,曲率范围越大,低频区的覆盖区范围更宽,增加了低频段到变换域的完整映射几率(图 2b)。
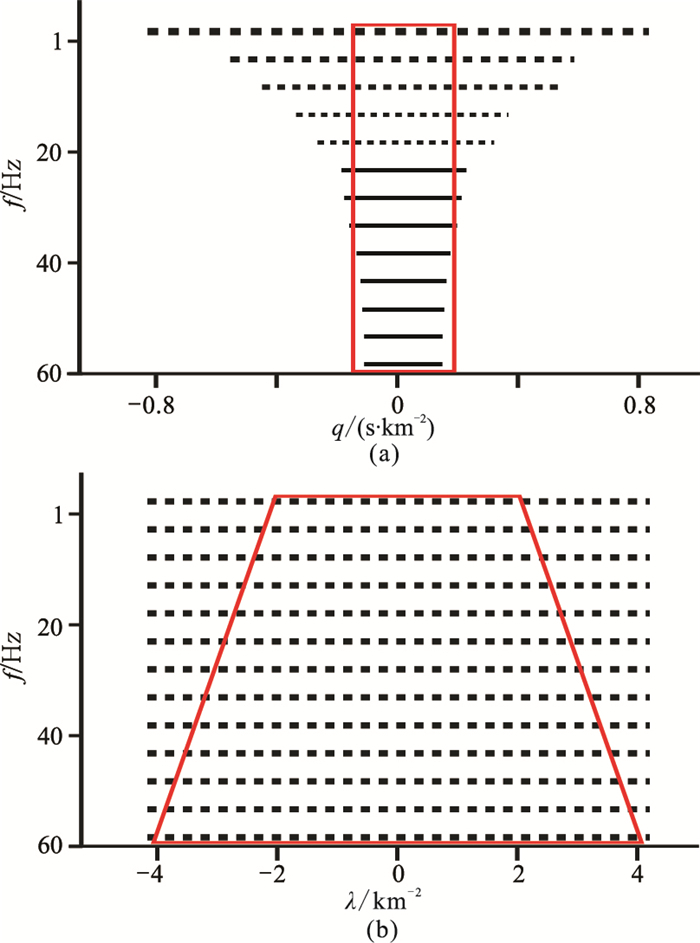
|
图 2 参数变量扫描范围示意图 (a)常规抛物Radon变换;(b)λ-f域抛物Radon变换 |
在实际资料处理中,利用抛物Radon变换压制多次波首先要对地震数据做动校正(NMO),然后根据一次波和多次波能量在变换域内分布位置的不同,通过手动方式定义切除区域,从而分离一次波和多次波能量团。对于海量三维地震数据而言,采用常规三维抛物Radon变换人为定义三维切除区,计算成本偏高。本文充分利用NMO后的一次波和多次波能量在λ-f域呈“窄直线”状分布特点,提出了一种椎体滤波方法,可以有效分离一次波和多次波能量,避免了人工定义切除区域的过程。实际Radon变换压制多次波的经验表明,为了满足浅层非多次波干扰区地震数据的保真性,通常在变换域内提取多次波能量,将其反变换回时空域,得到多次波模型数据,再采用自适应相减法从原始数据中去除多次波模型数据,以降低对有效波的伤害。基于此思路,在设计三维椎体滤波器时,以提取多次波能量为目标。设地震数据d(x, y, t)的λ-f域三维抛物Radon正变换为M(λx, λy, f),定义椎体滤波器为G(λx, λy, f),不同曲率的同相轴会映射到不同的椎体滤波区(图 3)。假设一次波同相轴经NMO后均被校平,视速度v趋近于∞,由公式q≈1/(2t0v2)可知,一次波的曲率近似为0,则一次波能量从椎体顶点附近垂向分布到椎体内部的切除区域。地震数据中多次波同相轴经NMO后变为具有一定曲率(范围为qmin~qmax)的抛物面,多次波能量从顶点附近呈直线辐射至椎体保留区域,则
| $ \boldsymbol{G}\left(\lambda_x, \lambda_y, f\right)= \begin{cases}0 & |r|<q_{\max } f \\ 1 & q_{\max } f \leqslant|r| \leqslant q_{\min } f \\ 0 & |r|>q_{\min } f\end{cases} $ | (19) |
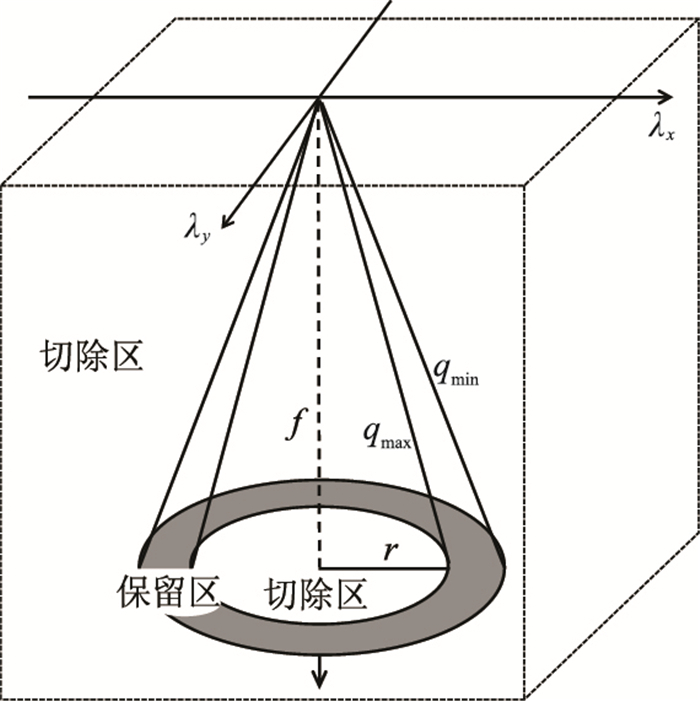
|
图 3 三维数据体λ-f域椎体滤波区域示意图 |
式中:
| $ \begin{gathered} \boldsymbol{M}_{\mathrm{mod}}\left(\lambda_x, \lambda_y, f\right)=\boldsymbol{G}\left(\lambda_x, \lambda_y, f\right)\left[\left(\boldsymbol{L}_{\lambda_x}^{\mathrm{H}} \boldsymbol{L}_{\lambda_x}+\mu \boldsymbol{I}\right)^{-1} \times\right. \\ \left.\boldsymbol{L}_{\lambda_x}^{\mathrm{H}} \boldsymbol{D}(f) \boldsymbol{L}_{\lambda_y}^{\mathrm{H}}\left(\boldsymbol{L}_{\lambda_y} \boldsymbol{L}_{\lambda_y}^{\mathrm{H}}+\mu \boldsymbol{I}\right)^{-1}\right] \end{gathered} $ | (20) |
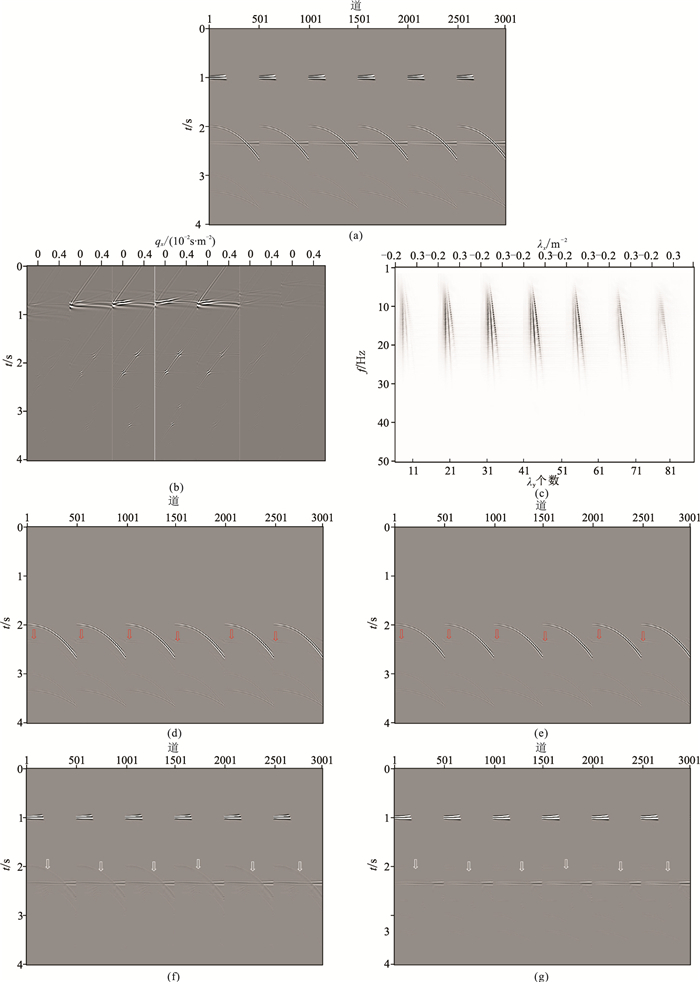
为了检验λ-f域三维抛物Radon变换方法的效果,以三维正演速度模型(图 4)为例进行多次波压制试算。图 5展示了图 4模型数据多次波压制效果。由图可见:①NMO三维模型数据的一次波同相轴均被校平,多次波同相轴仍为抛物形态(图 5a)。②常规三维抛物Radon正变换抽取一阶自由表面多次波能量最强位置,当一次波和多次波的截距时间较小时,由于存在能量团“拖尾”现象,部分能量交织在一起,很难分离多次波能量,在定义切除线过程中会损伤一次波能量或残留多次波能量(图 5b)。③λ-f域三维抛物Radon正变换结果的一次波能量垂直分布,而多次波能量具有一定斜率,因此根据空间位置可分离一次波和多次波(图 5c)。④常规三维抛物Radon变换和λ-f域三维抛物Radon变换均能有效提取多次波模型数据,但是在近炮检距位置都残留一次波(图 5d、图 5e红色箭头处)。这是由于近炮检距位置下层的一次波与上层的一阶自由表面多次波的NMO时差较小,很难有效分离所致,这也是Radon类方法在近炮检距位置多次波压制效果不佳的原因。⑤常规三维抛物Radon变换多次波压制结果明显残留多次波,这是由于常规三维抛物Radon变换的能量团收敛性差,在提取多次波能量过程中,为了减少一次波能量损伤,出现部分多次波能量泄露(图 5f白色箭头处)。⑥由于在λ-f域易于分离一次波和多次波能量,因此λ-f域三维抛物Radon变换较干净、彻底地压制了多次波(图 5g)。
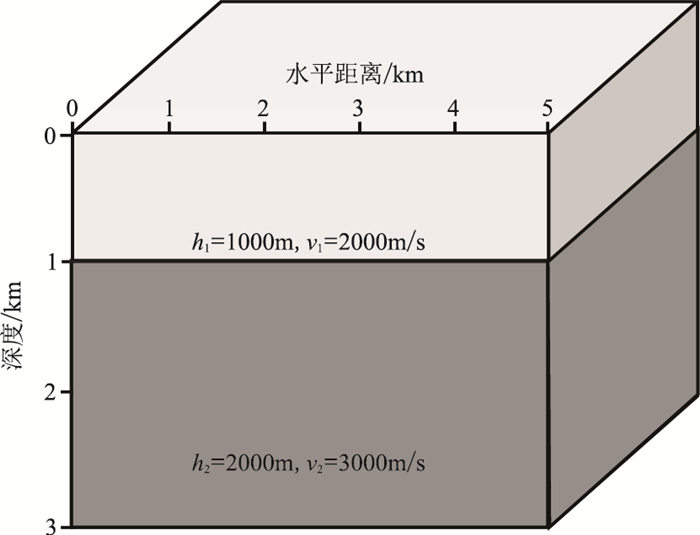
|
图 4 三维正演速度模型 模型包含两层水平层状介质,利用有限差分正演方法记录了上层的一阶和二阶自由表面多次波。模拟观测系统为规则网格,其中,纵、横向各500个网格点,网格间距为10m |
|
图 5 图 4数据多次波压制效果 (a)NMO三维模型数据(抽取6条排列显示);(b)常规三维抛物Radon正变换;(c)λ-f域三维抛物Radon正变换;(d)常规三维抛物Radon变换多次波模型;(e)λ-f域三维抛物Radon变换多次波模型;(f)图 5a与图 5d之差;(g)图 5a与图 5e之差 |
为了进一步分析常规三维抛物Radon变换和λ-f域三维抛物Radon变换的多次波压制精度,随机抽取图 5a、图 5f和图 5g同一位置的地震道(图 6),可见,后者的多次波压制精度高于前者。
表 1展示了利用不同方法压制多次波的计算效率,可见在采用相同的计算平台和计算参数情况下,对同一个节点的单线程运算,常规三维抛物Radon变换压制多次波方法的计算耗时(不包括人为定义切除过程)是λ-f域三维抛物Radon变换的8倍以上。因此,针对海量地震数据去噪,后者的计算高效性更明显,具有实用价值。
|
|
表 1 利用不同方法压制多次波的计算效率 |
理论上,二维抛物Radon变换压制多次波方法存储变换算子的矩阵维度不大,对于每个频率,重新计算变换算子的耗时较短。因此,λ-f域二维抛物Radon变换压制多次波的效率提升并不明显。常规三维抛物Radon变换压制多次波方法存储变换算子的维度大,对于每个频率切片,需要重复进行大量的矩阵运算,尤其是求取广义逆运算,会严重制约计算效率。因此,λ-f域三维抛物Radon变换压制多次波充分体现了计算效率优势。
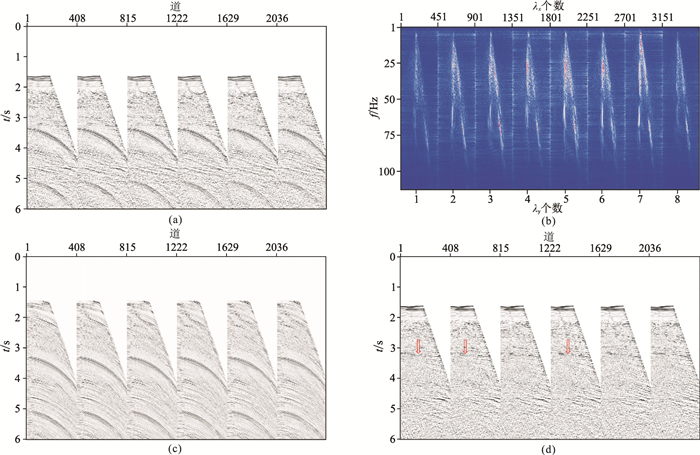
2.2 实际资料测试以海洋拖揽数据为例测试多次波压制效果。图 7为λ-f域三维抛物Radon变换压制海洋单炮记录多次波效果。由图可见:①NMO单炮记录中广泛存在一阶和二阶自由表面多次波,而且能量级别较大,部分有效波同相轴被掩盖(图 7a)。②λ-f域三维抛物Radon正变换结果的一次波能量在λx=0、λy=0区域附近几乎垂直分布,根据多次波的最大和最小视速度范围定义椎体滤波区域,可以分离有效波和多次波(图 7b)。③λ-f域三维抛物Radon变换有效恢复了能量强、曲率大的多次波(图 7c)。④经多次波压制,图 7a的强能量多次波均得到衰减,同时显现了部分能量较弱的一次波(图 7d红色箭头处)。
|
图 7 λ-f域三维抛物Radon变换压制海洋单炮记录多次波效果 (a)NMO单炮记录;(b)λ-f域三维抛物Radon正变换;(c)λ-f域三维抛物Radon变换多次波模型;(d)图 7a与图 7c之差共681炮数据,每激发一炮有6条拖缆接收,每条拖缆有408道,道间距为12.5m,拖缆间距为200m,地震记录长度为6s |
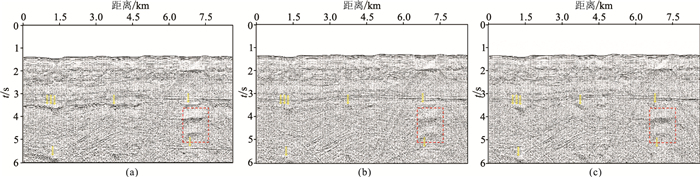
图 8为三维共炮检距剖面多次波压制效果。由图可见:原始数据存在强能量多次波,且地层具有一定倾角(图 8a箭头标注处);常规三维抛物Radon变换有效压制了大部分较平缓的一阶、二阶自由表面多次波,但在一些构造倾角较大位置仍残留多次波(图 8b);与图 8b相比,λ-f域三维抛物Radon变换干净、彻底地压制了多次波,尤其在一次波和多次波同相轴较接近的位置(t=3.3s),且未损伤有效信号(图 8c)。在相同的计算环境和计算参数情况下,常规三维抛物Radon变换处理681炮地震数据的耗时为684min,而λ-f域三维抛物Radon变换的耗时为71min,即后者的加速比提高了约9倍。
|
图 8 三维共炮检距剖面多次波压制效果 (a)原始数据;(b)常规三维抛物Radon变换;(c)λ-f域三维抛物Radon变换 |
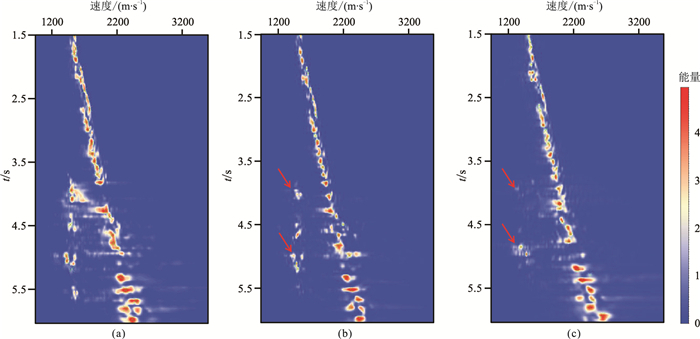
然而,尽管λ-f域三维抛物Radon变换方法的计算精度和效率高于常规三维抛物Radon变换方法,但在图 8的红色方框位置仍残留多次波。为了进一步验证,抽取该位置附近的叠前CMP道集速度谱(图 9)。可见,两种方法均存在明显的低速能量团,尤其在4.0s和4.7s位置附近。分析表明,在浅层(2s位置)存在绕射点,进而诱发强能量绕射多次波,其同相轴呈近似双曲线形态,不满足抛物Radon变换的假设条件,因此较难彻底压制。综上所述,利用λ-f域三维抛物Radon变换多次波压制方法去除海洋地震资料表面多次波的效果较好。
|
图 9 叠前CMP道集速度谱 (a)原始速度谱;(b)常规三维抛物Radon变换压制多次波后速度谱;(c)λ-f域三维抛物Radon变换压制多次波后速度谱 |
λ-f域三维抛物Radon变换是对常规三维Radon变换的改进,本文将其成功应用于三维地震资料多次波压制,理论模型和实际数据试算表明方法具有实用价值,适合于海量地震数据去噪,获得以下认识。
(1) 与常规三维Radon变换方法相比,λ-f域三维抛物Radon变换方法压制表面多次波更彻底,同相轴在λ-f域呈“窄直线”状分布,缓解了能量团“拖尾”现象,在多次波切除过程中降低了空间截断效应的影响。
(2) λ-f域三维抛物Radon变换通过对变换算子进行重构,消除了变换算子对频率的依赖,有效减少了矩阵求逆运算次数,较常规三维Radon变换方法的计算效率提高了约8倍以上。
(3) 利用λ-f域三维抛物Radon变换方法压制多次波时,需要根据多次波同相轴的视速度确定椎体滤波器的母线长度,即视速度越大,滤波器的切除线越向有效信号能量靠近。为了避免损伤有效信号,建议实际应用时不易选取过大的最大视速度。
尚需指出,λ-f域三维抛物Radon变换方法压制多次波时仍然存在Radon类方法的弊端,即当一次波和多次波速度差异较小时,在近炮检距位置无法得到较理想的多次波压制效果。
| [1] |
THORSON J R, CLAERBOUT J F. Velocity-stack and slant-stack stochastic inversion[J]. Geophysics, 1985, 50(12): 2727-2741. DOI:10.1190/1.1441893 |
| [2] |
ALKHAILIFAH T, TSVAMKIN I. Velocity analysis for transversely isotropic media[J]. Geophysics, 1995, 60(5): 1550-1566. DOI:10.1190/1.1443888 |
| [3] |
牛滨华, 孙春岩, 张中杰, 等. 多项式变换[J]. 地球物理学报, 2001, 44(2): 263-271. NIU Binhua, SUN Chunyan, ZHANG Zhongjie, et al. Polynomial Radon transform[J]. Chinese Journal of Geophysics, 2001, 44(2): 263-271. DOI:10.3321/j.issn:0001-5733.2001.02.014 |
| [4] |
黄新武, 吴律, 宋讳. 拉东投影法三维叠前深度偏移[J]. 地球物理学报, 2004, 47(2): 321-326. HUANG Xinwu, WU Lyu, SONG Wei. 3-D pre-stack depth migration with Radon projection[J]. Chinese Journal of Geophysics, 2004, 47(2): 321-326. DOI:10.3321/j.issn:0001-5733.2004.02.020 |
| [5] |
SCHONEWWILLE M A, DUIJNDAM A J W. Parabolic Radon transform, sampling and efficiency[J]. Geophysics, 2001, 66(2): 667-678. DOI:10.1190/1.1444957 |
| [6] |
高少武, 钱忠平, 孙鹏远, 等. 水陆检数据上下行波场分离方法[J]. 石油地球物理勘探, 2020, 55(5): 991-996. GAO Shaowu, QIAN Zhongping, SUN Pengyuan, et al. A separation method of up-going and down-going wavefields for dual-sensor seismic data[J]. Oil Geophysical Prospecting, 2020, 55(5): 991-996. |
| [7] |
HAMPSON D. Inverse velocity stacking for multiple elimination[J]. Journal of the Canadian Society of Exploration Geophysicists, 1986, 22(1): 44-55. |
| [8] |
KOSTOV C. Toeplitz structure in slant-stack inversion[C]. SEG Technical Program Expanded Abstracts, 1990, 9, doi: 10.1190/1.1890075.
|
| [9] |
SACCHI M D. High-resolution velocity gathers and offset space reconstruction[J]. Geophysics, 1995, 60(4): 1169-1177. DOI:10.1190/1.1443845 |
| [10] |
WOOD J C, DANIEL T. Radon transformation of time-frequency distribution for analysis of multicomponent signals[C]. IEEE Transactions on Signal Processing, 1994, 42(11): 3166-3178.
|
| [11] |
ABBAD B, URSIN B, PORSANI M J. A fast, modified parabolic Radon transform[J]. Geophysics, 2011, 76(1): V11-V24. DOI:10.1190/1.3532079 |
| [12] |
刘喜武, 刘洪, 李幼铭. 高分辨率Radon变换方法及其在地震信号处理中的应用[J]. 地球物理学进展, 2004, 19(1): 8-15. LIU Xiwu, LIU Hong, LI Youming. High resolution radon transform and its application in seismic signal processing[J]. Progress in Geophysics, 2004, 19(1): 8-15. DOI:10.3969/j.issn.1004-2903.2004.01.002 |
| [13] |
王维红, 裴江云, 张剑锋. 加权抛物Radon变换叠前地震数据重建[J]. 地球物理学报, 2007, 50(3): 851-859. WANG Weihong, PEI Jiangyun, ZHANG Jianfeng. Prestack seismic data reconstruction using weighted parabolic Radon transform[J]. Chinese Journal of Geophysics, 2007, 50(3): 851-859. DOI:10.3321/j.issn:0001-5733.2007.03.026 |
| [14] |
熊登, 赵伟, 张剑锋. 混合域高分辨率抛物Radon变换及其在衰减多次波中的应用[J]. 地球物理学报, 2009, 52(4): 1068-1077. XIONG Deng, ZHAO Wei, ZHANG Jianfeng. Hybrid-domain high-resolution parabolic Radon transform and its application to demultiple[J]. Chinese Journal of Geophysics, 2009, 52(4): 1068-1077. DOI:10.3969/j.issn.0001-5733.2009.04.024 |
| [15] |
石颖, 张振, 李婷婷, 等. λ-f域加权抛物Radon变换地震数据重建方法研究[J]. 地球物理学进展, 2014, 29(4): 1752-1757. SHI Ying, ZHANG Zhen, LI Tingting, et al. Investigation on seismic data reconstruction by λ-f domain weighted parabolic Radon transform method[J]. Progress in Geophysics, 2014, 29(4): 1752-1757. |
| [16] |
李志娜, 李振春, 王鹏. 基于改进线性Radon变换的井孔地震上下行波场分离方法[J]. 地球物理学报, 2014, 57(7): 2269-2277. LI Zhina, LI Zhenchun, WANG Peng. Wavefield separation by a modified linear Radon transform in borehole seismic[J]. Chinese Journal of Geophysics, 2014, 57(7): 2269-2277. |
| [17] |
王维红, 张振, 石颖, 等. λ-f域抛物Radon变换多次波压制方法[J]. 东北石油大学学报, 2015, 39(1): 17-22. WANG Weihong, ZHANG Zhen, SHI Ying, et al. Investigation of multiple suppression by parabolic Radon transform in λ-f domain[J]. Journal of Northeast Petroleum University, 2015, 39(1): 17-22. DOI:10.3969/j.issn.2095-4107.2015.01.003 |
| [18] |
LI Zhina, LI Zhenchun, WANG Peng, et al. Multiple attenuation using λ-f domain high-resolution Radon transform[J]. Applied Geophysics, 2013, 10(4): 433-441. DOI:10.1007/s11770-013-0405-1 |
| [19] |
薛亚茹, 唐欢欢, 陈小宏. 高阶高分辨率Radon变换地震数据重建方法[J]. 石油地球物理勘探, 2014, 49(1): 95-100, 131. XUE Yaru, TANG Huanhuan, CHEN Xiaohong. Seismic data reconstruction based on high order high resolution Radon transform[J]. Oil Geophysical Prospecting, 2014, 49(1): 95-100, 131. |
| [20] |
薛亚茹, 杨静, 钱步仁. 基于高阶稀疏Radon变换的预测多次波自适应相减方法[J]. 中国石油大学学报, 2015, 39(1): 43-49. XUE Yaru, YANG Jing, QIAN Buren. Multiples prediction and adaptive subtraction with high-order sparse Radon transform[J]. Journal of China University of Petroleum, 2015, 39(1): 43-49. DOI:10.3969/j.issn.1673-5005.2015.01.006 |
| [21] |
薛亚茹, 郭蒙军, 冯璐瑜, 等. 应用加权迭代软阈值算法的高分辨率Radon变换[J]. 石油地球物理勘探, 2021, 56(4): 736-744, 757. XUE Yaru, GUO Mengjun, FENG Luyu, et al. High resolution Radon transform based on the reweighted-iterative soft threshold algorithm[J]. Oil Geophysical Prospecting, 2021, 56(4): 736-744, 757. |
| [22] |
罗腾腾, 徐基祥, 孙夕平. 应用迭代收缩高分辨率Radon变换的绕射波分离与成像方法[J]. 石油地球物理勘探, 2021, 56(2): 313-322. LUO Tengteng, XU Jixiang, SUN Xiping. Diffraction wave separation and imaging based on high-resolution Radon transform on an iterative model shrinking approach[J]. Oil Geophysical Prospecting, 2021, 56(2): 313-322. |
| [23] |
唐欢欢, 毛伟建. 3D高阶抛物Radon变换地震数据保幅重建[J]. 地球物理学报, 2014, 57(9): 2918-2927. TANG Huanhuan, MAO Weijian. Amplitude preserved seismic data reconstruction by 3D high-order parabolic Radon transform[J]. Chinese Journal of Geo-physics, 2014, 57(9): 2918-2927. |
| [24] |
王亮亮, 毛伟建, 唐欢欢, 等. 快速3D抛物Radon变换地震数据保幅重建[J]. 地球物理学报, 2017, 60(7): 2801-2812. WANG Liangliang, MAO Weijian, TANG Huanhuan, et al. Amplitude preserved seismic data reconstruction by fast 3D parabolic Radon transform[J]. Chinese Journal of Geophysics, 2017, 60(7): 2801-2812. |
| [25] |
张全, 林柏栎, 杨勃, 等. CPU-GPU异构平台的抛物线Radon变换并行算法[J]. 石油地球物理勘探, 2020, 55(6): 1263-1270. ZHANG Quan, LIN Baiyue, YANG Bo, et al. Parabolic Radon transform parallel algoritnm for CPU-GPU heterogeneous platform[J]. Oil Geophysical Prospecting, 2020, 55(6): 1263-1270. |



 方云峰, 河北省涿州市华阳东路东方地球物理公司科技园物探技术研究中心处理技术研发部,072751。Email:
方云峰, 河北省涿州市华阳东路东方地球物理公司科技园物探技术研究中心处理技术研发部,072751。Email: 
