在地震数据处理中,地震噪声压制技术占据重要的地位[1]。目前,噪声压制方法主要有两种:一是在Bayes估计理论框架下,以信号满足线性假设、噪声满足高斯分布为基础,求解最佳的滤波器系数,形成最佳预测滤波器,实现对信号的最佳预测,如基于AR模型的f-x滤波、Wiener中心预测滤波等[2-5];另一种是在已知噪声统计特征的基础上,实现对噪声的精准预测,从而间接实现有效信号的恢复[6-7]。这两种方法在噪声压制中均有较为广泛的应用。在图像处理中,均值类滤波是压制高斯白噪的有效途径,但无法完整保留图像中的有效信号。
针对该问题,以高斯滤波器为基础,各向异性滤波器从保护图像边缘和细节信息的角度完善滤波器的性能[8-10]。Yaroslavsky[11]以Lee[12]提出的邻域滤波为基础,把邻域内各个数据点幅值相似程度作为滤波时的加权系数。假如滤波中心点即是噪声点,最好的噪声压制方式是将该点的幅值与邻域内所有噪声点的幅值进行加权平均。该过程需排除有效信息点,仅对噪声点进行加权平均。
邻域滤波器以幅值为约束,在一定程度上改善了滤波效果,但仍需发展更加有效的保护边缘信息的方法。Smith等[13]和Tomasi等[14]在邻域滤波器的基础上,提出兼顾邻域内数据点幅值相似程度和距离因素的双边滤波器。Paris等[15]阐述了双边滤波器的理论并展示了其应用效果。邻域滤波器与双边滤波器的区别在于处理空间分量的方式不同:对于邻域滤波器,在邻域空间内的所有数据点均会被统一均值处理;而对于双边滤波器,更接近滤波中心点的数据点被赋予了更大的权重。
Buades等[16-19]进一步拓展了邻域滤波器,提出非局部均值算法,该算法使用两个数据点对应的邻域间的相似程度评估这两点间的相似程度。
目前,已有很多保持图像边缘信息和结构的滤波方法,比如改进的数字图像均值滤波算法[20]、改进的反扩散图像平滑模型和自适应数值统计滤波算法[21]、改进的非局部均值图像去噪算法[22]、基于统计滤波的自适应双阈值的边缘检测算法[23]、自适应特征选择的相关滤波跟踪算法[24]和保持图像边缘信息的算法[25]等。
地震数据与常规图像之间存在很大的差异。地震数据本质上是由满足一定时距关系的地震同相轴与具有一定统计规律的随机噪声构成。地震记录是由地震子波构成的[26],在地震记录上,地震子波的波峰和波谷交替出现,幅值有正有负,使得同相轴具有一定宽度。常规图像可由二维函数f(x, y)定义,图像中每一个空间位置点(x, y)对应一个幅值f,即图像的灰度或强度[26-28]。在地震数据处理中,使用经典统计滤波器会影响地震数据中的同相轴信息,滤波效果不理想。杨葆军[29]和Chuai等[30]提出利用相干值扫描方法确定构造方向,将保结构的双边滤波方法应用于地震数据处理,这在一定程度上考虑了同相轴信息。考虑到局部的地震数据特征,基于地震波相似性,提出了自适应滤波器等非局部均值滤波[31-33]。为进一步保护同相轴信息,提出了自适应顺序统计滤波器和加权中值滤波器相结合的方法[34]、最大一致性倾角扫描方法[35]、自适应地震保边界方法[36]、基于非局部中值滤波的地震图像结构定向滤波方法[37]、改进的各向异性扩散滤波方法[38-39]、基于迭代启发网络算法的非平稳随机噪声压制方法[40]等。这些方法均可在压制噪声的同时,在一定程度上保留了地震同相轴局部变化信息。
在前人研究的基础上,本文设计了一种沿同相轴方向的各向异性滤波器。首先,利用相关系数提取同一同相轴相邻道的相似特征。然后,利用纵、横向方差比值划分区域,使滤波器在不同区域自适应地沿同相轴方向滤波,从而设计适合地震数据规律的滤波器。基于合成数据和实际数据,验证了该方法去噪的有效性并保持原有地震信号同相轴的有效信息。此外,本文对比了所提方法与图像处理中的各向同性滤波器(均值滤波器、高斯滤波器)、各向异性滤波器(邻域滤波器、双边滤波器、非局部均值滤波器)在地震数据处理中的优缺点。最后,根据信噪比、残差和误差曲线的定量、定性结果,分析了统计滤波在地震数据处理中应用的可能性和局限性。
1 方法原理 1.1 噪声模型地震数据可看作是确定性信号与满足各种概率分布的随机噪声的叠加[8-9]
| $ u(x, y)=s(x, y)+\eta(x, y) $ | (1) |
式中:u(x, y)表示观测数据的幅值,其中(x, y)表示第x道、第y个样点位置;s(x, y)表示地震信号;η(x, y)表示随机噪声。常见的噪声模型是高斯白噪声模型[8]。高斯分布是简单的、大数定律定义的有限分布。高斯白噪声具有的特点是功率谱密度服从均匀分布,幅值服从高斯分布。高斯随机变量n的概率密度函数[4]为
| $ p(n)=\frac{1}{\sigma \sqrt{2 \pi}} \mathrm{e}^{-\frac{(n-\overline n)^2}{\left(2 \sigma^2\right)}} $ | (2) |
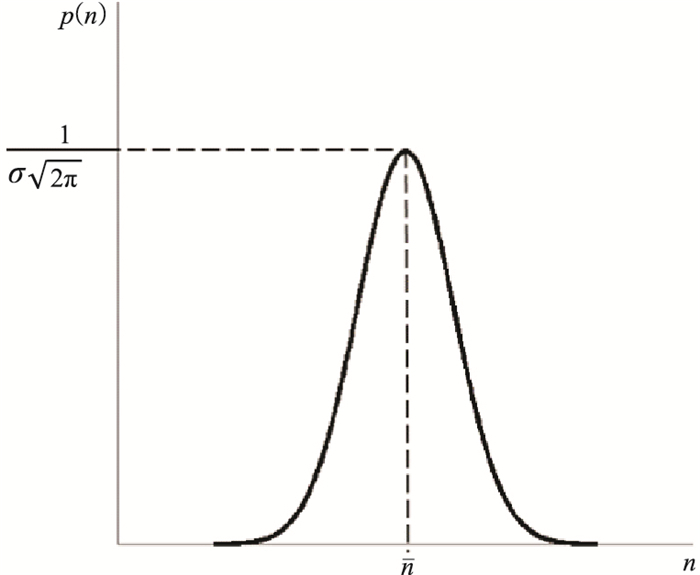
式中:n表示灰度值;n表示n的均值;σ表示n的标准差。高斯函数的曲线如图 1所示。
|
图 1 均值为n、标准差为σ的高斯概率密度函数 |
理论上,当地震数据包含的噪声为高斯白噪声时,均值滤波器是最佳的滤波器。根据概率理论,当邻域内噪声点的个数为N时,求取邻域内所有点的均值可使噪声标准差降低到原来标准差的
统计滤波的噪声压制思想是基于实测数据的统计特征,利用施加高斯白噪后的数据统计量信息,设计合适的统计滤波器。对含噪图像施加由滤波窗和参数确定的滤波算子,设计滤波器并滤波,使地震信号接近理论信号,并使随机噪声的统计量(期望、方差等)等于或接近零。统计量是随机数据的某种加权叠加,其结果依赖于施加高斯白噪后的数据的统计特征。高斯分布是一种大数定理定义的极限分布。
本文假设数据中包含的噪声是高斯白噪。地震数据是由带限的振荡子波组合而成,直接对其进行简单地加权求和处理会导致子波畸变。为此,设计沿同相轴方向的各向异性滤波器,在同相轴的方向进行加权叠加,尽可能地保留原始有效信号。该滤波器具有以下几点特征:沿着同相轴方向滤波;滤波窗是扁平的;邻域窗的形状和大小需根据地震信号特征变化进行设计。因此,在理论上若能沿着同相轴方向对地震信号进行滤波,滤波算子应有如下的性质
| $ \left\{\begin{array}{l} \mathrm{F} u(x, y)=\mathrm{Fs}(x, y)+\mathrm{F} \eta(x, y) \approx s(x, y) \\ E[\mathrm{F} \eta(x, y)]=0 \\ E[\mathrm{F}s(x, y)]=s(x, y) \end{array}\right. $ | (3) |
式中:F是滤波算子;E(·)表示求数学期望。因此,针对不同的结构特征,采取不同的滤波策略。理论上,只要沿着同相轴方向滤波,滤波后可以保护原始的同相轴信息。
本文通过计算邻道的相关系数求取局部的同相轴信息。两道的相关系数计算公式为
| $ \begin{aligned} &r\left(x, y, x^{\prime}, y^{\prime}\right)= \\ &\frac{\sum\limits_{a=-m}^m u(x-a, y) u\left(x^{\prime}-a, y^{\prime}\right)}{\sqrt{\sum\limits_{a=-m}^m u(x-a, y)^2 \sum\limits_{a=-m}^m u\left(x^{\prime}-a, y^{\prime}\right)^2}} \end{aligned} $ | (4) |
式中:(x′, y′)表示当前邻域窗内的某一点;a∈[-m, m],其中m是相关窗长度的一半。
获得相关系数后,通过邻域窗振幅和、相似系数范围、相似点总数三个参数表征数据之间的相似程度。其中,振幅和阈值用来排除不含同相轴信息的滤波点,相似系数范围和相似点总数用来提取相邻同相轴的相似特征。最后,根据同一同相轴相邻道的相似程度确定同相轴的方向。
由于地震子波具有一定的延续长度,邻域滤波窗应该设计成扁平状。子波宽度决定滤波器宽度,同相轴的平缓程度决定滤波器的长度。由于地震剖面往往包含噪声、弱反射、断层、不整合面等,因此有必要针对不同地质情况,构建不同尺寸的滤波器。本文通过纵、横向方差确定滤波器横向长度。方差纵横比定义为
| $ \left\{\begin{aligned} R=& \frac{\sigma_1}{\sigma_2} \\ \sigma_1^2=& \frac{1}{L}\left\{\left[u\left(x_1, y\right)-\bar{u}_y\right]^2+\right.\\ & {\left[u\left(x_2, y\right)-\bar{u}_y\right]^2+\cdots+} \\ & {\left.\left[u\left(x_L, y\right)-\bar{u}_y\right]^2\right\} } \\ \sigma_1^2=& \frac{1}{M}\left\{\left[u\left(x, y_1\right)-\bar{u}_x\right]^2+\right.\\ & {\left[u\left(x, y_2\right)-\bar{u}_x\right]^2+\cdots+} \\ & {\left.\left[u\left(x, y_M\right)-\bar{u}_x\right]^2\right\} } \end{aligned}\right. $ | (5) |
式中:σ12、σ22分别表示横向和纵向的方差值;ux、uy分别表示观测数据幅值在纵向和横向的均值;(xi, yj)表示邻域窗内点;M、L为邻域窗横、纵向尺寸。
选用几个不同尺寸的邻域窗,分别计算纵、横向方差比,根据比值粗略地划分不同的区域。最后,自适应地在不同区域采用不同尺寸的邻域窗进行滤波。
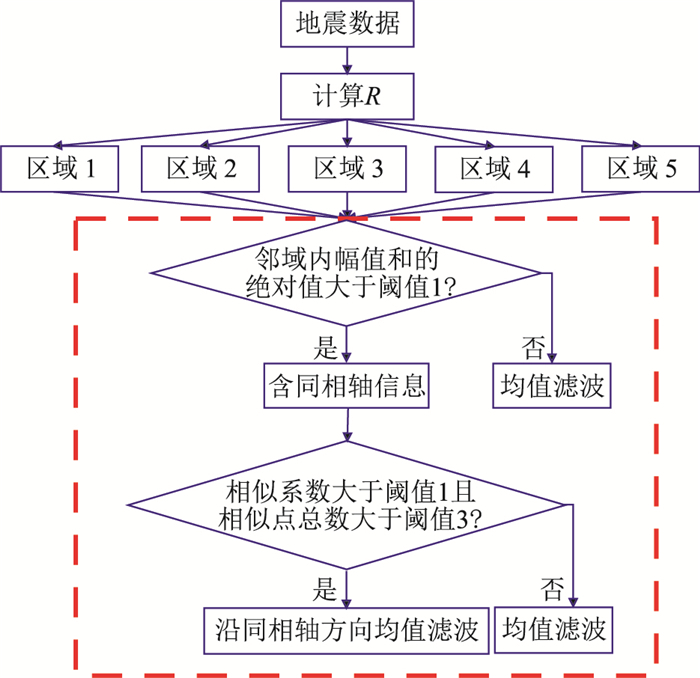
假设噪声是高斯白噪,通过综合衡量地震数据的相似程度,构建符合地震数据特征的滤波器,利用相关系数提取同一同相轴相邻道的相似特征,使得滤波器在不同区域自适应地沿同相轴方向滤波。本文提出的方法可以考虑地震数据中信号的变化特征,因此,可获得较好的滤波效果。图 2为本文所提统计滤波方法处理流程,可概括为:首先,计算地震数据的纵、横向方差比,划分不同的区域。然后,在某个区域的某个滤波点对应的邻域内,如果邻域内幅值和的绝对值小于阈值1,那么认为该滤波点是纯噪声点,进行均值滤波;反之,认为该邻域内含有同相轴信息。对于含有同相轴信息的邻域,如果相似系数大于阈值2且相似点总数大于阈值3,则沿根据相似程度确定的同相轴方向进行均值滤波;反之,认为该邻域内的大部分点为噪声点,直接进行均值滤波。
|
图 2 统计滤波方法处理流程 |
采用理论合成数据从定性和定量角度分别验证沿同相轴方向的各向异性滤波器压制噪声的可行性和有效性。图 3a为采用主频为30Hz的雷克子波合成的地震记录,该数据横向空间样点数为40,纵向时间样点数为300,时间采样间隔和空间采样间隔分别为2ms和1m。选取信噪比为6.94dB的水平同相轴数据,沿同相轴方向分别使用均值滤波器、高斯滤波器和邻域滤波器滤波,结果和相应残差如图 3c~图 3e所示,可见,残差中几乎不含有效信号,三种滤波方式均能有效去除噪声并保留有效信号。进一步计算三种方法处理结果的信噪比,分别为24.54、24.54、24.56dB。结果表明,本文方法在理论上是可行的;只要满足滤波器沿同相轴方向,分别和均值、高斯、邻域滤波器相结合均可获得很好的滤波效果,因此,本文方法仅采用沿同相轴方向均值滤波器。

|
图 3 对水平同相轴数据三种方法的滤波结果及残差对比 (a)原始数据;(b)加高斯白噪后的数据;(c)均值滤波器结果(左)及残差(右);(d)高斯滤波器结果(左)及残差(右);(e)邻域滤波器结果(左)及残差(右) |
对于信噪比为6.94、-2.07dB的水平同相轴数据沿同相轴方向做均值滤波,计算每个样点的相对误差,部分结果如图 4所示。图 4从定量角度表明,要使滤波结果相对误差降低到1%以下,对于信噪比为6.94dB数据,滤波器包含的样点长度至少达到80个;对于信噪比为-2.07dB的数据,滤波器包含的样点长度至少达到600个。因此信噪比越高,滤波器可以越短,对点数的限制越小。

|
图 4 对不同信噪比的合成水平同相轴数据均值滤波器结果的相对误差曲线 (a)6.94dB;(b)-2.07dB。1%的红色横线表示相对误差的基准线,Row-i表示第i个样点 |
统计滤波器可以达到理想滤波效果,即彻底压制地震数据中的随机噪声,但应用时需要尽量满足假设条件。而实际地震数据中的同相轴基本上不呈简单的直线型,数据更为复杂。因此,在实际数据应用中存在很大困难和局限性。
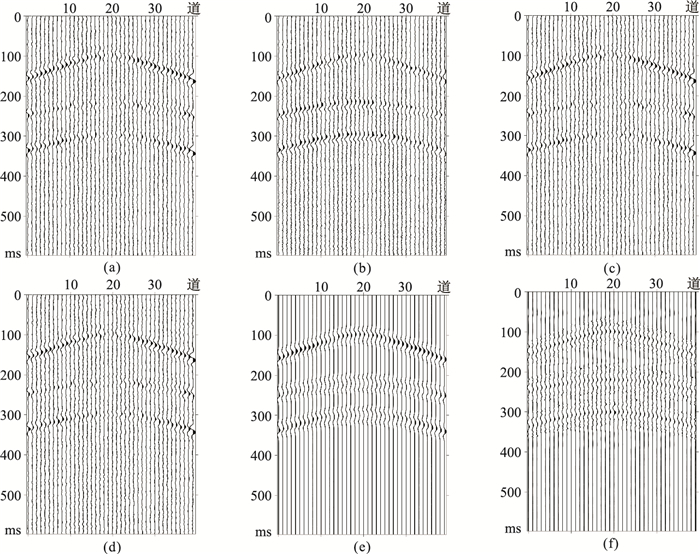
2.2 双曲型同相轴采用理论双曲型同相轴合成数据(图 5a),验证沿同相轴方向的各向异性滤波器在压制噪声和保持地震数据同相轴中有效信息的优势。图 5b是添加高斯白噪后的地震记录,信噪比为6.66dB。采用均值滤波器(图 5c)、高斯滤波器(图 5d)、邻域滤波器(图 5e)、双边滤波器(图 5f)、非局部邻域滤波器(图 5g)进行滤波,滤波结果的信噪比分别为11.81、8.86、12.09、12.10、4.91dB;采用邻域窗(37×37)和相关窗(17×1)滤波后地震记录(图 5h)的信噪比为20.97dB。可见,采用本文方法可有效去除噪声并保留有效信号,剖面的信噪比得到有效提升。图 6为图 5各滤波结果的残差,本文方法滤波结果的残差中几乎不含有效信号(图 6f),证明了该方法在保持同相轴中的有效信息里具有优势。

|
图 5 不同滤波器的滤波结果比较 (a)原始数据;(b)含高斯白噪数据;(c)均值滤波器;(d)高斯滤波器;(e)邻域滤波器;(f)双边滤波器;(g)非局部均值滤波器;(h)本文方法滤波器。图b~图h信噪比分别为6.66、11.81、8.86、12.09、12.10、4.91、20.97dB |
|
图 6 不同滤波器滤波后的残差对比 (a)均值滤波器;(b)高斯滤波器;(c)邻域滤波器;(d)双边滤波器;(e)非局部均值滤波器;(f)本文方法 |
采用较复杂的理论模型Sigsbee 2A测试本文方法的有效性和自适应分区域窗的必要性。图 7a为信噪比为6.63dB的部分Sigsbee 2A模型的成像剖面。模型的横向和纵向的采样点数均为541×261,纵、横向采样间隔均为10m。采用本文所提计算不同大小窗的方法,根据纵横向方差比划分的区域如图 7b所示。图 7c为采用固定窗的滤波结果,图 7d为图 7c与原始成像剖面的残差,图 7e为自适应分区域窗的滤波结果,图 7f为图 7e与原始成像剖面的残差。对比图 7c和图 7e发现,自适应地在不同区域采取不同的邻域窗参数进行滤波,可以考虑成像剖面中信号的变化特征,提高有效信号的保真度,获得较好的滤波结果。若不考虑信号特征,那么固定窗滤波能够有效地压制噪音,但残差中仍有较多的有效信息。

|
图 7 部分Sigsbee 2A模型数据的滤波结果 (a)含噪成像剖面;(b)方差比划分的区域;(c)固定窗的滤波结果;(d)图c与原始成像剖面的残差;(e)自适应分区域窗的滤波结果;(f)图e与原始成像剖面的残差 |
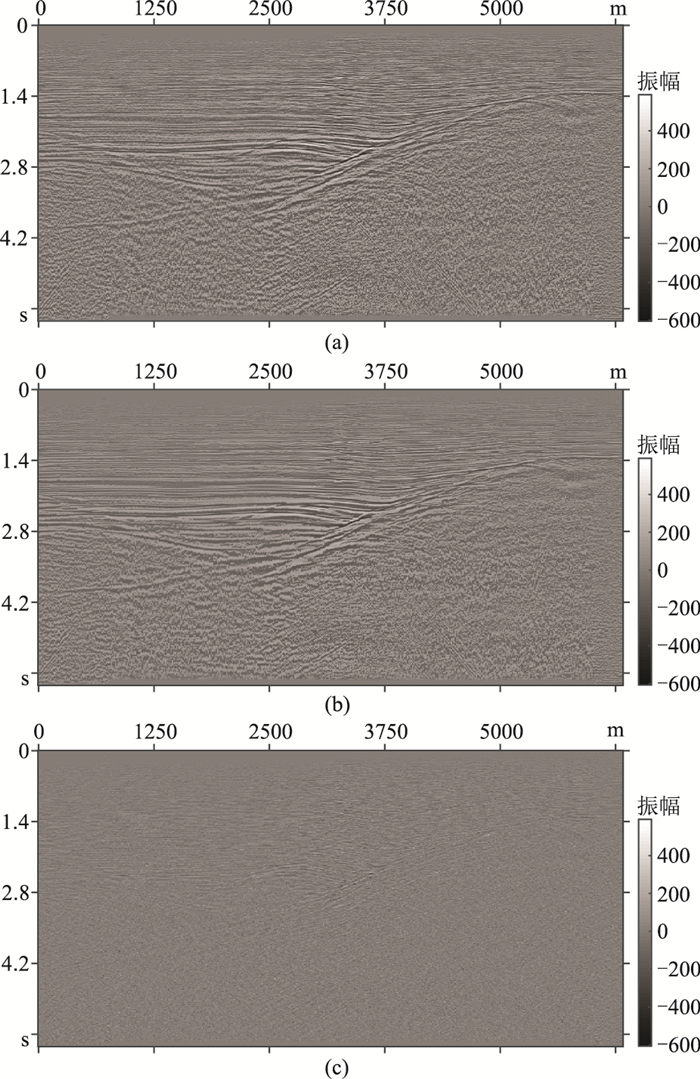
采用某地区实际数据测试本文方法的应用效果。偏移成像剖面如图 8a所示。在方差比分选出的不同区域中分别滤波得到成像剖面(图 8b),数据残差剖面(图 8c)中无明显的连续同相轴,在压制噪声的同时较好地保留了有效信号。可见,采用本文方法可较好地压制噪声,在保留原始同相轴和断层信息的同时,可提高同相轴的连续性。
|
图 8 实际数据滤波结果 (a)实际数据;(b)滤波结果;(c)残差 |
本文提出沿同相轴方向的各向异性滤波器,使滤波器沿同相轴方向在不同区域自适应地滤波。首先,滤波需从统计方面考虑;其次,统计滤波需跟随地震同相轴,自适应地设计与不同区域地质特征相匹配的扁平的窗函数。通过理论数据和实际数据测试,验证了本文所提方法可较好地压制噪声,保留的同相轴具有较好的相干性和连续性;最后,与经典的图像滤波方法相比,本文所提方法在地震数据滤波中适用性更强。但在实际的数据处理中,统计滤波器的长度和噪音的分布情况需要进一步分析和测试。
感谢中石油勘探开发研究院及西北分院、中海油研究院和湛江分公司、中石化物探技术研究院和胜利油田分公司对波现象与智能反演成像研究组(WPI)研究工作的资助与支持。
| [1] |
王华忠, 盛燊. 走向精确地震勘探的道路[J]. 石油物探, 2021, 60(5): 693-708, 720. WANG Huazhong, SHENG Shen. Pathway toward accurate seismic exploration[J]. Geophysical Prospecting for Petroleum, 2021, 60(5): 693-708, 720. DOI:10.3969/j.issn.1000-1441.2021.05.001 |
| [2] |
张力起, 张猛, 王华忠, 等. 高维地震数据Wiener中心滤波方法[J]. 石油物探, 2019, 58(3): 325-334. ZHANG Liqi, ZHANG Meng, WANG Huazhong, et al. Centralized Wiener filtering for high-dimensional seismic data[J]. Geophysical Prospecting for Petroleum, 2019, 58(3): 325-334. DOI:10.3969/j.issn.1000-1441.2019.03.002 |
| [3] |
刘彦萍, 张乃禄, 仵杰, 等. 利用波原子分解系数自适应Wiener滤波方法压制地震数据随机噪声[J]. 石油地球物理勘探, 2021, 56(5): 1022-1029, 1047. LIU Yanping, ZHANG Nailu, WU Jie, et al. Utilizing the method of wave atom decomposition coefficient with adaptive Wiener filtering to suppress seismic random noise[J]. Oil Geophysical Prospecting, 2021, 56(5): 1022-1029, 1047. |
| [4] |
许自龙, 宋林, 夏洪瑞. 一种从低信噪比地震资料中提取信号的方法[J]. 石油地球物理勘探, 2021, 56(2): 242-248. XU Zilong, SONG Lin, XIA Hongrui. A method of signal extracting in low SNR seismic data[J]. Oil Geo-physical Prospecting, 2021, 56(2): 242-248. |
| [5] |
SWÄRD J, ADALBJÖRNSSON S I, JAKOBSSON A. High resolution sparse estimation of exponentially decaying N-dimensional signals[J]. Signal Processing, 2016, 128: 309-317. DOI:10.1016/j.sigpro.2016.04.002 |
| [6] |
TAKEDA H, FARSIU S, MILANFAR P. Kernel regression for image processing and reconstruction[J]. IEEE Transactions on Image Processing, 2007, 16(2): 349-366. DOI:10.1109/TIP.2006.888330 |
| [7] |
程文婷, 方文倩, 付丽华. 基于自相似性和低秩先验的地震数据随机噪声压制[J]. 石油物探, 2020, 59(6): 880-889. CHENG Wenting, FANG Wenqian, FU Lihua. Seismic noise suppression via self-similarity and low-rank prior[J]. Geophysical Prospecting for Petroleum, 2020, 59(6): 880-889. DOI:10.3969/j.issn.1000-1441.2020.06.006 |
| [8] |
GONZALEZ R C, WOODS R E. Digital Image Processing[M]. 3rd Edition. Prentice-Hall Inc, Upper Saddle River, 2006.
|
| [9] |
SCHERZER O. Handbook of Mathematical Methods in Imaging[M]. Springer New York NY, New York, 2011.
|
| [10] |
ARCE G R. Nonlinear Signal Processing: A Statistical Approach[M]. John Wiley & Sons Inc, Hoboken, 2004.
|
| [11] |
YAROSLAVSKY L P. Digital Picture Processing[M]. Springer, Berlin, 1985.
|
| [12] |
LEE J S. Digital image smoothing and the sigma filter[J]. Computer Vision, Graphics, and Image Processi-ng, 1983, 24(2): 255-269. DOI:10.1016/0734-189X(83)90047-6 |
| [13] |
SMITH S M, BRADY J M. Susan: a new approach to low level image processing[J]. International Journal of Computer Vision, 1997, 23(1): 45-78. DOI:10.1023/A:1007963824710 |
| [14] |
TOMASI C, MANDUCHI R. Bilateral filtering for gray and color images[C]. Sixth International Conference on Computer Vision, 1998, 839-846.
|
| [15] |
PARIS S, KORNPROBST P, TUMBLIN J, et al. Bilateral filtering: theory and applications[J]. Foundations and Trends in Computer Graphics and Vision, 2016, 4(1): 1-73. |
| [16] |
BUADES A, COLL B, MOREL J M. A review of i-mage denoising algorithms, with a new one[J]. Multiscale Modeling & Simulation, 2005, 4(2): 490-530. |
| [17] |
BUADES A, COLL B, MOREL J M. A non-local algorithm for image denoising[C]. IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2005, 2: 60-65.
|
| [18] |
BUADES A, COLL B, MOREL J M. Nonlocal image and movie denoising[J]. International Journal of Computer Vision, 2008, 76: 123-139. DOI:10.1007/s11263-007-0052-1 |
| [19] |
BUADES A, COLL B, MOREL J M. Image denoising methods, A new nonlocal principle[J]. SIAM Review, 2010, 52(1): 113-147. DOI:10.1137/090773908 |
| [20] |
张旭, 陈树越. 一种基于统计特性的邻域均值滤波算法[J]. 科技情报开发与经济, 2005, 15(2): 146-147. ZHANG Xu, CHEN Shuyue. A neighborhood mean filter algorithm based on statistical features[J]. Sci-Tech Information Development & Economy, 2005, 15(2): 146-147. DOI:10.3969/j.issn.1005-6033.2005.02.084 |
| [21] |
黎健生. 基于数值统计滤波和偏微分方程的图像平滑去噪算法研究[D]. 广东汕头: 汕头大学, 2008. LI Jiansheng. A Study of Method for Image Smoo-thing and Denoising Based on Statistic Filtering and PDES[D]. Shantou University, Shantou, Guangdong, 2008. |
| [22] |
刘晓明, 田雨, 何微, 等. 一种改进的非局部均值图像去噪算法[J]. 计算机工程, 2012, 38(4): 199-201, 207. LIU Xiaoming, TIAN Yu, HE Wei, et al. Improved non-local means algorithm for image denoising[J]. Computer Engineering, 2012, 38(4): 199-201, 207. |
| [23] |
段军, 高翔. 基于统计滤波的自适应双阈值改进canny算子边缘检测算法[J]. 激光杂志, 2015, 36(1): 10-12. DUAN Jun, GAO Xiang. Adaptive statistical filtering double threshholds based on improved canny operator edge detection algorithm[J]. Laser Journal, 2015, 36(1): 10-12. |
| [24] |
刘万军, 孙虎, 姜文涛. 自适应特征选择的相关滤波跟踪算法[J]. 光学学报, 2019, 39(6): 234-247. LIU Wanjun, SUN Hu, JIANG Wentao. Correlation filter tracking algorithm for adaptive feature selection[J]. Acta Optica Sinica, 2019, 39(6): 234-247. |
| [25] |
LIU W, ZHANG P P, LEI Y J, et al. A generalized framework for Edge-Preserving and Structure-Preserving image smoothing[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021. DOI:10.1109/TPAMI.2021.3097891 |
| [26] |
陆基孟. 地震勘探原理[M]. 第3版. 北京: 石油工业出版社, 1982. LU Jimeng. The Principle of Seismic Exploration[M]. 3rd Edition. Beijing: Petroleum Industry Press, 1982. |
| [27] |
张贤达. 现代信号处理[M]. 第3版. 北京: 清华大学出版社, 2015. ZHANG Xianda. Modern Signal Processing[M]. 3rd Edition. Beijing: Tsinghua University Press, 2015. |
| [28] |
厉朗. 基于各向异性扩散方程的保持图像结构的去噪方法研究[D]. 上海: 同济大学, 2018. LI Lang. Research on Image-Structural-Preserving Denoising-Methods Based on Anisotropic Diffusion Equations[D]. Tongji University, Shanghai, 2018. |
| [29] |
杨葆军. 双边滤波保结构三维地震噪音压制技术[D]. 北京: 中国科学院大学, 2012. YANG Baojun. Structure Preserving Denoising 3D Seismic Data Using the Bilateral Filter Algorithm[D]. University of Chinese Academy of Sciences, Beijing, 2012. |
| [30] |
CHUAI Y Y, QIAO Z, XIE Z, et al. Adaptive bidirectional edge-preserving filtering microfaults recognition technology based on cepstrum[C]. SEG Technical Program Expanded Abstracts, 2020, 39: 1175-1179.
|
| [31] |
黄英, 文晓涛, 贺振华. 地震图像随机噪声的非局部均值去噪法[J]. 断块油气田, 2013, 20(6): 730-732. HUANG Ying, WEN Xiaotao, HE Zhenhua. Denoi-sing algorithm of random noise with seismic image based on nonlocal means[J]. Fault-Block Oil and Gas Field, 2013, 20(6): 730-732. |
| [32] |
SHANG S, HAN L G, LV Q T, et al. Seismic random noise suppression using an adaptive nonlocal means algorithm[J]. Applied Geophysics, 2013, 10(1): 33-40. |
| [33] |
赵冲, 李辉峰, 赵驰, 等. 基于地震波相似性的非局部均值滤波压制异常振幅噪音[J]. 海洋地质前沿, 2021, 37(3): 60-65. ZHAO Chong, LI Huifeng, ZHAO Chi, et al. Suppression of abnormal amplitude noise with seismic wave similarity non-local mean filter[J]. Marine Geo-logy Frontiers, 2021, 37(3): 60-65. |
| [34] |
陈仲委, 尧德中. 自适应顺序统计滤波在地震资料处理中的应用[J]. 石油地球物理勘探, 2006, 41(3): 271-274. CHEN Zhongwei, YAO Dezhong. Application of adaptive order statistic filtering in seismic data processing[J]. Oil Geophysical Prospecting, 2006, 41(3): 271-274. |
| [35] |
安勇, 魏立春, 杨长春. 地震资料保边的最大一致性倾角扫描去噪方法[J]. 应用地球物理(中文版), 2006, 3(4): 210-217. AN Yong, WEI Lichun, YANG Changchun. The most homogeneous dip-scanning method using edge preserving smoothing for seismic noise attenuation[J]. Applied Geophysics, 2006, 3(4): 210-217. |
| [36] |
范桃园, 杨长春. 自适应三维地震保边界去噪方法及应用[J]. 石油地球物理勘探, 2009, 44(5): 558-563. FAN Taoyuan, YANG Changchun. 3D adaptive seismic edge-preserving smoothing and its application[J]. Oil Geophysical Prospecting, 2009, 44(5): 558-563. |
| [37] |
GUO L Y, LIU Y, LIU C, et al. Structure-oriented filtering for seismic images using nonlocal median filter[C]. SEG Technical Program Expanded Abstracts. 2018, 37: 4623-4627.
|
| [38] |
FENG C, ZHANG H, PAN S, et al. Research on an improved anisotropic diffusion filtering method[C]. SEG Technical Program Expanded Abstracts, 2019, 38: 4705-4709.
|
| [39] |
王静, 张军华, 冯德永, 等. 利用不连续性的各向异性扩散滤波方法识别断层[J]. 石油地球物理勘探, 2020, 55(6): 1349-1357. WANG Jing, ZHANG Junhua, FENG Deyong, et al. Fault identification based on a discontinuous anisotropic diffusion filter[J]. Oil Geophysical Prospecting, 2020, 55(6): 1349-1357. |
| [40] |
张文征, 唐杰, 刘英昌, 等. 基于迭代启发网络算法的非平稳随机噪声压制[J]. 石油地球物理勘探, 2020, 55(5): 957-964, 972. ZHANG Wenzheng, TANG Jie, LIU Yingchang, et al. Iterative scheme inspired network for non-stationa-ry random denoising[J]. Oil Geophysical Prospecting, 2020, 55(5): 957-964, 972. |



 王华忠, 上海市杨浦区四平路街道1239号同济大学海洋与地球科学学院,200092。Email:
王华忠, 上海市杨浦区四平路街道1239号同济大学海洋与地球科学学院,200092。Email: 