在陆上地震勘探中,由于地震数据采集现场复杂的地震地质条件,加上采集设备、经济成本及禁采区等因素的限制,往往会产生坏道、地震道缺失、道间距过大等情况,从而造成所采集地震数据的不完整[1],包括有效信号缺失、信噪比低等。在海上,由于拖缆、洋流等因素也会造成空间假频、绕射噪声等问题,导致难以获得较高质量地震数据。为了满足后续处理对地震数据质量的较高要求,最直接有效的方法就是对缺失地震道进行补充采集和加密[2-3]。但受经济成本制约,大多难以再回现场补采数据,因此只能在后期采用有效的地震数据重建方法重建野外缺失的地震道。
地震数据重建方法有以下四种主要类型。一是基于滤波器的方法[4],该类方法通过插值滤波实现。因通常将非均匀网格采样数据当作规则数据处理,故易造成较大误差。二是波场延拓方法[5],该方法充分利用地下信息。因地下结构等先验信息通常是未知的,从而限制了该方法的应用。三是快速降秩方法[6-7],该方法将插值问题看作图像填充问题,计算速度快,参数设置简单,但在非均匀网格采样下的不规则缺失道重建及其反假频能力方面还存在局限性。四是基于数学变换方法,这类方法不需预知地下结构等先验信息,即能重建规则和不规则缺失地震道,且计算速度快,精度高。如Radon变换[8-9]、傅里叶变换[10-11]、小波变换[12]、Curvelet变换[13-15]、Seislet变换[16-17]等,是此类中的常用方法。本文研究的方法即属于第四类,通过改进传统算法,有效地重建出缺失地震数据。目前,基于傅里叶变换的地震数据重建方法已经产业化[18-19],但其重建精度有待进一步提高。为此,众多学者在傅里叶变换的基础上对Curvelet进行研究。Hennenfent等[20]提出了基于Curvelet数据重建的稀疏促进反演方法,成功重建了含有缺失道的地震数据。张华等[15]提出基于曲波变换和新阈值参数的重建方法,且实现了频率域中的三维地震数据重建。同时,人们还研究了基于曲波变换的重建方法[21-23]。但上述方法都是采用单一的迭代方法对地震数据进行重建,而单一方法难免存在局限性,如重建精度不够、收敛速度较慢,或需迭代较多次数才能达到预期的重建精度,这些均限制了相应方法的工业应用。
于是,研究人员提出了许多加速迭代方法,其中一类为Bregman正则化方法。该方法最早由Osher等[24]、Yin等[25]引入图像处理中,用于解决全变分(TV)的图像恢复问题。随后刘洋等[26]、郭萌等[27]、Cai等[28-29]应用线性Bregman方法进行地震数据重建,均取得较好效果。该方法参数设置简单,通过只阈值化下一次的梯度项系数加速收敛,提高迭代速度;但在每一次迭代过程中,由于部分未阈值化的系数参与重建,因此相比其他迭代法,线性Bregman方法重建效果有所下降。
由于迭代阈值收缩算法(Iterative Shrinkage Thresholding Algorithm,ISTA)参数设置简单[30-32],重建效果显著,在反演领域得到了广泛应用。但其运算速度较慢,需要迭代很多次才能达到满意效果。为了综合不同方法的优势,白兰淑等[33-34]将ISTA方法与线性Bregman方法结合,使联合方法的前期迭代加快,后期迭代精度提高。由于只采用普通线性Bregman方法及传统的线性阈值公式,因此重建精度和计算效率仍受到一定限制。
本文在此基础上,采用Curvelet变换作为稀疏基,引入加速线性Bregman方法(Acceleration linea-rized Bregman Method,ALBM)[35],并将其与ISTA联合;在此过程中,采用软阈值函数和指数阈值公式,且以新型线性和指数加权因子调节加速Bregman与ISTA方法的比重,充分发挥这两种算法的优点。理论和实际数据的重建结果表明,本文方法具有比传统方法更高的重建精度和计算效率。
1 算法原理 1.1 地震数据重建基本原理缺失道数据的重建过程,可假设为如下数学模型
| $ \boldsymbol{y}_{\mathrm{obs}}=\boldsymbol{M} \boldsymbol{f} $ | (1) |
式中:yobs∈Rm表示观测到的缺失数据;f∈RM(M≥m),表示需重建的完整地震数据;M∈Rm×M,表示采样矩阵。数据重建即是由不完整的观测数据yobs恢复完整的地震数据f的过程。由于地震数据在时间域不稀疏,本文拟采用具有多尺度多方向特性的曲波变换对地震数据进行稀疏处理,若用C表示曲波变换,x表示稀疏系数,则式(1)可写成
| $ \boldsymbol{y}_{\mathrm{obs}}=\boldsymbol{M C}^{\mathrm{H}} \boldsymbol{x} $ | (2) |
式中上标“H”表示共轭转置矩阵。
由于恢复缺失数据的过程即是求解欠定方程,则可将该问题转化为求L0范数稀疏约束最小化问题
| $ \boldsymbol{x}=\arg \min \|\boldsymbol{x}\|_0 \quad \text { s. t. } \quad \boldsymbol{y}_{\mathrm{obs}}=\boldsymbol{M} \boldsymbol{C}^{\mathrm{H}} \boldsymbol{x} $ | (3) |
式中||·||0指向量或矩阵中非零元素的个数。
由于求解零范数是一个NP-hard问题,则可将L0范数问题转化为L1范数问题
| $ \boldsymbol{x}=\operatorname{arg\;min}\|\boldsymbol{x}\|_1 \quad \text { s. t. } \quad \boldsymbol{y}_{\mathrm{obs}}=\boldsymbol{M} \boldsymbol{C}^{\mathrm{H}} \boldsymbol{x} $ | (4) |
式中||·||1是向量或矩阵中各个元素的绝对值之和。通过式(4),使得难以求解的L0范数问题转化为L1范数稀疏性线性规划问题。
由于野外采集数据都含有不同程度的噪声,为了有效地求解,通常采用正则化思想,在压缩感知理论框架下,式(4)的解可由以下泛函表达式得到
| $ \boldsymbol{x}=\arg \min \frac{1}{2}\|\boldsymbol{y}-\boldsymbol{A} \boldsymbol{x}\|_2+\lambda\|\boldsymbol{x}\|_1 $ | (5) |
式中:A=MCH;λ为正则化参数,它决定L1项与L2项之间的权重。式(5)求解L1范数问题可看作基追踪问题,要想从随机缺失地震数据重建满足后续处理要求的完整数据f,需采用有效反演算法。
1.2 迭代阈值收缩算法迭代阈值收缩算法在每次迭代过程中都会更新阈值,最小化式(5)中的二次方项;继而可通过阈值法投影到L1球上,逐渐收敛到式(5)的解,直到满足精度要求;再对N次迭代后的系数x做曲波反变换就可恢复缺失道信息。
阈值迭代法的迭代公式如下
| $ \begin{aligned} &\boldsymbol{x}_{k+1}=\boldsymbol{T}\left[\boldsymbol{x}_k+\boldsymbol{A}^{\mathrm{H}}\left(\boldsymbol{y}_{\mathrm{obs}}-\boldsymbol{A} \boldsymbol{x}_k\right)\right] \\ &k=1, 2, \cdots, N \end{aligned} $ | (6) |
式中T为阈值函数,分为硬阈值Th函数和软阈值Ts函数,其公式分别为
| $ \boldsymbol{T}_{\mathrm{h}}(\boldsymbol{x})= \begin{cases}\boldsymbol{x} & |\boldsymbol{x}|>\tau \\ 0 & |\boldsymbol{x}| \leqslant \tau\end{cases} $ | (7) |
| $ \boldsymbol{T}_{\mathrm{s}}(\boldsymbol{x})= \begin{cases}\boldsymbol{x}-\tau & x \geqslant \tau \\ \boldsymbol{x}+\tau & x \leqslant-\tau \\ 0 & |x|<\tau\end{cases} $ | (8) |
式中τ表示阈值因子。
1.3 加速线性Bregman算法线性Bregman方法通过将未阈值化的系数参与下一次迭代来加速收敛。该方法虽然在迭代初期收敛很快,但后期由于在恢复有效信号的同时也会将小于阈值的非有效信号吸收进来,导致最终的重建结果不佳。线性Bregman方法迭代公式为
| $ \left\{\begin{array}{l} \boldsymbol{z}_{k+1}=\boldsymbol{z}_k+\boldsymbol{A}^{\mathrm{H}}\left(\boldsymbol{y}_{\mathrm{obs}}-\boldsymbol{A} \boldsymbol{x}_k\right) \\ \boldsymbol{x}_{k+1}=\boldsymbol{T}\left(\boldsymbol{z}_{k+1}\right) \end{array}\right. $ | (9) |
为了进一步提高收敛速度,本文在传统Bregman算法基础上,引入加速线性Bregman方法(ALBM)[34],其迭代公式为
| $ \left\{\begin{array}{l} \boldsymbol{z}_{k+1}=\boldsymbol{z}_k+\boldsymbol{A}^{\mathrm{H}}\left(\boldsymbol{y}_{\mathrm{obs}}-\boldsymbol{A} \boldsymbol{x}_k\right) \\ \boldsymbol{z}_{k+1}=\alpha_k \boldsymbol{z}_{k+1}+\left(1-\alpha_k\right) \boldsymbol{z}_k \\ \boldsymbol{x}_{k+1}=\boldsymbol{T}\left(\boldsymbol{z}_{k+1}\right) \end{array}\right. $ | (10) |
式中αk为加速因子,一般选择为
在每次迭代过程中,通过加大未阈值化的曲波系数的比例,在迭代前期保留更大比例的有效信号,进一步提高了初期的收敛速度。
1.4 本文联合算法为了同时提高收敛速度和重建精度,将式(6)与式(10)联合,得到如下迭代式
| $ \left\{\begin{array}{l} \boldsymbol{z}_{k+1}=\beta \boldsymbol{z}_k+(1-\beta) \boldsymbol{x}_k+\boldsymbol{A}^{\mathrm{H}}\left(\boldsymbol{y}_{\mathrm{obs}}-\boldsymbol{A} \boldsymbol{x}_k\right) \\ \boldsymbol{z}_{k+1}=\alpha_k \boldsymbol{z}_{k+1}+\left(1-\alpha_k\right) \boldsymbol{z}_k \\ \boldsymbol{x}_{k+1}=\boldsymbol{T}\left(\boldsymbol{z}_{k+1}\right) \end{array}\right. $ | (11) |
式中β为加权因子,它的选取对于提高重建精度和计算效率均具有重要影响。为此,本文引入如下线性加权函数和指数加权函数两种公式进行对比
| $ \beta_1=1-\frac{k-1}{N-1} $ | (12) |
| $ \beta_2=\exp \left(\frac{k-1}{N-1} \ln 10^{-6}\right) $ | (13) |
通过加权因子的作用,可使Bregman加速项zk前期占比较大,提高迭代速度,加速收敛,后期ISTA稳定项xk占比较大,提高迭代的精度,并且使两种方法过渡得更平滑。
在实际数据处理过程中,软阈值避免了硬阈值的截断效应,使处理后的信号更光滑,但它将信号移向零并可能影响重建的准确性。硬阈值具有更好的幅度保留,但由于直接截断信号而引起抖动效果,即不光滑。本文为了消除硬阈值引起的抖动效果,选择软阈值函数进行处理。在迭代过程中,每次都会更新阈值,不断收敛到式(5)的解,直到满足精度要求;然后对最终迭代后的系数xN进行曲波反变换,即可恢复缺失道信息。迭代开始首先要使阈值较大强调L1项,随着迭代进行要使L2占较大影响,阈值因子τ慢慢递减逐渐逼近真实解。为此,阈值参数一般满足||Cy||∞=τ1>τ2>…>ε,ε为接近0的最小值。常用的线性阈值参数为[36]
| $ \tau_k=\operatorname{Max}-\frac{\operatorname{Max}-\varepsilon}{N-1}(k-1) $ | (14) |
式中Max为|Cy|的最大值,即稀疏变换系数的最大值。本文阈值参数选择为指数阈值参数[15],该参数相比线性阈值参数在保证求解精度的同时收敛速度更快,节省计算工作量,该阈值参数公式为
| $ \tau_k=\operatorname{Max} \cdot \exp \left[(\ln \varepsilon-\ln \operatorname{Max}) \sqrt{\frac{k-1}{N-1}}\right] $ | (15) |
为了检验本文方法的重建效果,定义信噪比公式
|
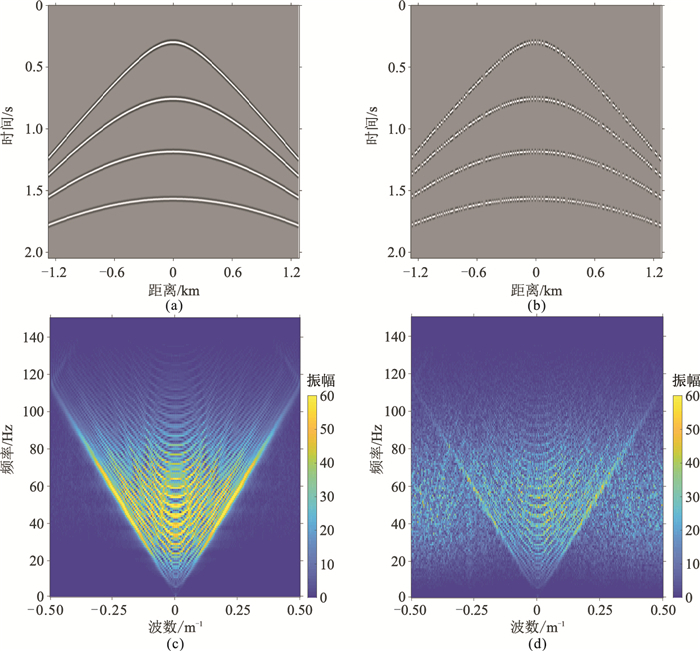
图 1 原始模型采样及f-k频谱 (a)理论模型;(b)50%随机欠采样;(c)理论数据f-k频谱;(d)随机采样数据f-k频谱 |
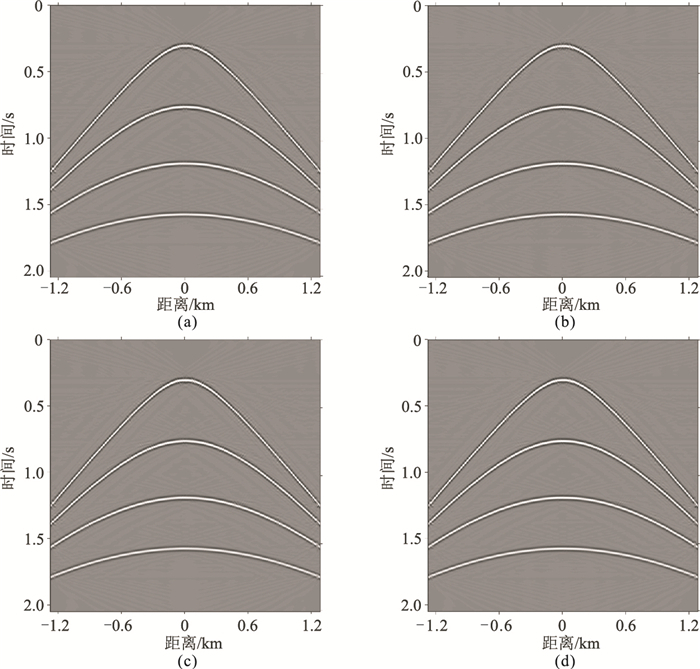
为了达到较好处理效果,本次重建模拟采用30次迭代,曲波变换的尺度为4,第二尺度上的方向值为32。图 2a、图 2b分别为阈值迭代法和加速线性Bregman法重建结果,其信噪比分别为14.99、14.87dB,图 2c为传统线性Bregman法与阈值迭代法联合(LBM+ISTA)重建结果,信噪比为15.44dB。图 2d为本文加速线性Bregman方法与阈值迭代法联合(ALBM+ISTA)重建结果,信噪比为16.35dB。可见每种方法都能将缺失的地震道有效地恢复出来,但与其他方法相比,本文方法重建后的信噪比最高,重建后的有效波同相轴与理论数据一致。
|
图 2 不同算法重建结果 (a)ISTA方法;(b)ALBM方法;(c)LBM+ISTA方法;(d)本文方法 |
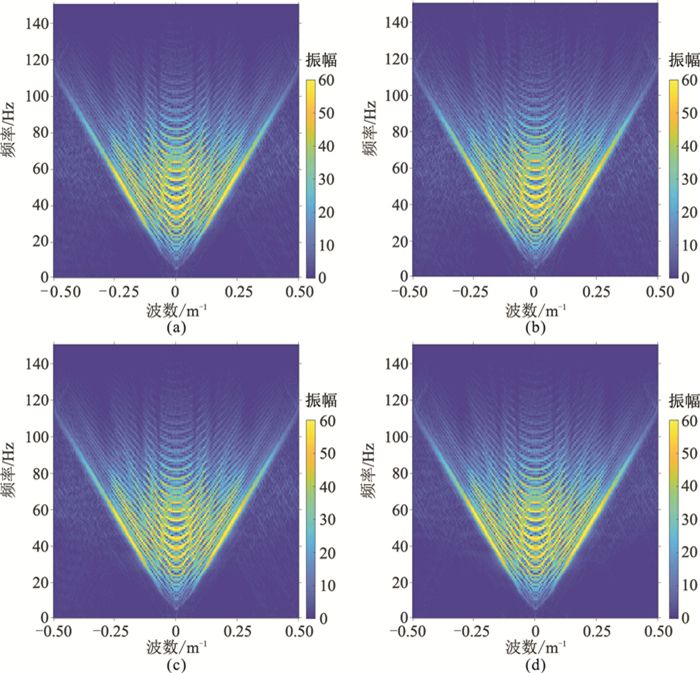
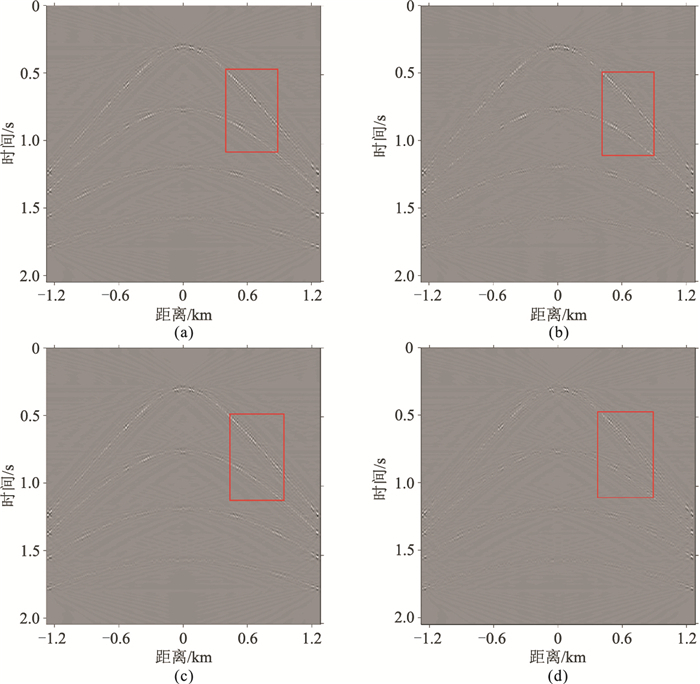
图 3a~图 3d为图 2对应的频谱图,可看出有效波能量都得到了明显收敛,消除了不相干的随机噪声,特别从图 3中的红色矩形可见,相比其他方法,本文方法重建后频谱与原始数据频谱最吻合。从相应的误差图(图 4)也可看出,本文所提联合算法重建误差最小,进一步证明了本文方法的有效性。
|
图 3 不同算法重建结果的频谱 (a)ISTA方法;(b)ALBM方法;(c)LBM+ISTA方法;(d)本文方法 |
|
图 4 不同算法重建结果的误差 (a)ISTA方法;(b)ALBM方法;(c)LBM+ISTA方法;(d)本文方法 |
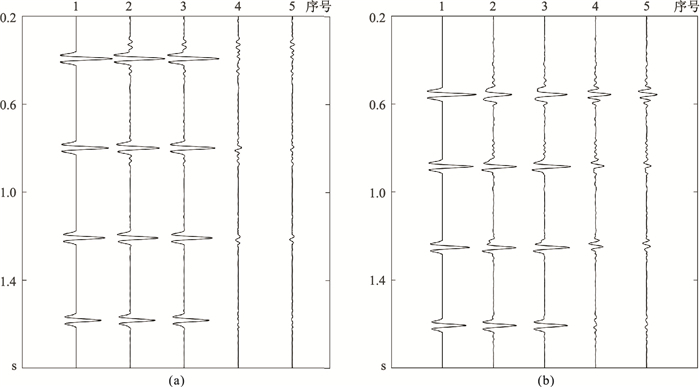
为了从细节体现本文方法的有效性,特意抽取某一单道曲线与传统联合方法进行对比(图 5)。图 5a和图 5b分别表示第102和178缺失道重建前、后的单道曲线,时窗为0.2~1.8s。对比为原始数据(第1条),LBM+ ISTA(第2条)和本文方法第3条重建后的单道曲线,以及其误差单道曲线(第4和第5条),可见本文方法重建结果与原始数据更吻合,重建后的精度高,误差小。
|
图 5 重建结果与误差的单道显示 (a)第102道重建前后曲线;(b)第178道重建前后曲线 1,原始单道记录;2、3,LBM+ISTA和本文方法重建后单道;4、5,对应2、3的误差记录 |
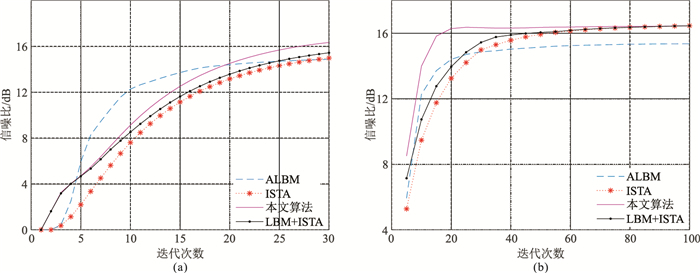
为了进一步比较各种算法在不同迭代次数下的重建信噪比,采用不同迭代次数进行重建,从而得到相应信噪比曲线。图 6a为最大迭代次数为30时的信噪比曲线,整体看初期线性ALBM收敛速度较快,但后期收敛速度变慢,且重建精度较低,而ISTA恰好相反。对于传统联合(LBM+ISTA) 方法,收敛速度和重建精度都较好,但整体来看,在相同迭代次数下,本文方法重建精度更高。图 6b为不同迭代次数下的信噪比曲线,可见ALBM在10次以内收敛速度较快,尔后收敛速度变慢,且重建精度也很难进一步提高。ISTA则随着迭代次数的增加,重建后的信噪比较高,传统联合方法吸收了线性Bregman方法和ISTA的优势,但相比本文所提方法,其收敛速度还是较慢,且可看出本文方法在20次以内就可达到较高信噪比,而后趋于稳定,显然本文方法更具优势。
|
图 6 重建后信噪比曲线 (a)30次迭代的信噪比;(b)不同算法迭代次数与信噪比关系 |
从以上结果还可看出联合算法结合了加速ALBM和ISTA的优点。前期迭代速度快,这是由ALBM方法完成的,后期ISTA方法使得信噪比得以提高。本文方法在20次迭代后就已经完全收敛,信噪比达到16.29dB,所需时间仅为121.77s。而ISTA和LBM+ISTA均在60次迭代后才开始收敛,约需80次迭代才可完全收敛,所需时间为613s。表 1为信噪比达到16dB的迭代次数和所需的时间,可见与ISTA和传统联合法相比,在达到满足后续重建精度信噪比的情况下节省了约3/4的时间。
|
|
表 1 信噪比达到16dB的迭代次数及时间 |
为了对比不同加权函数的重建效果,本文选取最大迭代次数5~60,然后记录不同加权函数的迭代次数与重建信噪比之间的关系曲线。图 7a为本文选取的线性加权阈值和指数加权阈值,这两个函数的加权值都是1~0,但指数阈值衰减更快,意味着ISTA项的比重快速上升。图 7b为两种加权因子的不同迭代次数的信噪比曲线,由于两种加权函数都是1~0,使得信噪比都是由低增至高,且随着迭代次数的增加,最终信噪比几乎相同。但由于指数加权函数衰减快,只需较少迭代次数就能使前期加速项衰减更快,在达到较高信噪比之后,稳定项的占比快速上升,最终获得良好的重建结果。

|
图 7 不同加权函数重建信噪比曲线 (a)加权函数曲线;(b)迭代次数不同时,不同加权函数信噪比 |
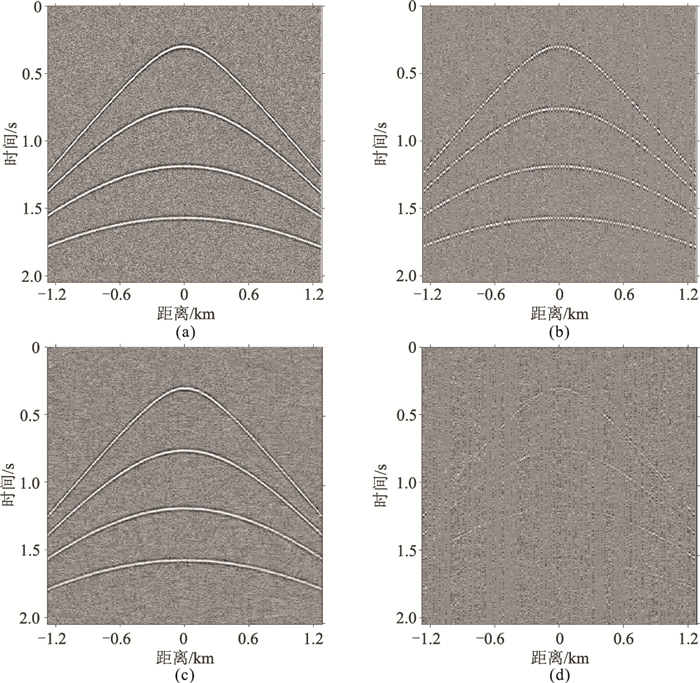
原始地震数据大多含有噪声,为了检验本文方法的抗噪重建能力,对图 1a加入随机高斯噪声(图 8a),再对其进行50%随机欠采样(图 8b),得到本文方法重建结果(图 8c)及其与原始数据的误差(图 8d)。从重建结果看,该含噪缺失数据的地震波同相轴较连续,有效波信号恢复较好,损失的有效波信息较少,说明本文方法有较强抗噪能力,可满足实际地震资料处理的要求。
|
图 8 含噪模型重建结果 (a)含噪模型;(b)50%随机欠采样;(c)本文方法重建结果;(d)重建误差 |
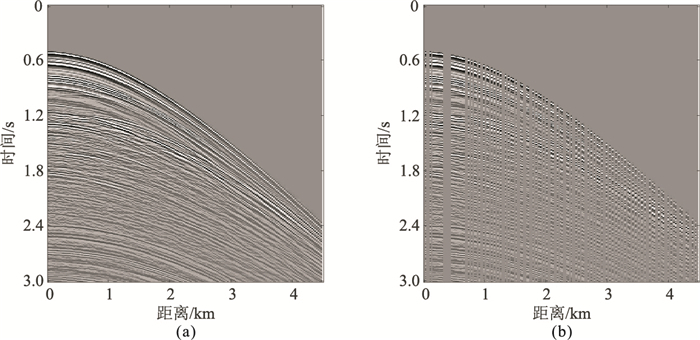
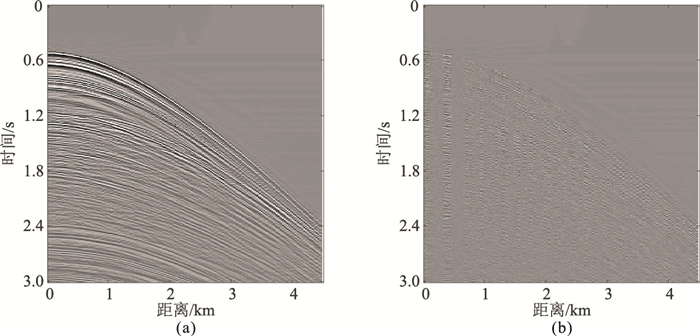
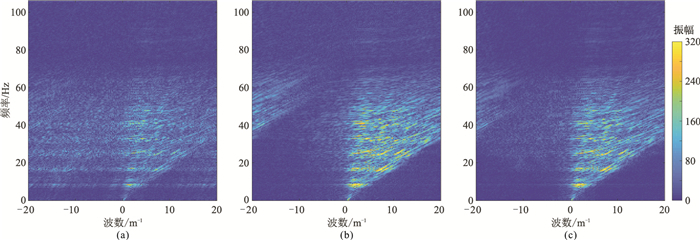
为了检验本文方法的实际意义,选取一块实际原始资料进行处理。图 9a是道距为25m、采样率为4ms、180道接收的实际单炮记录,对其进行50%随机欠采样和连续5道缺失采样(图 9b)。设定迭代次数为20次,曲波变换的尺度为4,第二尺度上的方向值为16,信噪比为8.01dB,得到本文方法重建结果(图 10a)及其与原始记录的误差剖面(图 10b)。可见缺失道信息得到有效重建,能量较弱的有效波也得到了保护,且在连续缺失5道的情况下,本文方法也能进行有效恢复。图 11是其对应的频谱,易见本文方法对有效波能量损伤小,效果明显。
|
图 9 实际单炮记录(a)及其随机欠采样记录(b) |
|
图 10 本文方法对实际单炮随机欠采样记录的重建结果(a)及误差剖面(b) |
|
图 11 实际(a)及其欠采样(b)和重建(c)地震数据的f-k频谱 |
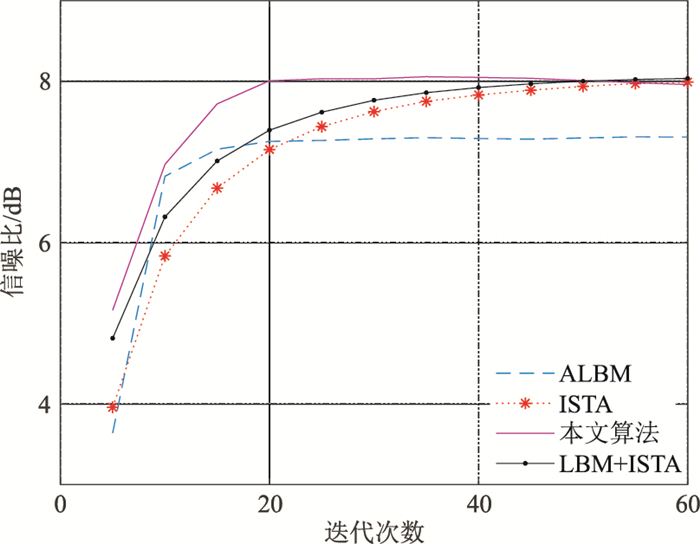
同时,也采用其他算法进行重建并做对比。图 12为不同迭代次数时ALBM、ISTA、LBM+ISTA及本文方法重建后的信噪比与迭代次数关系曲线,可见本文方法在20次迭代后就已开始收敛,而其他方法需40次才开始收敛,迭代60次才可达到与本文方法同样的重建效果。因此,在实际数据处理中,本文方法在迭代次数较少的情况下能有效地对缺失道进行了重建,提高了地震记录的信噪比,满足高精度地震勘探的要求。
|
图 12 实际数据不同算法迭代次数与信噪比关系 |
前述加速因子的选取非常重要,这也是区别于传统线性Bregman算法的关键所在。通常,该值随迭代次数增加而增加,变化范围是1~2。当然,不同的加速因子公式的计算效率不一样,本文引入传统加速因子公式,它随迭代次数的增加而缓慢增大,使得在每次迭代过程中,都可加大未阈值化曲波系数的比例。尽管引入了部分噪声,但保留了更大比例的有效信号,再通过与阈值迭代法进行联合,进一步提高加速项前期的比例,可大幅度提高计算速度,而引入的部分噪声可通过后期阈值迭代法滤除。
本文也尝试过选择指数加速因子公式做测试,但从最后的重建精度来看,其信噪比未能提高。这可能是加速因子呈指数快速增大后,会过多地加大未阈值化曲波系数的比例,尽管可提高部分计算精度,但后期阈值迭代法也不能有效滤除未阈值化的曲波系数带来的大量噪声,从而导致重建精度未能提高。当然还可选择其他加速因子计算公式,在保证计算效率的同时,力争或多或少提高重建精度。
另外,对于曲波变换的尺度和方向值的选择,通常若尺度选择较大,方向值选择较多,则越能反映信号的细节部分,重建精度会有所提高,但计算时间越长。本文综合考虑计算效率与重建精度,并通过多次测试对比,理论和实际数据尺度值都选择为4,方向值分别选择32和16能达到较好效果。
5 结论本文主要在压缩感知的基础上,采用曲波基作为稀疏表示基,在综合分析ALBM和ISTA两种算法优点的基础上,提出了加速联合迭代算法进行快速高精度数据重建,并采用指数加权因子控制ALBM中的加速项与ISTA中的稳定项的比例,使该加速联合迭代算法在前期计算中,ALBM起主要作用,加速算法的收敛,后期ISTA起主要作用,大幅度恢复前期所损失的有效波信号,从而提高重建精度,确保最后得到效率快、信噪比高的重建结果。与传统阈值迭代法、LBM+ISTA方法相比,在达到相同最高信噪比的情况下,本文方法的重建时间节省约70%(表 1),充分突显了本文方法用时少、精度高的特点。并且在加噪条件下和实际资料处理中也得到了较好重建效果,进一步体现了本文方法的广泛有效性,可完全满足海量地震数据处理的要求。
| [1] |
唐刚. 基于压缩感知和稀疏表示的地震数据重建与去噪[D]. 北京: 清华大学, 2010. TANG Gang. Seismic Data Reconstruction and Denoising Based on Compressive Sensing and Sparse Representation[D]. Tsinghua University, Beijing, 2010. |
| [2] |
张华, 陈小宏. 地震数据重建理论与方法[M]. 北京: 科学出版社, 2017. ZHANG Hua, CHEN Xiaohong. Theory and Method of Seismic Data Reconstruction[M]. Beijing: Science Press, 2017. |
| [3] |
霍志周, 熊登, 张剑锋. 地震数据重建方法综述[J]. 地球物理学进展, 2013, 28(4): 1749-1756. HUO Zhizhou, XIONG Deng, ZHANG Jianfeng. The overview of seismic data reconstruction methods[J]. Progress in Geophysics, 2013, 28(4): 1749-1756. |
| [4] |
张军华, 仝兆岐, 何潮观, 等. 在f-k域实现三维波场道内插[J]. 石油地球物理勘探, 2003, 38(1): 27-30. ZHANG Junhua, TONG Zhaoqi, HE Chaoguan, et al. 3-D seismic trace interpolation in f-k domain[J]. Oil Geophysical Prospecting, 2003, 38(1): 27-30. DOI:10.3321/j.issn:1000-7210.2003.01.006 |
| [5] |
NAGHIZADEH M, SACCHI M D. Beyond alias hie-rarchical scale curvelet interpolation of regularly and irregularly sampled seismic data[J]. Geophysics, 2010, 75(6): WB189-WB202. DOI:10.1190/1.3509468 |
| [6] |
MA J W. Three-dimensional irregular seismic data Reconstruction via low-rank matrix completion[J]. Geophysics, 2013, 78(5): V181-V192. DOI:10.1190/geo2012-0465.1 |
| [7] |
GAO J J, SACCHI M D, CHEN X H. A fast reduced-rank interpolation method for prestack seismic volumes that depend on four spatial dimensions[J]. Geophysics, 2013, 78(1): V21-V30. DOI:10.1190/geo2012-0038.1 |
| [8] |
薛亚茹, 唐欢欢, 陈小宏, 等. 高阶高分辨率Radon变换地震数据重建方法[J]. 石油地球物理勘探, 2014, 49(1): 95-100, 131. XUE Yaru, TANG Huanhuan, CHEN Xiaohong, et al. Seismic data Reconstruction based on high order high resolution Radon transform[J]. Oil Geophysical Prospecting, 2014, 49(1): 95-100, 131. |
| [9] |
唐欢欢, 毛伟建, 詹毅. 3D高阶抛物Radon变换在不规则地震数据保幅重建中的应用[J]. 地球物理学报, 2020, 63(9): 3452-3464. TANG Huanhuan, MAO Weijian, ZHAN Yi. Reconstruction of 3D irregular seismic data with amplitude preserved by high-order parabolic Radon transform[J]. Chinese Journal of Geophysics, 2020, 63(9): 3452-3464. |
| [10] |
罗腾. 基于压缩感知理论的地震数据重构方法研究[D]. 吉林长春: 吉林大学, 2015. LUO Teng. Study on the Reconstruction of Seismic Data Based on Compressive Sensing Theory[D]. Jilin University, Changchun, Jilin, 2015. |
| [11] |
温睿, 刘国昌, 冉扬. 压缩感知地震数据重建中的三个关键因素分析[J]. 石油地球物理勘探, 2018, 53(4): 682-693. WEN Rui, LIU Guochang, RAN Yang. Three key factors in seismic data reconstruction based on compressive sensing[J]. Oil Geophysical Prospecting, 2018, 53(4): 682-693. |
| [12] |
崔兴福, 刘东奇, 张关泉. 小波变换实现地震道内插[J]. 石油地球物理勘探, 2003, 38(增刊1): 93-97. CUI Xingfu, LIU Dongqi, ZHANG Guanquan. Seismic traces interpolation using wavelet transform[J]. Oil Geophysical Prospecting, 2003, 38(S1): 93-97. |
| [13] |
韩良良. 基于Curvelet变换的地震数据重建方法研究[D]. 山东青岛: 中国石油大学(华东), 2018. HAN Liangliang. The Study on Seismic Data Reconstruction Method Based on Curvelet Transform[D]. China University of Petroleum (East China), Qing-dao, Shandong, 2018. |
| [14] |
王本锋, 陆文凯, 陈小宏, 等. 基于3D Curvelet变换的频率域高效地震数据插值方法研究[J]. 石油物探, 2018, 57(1): 65-71. WANG Benfeng, LU Wenkai, CHEN Xiaohong, et al. Efficient seismic data interpolation using three-dimensional Curvelet transform in the frequency domain[J]. Geophysical Prospecting for Petroleum, 2018, 57(1): 65-71. |
| [15] |
张华, 陈小宏. 基于jitter采样和曲波变换的三维地震数据重建[J]. 地球物理学报, 2013, 56(5): 1637-1649. ZHANG Hua, CHEN Xiaohong. Seismic data reconstruction based on jittered sampling and curvelet transform[J]. Chinese Journal of Geophysics, 2013, 56(5): 1637-1649. |
| [16] |
刘财, 李鹏, 刘洋, 等. 基于seislet变换的反假频迭代数据插值方法[J]. 地球物理学报, 2013, 56(5): 1619-1627. LIU Cai, LI Peng, LIU Yang, et al. Iterative data interpolation beyond aliasing using seislet transform[J]. Chinese Journal of Geophysics, 2013, 56(5): 1619-1627. |
| [17] |
温睿. 基于Seislet变换的地震数据重建方法研究[D]. 北京: 中国石油大学(北京), 2018. WEN Rui. Study on Seismic Data Reconstruction Methods Based on Seislet Transform[D]. China University of Petroleum (Beijing), Beijing, 2018. |
| [18] |
ZHANG H, CHEN X H, WU X M. Seismic data reconstruction based on CS and Fourier theory[J]. Applied Geophysics, 2013, 10(2): 170-180. |
| [19] |
梁东辉. 基于傅里叶变换的地震数据规则化和插值[D]. 浙江杭州: 浙江大学, 2015. LIANG Donghui. Seismic Data Normalization and Interpolation Based on Fourier Transform[D]. Zhejiang University, Hangzhou, Zhejiang, 2015. |
| [20] |
HENNENFENT G, HERRMANN F J. Seismic denoising with nonuniformly sampled curvelets[J]. Computing in Science & Engineering, 2006, 8(3): 16-25. |
| [21] |
孔丽云, 于四伟, 程琳, 等. 压缩感知技术在地震数据重建中的应用[J]. 地震学报, 2012, 34(5): 659-666. KONG Liyun, YU Siwei, CHENG Lin, et al. Application of compressive sensing to seismic data reconstruction[J]. Acta Seismologica Sinica, 2012, 34(5): 659-666. |
| [22] |
ZHANG H, CHEN X H, ZHANG L Y. 3D simultaneous seismic data reconstruction and noise suppression based on the curvelet transform[J]. Applied Geo-physics, 2017, 14(1): 87-95. |
| [23] |
张岩, 任伟建, 唐国维. 基于曲波变换的地震数据压缩感知重构算法[J]. 吉林大学学报(信息科学版), 2015, 33(5): 570-577. ZHANG Yan, REN Weijian, TANG Guowei. Algorithm of compressed sensing reconstruction of seismic data based on curvelet transform[J]. Journal of Jilin University (Information Science Edition), 2015, 33(5): 570-577. |
| [24] |
OSHER S, BURGER M, GOLDFARB D, et al. An iterative regularization method for total variation-based image restoration[J]. Multiscale Modeling & Simulation, 2005, 4(2): 460-489. |
| [25] |
YIN W T, OSHER S, GOLDFARB D, et al. Bregman iterative algorithms for l1-minimization, with applications to compressed sensing[J]. SIAM Journal on Imaging Sciences, 2008, 1(1): 142-168. |
| [26] |
刘洋, 张鹏, 刘财, 等. 地震数据Bregman整形迭代插值方法[J]. 地球物理学报, 2018, 61(4): 1400-1412. LIU Yang, ZHANG Peng, LIU Cai, et al. Seismic data interpolation based on Bregman shaping iteration[J]. Chinese Journal of Geophysics, 2018, 61(4): 1400-1412. |
| [27] |
郭萌, 张会星, 刘明珠. 基于双重Bregman迭代的地震数据重构与去噪[J]. 石油物探, 2020, 59(5): 804-814. GUO Meng, ZHANG Huixing, LIU Mingzhu. Seismic data reconstruction and denoising based on dual Bregman iteration[J]. Geophysical Prospecting for Petroleum, 2020, 59(5): 804-814. |
| [28] |
CAI J F, OSHER S, SHEN Z W, et al. Linearized Bregman iterations for compressed sensing[J]. Mathe-matics of Computation, 2009, 78(267): 1515-1536. |
| [29] |
CAI J F, OSHER S, SHEN Z. Convergence of the linearized Bregman iterations for l1-norm minimization[J]. Mathematics of Computation, 2009, 78(268): 2127-2136. |
| [30] |
CANDES E J, ROMBERG J K. Signal recovery from random projections[C]. Electronic Imaging 2005, 2005: 76-86.
|
| [31] |
张华, 杨会, 刁塑, 等. 基于指数阈值迭代法的高精度地震数据重建[J]. 东华理工大学学报(自然科学版), 2017, 40(3): 253-260. ZHANG Hua, YANG Hui, DIAO Su, et al. High precision reconstruction of seismic data based on exponential threshold iteration method[J]. Journal of East China Institute of Technology (Natural Science Edition), 2017, 40(3): 253-260. |
| [32] |
HERRMANN F J, HENNENFENT G. Non-parametric seismic data recovery with curvelet frames[J]. Geophysical Journal International, 2008, 173(1): 233-248. |
| [33] |
白兰淑, 刘伊克, 卢回忆, 等. 基于压缩感知的Curvelet域联合迭代地震数据重建[J]. 地球物理学报, 2014, 57(9): 2937-2945. BAI Lanshu, LIU Yike, LU Huiyi, et al. Curvelet-domain joint iterative seismic data reconstruction based on compressed sensing[J]. Chinese Journal of Geophysics, 2014, 57(9): 2937-2945. |
| [34] |
BAI L S, LU H Y, LIU Y K, et al. A fast joint seismic data reconstruction by sparsity-promoting inversion[J]. Geophysical Prospecting, 2017, 65(4): 926-940. |
| [35] |
HUANG B, MA S Q, GOLDFARB D. Accelerated linearized bregman method[J]. Journal of Scientific Computing, 2013, 54(2): 428-453. |
| [36] |
ABMA R, KABIR N. 3D interpolation of irregular data with a POCS algorithm[J]. Geophysics, 2006, 71(6): E91-E97. |



 张华, 江西省南昌市经开区广兰大道418号东华理工大学地球物理与测控技术学院,330013。Email:
张华, 江西省南昌市经开区广兰大道418号东华理工大学地球物理与测控技术学院,330013。Email: