② 广西壮族自治区二七四地质队,广西北海 536005;
③ 塔里木油田公司勘探事业部物探工程部,新疆库尔勒 841000
② Guangxi No. 274 Geological Exploration Team, Beihai, Guangxi 536005;
③ Department of Geophysical Prospecting Engineering, PetroChina Tarim Oilfield Company, CNPC, Korla, Xinjiang 841000, China
炸药震源以其施工灵活、子波频率成分丰富、能量较强等特点,一直在复杂地表区地震勘探数据采集中广泛应用。以炸药为震源的数据采集中,药量是重要施工参数,它不仅影响地震资料质量,而且决定了施工成本。因此,药量设计方法的研究备受关注。
早期人们普遍认为:在药量处于某个范围内,子波能量随药量的增加而增加,加大药量是提高信噪比的必要手段[1-3]。该观点在信噪比较高地区的地震勘探中得到证实。但在低信噪比地区,刘树田[4]试验发现,当药量增加到一定程度后,虽然地震波有效能量随药量增加略有增加,但噪声能量增加更快,反而导致信噪比降低。钱荣钧[5]、Blair[6]等从炸药空腔半径与振幅能量的角度出发,对文献[4]所述现象做出了解释。蔡纪琰[7]认为单井柱状震源激发时,药量增加导致药柱长度增加,其能量向两边扩散,导致深层资料信噪比降低。于鲁洋等[8]通过爆炸数值模拟,进一步证实了文献[7]的观点。冯晓强等[9]通过提高药量使地层反射波同相轴信噪比得到显著提高。徐谦等[10]认为下传能量得以提升是长药柱各药段间激发的地震波存在叠加效应所致。
尽管人们在药量与信噪比关系的研究中取得了许多卓有成效的成果,但在实际地震数据采集中,药量参数确定还是以现场测试为主。其主要原因是炸药激发所形成的有效能量及噪声能量(信噪比)与药量、药型、激发岩性、地质构造、接收条件等因素构成了复杂的关系,而这种关系尚未被深刻认识和定量描述。
为了测定单井最佳激发药量,在中国西部多地采集了5种有代表性的样品,在实验室测得应力与应变关系、速度、密度等参数,建立相应力学模型;然后根据爆炸理论,选取3种药型,分别对5种模型用不同药量模拟激发获得波场数据;最后通过模拟分析,确定不同激发条件下的理论最佳药量。
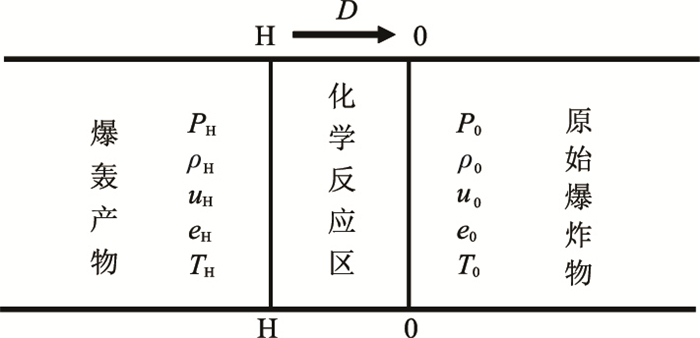
1 爆炸模拟理论炸药爆炸过程是一个剧烈的化学反应过程,点火后爆轰产物膨胀,化学能转化为动能,推动反应产物向前(图 1)。
|
图 1 炸药爆轰示意图 |
炸药爆轰过程可分为两个标志面:第一标志面在冲击波波阵面之前,其前的炸药尚未受到扰动即未发生化学反应;第二标志面在化学反应结束区之外。上述两个标志面分别以0-0、H-H断面表示,两面上的物理量分别以下标0、H标记,即PH、ρH、uH、eH、TH分别为爆轰产物的压力、密度、质点速度、比内能和温度,P0、ρ0、u0、e0、T0分别为炸药初始状态(未引爆)时的压力、密度、质点速度、比内能和温度。以波阵面前沿0-0和化学反应结束H-H面上的状态参量为研究对象,分别建立质量守恒(式(1))、动量守恒(式(2))和能量守恒(式(3))方程
| $ \rho_0 D=\rho_{\mathrm{H}}\left(D-u_{\mathrm{H}}\right) $ | (1) |
| $ P_{\mathrm{H}}-P_0=\rho_0 D u_{\mathrm{H}} $ | (2) |
| $ E_{\mathrm{H}}-E_0=\frac{1}{2}\left(P_{\mathrm{H}}+P_0\right)\left(u_0-u_{\mathrm{H}}\right)+Q $ | (3) |
式中:D为爆轰波定常传播速度;EH、E0分别为相应标志面的单位质量介质的总内能;Q表示爆轰反应过程中单位质量的炸药化学能的变化,即炸药所释放出的能量。
为求解围岩在炸药爆轰作用下的响应关系,需定义一个状态方程。本文采用在炸药爆轰数值模拟中应用广泛的JWL状态方程[11],它是描述炸药爆轰产物做功能力的一种不显含化学反应的形式,即
| $ P=A\left(1-\frac{\omega}{R_1 V}\right) \mathrm{e}^{-R_1 V}+B\left(1-\frac{\omega}{R_2 V}\right) \mathrm{e}^{-R_2 V}+\frac{\omega E}{V} $ | (4) |
式中:P为压力;A、B、R1、R2、ω均为爆轰相关系数,在实验室通过圆筒试验测得;V为相对体积;E为单位体积炸药的内能,其中ρ为密度。
围岩的受迫振动可由本构关系和控制方程描述[12]。其中,本构关系为
| $ \left\{\begin{array}{l} \tau_{x y}=\mu\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)=\tau_{y x} \\ \tau_{y z}=\mu\left(\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y}\right)=\tau_{z y} \\ \tau_{z x}=\mu\left(\frac{\partial w}{\partial x}+\frac{\partial u}{\partial z}\right)=\tau_{x z} \end{array}\right. $ | (5) |
| $ \left\{\begin{array}{l} p=-\frac{1}{3}\left(\sigma_{x x}+\sigma_{y y}+\sigma_{z z}\right) \\ \sigma_{x x}=p-2 \mu \frac{\partial u}{\partial x} \\ \sigma_{y y}=p-2 \mu \frac{\partial v}{\partial y} \\ \sigma_{z z}=p-2 \mu \frac{\partial w}{\partial z} \end{array}\right. $ | (6) |
式中:τ为剪应力;v、w、u对应为直角坐标方向x、y、z上的速度;μ为运动黏度;t为时间;p为压强;σ为正应力。
围岩受迫振动不同于炸药化学反应过程,但同样由相应的物理量守恒定律建立控制方程,则相应的质量守恒、动量守恒、能量守恒方程表示为
| $ \frac{\partial \rho}{\partial t}+\nabla \cdot \rho \boldsymbol{v}=0 $ | (7) |
| $ \frac{\partial \mathit{\boldsymbol{v}}}{\partial t}+(v \cdot \nabla) v=f-\frac{1}{\rho} \nabla p+\mu \Delta \mathit{\boldsymbol{v}} $ | (8) |
| $ \frac{\partial E}{\partial t}+(E \cdot \nabla) \mathit{\boldsymbol{v}}=\mathit{\boldsymbol{f}} \mathit{\boldsymbol{v}}-\frac{1}{\rho} \nabla(p \cdot \mathit{\boldsymbol{v}}) $ | (9) |
式中:v为流速;▽为哈密顿算子;Δ为拉普拉斯算子;E为单位体积流体的内能;f为单位体积微元的质量力。
用有限单元法求解以上方程,可得到炸药在围岩中激发生成的弹性子波的形态。其中炸药爆炸力学参数以及激发岩性的物理性质决定了爆炸模拟的结果及其准确性。炸药模型所采用的爆炸力学参数如表 1所示,该参数表在科技文献与工程应用中广泛引用,极具参考价值[13]。岩性参数则应用实际工区的岩样测试结果中的各项相关数值。
|
|
表 1 炸药爆炸相关力学参数 |
为了准确获取研究炸药激发层围岩力学参数,为炸药震源模拟提供依据,在中国西部新疆、四川、重庆、贵州等地进行了野外采样,获取了50余份岩(土)样(图 2),分别为8%砾石、10%砂岩、14%砂质泥岩、17%泥岩、25%黄土、6%井口钻返屑、4%砾石胶结物、2%砂岩粉末(风化)以及8%沙漠沙、6%灰岩;室内测试得到49份有效岩样测试数据。样本的详尽信息如图 2所示。岩样测试包含0.5MPa围压的纵、横波速度、弹性模量及受压变形直至破碎的应力—应变曲线。

|
图 2 现场采集的部分岩样及其不同岩性的占比 |
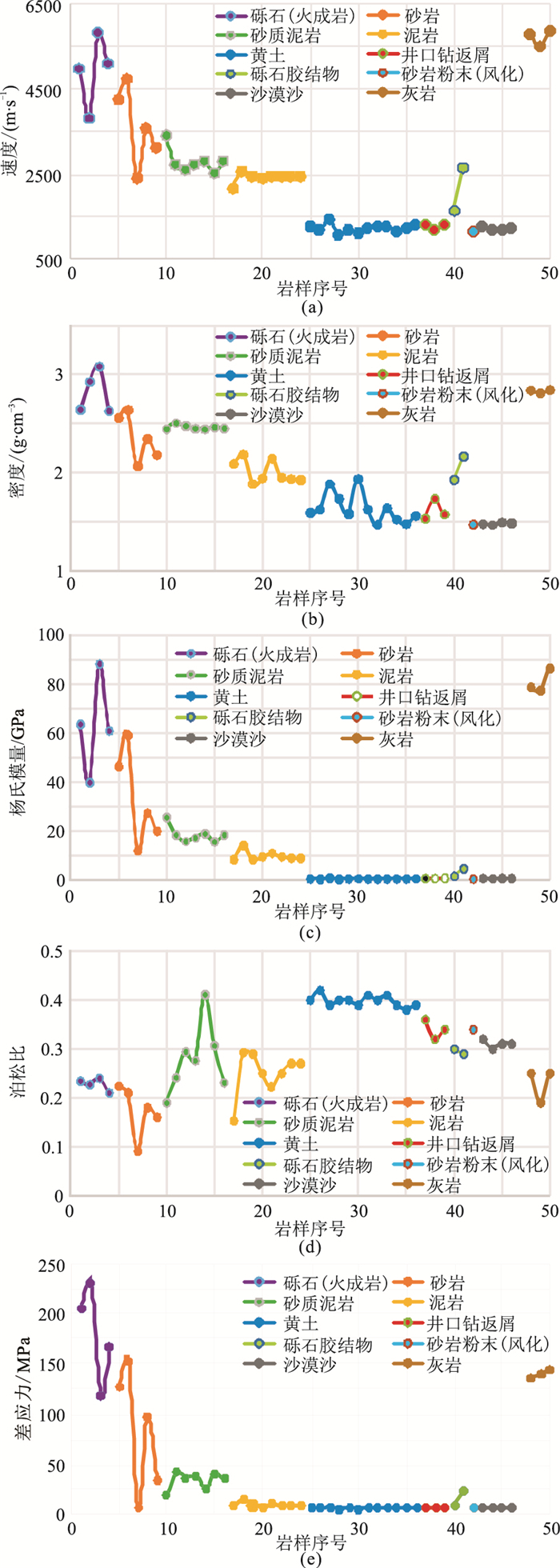
图 3展示了所取岩样的五类测试数据(曲线)。可见固结岩样的纵波速度大多超过2500m/s,灰岩、砾石(火成岩)、砂岩、泥岩等岩样速度依次降低;黄土样与沙漠沙样相似,速度约为1200m/s;土质疏松,具有较大空隙,受压变形量更大,泊松比较固结岩石大;屈服强度则相反,土质受压时会更快地进入塑性变形阶段,弹性变形范围很窄。
|
图 3 岩样不同物理参数测试结果 (a)纵波速度;(b)密度;(c)杨氏模量;(d)泊松比;(e)屈服应力 |
综合对比以上岩样的各项物性特征,选取5种差异较大并具有地区代表性的岩性,建立围岩力学模型,其岩性参数如表 2所示。
|
|
表 2 不同岩样的岩性参数 |
由于各种岩性(岩样)的应力、应变差异较大,为方便对比分析,对岩样有效应力与有效塑性应变均作对数处理(图 4)。可见黄土的杨氏模量很小,随着应力提升其应变显著变化;灰岩、火成岩、砂岩曲线相近,火成岩屈服应力(差应力)最大;泥岩的杨氏模量和屈服应力均较小,相同应变下,应力值小于灰岩、火成岩和砂岩。

|
图 4 五种典型岩样应力—应变对数关系 |
将岩样测试得到的数据代入爆炸控制方程,可对地震子波进行数值模拟。参考野外激发施工标准,在有限元模拟软件中构建几何模型(图 5)[14-15]。
|
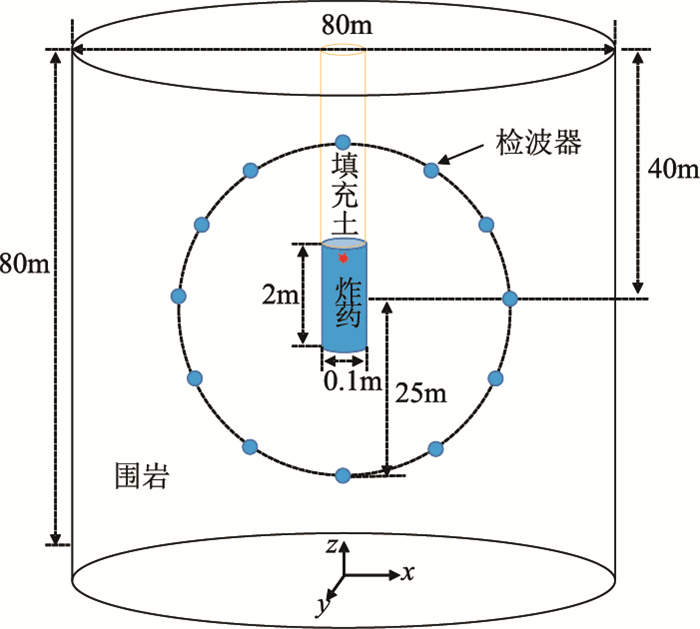
图 5 有限元模型示意图 |
模型采用底面直径80m、高80m的圆柱体,井筒直径为0.1m。井筒深度40m处填充炸药材料,随着药量增加,炸药长度相应加长(图 5以2m为例);炸药上部的井筒空间使用土壤材料填充封井,下方及侧方均为围岩。观测系统以炸药柱中心为圆心,在竖直平面内布置成半径为25m的圆形,圆周上每间隔2.5°布置一个检波器(图 5)。
模型单元采用支持炸药爆轰作用的非线性特性的三维显式结构实体单元,每个单元由8个节点构成[15]。由于圆柱模型存在竖直方向的轴对称性质,因此采用四分之一对称建模,在x和y方向的对称平面添加对称边界条件,面上的所有节点均施加平动位移约束,减少内存占用以提升计算效率。模型顶部定义为地表允许边界反射,模型底部与侧面均施加无反射边界条件,模拟地下半无限空间,避免反射波对观测点的干扰。
炸药选用表 1中高密度硝铵,激发方式为顶部激发,起爆点设置于距药柱上顶面25cm处的炸药内部,以逼近实际施工中起爆雷管的安装位置,如图 5红色爆炸点所示。
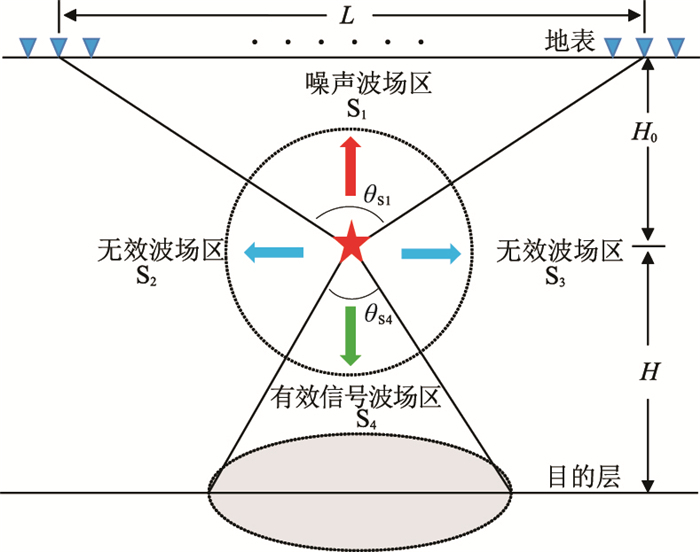
3.2 最佳激发效率分析徐峰等[16]将震源激发的波场划分为四个场区,如图 6所示。
|
图 6 震源波场能量分区示意图 L为检波器排列长度;H为震源距目标层深度;H0为震源离地表的距离;θS1为震源对排列的张角;θS4为震源对目的层的张角 |
S1区能量首先向地表传播,对检波器排列形成直接噪声干扰,是地震资料噪声的主要来源,因此将S1区定义为“噪声波场区”。激发参数的设计致力于降低该区(S1)的波场能量,提高地震资料信噪比。S2、S3区的能量向无限远处传播,对有效信号贡献不大,因此定义为“无效波场区”。S4区才是地震勘探所需能量,也是地震资料有效信号的能量来源,为“有效波场区”。
将S1~S4区传播能量分别记作ES1~ES4,则可定义激发效率
| $ \eta=\frac{E_{\mathrm{S}_4}}{E_{\mathrm{S}_1}+E_{\mathrm{S}_2}+E_{\mathrm{S}_3}+E_{\mathrm{S}_4}} $ | (10) |
为评判震源激发效果的标准函数。
固定力学模型和药型,激发效率与药量形成函数关系。当η具有极大值时,所对应的药量即为理论最佳药量。
3.3 子波能量分析以2kg高密度硝铵炸药激发为例。提取5个模型中震源正下方记录的波形曲线,分析其地震子波。
图 7中横坐标为时间,记录时长为20ms,纵坐标为应力,表征为子波的能量强度。从子波振幅看,灰岩振幅最大,振荡剧烈且频率较高;砂岩、火成岩、砂泥岩的子波形态相似、振幅大小相近,因波速的快慢而先后出现;黄土模型的子波速度最小,且振幅最小(能量最弱)。可见黄土地层作为低速带对爆炸子波的吸收能力较强,导致子波能量衰减快。从子波的频率看,从高到低分别为灰岩、砂岩、火成岩、泥岩和黄土。

|
图 7 子波的时间—应力关系 |
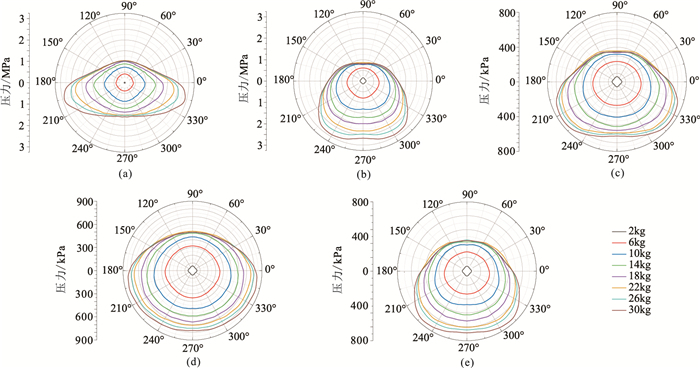
计算每个检波点记录的波形曲线的均方根能量值,作为爆炸能量在该点所在方向上的传播能量。以炸药包几何中心为极点,以x轴正方向(图 5)为极轴,绘制成能量极坐标图(图 8),为了比较不同药量激发效果,将各药量激发的能量分布叠加显示。
|
图 8 爆炸冲击波空间能量分布示意图 (a)黄土;(b)灰岩;(c)火成岩;(d)泥岩;(e)砂岩 |
从图 8可见,随着药量增加,所有模型在各个方向上的能量均有所增加,2~10kg内增幅尤为明显。上传能量在药量达到22kg时无明显提升。这是长药柱采取顶部激发的优点体现,因为药柱连续引爆,导致出现应力波场叠加的多普勒效应[17],该现象有利于减弱噪声波场区的能量传播。下传能量呈现出不同的增长趋势:黄土模型在药量达到22kg时能量达到饱和值且能量往药柱径向方向(无效波场区的主要方向)扩散严重;灰岩和砂岩中两侧传播的能量较少,下传方向能量较强;火成岩和泥岩不仅增加了无效波场区的能量,也对有效波场区传播的能量有一定贡献。
固定炸药类型和岩石力学模型,仅改变药量可得到不同药量与激发效率的关系曲线。根据激发波场能量分区,有效波场区的角度边线经过震源的夹角表示为
| $ \theta_{\mathrm{s}_4}=2 \arctan \frac{L}{4 H} $ | (11) |
根据排列长度与勘探目的层深度的一般关系,计算有效能量区角度约为45°,在本实验对称模型中取22.5°。
根据式(10)中激发效率定义,目标函数采用下式计算
| $ \eta(k)=\frac{\sum\limits_{\theta=\theta_1}^{\theta_2} E_{\mathrm{rms}}(k, \theta)}{\sum\limits_{\theta=0^{\circ}}^{360^{\circ}} E_{\mathrm{rms}}(k, \theta)} $ | (12) |
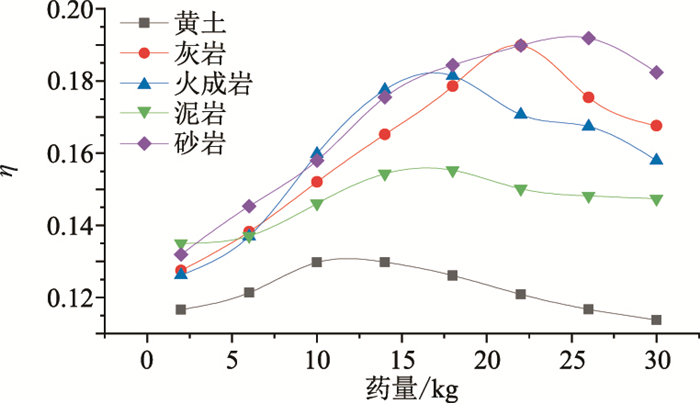
式中:k为药量;θ1、θ2为有效能量区边线的极角;Erms为检波器记录子波的均方根能量。计算得到图 9所示的药量与激发效率的关系。
|
图 9 炸药激发效率与药量关系 |
可见在2~10kg范围提升药量时,各岩性激发效率均有提升,超过14kg后黄土的激发效率持续下降,说明超过该药量时,激发能量对有效波场区的能量贡献较低,更多地消耗于噪声波场区,因此可认为14kg是黄土模型的最佳激发药量。如此类推,灰岩、火成岩、泥岩和砂岩的最佳激发药量分别认定为22、14、18、26kg。
根据上述分析方法进一步可知,TNT、铵梯炸药分别在黄土、灰岩、火成岩、泥岩、砂岩中激发所对应的最佳激发药量分别为6、18、10、14、18kg,18、30、22、22、30kg。3种炸药对应5个模型的最佳激发药量所对应的激发效率如表 3所示。
|
|
表 3 不同岩样最佳药量参数及对应激发效率 |
特别应注意的是,由于黄土未成岩,其杨氏模量和纵波速度很低,无论是TNT、铵梯还是高密度硝铵激发,其最佳药量都很小,对应的激发效率偏低,这可能是该类地区资料品质较差的缘由之一。
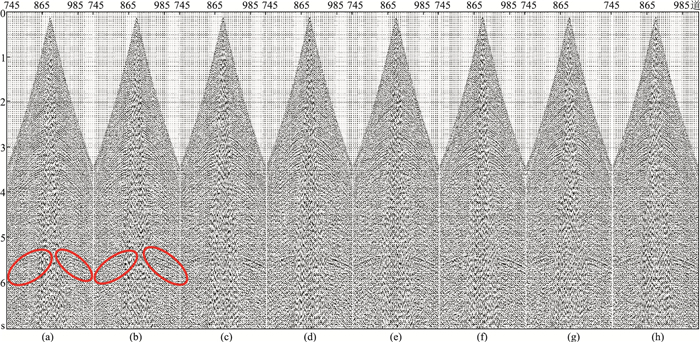
4 实例分析在M黄土地区应用高密度硝铵炸药做激发药量对比试验,各药量激发的地震记录如图 10所示。可见2kg与4kg药量激发效果较差,深部地层反射波能量较弱(椭圆)。随着药量的增加,反射波能量得到提升,地层的分辨能力逐渐提高。提取地震记录中的目标地层反射波计算下传能量(图 11)。
|
图 10 不同药量的地震记录 (a)2kg;(b)4kg;(c)6kg;(d)8kg;(e)10kg;(f)12kg;(g)14kg;(h)16kg |

|
图 11 局部地震记录 |
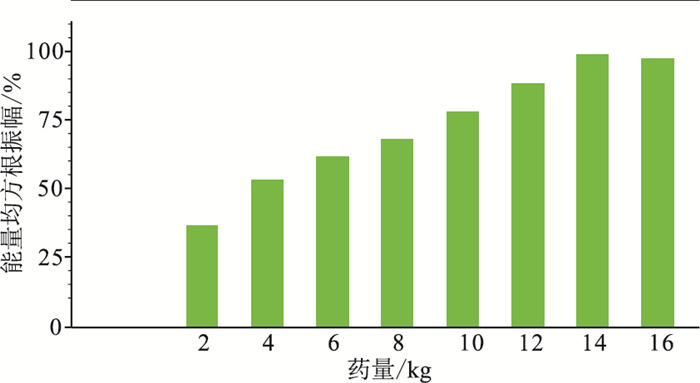
图 11为从地震记录抽取的部分道集,其中绿线区间为截取的目标地层(红线)反射波分析时窗。计算时窗内反射波均方根能量,得到不同药量的反射波能量值及其随药量变化的关系(图 12)。可见2kg药量的能量较低,能量随药量增加而逐渐提高;药量增至14kg时达到峰值。因此,14kg为该区炸药激发最佳药量,与理论最佳药量分析结果相一致。
|
图 12 激发能量与药量关系 |
单井长药柱激发的子波,其能量空间分布不均匀。该不均匀性与药量、药型及围岩有关。本文从模拟数据分析得知,药量与下传能量是非线性关系。
震源附近子波空间能量的分布特征与单炮记录的信噪比具有相关性,激发效率可作为分析激发效果的依据,也可作为最佳药量设计的目标函数。
单井条件下,不同药型在不同围岩中激发时理论计算的最佳药量不同。无论是TNT、高密度硝铵还是铵梯激发时,其杨氏模量(纵波速度)越大,屈服应力越大,最佳药量越大。
单井长药柱激发对于黄土覆盖区存在理论上的局限性,为提高该类地区地震采集资料的信噪比,应强化组合激发和大井径激发技术的研究。
本文提出的最佳药量设计思路可供同行参考。由于研究所用岩样的局限性,最佳药量的最终设定应根据具体工区激发岩性的特点,做充分论证。
| [1] |
HEELAN P A. Radiation from a cylindrical source of finite length[J]. Geophysics, 1953, 18(3): 685-696. DOI:10.1190/1.1437923 |
| [2] |
李庆忠. 地震高分辨率勘探中的误区与对策[J]. 石油地球物理勘探, 1997, 32(6): 751-783. LI Qingzhong. Some mistaken conceopts in high-re-solution seismic exploration and the corresponding countermeasures[J]. Oil Geophysical Prospecting, 1997, 32(6): 751-783. DOI:10.3321/j.issn:1000-7210.1997.06.001 |
| [3] |
钱绍瑚, 刘江平, 谷永兴, 等. 炸药震源爆炸机制及激发条件的研究[J]. 石油物探, 1998, 37(3): 1-14, 33. QIAN Shaohu, LIU Jiangping, GU Yongxing, et al. The research on the explosive mechanism and excitation condition of dynamite source[J]. Geophysical Prospecting for Petroleum, 1998, 37(3): 1-14, 33. |
| [4] |
刘树田. 地震勘探中炸药震源药型选择问题研究[J]. 石油物探, 1999, 38(4): 66-73. LIU Shutian. Research on the problem of dynamite type selection in seismic prospecting[J]. Geophysical Prospecting for Petroleum, 1999, 38(4): 66-73. |
| [5] |
钱荣钧. 炸药震源激发效果分析[J]. 石油地球物理勘探, 2003, 38(6): 583-588. QIAN Rongjun. Analysis of explosive effects of dynamite source[J]. Oil Geophysical Prospecting, 2003, 38(6): 583-588. DOI:10.3321/j.issn:1000-7210.2003.06.001 |
| [6] |
BLAIR D P. A comparison of Heelan and exact solutions for seismic radiation from a short cylindrical charge[J]. Geophysics, 2007, 72(2): E33-E41. DOI:10.1190/1.2424543 |
| [7] |
蔡纪琰. 近地表条件下爆炸震源有效激发方法研究[D]. 山东青岛: 中国石油大学(华东), 2013. CAI Jiyan. Study on Effective Excitation of Explosion Source with Near-surface Consideration[D]. China University of Petroleum(East China), Qingdao, Shandong, 2013. |
| [8] |
于鲁洋, 王益民, 田钢. 砂岩中炸药震源不同激发参数数值模拟研究[C]. 浙江省信号处理学会2015学术年会论文集, 2015, 245-253. YU Luyang, WANG Yimin, TIAN Gang. Numerical simulation of different excitation parameters of explosive source in sandstone[C]. Proceedings of the 2015 Annual Conference of Zhejiang Signal Processing Society, 2015, 245-253. |
| [9] |
冯晓强, 朱峰, 石一青, 等. 复杂地区高精度三维采集方法应用及效果[J]. 石油物探, 2021, 60(增刊1): 42-53. FENG Xiaoqiang, ZHU Feng, SHI Yiqing, et al. Application and analysis of the effect of high-precision three-dimensional acquisition in complex areas[J]. Geophysical Prospecting for Petroleum, 2021, 60(S1): 42-53. |
| [10] |
徐谦, 王仲琦. 轴向分布式药包激发地震波场模型[J]. 爆炸与冲击, 2021, 41(7): 48-57. XU Qian, WANG Zhongqi. Model of seismic wave field excited by axially distributed explosive[J]. Explosion and Shock Waves, 2021, 41(7): 48-57. |
| [11] |
罗兴柏, 张玉令, 丁玉奎. 爆炸力学理论教程[M]. 北京: 国防工业出版社, 2016.
|
| [12] |
宁建国, 马天宝. 计算爆炸力学[M]. 北京: 国防工业出版社, 2015.
|
| [13] |
门建兵, 蒋建伟, 王树有. 爆炸冲击数值模拟技术基础[M]. 北京: 北京理工大学出版社, 2015.
|
| [14] |
HALLQUIST J O. LS-DYNA3D Theoretical Manual [M]. LSTC, Livermore, 1998.
|
| [15] |
胡仁喜, 康士廷, 等. ANSYS 18.0/LS-DYNA非线性有限元分析实例指导教程[M]. 北京: 机械工业出版社, 2018.
|
| [16] |
徐峰, 刘福烈, 梁向豪. 基于相控理论的炮点组合设计技术[J]. 石油地球物理勘探, 2011, 46(2): 170-175. XU Feng, LIU Fulie, LIANG Xianghao. A method for source array design based on the phased-array theo-ry[J]. Oil Geophysical Prospecting, 2011, 46(2): 170-175. |
| [17] |
王卫华. 纵波勘探中的炸药激发方式分析[J]. 石油地球物理勘探, 1999, 34(3): 249-259. WANG Weihua. Analysis of dynamite source pattern in compressional wave exploration[J]. Oil Geophysical Prospecting, 1999, 34(3): 249-259. |



 徐峰, 四川省成都市新都区新都大道8号西南石油大学地球科学与技术学院,610500。Email:
徐峰, 四川省成都市新都区新都大道8号西南石油大学地球科学与技术学院,610500。Email: