反射地震是水合物地球物理勘探的重要技术。赋存天然气水合物的海底沉积物的反射地震响应往往存在似海底反射(BSR)特征[1]。BSR是由上覆高速的含水合物层与下伏低速的含游离气层之间的阻抗差异产生的,大体平行于海底,指示天然气水合物稳定带的底部,具有负极性、强振幅特征。但天然气水合物和游离气与BSR特征的关系仍欠明确,基于BSR的天然气水合物识别具有多解性[2]。此外,BSR仅能指明天然气水合物底部位置,却无法用于水合物含量的定量解释。
地震波的吸收衰减是天然气水合物地层地震响应的一个显著特征。研究发现,在加拿大Mallik冻土带、日本南海海槽等水合物探区BSR位置的上方存在与天然气水合物有关的低地震振幅或振幅“空白”带[3]。虽然空白的成因尚不完全清楚,但人们普遍认为空白的“强度”与地震波吸收衰减直接相关,可作为天然气水合物分布的一项指标。多个水合物探区的声波测井波形也显示,天然气水合物的存在导致了异常的衰减值[4]。国内外学者针对性地开展了岩石物理实验和理论研究,目的是探索地震波衰减机制及其与天然气水合物含量的定量关系,提高水合物储量的预测能力。
本文概述了不同探区天然气水合物储层的地震波吸收衰减特征,探讨并总结了水合物储层可能存在的衰减机制及相关的岩石物理理论模型研究现状,展望了水合物储层吸收衰减特性的应用及岩石物理模型构建的未来发展方向。
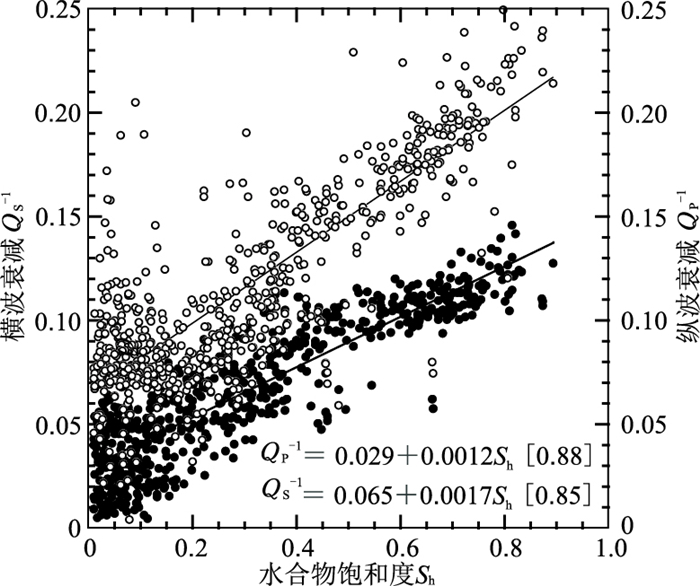
1 不同地区天然气水合物储层的地震波吸收衰减特征 1.1 加拿大Mallik冻土带Mallik冻土带位于加拿大西北部的Mackenzie三角洲,是世界上已经证实的冻土带中含有天然气水合物的典型地区。该区2L38井的阵列声波测井波形记录结果显示,含水合物地层的波形振幅发生明显减弱[4](图 1),表明声波在含水合物地层中传播时可能发生了强烈吸收衰减。Guerin等[4]利用质心频率偏移法分别计算了纵波和横波衰减,发现在含水合物地层二者都表现为高衰减值。文中用品质因子Q的倒数(逆品质因子Q-1)表示衰减强度,则高衰减对应高Q-1值或低Q值。进而对含水合物饱和度和纵、横波衰减(QP-1、QS-1)进行交会分析,得知纵、横波衰减与水合物饱和度大致呈线性关系,且相同含水合物饱和度条件下,横波衰减大于纵波衰减(图 2)。这也是在含水合物地层吸收衰减特性分析研究中,首次将纵、横波衰减特性与含水合物饱和度进行定量分析。

|
图 1 加拿大Mallik-2L38井声波成像仪记录的声波波形[4] 方框中为已识别出的水合物层段 |
|
图 2 Mallik-2L38井中利用电阻率法估算的天然气水合物饱和度与声波衰减之间的关系[4] 实心点表示纵波,空心点表示横波 |
Pratt等[5]和Bauer等[6]利用基于射线的层析成像技术对井间地震资料进行了衰减剖面的成像。结果显示,在含水合物地层地震波衰减也表现出明显的高值异常。由于声波测井频率一般在100~25kHz,而井间地震数据频率是在100~1000Hz(如采用美国Tomoseis公司的压电震源、10单元有源阵列接收系统,扫描频率为100~2000Hz,处理后频率为100~1000Hz),因此Pratt等[5]和Bauer等[6]的研究是对Guerin等[4]分析结果的重要补充。
1.2 日本南海海槽日本南海海槽是上新世以来菲律宾海板块向欧亚板块俯冲形成的年轻海沟,在水深800~2000m的内陆坡,分布数个新近系沉积充填的弧前沉积盆地。在弧前盆地的外侧,较深的陆坡处发育增生楔[7]。
由于该区在早期地震调查中识别出广泛分布的BSR,为了进一步确认天然气水合物藏的存在,JMITI(Japanese Ministry of International Trade and Industry)在日本南海海槽展开钻探,采集到含有大量天然气水合物的砂岩岩心。与加拿大Mallik冻土带相似,在该区的阵列声波测井中,声波波形振幅也发生明显减弱。Matsushima[8]使用质心频率偏移法对阵列声波测井波形记录数据分别计算了纵波和横波衰减,虽然该区含水合物地层较薄,且水合物饱和度较低,但纵、横波衰减仍然都表现为高值异常,并且纵、横波衰减与含水合物饱和度也大致呈线性关系。Matsushima[9]又利用VSP数据进行了吸收衰减参数的提取,在地震频带范围内进一步研究了日本南海海槽含水合物地层的地震波吸收衰减特性。结果显示在含游离气区域,纵波衰减表现出明显高值异常,而在含水合物地层位置,VSP提取的衰减参数并没有明显的异常(图 3)。因此Matsushima认为,含水合物地层的吸收具有频率选择性,在30~110Hz的频率范围内,含水合物地层并未对地震波产生强烈的吸收作用。

|
图 3 对日本南海海槽PSW1现场VSP数据利用谱比法(a) 和质心频率偏移法(b)估算的纵波逆品质因子[9] 浅灰色为含水合物区,深灰色为含游离气区,不同曲线对应不同道的数据 |
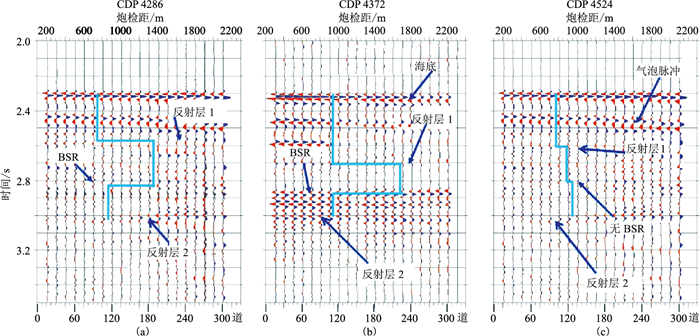
Makran增生楔位于西印度洋阿拉伯海海域,该区虽无井资料直接证明天然气水合物的存在,但Sain等[10]、Ojha等[11]基于该区地震资料通过多种方法证明了天然气水合物和游离气藏的存在。为了分析该区含水合物地层的地震波吸收特征,Sain等[12]在叠前道集上利用谱比法针对三个典型CDP处的水合物上覆地层、水合物稳定带及游离气层分别求取层间品质因子(图 4),这三个CDP分别对应强BSR、弱BSR及无BSR三个典型位置。分析这三个CDP处的地层品质因子变化规律可知,Makran增生楔地区含水合物地层吸收效应较弱,而BSR下部游离气藏的吸收效应较强。Sain等[12]指出,在Makran增生楔地区,含水合物地层的地震吸收特征与Mallik地区和日本南海海槽区的特征不一致,可能缘于该区含水合物地层中只有水合物和岩石骨架两相,而不存在流体,水合物与骨架的胶结作用增加了岩石的硬度从而造成地层吸收效应减弱。
|
图 4 Makran增生楔地区CDP 4286(a)、4372(b)和4524(c)处的地震道集分别与估计的层间品质因子Q叠加[12] |
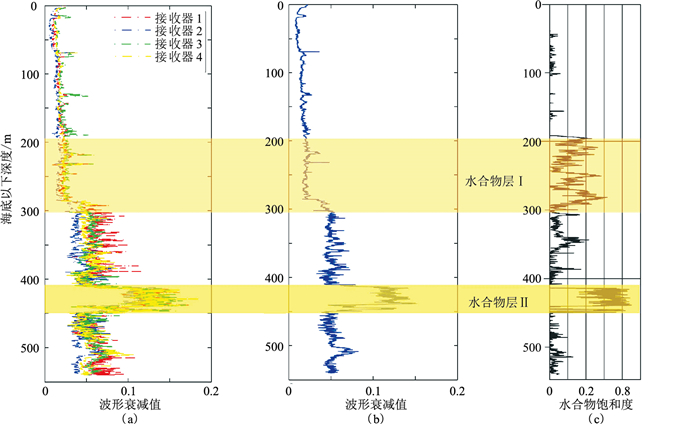
墨西哥湾西北陆缘是油气十分富集的被动大陆边缘,中新生代沉积盆地发育了巨厚海相碳酸盐岩,形成大规模的盐底辟构造和断裂构造。目前在众多区块识别出BSR[13-15],并采集到大量天然气水合物样品。在该区阵列声波测井中,声波振幅也发生明显减弱。王吉亮等[16]使用质心频率偏移法对墨西哥湾GC955H井的阵列声波测井波形数据计算了纵波衰减(图 5)。该区含有两种不同类型的含水合物地层,裂隙填充型的水合物层Ⅰ及孔隙填充型的砂岩水合物层Ⅱ。前者衰减大小与上覆背景泥岩层段相比并无明显变化,推测原因有三:①泥岩层水合物对衰减无影响;②泥岩层段内水合物饱和度太低;③可能是因为水合物充填于垂直裂隙中,对进入地层垂向传播的声波作用不大。而后者表现出明显的衰减高值异常,并且纵波衰减与含水合物饱和度也大致呈线性关系,随着水合物饱和度增加,纵波衰减逐渐增强。
|
图 5 墨西哥湾GC955H井声波衰减计算结果[16] (a)由4组声波波形分别计算得到的衰减值;(b)4组衰减的平均值;(c)水合物饱和度值 |
位于南海北部陆缘的珠江口盆地珠二坳陷白云凹陷南侧的神狐海域是中国近年来天然气水合物勘探的重点目标。广州海洋地质调查局于2007年及2015年先后在神狐海域进行了GMGS1、GMGS3两航次水合物钻探,均获得了水合物实物样品。钻探资料研究结果表明,神狐海域水合物储集层以黏土质粉砂细粒沉积物为主,局部存在具有较高孔渗性的粉砂细粒沉积物,水合物以分散式或者胶结式充填在其孔隙中[17]。GMGS1钻探区的水合物分布在海底以下约200m,厚度处于10~47m,平均饱和度约20%,最高达48%。GMGS3钻探区的水合物主要分布于海底以下100~250m,饱和度介于0~76%,较GMGS1钻探区厚度大、饱和度高、展布规模及储量大[18]。目前,针对中国南海水合物地震吸收衰减特征的研究较少。Li等[19]对神狐海域天然气水合物的反射地震数据分析表明,含水合物层的吸收衰减明显低于相邻地层。Wang等[20]利用神狐海域垂直电缆地震(VCS)资料,采用谱比法估算了海底各层品质因子Q值,研究发现,含水合物地层的Q值比不含水合物或游离气地层的Q值大,即吸收衰减弱,含游离气地层的Q值比不含水合物或游离气地层的Q值小,即吸收衰减强,但造成这一特征的主要原因和影响因素有待进一步研究。
1.6 人造岩样实验室测量结果Priest等[21]在实验室合成水合物饱和岩石样品,利用共振法在频率50~400Hz下对13个含不同体积水合物的砂岩样本进行了衰减值的测量。结果(图 6)显示:在水合物饱和度3%~5%范围内,纵横波衰减随饱和度增加迅速增至最大值,尔后纵波衰减迅速降低,接着又呈现缓慢增加的趋势,而横波衰减迅速减小且逐渐保持平稳,但仍比不含水合物地层的衰减值高2~3倍;当水合物饱和度增至3%~5%的临界饱和度时,衰减达到最强。

|
图 6 Priest实验试样H4-1及H5-1在500kPa围压下纵波衰减QP-1及横波衰减QS-1随水合物饱和度变化[21] |
Priest等[21]认为,实验室合成的含水合物砂岩样品为部分饱和,包含岩石骨架、水合物、吸附水和游离气等多个相态。在岩石中的水合物形成之前,地震波传播会引起吸附水和游离气在岩石裂隙和孔隙中产生喷射流,从而造成地震波能量的衰减。当水合物形成之后,水合物与岩石骨架的胶结会增加裂缝和孔隙的长度,从而加剧衰减作用。随着水合物饱和度进一步增加,水合物与岩石的胶结会逐渐完全堵塞裂隙和孔隙,吸附水和游离气被束缚,喷射流效应减弱,因而吸收作用逐渐减弱,但由于水合物本身也是多孔隙结构,吸附水和游离气可能在水合物内部结构中也会产生一定的喷射流效应,所以此时含水合物地层的吸收衰减效应仍强于不含水合物地层。对于横波的衰减只在水合物饱和度小于3%~5%时才会有敏感变化,该结论与Mallik地区的测井分析结果并不一致。在Mallik地区,随着水合物饱和度增加,横波衰减要比纵波衰减严重。Priest等[21]认为这主要是因为Mallik地区为完全饱和岩石,只含有岩石骨架、水合物和流体水三种相态,而实验样本含气体,气体的膨胀压缩作用,导致纵波衰减的变化更明显。
1.7 小结为便于对比,将五个水合物探区及人工岩样的纵、横波衰减特征进行归纳总结(表 1)。可以发现,对于不同的水合物探区或样品、使用不同的资料,地震波表现出不同的衰减特征,目前人们对此现象并未达成共识,这也是后续开展水合物地层吸收衰减机制及岩石物理研究的主要论题之一。
|
|
表 1 各水合物探区及人工岩样的地震波衰减特征对比 |
地下油气储层为多孔隙介质,孔隙结构的不规则性和孔隙介质的多相性导致多孔介质的宏观物理性质对孔隙流体含量、流体性质或孔隙结构的细小变化十分敏感。因此,当地震波在多孔隙介质中传播时,受其影响,介质孔隙发生闭合或张开、流体产生相对运动,致使多孔隙岩石的宏观物理性质甚至化学性质发生变化,从而引起地震波传播速度的频散、能量和振幅的频率依赖性衰减。可见,研究地震波在多孔隙介质中传播特性随孔隙流体及孔隙结构动态变化的关系,认识地震波在其中的传播规律,对于解决譬如储层流体预测等问题有重要的理论与实际意义。
国内外学者对含流体孔隙介质中的地震波传播与衰减问题进行了大量研究,建立了多种双相孔隙介质波动理论模型,如经典的Biot理论[22]、White模型[23]、BISQ理论[24]等。这些理论模型广泛应用于常规的油气储层研究,并取得了显著的应用效果[25]。而天然气水合物因其自身物理状态(冰态、结晶状化合物)及赋存方式(常见孔隙填充型、颗粒支撑性、胶结型)的特殊性,对储层流变性质及孔隙结构的影响远比油气层复杂得多,基于传统的理论来模拟天然气水合物与其宿主沉积物之间的相互作用、了解能量耗散过程,结果并不准确。因此学者们基于以上理论,考虑了各种水合物存在时可能带来的附加衰减机制,用来描述含水合物储层的地震波吸收衰减现象,由此形成了一系列岩石物理模型,如Leclaire模型[26]、CT模型[27]、改进的Leclaire模型[28]、HEG模型[29]、HBES模型[30]等,并结合水合物探区实际数据取得了较好的理论模拟及应用效果,为利用地震波衰减属性进行水合物储层识别及定量评价奠定了理论基础。
2.1 Leclaire模型(三相Biot理论)Biot[22]最早(1956年)提出的描述含饱和流体孔隙介质的弹性波理论——Biot双相介质理论,奠定了孔隙介质弹性波理论的基础。该理论假设介质为各向同性、孔隙空间连续,且孔隙流体是相对于固体骨架可以进行Poiseuille流动的牛顿流体,并将孔隙介质受到的力分解为作用于固体骨架和孔隙流体两部分的应力,当地震波传播经过孔隙介质时,导致了固体骨架和孔隙流体之间的相互运动,其能量由于黏性摩擦而发生衰减,这就是Biot耗散机制。Biot理论不仅首次提出了流固耦合作用及其对地震波响应的影响,还预测了慢纵波的存在。
Leclaire等[26]认为在0℃以下,孔隙空间中的水和冰晶共存,并将结冰过程中的冰晶从连续态转化为不连续态,将适用于饱和流体多孔介质的Biot理论拓展到包含岩石颗粒、冰晶和孔隙流体三相的多孔介质,称其为Leclaire模型或三相Biot理论(图 7)。该模型有两个重要假设,一是岩石颗粒与冰晶之间无直接接触;二是最小波长大于孔径,使骨架在宏观上可看成有效介质。模型基于连续介质力学给出了介质的动能、势能和耗散能量,推导出在岩石颗粒、冰晶、孔隙流体三相介质中波的传播方程
| $\left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{R}}}\nabla \varphi = {\mathit{\boldsymbol{\rho }}}\ddot \varphi + {\mathit{\boldsymbol{F}}}\ddot \varphi }\\ {{\mathit{\boldsymbol{\mu }}}\nabla \psi = {\mathit{\boldsymbol{\rho }}}\ddot \psi + {\mathit{\boldsymbol{F}}}\ddot \psi } \end{array}} \right.$ | (1) |

|
图 7 含岩石颗粒、冰晶和孔隙流体的Leclaire模型[26] |
式中:φ和ψ表示波的纵向和横向位移,上标点表示对时间求导;R、μ、ρ和F分别表示刚度、剪切模量、质量密度和摩擦系数矩阵,且有
| $\left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{R}}} = \left[ {\begin{array}{*{20}{l}} {{R_{11}}}&{{R_{12}}}&{{R_{13}}}\\ {{R_{12}}}&{{R_{22}}}&{{R_{23}}}\\ {{R_{13}}}&{{R_{23}}}&{{R_{33}}} \end{array}} \right]}\\ {{\mathit{\boldsymbol{\mu }}} = \left[ {\begin{array}{*{20}{c}} {{\mu _1}}&0&{{\mu _{13}}}\\ 0&0&0\\ {{\mu _{13}}}&0&{{\mu _3}} \end{array}} \right]}\\ {{\mathit{\boldsymbol{\rho }}} = \left[ {\begin{array}{*{20}{l}} {{\rho _{11}}}&{{\rho _{12}}}&{{\rho _{13}}}\\ {{\rho _{12}}}&{{\rho _{22}}}&{{\rho _{23}}}\\ {{\rho _{13}}}&{{\rho _{23}}}&{{\rho _{33}}} \end{array}} \right]}\\ {{\mathit{\boldsymbol{F}}} = \left[ {\begin{array}{*{20}{c}} {b_{11}^{\rm{F}}}&{ - b_{11}^{\rm{F}}}&0\\ { - b_{11}^{\rm{F}}}&{b_{11}^{\rm{F}} + b_{33}^{\rm{F}}}&0\\ { - b_{33}^{\rm{F}}}&{b_{33}^{\rm{F}}}&0 \end{array}} \right]} \end{array}} \right.$ | (2) |
式中:下标1、2、3分别对应岩石颗粒、孔隙流体及冰晶三相;下标ij表示相i与相j之间某种形式的耦合或相互作用,下标i或ii表示相i自身的性质;biiF为摩擦系数元素。
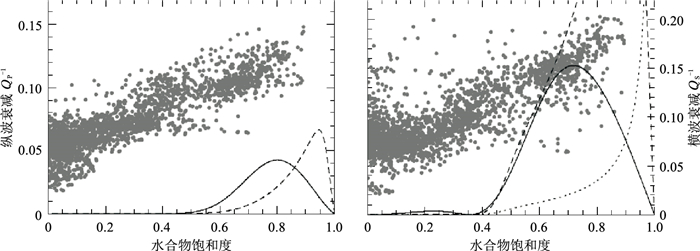
Guerin等[4]将Leclaire模型中的冰晶替换为水合物,分析了不同水合物饱和度下储层衰减变化(图 8)。模型孔隙度设置为35%,纵波频率采用12kHz,横波频率为2.5kHz,图中点线、虚线、实线分别对应地层渗透率κ为10-8m2、10-9m2、10-10m2,黑点为加拿大Mallik冻土区2L38含水合物井的实测数据。分析发现虽然模型与实测数据κ=10-10m2的条件下能匹配,但模型曲线并未很好地描述实际数据的趋势,其主要原因是该模型未考虑岩石颗粒与冰晶之间的相互作用。
|
图 8 纵(左)、横(右)波逆品质因子随水合物饱和度的变化[4] 其中黑点为测井数据,黑线为Leclaire模型预测结果 |
模型和实际数据还表明,QS-1通常高于QP-1,且相对于QP-1,QS-1在水合物低饱和度时就开始增加。此现象也解释了为何在水合物饱和度不超过15%的布莱克海脊含水合物探区中,只存在横波衰减[31]。
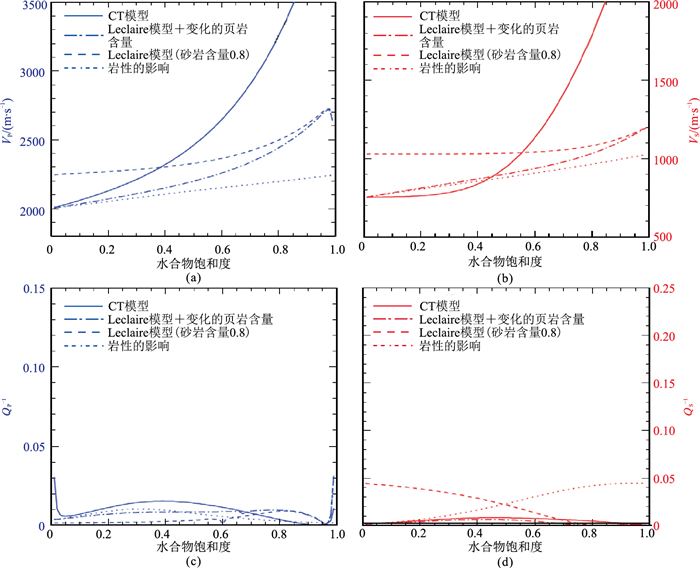
2.2 CT模型Carcione等[27]考虑了岩石颗粒与冰晶之间接触而产生的势能与动能,发展了Leclaire理论,即CT(Carcione Tinivella)模型,并将CT模型中的冰晶替换为水合物颗粒,应用于计算水合物沉积地层的弹性波速度。但CT模型忽略了岩石颗粒与水合物之间的相互摩擦。Guerin等[28]利用Leclaire模型和CT模型分析了水合物饱和度及岩性对含水合物沉积层纵、横波速度及衰减的影响(图 9)。相比Leclaire模型,CT模型中纵、横波速度随水合物饱和度增大的趋势更明显。此外,横波速度曲线表明:当水合物饱和度小于30%时,横波速度的增量可忽略;而当水合物饱和度较高时,横波速度的增加非常显著。但布莱克海脊数据表明,横波速度在低水合物饱和度时也有明显变化,与模型不相符[31]。Leclaire模型和CT模型均考虑了黏性流体摩擦,但衰减特征并不显著,这与Mallik冻土区(图 8)数据明显矛盾,其原因是Guerin等[4]使用水合物渗透率和剪切模量的极值。表明Leclaire模型和CT模型均不能准确描述该含水合物地层的衰减现象。
|
图 9 Leclaire模型和CT模型的模拟结果[28] (a)VP;(b)VS;(c)QP-1;(d)QS-1。不同曲线代表不同的模型及岩性的影响 |
Guerin等[28]假设天然气水合物和沉积物颗粒之间的胶结作用可用耦合剪切模量来描述。使用类似于Johnson等[32]固结模型中剪切模量的表达式,该模量的简单表达式为岩石颗粒和天然气水合物体积分数的二阶多项式函数
| ${\mu _{{\rm{sh}}}} = {\mu _{{\rm{sh}}0}}{\left( {{\phi _{\rm{h}}}{\phi _{\rm{s}}}} \right)^2} = {\mu _{{\rm{sh}}0}}{\left[ {{\phi _{\rm{h}}}(1 - \phi )} \right]^2}$ | (3) |
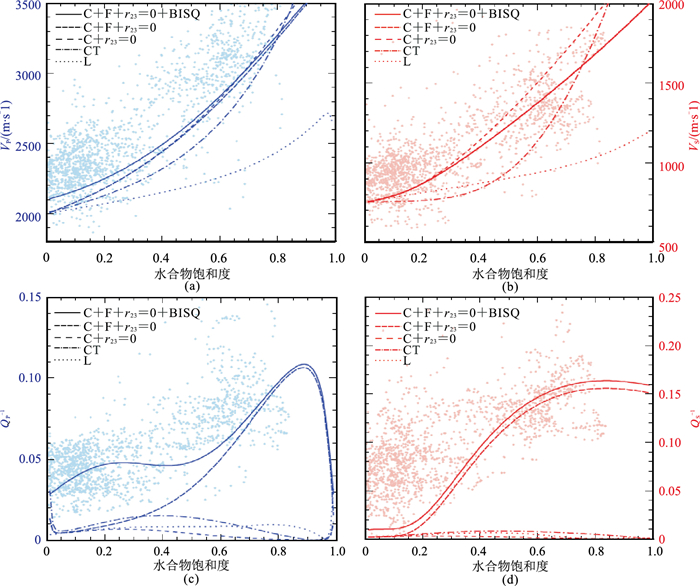
式中:ϕh、ϕs和ϕ分别为水合物的体积分数、沉积物颗粒的体积分数及孔隙度;μsh0为假定的初始耦合剪切模量,其值通过迭代确定,使得在最大水合物饱和度下的VP与CT模型结果相似。对比图 9中CT模型模拟结果与图 10中标记为“C”的结果,可发现引入沉积物颗粒与水合物之间的胶结作用后,预测横波速度的增加比CT模型更缓慢,纵波衰减QP-1略有增强,但无横波衰减。
|
图 10 各Leclaire模型模拟结果(线)与Mallik-2L38井数据(点)对比[28] (a)VP;(b)VS;(c)QP-1;(d)QS-1。改进的Leclaire模型包括增加胶结(C)、摩擦(F)和喷射流(BISQ),以及惯性耦合的变化(r23) |
岩石矿物颗粒与天然气水合物之间的胶结作用是速度随水合物饱和度增加而增加的必要条件[32],这两相之间可能发生接触和摩擦,而Leclaire模型和CT模型都忽略了摩擦。Berryman等[33]描述了双孔隙、双渗透率介质中固相之间的摩擦。Guerin等[28]假设固体颗粒与水合物之间的摩擦力是其间速度差的线性函数,类似于对孔隙流体的黏性摩擦力,并定义新的摩擦系数为天然气水合物和沉积物组分的二阶多项式函数,类似于Berryman等[33]计算的阻力系数,从而给出摩擦矩阵,将沉积物颗粒与水合物之间的摩擦损耗引入Leclaire模型:
| $\left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{F}} = \left[ {\begin{array}{*{20}{c}} {b_{11}^{\rm{F}} + {{\rm{b}}_{33}}}&{ - b_{11}^{\rm{F}}}&{ - b_{13}^{\rm{F}}}\\ { - b_{11}^{\rm{F}}}&{b_{11}^{\rm{F}} + b_{33}^{\rm{F}}}&{ - b_{33}^{\rm{F}}}\\ { - b_{13}^{\rm{F}}}&{ - b_{33}^{\rm{F}}}&{b_{33}^{\rm{F}} + b_{13}^{\rm{F}}} \end{array}} \right]}\\ {b_{13}^{\rm{F}} = {{\left[ {b_{13}^{{\rm{Fo}}}{\phi _{\rm{h}}}(1 - \phi )} \right]}^2}} \end{array}} \right.$ | (4) |
式中b13F0为假定的岩石矿物颗粒与水合物之间的初始摩擦系数。
如图 10所示,考虑沉积物颗粒与水合物之间的摩擦作用后,会产生更高纵波衰减QP-1,且随天然气水合物饱和度的增加,横波衰减明显增加。Guerin等[28]认为,天然气水合物与沉积物颗粒之间的摩擦可能是造成前期研究中观察到的横波能量耗散的原因。
2.3.3 考虑沉积物颗粒、水合物、孔隙水之间的惯性耦合在现有模型中引入摩擦和胶结,必须重新考虑模型中弯曲度aij和惯性耦合系数rij,它们定义了物理边界分离相的几何形状,对应于具有明确颗粒和孔隙几何形状的多孔介质。Leclaire等[26]用r23=0.5表示冰/孔隙水界面的几何形状,Carcione等[34]建议颗粒/水合物界面的值为r13=r31=0。Guerin等[28]发现,减少r23会显著增加模型预测的衰减值。图 10显示r23=0.1和r23=0的结果,可与原始值(r23=0.5)结果(图 9)做对比。从图 10c和图 10d可见,当r23=0时,得到QP-1和QS-1的最高值,表明天然气水合物与孔隙水之间几乎无惯性耦合。
2.3.4 考虑喷射流尽管由于上述综合物理机制导致水合物饱和度增加,衰减增加,但这些结果均未预测低水合物饱和度下的任何衰减。除了包含的孔隙流体的黏性摩擦外,不存在独立于水合物的能量耗散机制。Leclaire等[26]及Carcione等[34]只考虑波了传播方向上的能量耗散。为了将喷射流BISQ引入Leclaire模型,Guerin等[28]通过扩展三相介质的Diallo和Appel[35]孔隙压力公式来替换孔隙流体应力/应变关系,改变刚度矩阵R12、R23和R22(式(2))中与孔隙流体相关的弹性系数表达式。图 10显示,在低天然气水合物饱和度下,喷射流的加入增加了纵波衰减。在较高饱和度下,随着有效渗透率的降低,喷射流的贡献变得微不足道。由于孔隙流体不传递剪切能量,因此喷射流的加入对横波衰减没有影响。因此,在图 10d中,r23=0的QS-1曲线,有、无喷射流的结果完全重叠。然而,图 9d仍然预测在相对较低的水合物饱和度(约15%)下横波衰减显著增加。
将以上模型结果与Mallik-2L38井实际数据对比发现,在三相Leclaire模型中,摩擦、胶结和喷射流动机制的组合(无惯性耦合),能够较合理地再现Mallik探区速度和衰减随水合物饱和度增加而增加的情况。
2.4 HEG(Hydrate Effective Grains)模型 2.4.1 BSM模型与存在问题Stoll等[36]假设松散海洋沉积物骨架中存在全局摩擦损耗。在Biot理论中引入常数复骨架剪切模量和体积模量,这种对Biot理论的扩展,称为Biot-Stoll模型(BSM)。Stoll[37]的实验室数据表明,在松散的细粒海相沉积物中,纵波与横波的对数衰减率非常接近。因此,如果给定了复剪切模量,则可以通过假设骨架的合理泊松比估计无法通过测量直接获得的复骨架体积模量;Stoll[38]实验室数据进一步解释了此结果,认为细粒海洋沉积物中,存在由于骨架中的局部黏弹性损失引起的附加频率依赖性衰减,即全局骨架摩擦损耗,还使用Cole-Cole模型[39]中的公式引入复剪切模量。通过与实际数据对比,发现Biot理论明显低估了衰减,而Biot-Stoll模型也给出了低估的衰减值。Wood等[40]认为为了匹配这些数据而假设一个更高的剪切模量是不合理的,因为会导致很高的纵波速度。
2.4.2 EGM模型Leurer[41]认为需一个附加衰减机制来增加纵波能量的衰减,该机制在加载期间分别通过纯压缩和膨胀激活,即使剪切波对其吸收应非常高,也对纵波速度和衰减的影响很小,因为细颗粒近地表海洋沉积物的剪切模量很低[42]。因此Leurer[41]提出了等效颗粒模型(Effective-Grain Model,EGM模型),认为通常假设的体积模量对沉积物颗粒的描述是不充分的,因而假设沉积物具有较多的黏土组分,并且存在膨胀性的黏土矿物(以蒙脱石为代表),因为在几乎所有含黏土的海洋沉积物中都有不同数量的膨胀性黏土矿物。由于膨胀,即吸水,蒙脱石变成一个两相体系。为了描述等效颗粒材料的动态行为,膨胀蒙脱石被认为是均匀各向同性的平面柱状包裹体,假设包裹体被晶内水饱和,包裹体边缘与自由孔隙水所占据的孔隙空间相连。因此,颗粒材料被视为对应力具有黏弹性响应的等效介质,引入复体积模量来描述。衰减机制为应力诱导挤压引起的流体运动,因此可视为喷射流动过程,这一现象的一般特征是从低纵横比包裹体到纵横比接近统一的孔隙的局部流体流动。
2.4.3 EGM的拓展——含水合物层HEG模型Priest等[43-44]使用过量气(Excess gas)和过量水(Excess water)两种方法在砂岩样本中形成甲烷水合物。过量气法包括将已知质量的水分布在整个砂样中,用甲烷气体使部分水饱和的砂饱和,水倾向于覆盖湿砂粒,甲烷与水反应形成颗粒覆盖型水合物,其中一部分作用于在颗粒接触处胶结颗粒[45]。相比之下,过量水法需要向砂样中注入甲烷气体,然后用水冲洗砂样,这被认为产生了一种孔隙填充型水合物形态,因为甲烷气体倾向于分布在砂岩的孔隙空间中,周围是自然附着在湿砂颗粒上的水。该解释分别得到了文献[44]和文献[46]中报告的速度和弹性模量结果的支持。Best等[29]提出水合物颗粒可认为是含有气体或水的柔性材料,而不是单纯的固体矿物。包裹体是在Excess gas或Excess gas条件下水合物形成过程中捕获的孤立气或水的结果。在此情况下,水合物可能以与沉积物和岩石中其他微孔、柔性矿物类似的方式,产生局部黏性流体(喷射流)。Ecker等[47-48]不仅给出关于颗粒胶结水合物的骨架模量表达式,还给出承载型和孔隙填充型水合物的骨架体积和剪切模量的表达式,并将这些骨架模量值输入到Gassman[49]方程,以计算流体饱和沉积物中的地震速度。Best等[29]将其引入Biot理论中,以预测频率相关的纵波和横波速度和衰减。为了解释与微孔水合物颗粒相关的喷射流,Best等[29]使用Leurer等[41, 50]的EGM方法,使骨架弹性模量是与频率相关的复模量。这里,Ecker等[47-48]表达式中的固体水合物相的体积模量和剪切模量被含有流体包裹体的等效水合物颗粒的体积模量和剪切模量代替。并遵循Johnston等[51]的方案,利用对应性原理引入频率相关的复包裹材料弹性模量,使水合物的等效颗粒模量为频率相关的复模量。由此提出水合物等效颗粒模型(Hydrate Effective Grains,HEG,图 11)。

|
图 11 水合物等效颗粒模型示意图[47] |
Best等[29]模拟发现,胶结水合物HEG模型估算的衰减可忽略不计;孔隙填充水合物HEG模型只能解释饱和水条件下纵波衰减的增加(预测横波衰减为零);承载HEG模型预测纵波和横波衰减的增加。
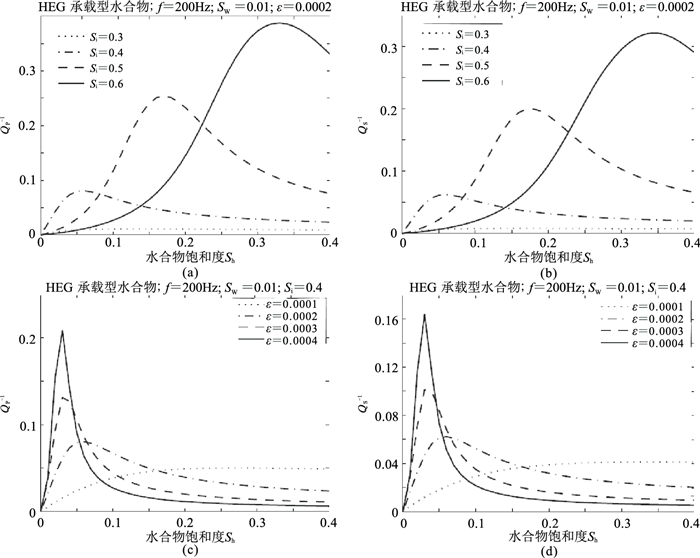
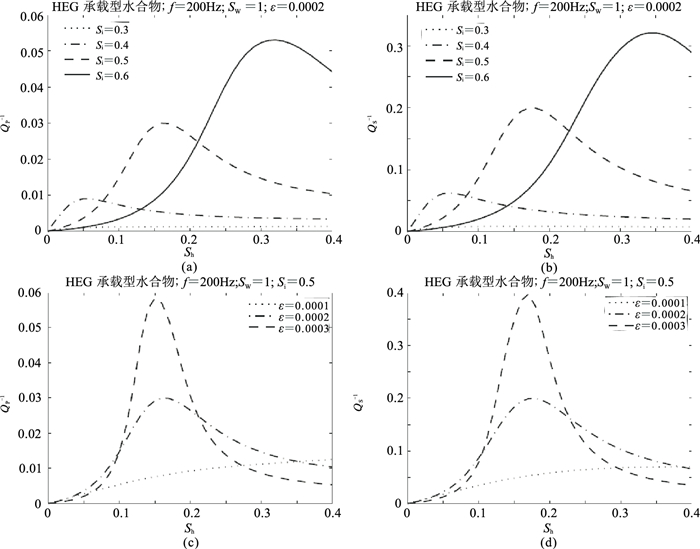
如图 12所示,对于饱和气体(Sw=0.01)承载型水合物,固定包裹体纵横比ε时,QP-1和QS-1显示为包裹体浓度Si的函数,以及固定包裹体浓度Si时为包裹体纵横比ε的函数,在水合物饱和度约为0.05时产生衰减峰值。Si控制衰减峰值相对于水合物饱和度Sh的位置,而ε控制衰减峰值大小(对于给定频率)。对于给定的水合物饱和度,预测的QP-1值略大于预测的QS-1值。
图 13显示含水饱和(Sw=1)、承载型水合物的类似结果,图 13c和图 13d显示通过固定Si=0.5和不同的包裹体纵横比预测Sh=0.15时衰减峰值。
|
图 13 水饱和时承载型HEG模型模拟结果(同图 12) |
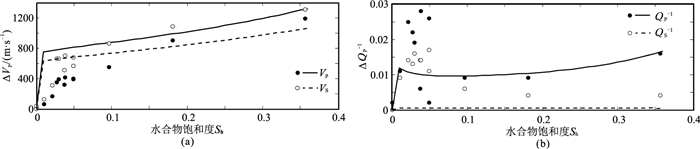
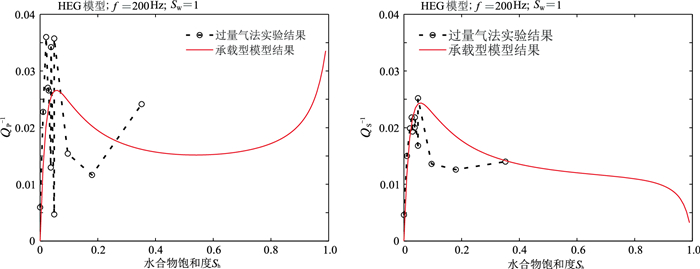
如图 14所示,通过将承载型HEG模型与Best等[29]的实验结果进行对比,可以发现尽管模型预测的QP-1略低,但预测了正确量级的衰减峰值。同时承载型HEG模型表明,高水合物饱和度时QP-1迅速增加,但QS-1迅速下降。
|
图 14 承载型HEG模型结果与Best等[29]实验数据对比 |
Marín-Moreno等[30]给出含水合物沉积物微观结构的理想状态(图 15)。他们将HEG模型[29]引入的水合物中流体包裹体与孔隙之间的流动称为亚微米喷射流,并以HEG模型和Biot-Stoll模型[36]为基础,将水合物生成孔隙和原始孔隙(如砂岩骨架主孔隙)之间的微米喷射流以及气泡阻尼引起的衰减加入其中,提出含水合物等效沉积物模型(Hydrate-Bearing Effective Sediment,HBES),模拟多重衰减机制下纵波衰减随水合物饱和度的变化。图 16模型示意图展示了不同的单独衰减机制,含水合物沉积物中的总能量损失由每种衰减机制的贡献给出。

|
图 15 含水合物沉积物微观结构的理想状态[30] |

|
图 16 含水合物有效沉积物(HBES)模型流程图[30] |
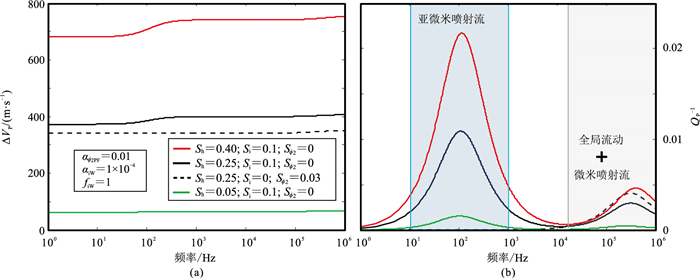
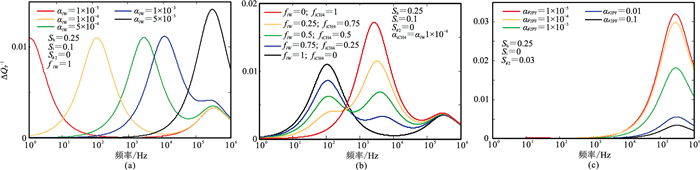
图 17为孔隙填充型水合物层的的纵波衰减随频率及饱和度的变化,地震频率下显示的衰减峰值是由水合物(亚微米喷射流)中的流体包裹体引起的,而在超声波频率下,衰减峰值是由孔隙填充水合物存在导致的初始孔隙度降低和不同纵横比孔隙的引起的。水合物中流体包裹体产生的亚微喷射流的衰减最大值出现在整个频率范围内,这取决于包裹体中流体的纵横比和类型(图 18a和图 18b),而不同纵横比孔隙产生的微喷射流的峰值出现在声波频率和超声波频率下,与孔隙的纵横比无关(图 18c)。本质上,水合物中流体包裹体的类型控制着衰减变化的幅度和衰减峰值对应频率。相比之下,水合物中流体包裹体的纵横比仅控制衰减峰值的频率依赖性,而包裹体的浓度仅控制衰减幅度。
|
图 17 孔隙填充型HBES模型结果[30] (a)ΔVP;(b)ΔQP-1(相对于不含水合物的值)。不同颜色线型对应不同的水合物饱和度Sh、包裹体浓度Si及水合物生成的不同纵横比孔隙占比Sϕ2 |
|
图 18 孔隙填充型HBES模型QP-1变化模拟结果(相对于不含水合物)[30] 不同颜色代表不同的水包裹体纵横比αiw、水包裹体占比fiw、甲烷包裹体占比fiCH4及孔隙填充型水合物生成的孔隙纵横比αϕ2PF |
将HBES模型结果(图 19)与Priest等[21]实验数据对比,可发现模型预测的纵横波速度与实验数据吻合较好,也同样预测了较低饱和度下的纵波衰减峰值,但结果偏低,而预测的横波衰减为零,与数据不符。
2.6 小结为方便读者对比,本文将各种岩石物理模型的假设条件与优缺点、衰减机制、模拟结果及对实际探区或实验数据的适用性进行了归纳总结(表 2)。
|
|
表 2 各模型假设条件与优缺点、衰减机制、模拟结果及对实际探区或实验数据适用性分析对比 |
本文回顾了国内外多探区天然气水合物地震波吸收衰减特征,综述了水合物储层可能存在的衰减机制及相关岩石物理理论,得到以下几点认识:
(1) 很多地区的水合物地层的地震数据呈现较明显的吸收衰减特征,但是相互之间存在较大的差异,造成差异的主要原因是水合物的赋存状态不同,以及储层是否含流体。
(2) 地震衰减具频散特征,但现有的现场观测和实验测试数据有限,难以全面体现衰减随频率变化的性质。
(3) 水合物对衰减的作用还不明确,现有的吸收衰减机制和岩石物理理论在一定程度上能够描述地震波衰减随水合物饱和度的关系,例如改进的Leclaire模型与井数据相匹配,HEG模型与Best的实验数据的趋势相一致,但是适用性和精度还需要进一步结合实际数据进行分析和验证。
(4) 由于实验室内较难合成与原位地层条件相同的水合物样品,基于人工合成岩心的岩石物理实验得到的水合物与各种岩石物理参数之间的关系,并不能准确描述实际地层的情况。
(5) 与天然气水合物存在有关的测井声波波形异常及低地震振幅或振幅“空白”带,与地震波吸收衰减直接相关,可作为天然气水合物量化的一个指标。但由于我们对沉积物中的衰减机制,特别是水合物的作用认识有限,因此对声波测井或者地震衰减测量的解释是不确定的,很难定量地将吸收衰减与特定的水合物或沉积物条件联系起来,但实验室研究可为其提供理论基础。
基于以上认识,本文认为:
(1) 基于孔隙介质地震波传播理论,开展一系列赋存方式和分布特征各异的含水合物储层的吸收衰减机制、岩石物理理论和衰减特征研究,对实验和现场数据的更可靠解释具有决定性的作用,可提高将地震振幅与天然气水合物含量联系起来的可能性,提高估算水合物储量的能力。
(2) 对于含水合物沉积物,研究水合物对岩石微观结构改变的作用机理,分离固有损耗机制并准确预测其依赖性(如测量频率、等效压力、温度、渗透率、孔隙流体类型和饱和度、水合物饱和度和形态),从而建立描述这种衰减机理的最佳岩石物理模型,仍是目前的主要挑战。
| [1] |
SHIPLEY T H, HOUSTON M H, BUFFLER R T, et al. Seismic evidence for widespread possible gas hydrate horizons on continental slopes and rises[J]. AAPG Bulletin, 1979, 63(12): 2204-2213. |
| [2] |
KVENVOLDEN K A. A primer on the geological occurrence of gas hydrate[J]. Geological Society Special Publications, 1998, 137(1): 9-30. DOI:10.1144/GSL.SP.1998.137.01.02 |
| [3] |
LEE M W, DILLON W P. Amplitude blanking rela-ted to the pore-filling of gas hydrate in sediments[J]. Marine Geophysical Researches, 2001, 22(2): 101-109. DOI:10.1023/A:1010371308699 |
| [4] |
GUERIN G, GOLDBERG D. Sonic waveform attenua-tion in gas hydrate-bearing sediments from the Mallik 2L-38 research well, Mackenzie Delta, Canada[J]. Journal of Geophysical Research—Solid Earth, 2002, 107(B5): EPM 1-1-EPM 1-11. |
| [5] |
PRATT R G, HOU F, BAUER K, et al. Waveform tomography images of velocity and inelastic attenuation from the Mallik 2002 crosshole seismic surveys[Z]. Scientific Results from the Mallik 2002 Gas Hydrate Production Research Well Program, Mackenzie Delta, Northwest Territories, Canada. Geological Survey of Canada, Vancouver, BC, Canada, 2005, Bulletin 585.
|
| [6] |
BAUER K, PRATT R G, WEBER M H, et al. Mallik 2002 cross-well seismic experiment: project design, data acquisition, and modelling studies[Z]. Scientific Results from the Mallik 2002 Gas Hydrate Production Research Well Program, Mackenzie Delta, Northwest Territories, Canada. Geological Survey of Canada, 2005, Bulletin 585.
|
| [7] |
宋海斌, 松林修. 日本南海海槽天然气水合物研究现状[J]. 地球物理学进展, 2001, 16(2): 88-98. SONG Haibin, MATSUBAYASHI O. A summary of gas hydrate researches in adjacent sea regions around Japan especially the Nankai Trough[J]. Progress in Geophysics, 2001, 16(2): 88-98. DOI:10.3969/j.issn.1004-2903.2001.02.012 |
| [8] |
MATSUSHIMA J. Attenuation measurements from sonic waveform logs in methane hydrate-bearing sediments at the Nankai Trough exploratory well of Tokai, central Japan[J]. Geophysical Research Letters, 2005, 32(3): L03306. |
| [9] |
MATSUSHIMA J. Seismic wave attenuation in methane hydrate-bearing sediments: Vertical seismic profiling data from the Nankai Trough exploratory well, offshore Tokai, central Japan[J]. Journal of Geophysical Research—Solid Earth, 2006, 111(B10): B10101. DOI:10.1029/2005JB004031 |
| [10] |
SAIN K, MINSHULL T A, SINGH S C, et al. Evidence for a thick free gas layer beneath the bottom simulating reflector in the Makran accretionary prism[J]. Marine Geology, 2000, 164(1/2): 3-12. |
| [11] |
OJHA M, SAIN K. Seismic attributes for identifying gas hydrates and free gas zones: application to the Makran accretionary prism[J]. Episodes, 2009, 32(4): 264-270. DOI:10.18814/epiiugs/2009/v32i4/003 |
| [12] |
SAIN K, SINGH A K. Seismic quality factors across a bottom simulating reflector in the Makran Accretionary Prism, Arabian Sea[J]. Marine and Petroleum Geology, 2011, 28(10): 1838-1843. DOI:10.1016/j.marpetgeo.2011.03.013 |
| [13] |
SASSEN R, MACDONALD I R. Evidence of structure H hydrate, Gulf of Mexico continental slope[J]. Organic Geochemistry, 1994, 22(6): 1029-1032. DOI:10.1016/0146-6380(94)90036-1 |
| [14] |
KRASON J, FINLEY P, RUDLOFF B. Geological Evolution and Analysis of Confirmed or Suspected Gas Hydrate Localities. Volume 3. Basin Analysis, Formation and Stability of Gas Hydrates in the Wes-tern Gulf of Mexico[R]. Geoexplorers International, Inc., Denver, CO USA, 1985.
|
| [15] |
HUTCHINSON D R, HART P E, COLLETT T S, et al. Geologic framework of the 2005 Keathley Canyon gashydrate research well, northern Gulf of Mexico[J]. Marine and Petroleum Geology, 2008, 25(9): 906-918. DOI:10.1016/j.marpetgeo.2008.01.012 |
| [16] |
王吉亮, 吴时国. 墨西哥湾GC955H井天然气水合物储层声波衰减特征[J]. 地球物理学报, 2016, 59(4): 1535-1542. WANG Jiliang, WU Shiguo. The characteristics of sonic wave attenuations of gas hydrate reservoirs at Well GC955H, Gulf of Mexico[J]. Chinese Journal of Geophysics, 2016, 59(4): 1535-1542. |
| [17] |
张伟, 梁金强, 陆敬安, 等. 中国南海北部神狐海域高饱和度天然气水合物成藏特征及机制[J]. 石油勘探与开发, 2017, 44(5): 670-680. ZHANG Wei, LIANG Jinqiang, LU Jing'an, et al. Accumulation features and mechanisms of high saturation natural gas hydrate in Shenhu area, northern South China Sea[J]. Petroleum Exploration and Development, 2017, 44(5): 708-719. |
| [18] |
张伟, 梁金强, 何家雄, 等. 南海北部神狐海域GMGS1和GMGS3钻探区天然气水合物运聚成藏的差异性[J]. 天然气工业, 2018, 38(3): 138-149. ZHANG Wei, LIANG Jinqiang, HE Jiaxiong, et al. Differences in natural gas hydrate migration and accumulation between GMGS1 and GMGS3 drilling areas in the Shenhu area, northern South China Sea[J]. Natural Gas Industry, 2018, 38(3): 138-149. |
| [19] |
LI C H, LIU X W. Seismic wave attenuation in hydrate-bearing sediments based on the patchy saturation model in the Shenhu area, South China Sea[J]. Interpretation, 2017, 5(3): SM25-SM32. DOI:10.1190/INT-2016-0139.1 |
| [20] |
WANG X C, LIANG L H, WU Z L. Research on seismic wave attenuation in gas hydrates layer using vertical cable seismic data[J]. Pure and Applied Geophysics, 2018, 175(10): 3451-3462. DOI:10.1007/s00024-018-1918-6 |
| [21] |
PRIEST J A, BEST A I, CLAYTON C R I. Attenuation of seismic waves in methane gas hydrate-bearing sand[J]. Geophysical Journal International, 2006, 164(1): 149-159. DOI:10.1111/j.1365-246X.2005.02831.x |
| [22] |
BIOT M A. Theory of propagation of elastic waves in a fluid-saturated porous solid. Ⅰ. low-frequency range[J]. The Journal of the Acoustical Society of America, 1956, 28(2): 168-178. DOI:10.1121/1.1908239 |
| [23] |
WHITE J E. Computed seismic speeds and attenuation in rocks with partial gas saturation[J]. Geophy-sics, 1975, 40(2): 224-232. |
| [24] |
DVORKIN J, MAVKO G, NUR A. Squirt flow in fully saturated rocks[J]. Geophysics, 1995, 60(1): 97-107. DOI:10.1190/1.1443767 |
| [25] |
张聿文, 刘学伟, 金玉洁. 含天然气水合物地层的速度和衰减研究[J]. 石油地球物理勘探, 2004, 39(2): 205-214. ZHANG Yuwen, LIU Xuewei, JIN Yujie. Study of velocity and attenuation for gas-bearing hydrate formation[J]. Oil Geophysical Prospecting, 2004, 39(2): 205-214. DOI:10.3321/j.issn:1000-7210.2004.02.017 |
| [26] |
LECLAIRE PCOHEN-TÉNOUDJI F, AGUIRRE-PUENTE J. Extension of Biot's theory of wave pro-pagation to frozen porous media[J]. The Journal of the Acoustical Society of America, 1994, 96(6): 3753-3768. DOI:10.1121/1.411336 |
| [27] |
CARCIONE J M, TINIVELLA U. Bottom-simu-lating reflectors: Seismic velocities and AVO effects[J]. Geophysics, 2000, 65(1): 54-67. DOI:10.1190/1.1444725 |
| [28] |
GUERIN G, GOLDBERG D. Modeling of acoustic wave dissipation in gas hydrate-bearing sediments[J]. Geochemistry, Geophysics, Geosystems, 2005, 6(7): 1-16. |
| [29] |
BEST A I, PRIEST J A, CLAYTON C R I, et al. The effect of methane hydrate morphology and water sa-turation on seismic wave attenuation in sand under shallow sub-seafloor conditions[J]. Earth and Planetary Science Letters, 2013, 368: 78-87. DOI:10.1016/j.epsl.2013.02.033 |
| [30] |
MARÍN-MORENO H, SAHOO S K, BEST A I. Theoretical modeling insights into elastic wave at-tenuation mechanisms in marine sediments with pore-filling methane hydrate[J]. Journal of Geophysical Research—Solid Earth, 2017, 122(3): 1835-1847. |
| [31] |
GUERIN G, GOLDBERG D, MELTSER A. Characterization of in situ elastic properties of gas hydrate-bearing sediments on the Blake Ridge[J]. Journal of Geophysical Research—Solid Earth, 1999, 104(B8): 17781-17795. DOI:10.1029/1999JB900127 |
| [32] |
JOHNSON D L, PLONA T J. Acoustic slow waves and the consolidation transition[J]. The Journal of the Acoustical Society of America, 1998, 72(2): 556-565. |
| [33] |
BERRYMAN J G, WANG H F. Elastic wave propagation and attenuation in a double-porosity dual-permeability medium[J]. International Journal of Rock Mechanics and Mining Sciences, 2000, 37(1/2): 63-78. |
| [34] |
CARCIONE J M, SERIANI G. Wave simulation in frozen porous media[J]. Journal of Computational Physics, 2001, 170(2): 676-695. DOI:10.1006/jcph.2001.6756 |
| [35] |
DIALLO M S, APPEL E. Acoustic wave propagation in saturated porous media: reformulation of the Biot/Squirt flow theory[J]. Journal of Applied Geophy-sics, 2000, 44(4): 313-325. DOI:10.1016/S0926-9851(00)00009-4 |
| [36] |
STOLL R D, BRYAN G M. Wave attenuation in sa-turated sediments[J]. The Journal of the Acoustical Society of America, 1970, 47(5B): 1440-1447. DOI:10.1121/1.1912054 |
| [37] |
STOLL R D. Marine sediment acoustics[J]. The Journal of the Acoustical Society of America, 1983, 74(S1): S57. |
| [38] |
STOLL R D. Sediment Acoustics[M]. Berlin: Springer-Verlag, 1989: 83-96.
|
| [39] |
COLE K S, COLE R H. Dispersion and absorption in dielectrics[J]. The Journal of Chemical Physics, 1941, 9(4): 341-351. DOI:10.1063/1.1750906 |
| [40] |
WOOD A B, WESTON D E. The propagation of sound in mud[J]. Acta Acustica United with Acustica, 1964, 14(3): 156-162. |
| [41] |
LEURER K C. Attenuation in fine-grained marine sediments: extension of the Biot-Stoll model by the "effective grain model" (EGM)[J]. Geophysics, 1997, 62(5): 1465-1479. DOI:10.1190/1.1444250 |
| [42] |
THEILEN F, PECHER I A. Assessment of shear strength of the sea bottom from shear wave velocity measurements on box cores and in-situ // HOVEM J M, RICHARDSON M D, STOLL R D. Shear Waves in Marine Sediments[M]. Springer Netherlands, Dordrecht, 1991, 67-74.
|
| [43] |
PRIEST J A, BEST A I, CLAYTON C R I. A laboratory investigation into the seismic velocities of me-thane gas hydrate-bearing sand[J]. Journal of Geophy-sical Research—Solid Earth, 2005, 110(B4): B04102. |
| [44] |
PRIEST J A, REES E V L, CLAYTON C R I. Influence of gas hydrate morphology on the seismic velocities of sands[J]. Journal of Geophysical Research—Solid Earth, 2009, 114(B11): B11205. |
| [45] |
CHAND S, MINSHULL T A, PRIEST J A, et al. An effective medium inversion algorithm for gas hydrate quantification and its application to laboratory and borehole measurements of gas hydrate-bearing sediments[J]. Geophysical Journal International, 2006, 166(2): 543-552. DOI:10.1111/j.1365-246X.2006.03038.x |
| [46] |
CLAYTON C R I, PRIEST J A, REES E V L. The effects of hydrate cement on the stiffness of some sands[J]. Géotechnique, 2010, 60(6): 435-445. DOI:10.1680/geot.2010.60.6.435 |
| [47] |
ECKER C, DVORKIN J, NUR A M. Sediments with gas hydrates: internal structure from seismic AVO[J]. Geophysics, 1998, 63(5): 1659-1669. DOI:10.1190/1.1444462 |
| [48] |
ECKER C, DVORKIN J, NUR A M. Estimating the amount of gas hydrate and free gas from marine seismic data[J]. Geophysics, 2000, 65(2): 565-573. DOI:10.1190/1.1444752 |
| [49] |
GASSMANN F. Elastic waves through a packing of spheres[J]. Geophysics, 1951, 16(4): 673-685. DOI:10.1190/1.1437718 |
| [50] |
LEURER K C, BROWN C. Acoustics of marine sediment under compaction: binary grain-size model and viscoelastic extension of Biot's theory[J]. The Journal of the Acoustical Society of America, 2008, 123(4): 1941-1951. DOI:10.1121/1.2871839 |
| [51] |
JOHNSTON D H, TOKSOZ M N, TIMUR A. Attenuation of seismic waves in dry and saturated rocks: Ⅱ. Mechanisms[J]. Geophysics, 1979, 44(4): 691-711. DOI:10.1190/1.1440970 |



 张峰,北京市昌平区府学路18号中国石油大学(北京)地球物理学院,102249。Email:
张峰,北京市昌平区府学路18号中国石油大学(北京)地球物理学院,102249。Email: