② 南方海洋科学与工程广东省实验室(广州),广东广州 511458;
③ 天然气水合物勘查开发国家工程研究中心,广东广州 511458
② Southern Marine Science and Engineering Guangdong Laboratory (Guangzhou), Guangzhou, Guangdong 511458, China;
③ National Engineering Research Center of Gas Hydrate Exploration and Development, Guangzhou, Guangdong 511458, China
海洋可控源电磁(MCSEM)法是有效探测海底电阻率异常体的重要方法之一,在海洋地质调查(海洋底构造、洋脊扩张、火山运动等)、海底资源(油气、水合物、地下水、多金属硫化物等)探测等诸多领域得到了成功应用[1-7]。该方法的优势在于:①相较于海洋地震方法,勘探成本低;②电磁响应对异常体的电阻率差异灵敏度高,可有效降低油藏勘探和开发的风险;③是地震勘探方法的有效补充,如在天然水合物调查中,对于地震方法无法识别的天然水合物顶界,电磁法可以有效识别。浅海的可燃冰储层具有高电阻率特性,利用MCSEM勘探不仅可以估算可燃冰的饱和度分布,也可与地震勘探结合,优势互补,显著降低钻探风险、提高钻探成功率[8]。中国的MCSEM勘探始于2016年在琼东南海域利用自主研制的海底电磁接收机开展的可燃冰探测试验[9]。
MCSEM的正演是反演以及实际应用研究的基础。由于海底地层的电性结构可能非常复杂[10],因此开发一个适用于MCSEM复杂三维模型的稳定且有效的正演算法至关重要。本文提出一种基于预条件迭代求解的频率域矢量有限元电磁模拟方法,可高效地进行复杂海底地形条件下的MCSM模型正演模拟。
MCSEM正演模拟的数值方法主要包括有限差分法、有限元方法、积分方程法、多网格法[11]等,这些方法各有优、缺点。有限元方法构造的源项采用单元积分方法,相比有限差分的加权平均方法更精确,因此有限元方法的求解精度理论上更高,并且更适用于复杂地质模型的构建。已证明有限元方法是一个适用于地球物理问题中任何复杂的二维或三维结构的数值分析的有效工具,其中矢量有限元方法因其算法稳定、求解效率高且适合于复杂几何形状模型的模拟,一直是电磁模型领域的研究热点[12-15]。矢量有限元(比如六面体单元)方法中,单元内的电场之间具有更紧密的耦合关系,且插值函数具有严格的无散性。Mitsuhata等[16]提出了一种基于矢量有限元的大地电磁建模算法。Schwarzbach等[17]基于线性高阶矢量有限元,利用四面体单元离散对MCSEM数据进行建模,精确地再现了真实海洋深水模型。
三维模型模拟中,曲面的离散可使用普通网格、六面体单元或四面体单元。对于三维矢量有限元模拟,四面体单元具有结构可任意离散化的特点[18-19]。比较而言,基于六面体单元的矢量有限元则更易实现结构化网格[20]、模型加密,具有正反演网格操作简单[21]等优势,集合了有限差分易于离散和矢量有限元对复杂模型适应性强的优势,得到了广泛的应用[22-24]。Nam等[25]利用规则六面体单元的矢量有限元建立了大地电磁三维模型,研究了海洋火山地形与水深对不同频段大地电磁数据的影响,并进行了数值分析。Kordy等[26]将直接求解法应用于不规则六面体单元的矢量有限元方法,并进行了散度校正,结果证明该方法可用于准确求解复杂地形的电磁响应。
在有限元求解框架下搭载稳定、高效的矩阵可显著提高求解效率。迭代方法是计算有限元稀疏矩阵的重要方法,其优点是计算量小、对计算机的存储要求低[13, 27]。预条件方法在矩阵迭代求解中具有非常重要的作用,最重要的一种预条件方法是对矩阵的不完全分解,常见的是不完全LU(ILU)分解。考虑矩阵对称情形,当矩阵正定性较强时,不完全Cholesky分解[28]也是非常有效的预条件手段。Um等[29]提出电磁场散射公式的有效ILU预条件的有限元迭代策略,并在多源、多频、多模型等不同条件下全方位地对几种预条件方法的效率进行了评价,提出正确选择预条件方法可以大大减少复杂海底模型的计算量和计算时间。
针对复杂电性结构海底地层模型,本文提出一种基于预条件迭代求解的频率域矢量有限元电磁正演模拟方法,基于ILU分解的预条件方法,提高了迭代求解效率。建立层状海洋电磁模型,通过模拟电场响应,并与解析解进行对比,验证了本文算法的有效性。基于结构化任意六面体单元建立了中国南海某海域真实地电框架模型,并针对不同构造矿藏储层特征,分别建立了深埋藏油气储层模型、可燃冰矿体模型及复杂基底地质模型,应用前述方法计算电场响应,对不同激发、接收模式下的MCSEM响应特征进行分析,并进一步总结出适宜的探测参数设置条件。
1 方法原理 1.1 控制方程地球物理勘探领域中常用到低频电磁场需满足的宏观电动力方程,即Maxwell方程组。在稳场近似下,可忽略位移电流。假设时间谐变因子为eiωt,频率域Maxwell方程组可表示为
| $\left\{ {\begin{array}{*{20}{l}} {\nabla \times {\mathit{\boldsymbol{E}}} = - {\rm{i}}\omega \mu {\mathit{\boldsymbol{H}}} - {\mathit{\boldsymbol{M}}}}\\ {\nabla \times {\mathit{\boldsymbol{H}}} = \sigma {\mathit{\boldsymbol{E}}} + {\mathit{\boldsymbol{J}}}}\\ {\nabla \cdot {\mathit{\boldsymbol{B}}} = 0}\\ {\nabla \cdot {\mathit{\boldsymbol{D}}} = q} \end{array}} \right.$ | (1) |
式中:E表示空间电场;H表示空间磁场;ω表示圆频率;磁导率μ=μtμ0=4π×10-7H/m,其中μt和μ0分别表示相对磁导率和真空中的磁导率;J和M分别表示电流密度和磁流密度;q表示体电荷密度;σ为介质电导率;B表示磁感应强度;D表示电位移矢量。
由于背景场在源附近急剧变化,用有限元法直接求解总场时,在边界处可采用稀疏网格,在场源附近则需采用精细网格。为了提高计算效率,可以采用求解异常场的方法求解总场。以电场E为例,首先将其分解为异常场Ea与背景场Eb之和,即E=Ea+Eb,Eb可以通过求解全空间或半空间的解析解得到,这样可得到基于电场异常场Ea的二阶偏微分方程
| $\nabla \times \left( {{\mu ^{ - 1}}\nabla \times {{\mathit{\boldsymbol{E}}}^{\rm{a}}}} \right) + {\rm{i}}\omega \sigma {{\mathit{\boldsymbol{E}}}^{\rm{a}}} = - {\rm{i}}\omega \left( {\sigma - {\sigma ^{\rm{b}}}} \right){{\mathit{\boldsymbol{E}}}^{\rm{b}}}$ | (2) |
式中上标“b”代表背景。对使用偶极子源进行激发的情形,采用异常场方法构造的源项更加平滑,有利于数值求解。背景场为均匀全空间或者层状介质的电场分布,可由快速汉克尔变换方法求得[30]。
为了表示的简洁性,后文中用E代表电场异常场Ea。假设求解目标在三维长方体域Ω内满足狄利克雷边界条件的解,式(2)可以表示为算子的简单形式
| ${\mathit{\boldsymbol{AE}}} + {\rm{i}}\omega \sigma {\mathit{\boldsymbol{E}}} = {\mathit{\boldsymbol{b}}}$ | (3) |
式中:A=∇×μ-1∇×;b=-iω(σ-σb)Eb。数值求解得到电场E后,可根据法拉第定律直接求解磁场
| ${\mathit{\boldsymbol{H}}} = - \frac{1}{{{\rm{i}}\omega \mu }}\nabla \times {\mathit{\boldsymbol{E}}}$ | (4) |
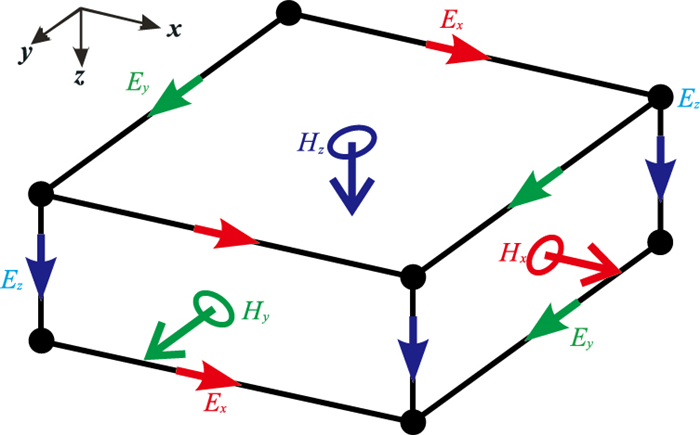
本文使用矢量有限元方法求解式(3),将矢量形函数定义在单元的边上,然后通过插值表示单元中各点的场值。这里采用六面体单元,六面体单元中节点和电/磁场的位置如图 1所示。
|
图 1 六面长方体单元中节点和电/磁场位置示意图 |
定义单元e沿x、y和z方向的边长分别为Δxe、Δye和Δze,单元内任一点的电场分量可以表示为
| $E_p^{\rm{e}} = \sum\limits_{i = 1}^4 {N_{pi}^{\rm{e}}} E_{pi}^{\rm{e}}\quad p = x, y, z$ | (5) |
式中Npie和Epie分别表示六面体单元的第i(i=1~4)条边上p(x, y, z)方向的单元基函数和切向电场。
矢量基函数在单元边界也是连续的,因此基于矢量有限元的公式也适用于无源条件下的电磁场模拟。采用Galerkin方法[30],设残差函数(式(2))的弱形式为零
| $\begin{align} & f({\mathit{\boldsymbol{E}}})=\iiint_{\mathit{\Omega }}{{{{\mathit{\boldsymbol{N}}}}_{j}}}\cdot \left[ \nabla \times \left( {{\mu }^{-1}}\nabla \times {\mathit{\boldsymbol{E}}} \right)+ \right. \\ & \ \ \ \ \ \ \ \ \ \ \ \ \left. \text{i}\omega \sigma {\mathit{\boldsymbol{E}}}+\text{i}\omega \left( \sigma -{{\sigma }^{\text{b}}} \right){{{\mathit{\boldsymbol{E}}}}^{\text{b}}} \right]\text{d}V=0 \\ \end{align}$ | (6) |
式中Nj表示第j个插值函数。基于矢量恒等式和第一矢量格林定理,对于单元e,式(6)可写成
| $\begin{array}{l} {f^e}({\mathit{\boldsymbol{E}}}) = \sum\limits_{e = 1}^{{n_{\rm{e}}}} {\left[ {{{\mathit{\boldsymbol{G}}}_e}{\mathit{\boldsymbol{E}}} + {\rm{i}}\omega {{\mathit{\boldsymbol{M}}}_e}{\mathit{\boldsymbol{E}}} + } \right.} \\ \;\;\;\;\;\;\;\;\;\;\;\left. {{\rm{i}}\omega \left( {\sigma - {\sigma ^{\rm{b}}}} \right){{\mathit{\boldsymbol{M}}}_e}{{\mathit{\boldsymbol{E}}}^{\rm{b}}}} \right] = 0 \end{array}$ | (7) |
式中:ne表示与单元e插值相关的单元个数;Ge和Me分别为单元刚度矩阵和单元质量矩阵,其表达式为
| $\left\{ \begin{array}{*{35}{l}} {{G}_{e, ij}}=\iiint_{{{\mathit{\Omega }}^{e}}}{{{\mu }^{-1}}}\left( \nabla \times {\mathit{\boldsymbol{N}}}_{i}^{e} \right)\cdot \left( \nabla \times {\mathit{\boldsymbol{N}}}_{j}^{e} \right)\text{d}{{\mathit{\boldsymbol{v}}}^{e}} \\ M_{e, ij}^{\text{e}}=\iiint_{{{\mathit{\Omega }}^{e}}}{{\mathit{\boldsymbol{N}}}_{i}^{e}}\cdot {\mathit{\boldsymbol{N}}}_{j}^{e}~\text{d}{{\mathit{\boldsymbol{v}}}^{e}}\quad e=1\tilde{\ }{{n}_{e}} \\ \end{array} \right.$ | (8) |
将单元刚度矩阵Ge整理到总刚度矩阵G即可得到最后的线性方程组,借助相应的矩阵求解器,即可直接求解三维电场E的分布。
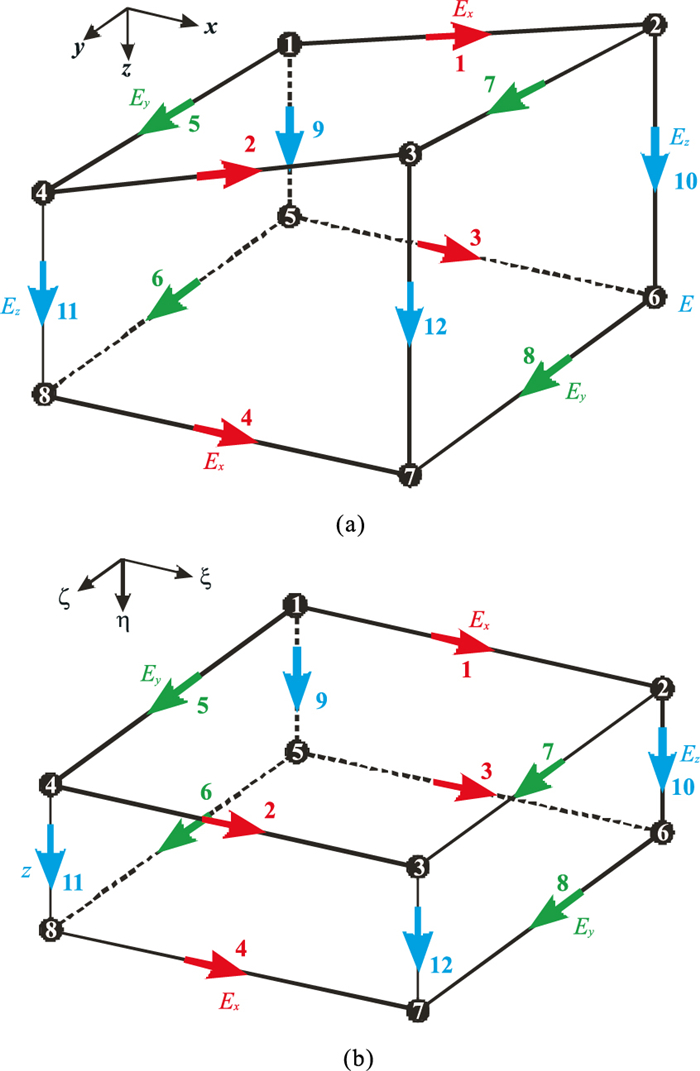
通常情况下,仅仅使用长方体网格无法精确模拟复杂地球物理模型[31]。在海洋电磁模拟中,电磁响应受地形起伏的影响很明显,粗糙的网格剖分会严重影响模拟结果对目标的分辨率。因此,基于不规则六面体单元的有限元方法在结果验证和数据补充方面具有重要的意义。可采用坐标变换将基于xyz坐标系的任意六面体单元(图 2a)映射为基于ξηζ坐标系的长方体单元(图 2b)
| $\left\{ {\begin{array}{*{20}{l}} {x = \sum\limits_{j = 1}^8 {N_j^{\rm{e}}} (\xi , \eta , \zeta )x_j^{\rm{e}}}\\ {y = \sum\limits_{j = 1}^8 {N_j^{\rm{e}}} (\xi , \eta , \zeta )y_j^{\rm{e}}}\\ {z = \sum\limits_{j = 1}^8 {N_j^{\rm{e}}} (\xi , \eta , \zeta )z_j^{\rm{e}}} \end{array}} \right.$ | (9) |
|
图 2 六面体单元从xyz坐标系(a)映射到ξηζ坐标系(b) |
其中
| $ \left\{ {\begin{array}{*{20}{l}} {\xi = \frac{{2\left( {x - x_{\rm{c}}^{\rm{e}}} \right)}}{{l_x^{\rm{e}}}}}\\ {\eta = \frac{{2\left( {y - y_{\rm{c}}^{\rm{e}}} \right)}}{{l_y^{\rm{e}}}}}\\ {\zeta = \frac{{2\left( {z - z_{\rm{c}}^{\rm{e}}} \right)}}{{l_z^{\rm{e}}}}} \end{array}} \right. $ |
式中:下标j表示单元节点编号;(xce, yce, zce)表示单元棱边的中点坐标;lxe、lye、lze表示单元边长;(xje, yje, zje)表示第j个顶点的坐标;Nje表示节点有限元的形函数,其表达式为
| $N_j^{\rm{e}}(\xi , \eta , \zeta ) = \frac{{\left( {1 + {\xi _j}\xi } \right)\left( {1 + {\eta _j}\eta } \right)\left( {1 + {\zeta _j}\zeta } \right)}}{8}$ | (10) |
为了建立平行于ξ轴的四个边的形函数,首先定义ξ为常数的面。由于该面垂直于ξ轴,在面上∇ξ只有法向分量,这样通过∇ξ定义的形函数只在平行于ξ轴的边上才有非零切向分量。根据式(10)建立六面体单元的矢量形函数
| $\left\{ {\begin{array}{*{20}{l}} {N_i^{\rm{e}}(\eta , \zeta ) = \frac{{l_i^{\rm{e}}}}{8}\left( {1 + {\eta _j}\eta } \right)\left( {1 + {\zeta _j}\zeta } \right)\nabla \xi }\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {i = 1\sim 4}\\ {N_i^{\rm{e}}(\xi , \zeta ) = \frac{{l_i^{\rm{e}}}}{8}\left( {1 + {\xi _j}\xi } \right)\left( {1 + {\zeta _j}\zeta } \right)\nabla \eta }\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {i = 5\sim 8}\\ {N_i^{\rm{e}}(\xi , \eta ) = \frac{{l_i^{\rm{e}}}}{8}\left( {1 + {\xi _j}\xi } \right)\left( {1 + {\eta _j}\eta } \right)\nabla \zeta }\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {i = 9\sim 12} \end{array}} \right.$ | (11) |
式中:lie表示第i条边的边长;(ξj,ηj,ζj)表示变换坐标系下第j个节点的坐标。
矢量形函数满足插值电场在切向分量上的连续性,因而可有效压制伪解的产生。对六面体单元e,与式(8)对应的形式为
| $\left\{ {\begin{array}{*{20}{l}} {A_{ij}^{\rm{e}} = \int_{ - 1}^1 {\int_{ - 1}^1 {\int_{ - 1}^1 {{\mu ^{ - 1}}} } } \left( {\nabla \times N_i^{\rm{e}}} \right) \cdot \left( {\nabla \times N_j^{\rm{e}}} \right)\det (\mathit{\boldsymbol{J}}){\rm{d}}\xi {\rm{d}}\eta {\rm{d}}\zeta }\\ {M_{ij}^{\rm{e}} = \int_{ - 1}^1 {\int_{ - 1}^1 {\int_{ - 1}^1 {N_i^{\rm{e}}} } } N_j^{\rm{e}}\det (\mathit{\boldsymbol{J}}){\rm{d}}\xi {\rm{d}}\eta {\rm{d}}\zeta } \end{array}} \right.$ | (12) |
式中J为Jacobian矩阵。
将式(9)和式(10)代入式(12)可得
| $\begin{array}{l} {\mathit{\boldsymbol{J}}}(\xi , \eta , \zeta ) = \frac{1}{8}\sum\limits_{j = 1}^8 {\left\{ {{\mathop{\rm diag}\nolimits} \left[ {\begin{array}{*{20}{l}} {{\xi _j}\left( {1 + {\eta _j}\eta } \right)\left( {1 + {\zeta _j}\zeta } \right)}\\ {{\eta _j}\left( {1 + {\xi _j}\xi } \right)\left( {1 + {\zeta _j}\zeta } \right)}\\ {{\zeta _j}\left( {1 + {\xi _j}\xi } \right)\left( {1 + {\eta _j}\eta } \right)} \end{array}} \right] \times } \right.} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left[ {\begin{array}{*{20}{l}} {x_j^{\rm{e}}}&{y_j^{\rm{e}}}&{z_j^{\rm{e}}}\\ {x_j^{\rm{e}}}&{y_j^{\rm{e}}}&{z_j^{\rm{e}}}\\ {x_j^{\rm{e}}}&{y_j^{\rm{e}}}&{z_j^{\rm{e}}} \end{array}} \right]} \right\} \end{array}$ | (13) |
式中diag(·)表示对角线矩阵。
六面体单元的矢量形函数式(11)的旋度为
| $\left\{ \begin{array}{l} \nabla \times N_i^e = \frac{{l_i^{\rm{e}}}}{8}\left( {{\eta _i}\nabla \eta + {\zeta _i}\nabla \zeta + {\eta _i}{\zeta _i}\eta \nabla \zeta + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\left. {{\eta _i}{\zeta _i}\zeta \nabla \eta } \right) \times \nabla \xi \quad\quad i = 1\sim 4\\ \nabla \times N_i^{\rm{e}} = \frac{{l_i^{\rm{e}}}}{8}\left( {{\xi _i}\nabla \xi + {\zeta _i}\nabla \zeta + {\xi _i}{\zeta _i}\xi \nabla \zeta + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\left. {{\xi _i}{\zeta _i}\zeta \nabla \xi } \right) \times \nabla \eta \quad\quad i = 5\sim 8\\ \nabla \times N_i^{\rm{e}} = \frac{{l_i^{\rm{e}}}}{8}\left( {{\xi _i}\nabla \xi + {\eta _i}\nabla \eta + {\xi _i}{\eta _i}\xi \nabla \eta + } \right.\\ \left. {\;\;\;\;\;\;\;\;\;\;\;\;{\xi _i}{\eta _i}\eta \nabla \xi } \right) \times \nabla \zeta \quad \quad i = 9\sim 12 \end{array} \right.$ | (14) |
确定了形函数及形函数的旋度后,式(13)可用三维数值积分的方法(如八点高斯积分)进行求解[20],得到
| $\begin{array}{l} \int_{ - 1}^1 {\int_{ - 1}^1 {\int_{ - 1}^1 f } } (\xi , \eta , \zeta ){\rm{d}}\xi {\rm{d}}\eta {\rm{d}}\zeta = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{k = 1}^2 {\sum\limits_{j = 1}^2 {\sum\limits_{i = 1}^2 {{W_i}} } } {W_j}{W_k}f\left( {{\xi _i}, {\eta _j}, {\zeta _k}} \right) \end{array}$ | (15) |
式中:ξi、ηj和ζk分别为高斯积分点;Wi、Wj和Wk分别为加权系数。
1.3 基于ILU分解的预条件迭代方法ILU分解预条件方法给大型稀疏方程组的求解带来很多新的思路和灵活选择。比如多重网格方法,在规则网格的假设下可进行完美的多级求解[30],但对非规则网格问题往往不能达到理想效果。利用ILU以及改进ILU(MILU)可实现有效的多级求解。对系数矩阵C,定义最简单的ILU分解为
| ${\mathit{\boldsymbol{C}}} = {\mathit{\boldsymbol{LU}}} + {\mathit{\boldsymbol{\delta }}}$ | (16) |
式中:δ表示残差;L和U分别代表下三角和上三角矩阵,且与矩阵C的上三角和下三角部分具有完全相同的稀疏性,即非零元素的结构一致,这种情况被称为ILU0分解。ILU0分解可通过按行进行的高斯消元法实现,并舍弃所有零元素对应位置的元素。基于这样的定义,ILU0分解对矩阵的分解精度不高,在一定程度上甚至会破坏对角线元素的占优性。
本文提出一种Jacobian+ILU0的预条件方法,具体分为两步:首先,将系数矩阵C分成上三角和下三角部分,并把上三角部分赋给U;然后,用ILU0分解计算L,L的对角线元素均为1。
2 数值算例 2.1 正演模拟算法有效性验证 2.1.1 精度验证建立两个MCSEM层状模型,这两个模型的区别在于异常层的厚度和深度不同,通过模拟这两个模型的电磁响应分析本文求解方法的精度。
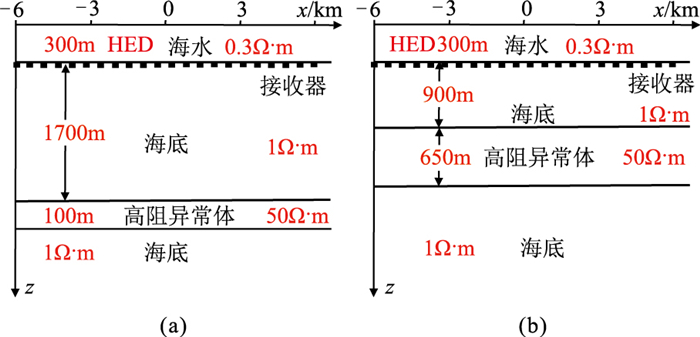
模型(图 3)包括海水层、海底地层、高阻异常层以及基底,两个模型的区别在于高阻异常层的厚度(分别为100、650m)和深度(分别为2000、1200m)。假设水平电偶极子(HED)源沿x方向置于海底以上50m,源中心点的x坐标为0,以100A·m的电偶极矩发射方波电信号。接收器置于海底,测量x方向的电场Ex。下文针对非异常体和异常体区域分别对采用长方体网格和不规则网格情况下的电磁模拟精度进行对比。
|
图 3 高阻层不同厚度和深度的MCSEM模型 (a)厚度100m,深度2000m;(b)厚度650m,深度1200m |
(1) 非异常体区域
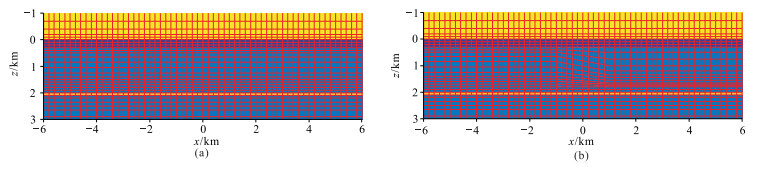
对图 3a模型的z∈[-1km, 1km]分别用长方体和不规则矩形网格进行划分,结果见图 4a和图 4b。设背景电场响应振幅为Eb,解析解为Et,数值解为Es。根据下式计算电场模拟的相对误差
| $\varepsilon = \frac{{\left| {{E^{\rm{t}}} - {E^{\rm{s}}}} \right|}}{{\left| {{E^{\rm{t}}}} \right|}} \times 100\% $ | (17) |
|
图 4 图 3a模型非异常体区域网格划分方案 (a)长方体网格剖分;(b)不规则矩形网格剖分 |
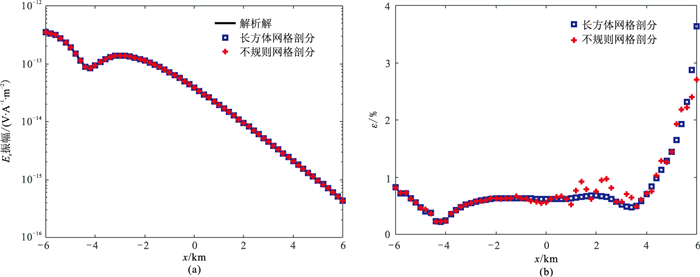
0.25Hz的电场分量Ex模拟结果见图 5。迭代过程中迭代残差范数设定为1×10-6。可以看出,有限元分析结果与半解析解吻合较好,两种网格的模拟结果相对误差均小于4.0%,规则网格剖分和非规则网格剖分的模拟结果最大相对误差分别为3.8%和2.9%。可见,非规则矩形网格划分情况下的模拟精度略高,尤其是在收发距较大的情况下。
|
图 5 图 4两种网格剖分的MCSEM模型电场响应Ex振幅(a)及相对误差(b) z |
(2) 异常体区域
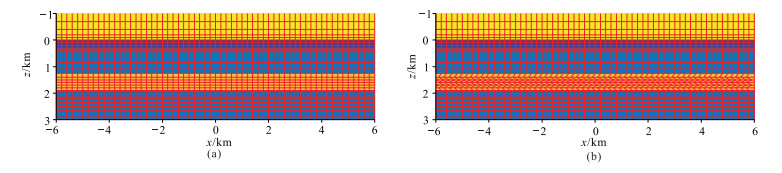
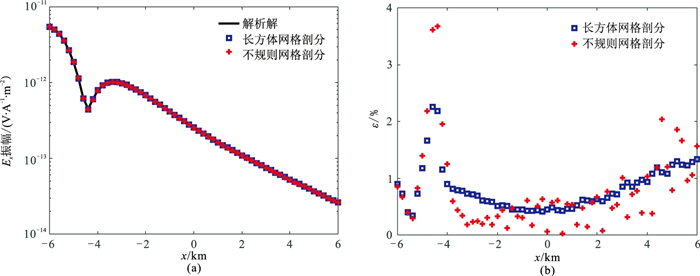
对图 3b模型中的高阻异常层分别进行长方形网格和不规则矩形网格剖分(图 6)。0.25Hz时的Ex振幅模拟结果见图 7。可以看出,使用长方体网格和不规则矩形网格对高阻异常层进行剖分时,对应的模拟最大振幅相对误差分别为3.7%和2.3%,可见整体上非规则矩形网格剖分情况下的模拟误差更小。
|
图 6 图 3b模型中高阻异常层的长方体网格剖分(a)和不规则矩形网格剖分(b) |
|
图 7 图 6两种网格剖分的模型电场响应Ex振幅(a)及相对误差(b) |
利用前文提到的三种预条件方法(Jacobian预条件方法、ILU0预条件方法及ILU0 + Jacobian预条件方法)进行数值算例测试,以评估不同预条件方法的有效性和可行性。
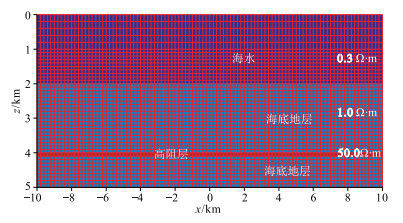
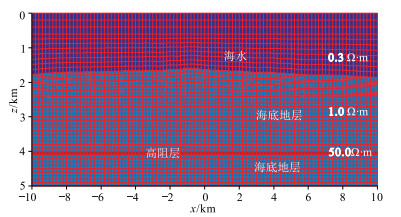
建立两种MCSEM模型进行预条件算法算例测试,即图 8模型(平坦海底地形)和图 9模型(崎岖海底地形)。将HED源中点置于x=-6.0km、z=1.6km处进行激发,并用有限元方法正演计算电磁响应。对这两个模型分别剖分为长方体网格和不规则四边形网格。
|
图 8 平坦海底层状MCSEM模型及网格剖分 |
|
图 9 崎岖海底层状MCSEM模型及网格剖分 |
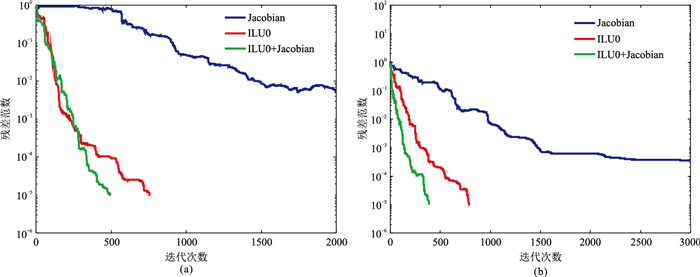
本文采用拟最小残差法(QMR)迭代求解,不同预条件方法下的迭代收敛曲线见图 10。可以看出:采用Jacobian预条件方法的迭代收敛效果最差,平坦海底模型(图 8)经过2000次迭代后的残差范数为5.290×10-3,而崎岖海底地形模型(图 9)经3000次迭代后的残差范数为3.489×10-4;ILU0预条件方法较Jacobian预条件方法的迭代收敛效果略好,图 8模型经758次迭代后的残差范数为9.931×10-6,而图 9模型经796次迭代后的残差范数为9.996×10-6;采用Jacobian+ILU0预条件方法的迭代效果最优,图 8模型经498次迭代后的残差范数为9.884×10-6,图 9模型经388次迭代后的残差范数为9.761×10-6。
与其他两种预条件方法相比,本文提出的Jacobian+ILU0预条件方法对图 8和图 9模型所需迭代次数更少,收敛更平滑,尤其对崎岖海底地形模型的迭代表现出了较强的适用性。因此,Jacobian+ILU0预条件方法在MCSEM模型有限元正演模拟中表现出了较好的收敛性能,即便对崎岖海底地形模型也表现出较好的模拟收敛效果。
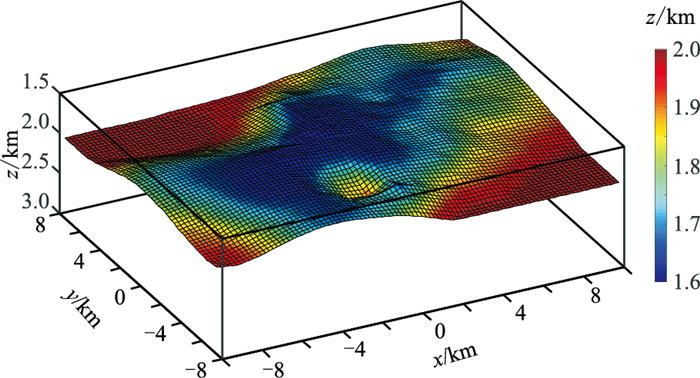
2.2 MCSEM深水模型仿真模拟受浅水域空气波的影响,深水模型的异常体较浅水模型的异常体响应更明显[32],但前提是海底地形是平坦的。当海底地形崎岖时,深水模型异常体的响应特征有待研究,为此,建立深水崎岖海底模型进行仿真模拟。基于公开的中国南海某海域海底地形数据(图 11),建立不同的三维储层模型,进行MCSEM有限元仿真模拟。
|
图 11 中国南海某海域三维海底地形 |
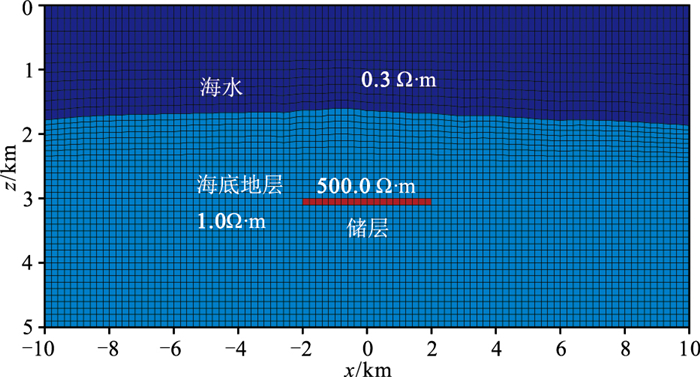
图 12所示三维储层模型包含海底地形信息,油气储层为4km(x)×4km(y)×100m(z)的长方体,油藏顶面位于海平面以下3km处。HED源(Tx)沿x方向在-10~10km范围内拖曳前行,距离海底的高度始终保持为50m。接收器(Rx)放置于海底,沿x方向均匀布设,测量-10~10km范围内的水平电场Ex,源Tx与测线位于同一xOz平面[33]。
|
图 12 考虑海底地形的三维MCSEM储层模型及网格剖分 |
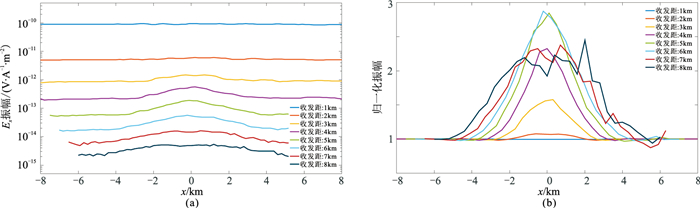
图 13a为水平电场Ex振幅随Tx-Rx偏移距(这里指Tx中点在海底的投影点与Rx的x坐标之差,后文简称收发距)的变化曲线,参考背景幅度为直线。可以看出,在收发距较小(1~3km)的情况下,异常体的电场分量Ex振幅较大,即异常体所在的平面位置附近Ex振幅出现正异常,但异常幅值总体不大,局部被地形影响抵消。可见收发距在3km以内时,地形对水平电场的影响较为明显,即使在储层埋藏较浅的情形下也难以明确判断储层范围。随着收发距的增加(4~6km),异常体响应逐渐变得明显,由于地形对电场振幅的影响较小,曲线较为光滑。因此,对于该模型,在地形变化不太剧烈情况下进行储层识别的适宜收发距是4~6km。当收发距进一步增大(7~8km)时,异常体响应减弱,曲线剧烈震荡,这是地形与异常体共同作用的结果,在这个收发距范围内,仅通过Ex振幅曲线已经无法有效识别储层。
|
图 13 图 12模型模拟Ex振幅(a)及归一化振幅(b)曲线 |
以1500m水深的均匀海底地层模型(含海底地形)的电场响应作为背景场,计算Ex振幅与背景场的比值,得到归一化曲线(图 13b)。可见归一化曲线与图 13a振幅曲线的变化趋势一致,但根据归一化曲线可较直观地判断储层的平面分布范围。整体而言,收发距较小时的Ex振幅归一化曲线,尤其是2km时,曲线异常范围与高阻油藏的水平范围基本吻合。随着收发距逐步增大,归一化振幅随之增大,归一化曲线异常边界逐渐模糊。当收发距大于6km时,归一化振幅开始变小,同时地形的影响开始增大,油藏的响应逐渐被淹没。
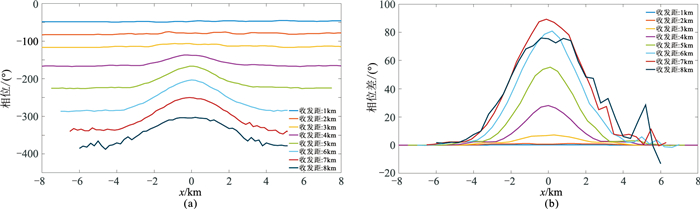
与图 13对应的Ex相位及相位差见图 14。由图可见,相位曲线(图 14a)与振幅曲线(图 13a)特征基本一致。需指出的是,相位对地形起伏不敏感,尤其是在储层响应最明显的4~6km收发距范围内,相位曲线非常平滑。当收发距增大到7~8km时,在相位曲线上可以同时观察到明显的储层(低频信号)和地形(高频信号)响应叠加在一起形成的锯齿状响应。与归一化Ex振幅(图 13b)相比,相位差曲线(图 14b)上出现相同特征所对应的收发距大于1km,且曲线更平滑。
|
图 14 图 12模型模拟Ex相位(a)及相位差(b) |
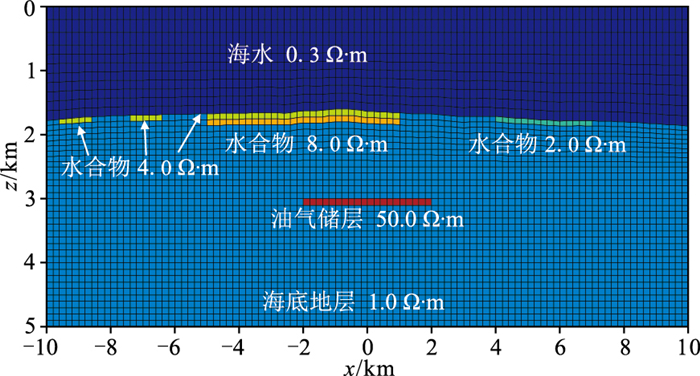
中国南海海域具有丰富的可燃冰资源。可燃冰形成于低温高压环境,因此通常分布于近海底区域,在可燃冰稳定区域之下常常会有高饱和的伴生天然气,造成近海底地层电阻率明显增大。可燃冰在海底一般是非均匀分布的。基于图 12所示模型,在海底增加四个不连续分布的可燃冰矿体,矿体沿y方向的延伸范围与储层范围一致(4km),建立考虑地形和近海底可燃冰分布的油气储层模型(图 15),网格剖分方案同图 12。
|
图 15 考虑海底地形和近海底可燃冰分布的三维油气储层模型及网格剖分 |
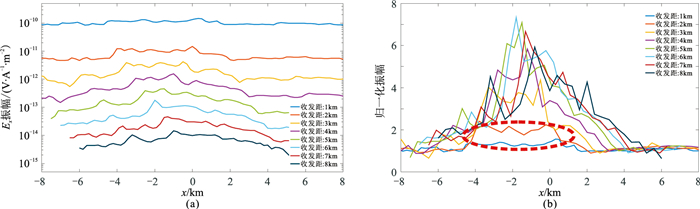
应用本文正演方法得到不同收发距下纵测线水平电场Ex振幅及归一化振幅曲线(图 16)。与仅考虑海底地形的情况(图 12)相比,含可燃冰矿体模型的归一化振幅的最大值增大约2倍,曲线扭曲严重,仅收发距较小时所对应的归一化振幅曲线可较清楚地分辨可燃冰矿体的分布范围(图 16b中虚线椭圆所示),但储层分布范围难以判断。据图 16还可以看出,含海底地形和可燃冰矿体的油藏模型电场响应非常复杂,可燃冰矿体的电场响应与海底地形耦合所产生的响应叠合在一起,使储层响应难以识别。可燃冰矿体分布的非均质性越强,响应越复杂。特别地,当可燃冰矿体与油气储层的水平分布范围大致相同时,二者的响应会叠加在一起,对目标储层的识别则愈加困难。进一步地,若目标储层水平分布范围较小,要对其进行识别就更难以实现。
|
图 16 图 15模型模拟Ex振幅(a)及归一化振幅(b)曲线 |
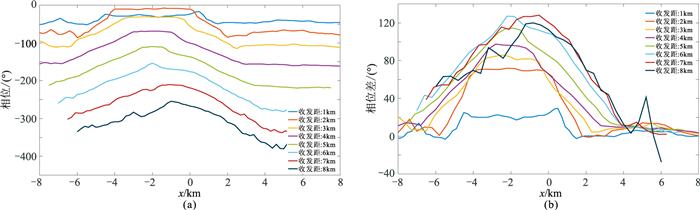
图 17所示为电场分量Ex相位及相位差曲线。从图 17a所示相位曲线可以看出,可燃冰矿体引起的异常范围随着收发距的增大逐渐减小,当收发距达到6km时已无法观察到可燃冰矿体引起的明显扰动。收发距逐渐增大,可燃冰矿体的电磁响应与储层响应逐步发生叠合,因此异常极大值点明显渐渐向右偏移。从图 17b所示相位差曲线可以看出,收发距为1km时,可清楚识别可燃冰矿体的分布范围,但可燃冰矿体和储层响应难以区分;收发距增加到2km时,较1km收发距时相位差增大,但可燃冰矿体和储层响应仍难以区分;当收发距逐渐增大至6km时,可燃冰矿体的响应逐步减弱,相位差曲线的中心点逐渐向储层中心移动,可较准确地判断储层的平面位置,这与图 16b揭示的特征一致。因此,若存在可燃冰矿体时,在保证信噪比的前提下,为更好地识别油气藏,应尽量采用较大的收发距。
|
图 17 图 15模型模拟Ex相位(a)及相位差(b) |
利用电磁数据可较准确地解释电性异常体的横向(平面)分布范围,其缺点是纵向分辨率较低,难以精确重建地层模型,而地震勘探的优点在于纵向分辨率高,与电磁方法形成互补关系。因而,开展高精度电磁勘探时,结合地震解释成果对电性层位进行深度标定,是提高电磁勘探效果的重要手段。利用地震资料的处理和解释成果能较精确地确定海底标志层,结合电磁法对电性异常体的平面分布解释成果,可建立区域地球物理框架,建立相应的地电模型,为高精度电磁勘探提供基础数据。
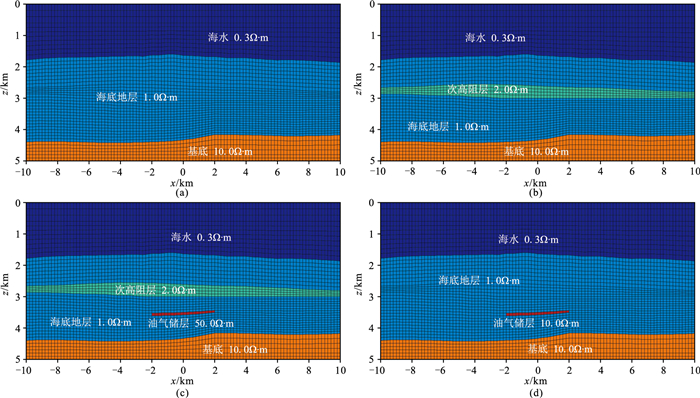
根据中国海南某海域地震解释成果和电磁资料,建立一个三层的地球物理框架,框架包括海底地形及海底地层。基于此框架,分别建立四个模型M0、M1、M2和M3(图 18):M0只考虑海底地形和基底;M1考虑海底地形、次高阻层和基底;M2综合考虑海底地形、次高阻层、基底及高阻油气储层;M3考虑海底地形、基底和高阻油气储层。
|
图 18 基于海南某海域地球物理框架建立的电阻率模型 (a)模型M0; (b)模型M1; (c)模型M2; (d)模型M3 |
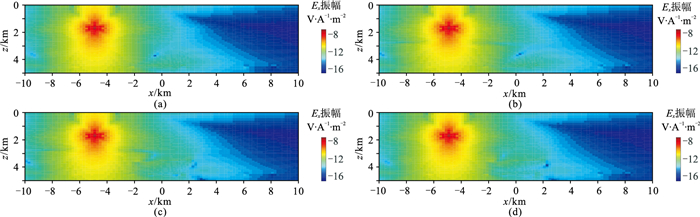
采用2.2.1节的激发、接收参数,这里仅分析源位于-5km时的情形。图 19是这四个模型的模拟Ex振幅剖面,频率为0.25Hz。从图 19b和图 19c可以看出,虽然模型中存在厚度较大的次高阻层,但由于与背景电阻率差异(2倍)较小,Ex振幅曲线并无明显异常。从图 19d可以看出,虽然模型M3中油气储层的厚度和分布范围都比模型M1和M2中的次高阻体小得多,但却引起了较明显的电场变化,这是由于储层与围岩的电阻率差较大(50倍)。
|
图 19 CSEM模型模拟Ex振幅剖面 (a)模型M0; (b)模型M1; (c)模型M2; (d)模型M3 |
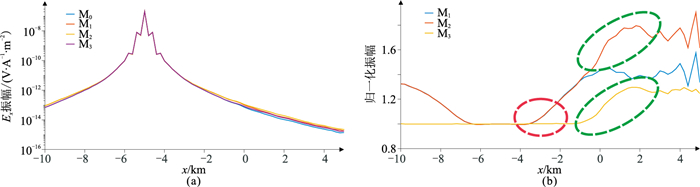
以模型M0的模拟数据为背景场,对模型M1、M2、M3的Ex振幅(图 20a)进行归一化,结果见图 20b。从图 20b所示归一化曲线上可以看出,收发距为2km曲线上次高阻体的特征比较明显(图 20b中红色虚线框所示),而油气储层的响应(图 20b中的绿色虚线框所示)则在收发距大于5km才可看出明显异常。这说明不同埋藏深度的电阻率异常体所对应的电磁响应会体现在不同收发距的电场数据中。同时还可以看出,在收发距大于9km(即对应坐标4km位置)时,油气储层的响应依然很明显,但振幅较小,这样的有用信号在实际勘探中容易被噪声淹没。
|
图 20 模型M0、M1、M2和M3的模拟Ex振幅(a)及归一化振幅(b)曲线 |
图 21是模型M0、M1、M2和M3正演电场分量Ex的相位及相位差曲线,其中背景响应采用模型M0的相位数据。
|
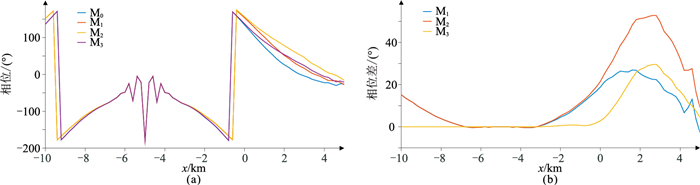
图 21 模型M0、M1、M2和M3模拟Ex相位(a)及相位差(b)曲线 |
由图 21可见,相位参数可更直观地显示不同模型电场响应的差异。根据图 21a,四条曲线整体上可分成两簇,一簇是模型M0和模型M3响应曲线,另一簇是模型M1和模型M2响应曲线。这两簇曲线在收发距为-2.5km处出现分歧,这与浅部次高阻层的位置有关;随着收发距逐渐增至约5km时,两簇曲线中的两支曲线均发生分离,相位差逐渐增大,这与油气储层的平面分布范围有关;随着收发距进一步增大,四条曲线最终在收发距为10km处趋于一致,表明此处已无法观测到浅部次高阻体或深部高阻油藏引起的电磁异常。图 21b相位差曲线也显示出与图 21a类似的特征,其中模型M2和M3中油藏产生的相位差分别约为60°和30°,而浅部异常体产生的相位差则很小。
3 结论基于预条件迭代求解的频率域矢量有限元模拟,本文实现了结构化任意六面体单元的三维海洋可控源电磁响应模拟,通过与层状模型的解析解对比验证了算法的正确性和有效性。本文提出了简化的ILU0预条件方法,有效提高了迭代求解的效率,收敛曲线更平滑,在崎岖海底地形模型的模拟中表现出较好的适应性。
基于中国南海某海域真实深水(1600~2000m)地形数据,分别建立了常规油气储层模型、考虑可燃冰分布的油气储层模型及考虑基底起伏的复杂地质模型。通过对这些模型的模拟及分析得出以下认识。
(1) 在近收发距区域,海底地形对水平电场的影响较明显,即使在储层埋藏较浅的情形下也难以分辨其水平分布范围;随着收发距的增加,储层响应逐渐增大,同时海底地形对电场振幅的影响变小,在地形起伏不太剧烈的情况下可识别储层的平面分布范围;当收发距进一步增大,异常体响应随之减弱,海底地形与油藏响应共同作用,造成电场曲线剧烈震荡,无法对高阻油藏进行有效识别。
(2) 若可燃冰矿体埋藏浅,其电场响应明显,但会与海底地形耦合,因而只在近收发距区域能比较清楚地识别可燃冰矿体的分布范围。特别地,可燃冰矿体与油气储层的水平分布范围接近,二者的响应会产生重叠和耦合,则需基于更大收发距的电场数据才能识别出深部高阻油藏。
(3) 埋深不同的电阻率异常体,其响应特征会体现在不同收发距范围的电场数据中。收发距稍大(这是一个相对数值,不同条件对应的适宜收发距会有所不同)条件下的电场数据中,深水油气储层的响应依然明显,而海底地形的影响则可忽略。
| [1] |
柳建新, 郭天宇, 王博琛, 等. 油气勘探中海洋电磁技术的研究进展[J]. 石油物探, 2021, 60(4): 527-538. LIU Jianxin, GUO Tianyu, WANG Bochen, et al. Review of marine electromagnetic methods for hydrocarbon exploration[J]. Geophysical Prospecting for Petroleum, 2021, 60(4): 527-538. DOI:10.3969/j.issn.1000-1441.2021.04.001 |
| [2] |
刘勇, 李文彬, 邓方顺, 等. 海洋可控源电磁法深海油藏开采监测仿真[J]. 石油地球物理勘探, 2022, 57(1): 237-244. LIU Yong, LI Wenbin, DENG Fangshun, et al. Simulation of deep-sea reservoir development monitoring using marine controlled-source electromagnetic me-thod[J]. Oil Geophysical Prospecting, 2022, 57(1): 237-244. |
| [3] |
ANDRÉIS D, MACGREGOR L. Controlled-source electromagnetic sounding in shallow water: principles and applications[J]. Geophysics, 2008, 73(1): F21-F32. |
| [4] |
CONSTABLE S, SRNKA L J. An introduction to marine controlled-source electromagnetic methods for hydrocarbon exploration[J]. Geophysics, 2007, 72(2): WA3-WA12. DOI:10.1190/1.2432483 |
| [5] |
SRNKA L J, CARAZZONE J J, EPHRON M S, et al. Remote reservoir resistivity mapping[J]. The Leading Edge, 2006, 25(8): 972-975. DOI:10.1190/1.2335169 |
| [6] |
UM E S, HARRIS J M, ALUMBAUGH D L. An ite-rative finite element time-domain method for simulating three-dimensional electromagnetic diffusion in earth[J]. Geophysical Journal International, 2012, 190(2): 871-886. DOI:10.1111/j.1365-246X.2012.05540.x |
| [7] |
ZHDANOV M S. Electromagnetic geophysics: notes from the past and the road ahead[J]. Geophysics, 2010, 75(5): 75A49-75A66. DOI:10.1190/1.3483901 |
| [8] |
裴发根, 方慧, 裴亮, 等. 天然气水合物电磁勘探研究进展[J]. 地球物理学进展, 2020, 35(2): 775-785. PEI Fagen, FANG Hui, PEI Liang, et al. Advances in electromagnetic exploration research of gas hydrate[J]. Progress in Geophysics, 2020, 35(2): 775-785. |
| [9] |
景建恩, 伍忠良, 邓明, 等. 南海天然气水合物远景区海洋可控源电磁探测试验[J]. 地球物理学报, 2016, 59(7): 2564-2572. JING Jian'en, WU Zhongliang, DENG Ming, et al. Experiment of marine controlled-source electromagnetic detection in a gas hydrate prospective region of the South China Sea[J]. Chinese Journal of Geophy-sics, 2016, 59(7): 2564-2572. |
| [10] |
DA SILVA N V, MORGAN J V, MACGREGOR L, et al. A finite element multifrontal method for 3D CSEM modeling in the frequency domain[J]. Geophysics, 2012, 77(2): E101-E115. DOI:10.1190/geo2010-0398.1 |
| [11] |
杨军, 刘颖, 吴小平. 海洋可控源电磁三维非结构矢量有限元数值模拟[J]. 地球物理学报, 2015, 58(8): 2827-2838. YANG Jun, LIU Ying, WU Xiaoping. 3D simulation of Marine CSEM using vector finite element method on unstructured grids[J]. Chinese Journal of Geophysics, 2015, 58(8): 2827-2838. |
| [12] |
殷长春, 贲放, 刘云鹤, 等. 三维任意各向异性介质中海洋可控源电磁法正演研究[J]. 地球物理学报, 2014, 57(12): 4110-4122. YIN Changchun, BEN Fang, LIU Yunhe, et al. MCSEM 3D modeling for arbitrarily anisotropic media[J]. Chinese Journal of Geophysics, 2014, 57(12): 4110-4122. DOI:10.6038/cjg20141222 |
| [13] |
周峰, 张志勇, 陈煌, 等. 基于非结构网格的三种CSEM有限元三维正演系统分析[J]. 石油地球物理勘探, 2021, 56(5): 1190-1202. ZHOU Feng, ZHANG Zhiyong, CHEN Huang, et al. Analysis of 3D finite-element forward modeling of CSEM data using three different formulas and unstructured grids[J]. Oil Geophysical Prospecting, 2021, 56(5): 1190-1202. |
| [14] |
KOLDAN J, PUZYREV V, DE LA PUENTE J, et al. Algebraic multigrid preconditioning within parallel finite-element solvers for 3-D electromagnetic modelling problems in geophysics[J]. Geophysical Journal International, 2014, 197(3): 1442-1458. DOI:10.1093/gji/ggu086 |
| [15] |
LELIÈVRE P G, FARQUHARSON C G. Gradient and smoothness regularization operators for geophysical inversion on unstructured meshes[J]. Geophysical Journal International, 2013, 195(1): 330-341. DOI:10.1093/gji/ggt255 |
| [16] |
MITSUHATA Y, UCHIDA T. 3D magnetotelluric modeling using the T-Ω finite element method[J]. Geophysics, 2004, 69(1): 108-119. DOI:10.1190/1.1649380 |
| [17] |
SCHWARZBACH C, BÖRNER R U, SPITZER K. Three-dimensional adaptive higher order finite element simulation for geo-electromagnetics: a marine CSEM example[J]. Geophysical Journal International, 2011, 187(1): 63-74. DOI:10.1111/j.1365-246X.2011.05127.x |
| [18] |
SCHWARZBACH C, HABER E. Finite element based inversion for time-harmonic electromagnetic problems[J]. Geophysical Journal International, 2013, 193(2): 615-634. DOI:10.1093/gji/ggt006 |
| [19] |
NAM M J, KIM H J, SONG Y, et al. Three-dimensional topographic and bathymetric effects on magnetotelluric responses in Jeju Island, Korea[J]. Geophysical Journal International, 2009, 176(2): 457-466. DOI:10.1111/j.1365-246X.2008.03993.x |
| [20] |
CAI H Z, XIONG B, HAN M R, et al. 3D controlled-source electromagnetic modeling in anisotropic medium using edge-based finite element method[J]. Computers & Geosciences, 2014, 73: 164-176. |
| [21] |
BADEA E A, EVERETT M E, NEWMAN G A, et al. Finite-element analysis of controlled-source electromagnetic induction using Coulomb-gauged potentials[J]. Geophysics, 2001, 66(3): 786-799. |
| [22] |
KEY K, WEISS C. Adaptive finite-element modeling using unstructured grids: the 2D magnetotelluric example[J]. Geophysics, 2006, 71(6): G291-G299. DOI:10.1190/1.2348091 |
| [23] |
LI Y G, KEY K. 2D marine controlled-source electromagnetic modeling: part 1-an adaptive finite-element algorithm[J]. Geophysics, 2007, 72(2): WA51-WA62. DOI:10.1190/1.2432262 |
| [24] |
MUKHERJEE S, EVERETT M E. 3D controlled-source electromagnetic edge-based finite element mo-deling of conductive and permeable heterogeneities[J]. Geophysics, 2011, 76(4): F215-F226. DOI:10.1190/1.3571045 |
| [25] |
NAM M J, KIM H J, SONG Y, et al. 3D magnetotelluric modelling including surface topography[J]. Geo-physical Prospecting, 2007, 55(2): 277-287. DOI:10.1111/j.1365-2478.2007.00614.x |
| [26] |
KORDY M, WANNAMAKER P, MARIS V, et al. 3D magnetotelluric inversion including topography using deformed hexahedral edge finite elements and direct solvers parallelized on SMP computers-part Ⅰ: forward problem and parameter Jacobians[J]. Geophysical Journal International, 2015, 204(1): 74-93. |
| [27] |
GU X M, HUANG T Z, LI L, et al. Quasi-minimal residual variants of the COCG and COCR methods for complex symmetric linear systems in electromagnetic simulations[J]. IEEE Transactions on Microwave Theory and Techniques, 2014, 62(12): 2859-2867. DOI:10.1109/TMTT.2014.2365472 |
| [28] |
LI L, HUANG T Z, JING Y F, et al. Application of the incomplete Cholesky factorization preconditioned Krylov subspace method to the vector finite element method for 3-D electromagnetic scattering problems[J]. Computer Physics Communications, 2010, 181(2): 271-276. DOI:10.1016/j.cpc.2009.09.019 |
| [29] |
UM E S, COMMER M, NEWMAN G A. Efficient pre-conditioned iterative solution strategies for the electromagnetic diffusion in the Earth: finite-element frequency-domain approach[J]. Geophysical Journal International, 2013, 193(3): 1460-1473. DOI:10.1093/gji/ggt071 |
| [30] |
BÖRNER R U. Numerical modelling in geo-electromagnetics: advances and challenges[J]. Surveys in Geophysics, 2010, 31(2): 225-245. DOI:10.1007/s10712-009-9087-x |
| [31] |
尚晓荣, 岳明鑫, 杨晓冬, 等. 起伏地形对三维可控源电磁响应的影响研究[J]. 石油地球物理勘探, 2022, 57(1): 222-236. SHANG Xiaorong, YUE Mingxin, YANG Xiaodong, et al. Influence of undulating terrain on three-dimensional controlled-source electromagnetic response[J]. Oil Geophysical Prospecting, 2022, 57(1): 222-236. |
| [32] |
沈金松, 陈小宏. 海洋油气勘探中可控源电磁探测法(CSEM)的发展与启示[J]. 石油地球物理勘探, 2009, 44(1): 119-127. SHEN Jinsong, CHEN Xiaohong. Development and enlightenment of controlled-source electromagnetic (CSEM) surveying method in marine oil/gas exploration[J]. Oil Geophysical Prospecting, 2009, 44(1): 119-127. DOI:10.3321/j.issn:1000-7210.2009.01.023 |
| [33] |
任文静, 何展翔, 孙卫斌, 等. 海底节点式时频双域电磁采集系统及试验[J]. 石油地球物理勘探, 2021, 56(2): 398-406. REN Wenjing, HE Zhanxiang, SUN Weibin, et al. Benthic nodal time-frequency dual-domain electromagnetic acquisition system and test[J]. Oil Geophysical Prospecting, 2021, 56(2): 398-406. |



 马超,广东省广州市南沙区南沙街海滨路1133号广州海洋地质调查局,511458。Email:
马超,广东省广州市南沙区南沙街海滨路1133号广州海洋地质调查局,511458。Email: