塔里木盆地广泛发育碳酸盐岩储层,其中缝洞体是油气勘探、开发的重要目标之一,通常是由相互连通的洞穴、次生溶蚀孔洞和裂缝组成的油气储集体。由于溶蚀作用的非均一性,碳酸盐岩缝洞体的发育规模、空间形态以及油气富集程度差异非常大,再加上复杂的地表条件、埋深极大等因素,给油气勘探和开发带来很大困难。因此,准确地刻画碳酸盐岩缝洞体边界是碳酸盐岩缝洞型储层量化雕刻的重要工作之一。
近年来,许多地震属性刻画方法在碳酸盐岩储层预测中均取得不错的效果,包括相干、曲率、蚂蚁体、振幅变化率等,而目前较理想的刻画碳酸盐岩缝洞体边界的方法则是由图像处理领域引入地震解释领域的GST属性技术。
在图像处理领域,描述数字图像结构的局部方向特征时首次提出GST的概念[1-2]并逐步成为研究热点,其应用包括不同目标纹理单元的检测、自适应的多维度滤波等[3-4]。Randen等[5-6]利用三维地震数据的GST提取地震数据的不连续性描述断层发育特征。Bakker[7]将GST系统地引入地震解释领域,广泛用于提取地震数据结构以及地层特征,在断层自动识别、河道刻画等方面获得良好效果。Luo等[8]将GST矩阵构造过程的三维高斯低通滤波函数转化为由复地震道瞬时能量作为加权值的数据自适应低通滤波方法,有效提高了倾角和方位角估算结果的空间一致性。随着GST技术的深入研究与应用,大量关于优化GST的相干体技术在地震解释领域获得了良好效果[9-10]。陈强等[11]利用GST矩阵特征值计算Chaos和边缘属性,精细描述与解释了不同类型的采空区。问雪等[12]利用地震图像的GST特征设计结构导向平滑滤波器,在压制噪声的同时有效保留了断层的不连续信息,为断层识别提供了高质量地震资料。王清振等[13]基于GST的不连续性检测技术识别盐丘边界与断层,与常规地震属性方法相比,在岩盐广泛发育地区能更好地甄别由高陡地层引起的不连续假象。彭达等[14]根据GST求取倾角信息,再通过构建梯度相关矩阵计算局部地震数据的梯度能量熵值,可以刻画三维地震数据的不连续空间结构特征,从而增强不连续边界的清晰度、提高断层边界的连续性。崔正伟等[15]结合构造导向滤波与GST相干算法,精细识别了储层裂缝。王震等[16]利用GST的第二特征值刻画断溶体边界。
中国业界利用GST刻画碳酸盐岩缝洞体边界的应用相对较少。为此,基于前人的GST技术方法,本文针对GST属性的详细计算方法及其几何意义,分析各计算环节对计算结果的影响,以期为碳酸盐岩缝洞型储层量化雕刻提供参考。
1 技术原理分析传统的图像处理中滤波与边缘检测主要针对相对简单的邻域范围,即被不连续区域分开的均质区域通常仅呈现图像数值的高、低差异。然而,除了图像数值的高、低差异之外,某个局部邻域范围内依然可能会包含一种模式或类型,如果这种模式具备某种有规律的结构特征,则称之为纹理。如果用参数描述这些纹理特征则需要进一步明确与简化,而纹理可以由线性结构组成。N维空间的线性结构定义为至少在一个方向是位移不变的,但并不包括所有方向是位移不变的。由此可见,地震数据的层状沉积结构特征满足线性结构定义,因此可以利用GST分析地震数据的结构特征,并由参数化提取用于地震解释。
地震解释领域中结构张量矩阵通常由地震数据的梯度构建,为了明确计算过程细节以增强该项技术方法的可复制性,本文将详细分析与探讨各关键计算步骤。
以三维地震数据GST属性计算为例,共分三个步骤:①求取地震数据的梯度;②构建结构张量矩阵,并对张量矩阵的元素分别平滑或积分;③特征值分解并进行排序。
通过对三维地震数据分别在垂直、Inline与Crossline三个方向求取一阶偏导数g1、g2、g3,便可得到原始三维地震数据对应的每个数据样点位置的梯度矢量
| $ \boldsymbol{g}=\left(g_{1}, g_{2}, g_{3}\right)^{\mathrm{T}} $ | (1) |
g不能直接构建张量矩阵求解特征值,因为直接构建的张量矩阵
| $ \boldsymbol{T}_{\mathrm{grad}}=\boldsymbol{g} \boldsymbol{g}^{\mathrm{T}}=\left(\begin{array}{lll} g_{1} g_{1} & g_{1} g_{2} & g_{1} g_{3} \\ g_{1} g_{2} & g_{2} g_{2} & g_{2} g_{3} \\ g_{1} g_{3} & g_{2} g_{3} & g_{3} g_{3} \end{array}\right) $ | (2) |
的秩不大于1,即使对g1、g2、g3分别进行平滑再构建张量矩阵也是如此。
当Tgrad的元素均不为零时,Tgrad的三个特征值λ1、λ2、λ3中只有一个不为零(如λ1≠0,λ2=λ3=0),则
| $ \lambda_{1}=\|\boldsymbol{g}\|^{2}=g_{1}^{2}+g_{2}^{2}+g_{3}^{2} $ | (3) |
本文称λ1为梯度的能量。
构建结构张量矩阵包含两个关键步骤:首先利用梯度与其转置相乘形成3阶方阵(也称为并矢积);其次对方阵中每一个元素分别平滑(或称局部平均),得到一定尺度范围内平均的结构张量矩阵[17]
| $ \boldsymbol{T}=\left\langle\boldsymbol{g g}^{\mathrm{T}}\right\rangle=\left(\begin{array}{lll} \left\langle g_{1} g_{1}\right\rangle & \left\langle g_{1} g_{2}\right\rangle & \left\langle g_{1} g_{3}\right\rangle \\ \left\langle g_{1} g_{2}\right\rangle & \left\langle g_{2} g_{2}\right\rangle & \left\langle g_{2} g_{3}\right\rangle \\ \left\langle g_{1} g_{3}\right\rangle & \left\langle g_{2} g_{3}\right\rangle & \left\langle g_{3} g_{3}\right\rangle \end{array}\right) $ | (4) |
式中〈·〉表示对角括符内的对象平滑,通常采用高斯滤波的方式。由张量矩阵的对称性可知,只需进行6个元素的平滑即可完成对9个元素的平滑。如果对g1、g2、g3也进行平滑,则总共需要9个三维数据体的平滑计算。对梯度元素的平滑计算可以压制由地震噪声引起的局部梯度异常,从而增强后续计算的鲁棒性;对张量元素的平滑计算使张量矩阵不仅包含最大梯度能量方向的特征,并且还包含所有正交方向的变化特征。
高斯滤波器在低通滤波或者平均计算等方面优点很多且应用广泛,高斯核函数卷积平滑计算的本质为局部尺度范围内的加权平均,通常一维高斯函数定义为
| $ G(t, \sigma)=\frac{1}{\sqrt{2 \pi} \sigma} \mathrm{e}^{-t^{2} /\left(2 \sigma^{2}\right)} $ | (5) |
式中:σ为标准差,用于表征高斯函数的半宽度;t为采样点数。
图 1为σ=1的高斯函数。可见,距离中心样点越远则权重值越小,当|t|>4时权重值趋近于零。确定一个非负σ值时,滤波器的有效长度可近似截断为-4σ≤t≤4σ。当滤波器有效长度较小(σ < 3)时,宜直接进行卷积计算;当滤波器的有效长度较大时,可采用递归高斯滤波有效提高运算效率[18]。文中的高斯滤波方式均采用有效长度内的离散样点进行卷积计算,即当给定σ为某一正整数时,取有效离散采样点数为8σ+1。对于三维地震数据而言,卷积的方式分为两种,第一种是利用三维高斯核函数直接计算一个三维空间卷积核,另一种则是沿垂直、Inline与Crossline三个方向分别进行一维高斯滤波器的卷积,两种方式均可实现同样的目标。

|
图 1 σ=1的高斯函数 |
由于构建的张量矩阵是实对称矩阵,属于半正定二次型,因此具有三个非负特征值,且对应的三个特征向量两两正交。对每个数据样点处的结构张量矩阵特征分解能够得到表征图像结构的各向异性参数与方向特征[19]。对于任意三维数据的结构张量矩阵而言,其特征分解均可表示为[20]
| $ \boldsymbol{T}=\lambda_{1} \boldsymbol{u} \boldsymbol{u}^{\mathrm{T}}+\lambda_{2} \boldsymbol{w} \boldsymbol{v}^{\mathrm{T}}+\lambda_{3} \boldsymbol{w} \boldsymbol{w}^{\mathrm{T}} $ | (6) |
式中:λ1≥λ2≥λ3≥0按大小顺序命名为第一、第二和第三特征值;u、v和w分别为λ1、λ2和λ3对应的单位特征向量,称为第一、第二和第三特征向量。对常规三维地震数据而言,通常u的方向垂直于反射同相轴的局部平面,v、w位于反射同相轴的局部平面内,并且v、w表征横向不连续变化方向,如由断层或者河道反射特征引起的地震数据变化。由于λ1、λ2和λ3分别反映对应方向的变化特征,因此通过优选三个特征值及其不同组合计算地震数据纹理类属性,便可解释目标地质体。在以河道及断层为研究目标时,u垂直于沿反射同相轴解释的空间曲面,v在局部范围内垂直于河道和断层走向,而w则呈局部平行的规律。对于碳酸盐岩缝洞体而言,河道及断层响应均属于不连续异常反射,而缝洞体引起的强反射异常区域在三维地震数据体中呈复杂三维空间立体结构的不连续变化,在局部三维空间尺度内沿各个方向均有振幅变化,因此λ1反映主要的层状反射特征,λ2和λ3刻画了缝洞体反射异常区域,类似于沿不同的视角对一个三维立体结构成像。由于特征值无量纲,因此在刻画目标缝洞体时阈值选取便成为一个不可避免的问题。
2 实际应用测试 2.1 二维GST属性分析为了验证不同平滑方案的影响,选取塔里木油田塔北A区典型地震剖面(图 2)计算二维GST属性,以识别碳酸盐岩缝洞体异常区域及其外部轮廓。

|
图 2 塔北A区典型地震剖面 5050ms位置处的解释层位为奥陶系碳酸盐岩吐木休克组底界(TO3t),目的层范围内明显可见由缝洞体引起的反射振幅异常区域 |
根据GST属性计算方法可知,在二维情况能求解两个特征值,针对该地震剖面进行以下测试:①不做任何平滑,直接利用梯度构建结构张量矩阵进行特征值分解;②对梯度元素平滑;③对张量元素平滑;④对梯度元素及张量元素均平滑。平滑计算会对分解结果的值域产生一定影响,故采用归一化策略将最终结果的值域调整为0~100再进行对比、分析,实际计算结果均表现为高值分布较少(90%以上均小于20),故色标显示范围调整为0~20。
图 3为不做任何平滑及对梯度元素平滑求解的λ1。可见,λ2=0,λ1反映了地震数据梯度的能量,仅对梯度元素平滑表现出低通滤波效果(图 3b),λ1并不能刻画碳酸盐岩缝洞体边界。

|
图 3 不做任何平滑(a)及对梯度元素平滑(b)求解的λ1 垂直方向与水平方向的平滑参数一致(σ=3) |
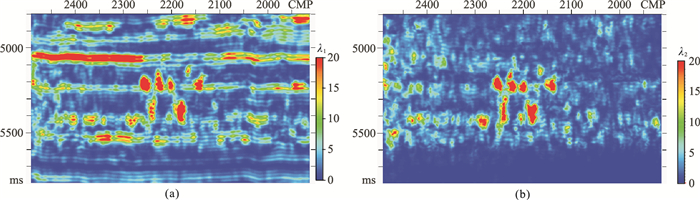
图 4为对张量元素平滑求解的λ1及λ2。可见:λ1主要反映了地震数据层状反射的主要结构特征,由于缝洞体区域的地震剖面依然具有垂直方向的反射振幅变化,因此在层状结构特征的背景上还存在缝洞体反射特征(图 4a);λ2与碳酸盐岩缝洞体反射异常区域一致性较高,且不受层状结构特征影响,将显示色标选取确定的阈值进行低值截取,可自动刻画碳酸盐岩缝洞体边界(图 4b)。
|
图 4 对张量元素平滑求解的λ1 (a)及λ2 (b) 垂直方向与水平方向的平滑参数一致(σ=3) |
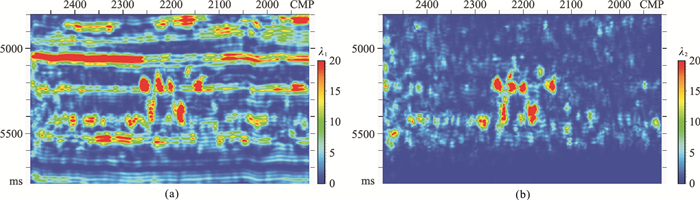
图 5为对梯度元素及张量元素均平滑求解的λ1及λ2。可见,整体特征与图 4基本一致,局部细节部分有细微差异,但对缝洞体边界刻画影响较小,梯度元素平滑对背景噪声具有一定压制作用。
|
图 5 对梯度元素及张量元素均平滑求解的λ1 (a)及λ2 (b) 垂直方向与水平方向的平滑参数相同,张量平滑尺度为梯度平滑尺度的3~10倍,梯度元素平滑时σ=1,张量元素平滑时σ=3 |
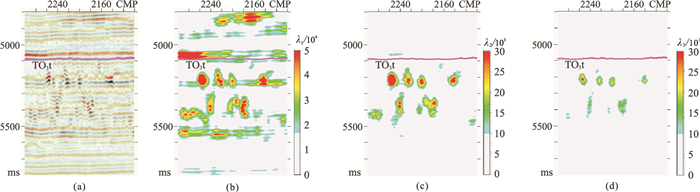
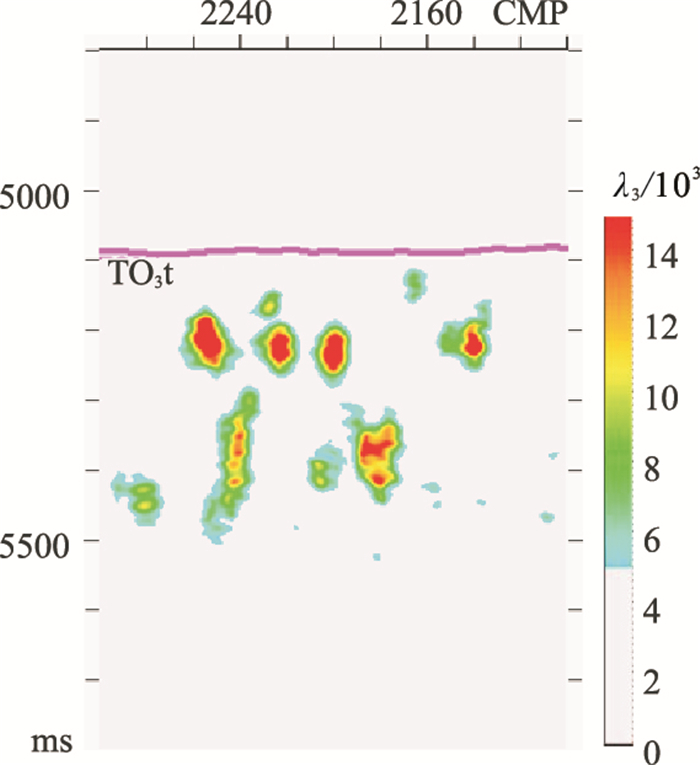
在塔北A区切取5km×5km的三维地震数据计算GST属性。图 6为对梯度元素及张量元素均平滑的三维GST求解结果。将显示色标选取一定的阈值进行低值截取,其中λ2(图 6c)与λ3(图 6d)的动态显示范围相同,即使显示范围较大,λ3依然反映了缝洞体异常反射区域的特征(图 6d)。由于λ3的整体值域约为λ2的一半,因此将λ3的显示范围减小一半(图 7),此时λ3与碳酸盐岩缝洞体异常反射区域对应较好,与λ2整体特征(图 6)相似但细节差异明显,表现为不同的观测视角。
|
图 6 对梯度元素及张量元素均平滑的三维GST求解结果
(a)地震剖面;(b)λ1;(c)λ2;(d)λ3
垂直、Inline与Crossline三个方向的平滑参数相同,相当于在有效尺度内由中心样点向三维空间均匀降低权重(各向同性高斯函数平滑),梯度元素平滑时σ=1,张量元素平滑时σ=3 |
|
图 7 将图 6中λ3的动态显示范围调整为λ2的一半的结果 |
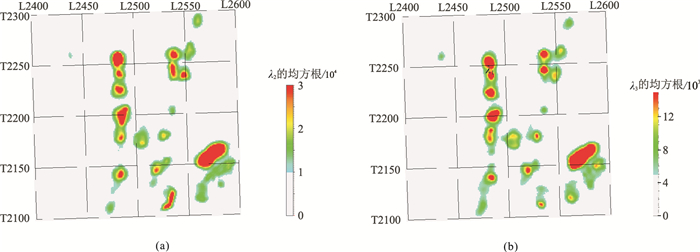
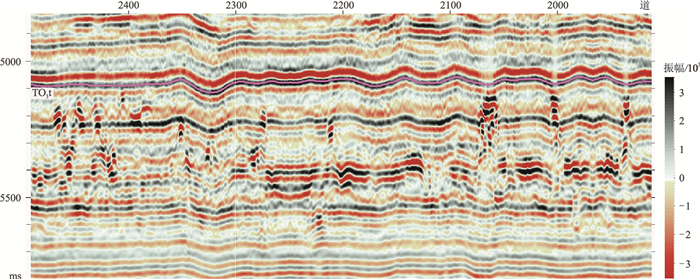
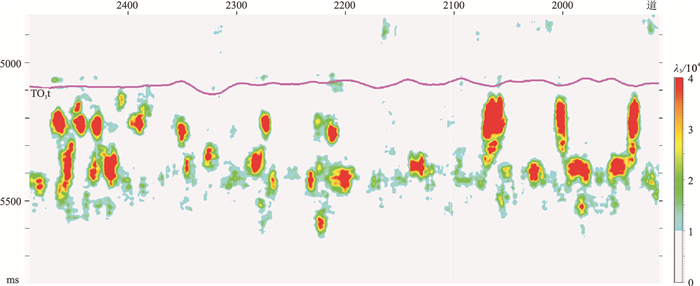
为了进一步明确λ2与λ3对平面刻画的差异,对解释层位(TO3t)向下取相同的时窗(300ms)分别计算λ2与λ3的均方根(图 8),可见λ2(图 8a)与λ3的均方根(图 8b)也表现出整体相似但又有差异的现象。切取一条尽量穿过所有平面属性高值异常区的任意线地震剖面(图 9)、λ2剖面(图 10) 与λ3剖面(图 11),可见后两者在一定的低值截取与显示动态范围内有效刻画了前者的形态各异的碳酸盐岩缝洞体反射异常,且较符合碳酸盐岩缝洞体溶蚀规律,但在不了解缝洞体真实空间形态的情况下,很难判断λ2、λ3或两者的组合计算结果的客观性。
|
图 8 沿TO3t向下取300ms的λ2(a)与λ3(b)的均方根 |
|
图 9 穿过所有平面属性高值异常区的任意线地震剖面 |

|
图 10 穿过所有平面属性高值异常区的任意线λ2剖面 |
|
图 11 穿过所有平面属性高值异常区的任意线λ3剖面 |
对实际生产应用而言,可以考虑利用工区钻井资料作为验证信息进行统计、分析,优选λ2、λ3或两者的组合计算结果作为碳酸盐岩缝洞体边界刻画的敏感地震属性,从而降低储层预测的多解性。
3 阈值选取策略通过GST矩阵求解得到的特征值为无明确物理量纲的数值,不具有明确的地质意义,如果仅仅根据经验选取储层的刻画阈值则依然属于定性描述范畴。实际应用中可采用钻时曲线交会分析确定储层刻画阈值的选取依据,也可采用气测显示、放空、漏失深度等信息标定钻遇储层边界以选取阈值,实质均为利用实钻信息判断钻遇碳酸盐岩储层位置,从而截取低值与控制显示动态范围,不失为一种合理的阈值选取策略。
由计算原理可知,在缝洞体异常区域特征值数值的高低与储层发育程度并无明确的映射关系,并且计算结果受地震资料信噪比、平滑尺度参数等多重因素影响。此外,在同一工区选择不同的钻井信息选取阈值时通常会出现阈值不一致的情况,因此直接利用GST属性不能定量刻画碳酸盐岩缝洞体。为了区别定性描述与定量刻画,本文提出标尺定量的概念,标尺定量即为无量纲的地震属性以实钻信息作为标尺而赋予刻画阈值的意义。对于定性刻画来说,标尺定量可以有效降低缝洞体刻画的多解性,不同的钻井数据作为标尺可能存在刻度差异,可以采取统计优选、平均计算以及多重约束的策略选取最终采用方案。
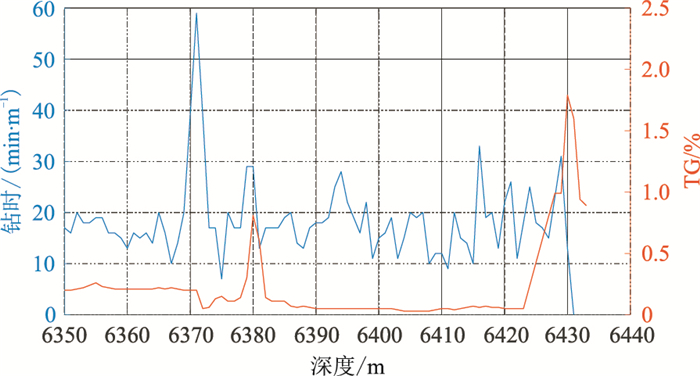
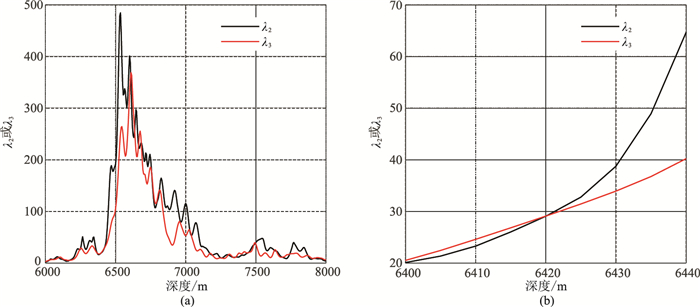
塔北A区有A、B、C、D、E等5口钻井,采用归一化将得到的λ2、λ3的值域控制在0~1000。图 12为C井钻时曲线与气测(全烃,TG)曲线交会图。可见,钻至6430m深度处钻时降为0,发生放空且漏失钻井液,TG曲线值达到1.8%,因此C井于该深度处钻遇缝洞体。沿C井轨迹抽出λ2、λ3曲线(图 13a),两者的整体相似性较高,但缝洞体位置对应λ2=38、λ3=33(图 13b)——C井的两个标尺刻度值。以同样的方式统计其余钻井的标尺刻度值(表 1),可见每口井的标尺刻度并不一致。设定x1与x2两个权重系数和期望阈值k,构造线性方程组
| $ \boldsymbol{M X}=\boldsymbol{K} $ | (7) |
其中
| $ \boldsymbol{M}=\left(\begin{array}{ll} \lambda_{2, \mathrm{~A}} & \lambda_{3, \mathrm{~A}} \\ \lambda_{2, \mathrm{~B}} & \lambda_{3, \mathrm{~B}} \\ \lambda_{2, \mathrm{C}} & \lambda_{3, \mathrm{C}} \\ \lambda_{2, \mathrm{D}} & \lambda_{3, \mathrm{D}} \\ \lambda_{2, \mathrm{E}} & \lambda_{3, \mathrm{E}} \end{array}\right) $ |
| $ \boldsymbol{X}=\left(\begin{array}{l} x_{1} \\ x_{2} \end{array}\right) $ |
| $ \boldsymbol{K}=\left(\begin{array}{l} k \\ k \\ k \\ k \\ k \end{array}\right) $ |
|
图 12 C井钻时曲线与气测曲线交会图 |
|
图 13 C井λ2与λ3曲线(a)及其缝洞体位置局部显示(b) |
|
|
表 1 塔北A区钻井标尺刻度值统计 |
式中λ2,i、λ3,i的i=A, B, C, D, E代表井号。式(7)为超定方程,设定k=50,利用最小二乘法求解得到x1=1.8107,x2=-0.5099。利用公式
| $ \lambda=x_{1} \lambda_{2}+x_{2} \lambda_{3} $ | (8) |
得到λ2、λ3的线性组合结果,并将整个三维体范围计算结果作为最终刻画缝洞体的特征值属性。图 14为过C井剖面特征值计算结果。可见,线性组合的结果λ(图 14d)融合了λ2(图 14b)与λ3(图 14c)的细节特征,设定的期望阈值与地震反射特征(图 14a)、钻井信息(图 12、图 13)高度吻合。图 15为塔北A区缝洞体刻画平面图,显示该区西部发育的断裂带与缝洞体分布一致,结合标尺定量获得的最终刻画阈值与λ2、λ3的线性组合结果(图 14d)可以有效解决不同钻井标尺刻度不一致的问题。

|
图 14 过C井地震剖面及特征值计算结果 (a)地震剖面;(b)λ2;(c)λ3;(d)λ |

|
图 15 塔北A区缝洞体刻画平面图 |
梯度结构张量属性可更连续地刻画碳酸盐岩缝洞体,通常还能在一定程度上反映溶蚀规律。技术原理分析及实际地震资料测试表明:
(1) 对张量元素的平滑计算是整个技术的关键,使结构张量矩阵不仅包含最大梯度能量方向的特征,并且还包含所有正交方向的变化特征,而梯度元素的平滑对背景噪声具有一定压制作用,可以提高最终计算结果的信噪比。
(2) 第二特征值与第三特征值对碳酸盐岩缝洞体均具有一定刻画能力,反映了不同观测视角的缝洞体三维空间形态特征,并且刻画结果较符合碳酸盐岩缝洞体溶蚀规律。结合实际研究区地质认识,优选或组合第二与第三特征值属性,在合适的低值截取与显示范围内可以有效刻画碳酸盐岩缝洞体边界。
(3) 本文提出了一种利用钻井信息作为标尺刻度无量纲特征值的方案,求解的特征值线性组合结果本质上是研究区基于钻井信息的多重约束解,融合了第二与第三特征值的细节特征,并且有效解决了不同钻井刻度值不一致的问题,但标尺定量刻画不是完全定量刻画。
| [1] |
KASS M, WITKIN A. Analyzing oriented patterns[J]. Computer Vision, Graphics and Image Proces-sing, 1987, 37(3): 362-385. DOI:10.1016/0734-189X(87)90043-0 |
| [2] |
KNUTSSON H. Representing local structure using tensors[C]. Proceedings of 6th Scandinavian Confe-rence on Image Analysis, 1989, 545-556.
|
| [3] |
RAO A R, SCHUNCK B G. Computing oriented texture fields[J]. CVGIP: Graphical Models and Image Processing, 1991, 53(2): 157-185. DOI:10.1016/1049-9652(91)90059-S |
| [4] |
HAGLUND L. Adaptive Multidimensional Filtering[D]. Linköping University, Linköping, Sweden, 1992.
|
| [5] |
RANDEN T, MONSEN E, SIGNER C, et al. Three-dimensional texture attributes for seismic data analysis[C]. SEG Technical Program Expanded Abstracts, 2000, 19, SEG-2000-0668.
|
| [6] |
RANDEN T, PEDERSEN S I, SØNNELAND L. Automatic extraction of fault surface from three-dimensional seismic data[C]. SEG Technical Program Expanded Abstracts, 2001, 20: 551-554.
|
| [7] |
BAKKER P. Image Structure Analysis for Seismic In-terpretation[D]. Delft University of Technology, Delft, Netherlands, 2002.
|
| [8] |
LUO Y, WANG Y E, ALBINHASSAN N M, et al. Computation of dips and azimuths with weighted structural tensor approach[J]. Geophysics, 2006, 71(5): V119-V121. DOI:10.1190/1.2235591 |
| [9] |
陈双全, 季敏. 地震数据结构张量相干计算方法[J]. 石油物探, 2012, 51(3): 233-238. CHEN Shuangquan, JI Min. Structure tensor cohe-rence computation method of seismic data[J]. Geophysical Prospecting for Petroleum, 2012, 51(3): 233-238. DOI:10.3969/j.issn.1000-1441.2012.03.004 |
| [10] |
唐成勇. 基于局部结构的地震几何属性研究与应用[D]. 四川成都: 西南交通大学, 2012.
|
| [11] |
陈强, 许玉莹, 曾维望. 基于地震数据结构梯度张量属性的采空区识别方法[J]. 中国煤炭地质, 2013, 25(7): 42-47. CHEN Qiang, XU Yuying, ZENG Weiwang. Goaf identification method based on seismic data gradient structure tensor (GST) attributes[J]. Coal Geology of China, 2013, 25(7): 42-47. DOI:10.3969/j.issn.1674-1803.2013.07.10 |
| [12] |
问雪, 陈雪芳, 陈胜红, 等. 利用结构导向平滑方法解释断层[J]. 石油地球物理勘探, 2017, 52(1): 146-151. WEN Xue, CHEN Xuefang, CHEN Shenghong, et al. Faults interpretation based on structure-oriented smoothing method[J]. Oil Geophysical Prospecting, 2017, 52(1): 146-151. |
| [13] |
王清振, 张金淼, 姜秀娣, 等. 利用梯度结构张量检测盐丘与断层[J]. 石油地球物理勘探, 2018, 53(4): 826-831. WANG Qingzhen, ZHANG Jinmiao, JIANG Xiudi, et al. Salt dome and fault detection based on the gradi-ent-structure tensor[J]. Oil Geophysical Prospecting, 2018, 53(4): 826-831. |
| [14] |
彭达, 肖富森, 冉崎, 等. 基于倾角导向梯度能量熵的断层检测方法[J]. 石油地球物理勘探, 2019, 54(1): 191-197. PENG Da, XIAO Fusen, RAN Qi, et al. Fault identification based on dip-oriented gradient-energy-entroy coherence estimation[J]. Oil Geophysical Prospecting, 2019, 54(1): 191-197. |
| [15] |
崔正伟, 程冰洁, 徐天吉, 等. 基于构造导向滤波与梯度结构张量相干属性的储层裂缝预测方法及应用[J]. 石油地球物理勘探, 2021, 56(3): 555-563. CUI Zhengwei, CHENG Bingjie, XU Tianji, et al. Reservoir fracture prediction method and application based on structure-oriented filtering and coherent attributes of gradient structure tensor[J]. Oil Geophysical Prospecting, 2021, 56(3): 555-563. |
| [16] |
王震, 文欢, 邓光校, 等. 塔河油田碳酸盐岩断溶体刻画技术研究与应用[J]. 石油物探, 2019, 58(1): 149-154. WANG Zhen, WEN Huan, DENG Guangxiao, et al. Fault-karst characterization technology in the Tahe Oilfield, China[J]. Geophysical Prospecting for Petroleum, 2019, 58(1): 149-154. |
| [17] |
WU X M. Directional structure-tensor-based cohe-rence to detect seismic faults and channels[J]. Geophysics, 2017, 82(2): A13-A17. DOI:10.1190/geo2016-0473.1 |
| [18] |
HALE D. Recursive Gaussian Filters[R]. Colorado School of Mines, CWP Report 546, 2006.
|
| [19] |
FEHMERS G C, HÖCKER C F. Fast structural interpretation with structure-oriented filtering[J]. Geophysics, 2003, 68(4): 1286-1293. DOI:10.1190/1.1598121 |
| [20] |
HALE D. Structure-Oriented Smoothing and Semblance[R]. Colorado School of Mines, CWP Report 635, 2009.
|



 张晟,新疆维吾尔自治区库尔勒市石化大道26号塔指小区勘探开发研究院2号实验楼地球物理所,841000。Email:
张晟,新疆维吾尔自治区库尔勒市石化大道26号塔指小区勘探开发研究院2号实验楼地球物理所,841000。Email: