② 福建农林大学交通与土木工程学院,福建福州 350002;
③ 深圳市欧圣达科技有限公司,安徽合肥 230001;
④ 中国石油化工股份有限公司石油物探技术研究院,江苏南京 211103
② College of Transportation and Civil Engineering, Fujian Agriculture and Forestry University, Fuzhou, Fujian 350002, China;
③ Shenzhen Osdiot Technology Co., Ltd., Hefei, Anhui 230001, China;
④ SINOPEC Geophysical Research Institute, Nanjing, Jiangsu 211103, China
时移地震技术最早出现于20世纪80年代初期,Atlantic Richfield Company(ARCO)为了提高注采检测效果,在三维地震数据上考虑了时间项(也称四维地震技术),首次运用时移地震技术。1983年,ARCO在SEG会议上介绍了时移地震技术[1-2]。此后的近40年时间里,人们广泛研究了时移地震方法,为监测油气藏动态提供了理论基础[1-5],并获得了较好的应用效果。
陈小宏等[3]于1998年对四维地震油藏监测技术进行了应用研究,指出四维地震的重要研究手段是高分辨率地震成像。随后,Abubakar等[4]分析了时移地震非线性反演的可行性,Gluck等[5]提出时移地震波阻抗反演,引起了业界关注。李景叶等[6-7]应用时移地震AVO反演定量解释油藏,推导了多波时移地震AVO反演的计算方法,实现了时移地震数据从定性解释到定量解释的跨越。陈小宏等[8]由时移地震非线性反演压力、饱和度的变化,认为非线性反演方法(非线性反演方法不受油藏参数变化范围的影响)优于线性化反演方法。Buland等[9]首次提出了基于贝叶斯理论的时移地震差异反演方法,提高了反演效率。Eidsvik[10]建立了时移地震AVO块反演模型并用于挪威海域数据,更好地反演了不同时间的弹性参数差异。陈勇等[11]将全变分多重网格法引入时移地震,不仅能较好地识别非连续介质模型边缘,同时也提高了计算效率。Kato等[12]提出了基于贝叶斯理论的AVO同时反演方法,通过测试油田不完整的时移多分量数据集,发现反演结果与真实结果基本一致。Zhu等[13]提出了基于时移地震差分资料的时移地震反演方法,能够有效地展示储层变化。王守东等[14]提出了基于贝叶斯理论的AVO波形反演方法,能够抑制反演假象,从而获得高分辨率的弹性参数信息。
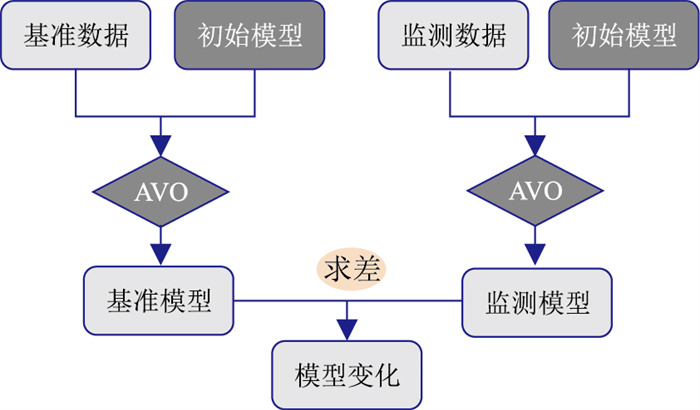
目前基于Zoeppritz方程[15]及其近似的AVO技术广泛用于油气勘探,同时也取得了许多重要成果。相比于其他反演方法,时移地震AVO反演技术通过重复地震观测获得油气藏开发前、后的数据差异,同时结合钻井、测井等相关信息解译差异数据,从而监测储层油气运移情况、探测和发现剩余油气,进而提高油藏采收率[16-17]。一般来说,储层变化是由两组叠前数据(基准数据和监测数据)反演的弹性参数差异表征。传统的时移地震AVO反演分别反演基准和监测资料,分别获得基准模型和监测模型,然后对反演结果求差,得到模型变化(图 1)。
|
图 1 传统的时移地震AVO反演策略 基于同一初始模型,对基准数据与监测数据分别进行反演 |
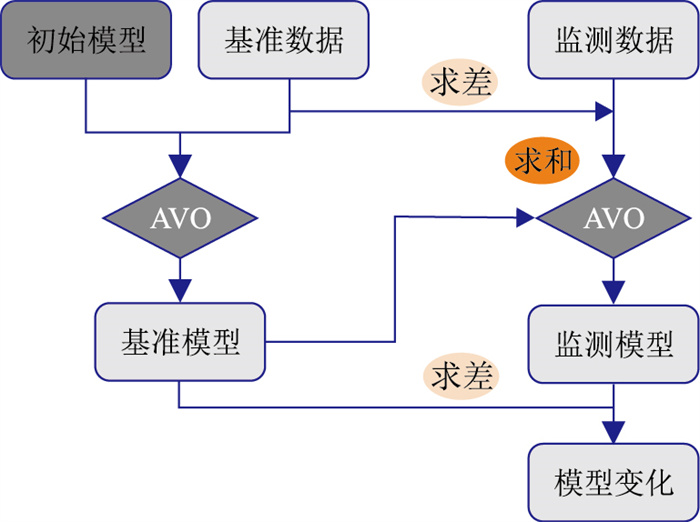
本文引入双差反演(Double-Difference Inversion,DDI)策略(图 2),直接反演差异数据得到储层参数变化[18-20]。由于其优异的目标导向性,可有效减少目标区域(存在储层参数变化的区域)外的反演假象,目前常用于时移全波形反演(FWI)[21-25],没有用于时移AVO反演。事实上,时移地震AVO反演与时移FWI类似,基准模型反演和监测模型反演的不一致也会导致目标区域外的反演假象。本文针对一维、二维模型,分别测试、对比传统反演策略和DDI策略的效果,反演了储层参数变化及其上覆地层压力变化引起的弹性参数变化。
|
图 2 双差反演策略 基于初始模型,先对基准数据反演,得到基准模型;再以基准模型为新的初始模型,对新监测数据(监测数据减去基准数据再加上基准模型合成的新基准数据)进行反演 |
Zoeppritz[15]方程为AVO反演的理论基础,但精确求解Zoeppritz方程难度较大,难以直接反演纵、横波阻抗。因此,人们对Zoeppritz方程进行了合理的简化处理,得到不同形式的反射系数近似公式,并发展了相应的AVO反演方法。但是,目前大部分的AVO反演方法仍存在一些问题,如:在大入射角、大阻抗差等情况下,反射系数近似公式与精确公式之间还存在一定误差;在同步反演密度、横波速度、纵波速度这三个参数时,反演问题病态程度高等[26]。Fu等[26]提出了基于改进的射线参数域地震纵波反射系数近似方程,建立了地震纵波反射系数与纵、横波阻抗的非线性关系,能够很好地处理上述问题,获得了较好的应用效果。本文基于改进的射线参数域地震纵波反射系数近似方程,结合广义线性反演(GLI)理论和贝叶斯理论[27],并同时引入FWI中的DDI策略,发展了基于DDI策略的时移地震AVO反演方法。改进的射线参数域地震纵波反射系数近似方程[21, 26]为
| $R\left( {{\theta _i}} \right) = \frac{{\frac{{{\rm{A}}{{\rm{I}}_{i + 1}}}}{{\cos {\varphi _i}}} - \frac{{{\rm{A}}{{\rm{I}}_i}}}{{\cos {\theta _i}}}}}{{\frac{{{\rm{A}}{{\rm{I}}_{i + 1}}}}{{\cos {\varphi _i}}} + \frac{{{\rm{A}}{{\rm{I}}_i}}}{{\cos {\theta _i}}}}}{\rm{ + 2(}}r + 2{\rm{)}}\frac{{{{\left[ {1 - {{\left( {\frac{{{\rm{S}}{{\rm{I}}_{i + 1}}}}{{{\rm{A}}{{\rm{I}}_{i + 1}}}}} \right)}^2}{{\sin }^2}{\varphi _i}} \right]}^{1 - {{\left( {\frac{{{\rm{S}}{{\rm{I}}_{i + 1}}}}{{{\rm{A}}{{\rm{I}}_{i + 1}}}}} \right)}^2}{{\sin }^2}{\varphi _i}}} - {{\left[ {1 - {{\left( {\frac{{{\rm{S}}{{\rm{I}}_i}}}{{{\rm{A}}{{\rm{I}}_i}}}} \right)}^2}{{\sin }^2}{\theta _i}} \right]}^{1 - {{\left( {\frac{{{\rm{S}}{{\rm{I}}_i}}}{{{\rm{A}}{{\rm{I}}_i}}}} \right)}^2}{{\sin }^2}{\theta _i}}}}}{{{{\left[ {1 - {{\left( {\frac{{{\rm{S}}{{\rm{I}}_{i + 1}}}}{{{\rm{A}}{{\rm{I}}_{i + 1}}}}} \right)}^2}{{\sin }^2}{\varphi _i}} \right]}^{1 - {{\left( {\frac{{{\rm{S}}{{\rm{i}}_{i + 1}}}}{{{\rm{A}}{{\rm{I}}_{i + 1}}}}} \right)}^2}{{\sin }^2}{\varphi _i}}} + {{\left[ {1 - {{\left( {\frac{{{\rm{S}}{{\rm{I}}_i}}}{{{\rm{A}}{{\rm{I}}_i}}}} \right)}^2}{{\sin }^2}{\theta _i}} \right]}^{1 - {{\left( {\frac{{{{\rm{S}}_i}}}{{{\rm{A}}{{\rm{i}}_i}}}} \right)}^2}{{\sin }^2}{\theta _i}}}}} $ | (1) |
式中:R(θi)为第i个反射界面的PP波反射系数,θi为第i个界面纵波入射角;φi为第i个界面纵波透射角;AIi+1、AIi分别为第i+1层、第i层纵波阻抗;SIi+1、SIi分别为第i+1层、第i层横波阻抗;r为密度与横波反射系数之比(可从测井数据中获得,其误差对反演结果影响很小),在反演过程中设定为常数。
式(1)同时包含了θi和φi。在共射线参数道集中,上一反射界面的透射角与下一反射界面的入射角相同。但是一般的叠前反演道集属于共反射角域,而在共入射角道集中,上一反射界面的纵波透射角并不等于下一反射界面的入射角。因此在获得每一采样点的纵波入射角的同时,还要获得对应的透射角才能精确反演R(θi)。在实际资料中,一般通过
| $ \sin \theta_{i}=\frac{\alpha_{i}}{\alpha_{\mathrm{rms}_{i}}} \sqrt{\frac{x^{2}}{x^{2}+\alpha_{\mathrm{rms}_{i}}^{2} t_{0}^{2}}} $ | (2) |
将炮检距域资料转换到入射角域。式中:αi为第i层纵波层速度;αrmsi为第i层均方根速度;x为炮检距;t0为零炮检距双程旅行时。
结合式(2)和Snell定理,通过
| $\sin \theta_{i+1}=\frac{\alpha_{i+1}}{\alpha_{i}} \sin \theta_{i}=\frac{\alpha_{i+1}}{\alpha_{\mathrm{rms}_{i}}} \sqrt{\frac{x^{2}}{x^{2}+\alpha_{\mathrm{mms}_{i}}^{2} t_{0}^{2}}} $ | (3) |
获得φi。
应用Cook等[28]提出的GLI方法,以柯西约束作为正则化项[29]增强弱反射,最终的目标函数为
| $ \begin{aligned} J(\Delta \boldsymbol{m})=&(\Delta \boldsymbol{R}-\boldsymbol{G} \Delta \boldsymbol{m})^{\mathrm{T}}(\Delta \boldsymbol{R}-\boldsymbol{G} \Delta m)+\\ & 2 \sigma_{\mathrm{n}}^{2} \sum\limits_{i=1}^{M} \ln \left[1+\frac{\left(\Delta m_{i}\right)^{2}}{\sigma_{m}^{2}}\right] \end{aligned} $ | (4) |
式中:ΔR为反射系数残差项;G为反射系数的雅克比矩阵;Δm为模型参数扰动量;σn为误差项(ΔR-GΔm)的标准差;σm为Δm的标准差;Δmi为第i个(i=1, 2, …, M)待反演参数扰动量,M为Δm的总长度。利用高斯—牛顿法求解式(4),可以得到纵、横波阻抗[30]。
2.2 时移反演方法对于传统的时移地震AVO反演策略,需要单独反演基准数据以及监测数据,然后将反演结果求差得到地下弹性参数变化,其中两次AVO反演使用的模型相同。在DDI策略中,第一次AVO反演与传统的时移地震AVO反演策略相同,即利用基准数据和初始模型反演基准模型;第二次反演以第一次反演的基准模型作为新初始模型,对新监测数据
| $ \boldsymbol{R}_{2}=\boldsymbol{S}_{\text {basseline }}+\left(\boldsymbol{R}_{\text {moonitor }}-\boldsymbol{R}_{\text {basseline }}\right) $ | (5) |
进行反演(图 2)。式中:R2为第二次反演使用的反射纵波数据;Sbaseline为第一次反演得到的基准模型(通过式(1)和反演的基准模型得到的不同角度的合成角道集或合成基准数据);Rmonitor为监测数据;Rbaseline为由基准数据合成的新基准数据。从本质上讲,反演要使合成数据与观测数据最匹配,因此上述反演的目标函数为
| $ E_{\mathrm{DDI}}=\frac{1}{2}\left\|\left(\boldsymbol{R}_{\text {monitor }}-\boldsymbol{S}_{\text {monitor }}\right)-\left(\boldsymbol{R}_{\text {bassline }}-\boldsymbol{S}_{\text {baseline }}\right)\right\|_{2}^{2} $ | (6) |
式中Smonitor为监测模型模拟的合成数据,是由式(1)和反演监测模型(即纵、横波阻抗)得到的不同角度的纵波反射系数。式(6)含有两个差值项[31],可见,监测反演的实质是使基准反演与监测反演的数据残差相同,即反演监测模型和基准模型的收敛程度相同。因此,DDI策略可以减少目标区域外的反演假象。
3 合成数据实例 3.1 一维模型测试以一维模型为例,分别采用基于传统的时移地震AVO反演策略与基于DDI策略的时移地震AVO反演方法进行反演,并对比两种方法的差别。
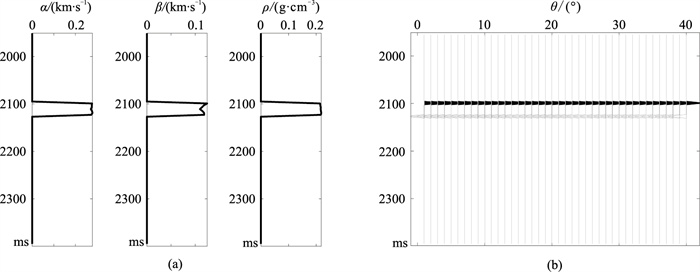
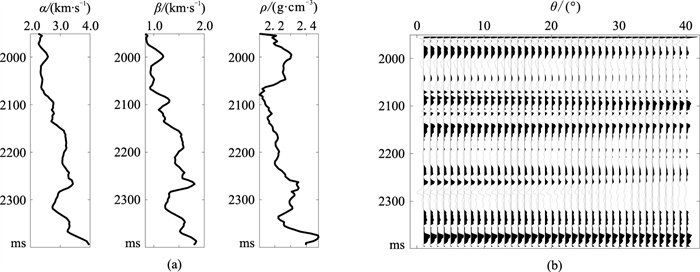
以BH地区测井曲线[32]为基准模型(图 3a),并采用卷积法生成共入射角合成地震记录(图 3b),其中在2100ms附近存在一个清晰的砂岩储层响应。
|
图 3 BH地区测井曲线(基准模型)(a)及其合成的共入射角道集(基准数据)(b) α、β、ρ和θ分别代表纵波速度、横波速度、密度和入射角,下同 |
将图 3a数据的储层参数值增加10%作为监测模型(图 4a)模拟流体变化,同样采用卷积法生成合成地震记录(图 4b)作为监测数据。

|
图 4 图 3a数据的储层参数值增加10%的数据(监测模型)(a)及其合成的共入射角道集(监测数据)(b) |
为了更清楚地显示监测模型(数据)与基准模型(数据)的差别,计算了两者之差(图 5)。图 5为图 4与图 3数据之差,可以清楚地看到储层参数在2100ms附近存在明显的变化。
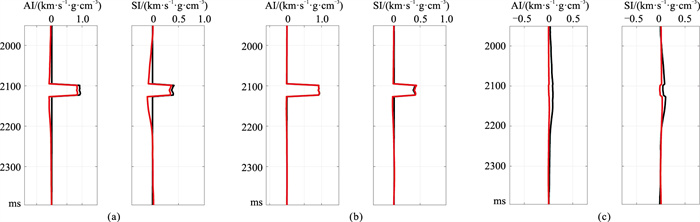
以图 5数据为基础,分别采用基于传统的时移地震AVO反演策略与基于DDI策略的时移地震AVO反演方法进行反演。图 6为反演的纵、横波阻抗(基准模型反演和监测模型反演的迭代次数均为10)。由图可见:①基于传统的时移地震AVO反演策略的反演结果与真实模型(基于时移模型得到的纵、横波阻抗变化)的变化趋势一致,但误差较大(图 6a、图 6c),其中横波阻抗的误差更明显(图 6a右);②基于DDI策略的反演结果与真实模型的变化趋势及数值均更吻合(图 6b);③基于DDI策略的反演结果的绝对误差(图 6c红色曲线)要小于基于传统的时移地震AVO反演策略(图 6c黑色曲线)。可见,基于DDI策略的时移地震AVO反演结果较基于传统的时移地震AVO反演策略能更准确地反映真实模型。
|
图 6 时移AVO反演的纵(左)、横波(右)阻抗(基准模型反演和监测模型反演的迭代次数均为10) (a)传统的时移地震AVO反演策略(黑色曲线代表真实值,红色曲线代表反演结果);(b)DDI策略(黑色曲线代表真实值,红色曲线代表反演结果);(c)图a(黑色)与图b(红色)的反演绝对误差 |
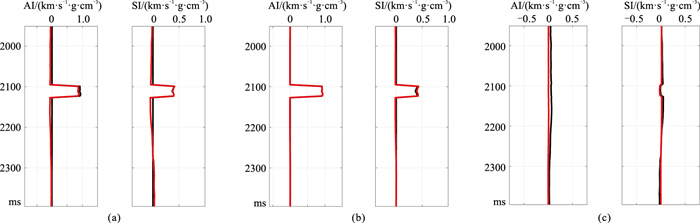
图 7为反演的纵、横波阻抗(基准模型反演和监测模型反演的迭代次数均为20)。对比图 6和图 7可知:①基于传统的时移地震AVO反演策略的反演结果(图 7a)的误差(图 7c)小于图 6a,即较差的基准模型(迭代次数较少)明显降低了传统的时移地震AVO反演精度;②基于DDI策略的反演结果(图 7b)与图 6b接近,即迭代次数对DDI策略影响较小。图 8为时移AVO反演的纵、横波阻抗(基准模型反演的迭代次数为10,监测模型反演的迭代次数为20),图 9为时移AVO反演的纵、横波阻抗(基准模型反演的迭代次数为20,监测模型反演的迭代次数为10)。由图可见,基准模型和监测模型反演的迭代次数不同,基于传统的时移地震AVO反演策略的反演结果的误差较大(图 8a、图 9a、图 8c、图 9c),基于DDI策略的反演结果误差较小(图 8b、图 9b、图 8c、图 9c)。因此,与传统的时移地震AVO反演策略相比,DDI策略反演结果的精度更高,且更集中于目标区域。另外,传统的时移地震AVO反演策略对基准模型和监测模型的反演迭代次数差异非常敏感,且会带来严重的反演假象,而DDI策略可以有效地压制假象,准确地反演储层变化。
|
图 7 时移AVO反演的纵(左)、横波(右)阻抗(基准模型反演和监测模型反演的迭代次数均为20) (a)传统的时移地震AVO反演策略(黑色曲线代表真实值,红色曲线代表反演结果);(b) DDI策略(黑色曲线代表真实值,红色曲线代表反演结果);(c)图a(黑色)与图b(红色)的反演绝对误差 |

|
图 8 时移AVO反演的纵(左)、横波(右)阻抗(基准模型反演的迭代次数为10,监测模型反演的迭代次数为20) (a)传统的时移地震AVO反演策略(黑色曲线代表真实值,红色曲线代表反演结果);(b) DDI策略(黑色曲线代表真实值,红色曲线代表反演结果);(c)图a(黑色)与图b(红色)的反演绝对误差 |

|
图 9 时移AVO反演的纵(左)、横波(右)阻抗(基准模型反演的迭代次数为20,监测模型反演的迭代次数为10) (a)传统的时移地震AVO反演策略(黑色曲线代表真实值,红色曲线代表反演结果);(b) DDI策略(黑色曲线代表真实值,红色曲线代表反演结果);(c)图a(黑色)与图b(红色)的反演绝对误差 |
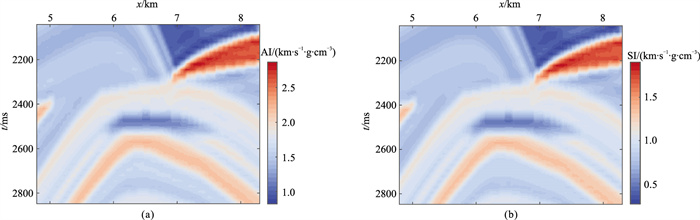
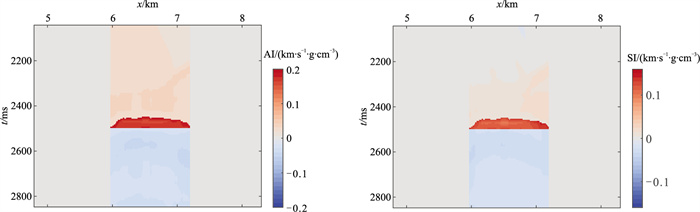
为进一步测试基于DDI策略的时移地震AVO反演,笔者构造了一个二维模型。图 10、图 11和图 12分别为二维基准模型、监测模型和时移模型。图 13为无噪声时DDI策略反演的时移模型。由图可见,DDI策略较好地反映了上覆地层的纵波阻抗变化(图 13a),但不能较好地反映横波阻抗变化,但依然清晰地分辨了上覆地层横波阻抗变化区域(图 13b)。图 14为信噪比为2时DDI策略反演的时移模型。由图可见:①DDI策略可以稳定、准确地反演储层纵、横波阻抗变化,但上覆地层压力造成的地层纵、横波阻抗变化较小,其反演质量不如储层反演结果,更易受噪声影响。②上覆地层的纵波阻抗变化反演结果受噪声影响较小(图 14a);上覆地层的横波阻抗变化由于数值较小,受噪声影响相对较大,但仍能够较好地分辨储层轮廓(图 14b),这也进一步验证了本文方法的合理性。
|
图 10 二维基准模型 (a)纵波阻抗;(b)横波阻抗 |
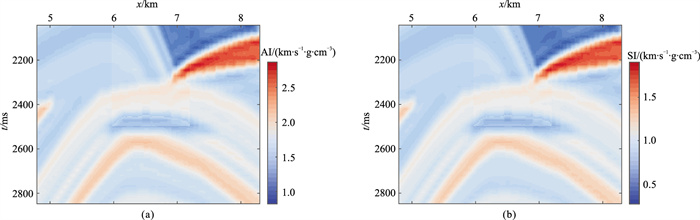
|
图 11 二维监测模型 (a)纵波阻抗;(b)横波阻抗 相对图 10,模型的储层参数值增加10%。为了模拟上覆地层压力变化造成的地层参数变化,上覆地层参数值增加2% |

|
图 12 二维时移模型 (a)纵波阻抗;(b)横波阻抗 |
|
图 13 无噪声时DDI策略反演的时移模型 (a)纵波阻抗;(b)横波阻抗 |

|
图 14 信噪比为2时DDI策略反演的时移模型 (a)纵波阻抗;(b)横波阻抗 |
本文基于改进的射线参数域地震纵波反射系数近似方程,结合GLI理论和贝叶斯理论[27],并同时引入FWI中的双差反演策略,发展了基于双差反演策略的时移地震AVO反演方法。该方法与传统AVO方法相比精度更高,更适应大阻抗差反射界面,且不易受纵、横波速度比为常数假设的限制。另外,基于双差反演策略的时移地震反演直接利用差异数据(监测数据减去基准数据)监测模型反演,不易受基准模型反演质量及基准模型反演和监测模型反演行为不一致的影响,可以有效压制目标区域外的反演假象,使反演结果集中在目标区域,可准确反映储层变化,提高了目标区域的反演精度,有利于解释储层。结合改进的地震纵波反射系数近似方程与双差反演策略可准确、稳定地反演储层纵、横波阻抗变化,并能有效反映由上覆地层压力改变引起的微小纵、横波阻抗变化。
需要注意的是,不一致的震源子波可能导致双差反演策略的结果产生较严重的反演假象。双差反演策略需要在监测数据与基准数据中进行代数运算,在执行该策略前,需要对基准数据或监测数据进行子波一致性校正,使基准数据与监测数据尺度、波形和带宽等一致,消除基准数据与监测数据中与地层变化无关的不一致性。
| [1] |
周长礼. 时移地震全波形反演方法研究[D]. 北京: 中国石油大学(北京), 2016.
|
| [2] |
周长礼, 王守东, 尹彦琼, 等. 时移地震全波形反演方法研究[C]. 2015中国地球科学联合学术年会论文集(十四)——专题40油气田与煤田地球物理勘探, 2015, 782.
|
| [3] |
陈小宏, 牟永光. 四维地震油藏监测技术及其应用[J]. 石油地球物理勘探, 1998, 33(6): 707-715. CHEN Xiaohong, MOU Yongguang. Four-dimensio-nal seismic reservoir monitoring technique and its application[J]. Oil Geophysical Prospecting, 1998, 33(6): 707-715. DOI:10.3321/j.issn:1000-7210.1998.06.001 |
| [4] |
ABUBAKAR A, VAN DEN BERG P M, FOKKEMA J T. A feasibility study on nonlinear inversion of time-lapse seismic data[C]. SEG Technical Program Expanded Abstracts, 2001, 20: 1664-1667.
|
| [5] |
GLUCK S, DESCHIZEAUX B, MIGNOT A, et al. Time-lapse impedance inversion of post-stack seismic data[C]. SEG Technical Program Expanded Abstracts, 2000, 19: 1509-1512.
|
| [6] |
李景叶, 陈小宏, 金龙. 时移地震AVO反演在油藏定量解释中的应用[J]. 石油学报, 2005, 26(3): 68-73. LI Jingye, CHEN Xiaohong, JIN Long. Application of time-lapse seismic AVO inversion to quantitative interpretation of reservoir[J]. Acta Petrolei Sinica, 2005, 26(3): 68-73. DOI:10.3321/j.issn:0253-2697.2005.03.015 |
| [7] |
李景叶, 陈小宏, 郝振江, 等. 多波时移地震AVO反演研究[J]. 地球物理学报, 2005, 48(4): 902-908. LI Jingye, CHEN Xiaohong, HAO Zhenjiang, et al. A study on multiple time-lapse seismic AVO inversion[J]. Chinese Journal of Geophysics, 2005, 48(4): 902-908. DOI:10.3321/j.issn:0001-5733.2005.04.024 |
| [8] |
陈小宏, 赵伟, 马继涛, 等. 时移地震非线性反演压力与饱和度变化研究[J]. 地球物理学进展, 2006, 21(3): 830-836. CHEN Xiaohong, ZHAO Wei, MA Jitao, et al. Pressure and saturation change nonlinear inversion method using time-lapse seismic data[J]. Progress in Geophysics, 2006, 21(3): 830-836. DOI:10.3969/j.issn.1004-2903.2006.03.022 |
| [9] |
BULAND A, OUAIR Y E. Bayesian time-lapse inversion[J]. Geophysics, 2006, 71(3). |
| [10] |
EIDSVIK J. Blocky inversion of time-lapse seismic AVO data[C]. SEG Technical Program Expanded Abstracts, 2009, 28: 3820-3824.
|
| [11] |
陈勇, 韩波, 肖龙, 等. 多尺度全变分法及其在时移地震中的应用[J]. 地球物理学报, 2010, 53(8): 1883-1892. CHEN Yong, HAN Bo, XIAO Long, et al. Multiscale total variation method and its application on time-lapse seismic[J]. Chinese Journal of Geophysics, 2010, 53(8): 1883-1892. DOI:10.3969/j.issn.0001-5733.2010.08.014 |
| [12] |
KATO A, STEWART R R. Joint AVO inversion for time-lapse elastic reservoir properties: Hangingstone heavy oilfield, Alberta[C]. SEG Technical Program Expanded Abstracts, 2010, 29: 4432-4437.
|
| [13] |
ZHU Z Y, JIANG X D, ZHAO W, et al. Time-lapse prestack elastic impedance inversion based on seismic difference data[C]. SEG Technical Program Expanded Abstracts, 2011, 30: 2497-2501.
|
| [14] |
王守东, 王波. 时移地震资料贝叶斯AVO波形反演[J]. 地球物理学报, 2012, 55(7): 2422-2431. WANG Shoudong, WANG Bo. Time-lapse Bayesian AVO waveform inversion[J]. Chinese Journal of Geophysics, 2012, 55(7): 2422-2431. |
| [15] |
ZOEPPRITZ K. Erdbebenwellen VⅡ b: über reflexion und durchgang seismischer wellen durch unstetig-keitsflächen[J]. Gottinger Nachr, 1919, 1: 66-84. |
| [16] |
廖仪, 周家雄, 刘巍, 等. 拟时移地震气藏剩余潜力研究[J]. 石油地球物理勘探, 2019, 54(3): 634-640. LIAO Yi, ZHOU Jiaxiong, LIU Wei, et al. Reminding gas potential study based on quasi time-lapse seismic[J]. Oil Geophysical Prospecting, 2019, 54(3): 634-640. |
| [17] |
郭奇, 庄天琳, 何书梅, 等. 基于时移地震资料的储层渗透率时变性研究[J]. 石油地球物理勘探, 2022, 57(1): 176-183. GUO Qi, ZHUANG Tianlin, HE Shumei, et al. Study of time-varying reservoir permeability based on time-lapse seismic data[J]. Oil Geophysical Prospecting, 2022, 57(1): 176-183. |
| [18] |
SHUEY R T. A simplification of the Zoeppritz equations[J]. Geophysics, 1985, 50(3): 609-614. |
| [19] |
付欣, 张峰, 李向阳, 等. 基于改进反射系数近似方程的纵横波阻抗同步反演[J]. 地球物理学报, 2019, 62(1): 276-288. FU Xin, ZHANG Feng, LI Xiangyang, et al. Simultaneous inversion of P-and S-wave impedances based on an improved approximation equation of reflection coe-fficients[J]. Chinese Journal of Geophysics, 2019, 62(1): 276-288. |
| [20] |
SARKAR S, GOUVEIA W P, JOHNSTON D H. On the inversion of time-lapse seismic data[C]. SEG Technical Program Expanded Abstracts, 2003, 22: 1489-1492.
|
| [21] |
ZHENG Y, BARTON P, SINGH S. Strategies for elastic full waveform inversion of time-lapse ocean bottom cable (OBC) seismic data[C]. SEG Technical Program Expanded Abstracts, 2011, 30: 4195-4200.
|
| [22] |
FU X, ROMAHN S, INNANEN K A. Double-wavelet double-difference time-lapse waveform inversion[C]. SEG Technical Program Expanded Abstracts, 2020, 39: 3764-3767.
|
| [23] |
FU X, INNANEN K A. An MCMC-based approach to time-lapse full-waveform inversion[C]. First International Meeting for Applied Geoscience & Energy Expanded Abstracts, 2021, 3484-3489.
|
| [24] |
刘宇航, 黄建平, 杨继东, 等. 弹性波全波形反演中的四种优化方法对比[J]. 石油地球物理勘探, 2022, 57(1): 118-128. LIU Yuhang, HUANG Jianping, YANG Jidong, et al. Comparison of four optimization methods in elastic full-waveform inversions[J]. Oil Geophysical Prospecting, 2022, 57(1): 118-128. |
| [25] |
李昕洁, 王维红, 郭雪豹, 等. 全波形反演正则化方法对比[J]. 石油地球物理勘探, 2022, 57(1): 129-139. LI Xinjie, WANG Weihong, GUO Xuebao, et al. Comparison of regularization methods for full-waveform inversion[J]. Oil Geophysical Prospecting, 2022, 57(1): 129-139. |
| [26] |
FU X, ZHANG F and LI X Y. Simultaneous inversion of P-and S-wave impedance based on an improved AVO equation[C]. SEG Technical Program Expanded Abstracts, 2007, 26: 828-833.
|
| [27] |
廖仪, 刘巍, 胡林, 等. 地震保幅高低频拓展与多尺度贝叶斯融合反演[J]. 石油地球物理勘探, 2021, 56(6): 1330-1339. LIAO Yi, LIU Wei, HU Lin, et al. Research on high- and low-frequency expansion of seismic amplitude preserving and multi-scale Bayesian fusion inversion[J]. Oil Geophysical Prospecting, 2021, 56(6): 1330-1339. |
| [28] |
COOKE D A, SCHNEIDER W A. Generalized linear inversion of reflection seismic data[J]. Geophysics, 1983, 48(6): 665-676. DOI:10.1190/1.1441497 |
| [29] |
ALEMIE W, SACCHI M D. High-resolution three-term AVO inversion by means of a Trivariate Cauchy probability distribution[J]. Geophysics, 2011, 76(3): R43-R55. DOI:10.1190/1.3554627 |
| [30] |
BOGDANOV A, KNUDSEN L R, LEANDER G, et al. PRESENT: An ultra-light weight block cipher[C]. Cryptographic Hardware and Embedded Systems- CHES 2007, 2007, 450-466.
|
| [31] |
YANG D, MEADOWS M, ⅡNDERWIESEN P, et al. Double-difference waveform inversion: Feasibility and robustness study with pressure data[J]. Geophysics, 2015, 80(6): M129-M141. DOI:10.1190/geo2014-0489.1 |
| [32] |
AVSETH P, MUKERJI T, MAVKO G. Quantitative Seismic Interpretation[M]. Cambridge University Press, 2005.
|



 张小龙, 安徽省合肥市蜀山区智能科技园A3座,230001。Email:
张小龙, 安徽省合肥市蜀山区智能科技园A3座,230001。Email: