② 中国石油化工股份有限公司石油勘探开发研究院,北京 100026;
③ 南方海洋科学与工程广东省实验室(广州),广东广州 511458
② Sinopec Petroleum Exploration and Production Research Institute, Beijing 102206, China;
③ Southern Marine Science and Engineering Guangdong Laboratory (Guangzhou), Guangzhou, Guangdong 511458, China
天然气水合物广泛分布于海域及冻土地带[1-2],其形成有较为严格的温度、压力限制条件,并且随不同温压和气源条件以不同形态赋存[3-6]。目前,人们意识到仅仅利用地震资料的海底浅层强反射(也称似海底反射层,Bottom Simulating Reflector,BSR)[7]探明天然气水合物的分布范围是远远不够的,还需要利用叠前地震反射特征探明天然气水合物的赋存形态以及天然气水合物的饱和度等参数[8-13]。为了实现这一目的,必须对天然气水合物及其赋存介质的岩石物理性质进行深入、细致地研究。
与常规的碎屑岩储层和碳酸盐岩储层不同,海域天然气水合物通常赋存于深海浅层疏松(泛指未固结或弱固结)沉积物中。常规岩石物理模型难以用来描述疏松沉积物—水合物这一复杂的沉积物体系。为此,众多地球物理学者提出了一些经验公式和理论模型用于研究水合物及其赋存介质的岩石物理性质。Lee等[14]改进Biot-Gassmann方程,提出了BGTL模型。Helgrud等[15]、Ecker等[16]提出了利用等效介质理论对水合物的岩石物理性质进行研究的基本方法和思路。宋海斌等[17]基于时间平均—Wood加权方程、三相介质波传播理论模型和弹性模量模型,计算并阐述了含天然气水合物岩石弹性参数与水合物饱和度、含游离气岩石弹性参数与游离气饱和度的关系,并研究了天然气水合物的叠前地震反射特征。刘欣欣等[18]针对孔隙充填和颗粒支撑两种分布模式的水合物地层,重点考虑水合物地层的微观孔隙结构及水合物的剪切性质,基于等效介质理论定量描述了地层矿物组分特征和孔隙连通性及形状,利用斑块饱和理论和广义Gassmann理论定量描述了孔隙充填水合物的剪切性质,并在此基础上构建了两种模式水合物地层的岩石物理模型。孟大江等[19]利用等效介质模型研究了天然气水合物横波预测的方法,并利用常规测井资料构建约束优化方程,其中以纵波速度、密度等作为约束、孔隙度和饱和度作为优化变量以寻找最优解,最后得到了与实测资料吻合度较高的建模结果。
现有的水合物岩石物理建模方法在一定程度上可满足需求,但也存在一些不足。首先,以基于时间平均方程的经验公式的方法过于简单,难以反映疏松沉积物—天然气水合物这一复杂沉积体系的弹性参数与物性参数的内在联系;其次,以Hertz-Mindlin公式为框架的岩石物理建模方法[15-16, 19]尽管在理论上比较完备,但是对横波速度的估计误差偏大,使方法的理论基础受到质疑;另外,以K-T模型及微分等效介质(DEM)模型为框架的岩石物理建模方法将岩石物理建模与反演过程相结合,可以得到与实测结果相吻合的结果,但是需要对多个参变量(孔隙度、水合物饱和度等)进行反演,存在一定的不确定性。
针对上述问题,本文提出了一种适用于海域疏松沉积物—天然气水合物的岩石物理建模方法。该方法仍以岩石物理等效介质理论为框架,因而可以反映沉积物物性与弹性参数的内在联系。同时,采用改进的Hertz-Mindlin模型估计疏松沉积物的弹性模量,提高了横波估算的精度,并使建模过程自洽。针对不同赋存形态的水合物沉积体系,讨论了其适用模型及不同赋存形态水合物沉积体系判别的大致原则;最后,针对研究区的具体情况,设计了岩石物理建模流程,以期提高水合物岩石物理建模的精度,增加对于海域天然气岩石物理性质的认识和理解。
1 岩石物理建模方法 1.1 疏松沉积物岩石物理建模方法海域天然气水合物只存在于海底浅层疏松沉积物的特定层段内,大部分海底浅层疏松沉积物内并不富集天然气水合物,因此饱和水的疏松沉积物是天然气水合物形成和赋存的背景介质。在进行水合物的岩石物理建模之前,应解决其背景介质的岩石物理建模问题。在疏松沉积物的岩石物理建模中,首先要计算临界孔隙度条件下沉积物的弹性模量。Helgerud等[15]利用Hertz-Mindlin公式求取在临界孔隙度条件下的疏松干岩石体积模量Khm和剪切模量Ghm,即
| $ K_{\mathrm{hm}}=\left[\frac{C^{2}\left(1-\varPhi_{\mathrm{c}}\right)^{2} G^{2}}{18 {\rm{ \mathsf{ π} }}^{2}(1-v)^{2}} P\right]^{\frac{1}{3}} $ | (1) |
| $ G_{\mathrm{hm}}=\frac{5-4 v}{5(2-v)}\left[\frac{3 C^{2}\left(1-\varPhi_{\mathrm{c}}\right)^{2} G^{2}}{2 {\rm{ \mathsf{ π} }}^{2}(1-v)^{2}} P\right]^{\frac{1}{3}} $ | (2) |
式中:C为配位数(与一个沉积颗粒直接接触的沉积颗粒的平均数目);Φc为沉积物的临界孔隙度;G、v分别为沉积物颗粒的剪切模量、泊松比;P为沉积颗粒间的有效应力。深度d处地层的有效应力为
| $ P(d)=\int_{0}^{d}\left[\rho_{\mathrm{m}}(h)-\rho_{\mathrm{w}}\right] \mathrm{d} h $ | (3) |
式中:ρm(h)为深度h处地层密度;ρw为海水的密度。
由式(2)估算的横波速度容易偏大,为此,Av-seth等[20]将估算的横波速度乘以一个小于1的系数,但这种解决办法需要人为调整系数,并且改变横波速度意味着剪切模量的改变,同时会影响纵波速度。单纯改变估算的横波速度而不调整纵波速度,是不自洽的过程。式(2)的基础是假设接触的沉积物颗粒间完全咬合在一起,而现实的情况是,在饱和海水条件下海水对接触颗粒可能起到润滑作用,会导致沉积物骨架的剪切模量降低。考虑到这一点,引入一个与润滑作用相关的系数f,可以得到改进的Mindlin公式[21]
| $ G_{\mathrm{hm}}=\frac{2+3 f-v(1+3 f)}{5(2-v)}\left[\frac{3 C^{2}\left(1-\varPhi_{\mathrm{c}}\right)^{2} G^{2}}{2 {\rm{ \mathsf{ π} }}^{2}(1-v)^{2}} P\right]^{\frac{1}{3}} $ | (4) |
当f=1时,表示完全没有润滑作用,式(4)可以退化为式(2);当f=0时,表示颗粒间完全没有摩擦作用存在。在建模的过程中,可以适当调节参数f,避免单纯调节横波速度。
当疏松沉积物的孔隙度(Φ)小于临界孔隙度(即Φ < Φc)时,假设沉积物由组分1、2组成。其中组分1为Φ=Φc的疏松沉积物;组分2为Φ=0,但是矿物组分与疏松沉积物相同。此种条件下,如果组分1与组分2的体积和为1,组分2的体积为Ω,那么所有的孔隙空间由组分1贡献,即
| $ (1-\varOmega) \varPhi_{c}=\varPhi $ | (5) |
由上式可以得到组分1、组分2的体积百分含量分别为Φ/Φc、1-Φ/Φc。此时,干疏松沉积物的弹性模量可以通过Hashine-Shtrikman的下限[22]求得,即
| $ \left\{\begin{aligned} &K_{\mathrm{dry}}=\left(\frac{\frac{\varPhi}{\varPhi_{\mathrm{c}}}}{K_{\mathrm{hm}}+\frac{4 G_{\mathrm{hm}}}{3}}+\frac{1-\frac{\varPhi}{\varPhi_{\mathrm{c}}}}{K+\frac{4 G_{\mathrm{hm}}}{3}}\right)^{-1}-\frac{4}{3} G_{\mathrm{hm}}\\ &G_{\mathrm{dry}}=\left(\frac{\frac{\varPhi}{\varPhi_{\mathrm{c}}}}{G_{\mathrm{hm}}+Z}+\frac{1-\frac{\varPhi}{\varPhi_{\mathrm{c}}}}{K+Z}\right)^{-1}-\frac{4}{3} Z\\ &Z=\frac{G_{\mathrm{hm}}}{6}\left(\frac{9 K_{\mathrm{hm}}+8 G_{\mathrm{hm}}}{K_{\mathrm{hm}}+2 G_{\mathrm{hm}}}\right) \end{aligned}\right. $ | (6) |
式中:Kdry和Gdry分别为疏松沉积物骨架的体积模量和剪切模量;K为疏松沉积物基质的体积模量。
当疏松沉积物的孔隙度大于临界孔隙度(Φ > Φc)时,仿照上述过程,利用Hashine-Shtrikman的上限公式[22],求取干疏松沉积物的弹性模量为
| $ \left\{\begin{aligned} &K_{\mathrm{dry}}=\left(\frac{\frac{1-\varPhi}{1-\varPhi_{\mathrm{c}}}}{K_{\mathrm{hm}}+\frac{4}{3} G_{\mathrm{hm}}}+\frac{\frac{\varPhi-\varPhi_{\mathrm{c}}}{1-\varPhi_{\mathrm{c}}}}{\frac{4}{3} G_{\mathrm{hm}}}\right)^{-1}-\frac{4}{3} G_{\mathrm{hm}}\\ &G_{\mathrm{dry}}=\left(\frac{\frac{1-\varPhi}{1-\varPhi_{\mathrm{c}}}}{G_{\mathrm{hm}}+Z}+\frac{\frac{\varPhi-\varPhi_{\mathrm{c}}}{1-\varPhi_{\mathrm{c}}}}{Z}\right)^{-1}-Z \end{aligned}\right. $ | (7) |
在求得干疏松沉积物的弹性模量后,利用Gassmann方程,可求得饱和流体的疏松沉积物的弹性模量(Ksat)、剪切模量(Gsat)及纵波速度(VP)、横波速度(VS)
| $ \left\{\begin{array}{l} K_{\mathrm{sat}}=K_{\mathrm{dry}}+\frac{\left(1-\frac{K_{\mathrm{dry}}}{K_{\mathrm{m}}}\right)^{2}}{\frac{\varPhi}{K_{\mathrm{f}}}+\frac{1-\varPhi}{K_{\mathrm{m}}}-\frac{K_{\mathrm{dry}}}{K_{\mathrm{m}}^{2}}} \\ G_{\mathrm{sat}}=G_{\mathrm{dry}} \\ V_{\mathrm{P}}=\sqrt{\frac{K_{\mathrm{sat}}+\frac{4}{3} G_{\mathrm{sat}}}{\rho}} \\ V_{\mathrm{s}}=\sqrt{\frac{G_{\mathrm{sat}}}{\rho}} \end{array}\right. $ | (8) |
式中:Kf、Km分别为流体、岩石基质的体积模量;ρ为岩石的密度。
1.2 天然气水合物赋存形态及适用模型不同的温压条件及气源条件下,天然气水合物呈现不同的赋存形态。Dai等[23]基于天然气水合物与沉积颗粒之间的微观结构关系,将天然气水合物的赋存形态分为六类(图 1)。不同赋存形态的天然气水合物在岩石结构中所起的力学作用不同,对岩石的弹性性质的影响也不同,因而需要使用不同的岩石物理模型进行描述。
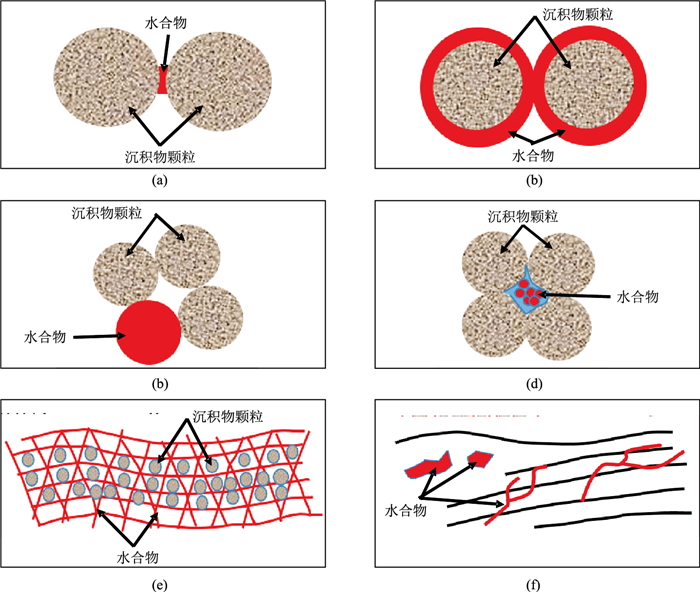
|
图 1 天然气水合物赋存形态示意图(据文献[23]修改) (a)第一类:水合物在沉积颗粒的接触处生长,水合物起胶结物作用;(b)第二类:水合物包裹沉积颗粒生长;(c)第三类:水合物在孔隙空间(红色)内生长并和沉积颗粒一同承担上覆地层压力;(d)第四类:水合物在孔隙空间内生长并作为流体(蓝色)的一部分;(e)第五类:水合物(水平红线)如冰层样均匀层状展布,水合物(斜交红线)作为岩石基质,而沉积物颗粒作为包体存在;(f)第六类:水合物(红色)呈结核状生长或沿地层裂缝(黑色)生长 |
(1) 第一类与第二类赋存形态的天然气水合物可以应用接触—胶结模型进行描述。该模型干沉积物的体积模量和剪切模量分别为[24]
| $ \left\{\begin{array}{l} K_{\mathrm{dry}}=\frac{C\left(1-\varPhi_{0}\right)}{6}\left(K_{\mathrm{h}}+G_{\mathrm{h}}\right) S_{\mathrm{n}} \\ G_{\mathrm{dry}}=\frac{K_{\mathrm{dry}}}{5}+\frac{C\left(1-\varPhi_{0}\right)}{3} G_{\mathrm{h}} S_{\tau} \end{array}\right. $ | (9) |
式中:Kh和Gh分别为天然气水合物的体积模量和剪切模量;Φ0为沉积物未发育天然气水合物时的孔隙度;Sn和Sτ分别为
| $ \left\{\begin{array}{l} S_{\mathrm{n}}=A_{\mathrm{n}}\left(\omega_{\mathrm{n}}\right) \alpha^{2}+B_{\mathrm{n}}\left(\omega_{\mathrm{n}}\right) \alpha+C_{\mathrm{n}}\left(\omega_{\mathrm{n}}\right) \\ A_{\mathrm{n}}\left(\omega_{\mathrm{n}}\right)=-0.024153 \cdot \omega_{\mathrm{n}}^{-1.3646} \\ B_{\mathrm{n}}\left(\omega_{\mathrm{n}}\right)=0.20405 \cdot \omega_{\mathrm{n}}^{-0.89008} \\ C_{\mathrm{n}}\left(\omega_{\mathrm{n}}\right)=-0.00024649 \cdot \omega_{\mathrm{n}}^{-1.9864} \\ \omega_{\mathrm{n}}=\frac{2 G_{\mathrm{h}}(1-v)\left(1-v_{\mathrm{h}}\right)}{{\rm{ \mathsf{ π} }} G(1-2 v)} \end{array}\right. $ | (10) |
| $ \left\{\begin{aligned} &S_{\tau}=A_{\tau}\left(\omega_{\tau}, v\right) \alpha^{2}+B_{\tau}\left(\omega_{\tau}, v\right) \alpha+C_{\tau}\left(\omega_{\tau}, v\right) \\ &A_{\tau}\left(\omega_{\tau}, v\right)=-0.01\left(2.26 v^{2}+2.07 v+2.3\right) \times \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \omega_{\tau}^{0.079 v^{2}+0.1754 v-1.342} \\ &B_{\tau}\left(\omega_{\tau}, v\right)=\left(0.0573 v^{2}+0.0937 v+0.202\right) \times \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \omega_{\tau}^{0.0274 v^{2}+0.0529 v-0.8765} \\ &C_{\tau}\left(\omega_{\tau}, v\right)= 10^{-4} \cdot\left(9.654 v^{2}+4.945 v+3.1\right) \times \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \omega_{\tau}^{0.01867 v^{2}+0.4011 v-1.8186} \\ &\omega_{\tau}=\frac{G_{\mathrm{h}}}{{\rm{ \mathsf{ π} }} G} \end{aligned}\right. $ | (11) |
式中:vh为天然气水合物的泊松比;参量α为胶结物接触半径与沉积物颗粒半径的比值。在第一类赋存形态下有
| $ \alpha=2\left[\frac{S_{\mathrm{gh}} \varPhi_{0}}{3 C\left(1-\varPhi_{0}\right)}\right]^{0.25} $ | (12) |
式中Sgh为水合物饱和度。在第二类赋存形态有
| $ \alpha=\left[\frac{2 S_{\mathrm{gh}} \varPhi_{0}}{3\left(1-\varPhi_{0}\right)}\right]^{0.5} $ | (13) |
(2) 第三类与第四类赋存形态的水合物都可以用上述疏松沉积物模型进行描述,只是在对水合物的处理方法上有所差异。对于第三类赋存形态模型,可将水合物作为沉积颗粒的一部分。对于第四类赋存形态模型,则将水合物作为孔隙流体的一部分。实际上第三类与第四类赋存形态的水合物可以同时存在,即一部分天然气水合物分散于孔隙流体中,一部分天然气水合物直接与沉积颗粒混杂接触起到颗粒支撑的作用。基于此,可以将第三类与第四类赋存形态的水合物作为一个整体进行考虑,并用疏松沉积物模型进行描述。在建模中引入参量γ表示起颗粒支撑作用水合物的占比,即
| $ \varOmega_{\mathrm{hm}}=\varPhi \cdot S_{\mathrm{gh}} \cdot \gamma $ | (14) |
| $ \varPhi^{\prime}=\varPhi\left(1-S_{\mathrm{gh}} \cdot \gamma\right) $ | (15) |
| $ S_{\mathrm{gh}}^{\prime}=\frac{S_{\mathrm{gh}} \cdot(1-\gamma)}{1-S_{\mathrm{gh}} \cdot \gamma} $ | (16) |
式中:Ωhm为单位体积的岩石内作为颗粒支撑水合物的体积;Φ'是水合物作为颗粒支撑后岩石的孔隙度;Sgh'是孔隙中流体部分的水合物的饱和度。在此条件下,沉积物基质体积模量和剪切模量分别为
| $ \begin{gathered} K=\frac{1}{2}\left[\left(\sum\limits_{i=1}^{N} \frac{\varGamma_{i} K_{i}}{1+\frac{\varPhi}{1-\varPhi} \cdot S_{\mathrm{gh}} \cdot \gamma}+\frac{K_{\mathrm{gh}}}{1+\frac{1-\varPhi}{\varPhi \cdot S_{\mathrm{gh}} \cdot \gamma}}\right)+\right. \\ \left.\left(\sum\limits_{i=1}^{N} \frac{\varGamma_{i}}{1+\frac{\varPhi}{1-\varPhi} \cdot S_{\mathrm{gh}} \cdot \gamma} \frac{1}{K_{i}}+\frac{\frac{1}{K_{\mathrm{gh}}}}{1+\frac{1-\varPhi}{\varPhi \cdot S_{\mathrm{gh}} \cdot \gamma}}\right)^{-1}\right] \end{gathered} $ | (17) |
| $ \begin{aligned} &G=\frac{1}{2}\left[\left(\sum\limits_{i=1}^{N} \frac{\varGamma_{i} G_{i}}{1+\frac{\varPhi}{1-\varPhi} \cdot S_{\mathrm{gh}} \cdot \gamma}+\frac{G_{\mathrm{gh}}}{1+\frac{1-\varPhi}{\varPhi \cdot S_{\mathrm{gh}} \cdot \gamma}}\right)+\right.\\ &\left.\left(\sum\limits_{i=1}^{N} \frac{\varGamma_{i}}{1+\frac{\varPhi}{1-\varPhi} \cdot S_{\mathrm{gh}} \cdot \gamma} \frac{1}{G_{i}}+\frac{\frac{1}{G_{\mathrm{gh}}}}{1+\frac{1-\varPhi}{\varPhi \cdot S_{\mathrm{gh}} \cdot \gamma}}\right)^{-1}\right] \end{aligned} $ | (18) |
式中:Γi、Gi、Ki分别为沉积物颗粒中第i种矿物的体积百分比、剪切模量、体积模量。孔隙流体的体积模量可以由Wood方程计算
| $ K_{\mathrm{f}}=\frac{S_{\mathrm{gh}}^{\prime}}{K_{\mathrm{h}}}+\frac{1-S_{\mathrm{gh}}^{\prime}}{K_{\mathrm{w}}} $ | (19) |
式中Kh、Kw分别为水合物、海水的体积模量。
(3) 第五类赋存形态的水合物沉积体系适用于采用经典的K-T模型和DEM模型进行描述。在此体系中,将天然气水合物作为岩石基质,而将沉积物颗粒作为包体。尽管从理论上可以计算在低饱和度条件下这类模型的弹性参数,但是在物理意义方面,作为岩石基质的成分必须占据足够的体积才能成为岩石基质。因此,在这种情况下,要求水合物的饱和度足够高,一般存在于永久冻土带中,海域水合物中较为少见。
(4) 对于第六类状态赋存的水合物,Lee[14]提出可以利用层状介质理论和Backus平均的方式描述。以此状态赋存的水合物局部饱和度较高。
在特定工区,可以由岩心观察或岩心CT及电阻率成像等方法获得天然气水合物的赋存形态,据此可以选择相应的模型进行岩石物理建模和分析,也可以利用各类模型对数据进行拟合,确定最优的模型和天然气水合物可能的赋存形态。有些准则可以用来大致判断水合物的赋存形态及其适用模型。首先,第五类赋存形态的水合物沉积体系纵波速度应该与水合物本身的速度接近;其次,第一类及第二类赋存形态存在的水合物沉积体系纵波速度远大于以第三类和第四类赋存形态存在的水合物沉积体系;最后,以第六类状态赋存的水合物沉积体系在密度测井曲线上会表现出局部低值,并在纵波速度、横波速度曲线上表现出局部高值的特点。根据这些准则并结合模型估算,可以大致判断水合物可能的赋存形态及其适用模型。
2 实际算例以A海域研究区六口浅钻井为例测试本文方法。由图 2可见,密度及纵波速度随深度增加而增大,反映了疏松沉积物随埋深增大而不断压实的趋势。同时,密度值在1.4~2.1g/cm3变化,没有接近于水或天然气水合物的密度异常值,表明不存在以第六类赋存形态为主的水合物沉积体系。纵波速度总体为低值(< 2200m/s),说明不存在以第五类赋存形态的天然气水合物沉积体系。因此,重点讨论在第一类~第四类水合物赋存形态中选择模型。
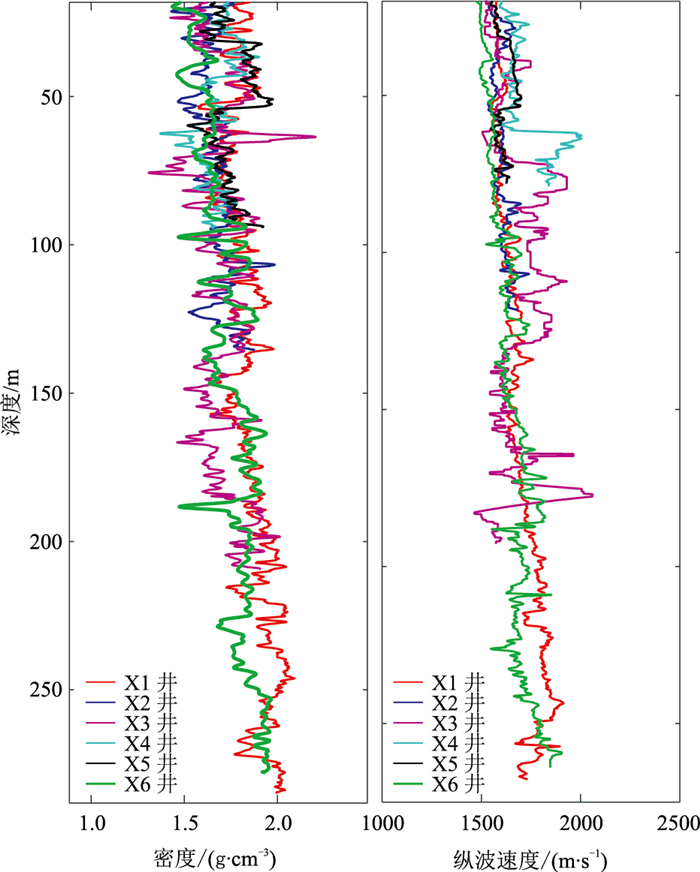
|
图 2 六口浅钻井密度(左)和纵波速度(右)测井曲线深度自海底起算 |
X1井井段较长,未发现天然气水合物,可以直接应用疏松沉积物的岩石物理模型提供全区使用的背景介质的建模参数。所有井都有放射性、密度、电阻率以及核磁测井等资料,通过测井解释可获得详细的矿物组分和孔隙度数据。由图 3可见,X1井疏松沉积物的孔隙度范围为40%~60%,造成这种超高孔隙度的原因一方面是由于沉积物的疏松性所致,另一方面也反映了沉积物颗粒的圆度系数较小。沉积颗粒为非规则圆球形状的孔隙度较规则球体的孔隙度大。根据文献[25],圆度系数在0.4左右的沉积颗粒的孔隙度可以达到70%,结合密度在1.75~2.00g/cm3变化,可以认为X1井孔隙度是可靠的。建模所用各组分的弹性参数如表 1所示。
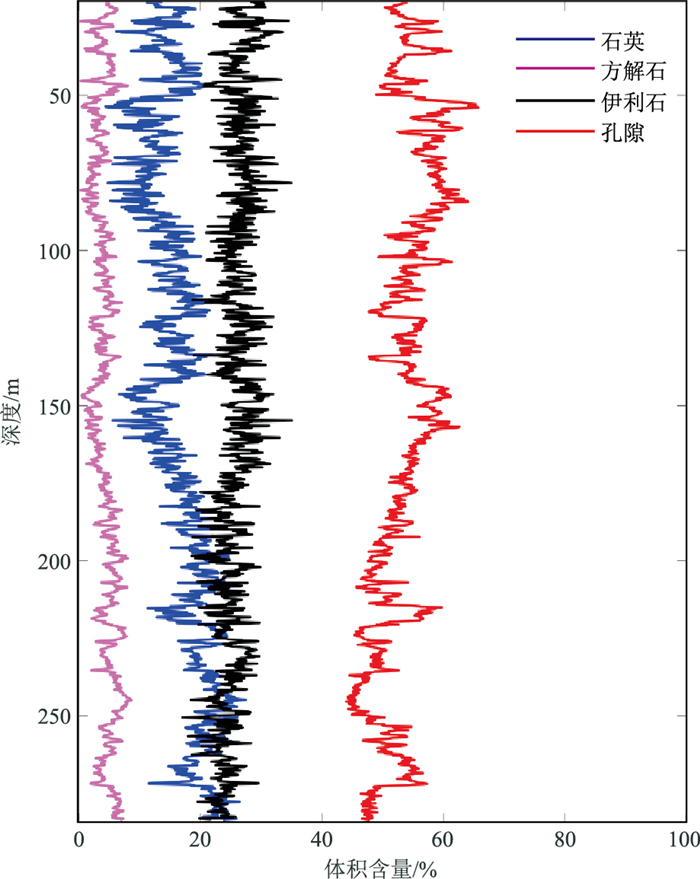
|
图 3 X1井的矿物含量及孔隙度曲线 |
|
|
表 1 建模所用各组分的弹性参数表 |
在应用式(1)~式(5)计算临界孔隙状态下疏松沉积物的体积模量过程中,本文根据Garcia等[26]确定沉积物的配位数。综合考虑研究区超高孔隙度状态,取Φc=0.65。图 4为利用上述参数进行岩石物理建模的结果与实测曲线的对比。由图可见,改进的Hertz-Mindlin模型建模结果与实测曲线吻合度较高,而传统Hertz-Mindlin模型的计算结果明显偏高,特别是估计的横波速度远大于实测速度(约高出实测横波速度的80%~100%)。
| $ C=4.46+\left(\varPhi_{c}-\varPhi\right)^{0.48} $ | (20) |
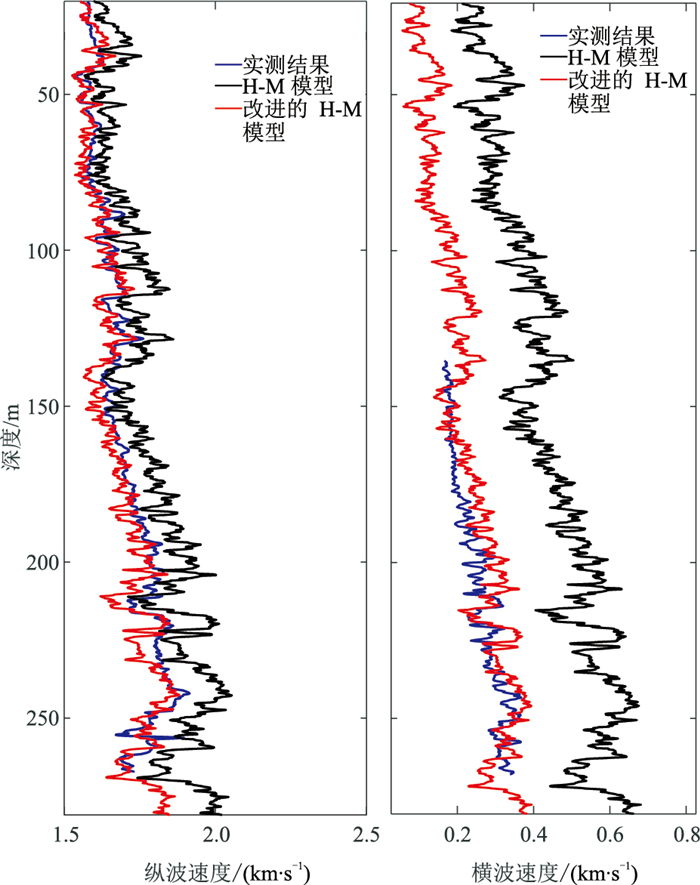
|
图 4 X1井不同岩石物理建模结果与实测曲线对比H-M模型为Hertz-Mindlin模型的简称 |
为进一步研究不同赋存形态天然气水合物对沉积体系纵波速度、横波速度的影响,改变X1井的天然气水合物饱和度(分别为10%、40%),并分别计算不同模型对应的纵波速度、横波速度(图 5)。由图可见,水合物以第一、第二类赋存形态存在时,沉积物的速度明显大于第三、第四类赋存形态。这说明水合物若以第一、第二类赋存形态存在,即使在饱和度很低的条件下(如10%),也会显著增加沉积物的纵波速度、横波速度。在低水合物饱和度条件下,第三类与第四类模型结果极为接近(图 5a中二者几乎完全重合),并与零饱和度条件下的测井曲线接近。这说明低饱和度条件下,第三、第四类赋存形态水合物对沉积物的纵波速度、横波速度影响较小。饱和度增大时(图 5b),第三类模型的纵波速度、横波速度有所增大,而第四类赋存形态的水合物则对沉积物的横波速度影响极小,这是因为其作为孔隙流体存在所决定的。
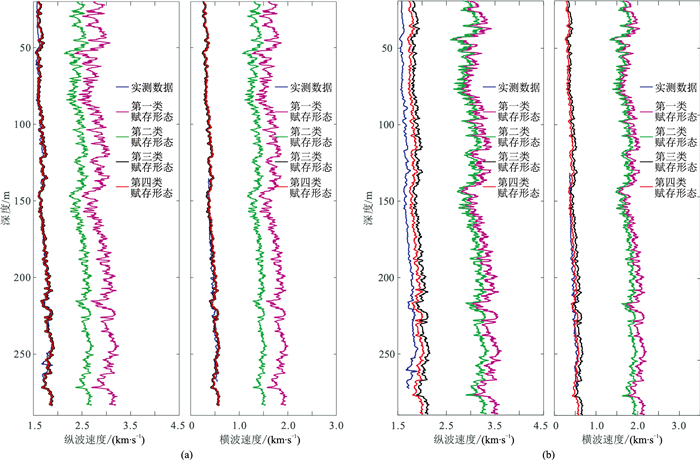
|
图 5 不同天然气水合物饱和度条件下X1井测井曲线与岩石物理建模纵波速度、横波速度对比 (a)10%;(b)40% |
观察区内六口浅钻井的纵波速度曲线(图 2右),可以排除水合物以第一、第二类赋存形态存在的可能性。研究区内水合物的饱和度整体不高,第三类、第四类赋存形态的建模结果接近(图 5)。从建模方法的角度看,第三类赋存形态模型可以包含第四类赋存形态模型。如前所述,将沉积物体系中的包含的水合物分为两部分,一部分按与沉积物颗粒做相同处理,一部分当作孔隙流体处理。因此,以第三、第四类赋存形态模型为基础,制定如下混合模型的岩石物理建模流程。
(1) 假设起颗粒支撑作用的水合物的体积占比初值γ=γ0。
(2) 利用式(17)、式(18)计算沉积颗粒(岩石基质)的体积模量和剪切模量;利用式(14)~式(16)修改沉积物的孔隙度及水合物的饱和度,利用式(19)计算孔隙流体的体积模量。
(3) 利用式(1)、式(4)计算临界孔隙状态的体积模量和剪切模量,利用式(6)~式(7)计算沉积物骨架的体积模量。
(4) 利用式(8)计算沉积体物的体积模量、剪切模量及纵波速度、横波速度。
(5) 对比建模结果与实测结果,若实测结果大于建模结果,则在(0,1)内增加γ值,反之则在(0,1)内减小γ值;返回步骤(2),进行循环。终止循环准则为γ值的变化小于某设定门槛值或者γ值达到0或1。
利用这一流程对研究区内的其他井进行了岩石物理建模,图 6为其中的一口井的建模结果。由图可见,所采用的模型模拟的纵波速度、横波速度精度较高。在少数数据点出现与实测速度偏离较大的现象,推测是由于横波测井解释的精度不高所致。
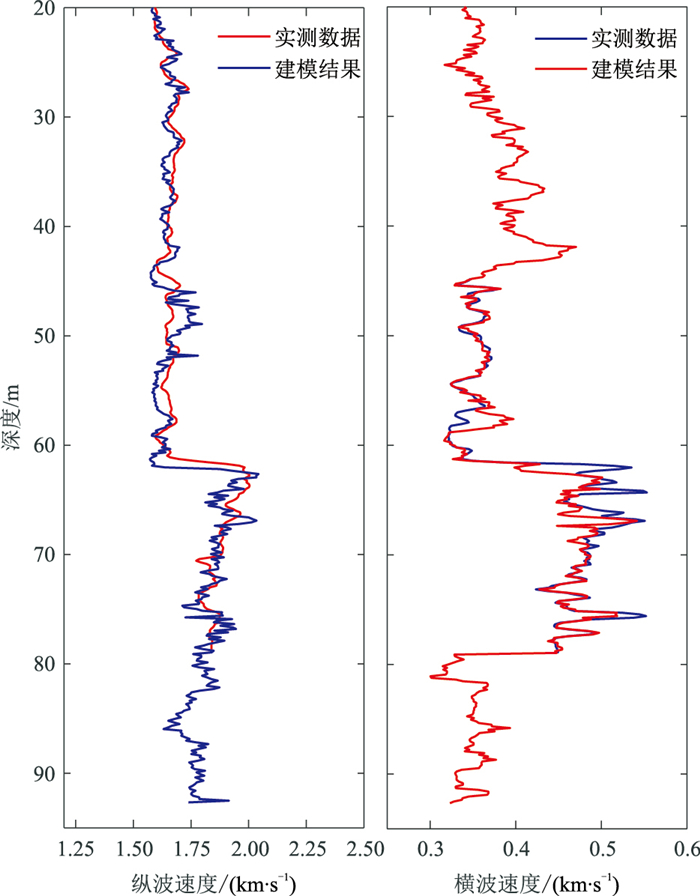
|
图 6 X4井实测与岩石物理建模波速度纵、横波速度对比 |
疏松沉积物是天然气水合物赋存的背景介质,针对疏松沉积物岩石物理建模中存在横波速度偏大的问题,引入了修正的Hertz-Mindlin方程,使建模过程自洽,并提高了建模精度。
本文讨论了天然气水合物可能的赋存形式及其适用模型。不同赋存形态的天然气水合物对沉积物的弹性性质影响不同,通过一些简单的准则可以快速判定(或排除)一些较为特殊的赋存形态。
建立了兼容第三、第四类赋存形态模型的岩石物理建模流程,获得了高精度的岩石物理建模结果。为进一步的理解水合物对沉积体系弹性性质的影响提供了理论和方法支撑。
目前,针对海域天然气水合物沉积体系的岩石物理方面的认识仍处在探索阶段。虽然利用现有的岩石物理模型进行组合可以较好地模拟水合物沉积体系的岩石物理性质,但是必须意识到,现有的理论和模型仍缺乏足够的实验数据支撑,特别是关于天然气水合物的赋存形态的模型尽管被广泛引用和论述,但是仍然需要勘探实践和实验室观测进一步证实。
| [1] |
MAKOGON Y F, HOLDITCH S A, MAKOGON T Y. Natural gas-hydrates—a potential energy source for the 21st Century[J]. Journal of Petroleum Science and Engineering, 2007, 56(1-3): 14-31. DOI:10.1016/j.petrol.2005.10.009 |
| [2] |
BOSWELL R, COLLETT T S. Current perspectives on gas hydrate resources[J]. Energy & Environmental Science, 2011, 4(4): 1206-1215. |
| [3] |
SLOAN E D. Clathrate Hydrates of Natural Gases[M]. Marcel Dekker, New York, 1998.
|
| [4] |
梁金强, 王宏斌, 苏新, 等. 南海北部陆坡天然气水合物成藏条件及其控制因素[J]. 天然气工业, 2014, 34(7): 128-135. LIANG Jinqiang, WANG Hongbin, SU Xin, et al. Natural gas hydrate formation conditions and the associated controlling factors in the northern slope of the South China Sea[J]. Natural Gas Industry, 2014, 34(7): 128-135. |
| [5] |
张光学, 梁金强, 陆敬安, 等. 南海东北部陆坡天然气水合物藏特征[J]. 天然气工业, 2014, 34(11): 1-10. ZHANG Guangxue, LIANG Jinqiang, LU Jing'an, et al. Characteristics of natural gas hydrate reservoirs on the northeastern slope of the South China Sea[J]. Natural Gas Industry, 2014, 34(11): 1-10. |
| [6] |
杜浩, 石万忠, 梁金强, 等. 琼东南盆地块体搬运沉积体系成因及其对水合物成藏的影响[J]. 石油地球物理勘探, 2021, 56(4): 869-881. DU Hao, SHI Wanzhong, LIANG Jinqiang, et al. Genesis of mass transport deposits and their effect on gas hydrate accumulation in the Qiongdongnan Basin[J]. Oil Geophysical Prospecting, 2021, 56(4): 869-881. |
| [7] |
CARCIONE J M, TINIVELLA U. Bottom-simulating reflectors: seismic velocities and AVO effects[J]. Geophysics, 2000, 65(1): 54-67. DOI:10.1190/1.1444725 |
| [8] |
赵群, 郭建, 郝守玲, 等. 模拟天然气水合物的岩石物理特性模型实验[J]. 地球物理学报, 2005, 48(3): 649-655. ZHAO Qun, GUO Jian, HAO Shouling, et al. Experiments of physical modeling for petrophysical properties of natural gas hydrate[J]. Chinese Journal of Geophysics, 2005, 48(3): 649-655. DOI:10.3321/j.issn:0001-5733.2005.03.024 |
| [9] |
张如伟, 张宝金, 黄捍东, 等. 天然气水合物沉积层的AVA特征[J]. 石油地球物理勘探, 2011, 46(4): 634-639. ZHANG Ruwei, ZHANG Baojin, HUANG Handong, et al. AVA characters on gas hydrate-bearing sedimentary deposit[J]. Oil Geophysical Prospecting, 2011, 46(4): 634-639. |
| [10] |
王新全, 刘晖, 王林, 等. 南祁连盆地天然气水合物地震勘探技术[J]. 石油地球物理勘探, 2017, 52(4): 644-650. WANG Xinquan, LIU Hui, WANG Lin, et al. Seismic exploration for natural gas hydrate in the South Qilian Basin[J]. Oil Geophysical Prospecting, 2017, 52(4): 644-650. |
| [11] |
霍元媛, 张明. 基于遗传算法的天然气水合物似海底反射层速度结构全波形反演[J]. 石油地球物理勘探, 2010, 45(1): 55-59. HUO Yuanyuan, ZHANG Ming. The genetic algorithm based velocity structure waveform inversion for gas hydrate bottom simulating reflection (BSR)[J]. Oil Geophysical Prospecting, 2010, 45(1): 55-59. |
| [12] |
杨静, 张雷, 王九拴, 等. 基于模型正演的天然气水合物定量描述[J]. 石油地球物理勘探, 2020, 55(2): 419-425. YANG Jing, ZHANG Lei, WANG Jiushuan, et al. Quantitative characterization of gas hydrate based on forward modeling[J]. Oil Geophysical Prospecting, 2020, 55(2): 419-425. |
| [13] |
张聿文, 刘学伟, 金玉洁. 含天然气水合物地层的速度和衰减研究[J]. 石油地球物理勘探, 2004, 39(2): 205-214. ZHANG Yuwen, LIU Xuewei, JIN Yujie. Study of velocity and attenuation for gas-bearing hydrate formation[J]. Oil Geophysical Prospecting, 2004, 39(2): 205-214. DOI:10.3321/j.issn:1000-7210.2004.02.017 |
| [14] |
LEE M W, HUTCHINSON D R, COLLETT T S, et al. Seismic velocities for hydrate-bearing sediments using weighted equation[J]. Journal of Geophysical Research-Solid Earth, 1996, 101(B9): 20347-20358. DOI:10.1029/96JB01886 |
| [15] |
HELGERUD M B, DVORKIN J, NUR A, et al. Elastic-wave velocity in marine sediments with gas hydrates: effective medium modeling[J]. Geophysical Research Letters, 1999, 26(13): 2021-2024. DOI:10.1029/1999GL900421 |
| [16] |
ECKER C, DVORKIN J, NUR A. Sediments with gas hydrates: internal structure from seismic AVO[J]. Geophysics, 1998, 63(5): 1659-1669. DOI:10.1190/1.1444462 |
| [17] |
宋海斌, OSAMU M, 杨胜雄, 等. 含天然气水合物沉积物的岩石物性模型与似海底反射层的AVA特征[J]. 地球物理学报, 2002, 45(4): 546-556. SONG Haibin, OSAMU M, YANG Shengxiong, et al. Physical property models of gas hydrate-bearing sediments and AVA character of bottom simulating reflector[J]. Chinese Journal of Geophysics, 2002, 45(4): 546-556. DOI:10.3321/j.issn:0001-5733.2002.04.012 |
| [18] |
刘欣欣, 印兴耀, 栾锡武. 天然气水合物地层岩石物理模型构建[J]. 中国科学(地球科学), 2018, 48(9): 1248-1266. LIU Xinxin, YIN Xingyao, LUAN Xiwu. Seismic rock physical modelling for gas hydrate-bearing sediments[J]. Scientia Sinica(Terrae), 2018, 48(9): 1248-1266. |
| [19] |
孟大江, 文鹏飞, 张如伟, 等. 天然气水合物横波速度等效介质模型预测方法[J]. 石油地球物理勘探, 2020, 55(1): 117-125. MENG Dajiang, WEN Pengfei, ZHANG Ruwei, et al. Gas hydrate S-wave velocity prediction method based on effective medium model[J]. Oil Geophysical Prospecting, 2020, 55(1): 117-125. |
| [20] |
AVSETH P, MUKERJI T, MAVKO G. Quantitative Seismic Interpretation: Applying Rock Physics Tools to Reduce Interpretation Risk[M]. Cambridge: Cambridge University Press, 2010.
|
| [21] |
MAVKO G, MUKERJI T, DVORKIN J. The Rock Physics Handbook: Tools for Seismic Analysis in Porous Media[M]. Cambridge: Cambridge University Press, 1998.
|
| [22] |
HASHIN Z, SHTRIKMAN S. A variational approach to the theory of the elastic behaviour of multiphase materials[J]. Journal of the Mechanics and Physics of Solids, 1963, 11(2): 127-140. DOI:10.1016/0022-5096(63)90060-7 |
| [23] |
DAI J C, SNYDER F, GILLESPIE D, et al. Exploration for gas hydrates in the deepwater, northern Gulf of Mexico: Part Ⅰ. A seismic approach based on geologic model, inversion, and rock physics principles[J]. Marine and Petroleum Geology, 2008, 25(9): 830-844. DOI:10.1016/j.marpetgeo.2008.02.006 |
| [24] |
DVORKIN J, NUR A. Elasticity of high-porosity sandstones: theory for two North Sea data sets[J]. Geophysics, 1996, 61(5): 1363-1370. DOI:10.1190/1.1444059 |
| [25] |
WADELL H. Volume, shape, and roundness of rock particles[J]. The Journal of Geology, 1932, 40(5): 443-451. DOI:10.1086/623964 |
| [26] |
GARCIA X, MEDINA E A. Hysteresis effects stu-died by numerical simulations: cyclic loading-unloading of a realistic sand model[J]. Geophysics, 2006, 71(2): F13-F20. DOI:10.1190/1.2181309 |



 张金强,北京市昌平区沙河镇百沙路197号中国石化科学技术研究中心,102206。Email:
张金强,北京市昌平区沙河镇百沙路197号中国石化科学技术研究中心,102206。Email: