② 中国石化弹性波理论与探测技术重点实验室,北京 100083;
③ 中国石化石油勘探开发研究院,北京 100083;
④ 齐鲁工业大学(山东省科学院)山东省科学院 海洋仪器仪表研究院,山东青岛 266061;
⑤ 中国石油大学(华东)深层油气重点实验室,山东青岛 266580
② SINOPEC Key Laboratory of Seismic Elastic Wave Technology, Beijing 100083, China;
③ SINOPEC Petroleum Exploration and Production Research Institute, Beijing 100083, China;
④ Institute of Oceanographic Instrumentation, Qilu University of Technology (Shandong Academy of Sciences), Qingdao, Shandong 266100, China;
⑤ Key Laboratory of Deep Oil and Gas, China University of Petroleum (East China), Qingdao, Shandong 266580, China
逆时偏移(RTM)方法[1-4]于20世纪80年代提出,该方法基于波动方程实现波场延拓,以其无倾角限制、能对多种波(反射波、多次波、棱柱波)成像而受到广泛关注[5-6]。弹性波逆时偏移(ERTM)算法[7-8]由McMechan研究组提出,采用更接近真实的弹性介质和弹性波场,与传统的声波RTM成像方法相比,理论假设与实际更接近,并能同时实现纵波和横波的深度域成像。
地震波波场分离是ERTM方法中的重要环节,也是得到纯波模式成像结果的关键一步。除了基于Helmholtz定理的波场分离方法[9-12]以外,目前常用的是解耦延拓方程法[13-16]。解耦延拓方程法可在波场延拓过程中实现均匀介质的纵、横波质点位移的解耦或者质点振动速度的矢量解耦,但在应力解耦时,横波应力存在能量串扰问题[17-19]。为解决横波应力中的纵波串扰问题,Du等[16-17]提出了伪横波应力构建方法,实现了纵波和横波应力的解耦。
共成像点道集(CIG)作为叠前深度偏移的重要输出道集,可以用于改善成像质量,提供反映地下岩性的振幅和相位等信息,同时能用于速度建模。CIG[20]主要分为共炮检距道集(Common-offset CIG,COCIG)和角度域道集(Angle-domain CIG,ADCIG)。Sava等[21]利用单程波偏移提取地下局部COCIG,通过转换获得ADCIG。三维情况下,Xu等[22-23]在频率—波数域通过传播方向求取反射角信息和方位角信息,利用合适的成像条件提取角道集,优点是角道集质量较好,缺点是计算量和存储量均较大。王保利等[24]在实现过程中利用波场延拓获得的质点振动速度和应力,提取了成像点处的Poynting矢量,从而确定入射波和反射波的传播方向,最后通过构建成像条件提取了ADCIG,该方法简单易行;汪天池等[25]将该方法拓展到倾角域进行反射波与绕射波分离以实现绕射波RTM。Zhao等[26]通过提取地下COCIG进而提取了PP波和PS波的ADCIG,并分析了二者的运动学特征。Wang等[27]通过构建Poynting矢量提取了PP波和PS波的ADCIG,但该方法没有考虑分离得到的横波应力存在的纵波能量串扰问题。
针对横波应力串扰问题,本文基于解耦延拓方程及伪横波应力构建方法,开展了基于Poynting矢量提取横波反射角的研究,构建了基于ERTM的PP波和PS波ADCIG求取方法;针对PP波ADCIG不同角度的成像特性,提出了把ADCIG按角度衰减的叠加成像策略。最后应用模型数据验证了本文方法的正确性。
1 方法原理 1.1 解耦延拓方程ERTM是利用弹性波动方程进行波场延拓,并结合波场分离方法得到解耦的震源端和检波端的纵/横波波场,然后运用弹性波成像条件得到最终的PP波和PS波成像结果。解耦延拓方程[14-19]能实现弹性波场的构建和解耦。其中,一阶弹性波波场方程[18]为
| $ \left\{\begin{array}{l} \rho \frac{\partial v_{x}}{\partial t}=\frac{\partial \tau_{x x}}{\partial x}+\frac{\partial \tau_{x z}}{\partial z} \\ \rho \frac{\partial v_{z}}{\partial t}=\frac{\partial \tau_{x z}}{\partial x}+\frac{\partial \tau_{z z}}{\partial z} \\ \frac{\partial \tau_{x x}}{\partial t}=(\lambda+2 \mu) \frac{\partial v_{x}}{\partial x}+\lambda \frac{\partial v_{z}}{\partial z} \\ \frac{\partial \tau_{z z}}{\partial t}=\lambda \frac{\partial v_{x}}{\partial x}+(\lambda+2 \mu) \frac{\partial v_{z}}{\partial z} \\ \frac{\partial \tau_{x z}}{\partial t}=\mu \frac{\partial v_{z}}{\partial x}+\mu \frac{\partial v_{x}}{\partial z} \end{array}\right. $ | (1) |
纵波方程为
| $ \left\{\begin{array}{l} \frac{\partial \tau_{\mathrm{P}}}{\partial t}=(\lambda+2 \mu)\left(\frac{\partial v_{x}}{\partial x}+\frac{\partial v_{z}}{\partial z}\right) \\ \frac{\partial v_{\mathrm{P}, x}}{\partial t}=\frac{1}{\rho} \frac{\partial \tau_{\mathrm{P}}}{\partial x} \\ \frac{\partial v_{\mathrm{P}, z}}{\partial t}=\frac{1}{\rho} \frac{\partial \tau_{\mathrm{P}}}{\partial z} \end{array}\right. $ | (2) |
横波波场可表示为
| $ \left\{\begin{array}{l} v_{\mathrm{S}, x}=v_{x}-v_{\mathrm{P}, x} \\ v_{\mathrm{S}, z}=v_{z}-v_{\mathrm{P}, z} \end{array}\right. $ | (3) |
式中:vx、vz分别为总弹性波场中x和z方向的质点振动速度分量;vP, x、vP, z为纵波波场的两个方向速度分量;vS, x、vS, z为横波波场的两个方向速度分量;τxx、τzz、τxz为总弹性波场应力分量;τP为纵波体应力;λ、μ和ρ分别为弹性介质的拉梅常数和密度。
总弹性波场应力分量减去纵波体应力τP,可以构建横波应力分量[15, 17]
| $ \left\{\begin{array}{l} \frac{\partial \tau_{\mathrm{S}, x x}}{\partial t}=-2 \mu \frac{\partial v_{z}}{\partial z} \\ \frac{\partial \tau_{\mathrm{S}, z z}}{\partial t}=-2 \mu \frac{\partial v_{x}}{\partial x} \\ \frac{\partial \tau_{\mathrm{S}, x z}}{\partial t}=\mu\left(\frac{\partial v_{x}}{\partial z}+\frac{\partial v_{z}}{\partial x}\right) \end{array}\right. $ | (4) |
式中τS, xx、τS, zz和τS, xz为横波应力分量。对上式进行时间积分,可得由弹性应变表示的横波应力
| $ \tau_{\mathrm{S}, i j}=2 \mu\left(\varepsilon_{i j}-b \delta_{i j}\right) $ | (5) |
式中:εij为弹性应变分量;b=εxx+εzz,为弹性体应变。由于弹性应变既包含纵波应变εP, ij,又包含横波应变εS, ij,则有
| $ \varepsilon_{i j}=\varepsilon_{\mathrm{P}, i j}+\varepsilon_{\mathrm{S}, i j} $ | (6) |
同时横波应力可以改写为
| $ \tau_{\mathrm{S}, i j}=2 \mu\left[\left(\varepsilon_{\mathrm{P}, i j}+\varepsilon_{\mathrm{S}, i j}\right)-\left(b_{\mathrm{P}}+b_{\mathrm{S}}\right) \delta_{i j}\right] $ | (7) |
式中:bP=εP, xx+εP, zz,为纵波体应变;bS=εS, xx+εS, zz,为横波体应变。可见横波应力除了横波应变作用2μ(εS, ij-bSδij)外,还有纵波应变作用2μ(εP, ij-bPδδij),因此,横波应力中含有纵波串扰。
为压制纵波能量在横波应力中的影响,Du等[16-17]基于横波质点振动速度提出了伪横波应力构建方程
| $ \left\{\begin{array}{l} \frac{\partial \tau_{\mathrm{qS}, x x}}{\partial t}=-2 \mu \frac{\partial v_{\mathrm{S}, z}}{\partial z} \\ \frac{\partial \tau_{\mathrm{qS}, z z}}{\partial t}=-2 \mu \frac{\partial v_{\mathrm{S}, x}}{\partial x} \\ \frac{\partial \tau_{\mathrm{qS}, x z}}{\partial t}=\mu\left(\frac{\partial v_{\mathrm{S}, x}}{\partial z}+\frac{\partial v_{\mathrm{S}, z}}{\partial x}\right) \end{array}\right. $ | (8) |
式中:τqS, xx和τqS, zz分别为x方向和z方向的伪横波正应力分量;τqS, xz为伪横波切应力。基于横波质点振动速度构建的伪横波应力与横波应力在形式上保持一致。不同于横波应力,伪横波应力只与横波质点振动速度相关,避免了纵波应变对横波应力的影响。由于横波质点振动速度满足
Poynting将能流密度矢量用于描述电磁能传播方向,即通过电场强度与磁场强度点乘得到电磁波的传播方向,后人把能流密度矢量称为Poynting矢量。Yoon等[28]给出了地震波场Poynting矢量表达式
| $ \boldsymbol{S}=-\boldsymbol{v} \cdot \boldsymbol{\tau} $ | (9) |
式中:v=(vx,vz)为质点振动速度矢量;τ为应力张量。
利用解耦的质点振动速度及应力,可以确定纵波和横波的Poynting矢量,进而确定纵波和横波能量传播方向。
图 1给出了纵波Poynting矢量与反射角的关系,其中SPs和SPr分别为纵波震源波场、检波点波场的Poynting矢量,β为纵波入射角(反射角)。根据余弦定理,可得纵波震源波场的Poynting矢量和纵波检波波场的Poynting矢量之间所确定的PP波开角
| $ \theta_{\mathrm{PP}}=\arccos \frac{\boldsymbol{S}_{\mathrm{P}}^{\mathrm{s}} \cdot \boldsymbol{S}_{\mathrm{P}}^{\mathrm{r}}}{\left|\boldsymbol{S}_{\mathrm{P}}^{\mathrm{s}}\right|\left|\boldsymbol{S}_{\mathrm{P}}^{\mathrm{r}}\right|} $ | (10) |

|
图 1 纵波Poynting矢量与反射角的关系示意图 |
由于纵波反射角等于入射角,因此开角的一半即为纵波反射角。根据Snell定律,纵波入射角β和横波反射角α之间满足sinβ/VP=sinα/VS,其中VP、VS为纵、横波传播速度。
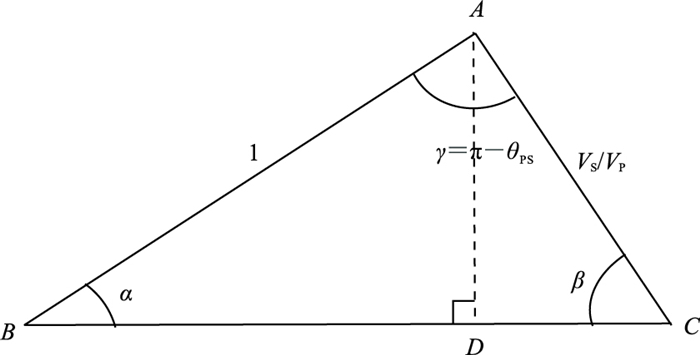
如图 2中ΔABC所示,取AB=1,AC=VS/VP,夹角∠ABC=α,即横波反射角,夹角∠ACB=β,即纵波入射角AD=sinα=VSsinβ/VP。那么,夹角∠BAC=γ=π-θPS,其中θPS=α+β为PS波开角,可以利用Poynting矢量确定,BC=
|
图 2 纵波入射角β与横波反射角α关系示意图 |
结合图 2,三角形ΔABC面积表示为ΦΔABC=AB·AC·sinγ/2=AB·BC·sinα/2,根据余弦定理,有
| $ \alpha=\arcsin \frac{V_{\mathrm{S}} \sin \theta_{\mathrm{PS}}}{\sqrt{V_{\mathrm{P}}^{2}+V_{\mathrm{S}}^{2}+2 V_{\mathrm{P}} V_{\mathrm{S}} \cos \theta_{\mathrm{PS}}}} $ | (11) |
式中
| $ \theta_{\mathrm{PS}}=\arccos \frac{\boldsymbol{S}_{\mathrm{P}}^{\mathrm{s}} \cdot \boldsymbol{S}_{\mathrm{S}}^{\mathrm{r}}}{\left|\boldsymbol{S}_{\mathrm{P}}^{\mathrm{s}}\right|\left|\boldsymbol{S}_{\mathrm{S}}^{\mathrm{r}}\right|} $ | (12) |
其中SSr为横波检波点波场的Poynting矢量。
由VP、VS和开角θPS就可以确定PS波反射角α。
由于Poynting矢量的非稳健性,往往采用在一定空间窗上进行平滑的方式求取θPP或θPS,即
| $ \theta=\arccos \frac{\sum\limits_{\varOmega} \boldsymbol{S}^{\mathrm{s}} \cdot \boldsymbol{S}^{\mathrm{r}}}{\sum\limits_{\varOmega}\left|\boldsymbol{S}^{\mathrm{s}}\right|\left|\boldsymbol{S}^{\mathrm{r}}\right|} $ | (13) |
式中Ω表示平滑的空间窗口。
1.3 PP波和PS波角度域道集提取方法获得纵波入射角β和横波反射角α后,便可以提取ADCIG以对成像过程进行质控,从而进一步提高成像精度。常规成像条件是对角道集所有角度的叠加,故不能直接用于提取ADCIG。为此,需对常规成像条件进行修改。借鉴王保利等[24]的方法,引入高斯采样函数,将常规成像条件拓展为PP波角度域共成像点成像条件
| $ \begin{array}{l} I_{\mathrm{PP}_{-} \mathrm{ADCIG}}\left(\boldsymbol{x}, \beta_{k}\right)\\ \ \ \ \ =\sum\limits_{i_{\mathrm{s}}} \frac{\sum\limits_{t=0}^{T_{\max }} \boldsymbol{v}_{\mathrm{P}}^{\mathrm{s}}(t, x) \cdot \boldsymbol{v}_{\mathrm{P}}^{\mathrm{r}}(t, x) \exp \left[-\frac{\left(\beta-\beta_{k}\right)^{2}}{2 \sigma^{2}}\right]}{\sum\limits_{t=0}^{T_{\max }} \boldsymbol{v}_{\mathrm{P}}^{\mathrm{s}}(t, \boldsymbol{x}) \cdot \boldsymbol{v}_{\mathrm{P}}^{\mathrm{s}}(t, \boldsymbol{x})} \end{array} $ | (14) |
式中:x为成像点坐标;IPP_ADCIG为PP波角度域共成像点道集;βk为第k个离散角;vPs和vPr分别表示震源端和检波端纵波质点振动速度场;is为炮号;Tmax为最大观测记录时间;σ表示高斯函数的方差。σ越大,则在离散角βk附近的道在成像中所占的权重越小,反射角分布越均匀;σ越小,则在离散角βk附近的道所占成像比重越大,反射角分布越集中。为权衡βk附近高成像比重和反射角分布均匀度,需要选取适度的方差σ,本文取值为0.6。
利用成像域PP波成像条件可以得到PP波的ADCIG,其中ERTM中PP波ADCIG的计算流程如下:
(1) 在炮域构建震源波场,计算每一时刻的纵波质点振动速度场,并将其存储至硬盘;
(2) 在炮域构建检波点波场,计算每一时刻的纵波质点振动速度场及应力场;
(3) 从硬盘读取纵波质点振动速度场,利用式(9)计算当前时刻的Poynting矢量,并利用式(10)计算纵波的开角和入射角;
(4) 利用式(13)进行角度平滑;
(5) 以离散角作为角道集输出的角度变量,利用式(14)输出PP波ADCIG。
类似地,利用得到的横波反射角α,本文给出了PS波ADCIG成像条件
| $ \begin{aligned} &I_{\mathrm{PS}_{-} \operatorname{ADCIG}}\left(\boldsymbol{x}, \beta_{k}\right) \\ &\ \ \ \ =\sum\limits_{i_{\mathrm{s}}} \frac{\sum\limits_{t=0}^{T_{\max }} v_{\mathrm{P}}^{\mathrm{s}}(t, \boldsymbol{x}) \cdot \boldsymbol{v}_{\mathrm{S}}^{\mathrm{r}}(t, x) \exp \left[-\frac{\left(\alpha-\beta_{k}\right)^{2}}{2 \sigma^{2}}\right]}{\sum\limits_{t=0}^{T_{\max }} \boldsymbol{v}_{\mathrm{P}}^{\mathrm{s}}(t, x) \cdot \boldsymbol{v}_{\mathrm{P}}^{\mathrm{s}}(t, \boldsymbol{x})} \end{aligned} $ | (15) |
式中:IPS_ADCIG表示PS波成像的ADCIG;vSr表示检波端横波质点振动速度场。
利用成像域PS波成像条件,可以得到PS波的ADCIG。其中ERTM中PS波ADCIG的计算流程如下:
(1) 在炮域构建震源波场,计算每一时刻的纵波质点振动速度场,并将其存储至硬盘;
(2) 在炮域构建检波点波场,计算每一时刻的横波质点振动速度场及应力场;
(3) 从硬盘读取纵波质点振动速度场,利用式(9)计算当前时刻的Poynting矢量,并求取纵波入射及横波反射之间的开角θPS;
(4) 结合Snell定律及波场传播关系,利用式(11)计算PS波反射角;
(5) 应用式(13)进行角度平滑;
(6) 以离散角作为角道集输出的角度变量,利用式(15)输出PS波ADCIG。
1.4 PP波ADCIG角度衰减+Laplace滤波的组合叠加成像策略受双程波动方程影响,ERTM方法进行PP波成像过程中引入了低波数噪声。低波数噪声反射角接近90°,主要存在于角道集的大角度区域,因此对角道集进行叠加时,可通过对大角度切除获得消除低波数噪声的RTM结果。但是,道集中大角度道也含有部分有效信息。
借鉴Laplace滤波的物理机制,本文提出了在PP波角道集中小角度按纵波入射角度余弦cosβk的方式进行叠加成像、大角度实施Laplace滤波的组合叠加成像的策略,即
| $ \begin{aligned} I_{\mathrm{PP}}(\boldsymbol{x})=& \sum\limits_{k=1}^{N_{\beta 1}} I_{\mathrm{PP}_{-} \mathrm{ADCIG}}\left(\boldsymbol{x}, \beta_{k}\right) \cos \beta_{k}+\\ & \nabla^{2} \sum\limits_{k=N_{\beta 1}}^{N_{\beta2}} I_{\mathrm{PP}_{-} \mathrm{ADCIG}}\left(\boldsymbol{x}, \beta_{k}\right) \end{aligned} $ | (16) |
式中:Nβ2为离散角度个数;Nβ1为小角度与大角度的分界点序号。分界角取值范围一般为30°~40°。
根据式(16)可知,本文的ADCIG叠加成像的策略利用了角道集中所有的角度成像,小角度cosβk值更大,因此最终成像结果中既突出了角度道集中小角度道的贡献,又避免了大角度道有效信息的损失。
需要指出的是,对于PS波成像,由于震源端P波与检波端S波传播路径不同,且振动方向也不一致,因此PS波成像不存在低波数噪声。为此,PS波角道集叠加成像时可以忽略低波数噪声影响,不需要大角度道集噪声压制。
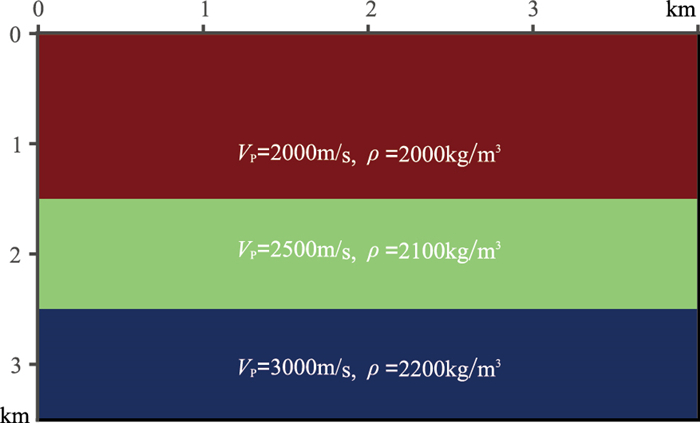
2 模型验证 2.1 水平层状模型构建水平层状模型验证本文的叠加成像策略的正确性。模型如图 3所示,网格数为400×350,尺寸为10m×10m,纵横波速度比为1.73。加载主频为15Hz的Ricker子波作为爆炸源,道间距为10m,炮间距为100m,在地表全覆盖,共接收40炮;时间采样间隔为1ms,记录长度为3.2s。采用时间二阶、空间十阶的有限差分算法进行数值模拟。
|
图 3 水平层状模型 |
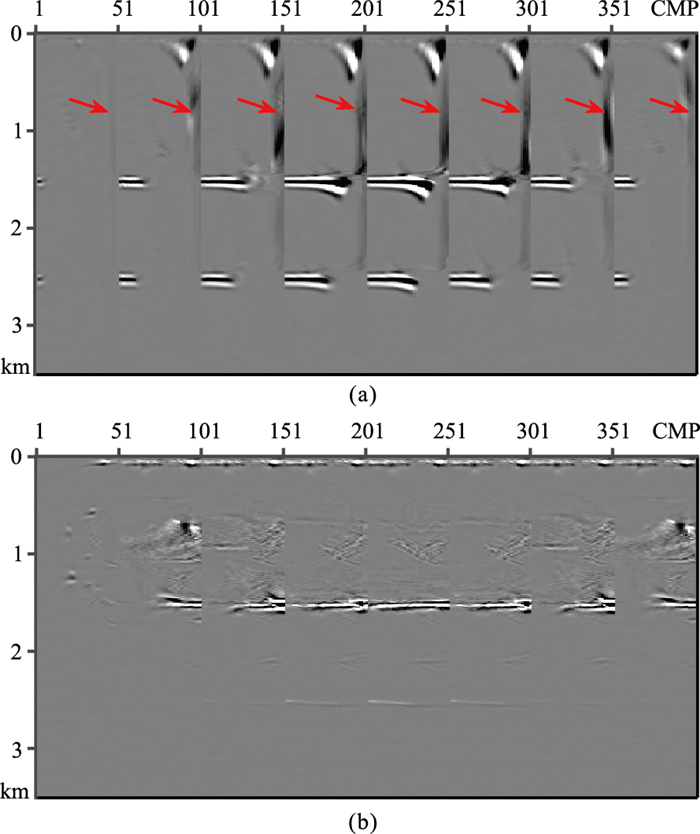
用式(14)和式(15)分别提取出水平层状模型的PP波角道集和PS波角道集,如图 4所示。其中,每个角道集角度范围为0°~90°,间隔为1°;每隔50个CMP抽取一个角道集显示。从PP波成像道集可以看出,同相轴水平,埋深1500m、2500m界面在ADCIG中的同相轴连续性较好,成像噪声较少。由红色箭头处可以看出,PP低波数噪声主要位于角道集的浅层大角度的位置。从PS波成像角道集可看出,虽然有多次波干扰,但是埋深1500m界面在ADCIG中同相轴是水平的,而且连续性较好。这证明了PP波角道集和PS波角道集提取方法的正确性。
|
图 4 水平层状模型的PP波(a)与PS波角道集(b) |
为便于AVO/AVA分析,利用Zoeppritz方程[29]计算深度1500m界面的PP波和PS波的理论反射系数曲线。提取深度1500m、CMP200处PP波角道集和PS波角道集振幅曲线并归一化,并其与理论反射系数对比(图 5)显示,提取的振幅随角度变化曲线与理论反射系数曲线基本一致,说明本文角道集提取方法基本可行。

|
图 5 1500m处界面PP波(a)和PS波(b)角道集归一化振幅曲线与理论反射系数曲线对比 |
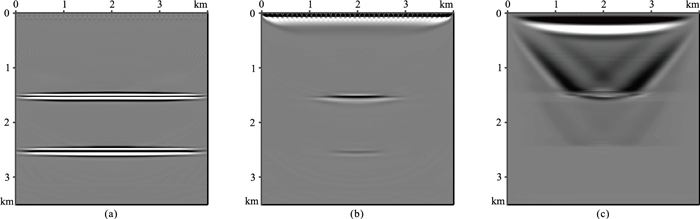
分别抽取水平层状模型PP波角道集中0°~40°、41°~70°及71°~90°的道进行叠加成像,分析角度对成像结果的影响(图 6)。0°~40°的叠加成像结果(图 6a)中几乎没有任何低波数噪声,41°~70°叠加成像结果(图 6b)中低波数噪声较少,而71°~90°的成像结果(图 6c)几乎全部是低频噪声,但有部分有效成像信息。
|
图 6 水平层状模型PP波不同角度范围的叠加成像结果 (a)0°~40°;(b)41°~70°;(c)71°~90° |
采用本文方法提出的PP波角度衰减+Laplace滤波的组合叠加成像策略(式(16)),取分界角度为40°,得到组合叠加成像结果(图 7a),并抽取CMP200处的0°~40°和40°~90°角道集(图 7b、图 7c),可见低波数噪声得以压制,且同相轴连续。

|
图 7 水平层状模型PP波组合叠加成像结果(a)及CMP200处0°~40°角道集(b)和41°~90°角道集(c) |
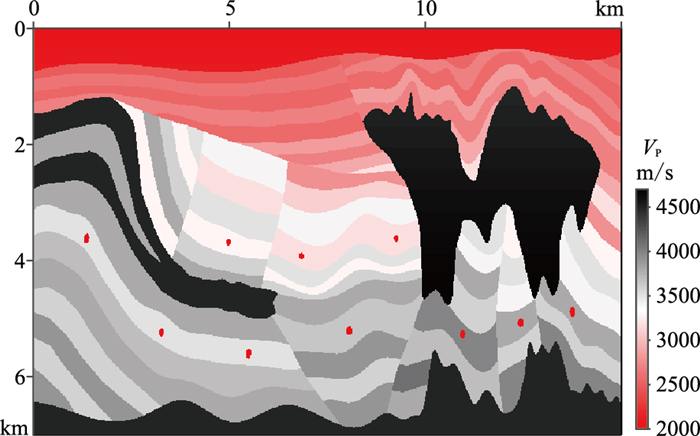
利用Salt模型(图 8)测试本文算法对复杂模型的成像精度和效果。模型网格数为1500×700,网格尺寸为10m×10m,纵横波速度比为1.73,密度取常数2.0g/cm3。数值模拟时,震源采用主频为30Hz的Ricker子波以爆炸形式加载至P波应力分量上;时间采样间隔为1ms;炮点间隔为100m,共150炮;在地表以10m为间隔均匀分布的检波点进行接收。采用在时间二阶、空间十阶的有限差分算法进行正向和反向波场延拓。
|
图 8 Salt纵波速度模型 |
提取的Salt模型的PP波的ADCIG如图 9a所示,角度范围为0°~90°,角度间隔为2°,每隔100个CMP抽取一个角道集进行展示。利用本文提出的组合叠加策略得到的PP波成像结果如图 9b所示。由图 9a可以看出,每个ADCIG的同相轴都是水平的,且存在低波数噪声。采用组合叠加策略后,成像结果的低波数噪声得到有效压制。
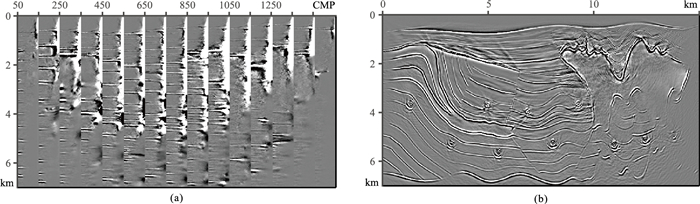
|
图 9 Salt模型PP波共成像点道集(a)和成像结果(b) |
用本文提出的基于伪横波应力角道集方法提取的Salt模型PS波ADCIG如图 10a所示。对0°~90°角道集进行叠加得到的PS成像结果如图 10b所示。由图可以看出,每个ADCIG上的同相轴都是水平的,验证了本文PS波角道集提取方法的正确性。在浅层PS波成像结果优于PP波,在深层PP波成像结果优于PS波。

|
图 10 Salt模型PS波共成像点道集(a)和成像结果(b) |
图 11a和图 11b分别为基于伪横波应力(本文方法)提取的PS波部分CMP角道集及0°~45°叠加成像结果;图 11c和图 11d分别为基于横波应力提取的PS波部分CMP角道集及0°~45°的叠加成像结果。图 11c中同相轴不连续,图 11d中含有低波数噪声;图 11a中同相轴较连续而且图 11b中不存在低波数噪声。原因在于图 11c和图 11d中构造的横波应力(式(4))中含有纵波成分,导致提取的PS波角道集也含有纵波成分,因此,基于横波应力提取的PS波角道集中存在纵波能量干扰和低波数噪声;相比之下,图 11a中基于伪横波应力(式(8))提取的PS波角道集较好压制了能量串扰。

|
图 11 基于伪横波应力的PS波角道集(a)及其0°~45°叠加成像结果(b)、基于横波应力提取的PS波角道集(c)及其0°~45°叠加成像结果(d) |
此外,对比PS波0°~45°角道集叠加结果(图 11b)与0°~90°全部角道集叠加的PS波成像(图 10b)结果发现,后者更优。
3 结论和认识(1) 基于解耦延拓方程及伪横波应力实现的弹性波逆时偏移方法,可以构建得到完全解耦的质点振动速度和应力;
(2) 根据余弦定理可以求得震源波场的Poyn-ting矢量与检波点波场的Poynting矢量的夹角,进而由纵、横波背景速度和开角确定PS波反射角;
(3) 通过引入时间窗、空间窗以及高斯函数构建的PP波和PS波共成像点道集成像条件,可稳健地实现PP波和PS波角道集的提取;
(4) 模型试验结果表明,组合叠加成像策略构建的PP波角道集可以保护部分大角度有效信息,并实现低波数噪声的有效压制。
| [1] |
WHITMORE N D. Iterative depth migration by backward time propagation[C]. SEG Technical Program Expanded Abstracts, 1983, 2: 382-385.
|
| [2] |
MCMECHAN G A. Migration by extrapolation of time-dependent boundary values[J]. Geophysical Pro-specting, 1983, 31(3): 413-420. DOI:10.1111/j.1365-2478.1983.tb01060.x |
| [3] |
BAYSAL E, KOSLOFF D D, SHERWOOD J W C. Reverse time migration[J]. Geophysics, 1983, 48(11): 1514-1524. DOI:10.1190/1.1441434 |
| [4] |
YOON K, SHIN C, SUH S, et al. 3D reverse-time migration using the acoustic wave equation: an experience with the SEG/EAGE data set[J]. The Leading Edge, 2003, 22(1): 38-41. DOI:10.1190/1.1542754 |
| [5] |
ZHANG Y, XU S, BLEISTEIN N, et al. True-amplitude, angle-domain, common-image gathers from one-way wave-equation migrations[J]. Geophysics, 2007, 72(1): S49-S58. DOI:10.1190/1.2399371 |
| [6] |
何兵寿, 张会星, 魏修成, 等. 双程声波方程叠前逆时深度偏移的成像条件[J]. 石油地球物理勘探, 2010, 45(2): 237-243. HE Bingshou, ZHANG Huixing, WEI Xiucheng, et al. Imaging conditions for two-way acoustic wave equation pre-stack reverse-time depth migration[J]. Oil Geophysical Prospecting, 2010, 45(2): 237-243. |
| [7] |
SUN R, MCMECHAN G A. Pre-stack reverse-time migration for elastic waves with application to synthetic offset vertical seismic profiles[J]. Proceedings of the IEEE, 1986, 74(3): 457-465. DOI:10.1109/PROC.1986.13486 |
| [8] |
CHANG W F, MCMECHAN G A. Elastic reverse-time migration[J]. Geophysics, 1987, 52(10): 1365-1375. DOI:10.1190/1.1442249 |
| [9] |
AKI K, RICHARDS P. Quantitative Seismology: Theory and Methods[M]. Freeman, San Francisco, 1980.
|
| [10] |
DU Q Z, ZHU Y T, BA J. Polarity reversal correction for elastic reverse time migration[J]. Geophy-sics, 2012, 77(2): S31-S41. |
| [11] |
NGUYEN B D, MCMECHAN G A. Excitation amplitude imaging condition for prestack reverse-time migration[J]. Geophysics, 2013, 78(1): S37-S46. DOI:10.1190/geo2012-0079.1 |
| [12] |
DUAN Y T, SAVA P. Scalar imaging condition for elastic reverse time migration[J]. Geophysics, 2015, 80(4): S127-S136. DOI:10.1190/geo2014-0453.1 |
| [13] |
ZHANG Q S, MCMECHAN G A. Direct vector-field method to obtain angle-domain common-image gathers from isotropic acoustic and elastic reverse time migration[J]. Geophysics, 2011, 76(5): WB135-WB149. DOI:10.1190/geo2010-0314.1 |
| [14] |
马德堂, 朱光明. 弹性波波场P波和S波分解的数值模拟[J]. 石油地球物理勘探, 2003, 38(5): 482-486. MA Detang, ZHU Guangming. Numerical modeling of P-wave and S-wave separation in elastic wavefield[J]. Oil Geophysical Prospecting, 2003, 38(5): 482-486. DOI:10.3321/j.issn:1000-7210.2003.05.005 |
| [15] |
李振春, 张华, 刘庆敏, 等. 弹性波交错网格高阶有限差分法波场分离数值模拟[J]. 石油地球物理勘探, 2007, 42(5): 510-515. LI Zhenchun, ZHANG Hua, LIU Qingmin, et al. Numeric simulation of elastic wavefield separation by staggering grid high-order finite-difference algorithm[J]. Oil Geophysical Prospecting, 2007, 42(5): 510-515. DOI:10.3321/j.issn:1000-7210.2007.05.006 |
| [16] |
DU Q Z, GUO C F, ZHAO Q, et al. Vector-based elastic reverse time migration based on scalar imaging condition[J]. Geophysics, 2017, 82(2): S111-S127. DOI:10.1190/geo2016-0146.1 |
| [17] |
DU Q Z, ZHANG X Y, GUO C F, et al. An elastic reverse time migration method based on the S-wave quasi-tensor[C]. Extended Abstracts of 80th EAGE Conference and Exhibition, 2018, A08.
|
| [18] |
TANG C, MCMECHAN G A. Multidirectional-vector-based elastic reverse time migration and angle-domain common-image gathers with approximate wavefield decomposition of P- and S-waves[J]. Geophy-sics, 2018, 83(1): S57-S79. |
| [19] |
慕鑫茹, 黄建平, 李振春, 等. 基于最佳平方逼近的TTI介质解耦qP波与qSV波逆时偏移[J]. 石油地球物理勘探, 2019, 54(6): 1280-1292. MU Xinru, HUANG Jianping, LI Zhenchun, et al. Reverse time migration of decoupled qP- and qSV-waves in TTI media with the optimal quadratic approximation[J]. Oil Geophysical Prospecting, 2019, 54(6): 1280-1292. |
| [20] |
XU S, CHAURIS H, LAMBARÉ G, et al. Common-angle migration: a strategy for imaging complex media[J]. Geophysics, 2001, 66(6): 1877-1894. DOI:10.1190/1.1487131 |
| [21] |
SAVA P C, FOMEL S. Angle-domain common-image gathers by wavefield continuation methods[J]. Geophysics, 2003, 68(3): 1065-1074. DOI:10.1190/1.1581078 |
| [22] |
XU S, ZHANG Y, TANG B. 3D common image gathers from reverse time migration[C]. SEG Technical Program Expanded Abstracts, 2010, 29: 3257-3262.
|
| [23] |
XU S, ZHANG Y, TANG B. 3D angle gathers from reverse time migration[J]. Geophysics, 2011, 76(2): S77-S92. DOI:10.1190/1.3536527 |
| [24] |
王保利, 高静怀, 陈文超, 等. 逆时偏移中用Poynting矢量高效地提取角道集[J]. 地球物理学报, 2013, 56(1): 262-268. WANG Baoli, GAO Jinghuai, CHEN Wenchao, et al. Extracting efficiently angle gathers using Poynting vector during reverse time migration[J]. Chinese Journal of Geophysics, 2013, 56(1): 262-268. |
| [25] |
汪天池, 刘少勇, 顾汉明, 等. 倾角域逆时偏移绕射波成像方法[J]. 石油地球物理勘探, 2020, 55(3): 591-598. WANG Tianchi, LIU Shaoyong, GU Hanming, et al. Seismic diffraction imaging by reverse time migration in dip angle domain[J]. Oil Geophysical Prospecting, 2020, 55(3): 591-598. |
| [26] |
ZHAO Y, LIU T, JIA X Y, et al. Surface-offset ga-thers from elastic reverse time migration and velocity analysis[J]. Geophysics, 2020, 85(1): S47-S64. DOI:10.1190/geo2018-0676.1 |
| [27] |
WANG W L, MCMECHAN G A. Vector-based elastic reverse time migration[J]. Geophysics, 2015, 80(6): S245-S258. DOI:10.1190/geo2014-0620.1 |
| [28] |
YOON K, MARFURT K J, STARR W. Challenges in reverse-time migration[C]. SEG Technical Program Expanded Abstracts, 2004, 23: 1057-1060.
|
| [29] |
张凌远, 张宏兵, 尚作萍, 等. 基于Zoeppritz方程的叠前和叠后混合多参数非线性地震反演[J]. 石油地球物理勘探, 2021, 56(1): 164-171. ZHANG Lingyuan, ZHANG Hongbing, SHANG Zuoping, et al. Nonlinear multi-parameter hybrid inversion of pre-stack and post-stack seismic data based on Zoeppritz equation[J]. Oil Geophysical Prospecting, 2021, 56(1): 164-171. |



 杜启振,山东省青岛市黄岛区长江西路66号中国石油大学(华东)深层油气重点实验室,266580。Email:
杜启振,山东省青岛市黄岛区长江西路66号中国石油大学(华东)深层油气重点实验室,266580。Email: