② 中国矿业大学(北京)地球科学与测绘工程学院, 北京 100083;
③ 中国石化石油勘探开发研究院, 北京 100083
② School of Geosciences & Surveying Enginee-ring, China University of Mining & Technology-Beijing, Beijing 100083, China;
③ SINOPEC Petroleum Exploration and Production Research Institute, Beijing 100083, China
绕射波作为地下局部不连续体的地震响应,携带了断裂、溶洞、尖灭、陷落柱等小尺度非均质体的重要信息,是提高地震勘探分辨率的重要工具[1]。然而,在地震记录中,绕射波能量比反射波能量低1~2个数量级,在偏移成像时,与绕射相关的小尺度异常体常被强能量的反射体掩盖,难以识别[2-3];同时,在以反射波为有效信号的传统地震数据处理流程中,绕射波也通常作为噪声被压制[4]。因此,对绕射波与反射波进行分离,并对绕射波单独成像,成为地下小尺度非均质体高分辨率成像的关键。
20世纪50年代,地球物理学家Krey[5]在研究含有断层或尖灭的反射地震记录时发现了绕射波。近年来,为提高小尺度地质体的成像分辨率,各种绕射波分离方法相继被提出。根据分离绕射波时所处的地震数据处理阶段,可以将绕射波分离方法分为以下两类。
(1) 在偏移前进行绕射波分离的方法。Nowak等[6]根据共炮点道集中绕射波与反射波同相轴横向位置差异,使用加权拉东变换,在变换域中提取绕射波。平面波破坏滤波器(PWD)在绕射波分离中应用广泛,Fomel[7]改进了该方法,只需局部平面波场斜率一个参数。孔雪等[8]根据绕射波与反射波在平面波记录上的几何形态差异,应用PWD压制反射波。朱生旺等[9]对共炮点道集记录进行平面波分解,首先利用局部倾角滤波方法分离绕射波大倾角信息成分,再利用预测反演方法分离绕射波低倾角信息成分,将两次分离结果相加得到最终分离的绕射波。魏巍等[10]在共炮点道集上通过动校正拉平反射波,增加其相干性,而绕射波无法被拉平,相干性弱;然后根据绕射波与反射波相干性差异,利用奇异值分解技术提取绕射波。Rad等[11]将共反射波面元方法扩展至叠前域,提出了一种基于波前属性的叠前绕射分离流程。Gong等[12]结合Radon变换、Stolt偏移和反偏移,在炮域分离绕射波。此外,多道奇异谱分析[13]、相干波场叠加方法[14]、在线字典学习方法[15]等也被用于绕射波分离。
(2) 在偏移后进行绕射波分离的方法。Khai-dukov等[16]提出了聚焦—反聚焦方法分离绕射波。Moser等[17]利用反稳相滤波器修正Kirchhoff偏移核函数,实现绕射波分离与成像。Silvestrov等[18]利用逆时偏移生成共成像点道集,根据反射波与绕射波在共成像点道集上的倾角差异分离反射波。Zhao等[19]根据马氏距离构建了振幅衰减函数,据此对Kirchhoff核函数进行修正,有效分离出绕射波。Yu等[20]基于局部平面波方程提出了数据规则化方法,实现了绕射波精确、稳定提取。在方位倾角道集中,反射波具有稀疏特性,而绕射波则表现为低秩分量,根据这种差异,Zhao等[21]提出一种稀疏低秩矩阵分解方法提取绕射波。Li等[22]构建了垂直旅行时差道集,在该道集中,绕射波是平坦的,而反射波表现为上凸形态,根据形态差异分离绕射波。汪天池等[23]证明了逆时偏移产生的倾角道集比Kirchhoff积分偏移产生的倾角道集具有更强的反射聚焦能力,更适合绕射波分离。罗腾腾等[24]在倾角域共成像点道集中,引入迭代收缩高分辨率Radon变换分离绕射波,具有良好的抗噪能力。刘培君等[25]通过构建反稳相滤波算子,在深度域进行绕射波分离与成像。
传统叠前绕射波分离方法大多在共炮检距道集开展,但由于深层绕射波能量分布范围大,因此造成绕射波能量损失。针对此问题,本文提出一种叠前绕射波分离方法,通过共虚震源变换将共炮点道集转换成共虚震源道集,并在共虚震源道集中进行偏移—反射波去除—反偏移处理,提取绕射波信号,解决在地震波场交叉和相切情况下绕射波弱信号难以分离的问题,最后通过共虚震源逆变换得到共炮点道集绕射波场。
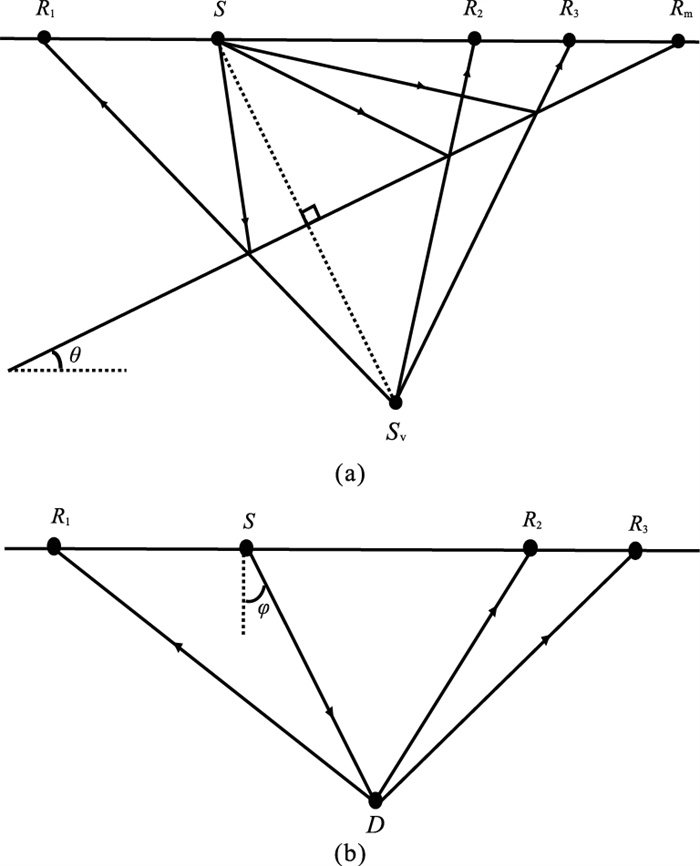
1 方法原理 1.1 共虚震源变换以均匀介质模型描述反射波和绕射波的旅行时特征(图 1)。根据反射定律,反射波旅行时可表示为
| $ t_{\mathrm{R}}^{2}=\frac{h^{2}+4 d^{2}+4 d h \sin \theta}{v^{2}} $ | (1) |
|
图 1 反射波和绕射波射线路径及聚焦特性示意图 (a)反射波;(b)绕射波。S为炮点;Ri(i=1, 2, 3)为接收点;Rm为界面与地表的交点;SV为虚震源 |
式中:v为地震波传播速度;h为炮检距;d为炮点到反射界面法向距离;θ为界面倾角。在共炮点道集中,炮点坐标固定,h变化,上式可写为
| $ v^{2} t_{\mathrm{R}}^{2}(h)=(h+2 d \sin \theta)^{2}+4 d^{2} \cos ^{2} \theta $ | (2) |
该旅行时曲线的顶点坐标为(-2dsinθ,2dcosθ/v),渐近线为±1/v。
绕射波旅行时可以表示为
| $ \left[v t_{\mathrm{D}}(h)+d_{1}\right]^{2}=\left(h+d_{1} \sin \varphi\right)^{2}+d_{1}^{2} \cos ^{2} \varphi $ | (3) |
式中:d1表示炮点至绕射体D的距离;φ为炮点至绕射体的射线角度。绕射波旅行时曲线的顶点坐标为(-d1sinφ,(d1+d1cosφ)/v),渐近线为±1/v。
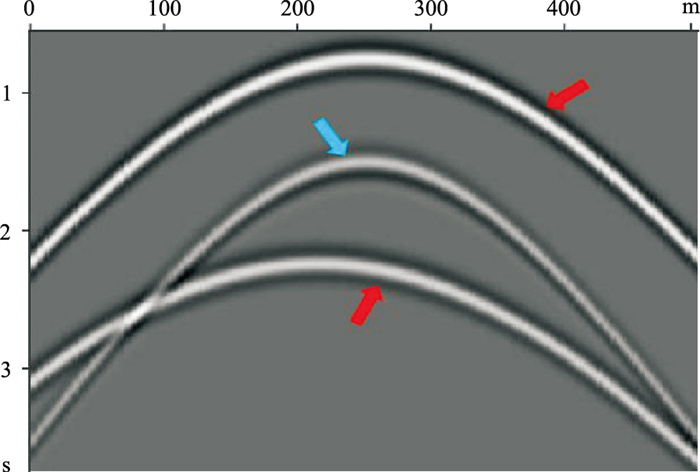
根据式(2)和式(3),绕射波(图 2的蓝色箭头所示)和反射波(图 2的红色箭头所示)都表现为双曲线形态,在共炮点道集中分离绕射波具有一定难度。
|
图 2 共炮点道集中绕射波和反射波形态示意图[26] |
事实上,绕射波和反射波具有不同的聚焦性。如图 1a所示,反射波在虚震源SV处聚焦,其旅行时等于从虚震源至接收点的时间。绕射波则在真正的绕射体位置聚焦,其旅行时等于从炮点到绕射体、再到接收点的时间(图 1b)。在一个共炮点道集中,同一个反射界面产生的反射波可以视为来自于一个公共虚震源,而绕射波则不能,因此可以利用反射波旅行时,将反射波映射到对应的虚震源位置上。通过这种方式,共炮点道集被转换成一个新的道集——共虚震源道集(CVSG)。
假设地下某一位置点是虚震源,将共炮点道集转换为CVSG可以表示为
| $ \begin{aligned} &V\left[S, S_{\mathrm{V}}(x, z), R\right]=\int U(S, R, t) \times \\ &\delta\left\{t-t_{\mathrm{R}}\left[S, S_{\mathrm{V}}(x, z), R\right]\right\} \mathrm{d} t \end{aligned} $ | (4) |
式中:x、z分别代表虚震源的水平位置和深度;R表示接收点;U表示记录时间为t的共炮点道集数据;V是对应的CVSG数据;在各向同性或等效介质中,由震源S激发、R点接收、对应(x, z)处虚震源的反射波走时可以简单地表示为
| $ \begin{aligned} &t_{\mathrm{R}}\left[S, S_{\mathrm{V}}(x, z), R\right]= \\ &t_{0}+\frac{\sqrt{W_{0}^{2}+2 W_{0} h \sin \alpha+h^{2}}-W_{0}}{v_{\mathrm{rms}}} \end{aligned} $ | (5) |
其中:t0是零炮检距双程旅行时,等于从虚震源SV到震源S的时间;W0为波前半径;α为射线的出射角;vrms为均方根速度。在直射线假设条件下,有
| $ \left\{\begin{array}{l} W_{0}=\sqrt{\left(x-x_{S}\right)^{2}+z^{2}} \\ t_{0}=\frac{W_{0}}{v_{\text {rms }}} \\ \sin \alpha=\frac{x_{S}-x}{W_{0}} \end{array}\right. $ | (6) |
式中xS表示震源的水平坐标。根据式(6),可求得式(4)中的反射波旅行时。值得注意的是,SV是一个假想的震源,并没有真实的速度信息,使用均方根速度vrms计算从虚震源SV到接收点的旅行时。在简单情况下,反射波的出射角等于界面的真倾角,因此,可以用已知的实际倾角范围限制SV的位置。
在共炮点道集向CVSG转换的过程中存在一个问题:如图 1a所示,当接收点位于界面延伸至地表位置Rm左侧时,可以计算从虚震源SV至接收点的反射旅行时;但是当接收点位于Rm右侧时,无法观察到反射波。一般情况下,可以用S和SV计算Rm的近似位置处理这一问题。转换过程中存在的另一个问题是:当虚震源和接收点相距较远时,会产生拉伸畸变现象。如图 3和式(4)所示,CSVG中的数据点和共炮点道集中的数据点具有一一对应的映射关系。当时差Δt小于时间采样间隔dt时,将会出现拉伸变形的现象。在均匀介质中,时差Δt可以表示为
| $ \begin{aligned} \Delta t &=t_{\mathrm{R}}\left[S, S_{\mathrm{V}}\left(x, z_{i+1}\right), R\right]-t_{\mathrm{R}}\left[S, S_{\mathrm{V}}\left(x, z_{i}\right), R\right] \\ &=\frac{L_{R S_{\mathrm{V}}}\left(x, z_{i+1}\right)-L_{R S_{\mathrm{V}}}\left(x, z_{i}\right)}{v_{\mathrm{rms}}} \end{aligned} $ | (7) |

|
图 3 炮集U和共虚震源道集V的映射关系示意图[23] j是时间t的离散序号 |
式中:i为深度z离散序号;LRSV(x, zi)表示接收点R到虚震源SV(x, zi)的距离。
当虚震源和接收点相距越远,Δt的值越小,拉伸变形就越严重,在界面陡峭和浅层情况下尤为突出。参考动校正的处理方法,当拉伸畸变无法接受时,切除变形严重的部分。
共炮点道集和CVSG具有精确的映射关系,可以通过逆变换由CVSG恢复炮集数据
| $\begin{aligned} &U(S, R, t)= \\ &\int V\left(S, S_{\mathrm{V}}(x, z), R\right) \delta\left[t-t_{\mathrm{R}}\left(S, S_{\mathrm{V}}(x, z), R\right)\right] \mathrm{d} S_{\mathrm{V}} \end{aligned} $ | (8) |
假设地下每一个点都是虚震源点,则可逐点给定坐标对共炮点道集数据进行共虚震源变换,来自同一反射面的反射事件将被校正到同一个虚震源。本文并不在虚震源位置进行反射波的聚焦叠加,而是依次排列成为线性同相轴(图 4红色箭头所示)。绕射波无虚震源,所以不会在共虚震源道集中表现为水平线性,而是表现为弯曲状(图 4蓝色箭头所示)。

|
图 4 CVSG中绕射波和反射波形态示意图[26] 红色圆点代表设置的虚震源位置 |
利用Stolt偏移、正则化PWD方法和反偏移在CVSG中提取绕射波弱信号。
Stolt偏移方法是目前最快速的偏移算法,广泛应用于地震数据处理。为了便于Stolt偏移,对共虚震源道集进行深时转换,转换后的CVSG在三维情况下可以写为V(x, y, z=0, t),其傅里叶变换为
| $\begin{aligned} \tilde{V}\left(k_{x}, k_{y}, 0, \omega\right) &=\iiint V(x, y, 0, t) \times \\ & \exp \left(\mathrm{i} k_{x} x+\mathrm{i} k_{y} y-\mathrm{i} \omega t\right) \mathrm{d} x \mathrm{~d} y \mathrm{~d} t \end{aligned} $ | (9) |
则成像数据M(x, y, z)的傅里叶变换为
| $ \begin{aligned} \widetilde{M}\left(k_{x}, k_{y}, k_{z}\right) &=-\frac{v_{\mathrm{m}} k_{z}}{2 \sqrt{k_{x}^{2}+k_{y}^{2}+k_{z}^{2}}} \times \\ & \tilde{V}\left(k_{x}, k_{y}, 0, \frac{v_{\mathrm{m}}}{2} \sqrt{k_{x}^{2}+k_{y}^{2}+k_{z}^{2}}\right) \end{aligned} $ | (10) |
式中vm为偏移速度。
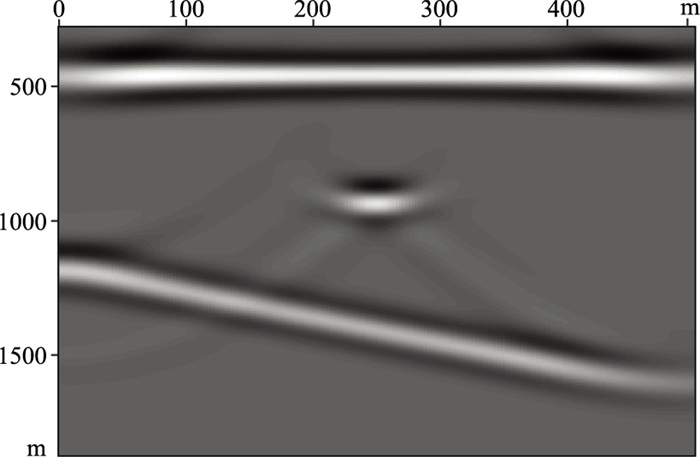
式(10)即为Stolt偏移公式。图 5为图 4的偏移结果,反射波表现为平面波,绕射波收敛为绕射点。
在CVSG经Stolt偏移后,反射波表现出线性连续特征具有平面波的性质,符合平面波假设,可以通过PWD滤波器预测[7]。然而,在偏移数据中,绕射波收敛为绕射点,绕射波不符合平面波假设,难以通过PWD滤波器预测,在预测过程中,绕射波会作为预测误差得到。因此,可以使用PWD方法得到偏移剖面中的绕射波
| $ \boldsymbol{C}(\boldsymbol{\sigma}) \boldsymbol{M}=Q(\boldsymbol{\sigma}) $ | (11) |
|
图 5 共虚震源道集偏移结果 |
式中:M=(m1, m2, …, mN),其中mi为第i道偏移数据,N为总道数;Q(σ)为预测误差,σ为斜率矢量;C(σ)是PWD算子,定义为
| $\boldsymbol{C}(\boldsymbol{\sigma})=\left[\begin{array}{ccccc} \boldsymbol{I} & & & & \\ -\boldsymbol{B}_{1, 2}\left(\boldsymbol{\sigma}_{1}\right) & \boldsymbol{I} & & & \\ & -\boldsymbol{B}_{2, 3}\left(\boldsymbol{\sigma}_{2}\right) & \boldsymbol{I} & & \\ & & \ddots & \ddots & \\ & & & -\boldsymbol{B}_{N-1, \mathrm{~N}}\left(\boldsymbol{\sigma}_{N-1}\right) & \boldsymbol{I} \end{array}\right] $ | (12) |
其中:I为单位矢量;Bl, n(σl)表示由第l道偏移数据预测第n道偏移数据的预测误差算子[7]。
从式(12)中可以看出,PWD算子所需要的唯一参数就是局部斜率σ,只需要求解局部斜率,再将其代入PWD算子,就可以利用式(11)得到绕射波。因此,获得绕射波的关键就是估计局部斜率。
求解局部斜率是一个迭代过程,可以使用高斯—牛顿法[7],在Q(σ)近似为零条件下,有
| $ \boldsymbol{C}^{\prime}\left[\boldsymbol{\sigma}^{(K)}\right] \Delta \boldsymbol{\sigma}^{(K)} \boldsymbol{M}+\boldsymbol{C}\left[\boldsymbol{\sigma}^{(K)}\right] \boldsymbol{M}=0 $ | (13) |
式中:K为迭代次数;C′[σ(K)]为C[σ(K)]关于σ(K)的微分;Δσ(K)为每次迭代中倾角斜率矢量的更新步长,局部斜率矢量的更新公式为σ(K+1)=σ(K)+ Δσ(K)。
上述是传统的求解局部斜率的过程,在求解过程中,并未考虑与断层等不连续地质体有关的地震数据对反演过程干扰作用和地震反射信号平滑特征,反演求解不稳定,局部斜率估计不准确,应用不准确的局部斜率分离绕射波,可能会导致反射波残留、分离出的绕射波不完整等问题。因此,为了避免上述问题,本文采用Yu等[20]提出的正则化局部斜率估计模型
| $ \begin{aligned} J^{\psi \cdot \beta}(\boldsymbol{\sigma})=& \frac{1}{2}\|\boldsymbol{Q}(\boldsymbol{\sigma})\|^{2}+\\ & \psi\left\langle\boldsymbol{L}_{1} \boldsymbol{\sigma}, \boldsymbol{\sigma}\right\rangle+\beta\left\langle\boldsymbol{L}_{2} \boldsymbol{\sigma}, \boldsymbol{\sigma}\right\rangle \rightarrow \min \end{aligned} $ | (14) |
式中:ψ、β均为正则化因子,用于平衡预测地震道和观测地震道的拟合情况;〈·, ·〉表示两个向量的内积;L1为负拉普拉斯算子,即
| $\boldsymbol{L}_{1}=\left[\begin{array}{ccccc} 1 & -1 & & & \\ -1 & 2 & -1 & & \\ & \ddots & \ddots & \ddots & \\ & & -1 & 2 & -1 \\ & & & -1 & 1 \end{array}\right] $ | (15) |
L2为差分算子,即
| $\boldsymbol{L}_{2}=\left[\begin{array}{ccccc} 1 & -1 & & & \\ & 1 & -1 & & \\ & & \ddots & \ddots & \\ & & & 1 & -1 \\ & & & & 1 \end{array}\right] $ | (16) |
上述正则化倾角估计模型保证了反演求解稳定性,也确保三维地震强反射信号估计准确性[20]。
为快速求解上述局部斜率估计模型,目标函数JΨ, β(σ)的梯度可表示为[20]
| $ \boldsymbol{g}(\boldsymbol{\sigma})=\frac{1}{2} \frac{\mathrm{d}}{\mathrm{d} \boldsymbol{\sigma}}\|\boldsymbol{Q}(\sigma)\|^{2}+\psi \boldsymbol{L}_{1} \boldsymbol{\sigma}+\beta \boldsymbol{L}_{2} \boldsymbol{\sigma} $ | (17) |
模型更新方案为
| $ \boldsymbol{\sigma}^{(K+1)}=A\left\{\boldsymbol{\sigma}^{(K)}-\boldsymbol{\xi}_{K} \boldsymbol{g}\left[\boldsymbol{\sigma}^{(K)}\right]\right\} $ | (18) |
其中:ξK为更新步长;对于任意ξK>0,A(·)表示斜率矢量的可行集投影。
在得到局部斜率后,可由式(11)得到预测误差Q(σ),即偏移数据中的绕射波。
在利用上述方法去除偏移数据中的反射波后,再进行反偏移
| $ \begin{array}{r} \widetilde{V}_{\mathrm{D}}\left(k_{x}, k_{y}, 0, \omega\right)=-\frac{4 \omega}{v_{\mathrm{m}}^{2} \sqrt{\left(\frac{2 \omega}{v_{\mathrm{m}}}\right)^{2}-\left(k_{x}^{2}+k_{y}^{2}\right)}} \times \\ \widetilde{M}_{\mathrm{D}}\left[k_{x}, k_{y}, \sqrt{\left(\frac{2 \omega}{v_{\mathrm{m}}}\right)^{2}-\left(k_{x}^{2}+k_{y}^{2}\right)}\right] \end{array} $ | (19) |
式中:
通过逆傅里叶变换可得CVSG绕射波
| $ \begin{aligned} &V_{\mathrm{D}}(x, y, 0, t)=\iint \tilde{V}_{\mathrm{D}}\left(k_{x}, k_{y}, 0, \omega\right) \times \\ &\quad \exp \left(-\mathrm{i} k_{x} x-\mathrm{i} k_{y} y+\mathrm{i} \omega t\right) \mathrm{d} k_{x} \mathrm{~d} k_{y} \mathrm{~d} \omega \end{aligned} $ | (20) |
最后,可以通过式(8)将绕射波CVSG变换为绕射波共炮点道集。
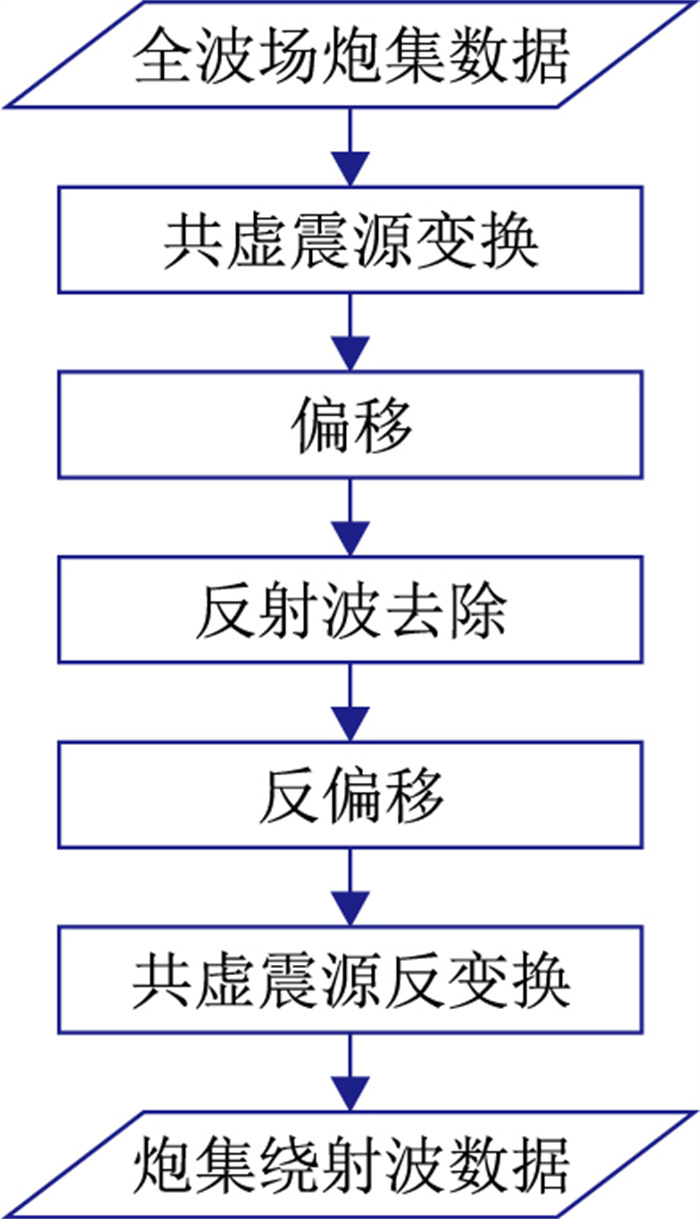
本文方法的处理流程如图 6所示。
|
图 6 叠前绕射波分离流程 |
构建岩溶—冲沟模型验证本文绕射波分离方法的效果,并与常规的PWD方法对比,阐明本文方法的优势;通过实际资料处理验证本文方法的适用性。
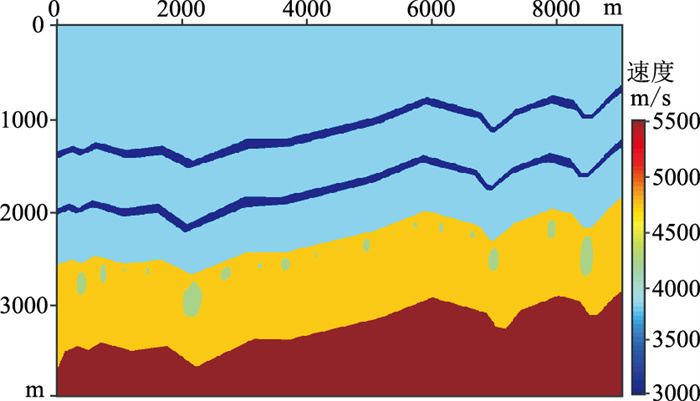
2.1 岩溶—冲沟模型岩溶-冲沟模型(图 7)尺寸为9000m×4000m,1000~2300m深度范围有两个薄层,2000~3500m深度范围内随机分布着一些形状、尺寸不同的岩溶体,最小的直径为4m,最大的直径为100m,填充速度为4200m/s,围岩的速度为4700m/s。图 8为模型的反射系数剖面,其中小尺度岩溶构造清晰,可用于对比分析不同分离方法的效果。对该模型使用Kirchoff正演算法生成合成数据,震源使用主频为25Hz的Ricker子波;共901炮,炮点位置从0到9000m变化,炮间距为10m;每炮901道,道间距为10m,采样间隔为4ms,其共炮检距剖面如图 9a所示。
|
图 7 岩溶—冲沟速度模型 |

|
图 8 岩溶—冲沟模型的反射系数剖面 |

|
图 9 岩溶—冲沟模型两种绕射波分离方法的共炮检距剖面对比 (a)全波场;(b)PWD方法;(c)本文方法 |
应用PWD法对图 9a所示的共炮检距剖面进行绕射波分离,结果如图 9b所示。PWD方法有效去除了平滑、连续的反射波,但绕射波也遭到严重的损伤,尤其在绕射波顶点,即绕射波与反射波相干处。
对模拟数据应用本文方法分离绕射波,并将分离结果(共炮点道集)抽成共炮检剖面,如图 9c所示。本文方法有效去除了剖面中平滑、连续的反射波,比PWD方法更完整地保留了绕射波信息,为绕射波的清晰成像奠定了基础。
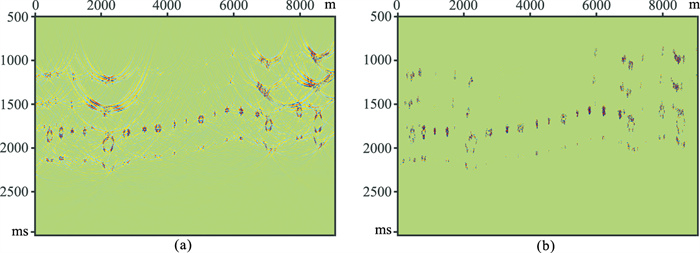
图 10a是PWD法分离的绕射波偏移成像结果,虽然绕射波弱信号在一定程度上突显,但由于分离的绕射波不完整,绕射点成像不清晰,信噪比较低。图 10b是使用本文方法分离的绕射波偏移成像结果,得益于反射波去除干净、绕射波保留完整,绕射点成像清晰完整,小尺度岩溶能够突显。
|
图 10 岩溶—冲沟模型两种方法分离的绕射波偏移剖面对比 (a)PWD法;(b)本文方法 |
实际资料采集于内蒙古杭锦旗。该区奥陶系缝洞型储集体发育,具有埋藏深、尺度小、非均质性强等特点,绕射波响应较弱。在常规反射成像剖面(图 11a)上缝洞型储集体反映不清晰,精细识别与刻画难度大,目的层的冲沟和岩溶体有显示(红色圆圈所示)。由于小尺度岩溶体的存在,平滑线性的反射层呈现向下弯曲的形态,但由于背景强反射的影响,分辨率较低,很难识别其中的小尺度岩溶体。对实际资料使用本文方法分离绕射波,并对分离结果进行成像(图 11b)。由于强反射已被移除,原来被强反射掩盖的小尺度岩溶突显(红色圆圈内),分辨率和聚焦性显著提高。相干体属性可用于断裂识别,图 12a是实际资料的反射波相干属性切片,虽然可以看到岩溶体和断裂,但小尺度岩溶体和断裂难以识别。图 12b为绕射波能量属性切片,可识别的小尺度岩溶体和断裂明显增多,小尺度岩溶体和断裂的边界、形态也更清晰(红色圆圈内)。

|
图 11 实际数据成像剖面对比 (a)全波场;(b)本文方法分离的绕射波场 |

|
图 12 反射波相干属性(a)与绕射波能量属性(b)的切片对比 |
本文通过共虚震源变换利用共炮点道集生成CVSG,对CVSG应用Stolt偏移使双曲形态的绕射波能量收敛,使用正则化PWD去除反射波,再利用反偏移重新得到CVSG,最后利用共虚震源反变换得到共炮点道集绕射波场。本文方法解决了反射与绕射波相切或相交时绕射波难以分离的问题,避免了传统方法在共炮检距道集上进行分离造成的深层绕射波能量损失。数值模型测试验证了本文提出的叠前绕射波分离方法可以提升小尺度地质体成像分辨率,实际资料的应用进一步证明了本文方法对探明缝洞型储集体具有积极意义。本文方法中共虚震源正、反变换虽然数学上是可逆的,但实现过程中有能量损失,如何减小这种损失是下一步的研究方向。
| [1] |
赵惊涛, 王真理, 于彩霞. 地震勘探中的边缘绕射波及其动力学识别方法[J]. 地球物理学进展, 2011, 26(1): 194-206. ZHAO Jingtao, WANG Zhenli, YU Caixia. Edge diffractive wave and its dynamic detection methods in seismic exploration[J]. Progress in Geophysics, 2011, 26(1): 194-206. DOI:10.3969/j.issn.1004-2903.2011.01.021 |
| [2] |
PRATT R G, WORTHINGTON M H. The application of diffraction tomography to cross-hole seismic data[J]. Geophysics, 1988, 53(10): 1284-1294. DOI:10.1190/1.1442406 |
| [3] |
李正伟, 张剑锋, 刘伟. 基于倾角—偏移距域道集的绕射波成像[J]. 地球物理学报, 2018, 61(4): 1447-1459. LI Zhengwei, ZHANG Jianfeng, LIU Wei. Diffraction imaging using dip-angle and offset gathers[J]. Chinese Journal of Geophysics, 2018, 61(4): 1447-1459. |
| [4] |
刘斌, 邸志新, 李晓峰, 等. 一种基于局部倾角估计的倾角域绕射波分离与成像方法[J]. 地球物理学进展, 2014, 29(5): 2204-2210. LIU Bin, DI Zhixin, LI Xiaofeng, et al. Separation and imaging method of diffraction based on local dip estimation in the dip-angle domain[J]. Progress in Geophysics, 2014, 29(5): 2204-2210. |
| [5] |
KREY T. The significance of diffraction in the investigation of faults[J]. Geophysics, 1952, 17(4): 843-858. DOI:10.1190/1.1437815 |
| [6] |
NOWAK E J, IMHOF M G. Diffractor localization via weighted Radon transforms[C]. SEG Technical Program Expanded Abstracts, 2004, 23: 2108-2111.
|
| [7] |
FOMEL S. Applications of plane-wave destruction filters[J]. Geophysics, 2002, 67(6): 1946-1960. DOI:10.1190/1.1527095 |
| [8] |
孔雪, 李振春, 黄建平, 等. 基于平面波记录的绕射目标成像方法研究[J]. 石油地球物理勘探, 2012, 47(4): 674-682. KONG Xue, LI Zhenchun, HUANG Jianping, et al. Diffracting objective imaging based on plane wave record[J]. Oil Geophysical Prospecting, 2012, 47(4): 674-682. |
| [9] |
朱生旺, 李佩, 宁俊瑞. 局部倾角滤波和预测反演联合分离绕射波[J]. 地球物理学报, 2013, 56(1): 280-288. ZHU Shengwang, LI Pei, NING Junrui. Reflection/diffraction separation with a hybrid method of local dip filter and prediction inversion[J]. Chinese Journal of Geophysics, 2013, 56(1): 280-288. |
| [10] |
魏巍, 高鸿, 刘忠岩. 奇异值分解技术在绕射波分离成像中的应用研究[J]. 石油物探, 2020, 59(2): 236-241. WEI Wei, GAO Hong, LIU Zhongyan. Separation and imaging of seismic diffractions using singular value decomposition[J]. Geophysical Prospecting for Petro-leum, 2020, 59(2): 236-241. DOI:10.3969/j.issn.1000-1441.2020.02.009 |
| [11] |
RAD P B, SCHWARZ B, GAJEWSKI D, et al. Common-reflection-surface-based prestack diffraction se-paration and imaging[J]. Geophysics, 2018, 83(1): S47-S55. DOI:10.1190/geo2016-0445.1 |
| [12] |
GONG X B, YU C X, WANG Z H. Separation of prestack seismic diffractions using an improved sparse apex-shifted hyperbolic Radon transform[J]. Exploration Geophysics, 2017, 48(4): 476-484. DOI:10.1071/EG16031 |
| [13] |
LIN P, PENG S P, ZHAO J T, et al. Diffraction separation and imaging using multichannel singular-spectrum analysis[J]. Geophysics, 2020, 85(1): V11-V24. DOI:10.1190/geo2019-0201.1 |
| [14] |
SCHWARZ B. Coherent wavefield subtraction for diffraction separation[J]. Geophysics, 2019, 84(3): V157-V168. DOI:10.1190/geo2018-0368.1 |
| [15] |
ZHAO J T, YU C X, PENG S P, et al. Online dictionary learning method for extracting GPR diffractions[J]. Journal of Geophysics and Engineering, 2019, 16(6): 1116-1123. DOI:10.1093/jge/gxz081 |
| [16] |
KHAIDUKOV V, LANDA E, MOSER T J. Diffraction imaging by focusing-defocusing: an outlook on seismic superresolution[J]. Geophysics, 2004, 69(6): 1478-1490. DOI:10.1190/1.1836821 |
| [17] |
MOSER T J, HOWARD C B. Diffraction imaging in depth[J]. Geophysical Prospecting, 2008, 56(5): 627-641. DOI:10.1111/j.1365-2478.2007.00718.x |
| [18] |
SILVESTROV I, BAINA R, LANDA E. Poststack diffraction imaging using reverse-time migration[J]. Geophysical Prospecting, 2016, 64(1): 129-142. DOI:10.1111/1365-2478.12280 |
| [19] |
ZHAO J T, PENG S P, DU W F, et al. Diffraction imaging method by Mahalanobis-based amplitude damping[J]. Geophysics, 2016, 81(6): S399-S408. DOI:10.1190/geo2015-0692.1 |
| [20] |
YU C X, WANG Y F, ZHAO J T. A seismic diffraction extraction method for the study of discontinuous geologies using a regularisation algorithm[J]. Exploration Geophysics, 2017, 48(1): 49-55. DOI:10.1071/EG15006 |
| [21] |
ZHAO J T, YU C X, PENG S P, et al. 3D diffraction imaging method using low-rank matrix decomposition[J]. Geophysics, 2020, 85(1): S1-S10. |
| [22] |
LI Z W, ZHANG J F. 3D diffraction imaging with Kirchhoff time migration using vertical traveltime difference gathers[J]. Geophysics, 2019, 84(6): S555-S566. DOI:10.1190/geo2018-0630.1 |
| [23] |
汪天池, 刘少勇, 顾汉明, 等. 倾角域逆时偏移绕射波成像方法[J]. 石油地球物理勘探, 2020, 55(3): 591-598. WANG Tianchi, LIU Shaoyong, GU Hanming, et al. Seismic diffraction imaging by reverse time migration in dip angle domain[J]. Oil Geophysical Prospecting, 2020, 55(3): 591-598. |
| [24] |
罗腾腾, 徐基祥, 孙夕平. 应用迭代收缩高分辨率Radon变换的绕射波分离与成像方法[J]. 石油地球物理勘探, 2021, 56(2): 313-322. LUO Tengteng, XU Jixiang, SUN Xiping. Diffraction wave separation and imaging based on high-resolution Radon transform on an iterative model shrinking approach[J]. Oil Geophysical Prospecting, 2021, 56(2): 313-322. |
| [25] |
刘培君, 黄建平, 李振春, 等. 一种基于反稳相的深度域绕射波分离成像方法[J]. 石油地球物理勘探, 2017, 52(5): 967-973. LIU Peijun, HUANG Jianping, LI Zhenchun, et al. A diffraction imaging method in the depth domain driven by anti-stationary phase strategy[J]. Oil Geophysical Prospecting, 2017, 52(5): 967-973. |
| [26] |
LI C J, ZHAO J T, PENG S P, et al. Prestack diffraction separation in the common virtual source gather[J]. Geophysics, 2021, 86(2): S113-S124. DOI:10.1190/geo2020-0105.1 |



 盛同杰, 北京市海淀区学院路丁11号中国矿业大学(北京)地球科学与测绘工程学院, 100083。Email:
盛同杰, 北京市海淀区学院路丁11号中国矿业大学(北京)地球科学与测绘工程学院, 100083。Email: 