② 山东科技大学地球科学与工程学院, 山东青岛 266590
② College of Earth Science and Engineering, Shandong University of Science and Technology, Qing-dao, Shandong 266590, China
对进入勘探开发中、后期的老油田,地震资料处理目标逐渐由“单块三维”转向“连片三维”,以实现对区域整体构造及各构造带之间转换关系的研究[1]。受地表条件等因素的影响,连片探区的不同区块往往采用多种震源和不同检波器进行观测接收,相同区块不同期次采集的资料品质参差不齐[2],导致相邻区块地震资料的振幅、频率、波形和相位等存在较大差异[3],严重影响了数据的连续对比分析和地质储层研究工作[4]。因而,连片资料的一致性校正处理尤为重要。
目前,解决不同区块连片资料拼接一致性问题的主要方法有反褶积参数调整法、匹配滤波法以及多种技术组合应用法。
反褶积参数调整法主要解决不同区块数据分辨率差异的问题,王西文等[5]通过在反褶积处理环节选择不同的预测步长,尽可能地实现有效频谱宽度、主频和优势频宽能量等的一致,这种方法在实际应用中具有一定的效果,但反褶积参数实验相对繁琐,对于十几或几十个区块进行资料拼接的大连片处理,选取合理的参数十分耗时、费力。
匹配滤波法可分为时变、时不变两类。时不变的匹配滤波法有子波处理法和直接匹配滤波法,其中子波处理法也称子波整形或子波匹配,子波处理法假设连片探区相同位置处反射系数相同,认为地震记录的差异由不同子波特征导致。王元波[6]在两个区块重叠区各选取多个面元的地震记录,分别进行混道和去噪处理后,求出相对稳定的子波,计算子波整形因子并应用其消除子波差异,该方法处理质量受拼接带资料质量的影响严重;宋玉龙[7]利用直接匹配滤波法对两个区块重叠区数据进行处理,采用最小二乘法直接计算匹配滤波算子,消除地震剖面间的振幅差异。时变的匹配滤波法包括基于小波变换的子波处理法和基于小波变换的匹配滤波法。王西文等[8]提出基于小波变换的子波处理法将重叠区的两期数据利用不同尺度的小波函数进行分频展开,沿时间方向开小时窗计算两者的能量标定量,并插值得到最佳重构系数,计算各尺度对应的重构系数后进行子波重构,实现一致性处理;程金星等[9]基于小波变换的匹配滤波法将重叠区的两期数据进行小波变换,在不同尺度上利用最小平方法分别计算两期数据的最佳匹配滤波因子,并应用其实现一致性处理的目的;为了实现振幅、时差、频率、相位和波形的全面校正,云美厚等[10]提出了互均衡处理技术,采用最小平方算法从叠后记录中求取多个匹配滤波算子进行一致性处理。
多种技术组合应用法利用多种振幅、频率、相位等一致性处理方法的组合应用解决连片数据的一致性问题。Mohan等[11]采用增益恢复、地表一致性反褶积和地表一致性均衡处理解决连片数据子波不一致问题;戴军文等[12]利用地表一致性振幅补偿、子波整形和振幅均衡处理消除连片处理中的能量不均带来的偏移画弧问题;裴江云等[13]针对叠前连片处理中不同区块的非一致性问题,联合应用几何扩散补偿、地表一致性振幅补偿、地表一致性反褶积和子波整形处理等技术以实现数据的一致性处理;Greer等[14]提出了一套连片一致性处理的流程,首先通过非平稳平滑滤波处理对高分辨率结果实现振幅和频率的均衡,随后利用局部相似扫描方法估计和消除两期数据剖面中的局部时移量,最后利用最小平方反演方法融合两期数据;蒋波[15]应用非刚性匹配、匹配滤波和谱整形等方法改善连片数据处理的子波一致性;曾华会等[16]综合利用叠前平均振幅谱匹配、混合震源相位匹配及叠前剩余时差校正等处理技术,消除了不同激发方式造成的地震资料品质差异。
匹配滤波法的一致性校正因子是通过两块资料的重叠区域数据计算得到,该方法适用的前提是必须存在一定范围的资料重叠区,其处理质量严重依赖于重叠区的资料品质,并且一般只适用于叠后数据的拼接处理。反褶积参数调整法和多种技术组合应用法可以处理叠前数据,但参数调整繁琐,且大都不具有时变处理能力。针对连片数据一致性处理方法存在的问题,本文提出一种基于Shearlet变换的连片数据一致性处理方法,可以处理叠前数据。该方法利用了Shearlet变换的多尺度和多方向性,在优选目标数据的基础上,利用Alpha-trim滤波方法估计待处理数据和目标数据在各尺度和方向上的时变均值和均方差,提取并消除两者的趋势差异,从而实现连片数据的一致性处理,并通过模型数据和实际资料对该方法进行了验证。
1 方法原理 1.1 Shearlet变换的基本原理Guo等[17-18]基于合成小波理论,利用仿射系统把几何分析和多尺度分析结合起来构造了Shearlet变换,其后又将该变换推广到三维空间。Shearlet变换的构造方法如下。
(1) 设
(2) 定义Shearlet波原子ψj, s, m为
| $ \psi_{j, s, m}=\left|\operatorname{det} \boldsymbol{M}_{\boldsymbol{A} \boldsymbol{S}}\right|^{-\frac{1}{2}} \psi\left[\boldsymbol{M}_{\boldsymbol{A} \boldsymbol{S}}^{-1}(\boldsymbol{x}-\boldsymbol{m})\right] $ | (1) |
式中:MAS=SsAa;m代表位置平移量; x为位置变量。令ψ∈L2(R2),其中,L2(R2)表示二维实数域上平方可积函数空间,并满足下列条件:
①
② ψ1为连续小波变换,
③ ψ2∈C∞(R),并满足suppψ2⊂[-1, 1];在区间(-1, 1),
函数f的Shearlet变换可定义为
| $ S_{f}(j, s, m)=\left\langle f, \psi_{j, s, m}\right\rangle $ | (2) |
式中〈·,·〉表示内积。
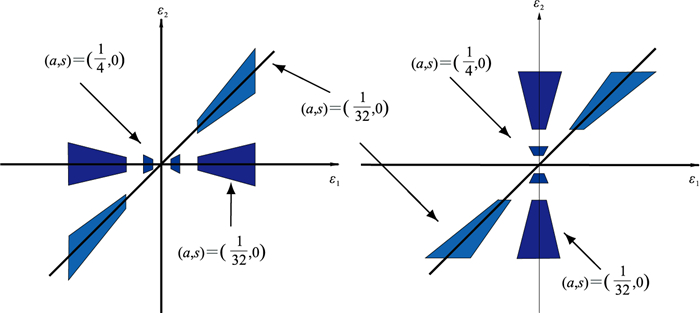
图 1是取不同a、s值所对应的水平方向和垂直方向的Shearlet波原子在频域的支撑[19],其分割方式与Curvelet变换相似。
|
图 1 不同a、s值对应的水平方向(左)和垂直方向(右)的Shearlet波原子在频域的支撑 |
对连片探区中各区块数据分别进行地表一致性振幅补偿和地表一致性反褶积处理,受资料品质、地层吸收差异等因素的影响,连片数据的时间、频率在空间上仍存在一定的差异。
选取一个处理的目标模型消除这种差异,凌云等[20]利用时频空间域球面发散与吸收补偿方法选取模型炮作为目标模型;熊艳梅等[21]优选部分炮检距数据作为目标模型,进行非刚性匹配处理实现数据的一致性处理。本文借鉴后者做法,在连片探区数据品质相对较好的区块内选取一定数量品质较好的数据作为目标模型,连片探区中的其他数据都以该目标数据为校正标准,估计Shearlet域的一致性校正因子,消除目标模型数据与待处理数据的统计差异量,实现连片探区的一致性处理。
一致性校正因子的估计包括两个方面,一个是反映目标模型数据时、频、空间变化的统计趋势估计,另一个是待处理数据的时、频、空间变化趋势的提取。
1.2.1 目标模型数据的时空变趋势估计在工区A中选取N炮质量相对较好的炮集数据作为模型数据,记为Xi,其中i=1, 2,…, N为模型炮的炮号。对Xi进行Shearlet变换,为便于表述,此处仅给出二维的情况,式(2)中位置参数m用二维变量mk1和mk2表示。变换后的Shearlet系数计算公式为
| $ S_{X}\left(i, j, s, m_{k_{1}}, m_{k_{2}}\right)=\left\langle x_{i}, \psi_{j, s, m_{k_{1}}, m_{k_{2}}}\right\rangle $ | (3) |
Alpha-trim均值滤波又称非线性平滑滤波[22],可以消除绝大部分极值因素的影响,同时保留数据非线性变化趋势。利用Alpha-trim均值滤波确定Shearlet系数SX(i, j, s, mk1, mk2)的时变均值,计算方法如下:
(1) 由小到大排序系数;
(2) 抛弃总数中α比例的极大值和极小值部分,其中0≤α≤0.5;
(3) 计算剩余部分的均值。
当α=0时该方法退化为均值滤波;当α=0.5时该方法退化为中值滤波。
第i个模型炮集数据经Shearlet变换后得到系数SX(i, j, s, mk1, mk2),对数据开一个长、宽分别为h、b的矩形窗wh, b,在矩形窗内进行Alpha-trim均值滤波处理,得到矩形窗口中心位置对应的均值,利用该均值进一步计算该窗口数据的均方差。滑动矩形窗wh, b,最终得到时空变的均值SXμ(i, j, s, mk1, mk2)和均方差SXσ(i, j, s, mk1, mk2)。
为了提高Shearlet系数时空变趋势估计结果的稳定性,对多个模型炮集数据的估计结果进行统计平均处理,得到尺度j、方向s下的Shearlet系数多炮统计平均时空变均值和时空变均方差
| $ \bar{S}_{X}^{\mu}\left(j, s, m_{k_{1}}, m_{k_{2}}\right)=\frac{1}{N} \sum\limits_{i=1}^{N} S_{X}^{\mu}\left(i, j, s, m_{k_{1}}, m_{k_{2}}\right) $ | (4) |
| $ \bar{S}_{X}^{\sigma}\left(j, s, m_{k_{1}}, m_{k_{2}}\right)=\frac{1}{N} \sum\limits_{i=1}^{N} S_{X}^{\sigma}\left(i, j, s, m_{k_{1}}, m_{k_{2}}\right) $ | (5) |
针对不同j和s循环上述步骤,直至全部遍历,完成模型炮集数据的时空变趋势估计。
1.2.2 待处理数据的时空变趋势估计由于Shearlet变换是基于频域中的二进尺度分割进行,因而在相同频带宽度下,高频端分解的尺度个数比低频端少,频带分割不精细,严重影响了频率一致性校正的精度。针对这一问题,在频域中分别计算模型数据和待处理数据的统计频谱,以模型数据的统计频谱为期望,计算频率一致性校正算子,对待处理数据进行统计频率一致性校正处理,处理结果记为Y。
将数据Y变换到Shearlet域,得到尺度j和方向s上的Shealet系数SY(j, s, mk1, mk2),对数据开大小为h×b的矩形窗wh, b(与1.2.1节目标模型数据时空变趋势估计的窗口大小保持一致),按照相同方式进行Alpha-trim均值滤波处理,并滑动窗口得到待处理数据的最终Shealet系数时空变均值SYμ(j, s, mk1, mk2)和均方差SYσ(j, s, mk1, mk2)。
当地层充填油气时,会导致地震数据时、空间存在局部能量强度异常,连片数据一致性校正处理时需要保留这种局部异常,同时消除连片区块间的宏观趋势异常。为了进一步消除二维Alpha-trim滑动滤波处理结果中残留的趋势异常,对SYμ(j, s, mk1, mk2)和SXσ(j, s, mk1, mk2)分别进行二维高斯滤波处理,以消除时空变的均值、均方差结果中的局部扰动,提高方法的稳定性。二维高斯函数为
| $ g\left(m_{c}, m_{d}\right)=\frac{1}{2 {\rm{ \mathsf{ π} }} \lambda^{2}} \cdot \exp \left[-\frac{1}{2 \lambda^{2}}\left(m_{c}^{2}+m_{d}^{2}\right)\right] $ | (6) |
式中:c、d表征二维高斯函数两个维度;λ为均方差。λ值越大,高斯窗函数越平坦,滤波效应越明显;λ值越小,高斯窗函数越陡峭,滤波效应降低。
设置滤波模板的半径为r,对式(6)进行归一化处理后,分别对SYμ(j, s, mk1, mk2)和Syσ(j, s, mk1, mk2)进行二维高斯滤波处理,即
| $ S_{Y}^{u, g}\left(j, s, m_{k_{1}}, m_{k_{2}}\right)=\frac{1}{\sum\limits_{m_{c}=-r}^{r} \sum\limits_{m_{d}=-r}^{r} g\left(m_{c}, m_{d}\right)} \cdot \sum\limits_{m_{c}=-r }^{r} \sum\limits_{m_{d}=-r}^{r} S_{Y}^{\mu, g}\left(j, s, m_{k_{1}}, m_{k_{2}}\right) g\left(m_{c}, m_{d}\right) $ | (7) |
| $ S_{Y}^{\sigma, g}\left(j, s, m_{k_{1}}, m_{k_{2}}\right)=\frac{1}{\sum\limits_{m_{c}=-r}^{r} \sum\limits_{m_{d}=-r}^{r} g\left(m_{c}, m_{d}\right)} \cdot \sum\limits_{m_{c}=-r}^{r} \sum\limits_{m_{d}=-r}^{r} S_{Y}^{\sigma, g}\left(j, s, m_{k_{1}}, m_{k_{2}}\right) g\left(m_{c}, m_{d}\right) $ | (8) |
经过二维Alpha-trim滑动滤波处理和二维高斯滤波处理后得到的时空变均值和均方差结果,基本消除了局部扰动异常,并且能够稳定地反映Shearlet系数随时间和空间的变化趋势。
1.2.3 一致性校正因子按照上述方法计算得到模型数据和待处理数据相对稳定的时空变均值和均方差后,通过下式计算一致性校正因子
| $ \begin{aligned} S_{\mathrm{e}}^{\mu}\left(j, s, m_{k_{1}}, m_{k_{2}}\right)=& \bar{S}_{X}^{\mu}\left(j, s, m_{k_{1}}, m_{k_{2}}\right)-\\ & S_{Y}^{\mu, g}\left(j, s, m_{k_{1}}, m_{k_{2}}\right) \end{aligned} $ | (9) |
| $ S_{\mathrm{e}}^{\sigma}\left(j, s, m_{k_{1}}, m_{k_{2}}\right)=\frac{\bar{S}_{X}^{\sigma}\left(j, s, m_{k_{1}}, m_{k_{2}}\right)}{S_{Y}^{\sigma, g}\left(j, s, m_{k_{1}}, m_{k_{2}}\right)} $ | (10) |
式中Sμe(j, s, mk1, mk2)和Sσe(j, s, mk1, mk2)分别表示时空变的均值和均方差校正量。
1.3 Shearlet域一致性校正处理计算出Shearlet域一致性校正因子后,按照下式调整待处理数据Shearlet系数的时变均值
| $ \begin{aligned} S_{Y}^{o_1}\left(j, s, m_{k_{1}}, m_{k_{2}}\right)=& S_{Y}\left(j, s, m_{k_{1}}, m_{k_{2}}\right)+\\ & S_{\mathrm{e}}^{\mu}\left(j, s, m_{k_{1}}, m_{k_{2}}\right) \end{aligned} $ | (11) |
并进一步调整SYo1(j, s, mk1, mk2)的均方差,得
| $ \begin{aligned} S_{Y}^{o_2}\left(j, s, m_{k_{1}}, m_{k_{2}}\right)=& S_{\mathrm{e}}^{\sigma}\left(j, s, m_{k_{1}}, m_{k_{2}}\right) \cdot \\ & S_{Y}^{o_1}\left(j, s, m_{k_{1}}, m_{k_{2}}\right) \end{aligned} $ | (12) |
式中SYo2(j, s, mk1, mk2)表示待处理炮集数据调整时变均值和均方差后的结果。将处理后的Shearlet系数反变换到时空域,得到最终的一致性处理结果。
在实际数据处理时,应注意通过定义时窗避开直达波和浅层折射波对一致性校正因子估计质量的影响。
2 模型试算与实际资料处理为了验证本文方法的可靠性和有效性,分别对模型数据和实际数据进行了一致性处理和分析。
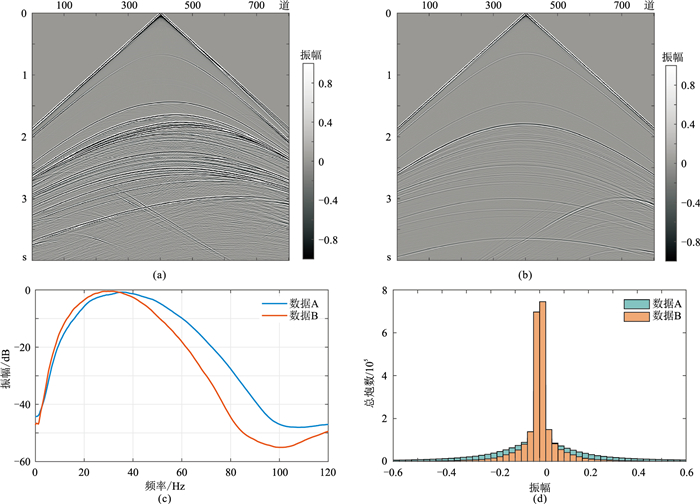
2.1 模型试算设计一个速度模型,在模型地表的不同位置利用主频为35Hz、极大值为2.5的Riker子波和主频为30Hz、极大值为1的Riker子波模拟激发,分别正演得到炮集数据A和数据B(图 2)。由图可见,数据A(图 2a)的能量比数据B(图 2b)强;由频谱统计图可以看出两者存在频率差异,数据A的主频略高并且频带略宽(图 2c);由数据A、数据B的振幅统计直方图可以看出(图 2d),二者的振幅幅值在零值附近分布居多,但数据A的幅值分布相对分散,较小值明显多于数据B,其统计直方图较“胖”,表明数据A的均方差较大。
|
图 2 正演模型数据及其统计频谱、振幅分析 (a)正演炮集数据A;(b)正演炮集数据B;(c)数据A和数据B的统计频谱;(d)数据A和数据B的振幅统计直方图 |
分别计算数据A和数据B中所有采样点值的均值E
| $ E=\sqrt{\frac{\sum\limits_{l=1}^{M} A_{l}}{M}} $ | (13) |
式中:M表示炮集数据中所有采样点的个数;Al表示第l个采样点的幅值。
再分别计算数据A、数据B的均方差σ
| $ \sigma=\sqrt{\frac{\sum\limits_{l=1}^{M}\left(A_{l}-E\right)^{2}}{M}} $ | (14) |
由式(13)计算出数据A、数据B的均值分别为EA=5.06×10-5和EB=1.20×10-4,两者均值差异很小,接近零值(均值反映了数据中直流分量的强弱)。利用式(14)计算出数据A、数据B的均方差分别为σA=2.7213和σB=0.6275,说明炮集数据的能量越强,其对应的均方差越大。下面以数据A作为目标模型,对数据B进行一致性处理。
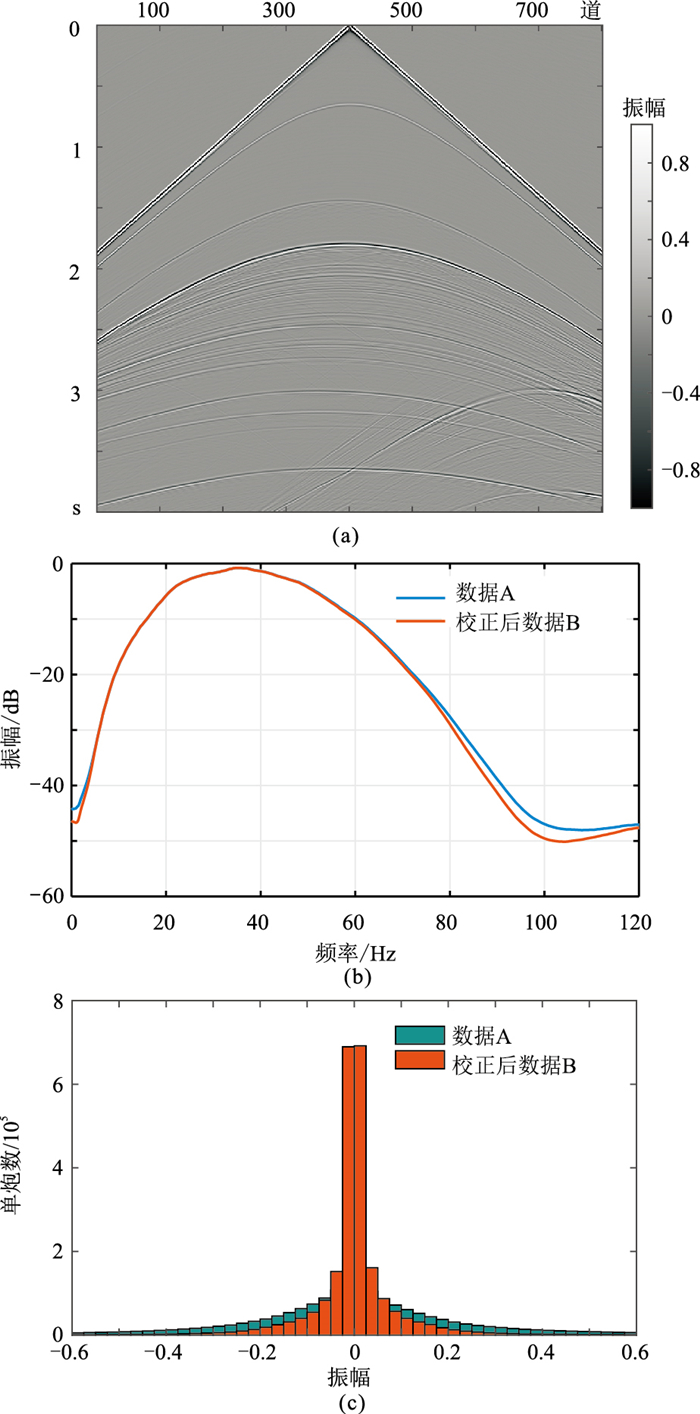
利用图 2c中数据A、B的统计频谱,设计频率一致性校正因子,对数据B进行频域统计一致性校正处理。图 3为处理结果,对比分析可以看出,处理前(图 2b)、后(图 3a)炮集数据的能量变化不明显。由图 3b可知,经过频率统计一致性处理后,数据B的统计频谱与目标模型数据A的统计频谱基本相吻合。对比处理前(图 2d)、后(图 3c)炮集数据的振幅统计直方图可知,处理后数据B中接近零值的数据个数急剧下降,朝着远离零值的趋势变化,但整体来看,数据B的振幅统计直方图依然较“瘦”,数据的均方差略有增加,但与数据A的振幅统计直方图相比,依然存在较大的差异。
|
图 3 频域统计一致性校正处理结果及其统计分析 (a)数据B频域一致性校正结果;(b)数据A和校正后数据B的统计频谱;(c)数据A和校正后数据B的振幅统计直方图 |
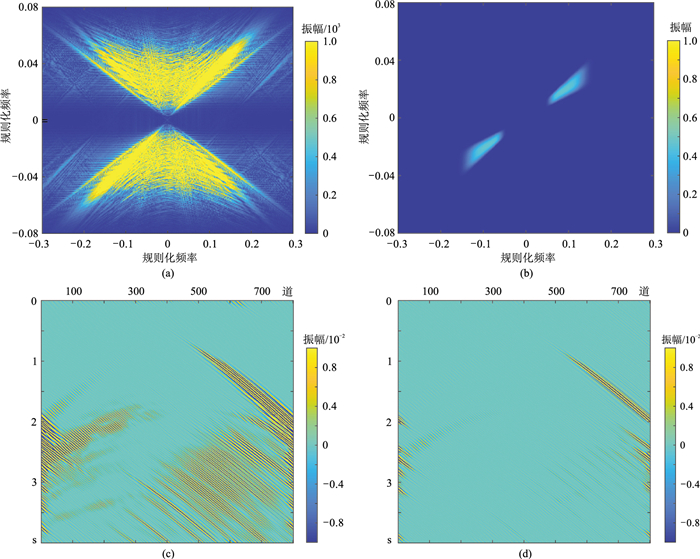
对数据A(图 2a)和频率一致性处理后的数据B(图 3a)进行Shearlet变换。图 4显示f-k域的Shearlet尺度分割及其变换系数的对比。图 4a为图 2a的f-k谱,图 4b为某个尺度和方向上的Shearlet的f-k域分割窗,利用该分割窗分别对数据A和频域一致性处理后的数据B进行分割,得到对应的Shearlet系数(图 4c、图 4d)。可以看出,由于模型数据和待处理数据的反射波能量、倾角和时空域分布都存在较大差异,经过Shearlet变换后,在相同尺度和方向上的系数也存在较大差异。
|
图 4 Shearlet变换的FK域分割及其变换系数对比 (a)数据A的f-k谱;(b)f-k域Shearlet变换的某个分割窗;(c)由分割窗计算出的数据A的Shearlet系数;(d)由分割窗计算出的数据B的Shearlet系数 |
图 4c、图 4d中Shearlet系数的幅度反映了局部数据在该尺度和方向的能量强弱,Shearlet局部系数依然是波形的形态特征。对于这种形态而言,均方差能够反映数据在特定尺度和方向的能量强弱,一般来说,数据能量越强,其Shearlet系数的均方差越大。
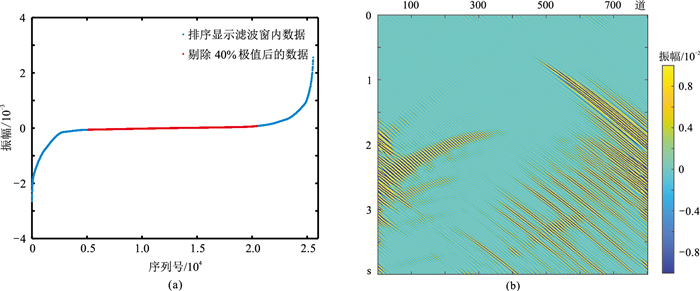
利用本文方法对图 4c、图 4d的Shearlet系数进行一致性校正因子估算。图 5a给出了二维滑动窗内数据由小到大排列及Alpha-trim滤波参数α=0.2时剔除了极值后的数据对比。由图可见,数据较大、较小值的数量均少但数值幅度较大,这会严重影响均值计算结果的质量,尤其是当数据中存在局部异常噪声的情况下。经Alpha-trim均值滤波处理剔除一定比例的较大、较小值后,能够消除局部极值对时变均值估计的影响,提高估计的稳定性。图 5b为图 4d的Shearlet系数经过一致性校正处理后的结果。综合对比可见,处理后数据B系数的几何特征(倾角、各反射间几何关系等)都与处理前保持一致,但能量分布的相对关系有较大改变,整体上与目标模型数据的Shearlet系数(图 4c)一致。
|
图 5 Shearlet系数一致性校正处理 (a)二维滑动窗内数据Alpha-trim滤波(参数α=0.2)剔除极值前、后对比;(b)图 4d中数据B的一致性校正结果 |
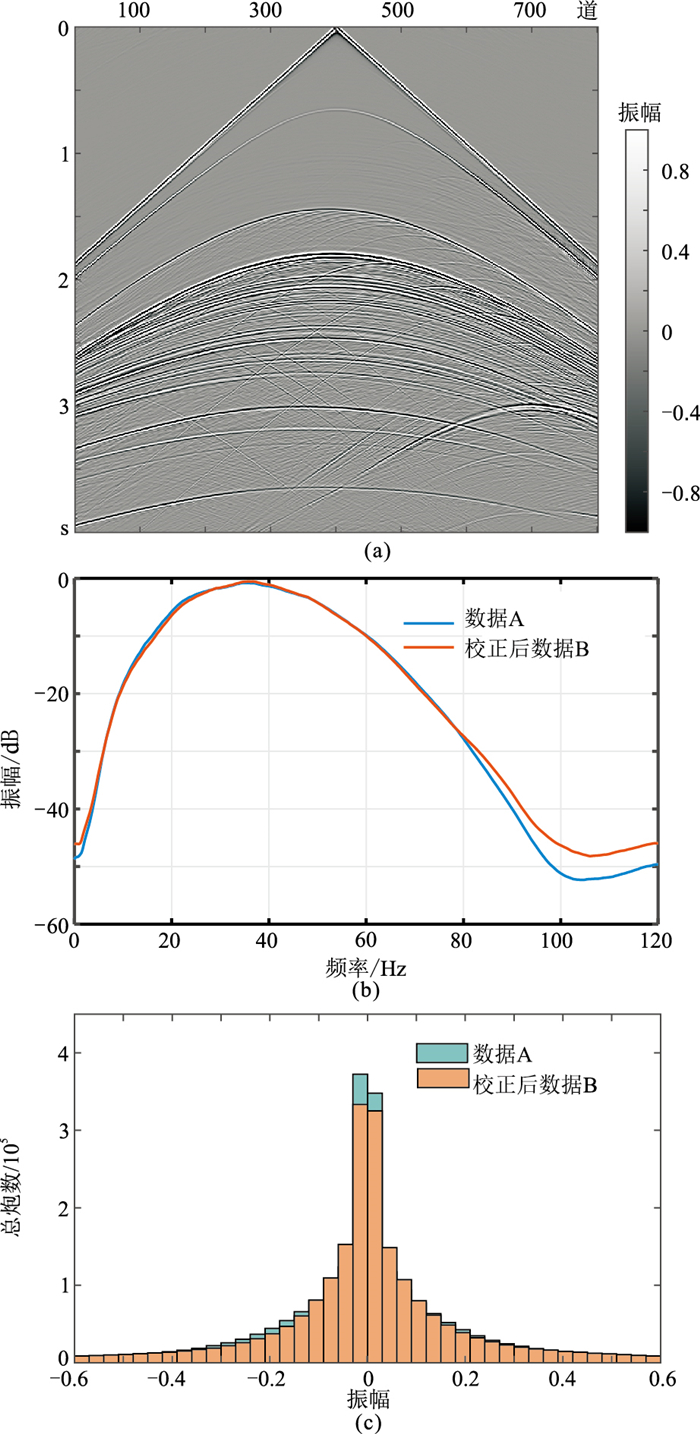
在Shearlet域完成各个尺度和方向的一致性校正处理,将处理后的系数反变换到时空域得到最终结果(图 6)。对比图 2a、图 3b和图 6a可以看出,经过Shearlet域一致性处理后,数据A和数据B的振幅强度在时空域的变化特征基本一致,并且反射、绕射波的特征也与处理前的数据特征保持一致,表明处理前、后炮集数据的几何特征和波动特征都得到较好的保持。进一步分析统计频谱(图 6b)可以看出,经过本文方法处理后,数据B的统计频谱与模型数据A基本一致,在80~120Hz频段内,处理后数据B的统计频谱能量有一定的提升,略高于数据A,侧面反映了随着频率的增加Shearlet变换对频率一致性的处理能力有所减弱。处理后数据B和数据A的振幅统计直方图(图 6c)显示,两者分布形态基本相似,除零值附近的分布特征略有不同外,其他幅度上的分布基本一致,表明处理后数据和模型数据在振幅统计上具有一致性。
|
图 6 Shearlet域一致性校正结果及其统计分析 (a)数据B Shearlet域一致性校正的处理结果;(b)数据A和校正后数据B的统计频谱;(c)数据A和校正后数据B的振幅统计直方图 |
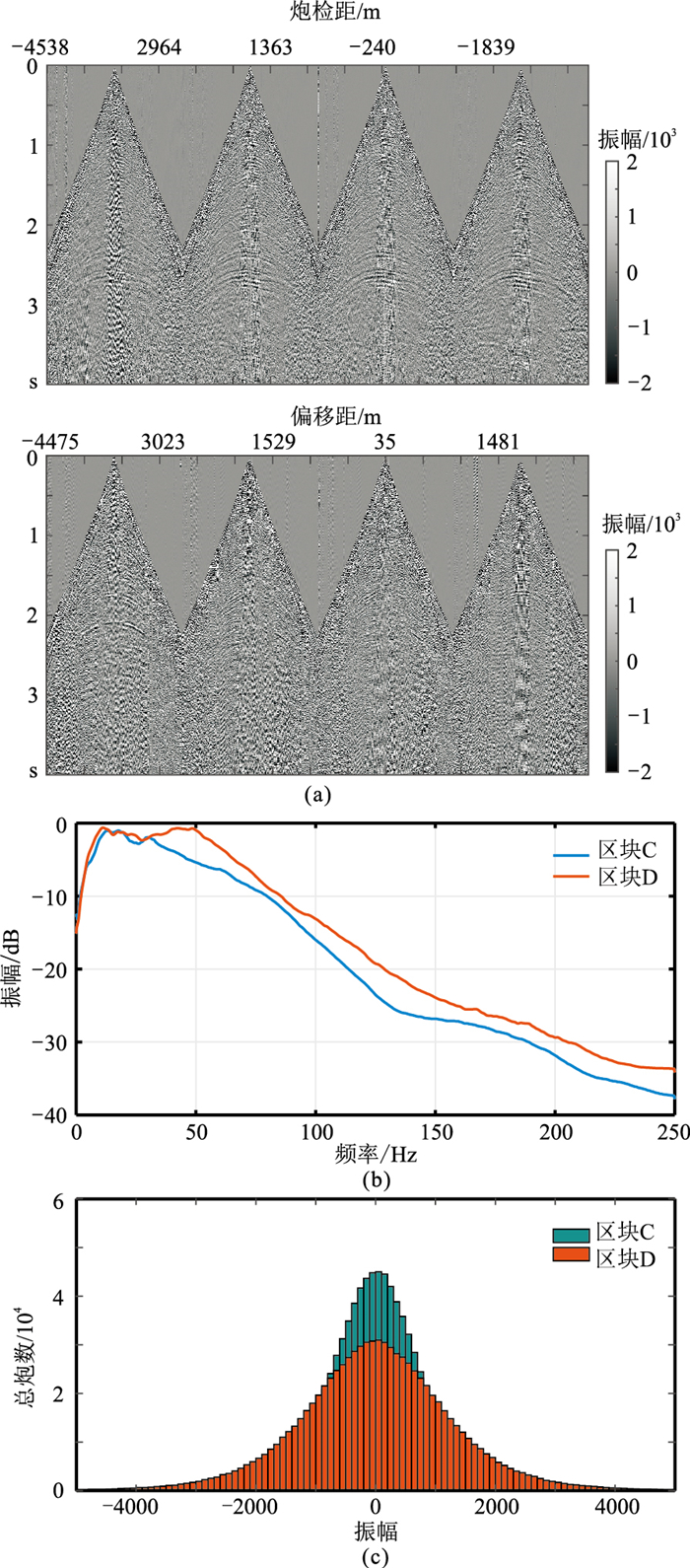
对实际连片区块C、区块D的炮集数据进行一致性校正处理,进一步验证本文方法的有效性。区块C(图 7a上)和区块D(图 7下)的数据都进行了地表一致性振幅补偿和地表一致性反褶积处理。对比可见,区块C数据的信噪比高于区块D数据。图 7c的统计频谱显示两块数据的频带宽度大致相当,区块D数据频带略宽,并且40~60Hz范围内的能量明显强于区块C。图 7d振幅统计直方图显示两者的振幅分布存在一定的差异,区块D数据的均方差略大,区块C数据振幅落在-1000~1000范围内的个数明显多于区块D。
|
图 7 实际观测数据及其统计分析 (a)区块C(上)、区块D(下)的实际炮集数据;(b)区块C和区块D数据的统计频谱;(c)区块C和区块D数据的振幅统计直方图 |
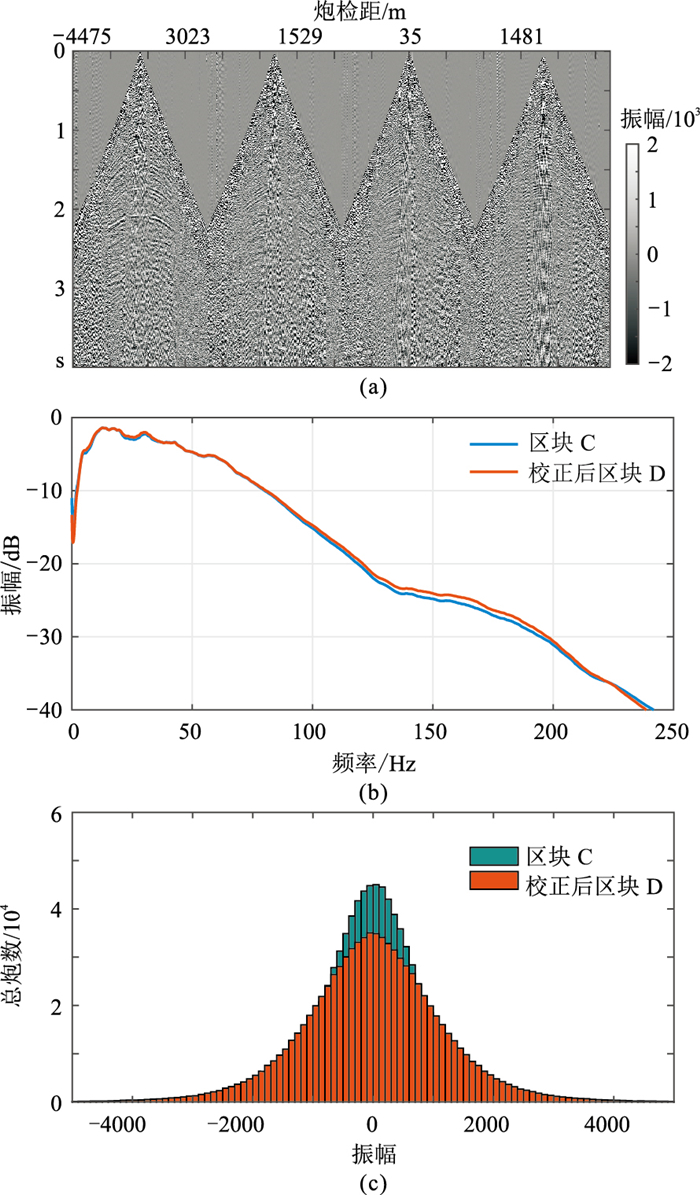
图 8为区块D数据进行频域一致性校正处理的结果,对比图 8a和图 7b炮集数据可以看出,两者无明显差异。图 8b统计频谱对比显示,经过频域一致性校正处理后,区块D数据的统计频谱与区块C数据的统计频谱基本一致。图 8d中振幅统计直方图对比可以看出,频域一致性校正处理后区块D数据振幅统计直方图的均方差略有降低,与区块C数据的振幅统计直方图吻合度有所提高。
|
图 8 频域统计一致性校正处理 (a)对区块D数据频域一致性校正处理结果;(b)区块C数据与校正后区块D数据的统计频谱;(c) 区块C数据与校正后区块D数据的振幅统计直方图 |
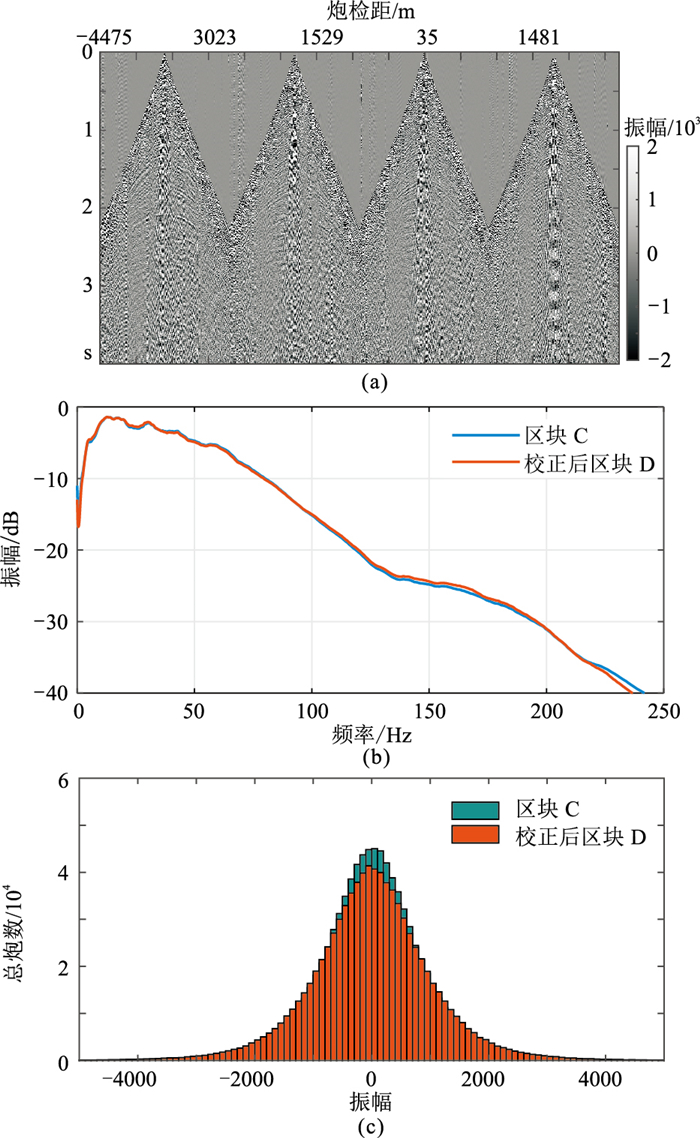
图 9为区块D数据采用本文方法一致性处理的最终结果,对比图 9a和图 7b的炮集数据可以看出,一致性处理后剖面的能量分布更加均衡,局部噪声也有所压制。对比处理后的统计频谱(图 9b)可以看出,本文方法能够较好地校正两区块数据间的统计频带差异,处理后两者的主频、频带宽度等都基本达到一致。对比处理后两区块数据的振幅统计直方图(图 9c)可见,本文方法极大地消除了两区块数据间的振幅统计分布差异,实现了两块数据振幅、频率的时空一致性,从而验证了本文方法的有效性。
|
图 9 Shearlet域一致性校正结果及其统计分析 (a)对区块D数据进行Shearlet域一致性校正处理的结果;(b)区块C数据与校正后区块D数据的统计频谱;(c)区块C数据与校正后区块D数据的振幅统计直方图 |
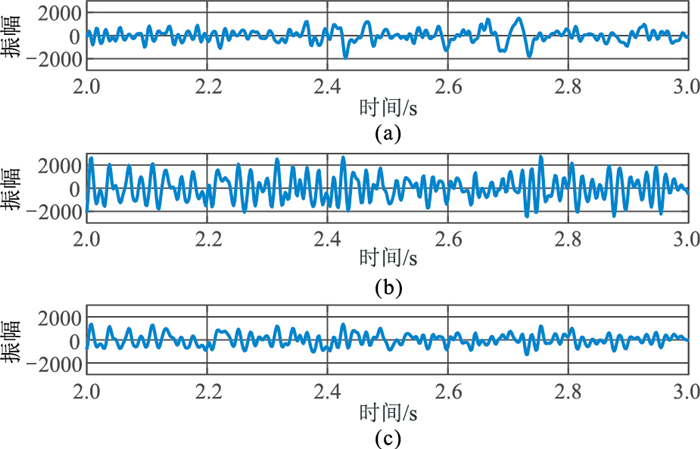
图 10进一步对比了区块D数据处理前、后地震道的波形变化,从图中可以看出,处理前区块C和区块D的地震记录的波形存在较大差异,区块D数据的振幅明显强于区块C数据。经过本文方法一致性处理后,区块D数据的振幅与区块C数据的振幅范围基本一致,进一步验证了本文方法一致性处理效果。
|
图 10 区块C和处理前、后区块D数据地震道波形对比 (a)区块C数据(第2炮、炮检距-1413m);(b)区块D数据(第2炮、炮检距-1425m);(c)处理后区块D数据(第2炮炮检距-1425m) |
需指出的是,受采集因素的影响,不同批次可控震源与炸药震源采集的数据往往存在较大的相位差异,在实际连片数据处理时,应进一步消除不同数据之间相位差异。上述方法仅消除了振幅、频率的时空上的差异,还需要采用小相位转换或相位旋转等处理手段消除不同区块间的相位差,最终实现连片数据振幅、频率、波形和相位的一致性处理。
3 结束语基于Shearlet变换的连片数据一致性处理方法是在Shearlet域通过二维Alpha-trim均值滑动滤波处理提取时变的均值,并进一步计算均方差,通过调整待处理数据和目标数据间的统计分布达到连片数据的振幅、频率在时空域相对一致的目的。不同频带的Shearlet变换尺度分割精细程度存在差异,高频段一致性校正能力较弱,为了解决这一问题,在Shearlet域一致性处理前,先在频域进行统计频谱的一致性处理。用本文方法进行模型试算和实际资料处理及对比分析,结果证实了方法的可靠性和有效性,具有一定的实际应用价值。
| [1] |
季占真, 柳世光, 张淑梅, 等. 连片叠前时间偏移技术在辽河盆地西部凹陷的应用[J]. 新疆石油地质, 2011, 32(4): 418-420. JI Zhanzhen, LIU Shiguang, ZHANG Shumei, et al. Application of merging pre-stack time migration technique in western sag of Liaohe Basin[J]. Xinjiang Petroleum Geology, 2011, 32(4): 418-420. |
| [2] |
王波, 聂其海, 陈进娥, 等. 四维多波地震在油藏动态监测中的应用[J]. 石油地球物理勘探, 2021, 56(2): 340-345. WANG Bo, NIE Qihai, CHEN Jin'e, et al. Application of 4D multi-component seismic survey in dynamic reservoir monitoring[J]. Oil Geophysical Prospecting, 2021, 56(2): 340-345. |
| [3] |
羊屋三维处理、解释一体化方法研究组. 三维地震数据的分析和监测方法研究[J]. 石油地球物理勘探, 2002, 37(5): 433-440. Research Group for Yangwu 3-D Processing and Interpretation Integration. Research on analyzing and monitoring method for 3-D seismic data[J]. Oil Geophysical Prospecting, 2002, 37(5): 433-440. DOI:10.3321/j.issn:1000-7210.2002.05.001 |
| [4] |
高军, 凌云, 林吉祥, 等. 相对保持储层信息的地震数据处理及其地球物理与地质监控[J]. 石油物探, 2010, 49(5): 451-459, 521. GAO Jun, LING Yun, LIN Jixiang, et al. Seismic data processing with relatively preserving reservoir reflection information and its geophysical & geological monitoring[J]. Geophysical Prospecting for Petroleum, 2010, 49(5): 451-459, 521. DOI:10.3969/j.issn.1000-1441.2010.05.004 |
| [5] |
王西文, 刘全新, 吕焕通, 等. 相对保幅的地震资料连片处理方法研究[J]. 石油物探, 2006, 45(2): 105-120. WANG Xiwen, LIU Quanxin, LYU Huantong, et al. Relative amplitude method to merging processing of 3-D seismic data from multi-area[J]. Geophysical Prospecting for Petroleum, 2006, 45(2): 105-120. |
| [6] |
王元波. 三维地震处理连片拼接技术[J]. 大庆石油地质与开发, 2001, 20(3): 67-68. WANG Yuanbo. Connecting technique of 3D seismic process[J]. Petroleum Geology & Oilfield Development in Daqing, 2001, 20(3): 67-68. |
| [7] |
宋玉龙. 滩浅海地区地震勘探存在问题及其解决方法[J]. 石油物探, 2005, 44(4): 343-347. SONG Yulong. Problems of seismic survey in neritic area and resolved methods[J]. Geophysical Prospecting for Petroleum, 2005, 44(4): 343-347. DOI:10.3969/j.issn.1000-1441.2005.04.009 |
| [8] |
王西文, 周立宏. 三维地震资料拼接中的地震子波处理[J]. 石油物探, 2002, 41(4): 448-451, 455. WANG Xiwen, ZHOU Lihong. Wavelet transform used in the concatenation of 3-D seismic data sets[J]. Geophysical Prospecting for Petroleum, 2002, 41(4): 448-451, 455. DOI:10.3969/j.issn.1000-1441.2002.04.014 |
| [9] |
程金星, 朱立华, 杨长春, 等. 基于小波变换的三维地震资料拼接方法[J]. 石油地球物理勘探, 2004, 39(4): 406-408. CHENG Jinxing, ZHU Lihua, YANG Changchun, et al. Method of putting 3-D seismic data together based on wavelet transform[J]. Oil Geophysical Prospecting, 2004, 39(4): 406-408. DOI:10.3321/j.issn:1000-7210.2004.04.008 |
| [10] |
云美厚, 丁伟, 王开燕, 等. 地震资料一致性处理方法研究与初步应用[J]. 石油物探, 2006, 45(1): 65-69. YUN Meihou, DING Wei, WANG Kaiyan, et al. Study and primary application on consistency proces-sing of seismic data[J]. Geophysical Prospecting for Petroleum, 2006, 45(1): 65-69. |
| [11] |
MOHAN T R M, YADAVA C B, KUMAR S, et al. Prestack merging of land 3D vintages: a case history from Kavery Basin, India[C]. SEG Technical Program Expanded Abstracts, 2007, 26: 437-441.
|
| [12] |
戴军文, 杨勇, 李振勇. GRISYS系统三维地震数据连片处理及关键技术[J]. 石油地球物理勘探, 2009, 44(增刊1): 52-56. DAI Junwen, YANG Yong, LI Zhenyong. 3D seismic data multi-survey merging processing and key techniques with GRISYS processing system[J]. Oil Geophysical Prospecting, 2009, 44(S1): 52-56. |
| [13] |
裴江云, 张丽艳, 王丽娜, 等. 松辽盆地深层地震资料叠前时间偏移连片处理技术研究[J]. 地球物理学报, 2011, 54(2): 294-303. PEI Jiangyun, ZHANG Liyan, WANG Lina, et al. Multi-survey joint pre-stack time migration proces-sing study of deep beds in Songliao Basin[J]. Chinese Journal of Geophysics, 2011, 54(2): 294-303. |
| [14] |
GREER S, FOMEL S. Matching and merging high-resolution and legacy seismic images[J]. Geophy-sics, 2018, 83(2): V115-V122. |
| [15] |
蒋波. 地震资料重处理的方法技术[J]. 石油物探, 2020, 59(4): 551-563. JIANG Bo. Seismic data reprocessing[J]. Geophysical Prospecting for Petroleum, 2020, 59(4): 551-563. |
| [16] |
曾华会, 王小卫, 苏勤, 等. 混合震源高精度匹配处理技术在中国西部复杂障碍区的应用[J]. 石油地球物理勘探, 2021, 56(3): 476-484. ZENG Huahui, WANG Xiaowei, SU Qin, et al. Research and application of mixed sources high-precision matching processing technology in the complex obstacle area in western China[J]. Oil Geophysical Prospecting, 2021, 56(3): 476-484. |
| [17] |
GUO K H, LABATE D. Optimally sparse multidimensional representation using shearlets[J]. SIAM Journal on Mathematical Analysis, 2007, 39(1): 298-318. |
| [18] |
GUO K H, LABATE D. Optimally sparse representations of 3D data with C2 surface singularities using parseval frames of shearlets[J]. SIAM Journal on Mathematical Analysis, 2012, 44(2): 851-886. |
| [19] |
YI S, LABATE D, EASLEY G R, et al. A shearlet approach to edge analysis and detection[J]. IEEE Transactions on Image Processing, 2009, 18(5): 929-941. |
| [20] |
凌云, 高军, 吴琳. 时频空间域球面发散与吸收补偿[J]. 石油地球物理勘探, 2005, 40(2): 176-182, 189. LING Yun, GAO Jun, WU Lin. Compensation for spherical dispersion and absorption in time-frequency-space domain[J]. Oil Geophysical Prospecting, 2005, 40(2): 176-182, 189. |
| [21] |
熊艳梅, 徐春梅, 邬达理, 等. 非刚性匹配技术在地震资料一致性处理中的应用[J]. 地球物理学进展, 2017, 32(1): 306-310. XIONG Yanmei, XU Chunmei, WU Dali, et al. Application of non-rigid matching technique in consistency processing of seismic data[J]. Progress in Geophy-sics, 2017, 32(1): 306-310. |
| [22] |
BEDNAR J, WATT T. Alpha-trimmed means and their relationship to median filters[J]. IEEE Tran-sactions on Acoustics, Speech, and Signal Processing, 1984, 32(1): 145-153. |



 田坤,山东省东营市北一路210号胜利油田物探研究院,257022。Email:
田坤,山东省东营市北一路210号胜利油田物探研究院,257022。Email: 