② 东方地球物理公司装备服务处装备研究中心,河北涿州 072751
② Geophysical Equipment Research Center, BGP Inc., CNPC, Zhuozhou, Hebei 072751, China
目前,海底勘探作业是发掘海洋油气资源的重要技术手段[1-3]。海底勘探施工过程(涉及海底电缆和海洋节点等)中一般采用长基线声学定位或初至波定位系统辅助确定铺放于海底的地震检波器的空间位置[4-7]。声学定位系统安装于专门的定位船上,可对铺于海底的声学应答器实时定位、指导释放海底电缆或海洋节点的放样导航船修正航线,从而保证铺放的电缆或节点满足放样精度要求而广泛应用。
近年来,学者对海洋长基线声学定位算法进行了相关研究,并取得了一定成效。基于距离交会定位基本方程,方守川[5]、赵建虎等[6]、刘慧敏等[7]提出了深度约束的交会定位方法,提高了在野外声学观测值组成的几何图形条件较差的情况下的定位精度,解决了控制点坐标存在垂直解不稳定问题。但其主要适用于海洋工程领域对海底控制点的定位,并不适用于海底勘探实时声学定位作业。方守川[5]和赵爽等[8]所述的差分定位方法,解决了作业船航迹对称及声场入射角不大的情况下的无需声速剖面的定位问题,提高了水下声学定位的精度,但它们均是针对野外数据观测值具有双边对称几何图形的情况。刘慧敏等[9]提出了顾及声线弯曲的浅海多目标水声定位算法,在声速测量不准且大入射角观测数据占比较大的情况下,通过改善观测方程数学模型显著提高定位精度。但其假设条件是相同的入射角具有近似的声线弯曲误差,这就需定位船围绕海底应答器全方位地采集声学信号或双边观测。
目前,实际生产作业中的实时定位软件普遍采用传统的最小二乘法估计的定位方法。而上述这些定位方法所处理的野外声学观测数据,均是在基于已完成数据采集的前提下进行的,一般适用于海洋工程领域中水底控制网的定位或数据后处理和质量控制工作,这与海底勘探实时声学定位的单一方向航行观测的方式不同。
结合实际生产作业过程中声学数据通过声学定位系统周期性的采集,其形成的观测值是定位船单一航行方向采集,并可能存在野值和粗差等不合格的观测值,从而影响实时定位精度的情况。基于以上问题,本文提出了一种基于抗差估计的海底勘探实时声学定位方法,首先给定观测值的可能范围并对其进行野值剔除处理,然后基于概率统计假设进行粗差探测,最后构建极值函数确定观测值权阵,通过迭代计算实现实时声学定位,从而满足放样导航船修正航线的需要和保证检波器放样精度要求。
1 传统实时定位原理海底勘探定位船一般配备全球导航定位系统(Global Navigation Satellite System,GNSS)、测深仪、声学定位系统及实时定位软件。其中,GNSS为船载声学探头提供绝对坐标,船载声学探头走航过程中与海底的应答器进行声波实时测距,通过不同时刻、不同船位距离交会方式即可确定海底应答器的位置。在海底地震勘探作业中,考虑到潮流影响,为提高放缆船或节点船放样导航的精度和作业效率,一般都会采用声学定位船跟随其后进行实时声学定位的作业方法(图 1)。

|
图 1 实时声学定位示意图 |
在这种工作模式下,定位船的实时定位采集软件根据设定好的定位采集间隔,对在其有效工作范围内的海底应答器进行呼叫,应答器返回应答信号。
定位船进行定位作业时,在不同时刻和位置会发射声波,其可获得接收声波的海底应答器与船载声学探头之间的距离观测值。类似于测边网距离交会方式[10],可构建如下观测方程,采用最小二乘法估计实时解算海底应答器的空间位置[5, 10]
| $ \begin{aligned} \rho_{\mathrm{vz}, i}=f\left(\boldsymbol{p}_{\mathrm{z}, i}, \boldsymbol{p}_{\mathrm{t}, i}\right)+\delta \rho_{\mathrm{i}} \end{aligned} $ | (1) |
| $ \delta \rho_{i} =\delta \rho_{\mathrm{t}, i}+\delta \rho_{\mathrm{v}, i}+\varepsilon_{\rho, i} $ | (2) |
式中:ρvz, i是声学观测值,为在i时刻定位船v声学探头到水下应答器z之间的观测距离;f(pz, i, pt, i)为i时刻声学探头t初始位置pt, i到水下应答器位置pz, i的几何距离函数;δρi为测距误差;δρt, i为时间延迟产生的系统误差;δρv, i为不同位置声速结构变化引起的系统误差;ερ, i为随机误差。
在给定初始值pz, 0情况下对式(1)线性化可得
| $ \rho_{\mathrm{vz}, i}-f\left(\boldsymbol{p}_{z, 0}, \boldsymbol{p}_{\mathrm{t}, i}\right)=\boldsymbol{a}_{\mathrm{vz}, i} \mathrm{~d} \boldsymbol{p}_{z, i}+\delta \rho_{i}+\boldsymbol{b}_{\mathrm{vz}, i} \mathrm{~d} \boldsymbol{p}_{\mathrm{t}, i} $ | (3) |
式中:avz, i为i时刻f(pz, i, pt, i)对pz, i的一次偏导系数;bvz, i为i时刻f(pz, i, pt, i)对pt, i的一次偏导系数;dpt, i为定位船声学探头在i时刻的空间位置误差。若定位船定位网络利用船体姿态修正后,对最后应答器定位的影响可忽略,即bvz, idpt, i≈0。式(3)中的各项具体形式分别为
| $ \left\{\begin{array}{l} \boldsymbol{p}_{\mathrm{z}, i}=\left[\begin{array}{l} x_{\mathrm{z}} \\ y_{z} \\ z_{\mathrm{z}} \end{array}\right] \\ \boldsymbol{p}_{\mathrm{t}, i}=\left[\begin{array}{l} x_{i} \\ y_{i} \\ z_{i} \end{array}\right] \\ \mathrm{d} \boldsymbol{p}_{\mathrm{z}, i}=\left[\begin{array}{l} \mathrm{d} x_{\mathrm{z}} \\ \mathrm{d} y_{\mathrm{z}} \\ \mathrm{d} z_{\mathrm{z}} \end{array}\right] \\ \mathrm{d} \boldsymbol{p}_{\mathrm{t}, i}=\left[\begin{array}{l} \mathrm{d} x_{i} \\ \mathrm{~d} y_{i} \\ \mathrm{~d} z_{i} \end{array}\right] \end{array}\right. $ | (4) |
| $ \left\{\begin{array}{l} \boldsymbol{a}_{\mathrm{vz}, i}=\left(\frac{\partial f_{i}}{\partial x_{\mathrm{z}}}, \frac{\partial f_{i}}{\partial y_{\mathrm{z}}}, \frac{\partial f_{i}}{\partial z_{\mathrm{z}}}\right) \\ \boldsymbol{b}_{\mathrm{vz}, i}=\left(\frac{\partial f_{i}}{\partial x_{i}}, \frac{\partial f_{i}}{\partial y_{i}}, \frac{\partial f_{i}}{\partial z_{i}}\right) \end{array}\right. $ | (5) |
| $ \begin{aligned} &f\left(\boldsymbol{p}_{z, 0}, \boldsymbol{p}_{\mathrm{t}, i}\right)= \\ &\sqrt{\left(x_{i}-x_{\mathrm{z}, 0}\right)^{2}+\left(y_{i}-y_{z, 0}\right)^{2}+\left(z_{i}-z_{z, 0}\right)^{2}} \end{aligned} $ | (6) |
| $ \left\{\begin{array}{l} \frac{\partial f_{i}}{\partial x_{z}}=\frac{x_{i}-x_{z, 0}}{f\left(\boldsymbol{p}_{z, 0}, \boldsymbol{p}_{\mathrm{t}, i}\right)} \\ \frac{\partial f_{i}}{\partial y_{z}}=\frac{y_{i}-y_{z, 0}}{f\left(\boldsymbol{p}_{z, 0}, \boldsymbol{p}_{\mathrm{t}, i}\right)} \\ \frac{\partial f_{i}}{\partial z_{z}}=\frac{z_{i}-z_{z, 0}}{f\left(\boldsymbol{p}_{z, 0}, \boldsymbol{p}_{\mathrm{t}, i}\right)} \end{array}\right. $ | (7) |
其中pz,0=(xz, 0, yz, 0, zz, 0)为应答器的初始位置,一般可由测线理论点坐标(或放样点的实际坐标)给定,fi为几何距离函数。
在最小二乘法估计的计算模型中,若定位船在n个时刻采样了n个航迹点,到每一个水下应答器就有n个观测距离,误差方程为
| $ \begin{aligned} v_{i}= \frac{\partial f_{i}}{\partial x_{\mathrm{z}, 0}} x_{\mathrm{z}}+\frac{\partial f_{i}}{\partial y_{\mathrm{z}, 0}} y_{\mathrm{z}}+\frac{\partial f_{i}}{\partial z_{\mathrm{z}, 0}} z_{\mathrm{z}}-\\ {\left[\rho_{\mathrm{vz}, i}-f\left(\boldsymbol{p}_{\mathrm{z}, 0}, \boldsymbol{p}_{\mathrm{t}, i}\right)\right] } \end{aligned} $ | (8) |
根据式(8)进行迭代计算,直到最终待估计的应答器的位置改正量小于所给定的误差即可。将式(8)写成矩阵形式,即
| $ \boldsymbol{V}=\boldsymbol{A} \hat{\boldsymbol{X}}-\boldsymbol{L} $ | (9) |
式中:
| $ \boldsymbol{V}=\left[\begin{array}{llll} v_{1} & v_{2} & \cdots & v_{n} \end{array}\right]^{\mathrm{T}} $ | (10) |
| $ \boldsymbol{A}=\left[\begin{array}{ccc} \frac{\partial f_{1}}{\partial x_{z, 0}} & \frac{\partial f_{1}}{\partial y_{z, 0}} & \frac{\partial f_{1}}{\partial z_{z, 0}} \\ \frac{\partial f_{2}}{\partial x_{z, 0}} & \frac{\partial f_{2}}{\partial y_{z, 0}} & \frac{\partial f_{2}}{\partial z_{z, 0}} \\ \vdots & \vdots & \vdots \\ \frac{\partial f_{n}}{\partial x_{z, 0}} & \frac{\partial f_{n}}{\partial y_{z, 0}} & \frac{\partial f_{n}}{\partial z_{z, 0}} \end{array}\right] $ | (11) |
| $\boldsymbol{L}=\left[\begin{array}{llll} l_{1} & l_{2} & \cdots & l_{n} \end{array}\right] $ | (12) |
| $ l_{i}=\rho_{\mathrm{vz}, i}-f\left(\boldsymbol{p}_{\mathrm{z}, 0}, \boldsymbol{p}_{\mathrm{t}, i}\right) \quad i=1, 2, \cdots, n $ | (13) |
根据最小二乘法估计,可得
| $\hat{\boldsymbol{X}}=\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{A}\right)^{-1} \boldsymbol{A}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{L} $ | (14) |
式中:P为对角权阵,在实际中可取为相应观测距离的倒数;li为i时刻观测值ρ与几何距离函数f的差值;n为总的观察值。
2 基于抗差估计的计算方法考虑到野外数据中可能存在的野值或粗差,为了得到最优且可靠的海底应答器实时声学定位的估计解,分三个步骤实现定位船实时声学定位的抗差估计,即通过野值剔除处理、粗差探测和构建极值函数确定观测值权阵,通过迭代计算求得最优解的抗差估计。
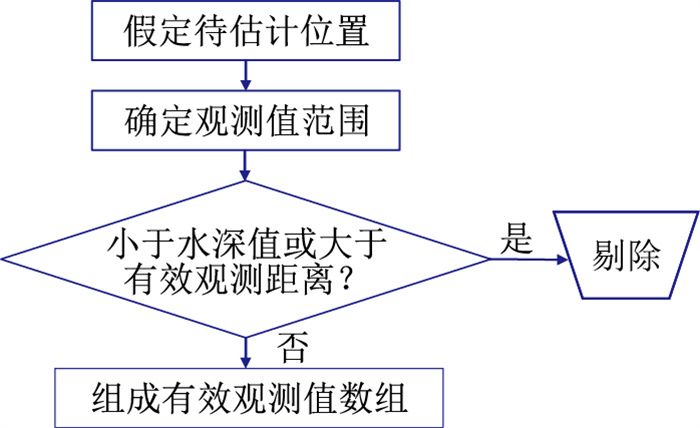
2.1 野值剔除处理野外作业中,实际不同类型的海底底质对声波传播会产生不可定量描述的影响,使声学定位过程中产生数据野值。为了获得可靠的高精度声学定位结果,在进行位置估计前,有必要根据如图 2所示步骤对可能存在的野值进行剔除处理。
|
图 2 野值剔除处理流程 |
经过野值剔除处理后,所得到的观测数据序列中可能还存在粗差。如果不处理这些可能存在的粗差,将导致声学定位计算结果不可靠。根据式(9)整理可得如下方程
| $ \boldsymbol{V}=\boldsymbol{A}(\hat{\boldsymbol{X}}-\widetilde{\boldsymbol{X}})-(\boldsymbol{L}-\boldsymbol{A} \widetilde{\boldsymbol{X}}) $ | (15) |
式中
将式(14)和
| $ \begin{aligned} \boldsymbol{V} &=\boldsymbol{A}\left(\boldsymbol{N}^{-1} \boldsymbol{A}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{L}-\boldsymbol{N}^{-1} \boldsymbol{A}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{A} \widetilde{\boldsymbol{X}}\right)+\boldsymbol{\varDelta} \\ &=\boldsymbol{A} \bf{N}^{-1} \boldsymbol{A}^{\mathrm{T}} \boldsymbol{P}(\boldsymbol{L}-\boldsymbol{A} \widetilde{\boldsymbol{X}})+\boldsymbol{\varDelta} \\ &=\left(\boldsymbol{I}-\boldsymbol{A} \bf{N}^{-1} \boldsymbol{A}^{\mathrm{T}} \boldsymbol{P}\right) \Delta=\boldsymbol{R} \boldsymbol{\varDelta} \end{aligned} $ | (16) |
式中R=I-AN-1ATP
式(16)两边取数学期望可得
| $ \boldsymbol{E}(\boldsymbol{V})=\boldsymbol{R E}(\boldsymbol{\varDelta}) $ | (17) |
由式(17)可知,若Δ只包含偶然误差时,不存在粗差,那么E(Δ)=0,E(V)=0也成立。V是Δ的线性函数,故V和Δ的概率统计都服从正态分布规则。
粗差探测的原假设可设定H0: E(vi)=0,即观测值序列L不存在粗差,vi服从正态分布vi~N(0, σ02Qvivi),其中Q为误差改正数vi的协方差矩阵,Qvivi为Q的元素,则可作标准正态分布统计量
| $ \sigma_{0}=\sqrt{\frac{\boldsymbol{V}^{\mathrm{T}} \overline{\boldsymbol{P}} \bf{V}}{n-3}} $ | (18) |
| $ \boldsymbol{u}=\frac{\boldsymbol{v}_{i}}{\sigma_{0} \sqrt{Q_{v_{i} v_{i}}}}=\frac{\boldsymbol{v}_{i}}{\sigma_{v_{i}}} $ | (19) |
式中:u是可作标准正态统计量;σ0为其中误差;
通过以上粗差探测法遍历观测值数组中的元素,循环一次可发现可能存在的粗差,剔除之,重新进行平差计算,再次构建统计量进行探测直至不再发现为止。
2.3 抗差估计定位船上的声学观测值是依据声学应答的时间间隔依次进入系统的。经过野值处理和可能存在的粗差探测处理,获得了一组比较干净的观测数据。为了确保最终的计算结果是最优且可靠的,还需设计一种能够抗差的最优估计方法。
在野外定位系统获得足够多的观测值下,经过野值剔除和粗差探测的处理后,可以获得其前一次最小二乘法估计解
| $ \hat{\boldsymbol{X}}=\left(\boldsymbol{A}^{\mathrm{T}} \overline{\boldsymbol{P}} \boldsymbol{A}\right)^{-1} \boldsymbol{A}^{\mathrm{T}} \overline{\boldsymbol{P}} \boldsymbol{L} $ | (20) |
| $ \boldsymbol{V}^{(1)}=\boldsymbol{A} \hat{\boldsymbol{X}}^{(1)}-\boldsymbol{L} $ | (21) |
式中:
| $ w_{1}\left(v_{i}\right)=\mathrm{e}^{-\frac{v_{i}^{2}}{2}} $ | (22) |
| $ w_{2}\left(v_{i}\right)=\frac{1}{\left(\left|v_{i}\right|+c\right)} $ | (23) |
式中c为不等于零的正常数。再重新组成误差方程组,两种权函数分别进行迭代计算
| $ \hat{\boldsymbol{X}}^{(k+1)}=\left[\boldsymbol{A}^{\mathrm{T}} \overline{\boldsymbol{W}}^{(k)} \boldsymbol{A}\right]^{-1} \boldsymbol{A}^{\mathrm{T}} \overline{\boldsymbol{W}}^{(k)} \boldsymbol{L} $ | (24) |
| $ \overline{\boldsymbol{W}}^{(k)}=\operatorname{diag}\left[w^{(k)}\left(v_{1}\right), w^{(k)}\left(v_{2}\right), \cdots, w^{(k)}\left(v_{n}\right)\right] $ | (25) |
式中k为迭代次数,w取w1或w2。
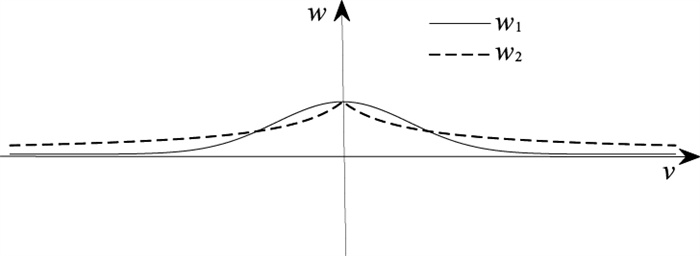
由图 3可见,权函数1和权函数2都具有以下特性:①均为|vi|的减函数;②都是有界函数;③均为连续函数(在自变量取值范围内);④权的值域为(0, 1]。
|
图 3 权函数图像 |
由于权因子是|vi|的非增函数,随|vi|的增大而减小。进一步说明残差的绝对值越大时,权因子越小,对估计值的贡献度越小。这两种权函数迭代计算方法的最优估值计算过程方便、简单,构建权因子过程参与的变量较少,适于实时的声学定位计算。
上述对权函数的迭代计算中,若|w(k+1)-w(k)| < s(给定的极小正数),则计算结束。同时分别计算其中误差σ0,与传统方法所得中误差(观测值与真值偏差的平方与观测次数比值的平方根)进行精度结果分析验证此方法的正确性。
3 方法验证为进一步验证上述方法的正确性,分别从模拟仿真和野外实际应用情况测试验证算法。
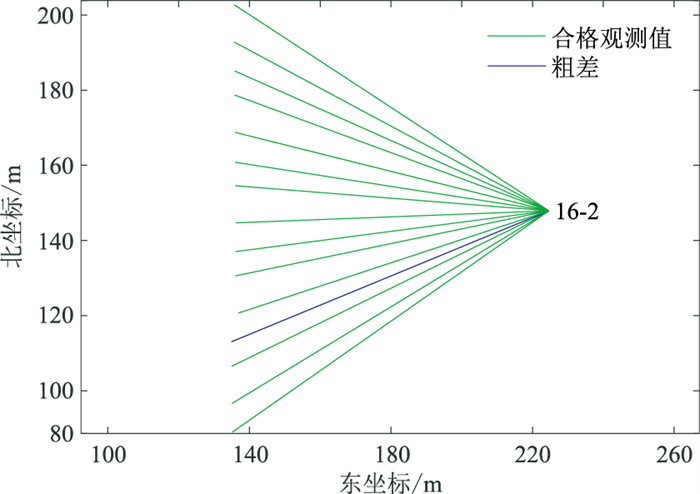
3.1 模拟仿真实例根据实时计算的特点利用声学定位系统厂商所提供的模拟仿真软件,模拟了声学定位船的GPS系统、测深仪及声学定位设备在野外实时声学定位的数据采集过程。模拟仿真软件模拟运行时,定位船由南向北航行(图 4)。在此过程中启动定位采集软件发送目标地址组号的应答器的呼叫命令并采集编号为16-2应答器的声学应答数据,并保存计算机内存中。
|
图 4 模拟声学定位观测值分布 |
由此过程采集到定位船船载探头的空间位置、测深仪的测深数据及声学定位系统输出的声学观测值(图 4)。共得到一组(共15个)声学定位数据,声速为1500m/s。为验证本文算法的有效性,模拟野外作业环境中可能存在的粗差现象,在第4个观测值上人为赋予了粗差(图 4)。
通过本文算法的粗差探测过程,发现第4序号数据存在粗差,在进行最终的估计之前,予以剔除。对剩下的观测值重新组成误差方程组进行最优估计计算,分析比较了传统的最小二乘法和本文抗差估计方法的定位解(表 1)。
|
|
表 1 不同估计定位解 |
由表 1可见,权函数1和权函数2的抗差估计比传统的最小二乘法估计的中误差分别提高了0.667m和0.786m,两种权函数抗差估计的内符合精度(测量值之间的偏差)均较好。
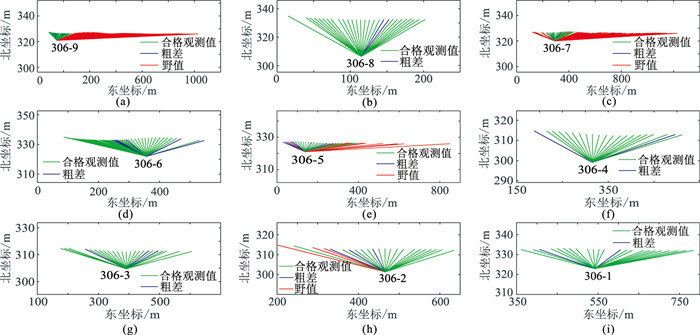
3.2 野外实际计算应用采用野外实际项目的数据,进一步验证算法的有效性。项目施工海域水深为15~20m,声速为1562m/s。定位船由西向东共采集了组号为306、地址号为1~9应答器的实时声学定位数据,其定位观测值分布、野值剔除及粗差探测结果如图 5所示。
|
图 5 不同地址号应答器的定位观测值分布、野值剔除及粗差探测结果 (a)地址号9;(b)地址号8;(c)地址号7;(d)地址号6;(e)地址号5;(f)地址号4;(g)地址号3;(h)地址号2;(i)地址号1 |
经本算法野值剔除处理验证发现:地址号为1、3、4、6、8应答器的观测值不存在野值;2号应答器存在3个野值;5号应答器存在11个野值;7号应答器存在36个野值;9号应答器存在58个野值。由图 5中红色线段可知,在野外作业环境中大入射角的观测值是野值的可能性更大。
再进行粗差探测验证得出,所有的应答器观测值在野值剔除后仍存在粗差(图 5)。地址号为1的应答器观测值存在3个粗差;2号应答器存在7个粗差;3号应答器存在3个粗差;4号应答器存在2个粗差;5号应答器存在7个粗差;6号应答器存在6个粗差;7号应答器存在8个粗差;8号应答器存在6个粗差;9号应答器存在3个粗差。
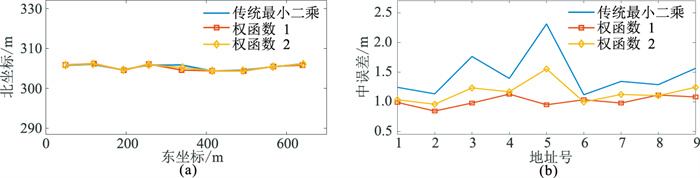
然后用三种算法计算得到最优估计结果(图 6)。由图 6a中可见,三种算法所得海底应答器的位置趋势基本相同,但两种权函数计算的位置比最小二乘法更相互趋近;由图 6b可见,用两种权函数计算的点位中误差结果优于传统最小二乘法估计解。
|
图 6 三种算法应答器的计算结果比较 (a)估计位置;(b)估计中误差 |
本文提出的基于抗差估计的实时声学定位方法,经模拟仿真实验和野外实际数据验证表明,此方法能够满足目前海底勘探过程中实时声学定位的需求,并可以得出如下结论:
(1) 对声学观测值中可能存在的野值进行了预处理,主要剔除了那些大入射角的声学观测值,从而阻断了其对最终计算结果的干扰;
(2) 基于统计假设的粗差检验方法,有效地发现了可能存在的粗差并剔除,能够保留一组不含粗差的较精确的观测值;
(3) 采用抗差自适应权阵构建的估计方法,选取两种有界函数作为极值函数,得到的抗差估计解比传统最小二乘法提高了内符合精度,达到了满意效果。
| [1] |
方守川, 秦学彬, 任文静, 等. 基于多换能器的声学短基线海底电缆定位方法[J]. 石油地球物理勘探, 2014, 49(5): 825-828, 845. FANG Shouchuan, QIN Xuebin, REN Wenjing, et al. Ocean buttom cable positioning based on multi transducer short baseline acoustic method[J]. Oil Geophysical Prospecting, 2014, 49(5): 825-828, 845. |
| [2] |
王忠成, 周华伟, 童思友, 等. 深水海底节点二次定位方法[J]. 石油地球物理勘探, 2020, 55(2): 242-247. WANG Zhongcheng, ZHOU Huawei, TONG Siyou, et al. Secondary positioning of deep ocean bottom nodes[J]. Oil Geophysical Prospecting, 2020, 55(2): 242-247. |
| [3] |
杨海申, 徐丽军, 马洁, 等. 矢量叠加初至波定位方法及精度评价[J]. 石油地球物理勘探, 2021, 56(1): 49-56. YANG Haishen, XU Lijun, MA Jie, et al. First-break positioning and accuracy evaluation based on vector superposition[J]. Oil Geophysical Prospecting, 2021, 56(1): 49-56. |
| [4] |
肖永新, 杨海申, 蒋先艺, 等. OBC勘探中扫描拟合二次定位方法[J]. 石油地球物理勘探, 2012, 47(3): 366-370. XIAO Yongxin, YANG Haishen, JIANG Xianyi, et al. A secondary positioning method by grid scanning and curved-surface fitting in OBC survey[J]. Oil Geo-physical Prospecting, 2012, 47(3): 366-370. |
| [5] |
方守川. 海底电缆地震勘探导航定位关键技术研究及系统研制[D]. 湖北武汉: 武汉大学, 2014. FANG Shouchuan. Research on Key Technique of Navigation & Positioning in Ocean Bottom Cable Seismic Operation and System Development[D]. Wuhan University, Wuhan, Hubei, 2014. |
| [6] |
赵建虎, 邹亚靖, 吴永亭, 等. 深度约束的海底控制网点坐标确定方法[J]. 哈尔滨工业大学学报, 2016, 48(10): 137-141. ZHAO Jianhu, ZOU Yajing, WU Yongting, et al. Determination of underwater control point coordinate based on constraint of water depth[J]. Journal of Harbin Institute of Technology, 2016, 48(10): 137-141. DOI:10.11918/j.issn.0367-6234.2016.10.020 |
| [7] |
刘慧敏, 王振杰, 赵爽. 深度约束的浅海多目标声学定位方法[J]. 石油地球物理勘探, 2019, 54(6): 1181-1187. LIU Huimin, WANG Zhenjie, ZHAO Shuang. A depth-constraint multi-target positioning acoustic approach in shallow waters[J]. Oil Geophysical Prospecting, 2019, 54(6): 1181-1187. |
| [8] |
赵爽, 王振杰, 吴绍玉, 等. 基于选权迭代的走航式水声差分定位方法[J]. 石油地球物理勘探, 2017, 52(6): 1137-1145. ZHAO Shuang, WANG Zhenjie, WU Shaoyu, et al. A ship-board acoustic difference positioning method based on selection weight iteration[J]. Oil Geophysical Prospecting, 2017, 52(6): 1137-1145. |
| [9] |
刘慧敏, 王振杰, 吴绍玉, 等. 顾及声线弯曲的浅海多目标水声定位算法[J]. 石油地球物理勘探, 2019, 54(1): 9-15. LIU Huimin, WANG Zhenjie, WU Shaoyu, et al. A positioning determination of multi-transponders with sound ray bending in shallow waters[J]. Oil Geophysical Prospecting, 2019, 54(1): 9-15. |
| [10] |
武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M]. 湖北武汉: 武汉大学出版社, 2014. Surveying Adjustment Discipline Group, School of Surveying and Mapping, Wuhan University. Error Theory and Foundation of Surveying Adjustment[M]. Wuhan, Hubei: Wuhan University Press, 2014. |
| [11] |
汪杨凯, 周良松, 李艳. 基于Fair函数的电力系统抗差估计[J]. 电力系统及其自动化学报, 2006, 18(3): 86-88. WANG Yangkai, ZHOU Liangsong, LI Yan. Robust state estimation of power system based on function of fair[J]. Proceedings of the CSU-EPSA, 2006, 18(3): 86-88. DOI:10.3969/j.issn.1003-8930.2006.03.019 |
| [12] |
王世超, 杨久东. 稳健估计权函数的对比研究[J]. 华北理工大学学报(自然科学版), 2019, 41(2): 1-6. WANG Shichao, YANG Jiudong. Comparison of robust estimation weight functions[J]. Journal of North China University of Science and Technology(Natural Science Edition), 2019, 41(2): 1-6. DOI:10.3969/j.issn.2095-2716.2019.02.001 |
| [13] |
周江文. 抗差估计论文集[M]. 北京: 测绘出版社, 1992. ZHOU Jiangwen. Papers on Robust Estimation[M]. Beijing: Surveying and Mapping Press, 1992. |
| [14] |
杨元喜. 等价权原理—参数平差模型的抗差最小二乘解[J]. 测绘通报, 1994(6): 33-35, 29. YANG Yuanxi. Equivalent weight principle-robust least square solution of parameter adjustment model[J]. Bulletin of Surveying and Mapping, 1994(6): 33-35, 29. |
| [15] |
姜佃高. 观测值不等权条件下稳健估计方法的稳健特性研究[D]. 山西太原: 太原理工大学, 2014. JIANG Diangao. Study on Robustness of Robust Estimation Methods under the Condition of Unequal Weighted Observations[D]. Taiyuan University of Technology, Taiyuan, Shanxi, 2014. |
| [16] |
李浩军, 王解先. 一种新的抗差估计方法及运算[J]. 辽宁工程技术大学学报(自然科学版), 2010, 29(4): 575-578. LI Haojun, WANG Jiexian. A new robust estimation method and its calculation[J]. Journal of Liaoning Technical University(Natural Science Edition), 2010, 29(4): 575-578. |



 方一涵, 湖北省武汉市鲁磨路388号中国地质大学(武汉)自动化学院,430074。Email:
方一涵, 湖北省武汉市鲁磨路388号中国地质大学(武汉)自动化学院,430074。Email: