② 中国海洋大学海洋地球科学学院,山东青岛 266100;
③ 青岛海洋科学与技术试点国家实验室海洋矿产资源评价与探测技术功能实验室,山东青岛 266100
② College of Marine Geosciences, Ocean University of China, Qingdao, Shandong 266100, China;
③ Functional Laboratory of Marine Mineral Resources Evaluation and Exploration Technology, Pilot National Laboratory for Marine Science and Technology (Qingdao), Qingdao, Shandong 266100, China
在实际地震资料的采集过程中,受现场条件的限制,会遇到炮点和检波点布设困难的情况,或者因设备损坏、故障等因素产生坏道,导致采集的地震数据在空间上不连续,出现地震道的缺失,给后续地震资料的进一步处理带来困难。因此需使用一定的处理方法,对缺失的地震道数据进行重构。
地震数据的重构技术可分为传统方法和基于机器学习的人工智能方法。传统的地震数据重构方法可分为以下四种。
第一种是基于波动方程的地震数据重构方法[1],该方法使用偏移算子对地震数据进行重构,可用于处理随机缺失和规则缺失的地震数据。但是,该方法需要一个近似的地下速度模型,并且计算量较大。
第二种是基于预测滤波的地震数据重构方法,该方法是通过设计预测误差的滤波器对存在空间假频的地震数据进行重构,通常用于存在规则道缺失的地震数据。Spitz[2]提出了经典的f-x域数据重构方法,能重构规则缺失的地震道记录。Porsani[3]进一步提出半步f-x域地震道重构方法,提高了数据重构的速度和精度。在此基础上,宜明理等[4]研究了f-k域抗假频地震数据重构方法,张军华等[5]采用并行算法在f-x域实现了三维地震数据重构。
第三种是基于多域变换的地震数据重构方法,是目前地震数据重构的主流方法。该类方法首先使用特定的数学变换,如傅里叶变换、拉东变换、小波变换等,将地震数据变换到其他域进行数据重构,然后对处理后的数据进行反变换,实现地震数据的重构。Duijndam等[5]首先提出了基于傅里叶变换的地震数据重构方法,使用最小二乘法估计傅里叶分量,对沿一个空间方向的不规则道缺失地震数据进行重构。Herrmann等[6]研发了一种基于Curvelet变换的地震数据重构方法,对存在多道缺失的地震数据进行重构。Fomel等[7]提出基于一种Seislet变换的反假频迭代地震数据重构方法,利用压缩感知Bregman迭代算法,对缺失的地震道重构。Ibrahim等[8]提出了一种基于拉东域的地震数据重构方法,利用全为零值的缺失地震道与未缺失地震道在拉东域中曲率范围不同这一特点,通过去除缺失地震道对应的拉东系数,再利用拉东逆变换变回t-x域实现重构不规则缺失地震数据。Gan等[9]提出了在POCS算法框架下应用Seislet变换重构地震数据的方法,可重构非规则道缺失的地震数据。
第四种是基于矩阵降秩的地震数据重构方法[10],该类方法利用当数据存在缺失时,数据在频率切片的Hankel矩阵的秩会升高这一原理,通过降低Hankel矩阵的秩或对数据降维重构数据。Zhang等[11]提出一种降秩与稀疏促进混合的数学模型,并将该模型用于三维地震数据的重构。Oropeza等[12]提出基于随机奇异值分解方法重构地震数据,解决了原始截断奇异值分解方法计算量较大的问题,提高了计算效率,低维地震数据的重构效果显著。
近年来,随着人工智能技术的发展,深度学习(Deep Learning,DL)方法越来越多地应用于地震数据重构。Wang等[13]利用存在道缺失的地震数据和完整的地震数据预先训练残差网络,然后使用训练后的网络对道缺失的地震数据进行重构。该方法只适用于重构规则道缺失的地震数据,对不规则道缺失的地震数据的重构效果较差。郑浩等[14]提出一种基于DL卷积神经网络的智能化地震数据重构方法,该方法首先利用大量地震数据训练搭建的卷积自编码器模型,然后使用训练后的卷积自编码器模型重构缺失地震道的数据重构。Alwon[15]和Oli-veira等[16]提出使用生成对抗网络重构道缺失的地震数据,但面对地质构造比较复杂的地震数据,会出现非地质伪影。Kaur等[17]进一步提出了使用生成对抗网络重构三维地震数据的方法。传统的有监督DL地震数据重构方法主要包括三个步骤:首先,构建训练集,训练集一般由道缺失的地震数据(输入)和对应的完整地震数据(期望输出,标签)构成;然后,使用构建的训练集训练网络模型,学习数据的特征;最后,使用训练后的网络模型重构道缺失的地震数据。一般利用DL解决地震数据重构问题的方法需使用大量合适的训练集训练网络,并且训练集的质量直接影响重构效果[18]。但是,从野外地震数据很难获得训练所用的标签。为此,本文提出一种基于无监督DL地震数据重构方法。该方法可直接对存在道缺失的不完整地震数据进行重构,而无需构建训练集预先训练网络,避免了有监督DL数据重构方法建立包含完整地震数据标签的训练集问题。
残差网络由He等[19]首先提出,其内部的残差单元使用了跳跃连接,提升了信息传递路径的数量、简化了网络的学习目标及难度、提升了网络的准确度。同时,残差网络通过训练使网络中多余层的残差为0,使得这些层变为恒等映射,解决了层数加深导致的网络退化问题,提升了网络性能。
与传统的DL方法不同的是,本文提出的基于无监督残差网络DL的地震数据重构方法无需使用完整的地震数据作为标签预先训练残差网络,而是用随机数据作为残差网络的输入,以缺失道的原始地震记录作为残差网络的期望输出,通过反向传播残差网络的预测输出与期望输出之间的误差,迭代优化残差网络参数,使网络输出与原始地震记录的差别最小,从而获得参数最优的残差网络,再用该网络计算缺失的地震道记录。在网络参数优化过程中,利用卷积的局部和平移不变性质,用卷积滤波器学习多尺度下地震数据邻域之间的相似特征,并在网络输出中呈现。因无需使用训练集,因此获得的残差网络具有很强的泛化能力,适于不同特征地震数据重构。使用Marmousi模型模拟地震数据和实测海洋拖缆数据进行测试,结果验证了本文方法的有效性。
1 深度残差网络地震数据重构原理 1.1 深度残差网络广泛应用的卷积神经网络(Convolutional Neural Networks,CNN)主要由卷积层、池化层和全连接层组成。其中卷积层用于局部感知、特征提取;池化层用于合并语义相似的特征。通常,卷积层与池化层相互连接配合,组成多个卷积—池化组逐层提取特征,最后通过全连接层完成数据的特征提取、综合与数据压缩。在训练阶段,数据通过自动特征提取层和分类层向前传播,得到CNN的预测输出,然后通过损失函数计算总体误差,通过反向传播更新网络参数,使总体误差最小化。
提高CNN模型的深度可增加网络中训练参数的种类和数量,从而提高网络模型的表达能力和特征提取能力。但是,当网络层数超过一定数目后,会导致模型出现梯度爆炸和梯度消失等现象,网络的训练误差升高、性能下降。为了克服这一缺陷,在网络模型中引入跳跃连接结构,通过训练使多余层的残差为0,从而使这些层变为恒等映射,解决了网络层数过大时引起的梯度消失和梯度爆炸等问题。
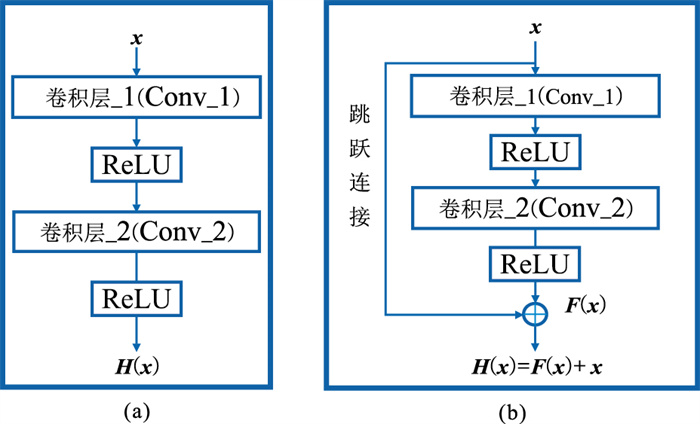
图 1为普通CNN的卷积单元与残差网络单元对比。如图 1a所示,假设某个神经网络单元的输入是x,实际输出为F(x),期望输出为H(x)。希望网络单元学习到一个恒等映射函数H(x)=x,但随着网络层数的增加,这个恒等映射会变得越来越难以拟合,增大了直接学习的难度。为解决这一问题,残差网络利用跳跃连接将残差单元的输出变为F(x)+x。残差单元不直接学习目标映射,而是转换为学习一个残差函数F(x)=H(x)-x,即网络的学习内容变为残差[20]。残差网络不仅解决了由于网络层数增加造成的退化问题,还简化了网络的学习目标、降低了深度神经网络的训练难度[21]。
|
图 1 不同单元结构对比 (a)普通卷积单元;(b)残差单元 |
深度残差网络(图 1b)由许多基本的残差单元(Residual Block)组成,经典的两层残差单元包含两个卷积层,每层卷积操作后使用ReLU激活函数激活后输入到下一层。每个残差单元的一般形式为
| $ \boldsymbol{y}_{t}=\boldsymbol{x}_{t}+\boldsymbol{F}\left(\boldsymbol{x}_{t} ; \boldsymbol{W}_{t}\right) $ | (1) |
| $ \boldsymbol{x}_{t+1}=\boldsymbol{h}\left(\boldsymbol{y}_{t}\right) $ | (2) |
式中:xt和xt+1分别是第t个残差单元的输入与输出;Wt={Wt,k|1≤k≤K}是与第t个残差单元相关联的一组权重和偏差,其中K是单个残差单元中的总层数(图 1b中K=2);k是当前层数;h(·)是激活函数。图 1b中常规基本残差单元使用的是ReLU激活函数。
如果h(·)是一个恒等映射,即xt+1=yt,则可得到
| $ \boldsymbol{x}_{t+1}=\boldsymbol{x}_{t}+\boldsymbol{F}\left(\boldsymbol{x}_{t} ; \boldsymbol{W}_{t}\right) $ | (3) |
将残差网络的输入与输出代入式(3),可得到残差函数的一般形式
| $ \boldsymbol{x}_{T}=\boldsymbol{x}_{0}+\sum\limits_{t=0}^{T-1} \boldsymbol{F}\left(\boldsymbol{x}_{t} ; \boldsymbol{W}_{t}\right) $ | (4) |
式中T为残差单元的总数。式(4)具有良好的反向传播特性,即使权重很小,层的梯度也不会消失。
1.2 地震数据重构方法在地震数据重构过程中,设X∈Si×j为理想的完整地震数据(S代表单炮地震数据,i、j分别代表采样点数和道数);X0∈Si×j为含缺失地震道的已知地震数据。是利用已知地震数据X0对缺失的地震道进行重构,得到完整的数据X。X0与X的关系可表示为
| $ \boldsymbol{X}_{0}=\boldsymbol{X} \circ \boldsymbol{s} $ | (5) |
式中:“°”表示哈达玛积(Hadamard Product);s∈(0, 1)i×j是采样算子,是由0和1组成的矩阵,存在道缺失的位置为0,其余为1。式(5)的目的是区分出原始地震数据中已有地震道与需要重构的地震道。由X0求X是一个不适定的反演问题,为求得一个合适的解,必须加入某种先验信息对反演进行约束。因此,将该反演问题转换为求下列目标函数的最优解x*
| $ \boldsymbol{x}^{*}=\underset{\boldsymbol{\theta}}{\arg \min }\left\{Q\left[f_{\boldsymbol{\theta}}(\boldsymbol{N}) \circ \boldsymbol{s}-\boldsymbol{X}_{0}\right]+R(\boldsymbol{x})\right\} $ | (6) |
式中:Q(·)是数据保真项,这里取Q(·)为二阶范数;R(·)是一个先验正则化函数;θ表示网络参数;N为输入网络的原始随机数据;fθ(·)代表网络参数为θ的CNN模型,表示输入与输出间的非线性映射函数。本文中去掉正则化函数R(·),改用神经网络参数来捕获数据中的内在属性。此时,上述反演问题便转换为求解神经网络的最优参数θ*
| $ \boldsymbol{\theta}^{*}=\underset{\boldsymbol{\theta}}{\arg \min } Q\left[f_{\boldsymbol{\theta}}(\boldsymbol{N}) \circ \boldsymbol{s}-\boldsymbol{X}_{0}\right] $ | (7) |
将式(7)改写为如下最小化问题
| $ \left\{\begin{array}{l} \boldsymbol{\theta}^{*}=\underset{\boldsymbol{\theta}}{\arg \min }\left\|\boldsymbol{X}^{\prime}-\boldsymbol{X}_{0}\right\|_{2}^{2} \\ \boldsymbol{X}^{\prime}=f_{\boldsymbol{\theta}}(\boldsymbol{N}) \circ \boldsymbol{s} \end{array}\right. $ | (8) |
式中:
网络参数θ由神经网络各层的深度、大小、核的个数、每个核中的元素以及每个核对应的偏差构成,其初始值随机确定,使用优化算法迭代更新θ,通过令网络输出fθ(N)与s相乘,使X′与X0之间的误差达到极小,获得网络最优参数θ*,从而得到完整的数据X
| $ \boldsymbol{X}=f_{\boldsymbol{\theta}^{*}}(\bf{N}) $ | (9) |
这样构建的残差网络,建立了从N到X0的之间的复杂映射关系。在网络参数优化过程中,通过卷积运算将地震数据相邻道之间的相似特征施加到输出的数据上。用该网络预测的X′与X0最匹配,从而能够重构缺失的地震道。
图 2、图 3对本文无监督学习方法与有监督学习方法进行了对比。一般的有监督学习方法地震数据重构流程如图 2所示。将完整的地震数据去掉一定的地震道后作为神经网络的输入,相应的完整地震数据作为标签,即期望输出。使用建立的大量训练数据集,对神经网络预先训练,学习训练数据集的特征,然后使用训练后的网络模型对存在道缺失的地震数据进行重构。

|
图 2 有监督学习方法数据重构流程 |
|
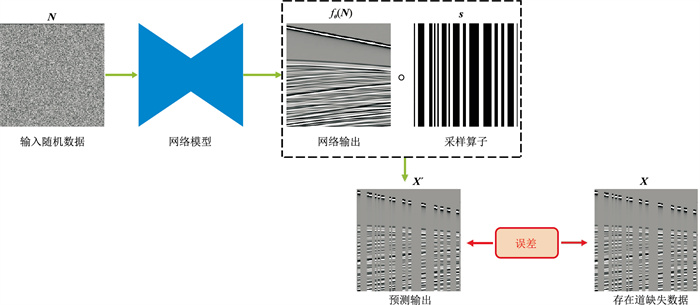
图 3 无监督学习方法数据重构流程 |
本文无监督学习方法地震数据重构流程如图 3所示。利用隐藏在已知地震道中的先验特征进行重构缺失道数据。其中,网络的输入为随机数据N,预测输出为X′,期望输出为X0。随机初始化网络参数θ,网络从输入N得到残差网络的输出fθ(N)。将fθ(N)与s作用后得到X′,对X0与X′之间的均方误差(MSE)进行反传,优化网络参数,使该均方误差最小化,得到网络的最优参数θ*。
具体步骤如下:首先,输入残差网络需要的数据,将随机数据N作为残差网络的输入,含缺失地震道的地震数据X0作为残差网络的期望输出,输入采样算子s;然后,随机初始化残差网络参数θ,将经残差网络计算得到的fθ(N)与采样算子s相乘得到X′,计算二者的误差
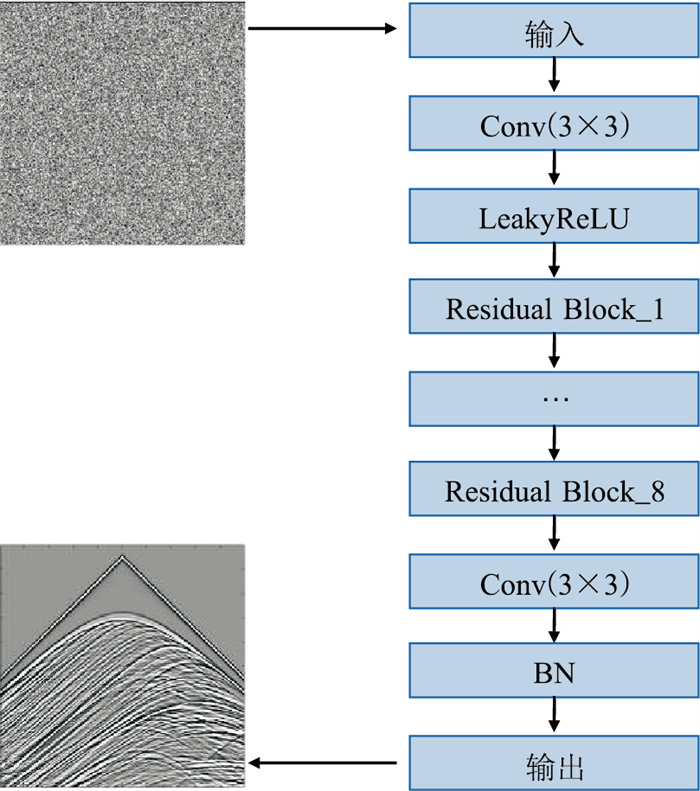
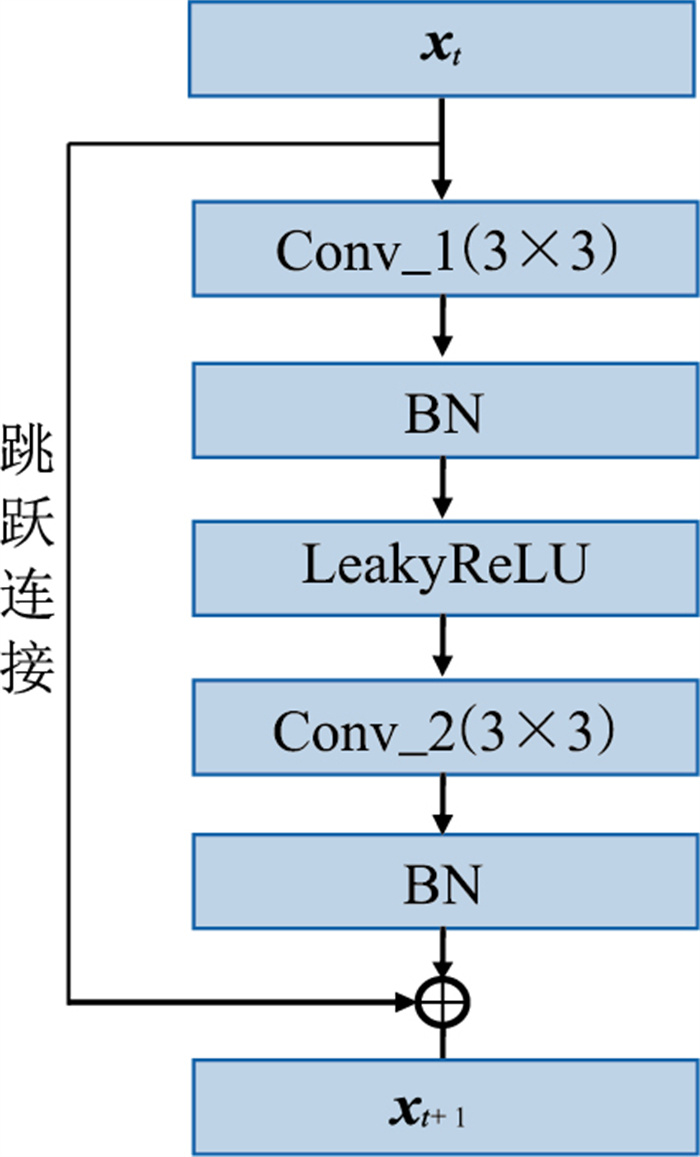
本文使用的残差网络整体框架如图 4所示,网络的第二层到最后一层之间由多个残差单元构成,并且使用了LeakyReLU激活函数,加入了批量归一化操作。残差单元的具体结构如图 5所示,每个残差单元由两个卷积层(Conv)、两个批量归一化层(BN)和一个LeakyReLU激活函数组成。残差网络的主体结构中,第一个卷积层的尺寸为3×3×32×64(包含64个卷积核为3×3的卷积滤波器,通道数为32),最后一个卷积层的尺寸为3×3×64×1(包含1个卷积核为3×3的卷积滤波器,通道数为64)。本文使用的残差网络一共包含8个残差单元,每个残差单元中的卷积层尺寸均为3×3×1×64(包含64个卷积核为3×3的卷积滤波器,通道数为1)。网络输入尺寸为512×512的随机数据,输出为重构的地震数据。
|
图 4 深度残差网络架构示意图 |
|
图 5 残差单元架构(Residual Block)示意图 |
该模型在64位工作站上进行训练,配置是NVDIA RTX 3090 GPU和Intel Core i9-10900k CPU,内存为64G,使用的是Python v3.6.1、Cuda11.1.0和Pytorch框架。
在网络模型的训练过程中,梯度消失和梯度爆炸会严重影响网络模型的收敛。为了解决该问题,在原始残差单元中加入了BN层。通过执行BN处理规范网络中各层的数据,使网络数据的均值为0、方差为1。上述处理可有效加快神经网络的学习速度,在解决梯度弥散问题的同时增加网络整体的稳定性和泛化能力[21]。
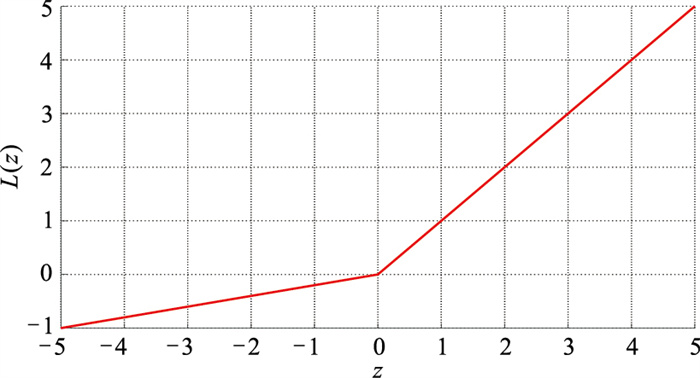
在残差网络中使用了性能更优异的LeakyReLU激活函数(图 6)。该函数的输出对于输入的负值具有很小的坡度,因此导数不会取到零值。这样可减少静默神经元的出现,避免了使用ReLU函数进入负区间后神经元不再继续学习的问题。使用LeakyReLU函数对上一层节点的输出做非线性变换,有助于残差网络更好地学习输入与输出间的复杂映射关系[22-23]。
|
图 6 LeakyReLU函数 |
LeakyReLU函数的具体公式如下
| $ L(z)=\left\{\begin{array}{cc} z & z>0 \\ 0.2 z & z \leqslant 0 \end{array}\right. $ | (10) |
式中:z是LeakyReLU函数的输入;L(z)表示LeakyReLU函数的输出。
本文残差网络使用自适应性矩估计(Adam)优化算法。与常规优化算法相比,Adam优化算法更高效、更准确,对内存需求更少,且网络参数的更新不受梯度变换影响,更适用于数据与参数较多的场景[24]。
网络的收敛性与设置的学习率密切相关,学习率不宜过大。为了使残差网络在较快收敛同时使网络的损失达到最小,本文采用0.001的学习率重构地震数据[25]。
2 模型数据测试为验证本文方法的地震道重构效果,利用理论模拟数据进行了测试。使用长10km、厚5km的Marmousi模型。检波器均匀分布于地表,检波器间距为20m;炮点位于地表距离首个检波器5km处;用20m×20m网格离散该模型,模型被离散成1000×500个矩形单元;震源采用主频为8Hz雷克子波;时间采样间隔为0.002s;记录时长为4s。用波动方程有限差分法模拟地震波[26]。
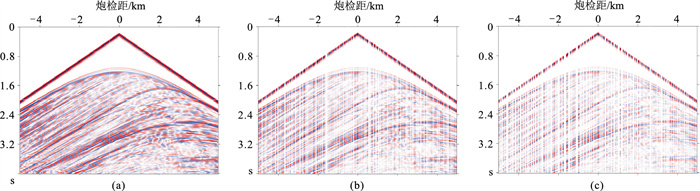
首先从模拟地震记录中按一定比例去除部分地震道,就得到存在缺失地震道的地震数据(图 7);然后用本文地震道重构方法重构整个地震数据。重构地震数据与原始地震数据有一定误差,相当于对原始地震数据引入了噪声。借用“信噪比(SNR)”定量说明对地震数据的重构效果。SNR计算式为
| $ \mathrm{SNR}=10 \lg \left(\frac{\|\boldsymbol{X}\|_{2}^{2}}{\left\|\boldsymbol{X}-\boldsymbol{X}^{\prime}\right\|_{2}^{2}}\right) $ | (11) |
|
图 7 模拟地震数据 (a)完整地震数据;(b)40%随机缺失数据;(c)60%随机缺失数据 |
SNR越大,表示重构的地震数据与原始地震数据之间的差异越小,即重构效果越好。
本文设计的损失函数如下
| $ \mathrm{MSE}=\left\|f_{\boldsymbol{\theta}}(\bf{N}) \circ \boldsymbol{s}-\boldsymbol{X}_{0}\right\|_{2}^{2} $ | (12) |
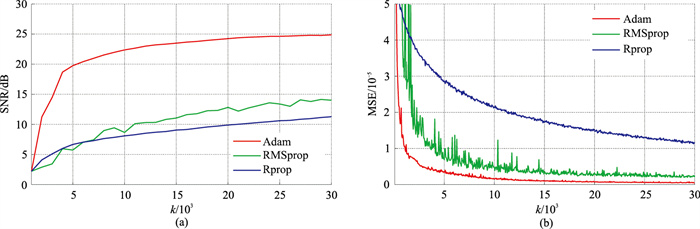
本文的深度残差网络选用了Adam网络优化算法,这里与Rprop、RMSprop算法进行对比测试,以说明选用Adam算法的优势。对模拟地震数据(图 7a)随机去除其中60%的地震道(图 7c),然后使用上述三个网络优化算法对缺失的地震数据进行重构。设置学习率为0.001,迭代次数k为30000。使用不同优化算法的网络重构数据的信噪比和MSE损失函数随迭代次数的变化如图 8a、图 8b所示。由图 8a可见,Adam优化算法重构结果信噪比曲线达到稳定时,得到的重构数据信噪比最高,而且相比于其他算法,Adam优化算法重构地震数据的信噪比随迭代次数上升得更快。由图 8b可见:使用Rprop优化算法的MSE损失曲线下降很慢;RMSprop的MSE损失曲线波动剧烈;使用Adam优化算法的MSE损失曲线更稳定、更快速收敛。
|
图 8 不同优化算法重构数据的SNR(a)与MSE(b)对比 |
因此,本文使用的Adam优化算法性能更好。
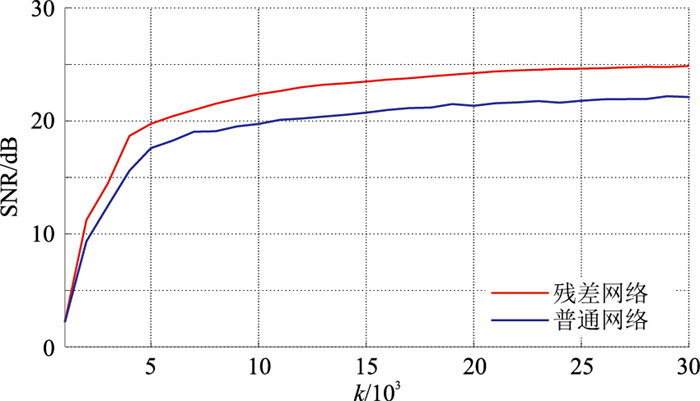
2.2 网络结构比较对本文使用的残差网络与不含跳跃连接结构的普通网络模型进行对比试验。分别使用残差网络和普通网络对图 7c进行重构。两种网络模型的SNR和MSE损失函数随迭代次数的变化如图 9、图 10所示。由图可见,随着迭代次数的增加,两种网络模型的MSE损失函数逐渐降低,重构地震数据信噪比逐渐增加,但残差网络相比于普通网络模型的MSE损失更低,重构数据SNR更高。
|
图 9 不同网络重构SNR对比 |

|
图 10 不同网络MSE对比 |
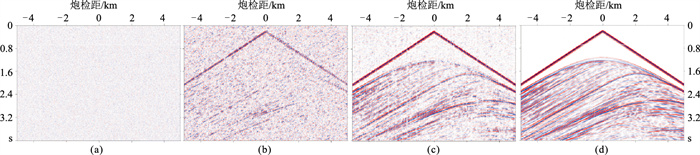
为了直观地展示使用本文方法对道缺失的地震数据重构的迭代过程,将图 7c作为原始地震数据进行完整数据重构。图 11所示是不同迭代次数的重构结果。由图可见:因网络输入是随机信号,迭代初期的输出表现为随机噪声(图 11a);随着迭代次数增加,能量强的地震波先逐渐重构出来(图 11b),然后,能量弱的地震波也被逐渐重构。当迭代次数达到170次时,地震资料的总体面貌开始被恢复,经过2000次迭代基本上恢复了地震资料。可见,以随机信号作为输入,通过对网络输出与原始含缺失道的地震数据之间的误差进行反馈,不断优化网络模型,达到重构完整地震数据的目的,避免了常用监督学习网络建立训练集的繁重环节。
|
图 11 本文方法不同迭代次数((a)~(d)对应10、90、170、2000次迭代)的重构结果 |
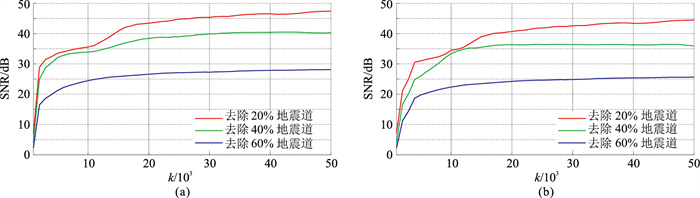
对图 7a数据分别规则和随机去除其中20%、40%和60%的地震道,使用本文方法对不同比例道缺失的地震数据重构。设置学习率为0.001、k为50000。重构地震数据的信噪比随迭代次数的变化如图 12所示。由图可见:道缺失数据的原始信噪比均低于10dB;经过1000次迭代后重构数据的SNR迅速提高,在20000次迭代后达到较高的重构质量并趋于稳定,说明本文方法在迭代次数较低时重构数据的SNR增长迅速,达到一定迭代次数后重构数据的SNR到达高位并保持稳定;数据缺失比例越大,重构数据的SNR越低,缺失的地震道越少重构效果越好;在数据缺失相同比例的情况下,对规则缺失数据的重构SNR要大于随机缺失数据的重构信噪比,这是因为随机缺失数据容易出现连续多道缺失的情况,使重构误差较大。
|
图 12 本文方法对不同比例的规则缺失(a)、随机缺失(b)数据重构SNR的对比 |
快速凸集投影软阈值(FPOCS-Soft)方法是一种较新的地震道插值方法,可直接重构道缺失地震数据,具有较高计算精度和稳定性[27]。为了说明本文方法的有效性和精度,分别使用本文方法和FPOCS-Soft方法对随机缺失40%地震道的数据进行重构,并对两种重构结果进行对比。
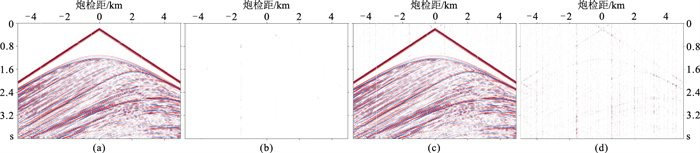
图 13是随机去除40%地震道的地震资料(图 7b)的重构结果。图 13a和图 13b分别为本文方法重构的完整地震记录及误差;图 13c和图 13d分别为使用FPOCS-Soft方法重构的完整地震记录及误差。由图可见:本文方法在连续缺失道数较少时重构数据的误差几乎为0,在连续缺失道数较多的情况时重构数据的误差会有所上升,但重构效果仍然远好于FPOCS-Soft方法。FPOCS-Soft方法对连续缺失道的重构误差更明显,并且在无地震数据的区域还会出现一些假的地震数据。使用本文方法和FPOCS-Soft方法重构的地震数据的SNR分别为36.41dB和18.6dB,均方误差分别为2.29×10-6、1.01×10-4。
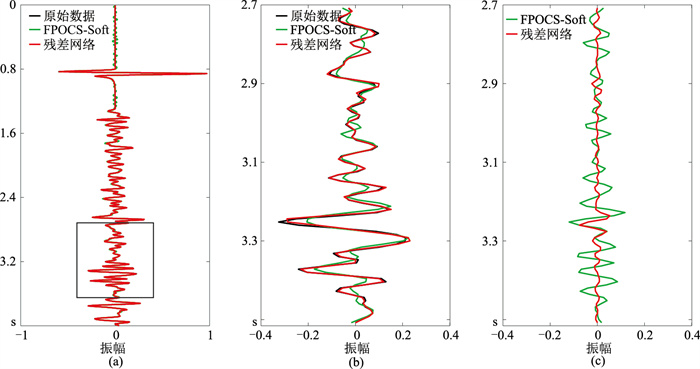
图 14为对图 7b中第162道数据的重构结果对比。由图可见,本文方法重构精度明显高于FPOCS-Soft方法。另外,由于随机缺失数据较规则缺失数据存在连续多道数据缺失,当连续缺失的地震道较多时,本文方法的重构精度会有所下降,但重构效果仍然明显优于FPOCS-Soft方法。
|
图 14 两种方法第162道模拟地震数据重构结果对比 (a)随机缺失单道重构结果;(b)图a中矩形框中的放大图;(c)对应图b的重构误差 |
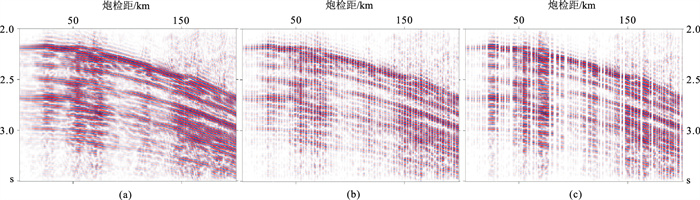
为了检验本文方法对实际数据的应用效果,将本文方法应用于南黄海海洋拖缆实测资料的单炮数据。对该地震数据分别进行规则和随机去除40%的地震道(图 15),分别用本文方法和FPOCS-Soft方法对缺失地震道重构。设置学习率为0.001,迭代次数为20000。
|
图 15 海洋拖缆某炮集数据 (a)完整海洋拖缆数据;(b)规则缺失40%数据;(c)随机缺失40%数据 |
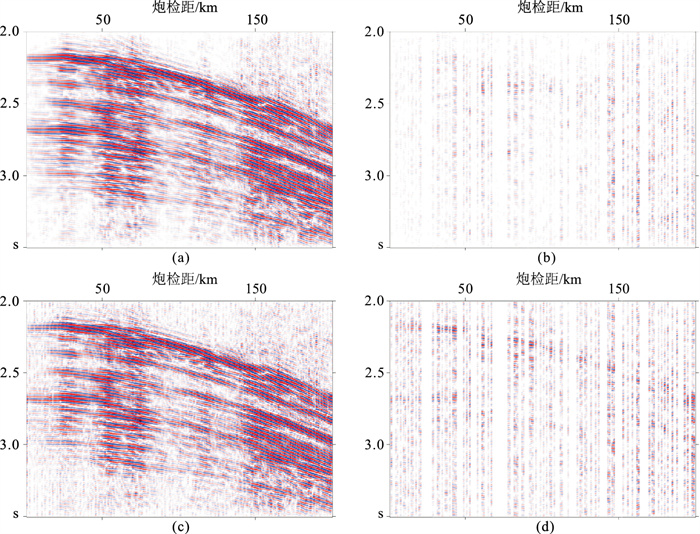
图 16是对图 15c分别用本文方法和FPOCS-Soft方法重构结果及误差分布,重构数据的信噪比分别为16.83dB和11.23dB,均方误差分别为4.32×10-4和1.30×10-3。可以看出,本文方法可以很好地重构缺失的拖缆数据,同相轴变得更连续,重构的结果与原始拖缆数据(图 15a)基本一致,在没有数据的位置不会出现假数据。而FPOCS-Soft方法对连续同相轴的重构结果存在较明显的误差,并且在重构数据中引入了新噪声。
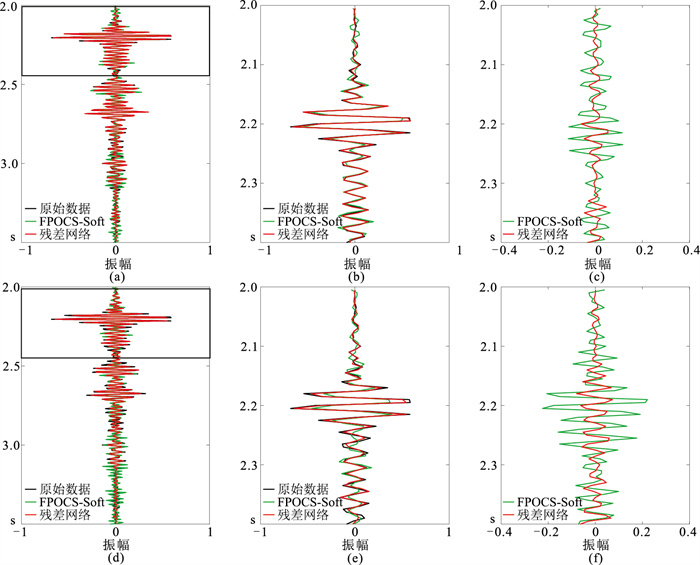
图 17是对图 15b和图 15c的第43道数据的重构结果及误差对比。可见不论对规则缺失还是随机缺失地震道的数据,与FPOCS-Soft方法结果相比,本文方法结果与原始地震数据(图 15a)基本一致,对缺失道数据的重构精度更高。对比规则缺失与随机缺失地震数据的重构结果,可见因随机缺失资料出现多道连续缺失的情况,本文方法的重构精度低于规则缺失数据,但仍然高于FPOCS-Soft方法对规则缺失数据的重构精度,说明了本文方法的良好应用效果和对不同缺失数据更强的适应性。
|
图 17 第43道海洋拖缆数据数据重构精度对比 (a)规则缺失单道重构结果;(b)图a中矩形框区域放大图;(c)图b的重构误差;(d)随机缺失单道重构结果;(e)图d中矩形框区域放大图;(f)图e的重构误差 |
本文提出了一种基于无监督残差网络的缺失地震数据重构方法。该方法以随机数据作为网络输入,通过对网络输出与含缺失道的地震数据之间的误差的反向传播,通过迭代优化网络参数;在迭代过程中,利用卷积的局部和平移不变性质,使用带有跳跃连接的残差网络结构,学习多尺度地震数据邻域之间的相似特征,并把这些先验特征反映在网络输出中;使用性能优良的Adam优化算法,进一步提高了构建的深度残差网络模型的性能。本文方法只需使用地震道缺失的数据和优化的残差网络便可重构完整的地震数据,无需由训练集训练残差网络模型,避免了常规基于深度学习方法的构建大型训练数据集和网络模型泛化能力的问题,实用性更强。
利用模拟地震数据和实测海洋拖缆地震数据对本文方法进行了测试,并与效果较好的FPOCS-Soft地震道插值方法效果进行了比较。结果表明,不论对规则缺失还是随机缺失地震道的地震数据,本文方法的重构精度都高于FPOCS-Soft方法,说明了本文方法的可行性和良好效果。对于存在连续缺失多道的地震数据,本文方法重构地震道的精度会降低,但仍然高于FPOCS-Soft方法。
| [1] |
FOMEL S. Seismic reflection data interpolation with differential offset and shot continuation[J]. SEG Tech-nical Program Expanded Abstracts, 2001, 20: 2045-2048. |
| [2] |
SPITZ S. Seismic trace interpolation in the F-X domain[J]. Geophysics, 1991, 56(6): 785-794. DOI:10.1190/1.1443096 |
| [3] |
PORSANI M J. Seismic trace interpolation using half-step prediction filters[J]. Geophysics, 1999, 64(5): 1461-1467. DOI:10.1190/1.1444650 |
| [4] |
宜明理, 严又生, 魏新, 等. F-K域抗假频道内插[J]. 石油物探, 2001, 40(2): 36-41. YI Mingli, YAN Yousheng, WEI Xin, et al. Using anti-alias trace interpolation in F-K domain[J]. Geophysical Prospecting for Petroleum, 2001, 40(2): 36-41. DOI:10.3969/j.issn.1000-1441.2001.02.005 |
| [5] |
DUIJNDAM A J W, SCHONEWILLE M A, HINDRIKS C O H. Reconstruction of band-limited signals, irregularly sampled along one spatial direction[J]. Geophysics, 1999, 64(2): 524-538. DOI:10.1190/1.1444559 |
| [6] |
HERRMANN F J, HENNENFENT G. Non-parame-tric seismic data recovery with curvelet frames[J]. Geophysical Journal International, 2008, 173(1): 233-248. DOI:10.1111/j.1365-246X.2007.03698.x |
| [7] |
FOMEL S, LIU Y. Seislet transform and seislet frame[J]. Geophysics, 2010, 75(3): V25-V38. DOI:10.1190/1.3380591 |
| [8] |
IBRAHIM A, SACCHI M D. Simultaneous source separation using a robust radon transform[J]. Geophysics, 2014, 79(1): V1-V11. DOI:10.1190/geo2013-0168.1 |
| [9] |
GAN S W, WANG S D, CHEN Y K, et al. Dealiased seismic data interpolation using seislet transform with low-frequency constraint[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(10): 2150-2154. DOI:10.1109/LGRS.2015.2453119 |
| [10] |
TRICKETT S, BURROUGHS L, MILTON A, et al. Rank-reduction-based trace interpolation[C]. SEG Technical Program Expanded Abstracts, 2010, 29: 3829-3833.
|
| [11] |
ZHANG D, ZHOU Y T, CHEN H M, et al. Hybrid rank-sparsity constraint model for simultaneous reconstruction and denoising of 3D seismic data[J]. Geophysics, 2017, 82(5): V351-V367. DOI:10.1190/geo2016-0557.1 |
| [12] |
OROPEZA V, SACCHI M. Simultaneous seismic data denoising and reconstruction via multichannel singular spectrum analysis[J]. Geophysics, 2011, 76(3): V25-V32. DOI:10.1190/1.3552706 |
| [13] |
WANG B F, ZHANG N, LU W K, et al. Deep-lear-ning-based seismic data interpolation: a preliminary result[J]. Geophysics, 2019, 84(1): V11-V20. DOI:10.1190/geo2017-0495.1 |
| [14] |
郑浩, 张兵. 基于卷积神经网络的智能化地震数据插值技术[J]. 地球物理学进展, 2020, 35(2): 721-727. ZHENG Hao, ZHANG Bing. Intelligent seismic data interpolation via convolutional neural network[J]. Progress in Geophysics, 2020, 35(2): 721-727. |
| [15] |
ALWON S. Generative adversarial networks in seismic data processing[C]. SEG Technical Program Expanded Abstracts, 2018, 37: 1991-1995.
|
| [16] |
OLIVEIRA D A B, FERREIRA R S, SILVA R, et al. Interpolating seismic data with conditional generative adversarial networks[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(12): 1952-1956. DOI:10.1109/LGRS.2018.2866199 |
| [17] |
KAUR H, PHAM N, FOMEL S. Seismic data interpolation using deep learning with generative adversa-rial networks[J]. Geophysical Prospecting, 2021, 69(2): 307-326. DOI:10.1111/1365-2478.13055 |
| [18] |
杨冠雨, 王璐, 孟凡顺. 基于深度卷积神经网络的地震数据重建[J]. 地球物理学进展, 2020, 35(4): 1497-1506. YANG Guanyu, WANG Lu, MENG Fanshun. Seismic data reconstruction via deep convolution neural network[J]. Progress in Geophysics, 2020, 35(4): 1497-1506. |
| [19] |
HE K M, ZHANG X Y, REN S Q, et al. Deep resi-dual learning for image recognition[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 2016, 770-778.
|
| [20] |
杨午阳, 杨佳润, 陈双全, 等. 基于U-Net深度学习网络的地震数据断层检测[J]. 石油地球物理勘探, 2021, 56(4): 688-697. YANG Wuyang, YANG Jiarun, CHEN Shuangquan, et al. Seismic data fault detection based on U-Net deep learning network[J]. Oil Geophysical Prospecting, 2021, 56(4): 688-697. |
| [21] |
张政, 严哲, 顾汉明. 基于残差网络与迁移学习的断层自动识别[J]. 石油地球物理勘探, 2020, 55(5): 950-956. ZHANG Zheng, YAN Zhe, GU Hanming. Automatic fault recognition with residual network and transfer learning[J]. Oil Geophysical Prospecting, 2020, 55(5): 950-956. |
| [22] |
IOFFE S, SZEGEDY C. Batch normalization: accele-rating deep network training by reducing internal covariate shift[C]. Proceedings of the 32nd International Conference on International Conference on Machine Learning, 2015, 448-456.
|
| [23] |
HE K M, ZHANG X Y, REN S Q, et al. Delving deep into rectifiers: surpassing human-level perfor-mance on ImageNet classification[C]. 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 2015, 1026-1034.
|
| [24] |
KINGMA D P, BA L J. Adam: a method for stochastic optimization[C]. International Conference on Learning Representations (ICLR), 2015, 1-15.
|
| [25] |
王静, 张军华, 芦凤明, 等. 构建三维深度监督网络的断层检测方法[J]. 石油地球物理勘探, 2021, 56(5): 947-957. WANG Jing, ZHANG Junhua, LU Fengming, et al. Research on fault detection method based on 3D deeply supervised network[J]. Oil Geophysical Prospecting, 2021, 56(5): 947-957. |
| [26] |
袁崇鑫. 波动方程有限差分正演技术研究[D]. 四川成都: 成都理工大学, 2015. YUAN Chongxin. Finite Difference Wave Equation Forward Modeling Technology Research[D]. Chengdu University of Technology, Chengdu, Sichuan, 2015. |
| [27] |
马泽川, 李勇, 陈力鑫, 等. 地震资料快速两步插值算法[J]. 石油地球物理勘探, 2020, 55(5): 997-1004. MA Zechuan, LI Yong, CHEN Lixin, et al. Fast two-step interpolation algorithm for seismic data[J]. Oil Geophysical Prospecting, 2020, 55(5): 997-1004. |



 张建中, 山东省青岛市松岭路238号中国海洋大学海洋地球科学学院,266100。Email:
张建中, 山东省青岛市松岭路238号中国海洋大学海洋地球科学学院,266100。Email: