② 东北石油大学人工智能能源研究院,黑龙江大庆 163318;
③ 黑龙江省网络化与智能控制重点实验室,黑龙江大庆 163318
② Artificial Intelligence Energy Research Institute, Northeast Petroleum University, Daqing, Heilongjiang 163318, China;
③ Heilongjiang Provincial Key Laboratory of Networking and Intelligent Control, Daqing, Heilongjiang 163318, China
在理想情况下,地震数据的采样规则且密集。但是,受复杂地表、地下地质条件、采集因素等的影响,易出现空间采样不足、地震数据缺失等不规则的问题,影响后续地震资料的处理、解释结果,因此地震缺失数据的规则化重建非常重要。
从二十世纪八十年代起,学者们就开始研究地震数据规则化重建方法[1]。目前常用的方法大致分为两类:一类是基于传统模型;另一类是基于深度学习。
基于传统模型的地震数据规则化方法主要分为五种,即:①基于相干倾角插值的方法[2-4],通过扫描时空窗内同相轴的倾角,然后沿着若干个倾角方向通过加权和的形式产生内插的地震道。此类方法处理过程复杂且易受噪声干扰,难以应用到实际场景中。②基于变换域的方法,利用地震数据在某个变换域的稀疏性进行重建[5-10],如利用Fourier变换[6]、Con-tourlet变换[7]、Ridgelet变换[8]、Curvelet变换[9]、快速离散曲波变换(Fast Discrete Curvelet Transform,FDCT)算法[10]等,可以较好地进行地震数据规则化。③基于波场延拓算子的方法[11-13],把缺失道作为零道,结合波动方程部分偏移对叠前地震数据进行重建。该类方法可将倾角时差处理(Dip-Moveout Processing,DMO)与反DMO相结合实现地震数据重建,但在地质信息缺失的情况下,存在重建精度低和运算量大的缺点。④基于滤波器的方法[14-16],通过褶积插值滤波器实现不规则数据重建,通常把某类插值滤波器应用于待规则化的数据,进行褶积操作。此类方法往往具有较高的计算复杂度。⑤基于压缩感知(Compressed Sensing,CS)[17-21]的规则化技术,将不规则地震数据作为完整地震数据的少量信号投影值,在处理端通过稀疏性约束正则化方法实现数据的近似重建,从而突破奈奎斯特采样定理的瓶颈。上述方法共同的问题是所建立的复杂模型通常求解困难,且仅适用于某个特定情况,模型的泛化能力较差。此外,部分模型在缺少地震数据先验知识(如偏移速度、均方根速度、叠加速度等)的情况下,地震数据规则化处理的质量会受到影响。
近年来,深度学习理论与方法逐渐用于地震数据重建。基本原理是通过学习大量的地震数据样本,得到目标区块地震数据分布特征的非线性映射函数,预测相应位置上缺失地震道的实际值,以达到恢复数据中缺失道、规则化地震数据的目的。常见的深度学习重建规则化地震数据的方法包括卷积神经网络(Convolutional Neural Networks, CNN)、生成对抗神经网络(Generative Adversarial Networks,GAN)和自编码器(Auto-Encoder, AE)三类。其中:①基于CNN的规则化方法中,Wang等[22]提出了一种基于ResNets网络的地震资料插值算法,在网络层数较深时效果较好,但需要事先对缺失的数据做预插值处理;Wang等[23]提出利用格林函数的空间互易性重建数据,降低了神经网络在训练过程中对样本多样性的依赖,但同样需要对网络输入的地震数据缺失部分做预插值;高静怀等[24]通过交替迭代求解地震数据重建的最小二乘法问题和预训练的网络模型对地震数据进行重建,同样需要在迭代初始以及输入网络前对缺失数据进行预处理。王钰清等[25]提出了一种基于数据生成和增广的CNN,可用于小样本的网络训练。②基于GAN的规则化方法中,Chang等[26]等提出了一种基于GAN的地震数据插值重建技术;Oliveira等[27]利用GAN对叠后地震数据进行重建。这两种方法均取得了较好的效果,但GAN网络主要存在的问题是训练过程不稳定,结果收敛困难。③基于AE的规则化方法中,郑浩等[28]利用卷积AE,学习完全采样地震数据与缺失重建数据的映射关系,通过残差学习预测缺失数据并进行重建输出,在测试模型上取得了较好的效果;Jia等[29]利用支持向量机重建规则欠采样的地震数据,需要对网络模型进行预插值;宋辉等[30]提出了一种基于卷积降噪AE,可以对地震数据以无监督的方式去噪。
上述深度学习规则化地震数据重建方法利用样本数据时域均方误差(Mean Square Error,MSE)信息损失作为约束,通过网络输出的规则化数据逼近实际完全采样的地震数据,可以达到较好的信噪比评价结果。Zhu等[31]考虑频域特征的提取,利用短时Fourier变换将时域的数据转化到频域,将实部和虚部传入CNN,通过逆变换得到时域的重建地震数据。此方法可以在频域上消除混叠效应,但在能量较弱区域效果不理想。基于深度学习的方法不需要建立复杂的数学模型,相对于传统的基于模型的方法,它能得到数据深层的特征信息,在缺少地下介质先验知识的条件下也可以取得较好的效果。但是,目前基于深度学习的方法还存在一些问题:①通常只关注地震数据单一域特征信息的提取,未挖掘数据联合域的特征信息;②在时域上重建地震数据的方法容易出现细节模糊或过于平滑的现象,丢失纹理信息,影响后续地震数据的解释;反之,若仅关注频域的特征信息,在地震数据能量较弱的区域重建的数据质量较差,无法反映实际的数据特征。
小波具有多尺度分析、多方向性的特点,在图像恢复领域取得了较好的效果。Anbarjafari等[32]提出了利用小波变换将图像从频域分解为平滑子图与细节子图的方法,并利用细节子图辅助恢复高质量的图像;Gao等[33]提出了一种混合小波的卷积网络,将输入数据分解成稀疏特征图谱,然后用另一个卷积网络进行稀疏编码、恢复图像;张岩等[34]考虑其他物理约束信息,提出了一种联合傅里叶域的去噪CNN,取得了较好的纹理保持效果和较高的信噪比;Wang等[35]引入阻抗域的损失,提出了一种基于闭环CNN测井约束地震反演方法,应用于真实地震数据,获得了较好的效果。
据此,本文提出基于联合小波域深度学习的地震数据规则化方法。首先,建立联合深度CNN学习地震数据在时域与小波域的分布特征,得到规则化数据的预测模型,将不规则地震数据的重建转化为CNN小波系数的预测;其次,设置结合时域与小波域的损失函数,通过地震数据的整体特征和局部细节信息约束网络模型,调节联合损失函数的平衡系数以调整网络模型学习的注意力。模型测试和实际数据应用均表明,该方法具有很好的细节保持效果,更具鲁棒性。
1 方法原理 1.1 不规则地震数据重建模型假设完整的地震数据为x。实际上,在缺道或稀疏采样等条件下,采集到的不规则地震数据y可以表示为
| $ \boldsymbol{y}=\boldsymbol{R} \boldsymbol{x} $ | (1) |
式中R为采样矩阵,表示从M道地震数据中采样得到M1道(M>M1)。基于深度学习的地震数据规则化重建过程,就是通过学习样本特征从y中重建得到完全采样地震数据的近似估计x′(x′≈x),利用多次迭代使训练结果趋于稳定,并逐渐逼近x。
1.2 基于小波变换的地震数据规则化以样本x作为时域的标签。通过滤波器组对x进行二维小波分解,即
| $ T_{j+1, m, n}(\boldsymbol{x})=\left\{\begin{array}{l} h_{\psi, -n}(\boldsymbol{x}) \oplus h_{\psi, -m}(\boldsymbol{x})=\boldsymbol{D}_{j, m, n}(\boldsymbol{x}) \\ h_{\psi, -n}(\boldsymbol{x}) \oplus h_{\varphi, -m}(\boldsymbol{x})=\boldsymbol{H}_{j, m, n}(\boldsymbol{x}) \\ h_{\varphi, -n}(\boldsymbol{x}) \oplus h_{\psi, -m}(\boldsymbol{x})=\boldsymbol{V}_{j, m, n}(\boldsymbol{x}) \\ h_{\varphi, -n}(\boldsymbol{x}) \oplus h_{\varphi, -m}(\boldsymbol{x})=\boldsymbol{A}_{j, m, n}(\boldsymbol{x}) \end{array}\right. $ | (2) |
式中:hψ为低通滤波器;hφ为高通滤波器;下标中的“-”表示卷积操作中的翻转操作;⊕表示卷积运算;j=0, 1, 2, …, J-1,J为最大尺度因子;m=n=0, 1, 2, …, 2j-1;A、V、H和D分别表示低频分量、水平高频分量、垂直高频分量和对角高频分量,对应小波域的标签C=(C1, C2, C3, C4)。
以y作为网络输入,利用网络G训练得到各频率分量的小波系数
| $ G(\boldsymbol{y})=\left\{\begin{array}{l} G_{\mathrm{D}}(\boldsymbol{y})=\boldsymbol{D}^{\prime} \\ G_{\mathrm{H}}(\boldsymbol{y})=\boldsymbol{H}^{\prime} \\ G_{\mathrm{V}}(\boldsymbol{y})=\boldsymbol{V}^{\prime} \\ G_{\mathrm{A}}(\boldsymbol{y})=\boldsymbol{A}^{\prime} \end{array}\right. $ | (3) |
式中:GA、GV、GH、GD分别为低频分量、水平高频分量、垂直高频分量、对角高频分量对应的映射;A′、V′、H′、D′分别表示为网络训练所得小波系数不同方向低频分量、水平高频分量、垂直高频分量、对角高频分量,对应网络训练的预测小波系数C′=(C′1, C′2, C′3, C′4)。
小波反变换后得到重建时域数据x′。联合计算时域与小波域的误差,设置全局损失函数ltotal作为约束,并通过正向传递和反向传播调整网络参数。经过多次迭代,网络训练结果趋于稳定,得到最终网络模型,将地震数据规则化问题转化为小波系数预测问题。
网络模型由一个非线性映射函数fθ表示,通过参数θ预测不规则地震数据yi对应的规则地震数据x′i,得到x′i=fθ(yi),其中i为样本编号。通常基于深度学习的重建方法从yi中估计xi的最大似然,通过
损失函数采用在数据采样点处x与x′的均方误差,即
| $ l_{\mathrm{mse}}\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)=\left\|\boldsymbol{x}-\boldsymbol{x}^{\prime}\right\|_{2}^{2} $ | (4) |
最小化均方误差损失仅利用了地震数据时域特征,忽略了高频纹理细节的约束,因此本文引入小波域的损失增强细节纹理部分的重建效果。模型映射函数Gθ(x)=[Gθ1(x), Gθ2(x), Gθ3(x), Gθ4(x)]的参数θ被优化为
地震数据的波前信息在时域上表现为复杂的纹理状曲线,尽管多层CNN具有较强的特征提取能力,但仅利用时域信息提取特征时具有很大的局限性。小波变换通过缩、放母小波的宽度获取信号的频率特征,平移小波基获取信号的时间信息[36]。信号的小波变换相当于利用母小波的缩、放和小波基的平移,并与原始信号卷积,得到小波系数(图 1)。

|
图 1 小波变换示意图 |
选择haar小波作为小波基,根据二维快速小波变换(Fast Wavelet Transform,FWT)[37]计算haar小波系数,图 2为地震数据进行小波分解的实例。由小波变换的系数分布特性可知,低频小波系数的预测可以保留地震数据全局的主要特征信息,高频小波系数的预测有利于地震数据细节的恢复。

|
图 2 时域(a)与小波域(b)地震数据对比 图b左上块对应地震数据低频子带;右上块对应水平方向的高频子带;左下块对应垂直方向的高频子带;右下块对应对角高频子带 |
为了充分利用小波域的特征,本文设计了小波预测损失和纹理损失两种损失函数。前者是小波域均方误差的加权形式,定义为
| $ l_{\text {wavelet }}=\sum\limits_{k=1}^{n} \lambda_{k}\left\|\boldsymbol{C}_{k}-\boldsymbol{C}_{k}^{\prime}\right\|_{2}^{2} $ | (5) |
式中:λk是平衡不同小波子带重要性的权重系数;n为小波系数分量数。赋予高频系数较大的权重,可以将训练注意力集中在局部高频细节重建上,生成细节效果较好的规则化地震数据。为了防止过拟合导致高频小波系数收敛到0,定义纹理损失为
| $ l_{\text {texture }}=\sum\limits_{k=q}^{n} \gamma_{k} \max \left(\alpha\left\|\boldsymbol{C}_{k}\right\|^{2}-\left\|\boldsymbol{C}_{k}^{\prime}\right\|^{2}+\varepsilon, 0\right) $ | (6) |
式中:q为约束高频小波系数的初始子带序号,本文采用一级小波分解,生成的低频分量子带保留数据主要信息分量,其余三个子带为不同方向的高频分量;γk、α和ε均为平衡系数,其中γk为各高频分量的权重,α略大于1,ε略大于0。ε保证了ltexture不为0,从而使高频小波系数非零,防止小波高频系数训练过拟合。
1.4 联合小波域深度学习网络设计本文设计的联合学习CNN模型G如图 3所示,由嵌入层网络、小波系数预测网络和联合损失计算3个子网组成。

|
图 3 网络模型结构 |
不规则的地震数据输入嵌入层网络后,经过多层卷积特征提取,将得到的特征图谱传递给后续网络。输入的不规则地震数据尺寸为128×128,嵌入层网络的所有卷积核尺寸均为3×3,步长为1。通过补“0”操作使特征图谱尺寸与输入数据相同。卷积后的特征图谱经过归一化和激活函数,再进入下一层操作。卷积层、归一化层和激活函数构成一个残差块,前、后残差块之间设置残差连接,可以加速收敛和防止梯度消失。每层卷积核的数量沿前向递增,分别是128、256、512、1024,为小波系数预测网络提供足够的特征信息。
1.4.2 小波系数预测网络小波系数预测网络由4个独立的并行子网络组成,它利用嵌入层网络提取的特征图谱学习、预测不同频率分量的小波系数。地震数据具有较强的曲线纹理特征。以一级小波分解为例,将小波预测网络分成4个独立的小波预测子网络;再通过CNN单独处理对应方向子带的小波系数,重建规则化的地震数据。每层网络的卷积核的尺寸为3×3,步长为1,网络预测的小波系数尺寸与不规则地震数据输入的尺寸相同。由于每个子网预测的小波系数相对独立,因此网络更具鲁棒性。
1.4.3 联合损失计算联合损失计算是对地震数据小波域和时域的损失进行评价。网络将各个独立小波预测子网的小波系数反变换为时域的规则化地震数据,使其与完全采样的地震数据进行对比、计算损失,再反向传递到网络中,从而更新网络参数权重。
1.5 联合损失函数网络的联合损失函数由三部分组成,即全局信息预测损失、小波系数预测损失和纹理细节预测损失。其中,全局信息损失是计算重建的时域规则化地震数据与完全采样地震数据之间的损失,以均方误差作为约束条件;小波系数预测损失是利用完全采样地震数据的小波系数对预测子网得到的小波系数施加约束;纹理细节预测损失是计算输入数据与标签之间小波变换高频分量的误差,加强此部分的约束可改善地震数据规则化的纹理细节效果。
设空间域的均方误差为全局损失lfull,联合误差函数为
| $ \begin{aligned} l_{\text {total }} &=l_{\text {wavelet }}+\mu l_{\text {texture }}+\nu l_{\text {full }} \\ &=\sum\limits_{k=1}^{n} \lambda_{k}\left\|\boldsymbol{C}_{k}-\boldsymbol{C}_{k}^{\prime}\right\|_{2}^{2}+\\ & \mu \sum\limits_{k=1}^{n} \gamma_{k} \max \left(\alpha\left\|\boldsymbol{C}_{k}\right\|^{2}-\left\|\boldsymbol{C}_{k}^{\prime}\right\|^{2}+\varepsilon, 0\right)+\\ & \nu\left\|\boldsymbol{x}-\boldsymbol{x}^{\prime}\right\|_{2}^{2} \end{aligned} $ | (7) |
式中μ和ν是平衡参数,可根据网络训练目标的侧重点进行调整,以改变网络学习的注意力。
由于小波系数与不规则的地震数据输入尺寸相同,因此通过CNN可使每个特征图谱的大小保持一致,可以降低训练难度、兼顾地震数据的全局拓扑信息和纹理细节信息。
2 模型测试 2.1 参数设置选择Marmousi模型测试本文方法。震源和检波器置于地表,通过中间放炮、两端接收的方式进行正演获取地震道集数据,检波器采样间隔为4ms,道间距为10m。完全采样实验样本数据裁剪尺寸为128×128的切片数据x,作为训练样本时域标签。从完整地震数据抽取比例为r的地震道作为不规则的地震数据样本,其他道为空道,分别以随机抽取和均匀抽取的方式仿真稀疏采样两种不规则情况。
地震数据重建效果的衡量指标采用信噪比(Signal-to-Noise Ratio,SNR)
| $ \mathrm{SNR}=10 \times \lg \frac{\sum\limits_{i=1}^{N} f^{2}\left(\boldsymbol{x}_{i}\right)}{\sum\limits_{i=1}^{N}\left[f\left(\boldsymbol{x}_{i}\right)-f\left(\boldsymbol{x}_{i}^{\prime}\right)\right]^{2}} $ | (8) |
式中N表示样本数量。
将10000组Marmousi模型数据按照8∶1∶1比例且不交叠的方式分别划分为训练集、验证集和测试集。在训练阶段,使用训练集数据进行训练并用验证集评估网络训练效果;当验证集结果趋近收敛时保存网络模型和参数,并用测试集数据对预训练模型进行评估。
2.2 网络模型测试针对均匀采样和随机采样两类情况,制作从10%~90%共9组不同采样率下的样本(每组采样率间隔为10%,两类采样样本共18组),分批次输入网络进行训练。不同采样率下训练的不同网络模型用来测试相应采样率下的地震数据。
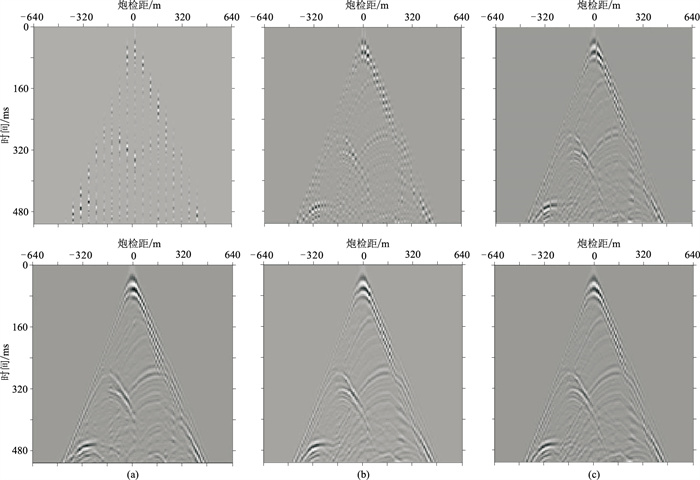
由图 4可见,在不同采样率条件下,本文方法(联合小波域的深度学习方法)均较好地保留了实际地震数据的特征;随着采样率不断提高,规则化效果也随之提升。
|
图 4 不同采样率条件下均匀采样数据(上)及其规则化重建结果(下) (a)20%;(b)50%;(c)80% |
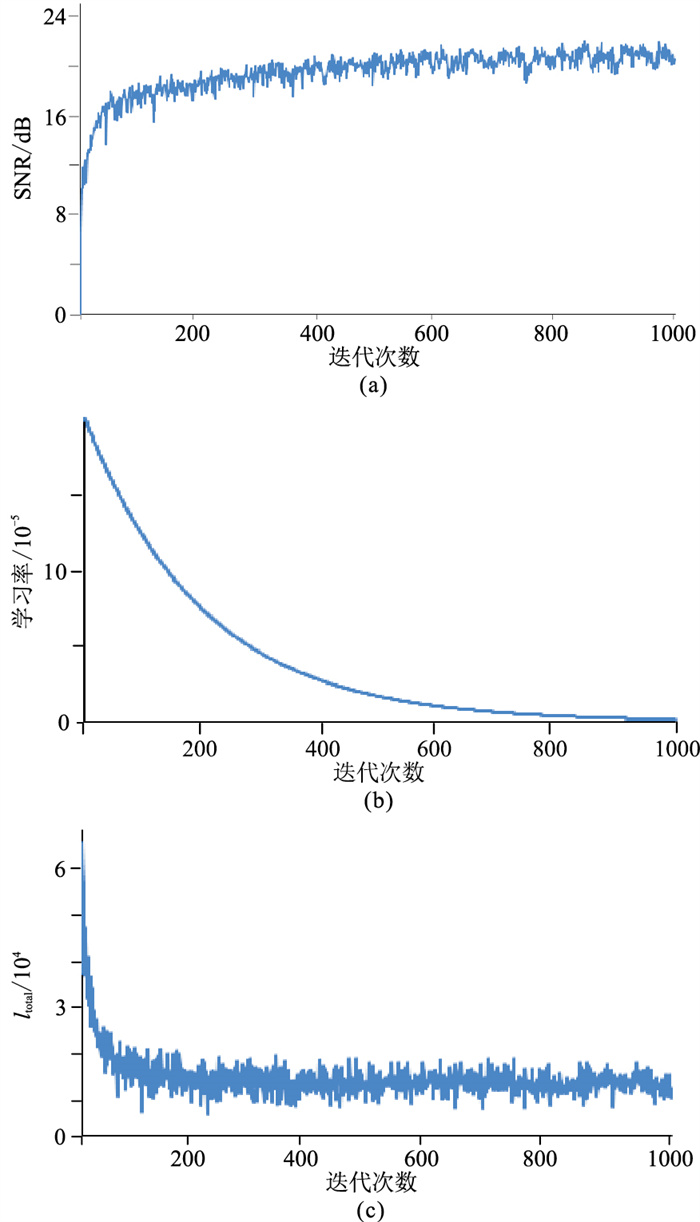
图 5为本文方法在验证集测试的评估结果。由图 5a可见,随着迭代次数增多,SNR逐步提高,重建效果不断增强;当达到1000次时,算法取得收敛,SNR基本稳定在最大值附近,说明本网络模型具有较好的收敛性和稳定性。为了使网络更好地收敛至最优解,防止训练后期学习率过大,本文采用指数衰减算法,设置初始学习率为2×10-4,每次迭代衰减指数为0.995(图 5b)。迭代初期用较大的学习率使结果快速收敛,所以前期联合误差数值变化相对较为剧烈(图 5c),有助于加速重建地震数据;后期减小学习率,使目标函数收敛至局部最小值,联合误差变化相对缓慢(图 5c),有利于重建规则数据细节信息。另外,在训练过程中网络调整参数导致结果振荡,但是网络会根据损失函数进行调整,从而使最终结果趋于稳定。
|
图 5 SNR(a)、学习率(b)和ltotal(c)随迭代次数变化趋势 |
为了验证本文方法对细节重建的有效性,测试样本在50%均匀采样条件下,对比联合小波域学习网络(SNR=19.8550dB)和仅使用时域学习网络(SNR=17.2667dB)的结果(图 6)。由图可见,联合小波域学习的网络局部细节特征更准确,更接近于真实地震数据。这证明了联合小波变换的CNN具有更好的纹理保持性能。

|
图 6 50%均匀采样条件下全采样(a)与未采用联合小波(b)、采用联合小波(c)的重建波形(上)及其局部(红框)放大(下) |
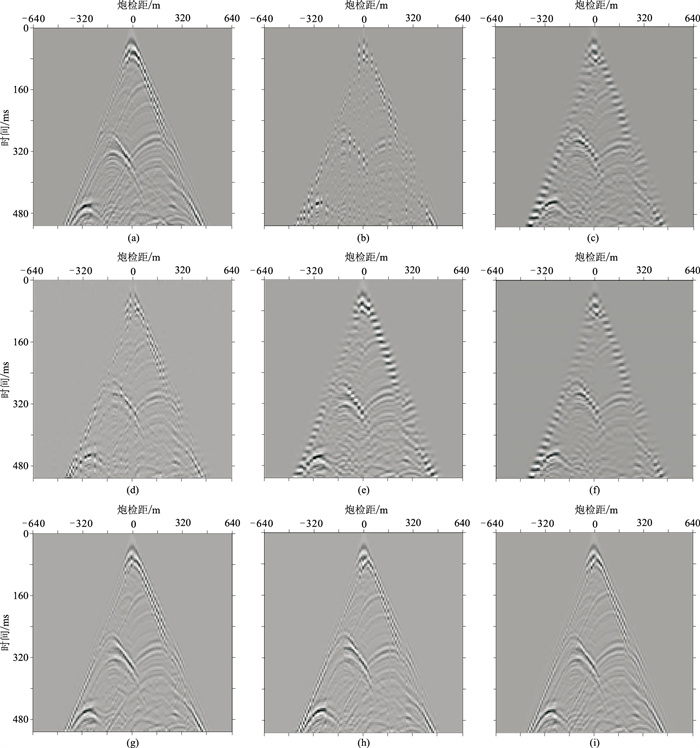
将本文方法应用于地震数据随机缺失的情况,并与当前较先进的重建算法进行对比(图 7)。由图可见,本文方法重建的地震数据波形连续性好、无突变,更逼近真实地震数据。
|
图 7 全采样数据与50%随机采样条件下不同算法重建结果对比 (a)全采样数据;(b)50%采样数据;(c)双三次插值法;(d)Curvelet;(e)BM3D[38];(f)KSVD[39];(g)VDSR[40];(h)EDSR[41];(i)联合小波神经网络(本文方法) |
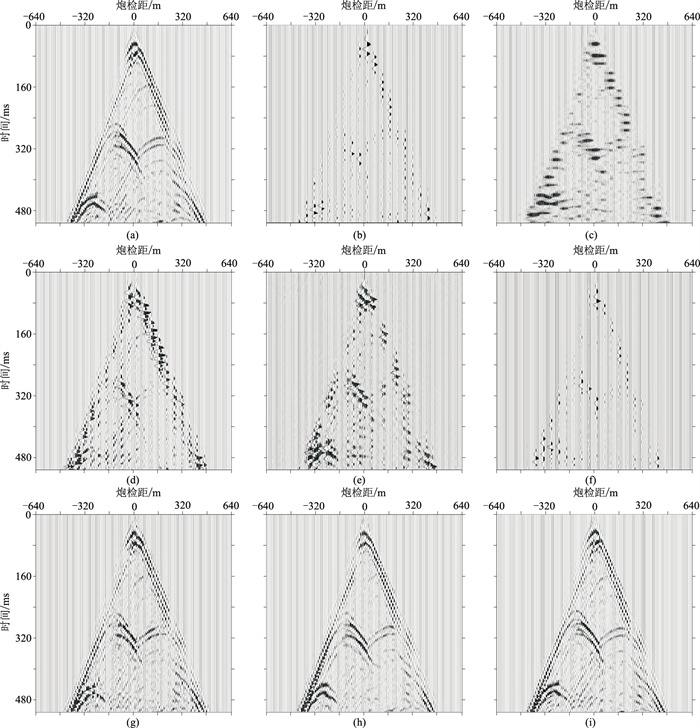
本文方法是从全局拓扑信息中预测小波系数,因此在低采样率情况下具有一定的优势。由图 8可见,在20%的低采样条件下,空道占据大部分,很难重建地震数据,因此基于物理建模重建的地震数据均出现大幅度缺失或失真;数据驱动方法重建地震数据整体效果得到大幅提升,但与真实数据相比仍存在细节缺失或重建精度不够的问题;在较低采样率(≤20%)且未考虑采样数据位置的情况下,本文方法重建的地震数据较好地保留了原始地震数据特征和波形信息,在细节处更逼近实际数据。这证明了本文方法对地震数据缺失位置不敏感,在地震数据规则化的过程具有鲁棒性。
|
图 8 全采样数据与20%均匀采样条件下不同算法重建结果对比 (a)全采样数据;(b)20%均匀采样数据;(c)双三次插值法;(d)Curvelet;(e)BM3D;(f)KSVD;(g)VDSR;(h)EDSR;(i)联合小波神经网络(本文方法) |
表 1和表 2分别对比了均匀采样与随机采样两种方式不同采样率条件下本文方法与其他方法测试集样本数据重建时SNR的均值对比。由表可见,本文方法显著优于基于模型的规则化方法,也优于同类基于深度学习的规则化方法。对于本文方法而言,在高采样率(>80%)时,无论是均匀采样还是随机采样,数据整体结构的特征均保持较完整,重建的数据效果比较接近;在中等采样率(20%~80%)时,均匀采样比随机采样能更好地保留数据的结构特性,均匀采样重建的效果要优于随机采样;在低采样率(≤20%)时,均匀采样和随机采样严重破坏了实际地震数据的结构特性,两种方法重建效果均较差。
|
|
表 1 均匀采样条件下不同方法重建地震数据的SNR均值对比 |
|
|
表 2 随机采样条件下不同方法重建地震数据的SNR均值对比 |
在50%随机采样条件下,比较不同深度学习方法训练效率。不同方法训练迭代1000次的训练完成时间如表 3所示。由表可见,联合小波学习方法相比于时域学习方法增加了计算时间,但增加幅度相对较小,重建地震数据SNR却得到了较大程度地提高。
|
|
表 3 不同深度学习方法训练所用时长及重建地震数据的SNR均值对比 |
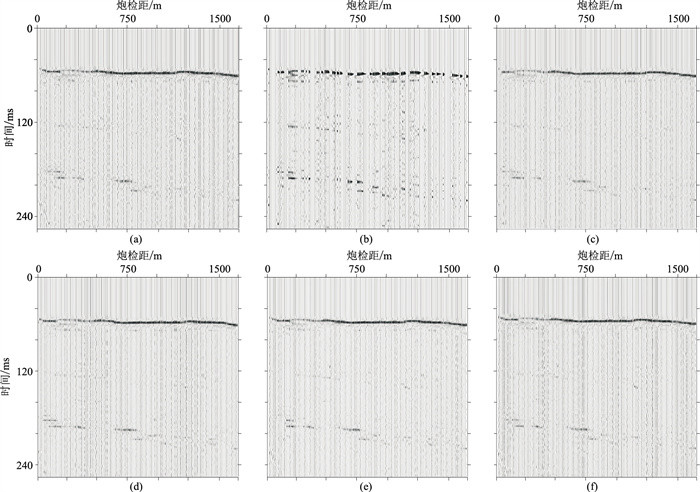
选取A油田实际地震数据测试本文方法规则化处理效果。震源和检波器置于地表,检波器采样间隔为2ms,道间距为12.5m。将实际样本数据共5000个按照8∶1∶1分别划分为训练集、验证集和测试集,使用训练集数据训练网络,再用测试集测试网络的有效性。任选1个测试集样本,实际地震数据不同方法重建波形对比如图 9所示。由图可见,本文方法重建的地震数据同相轴光滑、连续,可较好地重建缺失道和细节,具有较好的鲁棒性。
|
图 9 实际地震数据及不同方法重建波形对比 (a)原始地震数据;(b)随机50%采样;(c)双三次插值;(d)BM3D;(e)VDSR;(f)本文方法 |
为了验证本文网络的泛化能力,将B采油厂叠前和叠后地震数据各抽取5000组样本,制成一个样本增广的地震数据集,训练集、验证集和测试集按不交叠的方式划分比例为8∶1∶1,通过结合两种样本数据集进行网络训练。当训练收敛时,分别使用测试集中叠前和叠后数据分别进行测试。当测试数据为叠前数据时,规则化地震数据SNR=16.0539dB;当测试数据为叠后数据时,规则化地震数据SNR=16.331dB。这表明本文网络具有一定的泛化能力和适用性。
4 结束语本文提出的联合小波域深度学习的地震数据规则化方法有效利用了频域和时域的特征。对比基于模型的方法以及仅在时域学习条件下的重建效果,本文方法具有细节保持效果好、对地震数据缺失位置不敏感、在采样率较低的情况下具较好的重建效果的特点。实际地震数据重建结果验证了本文方法的准确性和有效性。需要指出的是,基于卷积神经网络的方法往往需要大量数据学习相应地震数据的特征,所以如何仅在有限量样本的情况下,提高模型的泛化能力,取得相对理想的效果,是进一步研究的方向。
| [1] |
霍志周, 熊登, 张剑锋. 地震数据重建方法综述[J]. 地球物理学进展, 2013, 28(4): 1749-1756. HUO Zhizhou, XIONG Deng, ZHANG Jianfeng. The overview of seismic data reconstruction methods[J]. Progress in Geophysics, 2013, 28(4): 1749-1756. |
| [2] |
HATTON L, LARNER K, GIBSON B S. Migration of seismic data from inhomogeneous media[J]. Geophysics, 1981, 46(5): 751-767. DOI:10.1190/1.1441213 |
| [3] |
俞寿朋, 蔡希玲, 苏永昌. 用地震信号多项式拟合提高叠加剖面信噪比[J]. 石油地球物理勘探, 1988, 23(2): 131-139. YU Shoupeng, CAI Xiling, SU Yongchang. Improvement of signal-to-noise ratio of stack section using polynomial fitting of seismic signals[J]. Oil Geophysical Prospecting, 1988, 23(2): 131-139. |
| [4] |
PIEPRZAK A W, MCCLEAN J W. Trace interpolation of severely aliased events[J]. SEG Technical Program Expanded Abstracts, 1988, 7: 658-660. |
| [5] |
THORSON J R, CLAERBOUT J F. Velocity-stack and slant-stack stochastic inversion[J]. Geophysics, 1985, 50(12): 2727-2741. DOI:10.1190/1.1441893 |
| [6] |
ZWARTJES P M, SACCHI M D. Fourier reconstruction of nonuniformly sampled, aliased seismic data[J]. Geophysics, 2004, 72(1): V21-V32. |
| [7] |
DO M N, VETTERLI M. The contourlet transform: an efficient directional multiresolution image representation[J]. IEEE Transactions on Image Proces-sing, 2005, 14(12): 2091-2106. DOI:10.1109/TIP.2005.859376 |
| [8] |
ZHANG H L, SONG S, LIU T Y. The ridgelet transform with non-linear threshold for seismic noise attenuation in marine carbonates[J]. Applied Geophysics, 2007, 4(4): 271-275. DOI:10.1007/s11770-007-0027-6 |
| [9] |
彭才, 常智, 朱仕军. 基于曲波变换的地震数据去噪方法[J]. 石油物探, 2008, 47(5): 461-464. PENG Cai, CHANG Zhi, ZHU Shijun. Noise elimination method based on curvelet transform[J]. Geophysical Prospecting for Petroleum, 2008, 47(5): 461-464. DOI:10.3969/j.issn.1000-1441.2008.05.006 |
| [10] |
CANDÈS E, DEMANET L, DONOHO D, et al. Fast discrete curvelet transforms[J]. Multiscale Modeling & Simulation, 2006, 5(3): 861-899. |
| [11] |
RONEN J. Wave-equation trace interpolation[J]. Geophysics, 1987, 52(7): 973-984. DOI:10.1190/1.1442366 |
| [12] |
CANNING A, GARDNER G H F. Regularizing 3-D data sets with DMO[J]. Geophysics, 1996, 61(4): 1103-1114. DOI:10.1190/1.1444031 |
| [13] |
吴丹, 龚仁彬, 王从镔, 等. 最小二乘叠前时间偏移在地震数据规则化中的应用[J]. 石油地球物理勘探, 2019, 54(1): 36-44. WU Dan, GONG Renbin, WANG Congbin, et al. Seismic data regularization via least-squares prestack time migration[J]. Oil Geophysical Prospecting, 2019, 54(1): 36-44. |
| [14] |
SPITZ S. Seismic trace interpolation in the F-X domain[J]. Geophysics, 1991, 56(6): 785-794. DOI:10.1190/1.1443096 |
| [15] |
李国发. F-K域与F-X域联合实现道内插[J]. 石油地球物理勘探, 1995, 30(5): 693-701. LI Guofa. Joint trace interpolation in F-K and F-X domains[J]. Oil Geophysical Prospecting, 1995, 30(5): 693-701. |
| [16] |
国九英, 周兴元. F-K域等道距道内插[J]. 石油地球物理勘探, 1996, 31(2): 211-218. GUO Jiuying, ZHOU Xingyuan. ISO-spaced trace interpolation in F-K domain[J]. Oil Geophysical Prospecting, 1996, 31(2): 211-218. |
| [17] |
CANDES E J, ROMBERG J, TAO T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509. DOI:10.1109/TIT.2005.862083 |
| [18] |
DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 |
| [19] |
ABMA R, KABIR N. 3D interpolation of irregular data with a POCS algorithm[J]. Geophysics, 2006, 71(6): E91-E97. |
| [20] |
HERRMANN F J, HENNENFENT G. Non-parametric seismic data recovery with curvelet frames[J]. Geophysical Journal International, 2008, 173(1): 233-248. |
| [21] |
陈杰, 牛聪, 李勇, 等. 基于数据驱动紧框架理论的三维地震数据去噪与重建[J]. 石油地球物理勘探, 2020, 55(4): 725-732. CHEN Jie, NIU Cong, LI Yong, et al. Denoising and reconstruction of 3D seismic data on a data-driven tight frame[J]. Oil Geophysical Prospecting, 2020, 55(4): 725-732. |
| [22] |
WANG B F, ZHANG N, LU W K, et al. Deep-lear-ning-based seismic data interpolation: a preliminary result[J]. Geophysics, 2019, 84(1): V11-V20. |
| [23] |
WANG F, CHEN S C. Residual learning of deep convolutional neural network for seismic random noise attenuation[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 16(8): 1314-1318. |
| [24] |
高静怀, 毛剑, 满蔚仕, 等. 叠前地震资料噪声衰减的小波域方法研究[J]. 地球物理学报, 2006, 49(4): 1155-1163. GAO Jinghuai, MAO Jian, MAN Weishi, et al. On the denoising method of prestack seismic data in wavelet domain[J]. Chinese Journal of Geophysics, 2006, 49(4): 1155-1163. |
| [25] |
王钰清, 陆文凯, 刘金林, 等. 基于数据增广和CNN的地震随机噪声压制[J]. 地球物理学报, 2019, 62(1): 421-433. WANG Yuqing, LU Wenkai, LIU Jinlin, et al. Random seismic noise attenuation based on data augmentation and CNN[J]. Chinese Journal of Geophysics, 2019, 62(1): 421-433. |
| [26] |
CHANG D K, YANG W Y, YONG X S, et al. Seismic data interpolation using dual-domain conditional generative adversarial networks[J]. IEEE Geoscience and Remote Sensing Letters, 2021, 18(10): 1856-1860. |
| [27] |
OLIVEIRA D A B, FERREIRA R S, SILVA R, et al. Interpolating seismic data with conditional generative adversarial networks[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(12): 1952-1956. |
| [28] |
郑浩, 张兵. 基于卷积神经网络的智能化地震数据插值技术[J]. 地球物理学进展, 2020, 35(2): 721-727. ZHENG Hao, ZHANG Bing. Intelligent seismic data interpolation via convolutional neural network[J]. Progress in Geophysics, 2020, 35(2): 721-727. |
| [29] |
JIA Y N, MA J W. What can machine learning do for seismic data processing? An interpolation application[J]. Geophysics, 2017, 82(3): V163-V177. |
| [30] |
宋辉, 高洋, 陈伟, 等. 基于卷积降噪自编码器的地震数据去噪[J]. 石油地球物理勘探, 2020, 55(6): 1210-1219. SONG Hui, GAO Yang, CHEN Wei, et al. Seismic noise suppression based on convolutional denoising autoencoders[J]. Oil Geophysical Prospecting, 2020, 55(6): 1210-1219. |
| [31] |
ZHU W Q, MOUSAVI S M, BEROZA G C. Seismic signal denoising and decomposition using deep neural networks[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(11): 9476-9488. |
| [32] |
ANBARJAFARI G, DEMIREL H. Image super resolution based on interpolation of wavelet domain high frequency subbands and the spatial domain input image[J]. ETRI Journal, 2010, 32(3): 390-394. |
| [33] |
GAO X, XIONG H K. A hybrid wavelet convolution network with sparse-coding for image super-resolution[C]. 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 2016, 1439-1443.
|
| [34] |
张岩, 李新月, 王斌, 等. 基于联合深度学习的地震数据随机噪声压制[J]. 石油地球物理勘探, 2021, 56(1): 9-25, 56. ZHANG Yan, LI Xinyue, WANG Bin, et al. Random noise suppression of seismic data based on joint deep learning[J]. Oil Geophysical Prospecting, 2021, 56(1): 9-25, 56. |
| [35] |
WANG Y Q, GE Q, LU W K, et al. Well-Logging constrained seismic inversion based on closed-loop convolutional neural network[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(8): 5564-5574. |
| [36] |
MALLAT S. Wavelets for a vision[J]. Proceedings of the IEEE, 1996, 84(4): 604-614. |
| [37] |
MALLAT S G. A theory for multiresolution signal decomposition: the wavelet representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1989, 11(7): 674-693. |
| [38] |
DABOV K, FOI A, KATKOVNIK V, et al. Image denoising by sparse 3-D transform-domain collaborative filtering[J]. IEEE Transactions on Image Processing, 2007, 16(8): 2080-2095. |
| [39] |
ELAD M, AHARON M. Image denoising via sparse and redundant representations over learned dictionaries[J]. IEEE Transactions on Image Processing, 2006, 15(12): 3736-3745. |
| [40] |
KIM J, LEE J K, LEE K M. Accurate image super-resolution using very deep convolutional networks[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 2016, 1646-1654.
|
| [41] |
LIM B, SON S, KIM H, et al. Enhanced deep residual networks for single image super-resolution[C]. 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 2017, 1132-1140.
|



 董宏丽, 黑龙江省大庆市高新技术开发区发展路199号东北石油大学人工智能能源研究院,163318。Email:
董宏丽, 黑龙江省大庆市高新技术开发区发展路199号东北石油大学人工智能能源研究院,163318。Email: