② 电子科技大学资源与环境学院,四川成都 611731;
③ 电子科技大学长三角研究院(湖州),浙江湖州 313000;
④ 中国石化石油勘探开发研究院,北京 100083
② School of Resources and Environment, University of Electronic Science and Technology of China, Chengdu, Sichuan 611731, China;
③ Yangtze Delta Region Institute of University of Electronic Science and Technology of China, Huzhou, Huzhou, Zhejiang 313000, China;
④ SINOPEC Petroleum Exploration and Production Research Institute, Beijing 100083, China
近几十年以来,常规地震勘探技术在石油、天然气等资源的勘察、开采等方面发挥了关键作用,目前正在向精细化、自动化、智能化等方向快速发展。然而,常规地震勘探技术无法回避波场单一(仅纵波)、信息量不足(缺横波)、精度不够高、多解性强等“瓶颈”问题。多波多分量地震勘探技术则可获得纵波(PP)、横波(S)、转换横波(PS)等多种类型的波场信息,具有多波联合成像、多波联合标定、多波联合反演、全波属性融合等独特优势,在有效解决“气云”(气烟囱)屏蔽成像、岩性判别、裂缝(各向异性)检测、流体(油、气、水)识别等复杂难题方面具有显著优势。
但是,要充分发挥多波多分量地震勘探技术的独特优势,首先需要解决多波地震信号的匹配问题[1]。目前,多波地震信号的匹配处理尚存在两方面主要问题:①时间、频率、相位等匹配精度不够高,尤其在信噪比较低的区域,多波匹配的可靠性较差;②匹配处理需要人工干预,效率低,缺乏自动化和智能化匹配方法。
近几年,人工智能技术已向油气领域快速扩张,地震勘探技术从采集、处理到解释向智能化方向发展已是大势所趋。尤其是深度学习(Deep Lear-ning,DL)方法,它作为机器学习的一个研究新领域,克服了浅层机器学习方法计算量大、离不开主观且繁琐的人工干预、学习速度慢、易陷入局部极值、易出现过拟合或欠拟合等一系列问题。自Hinton等[2]于2006年首先提出之后,DL逐渐成为人工智能的核心技术,在分析大数据、挖掘多维信息、智能搜索、提取复杂特征、识别复杂模式、解决非线性问题、解决低效率与长周期问题、处理图像、识别人脸、识别语音等方面展现出显著的优势。
然而,在多波多分量地震勘探中,因受DL方法的前沿性和多波理论的复杂性、数据处理解释和特征信息提取难度较大等诸多因素的影响,有关DL的研究与应用极少。仅极少数学者,如田高鹏等[3],基于卷积神经网络的DL方法开展了多波数据的小样本训练、多波储层预测等探索性研究。
基于PP波和PS波地震数据,本文针对多波匹配难题,采用DL方法,充分发挥计算机科学、地震、人工智能等多学科优势,创新建立了高精度、高效率、自动化和智能化的多波匹配技术,为多波联合沉积相识别、地层解释、断层追踪、储层预测、裂缝检测、含油气性识别等夯实基础。
1 方法原理 1.1 重采样信号重采样包含多种采样方式,本文运用重采样中的分数倍抽取方法对PS波信号进行时域压缩处理。主要运用的方法有插值、抽取和滤波等。插值的目的是增加信号的采样频率(时域拉伸)。插值倍率为N,即在序列相邻采样点之间插入N-1个点;抽取的目的是降低信号采样频率(时域压缩),可分为整数倍抽取和分数倍抽取。抽取倍率为整数M时,即在原序列信号中每隔M-1点抽取1点组成一个新的信号序列。
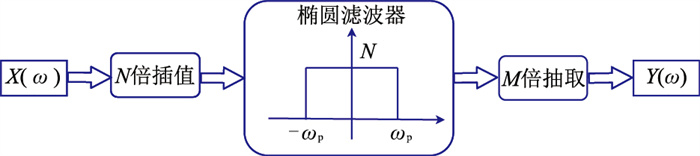
在进行地震信号处理时,PP波、PS波的时域长度比值往往不是整数,此时需进行分数倍抽取(图 1)。分数倍抽取是由插值与整数倍抽取结合而来,当抽取倍率为分数N/M倍时,可先执行N倍插值再执行M倍抽取。为消除镜像频谱和频谱混叠的影响,可选择在插值与抽取之间加入一个增益为N、截止频率ωp为min(π/N, π/M)的椭圆滤波器(考尔滤波器),相较于其他滤波器,该滤波器在阶数相同情况下具有最小的通带和阻带。
|
图 1 信号分数倍抽取流程 图中X(ω)和Y(ω)分别为输入、输出信号的频谱 |
按照图 1所示进行信号分数倍抽取具有许多优点:第一步进行插值保证了信号源不会损失;第二步使用一个滤波器就能同时实现滤除镜像频率、防止频谱混叠,滤波后再进行抽取能最大程度保留原有信号的特征。
1.2 卷积神经网络(CNN)卷积神经网络(Convolutional Neural Networks, CNN)是一类包含卷积计算且具有深度结构的前馈神经网络,通过仿造生物的视知觉机制而构建,是目前最具代表性、应用最广泛的DL算法。
基础的CNN由卷积层(Convolution)、激活层(Activation)和池化层(Pooling)三种结构组成。CNN输出的结果为每幅图像的特定特征空间。当处理图像分类任务时,把CNN输出的特征空间作为全连接层或全连接神经网络的输入,用全连接层完成从输入图像到标签集的映射,即可实现分类。
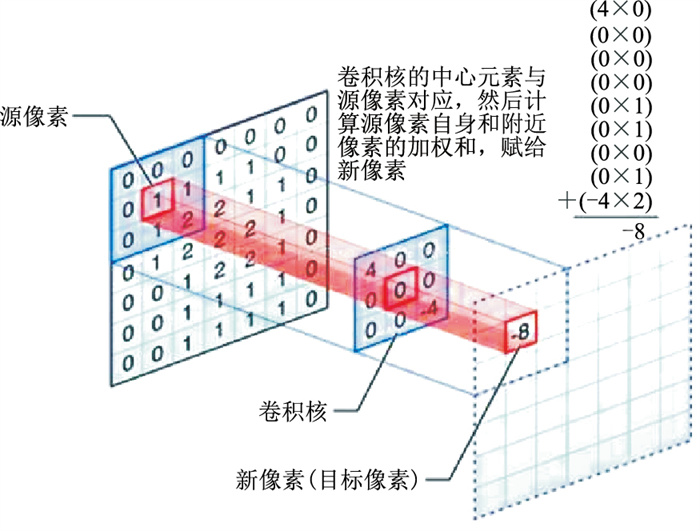
1.3 卷积特征提取卷积层是CNN在特征提取中最关键的部分,计算原理如图 2所示。其内部包含多个卷积核(滤波器),卷积核实质为一矩阵,其每个元素i都对应一个权重系数和一个偏差量Bias。通过滑动窗口机制,卷积核会依据特定步长在图像上进行滑动,依次进行局部矩阵卷积运算
| $ O=\sum\limits_{i} w_{i} x_{i}+\text { Bias } $ | (1) |
|
图 2 卷积核计算特征值原理 |
式中wi、xi分别是矩阵上对应i元素位置的权重、矩阵值,计算结果便是该步提取的特征值。
在一层卷积层中,单个卷积核能对图像提取一个特征图,对于极其复杂的地震数据,显然这是不够的,会有特征值提取不充分的问题,可添加多个卷积核,如64个卷积核,便能一次性地提取64种特征图。
卷积核大小可以指定为小于输入图像尺寸的任意值,卷积核越大,感受野越大,可提取的输入特征越复杂,但相应的计算量会更大。可选择反复使用小卷积核(如3×3)进行卷积计算,通过增加网络的深度,以保证感受野不低于大卷积核的情况下,大幅度地减小计算量。
1.4 梯度下降法梯度下降(Gradient Descent)是神经网络比较重要的部分,通常利用损失函数和参数的梯度进行反向传播,迭代更新权重、偏置参数找到损失最低点,使模型达到最优的效果。
Adam优化算法是目前执行梯度下降的常用算法之一,通过计算损失函数和参数梯度的一阶矩估计和二阶矩估计使梯度平滑过渡,可以适应不稳定的目标函数,同时也能为不同参数产生自适应的学习率。
1.5 方法实现流程基于以上原理,本文提出的多波地震信号匹配方法主要流程如下:首先,利用单波分层重采样,分数倍抽取PS波,将PS波初步压缩到PP波时间域;其次,训练CNN后提取部分网络参数搭建专用特征提取网络,并将8层卷积层结果组合后作为网络输出;再次,对PS波进行归一化、升维复制、切割处理后,利用神经网络提取PP波、PS波特征,定义“双加权”损失函数后利用梯度下降迭代更新PS波;最后,通过降噪、降维、反归一化等处理得到最终的输出结果。
本方法通过直接提取并改变图像特征匹配PP波、PS波,间接完成了频率和相位的匹配。
2 应用实例川西坳陷深层须家河组的致密碎屑岩气藏分布于四川盆地新场、合兴场、孝泉等地区,天然气储量丰富,资源开发潜力巨大;但同时具有储层埋藏深、致密化程度高、裂缝发育、气水分布复杂、圈闭边界不清晰等特征,勘探难度极大,常规的地震勘探技术难以奏效。
自2004年开始实施多波多分量(三维三分量,3D3C)地震勘探以来,在地层对比追踪解释、超致密砂岩储层预测、含气性识别、各向异性与裂缝检测等方面取得了重要进展,尤其在储量发现、圈闭优选、井位部署等勘探、开发环节发挥了关键作用。然而,受地震信号频带窄、PP波与PS波匹配精度不足等问题的制约,多波多分量地震勘探的技术优势仍然未能充分发挥。
本文试验以川西坳陷新场3D3C地震资料为基础,采用基于DL的多波地震信号智能匹配方法,对PP波与PS波叠后地震资料开展高精度、高效率、智能化和自动化匹配研究,为后续多波地层对比解释、多波属性提取等提供了基础。
2.1 单波分层重采样在利用CNN提取新场3D3C中PP波、PS波特征值之前,需将两种波形图转换到同一尺度,即将PS波压缩到PP波时间域。
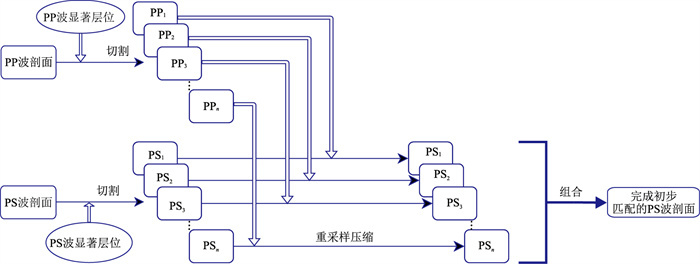
每次取得单道地震波数据(对应矩阵中的一列数据),如图 3所示,利用预提取的PP波、PS波层位数据,依据层位坐标将PP波与PS波在时间域分别切分为n部分,记作PP1、PP2、…、PPn和PS1、PS2、…、PSn。
|
图 3 单波分层重采样流程 |
计算PP1、PP2的长度比值I= N/M,对PS1进行N/M倍抽取,将其压缩到PP1时间域,后续对PS2、PS3…、PSn进行同样操作。完成n部分的压缩后进行拼接便得到一道完整的时域压缩PS波。对数据体中每一道PS波依次进行该操作后得到初步压缩到PP波时间域的完整PS波信号。
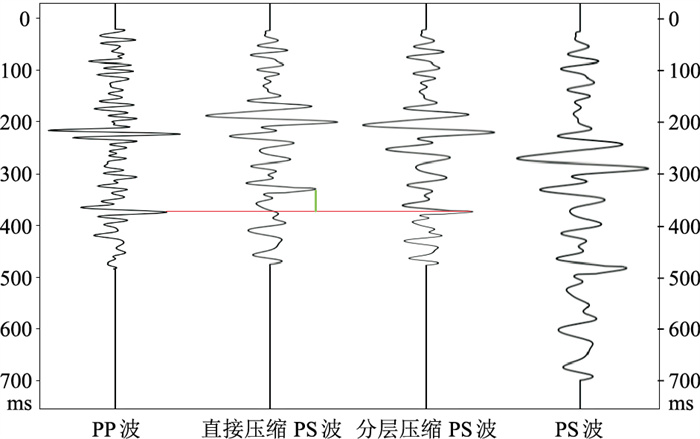
之所以不选择直接一次性将PS波压缩,是因为PP波、PS波在不同地质结构上传播速度比不同,导致两种波在不同时段的压缩比存在差异。若是依据某一压缩比,直接压缩可能导致部分需要对应的显著层位位置相距较远,位置偏差如图 4中绿线所示,后续神经网络处理时难度较大。而使用分层位压缩,能保证在时间域上显著层位完美对应,且细节层位初步匹配,后续只需在小范围内对各细节层位进行微小改动。
|
图 4 分层采样压缩效果 图中红线表示一个层位;绿线长度为直接压缩PS波与PP波层位的距离差 |
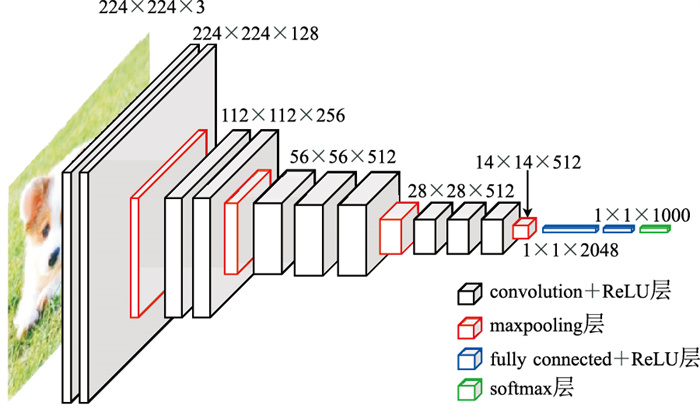
本文搭建的CNN结构如图 5所示,10层卷积层全部使用3×3卷积核,通过多次使用3×3小型卷积核替代大尺寸卷积核,在保证感受野不降低的情况下减小了参数计算量。卷积步长均为1,填充选择Same Padding,能保证模型卷积层输入、输出的图像尺寸不变。空间池化由4个最大池化(maxpooling)层进行,池化核尺寸均为2×2、步长为2,通过在卷积过程中多次穿插最大池化,能构建出多尺度的地震数据空间,从而采集到不同尺度地震数据特征值。网络设有两个全连接层:第一全连接有2048个通道;第二全连接(fully connected)执行1000维ILSVRC分类,包含1000个通道。两个全连接层都执行丢弃正则化。最后一层是softmax层,用于将第二全连接层中的1000个节点的输出映射为0~1的概率值,且所有概率值之和为1。所有隐藏层都配置了ReLU激活函数。
|
图 5 CNN结构 |
用于训练的数据集选择了ILSVRC-2012数据集,该数据集共包括1000个类别的图像,分为:训练集(130万张)、验证集(5万张)和测试集(10万张)三组。将原始图像进行归一化处理,并随机裁剪为224×224大小RGB图像。为了对训练集进行数据增强,裁切图像进行随机的水平翻转和随机的RGB颜色转换。
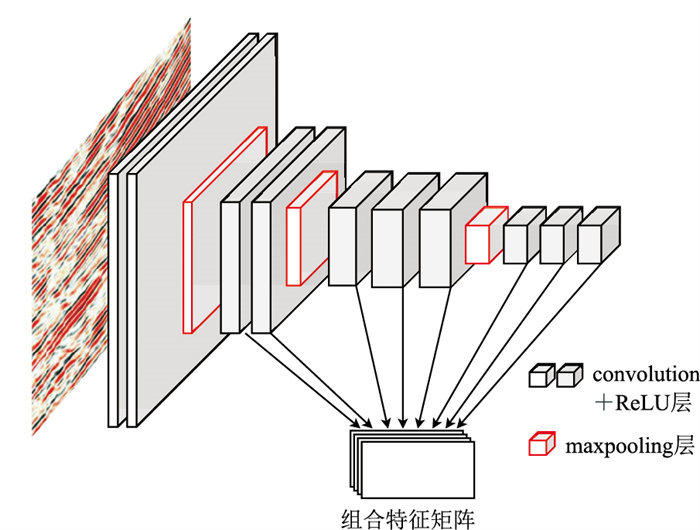
在完成训练后,还需利用已完成训练的CNN搭建专用网络模型以提取地震信号特征值:首先,选取原CNN前13层网络权重组成新的特征值提取网络;然后,输入层动态设置输入尺寸以适应不同剖面尺度的地震数据。由于不同深度的卷积层在提取地震剖面特征值时对全局和局部特征侧重不同,为保证信号在PP波和PS波的全局和局部特征的提取和映射匹配效果较好(图 6),保留模型后8层卷积提取的所有特征矩阵,组合8个特征矩阵作为神经网络的地震特征输出。
|
图 6 地震信号特征提取网络 |
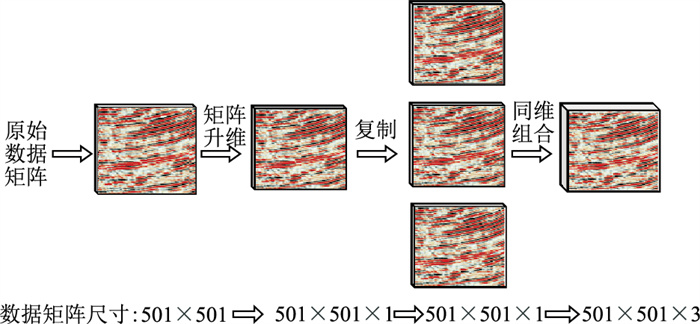
地震数据转为矩阵后可视作为单通道图片,但由于模型由三通道图片预训练而成,需将原始矩阵升维后进行复制,转换为三通道灰度图(图 7)。
|
图 7 信号扩维示意图 |
通常,三维地震数据由多条剖面数据组成。若在剖面边缘处信号突变,提取的波形特征也会突变,对匹配过程影响较大。因此,可将数据体依据剖面位置信息分割为多个小数据体(单个小数据即为单个剖面数据),对每个小数据体单独处理。
多波地震信号PP波和PS波振动方向、传播特性等一系列因素会导致两种波的振幅差异较大、数据大小可相差数倍。若直接将两种信号数据进行匹配,在计算损失函数时会导致较小数据值的特征值被直接忽略。因此,需将两种信号归一化到0~1;匹配完成后,在输出层再进行反归一化处理。
2.4 PP波与PS波特征匹配首先,将PS波数据复制为原始输出矩阵OUT,输入网络得到特征矩阵O,分别将PP波、PS波数据输入神经网络得到对应特征值矩阵P和S,再令Om、Pm、Sm分别为第m层卷积对OUT、PP波、PS波的卷积结果。
定义第n层卷积结果的平方距离损失函数为
| $ {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_n} = \frac{1}{2}\left[ {{w_{\rm{P}}}{{\left( {{\mathit{\boldsymbol{O}}_m} - {\mathit{\boldsymbol{P}}_m}} \right)}^2} + {w_{\rm{S}}}{{\left( {{\mathit{\boldsymbol{O}}_m} - {\mathit{\boldsymbol{S}}_m}} \right)}^2}} \right] $ | (2) |
式中wP、wS分别代表PP波和PS波特征权重值。
再定义总损失函数为
| $ \mathit{\boldsymbol{ \boldsymbol{\varGamma} }} = \frac{1}{8}\sum\limits_m {{w_m}} \cdot \frac{{{\mathop{\rm sum}\nolimits} \left( {{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_m}} \right)}}{{{\mathit{\boldsymbol{S}}_m}}} $ | (3) |
式中:wm是第m层卷积结果损失占总损失的权重;sum(Гm)代表将矩阵Гm中每个元素求和。
其次,便可求出总损失函数和输出矩阵的梯度,利用Adam优化算法执行梯度下降,迭代更新OUT,在完成梯度下降更新后,取OUT三个通道数据的平均值作为单通道数据。
最后,进行归一化和高斯滤波降噪处理,得到最终的输出数据。
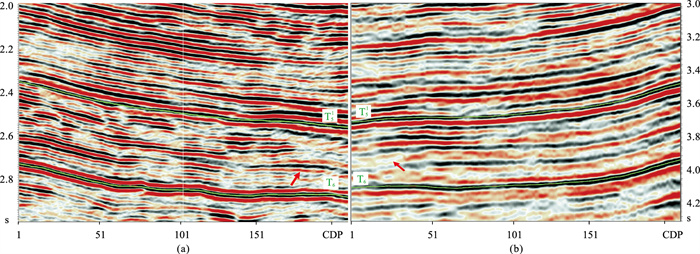
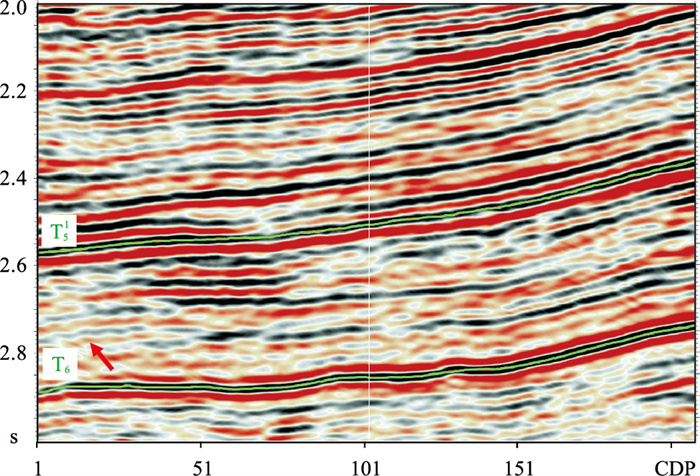
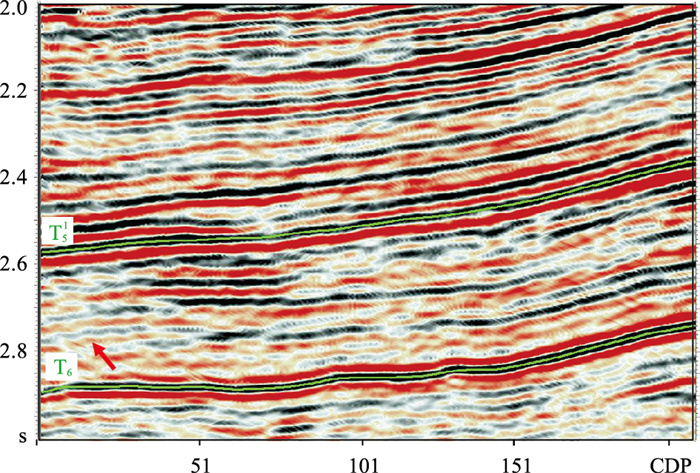
2.5 效果分析利用CNN及上述流程,基于川西坳陷新场3D3C地震资料,实现了PP波与PS波高精度、高效率、智能化和自动化匹配,获得了高品质的PS波匹配数据。图 8~图 11分别代表PP波、PS波的四个关键处理环节(处理前、重采样后、神经网络特征匹配、降噪)的剖面,重点对比分析PP波与PS波匹配前、后的剖面效果。由图可见,匹配后的PS波(图 10)在匹配前(图 8b)的基础上,实现了PP波时间域压缩,标志性地层(T51、T6)的波形特征较好地对应PP波。并且,对于之前难以匹配的非标志层或细节特征(红色箭头所指),在经过CNN处理后也获得了良好的匹配效果。整体上,PS波在保持原有特性的基础上,与PP波(图 8a)在传播时间、频率、相位、波形等运动学、动力学和几何学特征更加逼近,可更方便、更有效地应用于PP、PS波对比分析和地质解释。
|
图 8 新场3D3C测线PP波(a)与匹配前PS波(b)剖面 PP波与PS波剖面是镜像关系,下同 |
|
图 9 新场3D3C完成分层重采样的PS波地震剖面 |
|
图 10 新场3D3C完成神经网络特征匹配后的PS波剖面 |
|
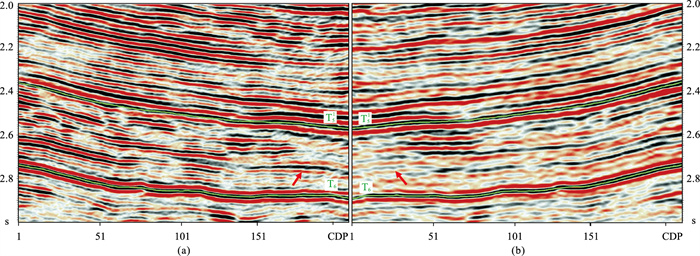
图 11 新场3D3C匹配后PP波(a)与完成降噪后最终输出PS波(b)剖面 |
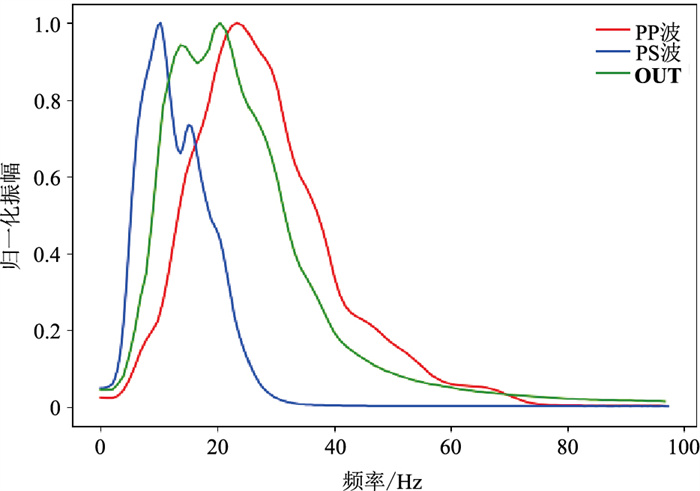
匹配后,PS波的主频提高、频宽拓展,与PP波的相位更接近。图 12为匹配前、后PP波与PS波的频谱关系。可见原始PP波、PS波频谱差异较明显,PS波的主频较低、频带较窄;匹配后,PS波在原有频谱特征基础上明显向PP波频谱特征逼近,匹配后PS波的主频提高、频带拓宽,在保持PS波原有特性的基础上,地层分辨能力进一步提升。
|
图 12 匹配前的PP波、PS波与匹配输出的PS波OUT频谱对比 数据范围:Inline1180;Crossline1050~1750 |
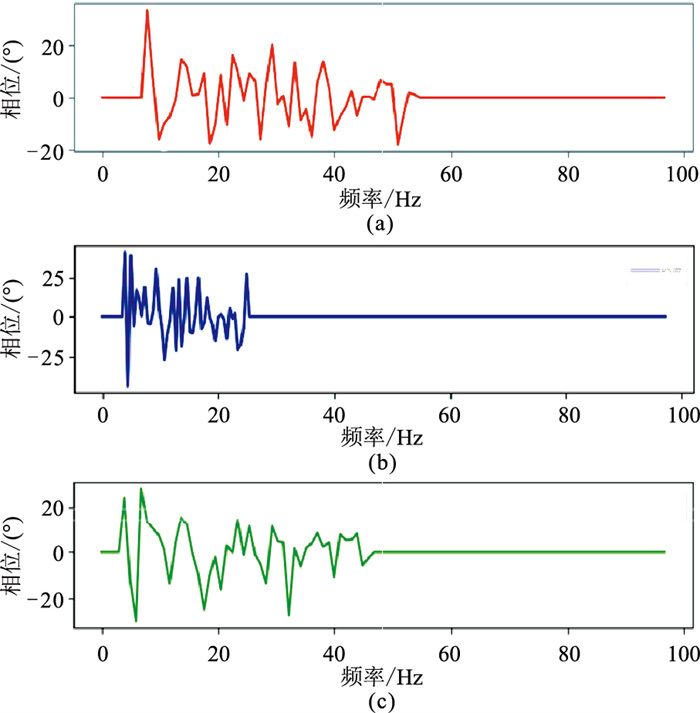
同时,匹配后,PS波的相位特征与PP波更加相似,有利于PP波与PS波的对比解释。在图 13所示的相位谱对比中,匹配前PP波与PS波相位差异较为明显,PP波相位集中在-20°~20°,PS波相位集中在-25°~25°。在完成匹配后,PS波的相位大部分已集中到-20°~20°,且在PS波原有相位特征基础上明显向PP波逼近,因此PP波与PS波相位特征匹配精度较高。
|
图 13 匹配前PP波(a)、PS波(b)与匹配后的匹配输出的PS波OUT(c)相位谱对比 数据范围:Inline1180;Crossline1050~1750 |
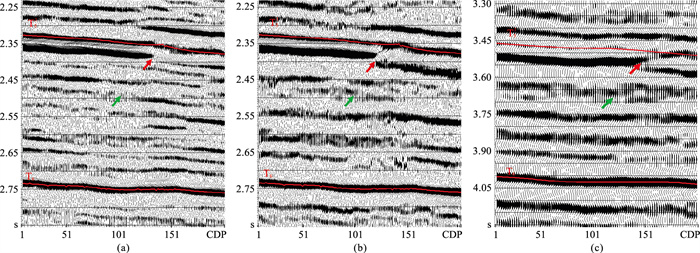
匹配后,PS波揭示的地层接触关系更清晰。如图 14,显示了新场3D3C某测线匹配前后PP波与PS波的剖面特征。由图可见,匹配后PS波的波形逼近PP波,断层接触关系更清晰(红色箭头),原复合波形被分解(绿色箭头),地层分辨能力提升,更有利于地层追踪解释。
|
图 14 新场3D3C另一测线匹配后PP波(a)、PS波(b)与匹配前PS波(c)剖面 |
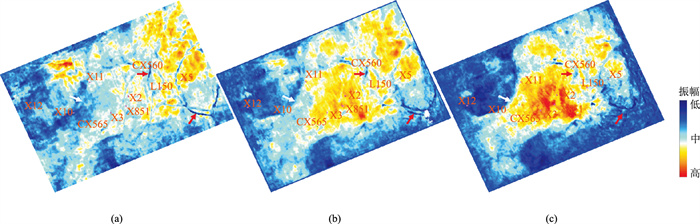
整体上,匹配后的PS波集中了PP波与匹配前PS波的在岩性边界刻画、断层识别等方面的优势。图 15显示了匹配前、后PP波、PS波沿T51层(以超致密泥岩为主,为下伏致密砂岩气藏提供了良好的封盖条件)的振幅变化特征。可见,匹配后PS波与PP波的振幅特征更逼近,更清晰地展示了断层分布(红色箭头);同样,也保持了原PS波的特色,较清晰地显示了泥岩盖层的边界及厚度变化(白色箭头)。
|
图 15 新场地区T51地层匹配后PP波(a)、PS波(b)与匹配前的PS波(c)振幅特征 |
川西坳陷新场地区实例分析表明,利用基于DL的多波地震信号智能匹配方法,在保持PS波原始传播特性的基础上,实现了与PP波的传播时间、频率、相位和波形等动力学、运动学和几何学特征匹配,证实了本文方法具有高精度、高效率、智能化和自动化等优点;匹配后的PS波主频提高、频带拓展,保持了匹配前的岩性和沉积相的边界刻画特性,断层和其他地质细节的分辨能力获得了有效提升。
3 结论与认识多波地震信号的高精度、高效率、自动化、智能化匹配是未来发展的趋势。基于DL的多波地震信号智能匹配方法,采用CNN能自动、高效地提取PP波和PS波的波形特征,将两者波形特征和输出特征的损失进行加权处理,可保证PS波的波形在整体特征不变的前提下,向PP波时间域逼近;通过PP波与PS波波形的匹配,自动完成时间、相位、频率等动力学、运动学和几何学特征匹配。
在川西坳陷新场3D3C地震资料的匹配应用表明:该方法适用于PP波与PS波匹配处理,匹配后的PS波在保持原始传播特性的基础上,在PP波时间域的主频、频宽、波形等逼近PP波;与匹配前相比,匹配后PS波分辨能力获得提升,地层接触关系更清晰,更有利于断层识别、岩性边界刻画、地层追踪等解释应用;同时,高精度匹配后的PS波,可为多波联合反演、沉积与构造对比解释等提供基础支撑。
| [1] |
徐天吉. 纵横波高精度匹配方法研究与应用[D]. 四川成都: 成都理工大学, 2012. XU Tianji. Study and Application of Methods on High-Precision Matching of P-Wave and S-Wave[D]. Chengdu University of Technology, Cheng-du, Sichuan, 2012. |
| [2] |
HINTON G E, SALAKHUTDINOV R R. Reducing the dimensionality of data with neural networks[J]. Science, 2006, 313(5786): 504-507. DOI:10.1126/science.1127647 |
| [3] |
田高鹏, 林年添, 张凯, 等. 多波地震油气储层的自组织神经网络学习与预测[J]. 科学技术与工程, 2021, 21(19): 7931-7941. TIAN Gaopeng, LIN Niantian, ZHANG Kai, et al. Prediction of seismic oil and gas reservoir using self-organizing neural network from multi-component seismic data[J]. Science Technology and Engineering, 2021, 21(19): 7931-7941. DOI:10.3969/j.issn.1671-1815.2021.19.011 |
| [4] |
常亮, 邓小明, 周明全, 等. 图像理解中的卷积神经网络[J]. 自动化学报, 2016, 42(9): 1300-1312. CHANG Liang, DENG Xiaoming, ZHOU Mingquan, et al. Convolutional neural networks in image understanding[J]. Acta Automatica Sinica, 2016, 42(9): 1300-1312. |
| [5] |
牟晋娟. 基于深度学习的图像风格迁移技术的研究[J]. 电子元器件与信息技术, 2019(4): 82-85. MOU Jinjuan. Research on image style transfer technology based on deep learning[J]. Electronic Component and Information Technology, 2019(4): 82-85. |
| [6] |
张顺, 龚怡宏, 王进军. 深度卷积神经网络的发展及其在计算机视觉领域的应用[J]. 计算机学报, 2019, 42(3): 453-482. ZHANG Shun, GONG Yihong, WANG Jinjun. The development of deep convolution neural network and its applications on computer vision[J]. Chinese Journal of Computers, 2019, 42(3): 453-482. |
| [7] |
方莉, 张萍. 经典图像去噪算法研究综述[J]. 工业控制计算机, 2010, 23(11): 73-74. FANG Li, ZHANG Ping. Overveiw on some arithmetics for image denoising[J]. Industrial Control Computer, 2010, 23(11): 73-74. DOI:10.3969/j.issn.1001-182X.2010.11.034 |
| [8] |
付燕. 人工地震信号去噪方法研究[D]. 陕西西安: 西北工业大学, 2002. FU Yan. Research on De-noising Methods of Seismic Data[D]. Northwestern Polytechnical University, Xi'an, Shaanxi, 2002. |
| [9] |
孙旭, 李晓光, 李嘉锋, 等. 基于深度学习的图像超分辨率复原研究进展[J]. 自动化学报, 2017, 43(5): 697-709. SUN Xu, LI Xiaoguang, LI Jiafeng, et al. Review on deep learning based image super-resolution restoration algorithms[J]. Acta Automatica Sinica, 2017, 43(5): 697-709. |
| [10] |
张一琛. 纵横波时间域匹配方法研究[D]. 北京: 中国石油大学(北京), 2019. ZHANG Yichen. Method Study on Time Domain Registration of P- and C-Waves[D]. China University of Petroleum(Beijing), Beijing, 2019. |
| [11] |
SIMONYAN K, ZISSERMAN A. Very Deep Convolutional Networks for Large-Scale Image Recognition[DB/OL]. (2014-09-04). https://arxiv.org/abs/1409.1556.
|
| [12] |
KINGMA D P, BA J. Adam: A Method for Stochastic Optimization[DB/OL]. (2014-12-22). https://ar-xiv.org/abs/1412.6980.
|
| [13] |
NIEPERT M, AHMED M, KUTZKOV K. Learning convolutional neural networks for graphs[C]. Proceedings of the 33rd International Conference on International Conference on Machine Learning, 2016, 2014-2023.
|
| [14] |
肖进胜, 刘恩雨, 朱力, 等. 改进的基于卷积神经网络的图像超分辨率算法[J]. 光学学报, 2017, 37(3): 94-102. XIAO Jinsheng, LIU Enyu, ZHU Li, et al. Improved image super-resolution algorithm based on convolutional neural network[J]. Acta Optica Sinica, 2017, 37(3): 94-102. |
| [15] |
吴正文. 卷积神经网络在图像分类中的应用研究[D]. 四川成都: 电子科技大学, 2015. WU Zhengwen. Application Research of Convolution Neural Network in Image Classification[D]. University of Electronic Science and Technology of China, Chengdu, Sichuan, 2015. |
| [16] |
何鹏程. 改进的卷积神经网络模型及其应用研究[D]. 辽宁大连: 大连理工大学, 2015. HE Pengcheng. Research of Improved Convolutional Neural Network Model and Its Application[D]. Dalian University of Technology, Dalian, Liaoning, 2015. |
| [17] |
陈立福, 武鸿, 崔先亮, 等. 基于迁移学习的卷积神经网络SAR图像目标识别[J]. 中国空间科学技术, 2018, 38(6): 45-51. CHEN Lifu, WU Hong, CUI Xianliang, et al. Convolution neural network SAR image target recognition based on transfer learning[J]. Chinese Space Science and Technology, 2018, 38(6): 45-51. |
| [18] |
毕华, 梁洪力, 王珏. 重采样方法与机器学习[J]. 计算机学报, 2009, 32(5): 862-877. BI Hua, LIANG Hongli, WANG Jue. Resampling methods and machine learning[J]. Chinese Journal of Computers, 2009, 32(5): 862-877. |
| [19] |
周庆龙, 江桦, 崔伟亮. 基于Lagrange插值的信号重采样方法研究[C]. 中国第二十届电路与系统学术年会暨2007年港澳内地电子信息学术研讨会论文集, 2007, 34-38. ZHOU Qinglong, JIANG Hua, CUI Weiliang. Research on signal resampling method based on Lagrange interpolation[C]. Proceedings of the 20th China Annual Conference on Circuits and Systems and the 2007 HongKong, Macao and Mainland Electronic Information Symposium, 2007, 34-38. |
| [20] |
周飞燕, 金林鹏, 董军. 卷积神经网络研究综述[J]. 计算机学报, 2017, 40(6): 1229-1251. ZHOU Feiyan, JIN Linpeng, DONG Jun. Review of convolutional neural network[J]. Chinese Journal of Computers, 2017, 40(6): 1229-1251. |
| [21] |
常德宽, 雍学善, 王一惠, 等. 基于深度卷积神经网络的地震数据断层识别方法[J]. 石油地球物理勘探, 2021, 56(1): 1-8. CHANG Dekuan, YONG Xueshan, WANG Yihui, et al. Seismic fault interpretation based on deep convolutional neural networks[J]. Oil Geophysical Prospecting, 2021, 56(1): 1-8. |
| [22] |
宋辉, 高洋, 陈伟, 等. 基于卷积降噪自编码器的地震数据去噪[J]. 石油地球物理勘探, 2020, 55(6): 1210-1219. SONG Hui, GAO Yang, CHEN Wei, et al. Seismic noise suppression based on convolutional denoising autoencoders[J]. Oil Geophysical Prospecting, 2020, 55(6): 1210-1219. |
| [23] |
周创, 居兴国, 李子昂, 等. 基于深度卷积生成对抗网络的地震初至拾取[J]. 石油物探, 2020, 59(5): 795-803. ZHOU Chuang, JU Xingguo, LI Ziang, et al. A deep convolutional generative adversarial network for first-arrival pickup from seismic data[J]. Geophysical Prospecting for Petroleum, 2020, 59(5): 795-803. |



 四川省成都市高新区(西区)西源大道2006号电子科技大学(清水河校区)创新中心,611731。
四川省成都市高新区(西区)西源大道2006号电子科技大学(清水河校区)创新中心,611731。