② 中国石化石油勘探开发研究院,北京 100083
② SINOPEC Petroleum Exploration and Production Research Institute, Beijing 100083, China
在地震勘探过程中,复杂地质环境通常产生严重的干扰波,对地震资料的处理、解释等带来不利影响。其中,地震多次波与一次波波组特征相似,尤其是层间多次波,剩余时差小,预测及压制难度大,严重影响构造及油气识别的准确性。因此,研究多次波压制方法在地震勘探领域具有重大意义。地震多次波通常分为表面多次波和层间多次波。其中,表面多次波压制技术已较成熟,而层间多次波压制技术在大规模应用方面效果仍不够理想。
现有的层间多次波压制方法主要是基于波动方程的预测减去法[1],根据地震资料预测层间多次波模型,再从原始数据中减去,包括模型驱动方法和数据驱动方法。模型驱动方法以地下地层的假设模型为基础,进行层间多次波预测。Verschuur等[2]将自由表面多次波压制(SRME)技术扩展到层间多次波压制,提出共聚焦点(CFP)策略,利用上覆地层的宏观速度信息预测层间多次波模型。而数据驱动类方法无需对地层做模型假设,从野外记录数据出发,进行层间多次波预测。Weglein等[3]基于散射理论,提出逆散射级数法(ISS),经过Luo等[4]、Wang等[5]改进后,能够压制二维和三维实际数据中的层间多次波,但该方法计算量巨大,限制了其用于大规模叠前数据。此外,Meles等[6]利用Marchenko自聚焦方法压制层间多次波,叶月明等[7]在SRME方法的基础上,提出了层间多次波压制的数据驱动迭代算法。但这些层间多次波压制技术在实际数据应用方面仍未成熟。
Ikelle[8]提出了利用地震数据中的虚同相轴进行层间多次波压制的方法,后人对该方法进行了多种改进,并应用于实际数据:An等[9]利用虚同相轴方法压制1.5维实际地震资料中的层间多次波;刘嘉辉等[10]、Liu等[11]、崔永福等[12]发展了虚同相轴方法并压制实际地震数据中的层间多次波,取得了较好效果。由于虚同相轴方法计算效率较低,一定程度上依赖于人工参数调整和层位拾取,且处理低信噪比数据时可能存在多次波泄露,限制了虚同相轴方法的规模化应用。
随着人工智能技术的发展和推广应用,借助深度学习模型的强大特征提取能力,对地震资料进行智能化处理、解释成为可能,例如初至拾取[13-14]、储层预测[15]、断层解释[16]等。目前,地震数据去噪成为人工智能技术在地球物理领域的应用热点之一,利用深度学习模型能够建立含噪数据与干净数据的映射关系,模型训练完成后实现对新数据集的自适应去噪,避免人为参数调整和耗时过长等问题[17]。在图像处理领域,Jain等[18]利用卷积神经网络(CNN)进行自然图像去噪,证明CNN能够有效学习从含噪图像到干净图像的非线性映射;此后,CNN由于具有较强的特征提取能力及更少的待训练参数,得到了快速发展。Ronneberger等[19]提出的U形编码与解码卷积神经网络(U-Net)以及Zhang等[20]提出的去噪卷积神经网络(DnCNN),均在图像去噪方面得到广泛应用。在有些应用领域,数据及标签数据获取难度大,训练数据的不足通常导致神经网络泛化能力不高,因此相继发展了不同的数据增广方法,包括几何变换[21]、噪声注入[22]、多数据混合[23]等。
在地震数据去噪方面,利用CNN进行地震随机噪声压制已比较成熟。韩卫雪等[24]利用DnCNN压制随机噪声,高好天等[25]对比了DnCNN与U-Net模型的随机噪声压制效果。王钰清等[26]提出基于数据增广的CNN随机噪声压制框架,通过几何变换及噪声注入的数据增广方法增加训练数据的多样性,取得了较好的实际数据随机噪声压制效果。
在多次波压制方面,神经网络方法已被用于压制表面多次波。Siahkoohi等[27]将原始数据和SRME算法的多次波初步预测模型作为输入,利用生成对抗网络(GAN)对实际数据中的表面多次波进行压制;Li等[28]也将SRME算法预测得到的表面多次波模型作为输入,利用CNN实现表面多次波预测模型,与原始数据的自适应匹配相减,取得了优于传统匹配相减算法的效果。此外,宋欢等[29]利用CNN对合成数据中的CMP道集进行多次波压制;Yu等[17]利用DnCNN压制合成地震数据中的表面多次波。然而,尚未见到神经网络方法应用于层间多次波压制。
本文将神经网络方法应用于层间多次波压制,设计较为适合层间多次波压制的深层编、解码卷积网络,并发展了两种数据增广方法,建立了基于数据增广的编解码卷积网络层间多次波压制框架。首先,利用虚同相轴方法对实际数据进行层间多次波压制,估计出一次波及层间多次波,将估计出的一次波作为标签;然后,构建两种增广训练集,通过改变层间多次波波场的数据增广提高网络对新数据集的泛化能力和适应性,通过高斯噪声注入的数据增广提高网络的抗噪性能;最后,基于增广训练集进行编解码网络的训练及预测。合成及实际数据的实验结果表明,本文提出的数据增广的编解码卷积网络层间多次波压制方法,能够有效压制复杂层间多次波并保护一次波,具有良好的泛化能力和抗噪性能,同时显著提高了计算效率。
1 方法原理数据增广的编解码卷积网络层间多次波压制算法主要包括深层编解码网络和两种数据增广方法,即改变层间多次波波场的数据增广和高斯噪声注入的数据增广。
1.1 神经网络层间多次波压制原理含层间多次波及随机噪声的地震数据可以表示为
| $ \boldsymbol{d}=\boldsymbol{p}+\boldsymbol{m}+\boldsymbol{n} $ | (1) |
式中:p为一次波数据;m、n分别为层间多次波、随机噪声。
利用神经网络压制噪声的目标是在无任何假设的情况下,从d中恢复p,即
| $ \hat{\boldsymbol{p}}=\operatorname{Net}(\boldsymbol{d} ; \boldsymbol{\theta}) $ | (2) |
式中:
| $ \left\{\begin{array}{l} \boldsymbol{w}^{(k)}=\boldsymbol{w}^{(k)}-\alpha \frac{\partial L(\boldsymbol{w}, \boldsymbol{b})}{\partial \boldsymbol{w}^{(k)}} \\ \boldsymbol{b}^{(k)}=\boldsymbol{b}^{(k)}-\alpha \frac{\partial L(\boldsymbol{w}, \boldsymbol{b})}{\partial \boldsymbol{b}^{(k)}} \end{array}\right. $ | (3) |
| $ L(\boldsymbol{w}, \boldsymbol{b})=\frac{1}{N} \sum\limits_{i=1}^{N}\left\|\hat{\boldsymbol{p}}_{i}-\boldsymbol{p}_{i}\right\|_{2}^{2} $ | (4) |
式中:L(w, b)为损失函数,是一次波数据与预测一次波数据的均方误差(MSE);N为输入数据个数;α为学习率,表征网络参数更新的幅度,训练初期使用较大学习率以便快速得到较优解,随后逐步减小学习率使模型稳定收敛。在进行层间多次波压制时,神经网络需要预测出输出数据每个样点的具体值,因此本质上属于回归问题。MSE是回归问题中的常用损失函数,能够让网络收敛快速稳定,本文将网络输出与标签数据的MSE作为损失函数。
1.2 深层编解码网络结构DnCNN是图像去噪领域常用的网络之一。网络使用的批归一化操作可以将每层神经网络的输入值归一化到较标准的分布,使非线性函数对输入更为敏感,缓解训练过程中的梯度消失问题[22],提高网络收敛速度。U-Net是图像分割领域的经典算法,它具备的编码与解码结构使网络随深度增加能够提取不同尺寸的信息,且编码、解码网络间的跳跃连接操作使网络融合多维信息,提取复杂特征。因此,结合DnCNN与U-Net两种网络的优点搭建层间多次波压制网络。
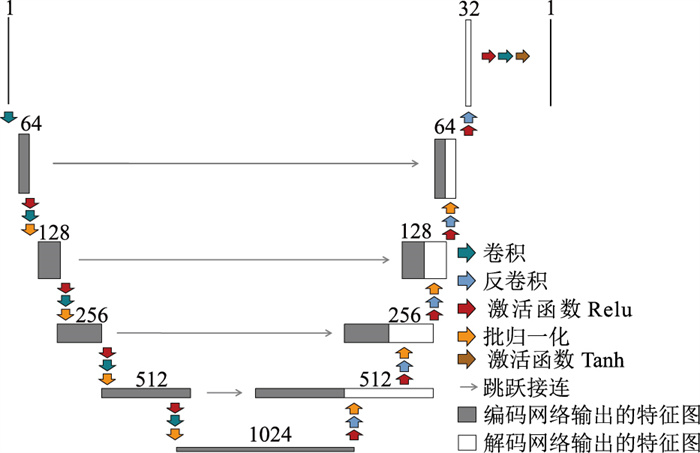
构建的网络结构如图 1所示,由编码网络和与之对称的解码网络构成。编码网络包含五层卷积层,卷积核尺寸设置为4×4,卷积核步长为2,使网络逐层提取特征并进行下采样,每个卷积层输出特征图的长与宽变为输入的1/2,以获取更大的感受野;卷积核数量从第二层后逐层翻倍,使输出特征图数目扩大2倍以充分保留有效特征;第二层以下的卷积层后加入批归一化操作以缓解梯度消失问题;之后使用Relu函数激活,加速网络收敛。
|
图 1 层间多次波压制的解编码网络结构 图中数字表示输出特征图个数 |
解码网络包括五层反卷积层,用于特征恢复,每层卷积核尺寸、数量及步长等与编码网络中同层卷积核的设置相同,则每次反卷积后输出特征图个数缩小为原来的1/2,尺寸增大2倍,使特征图最终恢复成原始图像尺寸;解码网络的第2~第5个反卷积层输出的特征图跳跃接连编码网络中同层特征图,使网络融合深层到浅层的多维信息,提取更精细的特征。网络最后加入只包含1个卷积核的卷积层,以复原输出通道数,并用Tanh函数激活后输出。网络输入为含层间多次波的原始数据,网络输出为预测得到的一次波。
1.3 改变层间多次波波场的数据增广神经网络处理训练集以外的、具有相同规律的新数据的能力即为网络的泛化能力。当训练数据有限时,通过数据增广丰富训练集中的特征多样性,能够提高网络的泛化能力。对于三维地震数据,不同剖面中的层间多次波在振幅、极性和旅行时上存在差异,这会由地下构造导致,也可能由接收仪器或不同处理流程产生的系统误差所致。据此设计了改变层间多次波波场的数据增广方法,简称波场增广方法,通过对层间多次波进行适当改变,模拟待处理的其余地震剖面数据的层间多次波,提高神经网络处理新数据的泛化能力。
首先利用虚同相轴方法处理原始数据,估计出一次波及层间多次波,然后对估计出的层间多次波数据进行振幅、极性、旅行时的改变,将改变后的层间多次波与一次波相加,以得到波场增广后的训练样本。由于一次波是网络的学习目标及期望输出,因此不对估计出的一次波进行改变,以保证网络的学习目标准确,输出结果可靠。
波场增广过程可表示为
| $ \left\{\begin{array}{l} \boldsymbol{d}(t)=\boldsymbol{p}_{0}(t)+\boldsymbol{m}_{0}(t) \\ \boldsymbol{m}_{1}(t)=\gamma \boldsymbol{m}_{0}(t+\Delta t) \\ \boldsymbol{d}^{\prime}(t)=\boldsymbol{p}_{0}(t)+\boldsymbol{m}_{1}(t) \end{array}\right. $ | (5) |
式中:p0、m0分别为利用虚同相轴方法估计出的一次波和层间多次波;m1为波场增广后的层间多次波;d′为波场增广后得到的训练样本,即估计一次波与波场增广后的层间多次波之和;Δt表示层间多次波波场在时间维度浮动的采样点数;γ表示层间多次波振幅与极性改变系数,取负数时表示极性反转,绝对值小于1表示振幅绝对值减小,γ-1表示振幅浮动的百分比。
需要注意的是,通过波场增广方法生成的数据需要与待处理的地震数据在旅行时、振幅与极性特征等方面基本吻合,以保证增广数据中的层间多次波满足实际的地下传播规律,才能准确模拟待处理数据,提高神经网络处理新数据集的效果。因此波场增广参数γ及Δt的取值需要根据实际地震数据中同相轴的振幅、极性、旅行时特征进行尝试后选择。对于构造或岩性变化较大地区,Δt及γ的取值范围可以适当增大;当岩性变化剧烈,以至于不同剖面中上、下地层波阻抗差符号相反时,γ可以取负值,模拟极性相反的同相轴。
得到波场增广的训练样本后,将虚同相轴方法估计的一次波数据作为对应的标签,并加入波场增广训练集,完成改变层间多次波波场的数据增广。
1.4 高斯噪声注入的数据增广实际地震数据通常信噪比较低,随机噪声的存在是影响虚同相轴方法效果的潜在因素之一。据此设计了高斯噪声注入的数据增广方法,使增广后训练样本包含层间多次波和高斯噪声两种干扰,以模拟低信噪比的地震数据。神经网络经过训练能够同时压制数据中的层间多次波及高斯噪声,具有较强的抗噪性能。
同样,首先利用虚同相轴方法对原始数据进行层间多次波压制,估计出一次波及层间多次波。需要注意的是,如果原始地震数据信噪比较低,影响了虚同相轴方法的层间多次波压制效果,需要通过已有的随机噪声压制方法对数据进行预处理,以保证虚同相轴方法生成的一次波标签准确。对原始地震数据加入不同信噪比的高斯噪声,以生成低信噪比地震数据,作为训练样本。信噪比可以表示为
| $ \mathrm{SNR}=10 \lg \frac{\|\boldsymbol{p}+\boldsymbol{m}\|_{2}}{\|\boldsymbol{n}\|_{2}} $ | (6) |
高斯噪声注入后的训练样本包含层间多次波和高斯噪声两种干扰,因此,神经网络在训练过程中能够同时学习两种干扰的特征,训练完成后具备同时压制两种干扰的能力。
得到高斯噪声注入的训练样本后,同样将虚同相轴方法估计的一次波作为对应的标签,加入训练集,完成高斯噪声注入的数据增广。
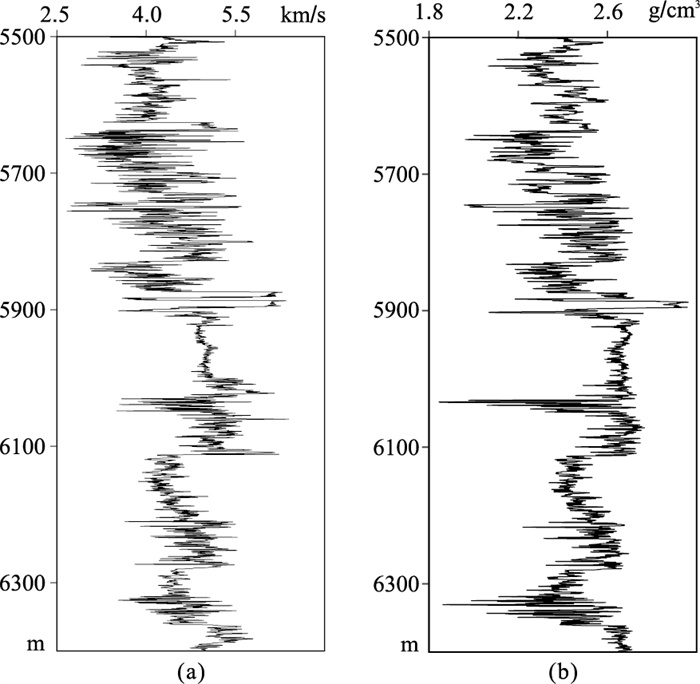
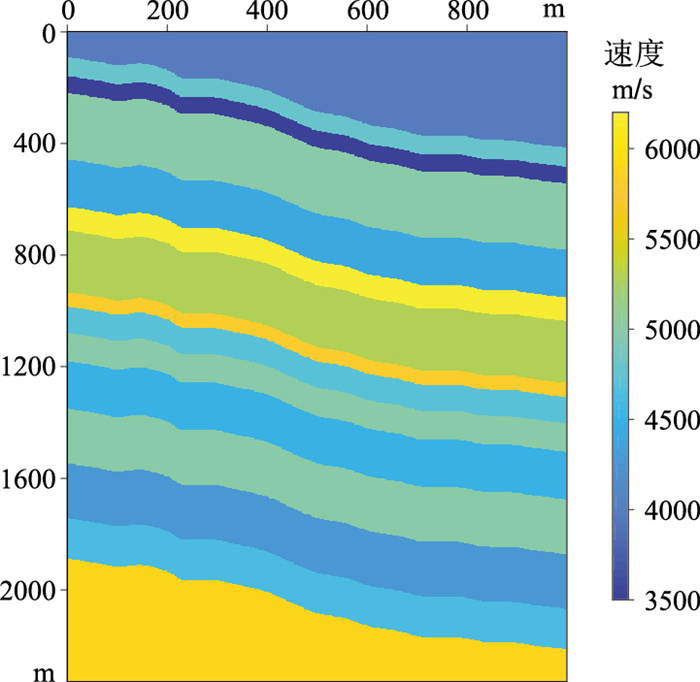
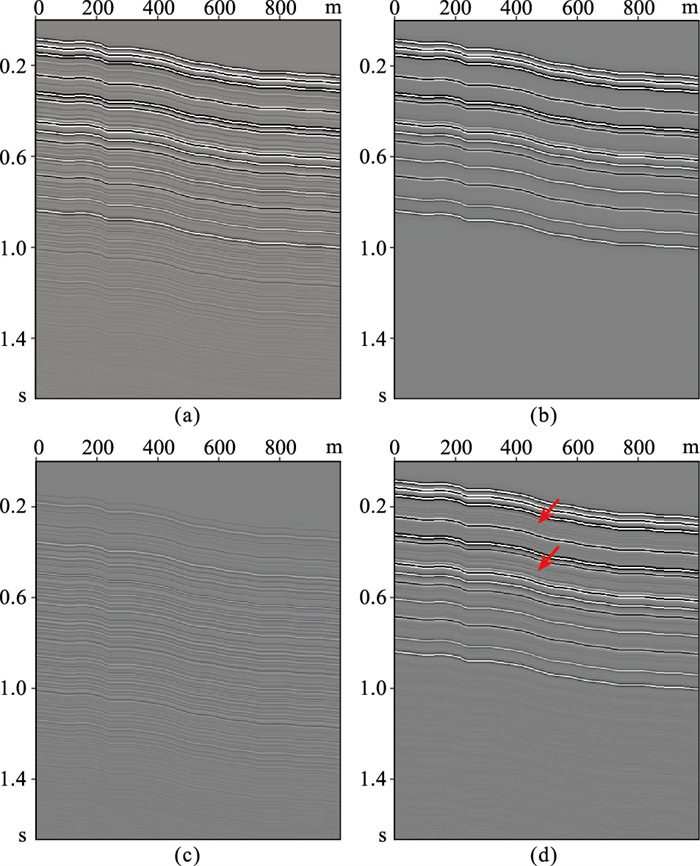
2 合成数据算例本文利用基于数据增广的编解码卷积网络层间多次波压制算法处理合成数据,并与虚同相轴方法的结果进行对比,以验证层间多次波压制效果。首先,参考塔里木盆地TH地区X井的测井数据(图 2),建立多层倾斜层状地质模型(图 3)。采用波场延拓层间多次波模拟法[30]对该模型进行地震正演,得到图 4a所示的合成数据,时间采样点数为416,采样间隔为4ms。图 4b和图 4c分别为合成数据的真实一次波与层间多次波,层间多次波在0.5、0.7、0.8s等处与一次波同相轴交叉,干扰了真实有效波信号。对该合成数据利用虚同相轴方法压制层间多次波以制作标签(图 4d),绝大部分层间多次波得到了较好的压制,尤其是1s以下已不存在明显的层间多次波同相轴,且一次波没有明显损失,说明虚同相轴法对合成数据的层间多次波压制较准确,是制作一次波标签的有效方法。
|
图 2 塔里木盆地TH地区X井测井曲线 (a)速度;(b)密度 |
|
图 3 倾斜层状速度模型 |
|
图 4 模型正演数据及虚同相轴法得到的一次波标签 (a)正演数据;(b)一次波数据;(c)多次波数据;(d)虚同相轴法得到的一次波标签数据。红箭头指示了微弱的层间多次波压制误差 |
得到一次波标签后,利用两种数据增广方法构建训练集、验证集及测试集,样本比例为10∶1∶1,三类数据集中的数据完全不重合,其中训练集包含400组带标签数据,并使用本文搭建的网络训练。训练过程中,通过验证集收敛情况确定合理的超参数,采用Adam优化算法更新参数,学习率随损失函数减小而逐步下降,网络训练600轮次,采用小批量训练法,每次以一个批量的地震数据为单元进行训练,批大小设置为2。
2.1 改变层间多次波波场的数据增广为了验证本文算法对变化较大的层间多次波的泛化性,选择波场增广参数Δt∈[0, 7],γ∈[0.5, 1.5]。得到增广数据集后,分别利用本文搭建的网络及DnCNN进行训练并测试,对比层间多次波压制效果。
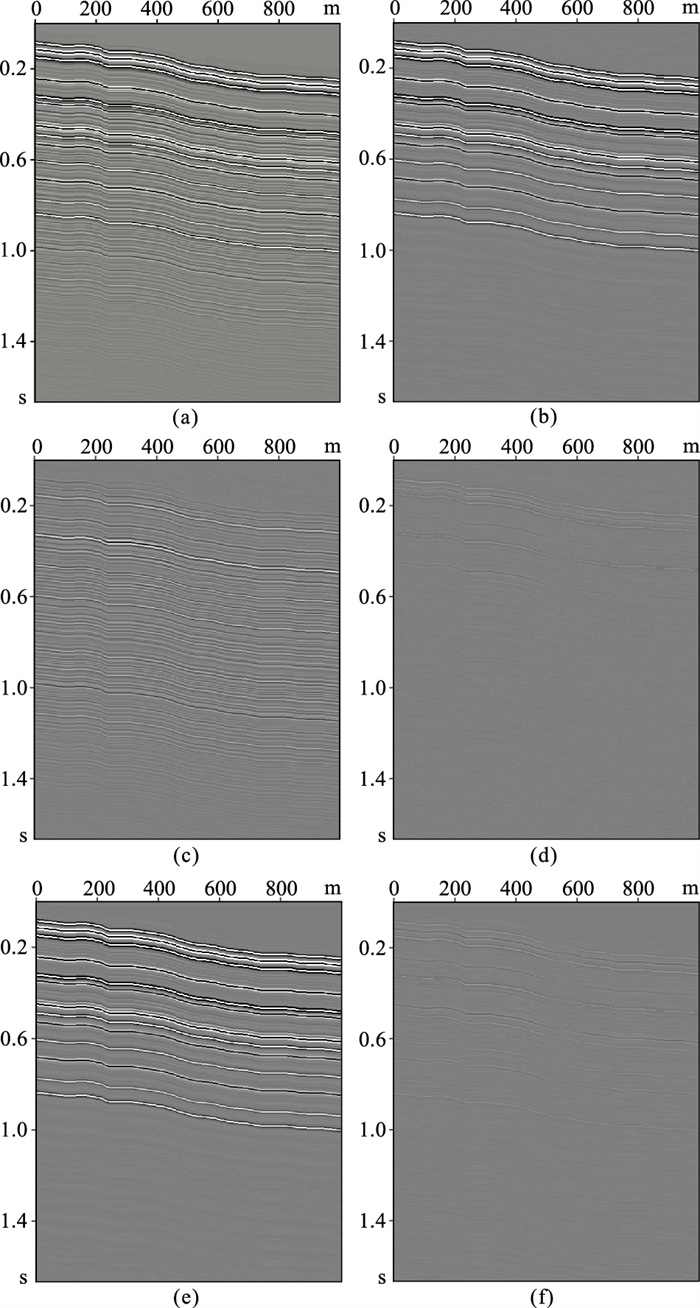
图 5是本文网络与DnCNN对波场增广后的倾斜模型正演数据进行层间多次波压制的结果。波场增广后的数据如图 5a所示,其中波场增广参数为Δt=6,γ=1.48。本文网络较精确地压制了振幅增大且旅行时改变的层间多次波(图 5b~图 5d)。神经网络对波场增广数据的压制结果表明,在仅有原始训练数据及标签的情况下,利用波场增广策略能够使训练好的神经网络对新数据集中层间多次波实现智能自适应压制,与传统方法相比显著提高了效率。图 5e、图 5f为DnCNN的层间多次波压制结果和误差,与本文网络压制结果相比,误差较大,存在部分一次波损失,因此本文设计的网络能够更有效地学习信号特征,压制复杂层间多次波的同时充分保护有效信号。
|
图 5 本文网络与DnCNN对波场增广后合成数据的层间多次波压制结果对比 (a)波场增广后的合成数据;(b)本文算法的压制结果;(c)本文算法预测的层间多次波;(d)本文算法压制结果与一次波标签数据的差;(e)DnCNN的压制结果;(f)DnCNN压制结果与一次波标签数据的差 |
为了验证本文算法的抗噪性能,利用高斯噪声注入的数据增广方法建立增广数据集,数据集信噪比为0~30dB,进行神经网络训练后,分别利用虚同相轴法及本文层间多次波压制方法对不同信噪比的地震数据进行层间多次波压制。
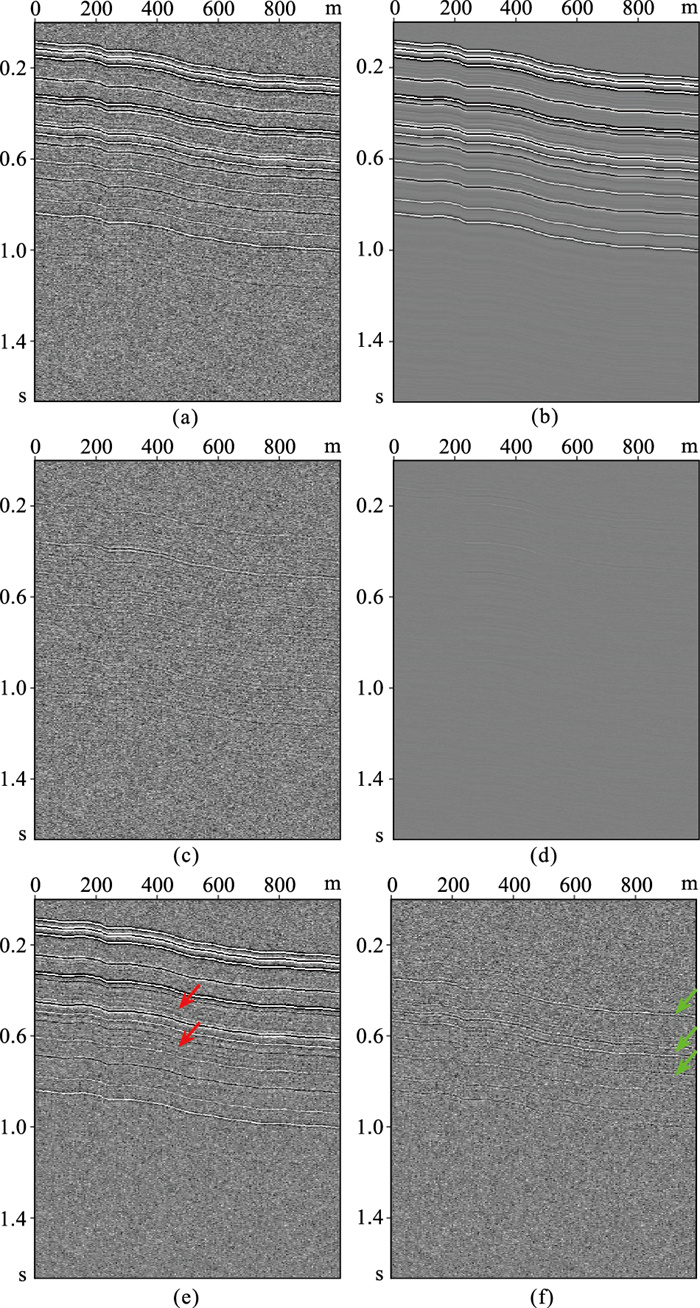
图 6为本文层间多次波压制算法对信噪比为5dB地震数据的层间多次波压制结果,并与虚同相轴方法进行对比。本文算法抗噪性强,对低信噪比数据中的层间多次波仍有较好压制效果,误差较小,且能同时压制高斯噪声与层间多次波(图 6b~图 6d)。相比之下,虚同相轴方法抗噪性较差,压制结果存在层间多次波残留(图 6e红色箭头所示),预测误差含有一次波能量损失(图 6f绿箭头所示)。
|
图 6 本文算法对噪声注入增广后合成数据的层间多次波压制结果 (a)噪声注入增广后的模拟数据;(b)本文算法压制结果;(c)本文算法压制的噪声;(d)本文算法压制结果与一次波标签数据的误差;(e)虚同相轴方法的压制结果;(f)虚同相轴方法压制结果与一次波标签数据的误差。红箭头指示层间多次波残留,绿箭头指示一次波损失 |
采用均方误差(MSE)作为定量指标验证两种方法对不同信噪比数据中层间多次波的压制效果(表 1)。在压制低信噪比数据中的层间多次波时,虚同相轴方法抗噪性差,尤其是当信噪比低于10dB时,虚同相轴方法压制结果存在较大误差,噪声和层间多次波有残留,一次波有损失。本文的神经网络方法层间多次波压制结果的MSE能够减小三个量级。神经网络作为数据驱动的算法,能够充分学习增广数据集中两种噪声的特征,在具备层间多次波压制能力的同时具有抗噪性能。因此,通过将神经网络与高斯噪声注入的数据增广方法结合,能够实现抗噪性能强的层间多次波压制。
|
|
表 1 不同信噪比数据两种算法压制结果的MSE统计 |
将本文算法应用于塔里木盆地TH地区三维偏移地震数据进行层间多次波压制。该地区地震数据包含700条主测线,时间采样点数为7000。利用虚同相轴方法对三维数据体中的不同主测线压制层间多次波以生成标签数据。
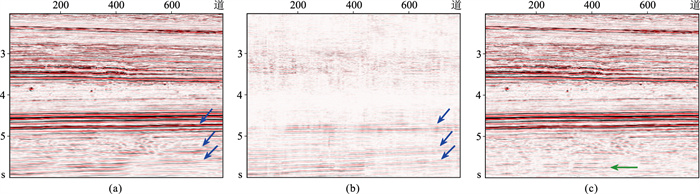
图 7为地震测线1902的偏移剖面及虚同相轴法压制层间多次波后的结果。原始剖面中3.5s和4.5s附近存在强振幅同相轴。虚同相轴方法压制了2.8~3.5s范围内的部分同相轴,并主要压制了4.8s附近的同相轴和5.0s以下的倾斜同相轴,如图 7a、图 7b中蓝色箭头所示。4.8s处的多次波可能由4.5s附近地层之间的多次反射产生。5.0s以下的倾斜同相轴与4.5s处强振幅同相轴之间的旅行时差大致等于4.5s与3.5s处强振幅同相轴之间的旅行时差,体现出了周期性的特征,即蓝色箭头指示的5.0s以下的倾斜同相轴可能是由地震波在4.5s与3.5s处的地层之间发生多次反射产生的。在原始剖面上,这些倾斜同相轴掩盖了绿箭头指示的水平同相轴能量(图 7c);多次波压制后,绿色箭头所示的水平同相轴能量得到了恢复。
|
图 7 塔里木盆地TH地区地震偏移剖面及其虚同相轴法的层间多次波压制结果 (a)地震测线1902偏移剖面;(b)虚同相轴法压制的层间多次波;(c)虚同相轴法层间多次波压制结果(一次波标签)。 绿箭头所示为原始数据中被倾斜多次波同相轴掩盖的水平同相轴;蓝箭头指示了4.5s以下的倾斜层间多次波同相轴 |
得到一次波标签后,将部分带标签测线数据作为训练集,其余作为测试集和验证集。不同主测线数据中同相轴形态、振幅及极性特征、旅行时等均有差异,因此对训练集以外的主测线进行测试能够验证网络的泛化性能。
训练集中数据的选取应取决于该地区构造变化程度,剧烈时应提供更多的带标签测线数据作为训练数据,以保证神经网络学习到不同主测线数据中的特征。塔里木盆地TH地区构造较为复杂,缝洞体、断层等发育,且不同的主测线数据间存在一定变化。本文在每2、6、8条带标签测线数据中选1条加入训练集,检验不同数量训练数据对神经网络层间多次波压制结果的影响。以固定间隔选择训练数据,能够使神经网络基于最少的训练数据,充分学习不同主测线数据的特征,缩短训练标签制作时间与网络训练时间。为提高神经网络在小样本训练情况下的表现,使用层间多次波波场增广方法扩充训练集。考虑到相邻测线中同相轴形态、振幅与极性特征及旅行时差别不大,本文设置了几组浮动范围较小的波场增广参数,并对比不同参数训练的网络在测试环节中取得的MSE值,最终选取的波场增广参数为Δt∈[0, 1],γ∈[0.9, 1.1],采用这组参数训练的网络在测试环节能够取得最小的MSE。
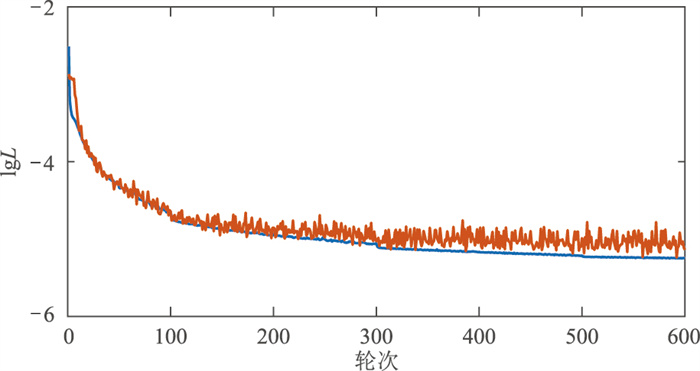
生成数据集后,对编解码网络进行训练。图 8为每2条带标签测线数据中选1条作为训练数据时,网络训练过程中损失函数的收敛情况。无论训练集还是验证集,损失函数的收敛均较稳定,前100轮次lgL从-3迅速下降到-5左右。随着训练轮次的进一步增加,lgL下降速度逐渐变慢,在第300轮次网络基本达到较稳定的收敛结果,而继续训练能使网络取得更好的层间多次波压制效果。网络训练完成后,利用本文算法对测试集中的主测线进行层间多次波压制,以验证方法的泛化性能,并与虚同相轴方法的一次波标签进行对比,采用MSE作为定量指标验证压制效果。
|
图 8 网络训练过程损失函数的收敛曲线 蓝色表示训练集收敛曲线,橙色代表验证集收敛曲线 |
表 2为训练数据量不同时,本文算法对测试集数据压制层间多次波后的MSE平均值,并对比了神经网络基于原始训练集与波场增广训练集训练后的层间多次波压制结果。随着训练数据的减少,神经网络的压制误差逐渐增大;而进行数据增广可以提高神经网络在小样本训练时的表现,当训练数据为主测线总数的1/6及1/8时,进行波场增广后MSE分别减小了6.5×10-6和5.6×10-6。对于构造复杂多变的实际地震资料,基于相同的训练数据时,神经网络结合波场增广方法后,能够对训练集以外的新测线数据取得更好的层间多次波压制效果,泛化能力更强。
|
|
表 2 不同数量训练集压制结果的MSE统计 |
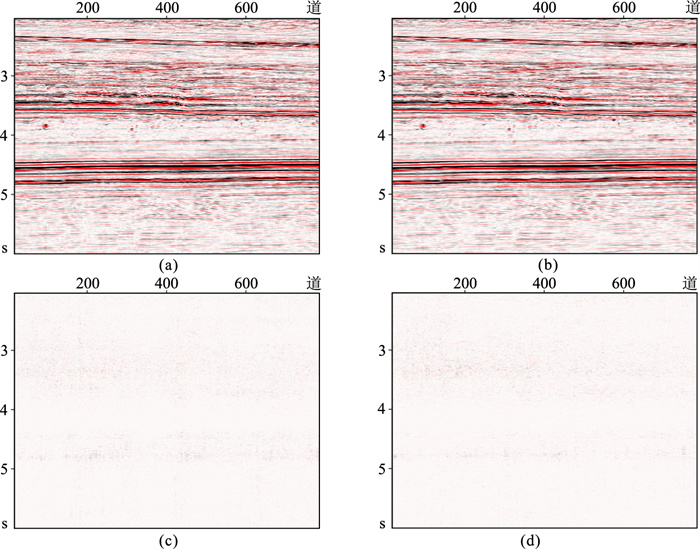
图 9为训练数据数量不同时,本文算法对第1902条主测线的层间多次波压制结果。当训练数据为主测线总数的1/2时,神经网络的压制结果较好,不存在明显误差(图 9a、图 9d)。当每6条或8条带标签测线数据中选1条作为训练数据时,由于训练数据较少,神经网络的压制误差较大,如图 9e、图 9f中3.0~3.5s以及4.7s处存在较大的误差。对于后两种情况,进行波场增广后,基于增广训练集训练的神经网络的层间多次波压制结果如图 10所示。增广训练后神经网络的压制误差明显变小,说明本文提出的波场增广方法能在一定程度上缓解神经网络训练过程中训练样本缺少的问题,提高网络压制新数据集中层间多次波的效果,使网络具有更强的泛化能力。

|
图 9 测线1902、不同数量训练集的层间多次波压制效果分析 (a)1/2训练集的压制结果;(b)1/6训练集的压制结果;(c)1/8训练集的压制结果;(d)图a与标签数据(图 7c)的差;(e)图b与标签数据的差;(f)图c与标签数据的差 |
|
图 10 测线1902、波场增广后的层间多次波压制效果 (a)1/6训练集压制结果;(b)1/8训练集压制结果;(c)图a与标签数据的差;(d)图b与标签数据的差 |
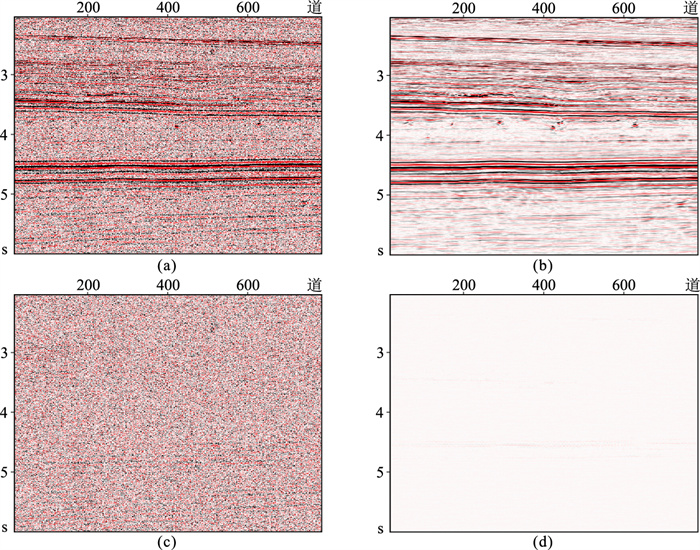
为了验证本文层间多次波压制算法的抗噪性,对塔里木盆地TH地区地震数据进行高斯噪声注入的数据增广,得到信噪比在0~30dB范围内的数据,生成训练集、验证集与测试集,并进行神经网络训练,训练完成后对测试集中的低信噪比数据进行层间多次波压制。图 11是测线1800信噪比为5dB噪声注入数据及本文算法的层间多次波压制结果、压制的噪声及压制误差。本文算法处理低信噪比数据时,能够同时压制高斯噪声以及层间多次波(图 11c),压制结果与一次波标签的误差较小,这是由于高斯噪声注入的数据增广方法使网络具备了抗噪能力。
|
图 11 测线1800高斯噪声注入后本文算法的层间多次波压制结果 (a)噪声增广数据;(b)压制结果;(c)压制的噪声,含高斯噪声与层间多次波;(d)压制误差(图b与标签数据的差) |
本文深层编解码网络在训练过程中的GPU内存占用为18559MB,整个网络的训练共耗时约4h10min。训练完成后,利用网络对700条主测线进行层间多次波压制仅需472s,即每条主测线数据的层间多次波压制只需花费0.67s。利用虚同相轴方法对每条主测线数据进行层间多次波压制需要花费266s,且压制前要求人为拾取层间多次波的来源层位。而本文方法在神经网络训练完成后,能够智能自适应压制数据中的层间多次波,有效避免人为拾取一次波,以及匹配相减中人为参数调整的过程,且大幅度提高了层间多次波压制效率。
由于实际地下介质和建立的速度模型有很大差别,且实际数据中层间多次波更复杂,导致实际数据与合成数据中地震同相轴形态、振幅和极性特征等差异很大。因此,对于实际地震数据的层间多次波压制网络,本文只利用实际数据及估计的一次波作为训练数据。然而,针对实际数据在训练层间多次波压制网络时,可以在基于模拟数据训练好的网络上进行迁移学习,加快网络训练过程。但迁移学习仍需要部分实际数据及其对应的一次波标签,才能保证网络应用于实际数据时取得准确的层间多次波压制结果。关于迁移学习对网络训练过程的影响,以及迁移学习时实际数据标签制作的要求等,将是下一步的研究方向。
4 结论本文提出了两种数据增广方法,并搭建了适于层间多次波压制的深层编解码网络,以此建立了基于数据增广的编解码卷积网络层间多次波压制框架。主要结论如下:
(1) 搭建的深层编解码网络融合了DnCNN中的批归一化及U-Net中的深层编解码结构、跳跃连接操作,具有更强的特征学习能力,适合进行层间多次波压制。
(2) 利用不同的数据增广方式能够使网络实现不同功能。波场增广能够提高网络压制新数据集中层间多次波的泛化性能;高斯噪声注入的数据增广能够使神经网络具有良好的抗噪性能。两种数据增广方法为网络训练提供了更丰富的特征,使训练好的网络具有更优的性能。
(3) 本文算法在虚同相轴方法的基础上,实现了对新数据集中层间多次波的自适应压制,避免了人为参数调整及人工拾取层位,显著提高了层间多次波的压制效率。
| [1] |
WEGLEIN A B. Multiple attenuation: an overview of recent advances and the road ahead(1999)[J]. The Leading Edge, 1999, 18(1): 40-44. DOI:10.1190/1.1438150 |
| [2] |
VERSCHUUR D J, BERKHOUT A J. Removal of internal multiples with the common-focus-point (CFP) approach: part 2 - application strategies and data examples[J]. Geophysics, 2005, 70(3): V61-V72. DOI:10.1190/1.1925754 |
| [3] |
WEGLEIN A B, GASPAROTTO F A, CARVALHO P M, et al. An inverse-scattering series method for attenuating multiples in seismic reflection data[J]. Geophysics, 1997, 62(6): 1975-1989. DOI:10.1190/1.1444298 |
| [4] |
LUO Y, KELAMIS P G, FU Q, et al. Elimination of land internal multiples based on the inverse scattering series[J]. The Leading Edge, 2011, 30(8): 884-889. DOI:10.1190/1.3626496 |
| [5] |
WANG M, HUNG B. 3D inverse scattering series method for internal multiple attenuation[C]. Exten-ded Abstracts of 76th EAGE Conference and Exhibition, 2014, 1-5.
|
| [6] |
MELES G A, LÖER K, RAVASI M, et al. Internal multiple prediction and removal using Marchenko autofocusing and seismic interferometry[J]. Geophy-sics, 2015, 80(1): A7-A11. |
| [7] |
叶月明, 赵昌垒, 姚根顺, 等. 数据驱动型层间多次波预测方法研究[J]. 石油地球物理勘探, 2014, 49(2): 244-251. YE Yueming, ZHAO Changlei, YAO Genshun, et al. Study of data-driven interbed multiple prediction[J]. Oil Geophysical Prospecting, 2014, 49(2): 244-251. |
| [8] |
IKELLE L T. A construct of internal multiples from surface data only: the concept of virtual seismic events[J]. Geophysical Journal International, 2006, 164(2): 383-393. DOI:10.1111/j.1365-246X.2006.02857.x |
| [9] |
AN S P, HU T Y, LIU J H, et al. Scheme of applying virtual event method for internal multiples on land seismic data[C]. International Geophysical Confe-rence, Qingdao, China, 2017, 391-394.
|
| [10] |
刘嘉辉, 胡天跃, 彭更新. 自适应虚同相轴方法压制地震层间多次波[J]. 地球物理学报, 2018, 61(3): 1196-1210. LIU Jiahui, HU Tianyue, PENG Gengxin. Suppres-sing seismic inter-bed multiples with the adaptive virtual events method[J]. Chinese Journal of Geophy-sics, 2018, 61(3): 1196-1210. |
| [11] |
LIU J H, HU T Y, PENG G X, et al. Removal of internal multiples by iterative construction of virtual primaries[J]. Geophysical Journal International, 2018, 215(1): 81-101. DOI:10.1093/gji/ggy270 |
| [12] |
崔永福, 刘嘉辉, 陈猛, 等. 虚同相轴方法及其在陆上地震层间多次波压制中的应用[J]. 石油地球物理勘探, 2019, 54(6): 1228-1236, 1245. CUI Yongfu, LIU Jiahui, CHEN Meng, et al. Land seismic peg-leg multiple attenuation with the virtual event method[J]. Oil Geophysical Prospecting, 2019, 54(6): 1228-1236, 1245. |
| [13] |
陈德武, 杨午阳, 魏新建, 等. 基于混合网络U-SegNet的地震初至自动拾取[J]. 石油地球物理勘探, 2020, 55(6): 1188-1201. CHEN Dewu, YANG Wuyang, WEI Xinjian, et al. Automatic picking of seismic first arrivals based on hybrid network U-SegNet[J]. Oil Geophysical Prospecting, 2020, 55(6): 1188-1201. |
| [14] |
周创, 居兴国, 李子昂, 等. 基于深度卷积生成对抗网络的地震初至拾取[J]. 石油物探, 2020, 59(5): 795-803. ZHOU Chuang, JU Xingguo, LI Ziang, et al. A deep convolutional generative adversarial network for first-arrival pickup from seismic data[J]. Geophysical Prospecting for Petroleum, 2020, 59(5): 795-803. |
| [15] |
付超, 林年添, 张栋, 等. 多波地震深度学习的油气储层分布预测案例[J]. 地球物理学报, 2018, 61(1): 293-303. FU Chao, LIN Niantian, ZHANG Dong, et al. Prediction of reservoirs using multi-component seismic data and the deep learning method[J]. Chinese Journal of Geophysics, 2018, 61(1): 293-303. |
| [16] |
常德宽, 雍学善, 王一惠, 等. 基于深度卷积神经网络的地震数据断层识别方法[J]. 石油地球物理勘探, 2021, 56(1): 1-8. CHANG Dekuan, YONG Xueshan, WANG Yihui, et al. Seismic fault interpretation based on deep convolutional neural networks[J]. Oil Geophysical Prospecting, 2021, 56(1): 1-8. |
| [17] |
YU S W, MA J W, WANG W L. Deep learning for denoising[J]. Geophysics, 2019, 84(6): V333-V350. DOI:10.1190/geo2018-0668.1 |
| [18] |
JAIN V, SEUNG H S. Natural image denoising with convolutional networks[C]. Proceedings of the 21st International Conference on Neural Information Processing Systems, 2008, 769-776.
|
| [19] |
RONNEBERGER O, FISCHER P, BROX T. U-Net: Convolutional networks for biomedical image segmentation[C]. Medical Image Computing and Computer-assisted Intervention, 2015, 234-241.
|
| [20] |
ZHANG K, ZUO W M, CHEN Y J, et al. Beyond a Gaussian denoiser: residual learning of deep CNN for image denoising[J]. IEEE Transactions on Image Processing, 2017, 26(7): 3142-3155. DOI:10.1109/TIP.2017.2662206 |
| [21] |
LECUN Y, BOTTOU L, BENGIO Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278-2324. DOI:10.1109/5.726791 |
| [22] |
MORENO-BAREA F J, STRAZZERA F, JEREZ J M, et al. Forward noise adjustment scheme for data augmentation[C]. 2018 IEEE Symposium Series on Computational Intelligence (SSCI), 2018, 728-734.
|
| [23] |
ZHANG H Y, CISSE M, DAUPHIN Y N, et al. Mixup: beyond empirical risk minimization[DB/OL]. 2017-10-25, https://arxiv.org/abs/1710.09412.
|
| [24] |
韩卫雪, 周亚同, 池越. 基于深度学习卷积神经网络的地震数据随机噪声去除[J]. 石油物探, 2018, 57(6): 862-869. HAN Weixue, ZHOU Yatong, CHI Yue. Deep lear-ning convolutional neural networks for random noise attenuation in seismic data[J]. Geophysical Prospecting for Petroleum, 2018, 57(6): 862-869. DOI:10.3969/j.issn.1000-1441.2018.06.008 |
| [25] |
高好天, 孙宁娜, 孙可奕, 等. DnCNN和U-Net对地震随机噪声压制的对比分析[J]. 地球物理学进展, 2021, 36(6): 2441-2453. GAO Haotian, SUN Ningna, SUN Keyi, et al. Comparative analysis of DnCNN and U-Net on suppression of seismic random noise[J]. Progress in Geophysics, 2021, 36(6): 2441-2453. |
| [26] |
王钰清, 陆文凯, 刘金林, 等. 基于数据增广和CNN的地震随机噪声压制[J]. 地球物理学报, 2019, 62(1): 421-433. WANG Yuqing, LU Wenkai, LIU Jinlin, et al. Random seismic noise attenuation based on data augmentation and CNN[J]. Chinese Journal of Geophysics, 2019, 62(1): 421-433. |
| [27] |
SIAHKOOHI A, VERSCHUUR D J, HERRMANN F J. Surface-related multiple elimination with deep learning[C]. SEG Technical Program Expanded Abstracts, 2019, 38: 4629-4634.
|
| [28] |
LI Z X, GAO H T. Feature extraction based on the convolutional neural network for adaptive multiple subtraction[J]. Marine Geophysical Research, 2020, 41(2): 1-20. |
| [29] |
宋欢, 毛伟建, 唐欢欢. 基于深层神经网络压制多次波[J]. 地球物理学报, 2021, 64(8): 2795-2808. SONG Huan, MAO Weijian, TANG Huanhuan. Application of deep neural networks for multiples atte-nuation[J]. Chinese Journal of Geophysics, 2021, 64(8): 2795-2808. |
| [30] |
匡伟康, 胡天跃, 段文胜, 等. 基于自适应变步长波场延拓的可控层分阶层间多次波模拟[J]. 地球物理学报, 2020, 63(5): 2043-2055. KUANG Weikang, HU Tianyue, DUAN Wensheng, et al. Modeling inter-layer multiples based on adaptive step-length-varying wavefield extrapolation[J]. Chinese Journal of Geophysics, 2020, 63(5): 2043-2055. |



 北京市海淀区颐和园路5号北京大学地球与空间科学学院,100871。Email:
北京市海淀区颐和园路5号北京大学地球与空间科学学院,100871。Email: