② 河南省瓦斯地质与瓦斯治理重点实验室——省部共建国家重点实验室培育基地,河南焦作 454000;
③ 中国石油集团测井有限公司,陕西西安 710077;
④ 东方地球物理公司综合物化探处,河北涿州 072751
② Key Laboratory of Gas Geology and Gas Control in Henan Province-National Key Laboratory Cultivation Base Co-constructed by Provincial Departments, Jiaozuo, Henan 454000, China;
③ China Petroleum Logging Co., Ltd, Xi'an, Shaanxi 710077, China;
④ GME & Geochemical Surveys, BGP Inc., CNPC, Zhuozhou, Hebei 072751, China
随着油气勘探的不断深入,勘探目标从传统的构造油气藏逐步转向复杂油气藏和隐蔽油气藏,勘探难度增加,对地球物理勘探技术的要求也越来越高。距井眼较远区域的地质构造、储层横向展布、裂缝发育及断层分布等信息对于油气藏探测具有重要意义。近些年,基于瞬变电磁理论的井孔时域电磁测井方法克服了传统频率域电磁测井仪器通过降低频率、增加源距实现远距离探测的技术局限性,通过测量电流脉冲关断过程激励的电磁衰变信号和晚期电磁场,采用较短的源距就可以达到频率域长源距才能实现的探测效果[1]。
瞬变电磁法经过近四十年的发展,取得了不错的效果,但目前该方法在测井领域的应用还处于探索阶段。Kaufman等[2]首先提出了时域感应测井理论;Anderson等[3]利用FFT变换,将频率域测井响应转换到时间域,模拟了井眼、薄层等因素的瞬态响应;周仕新等[4]对磁偶极源激发的井中瞬变电磁进行了模拟;Banning等[5]通过井中瞬变电磁三分量感应测井数值模拟及成像技术对地层倾角及视电阻率进行了估算;Onegova[6]讨论了垂直井眼环境下泥浆电阻率和线圈阵列长度发生变化时的装置相对偏心率与视电阻率之间的关系;Hagiwara[7]采用三轴感应测井方式,基于三轴响应比值估算了地层倾角和各向异性;李建慧等[8]开展了地—井瞬变电磁三维正演;Commer等[9]运用时域有限差分法,在直角坐标系下进行三维建模,计算了钢套管条件下的瞬变电磁响应;Swidinsky等[10]采用重叠回线模式的发射、接收线圈,研究了井中瞬变电磁波响应特征;李建慧等[11]采用非结构化四面体网格对局部区域进行网格加密,并运用矢量有限元方法计算了复杂回线源的脉冲响应;段书新等[12]研究了井中瞬变电磁法对井旁低阻介质的探测能力;Meng等[13]基于全空间瞬变电磁场表达式和Halley优化算法提出了一种视电阻率校正算法,对径向层状模型进行模拟,结果证明该算法可以消除径向低阻内层对瞬变电磁测井响应的影响;陈卫营等[14]分析了三维地—井瞬变电磁法的电场和磁场全分量探测效果;郭建磊等[15]基于有限差分法实现了地—井瞬变电磁三维各向异性正演,并分析了半空间模型和块状异常体模型的三分量响应特征。
近些年来,瞬变电磁法数值模拟技术日趋成熟,目前常用的方法包括有限元法[16-17]、有限差分法[18-19]、积分方程法[20-21]和有限体积法[22-23]等。针对这些瞬变电磁数值模拟方法,国内外学者大多在笛卡尔坐标系中进行数值模拟,但在测井问题中,井孔及地层非均匀介质的电导率在小尺度(套管、泥浆等)上存在剧烈变化。传统笛卡尔坐标系为了能够反映出小尺度上的介质参数变化,需要采用很细的剖分网格,这大大增加了计算区域的网格数量,通常情况下可达千万级(107)甚至超过亿级(108)。虽然当前计算机计算能力和性能得到了迅速提升,但若不改进建模方式,仍然难以满足实际计算需求。而圆柱坐标系能较好地模拟井眼及周围小尺度上的介质属性变化,可以有效减少网格剖分数量,提升计算效率。因此,本文在圆柱坐标系下开展模拟。
瞬变电磁法中发射波形是影响探测效果的重要指标之一,常用的发射波形有梯形波、半正弦波、三角波等,发射波形可分为开启(on-time)、稳定、关断(off-time)三个阶段。目前,许多学者将发射波形相关参数对瞬变电磁响应结果的影响作为研究重点[24]。齐彦福等[25]通过改变时间道上的瞬时电流强度,并运用有限元方法完成了三维航空电磁全波形正演模拟与响应特征分析。赵越等[26]利用梯形波、三角波和半正弦波对浅海瞬变电磁场进行了数值模拟,并分析了不同波形在开启和关断下的响应特征。Zeng等[27]采用有限元方法,对不同电导率的半空间进行了全波形正演模拟。Ji等[28]运用有限差分法分析了线性变化的斜坡关断时间对浅层异常体的全波瞬变电磁响应。
综上所述,在井孔地层非均匀介质条件下,如何有效减少网格数量进而降低方程组的求解规模,以及如何设置合理的发射波形及相关参数,对目前瞬变电磁方法的研究具有重要意义。本文在圆柱坐标系下对求解区域进行离散,基于有限体积法实现了套管井三维瞬变电磁正演模拟[29],重点对套管电导率、相对磁导率、厚度和内径变化对响应结果的影响进行了研究,对比了梯形波、三角波、半正弦波的响应特征,并分析了梯形波各阶段持续时间对电磁响应特征的影响。
1 正演理论 1.1 控制方程在准静态情况下,时间域麦克斯韦方程组可表示为
| $ \nabla \times \boldsymbol{E}+\frac{\partial \boldsymbol{B}}{\partial t}=\boldsymbol{S}_{1} $ | (1) |
| $\nabla \times \boldsymbol{H}-\boldsymbol{J}=\boldsymbol{S}_{2} $ | (2) |
式中:E表示电场强度;B表示磁感应强度;H表示磁场强度;J表示电流密度;S1表示外加回线源的磁流密度,下标“1”代表磁性源;S2表示外加线源的电流密度,下标“2”代表电性源;t表示时间。上式中场量之间的本构关系可表示为
| $\boldsymbol{J}=\sigma \boldsymbol{E} $ | (3) |
| $\boldsymbol{B}=\mu \boldsymbol{H} $ | (4) |
式中σ和μ分别表示电导率和磁导率。在时间域进行麦克斯韦方程离散,需要调用式(3)和式(4)的本构关系表示离散系统。时域问题的电磁场公式为
| $ \boldsymbol{C} \boldsymbol{E}+\frac{\partial \boldsymbol{B}}{\partial t}=\boldsymbol{S}_{1} $ | (5) |
| $ \boldsymbol{C}^{\mathrm{T}} \boldsymbol{M}_{\mu}^{\mathrm{f}}-1 \boldsymbol{B}-\boldsymbol{M}_{\sigma}^{\mathrm{e}} \boldsymbol{E}=\boldsymbol{S}_{2} $ | (6) |
其中
| $ \boldsymbol{E}=\left(\boldsymbol{M}_{\sigma}^{\mathrm{e}}\right)^{-1} \boldsymbol{C}^{\mathrm{T}} \boldsymbol{M}_{\mu-1}^{\mathrm{e}} \boldsymbol{B}-\left(\boldsymbol{M}_{\sigma}^{\mathrm{e}}\right)^{-1} \boldsymbol{S}_{2} $ | (7) |
将式(7)代入式(5)可得
| $ \boldsymbol{C}\left(\boldsymbol{M}_{\sigma}^{\mathrm{e}}\right)^{-1} \boldsymbol{C}^{\mathrm{T}} \boldsymbol{M}_{\mu-1}^{\mathrm{f}} \boldsymbol{B}+\frac{\partial \boldsymbol{B}}{\partial t}=\boldsymbol{C}\left(\boldsymbol{M}_{\sigma}^{\mathrm{e}}\right)^{-1} \boldsymbol{S}_{2}+\boldsymbol{S}_{1} $ | (8) |
对上式进行变形得到
| $\frac{\partial \boldsymbol{B}}{\partial t}=-\boldsymbol{C}\left(\boldsymbol{M}_{\sigma}^{\mathrm{e}}\right)^{-1} \boldsymbol{C}^{\mathrm{T}} \boldsymbol{M}_{\mu-1}^{\mathrm{f}} \boldsymbol{B}+\boldsymbol{C}\left(\boldsymbol{M}_{\sigma}^{\mathrm{e}}\right)^{-1} \boldsymbol{S}_{2}+\boldsymbol{S}_{1} $ | (9) |
式(5)~式(9)中:C表示边旋度算子;矩阵M表示内积算子;上标“e”和“f”分别代表网格单元的边和面;上标“T”表示转置。
1.2 有限体积离散有限体积法将待求解区域离散为互不重叠的体积单元,并对需要求解的微分方程进行体积积分。本文采用交错网格实现有限体积空间离散,将电场分量定义在网格单元的棱边中心,磁场分量定义在网格单元的面中心。基于圆柱坐标系可方便进行井眼建模,不会在井眼部位产生大量的离散网格,可有效提高计算速度。圆柱坐标系下网格单元离散形式如图 1所示,其中图 1a所示为未进行角度离散的完全对称网格单元,图 1b为包含角度离散的三维网格单元。本文选用图 1a所示剖分形式对求解区域进行离散。
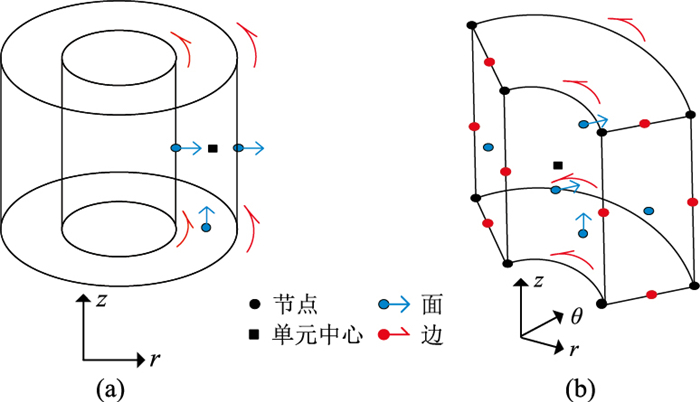
|
图 1 有限体积空间离散单元 (a)圆柱对称网格单元(未做角度离散);(b)三维圆柱网格单元(角度离散后)。r、θ分别表示半径和角度。 |
本文采用后向欧拉法对时间进行离散,其一阶差分形式为
| $\frac{\mathrm{d} g(t)}{\mathrm{d} t}=\frac{g(t)-g(t-\Delta t)}{\Delta t} $ | (10) |
式中:g(t)表示当前时刻数据;g(t-Δt)表示前一时刻数据,其中Δt是时间步长。本文在电流变化剧烈的阶段采用较小的时间步长,在平稳阶段采用稍大的时间步长,这样既能保证数据的稳定性又能提高计算效率。结合式(9),可通过下式求解第n+1个时间步长的场值
| $ \begin{aligned} \frac{\boldsymbol{B}^{(n+1)}-\boldsymbol{B}^{(n)}}{\Delta t}=&-\boldsymbol{C}\left(\boldsymbol{M}_{\sigma}^{\mathrm{e}}\right)^{-1} \boldsymbol{C}^{\mathrm{T}} \boldsymbol{M}_{\mu-1}^{\mathrm{f}} \boldsymbol{B}^{(n+1)}+\\ & \boldsymbol{C}\left(\boldsymbol{M}_{\sigma}^{\mathrm{e}}\right)^{-1} \boldsymbol{S}_{2}^{(n+1)}+\boldsymbol{S}_{1}^{(n+1)} \end{aligned} $ | (11) |
即
| $ \begin{aligned} &{\left[\boldsymbol{C}\left(\boldsymbol{M}_{\sigma}^{\mathrm{e}}\right)^{-1} \boldsymbol{C}^{\mathrm{T}} \boldsymbol{M}_{\mu-1}^{\mathrm{f}}+\frac{1}{\Delta t^{(n)}}\right] \boldsymbol{B}^{(n+1)}-\frac{1}{\Delta t^{(n)}} \boldsymbol{I B}^{(n)}} \\ &\quad=\boldsymbol{C}\left(\boldsymbol{M}_{\sigma}^{\mathrm{e}}\right)^{-1} \boldsymbol{S}_{2}^{(n+1)}+\boldsymbol{S}_{1}^{(n+1)} \end{aligned} $ | (12) |
式中:时间步长Δt(n)=t(n+1)-t(n),t(n+1)表示当前时刻,t(n)表示前一时刻;I表示单位矩阵。
假设在0时刻向磁性源中通入非阶跃电流,通过改变电流强度实现发射波形的瞬态响应模拟。这里分别采用梯形波、半正弦波和三角波三种发射波形,波形示意图见图 2,其激励函数分别为
| $ U_{1}(t)= \begin{cases}0 & t=0 \\ \frac{t}{t_{1}} & 0<t \leqslant t_{1} \\ 1 & t_{1}<t \leqslant t_{2} \\ \frac{t-t_{2}}{t_{3}-t_{2}} & t_{2}<t<t_{3} \\ 0 & t_{3} \leqslant t\end{cases} $ | (13) |
| $ U_{2}(t)= \begin{cases}0 & t=0 \\ \sin \left(\frac{\pi}{2} \times \frac{t}{t_{4}}\right) & 0<t \leqslant t_{4} \\ \cos \left(\frac{\pi}{2} \times \frac{t-t_{4}}{t_{5}-t_{4}}\right) & t_{4}<t<t_{5} \\ 0 & t_{5} \leqslant t\end{cases} $ | (14) |
| $U_{3}(t)= \begin{cases}0 & t=0 \\ \frac{t}{t_{4}} & 0<t \leqslant t_{4} \\ \frac{t-t_{4}}{t_{5}-t_{4}} & t_{4}<t<t_{5} \\ 0 & t_{5} \leqslant t\end{cases} $ | (15) |

|
图 2 发射波形示意图 (a)梯形波;(b)半正弦波;(c)三角波 |
为确保时域麦克斯韦方程组解的唯一性及合理性,需给出初始条件和边界条件。由于下阶跃波在0时刻前保持稳定的电流,会在整个空间产生稳定的磁场,因此0时刻的初始条件为H(0)=H0,这里H0表示0时刻的磁场分布,0时刻的电场分布为E(0)=0。但是,梯形波、半正弦波和三角波在0时刻之前并未接通电流,所以在整个空间任意位置的初始磁场和电场分布均为0,即H(0)=0,E(0)=0。本文使用Dirichlet边界条件,假设求解区域外边界Г的切向电场分量为0,即E×n=0|Г,这里n表示Г的外法向方向向量。最后采用直接求解器PARDISO对离散后的方程组进行计算。
1.3 正确性验证本文程序运行平台为Inter i5四核处理器,主频为1.6GHz,内存为12GB。为了验证本文程序的正确性,建立图 3所示均匀半空间模型,对模型正演模拟得到的数值解与解析解进行对比。观测装置收—发纵向偏移距为5m,线圈面积为1m2,发射电流为1A。模拟区域径向均匀网格的最小尺度为0.3m,最大为3.0m,纵向均匀网格最小尺度为1.0m,最大为3.0m,在扩展区域以1.3为等比因子进行扩充。在电流断开1×10-6~1×10-2s内选取41个时间点进行观测,早期时间步长为1×10-8s,随时间的推移,逐渐增大时间步长。一次正演计算耗时175s。数值解和解析解的计算结果如图 4所示,纵轴dBz/dt表示垂直磁感应分量Bz关于时间的导数。分析图 4可知,解析解和数值解吻合较好,说明本文瞬变电磁计算方法是正确的。
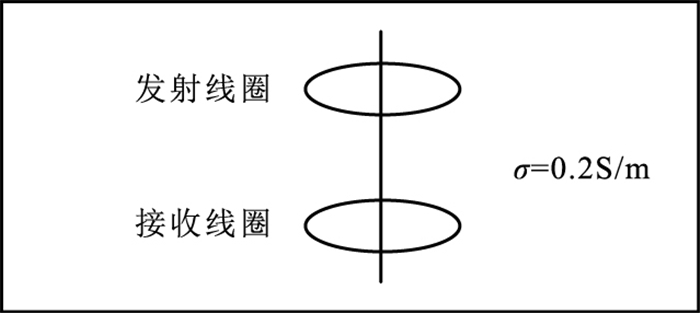
|
图 3 瞬变电磁均匀半空间模型 |
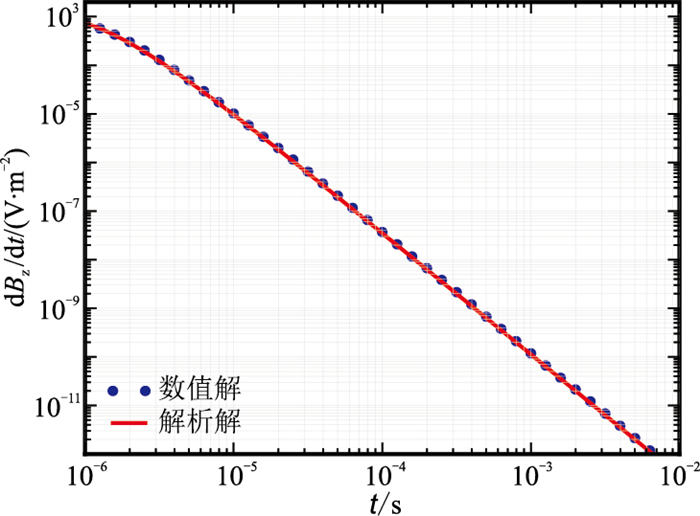
|
图 4 均匀半空间模型瞬变电磁响应 |
为了研究套管对瞬变电磁响应的影响,分别讨论套管电导率、相对磁导率、厚度和内径的响应特征。建立图 5a所示套管测井模型,采用图 5b所示套管井瞬变电磁装置,发射电流为5A。
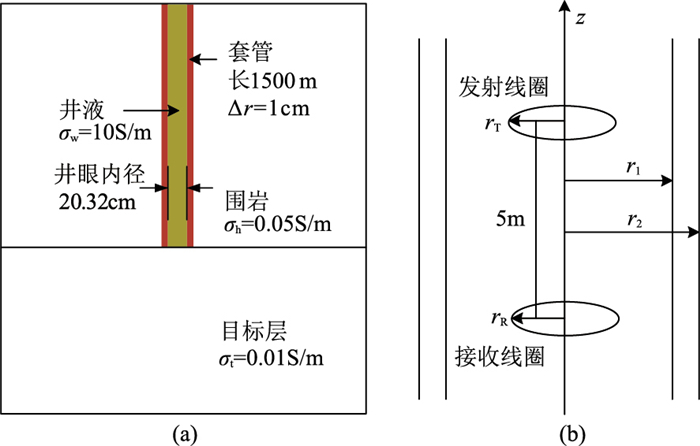
|
图 5 套管井模型(a)及瞬变电磁装置剖面示意图(b) r1、r2分别表示井眼内径和外径;Δr=r2-r1表示套管厚度;rT、rR分别表示发射线圈和接收线圈的半径,这里rT=rR=9.6cm;σh、σw、σt分别表示围岩、井液、目标层的电导率。 |
首先模拟不同套管电导率(σc)和相对磁导率μr(μr=μ/μ0,μ表示介质磁导率,μ0=4π×10-7H/m表示真空中的磁导率)条件下的瞬变电磁响应。μr=100,σc=1×105、5×105、1×106S/m的计算结果见图 6。由图可知,当其他参数不变时,σc越高,早期时间道的dBz/dt值越低,衰减越慢,衰减的时间也越长。σc=1×105S/m,μr=100、150、200的计算结果见图 7。可以看出,套管的μr越高,早期时间道上的响应信号幅值越低,信号衰减越慢。
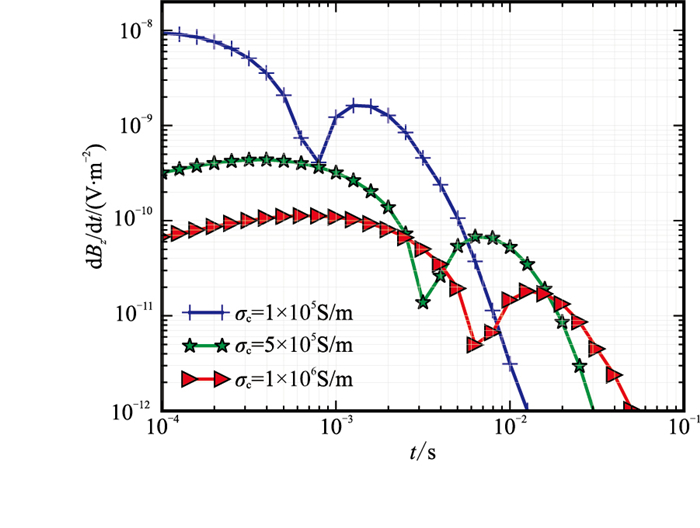
|
图 6 套管不同电导率σc下瞬变电磁响应曲线 |
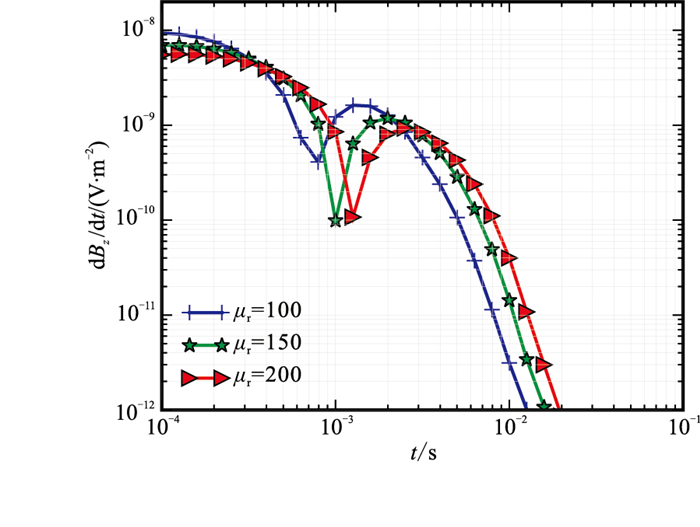
|
图 7 套管不同相对磁导率μr下瞬变电磁响应曲线 |
讨论了套管电导率和相对磁导率对瞬变电磁探测的影响后,假设其他参数不变,分析套管厚度Δr及内径r1对瞬变电磁响应信号的影响。
设套管电导率σc=1×105S/m,相对磁导率μr=100,套管厚度Δr分别为0.8、1.0、1.5cm的电磁响应计算结果见图 8。分析图 8可知,套管厚度越大,早期瞬变电磁响应信号越弱,且电磁响应信号衰减越慢。
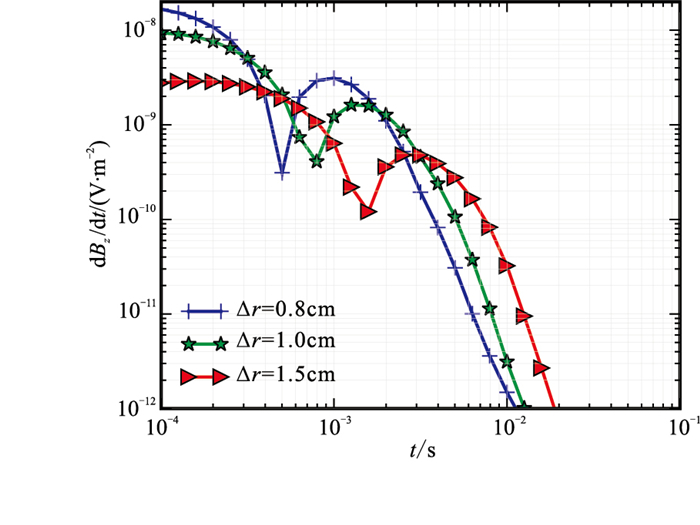
|
图 8 不同套管厚度Δr下瞬变电磁响应曲线 |
在其他参数不变的条件下,假设套管厚度Δr为1.0cm,内径r1分别为20.32、22.86、25.40cm时的响应曲线见图 9。可以看出,所有响应曲线的变化趋势一致,但套管内径r1越大,整个观测过程的信号幅值越低。
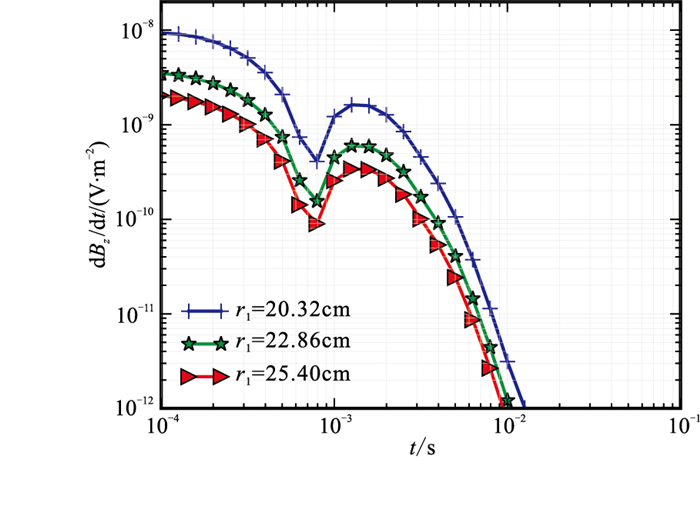
|
图 9 不同套管内径r1下瞬变电磁响应曲线 |
对瞬变电磁过套管响应特征的分析结果表明,对套管井进行瞬变电磁探测时,套管参数σc、μr、Δr、r1会对瞬态响应结果产生较强的影响,研究其如何影响电磁场是校正金属套管影响的基础。
2.2 不同发射波形响应特征分析采用上节基本模型研究不同发射波形(梯形波、半正弦波和三角波的波形)下的瞬变电磁套管井电磁响应特征。假设套管电导率σc=1×105S/m,相对磁导率μr=100,发射波形通电时间为6ms,其中梯形波的上升沿(0~t1)和下降沿(t2~t3)时长均为0.01ms,分别计算目标层电导率σt为0.20、0.01S/m时的电磁响应,结果见图 10。
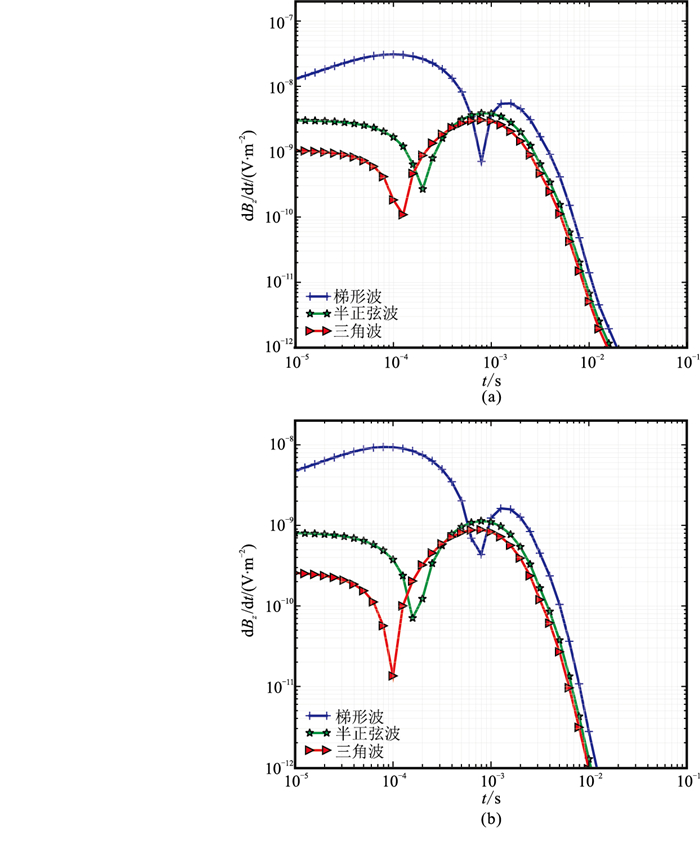
|
图 10 不同σt下瞬变电磁响应曲线 (a)σt=0.20S/m;(b)σt=0.01S/m |
对比图 10所示三种波形的响应曲线可知,电磁响应信号从高到低所对应的发射波形为梯形波、半正弦波和三角波。不同发射波形的响应信号特征受地下介质电导率的影响显著,且同种发射波形对高电导率目标层的响应信号强于低电导率目标层的响应信号。
2.3 梯形波各阶段响应特征分析在实际工作中,由于很难实现对发射电流的即开即断,所以分析梯形波各阶段电磁响应的差别对探测系统参数的设计具有重要意义。如图 2a所示,梯形波的供电过程包括三个阶段:开启阶段(0~t1)、稳定阶段(t1~t2)和关断阶段(t2~t3)。开启和关断过程中电流均会在地层中激发涡流,产生瞬变电磁信号,这些信号可能会相互叠加或相互抵消。电流断开后,利用观测装置测量地层中的感应信号并对其进行分析,可计算地层介质的地电信息。
假设目标层电导率σt为0.01S/m,开启时间t0和关断时长(t3-t2)均为0.1ms,其他参数不变,分别计算梯形波的稳定时长(t2-t1)为1、2、6、20、50ms时的瞬变电磁响应,结果见图 11。由图可知,在波形开启和关断时长固定的条件下,当波形稳定时长小于6ms时,稳定时长对响应结果的影响明显;当稳定时长大于6ms时,各时间道上测得的电磁响应结果基本不受影响。因此,在套管环境下开展瞬变电磁探测需设置合理的梯形波稳定时长,一方面要考虑探测效果,另一方面,稳定时长过长则需要更多的时间步长,会增加计算时间,在野外工作中也会增加能耗。
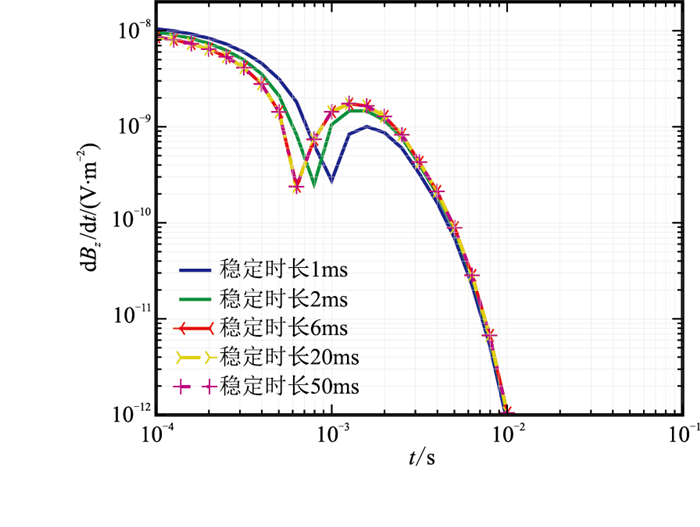
|
图 11 梯形波不同稳定时长的瞬变电磁响应曲线 |
假设梯形波的关断时长(t3-t2)为0.10ms,开启和稳定时长之和t2为6ms,其他参数不变,分别计算开启时间t1为0.01、0.10、1.00、2.00ms的电磁响应,结果见图 12。当然,波形稳定时长会随开启时间的增加而减少。由图 12可见,在波形开启和稳定时长总和不变的条件下,波形开启时间对电磁响应结果的影响差异很小,因此,在电流关断后进行观测时,可以忽略开启时间对电磁响应的影响。
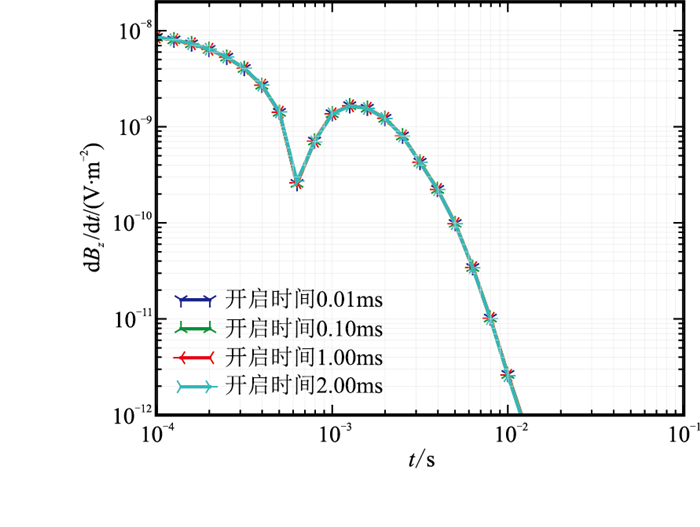
|
图 12 发射波形不同开启时间的瞬变电磁响应结果 |
发射波形的关断时间(t3-t2)是判断电磁探测设备性能的重要指标之一,因此,分析关断时间对电磁信号的影响非常重要。假设波形开启和稳定时间总和t2为6ms,开启时间t1为0.1ms,分别计算关断时间(t3-t2)为0.001、0.010、0.100、0.200ms的电磁响应,结果见图 13。分析图中衰减曲线可知:电流关断时间为0.010、0.100、0.200ms时,关断时间越短,早期时段观测信号越强,晚期时段观测信号曲线基本重合;关断时间为0.001ms与0.010ms的响应曲线几乎完全重合。可见,关断时间对响应信号的影响主要集中在早期,对晚期的影响很小,而早期电磁信号反映的是浅层信息,因此开展瞬变电磁勘探时,设计合理的梯形波关断时间尤为重要。
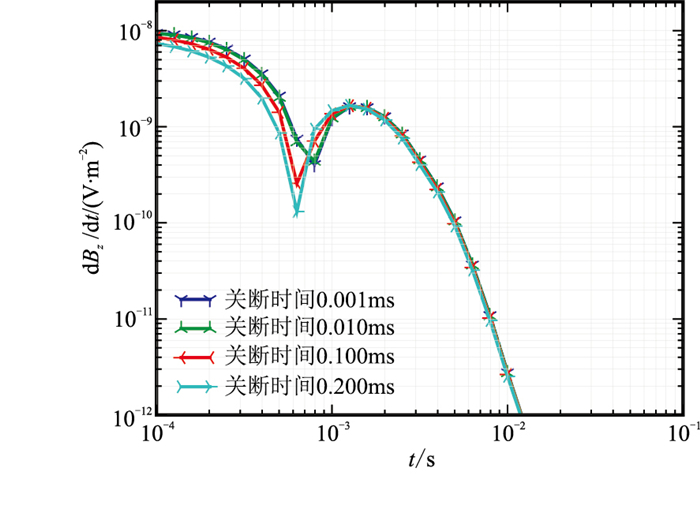
|
图 13 梯形波不同关断时间的瞬变电磁响应曲线 |
本文基于圆柱坐标系开展套管井瞬变电磁建模,运用有限体积法和后向欧拉法分别进行空间和时间离散,最终通过求解时域麦克斯韦方程组得到三维瞬变电磁过套管电磁响应。分别针对套管的电导率、相对磁导率、厚度和内径等参数对电磁场响应的影响特征进行分析,为瞬变电磁过套管数据的处理及探测装置参数的设计提供了技术支撑,得到如下结论。
(1) 套管的电导率越高或相对磁导率越大,三维瞬变电磁过套管响应信号的衰减时间越长,早期的响应幅值越低;套管的内径或厚度越大,早期的响应信号幅值越低。
(2) 发射波采用梯形波形、半正弦波形和三角波形,所对应的套管井瞬变电磁响应信号逐次减弱。
(3) 发射波采用梯形波形且波形开启和关断时间固定时,随稳定时间的增加,早期时间道上的电磁响应信号减弱,当稳定时间足够长时,稳定时间的变化对电磁响应的影响逐渐减弱;波形开启和稳定时间之和固定时,波形开启时间的长短对电磁响应的影响不大,可以忽略;发射波形的关断时间对电磁响应的影响主要集中在早期,对晚期电磁响应的影响较小。
| [1] |
袁习勇, 邓少贵, 胡旭飞, 等. 瞬变电磁波测井边界远探测方法研究[J]. 地球物理学报, 2020, 63(7): 2751-2761. YUAN Xiyong, DENG Shaogui, HU Xufei, et al. Detection of the remote boundary using the transient electromagnetic logging method[J]. Chinese Journal of Geophysics, 2020, 63(7): 2751-2761. |
| [2] |
KAUFMAN A A, KELLER G V. Frequency and Transient Soundings[M]. New York: Elsevier Scientific Pub. Co., 1983.
|
| [3] |
ANDERSON B, CHEW W C. Transient response of some borehole mandrel tools[J]. Geophysics, 1989, 54(2): 216-224. DOI:10.1190/1.1442645 |
| [4] |
周仕新, 岳建华. 巷道围岩中瞬变电磁场三维数值模拟[J]. 物探与化探, 2005, 29(6): 533-536, 540. ZHOU Shixin, YUE Jianhua. Numerical three-dimensional simulation of transient electromagnetic field in roadway and its surrounding rocks[J]. Geophysical and Geochemical Exploration, 2005, 29(6): 533-536, 540. DOI:10.3969/j.issn.1000-8918.2005.06.015 |
| [5] |
BANNING E J, HAGIWARA T, OSTERMEIER R M. Imaging of a subsurface conductivity distribution using a time-domain electromagnetic borehole conveyed logging tool[C]. SEG Technical Program Expanded Abstracts, 2007, 26: 648-652.
|
| [6] |
ONEGOVA E V. Effect of multicoil electromagnetic tool eccentricity on measured signals[J]. Russian Geology and Geophysics, 2010, 51(4): 423-427. DOI:10.1016/j.rgg.2010.03.009 |
| [7] |
HAGIWARA T. Transient tri-axial induction mea-surements: apparent dip and apparent anisotropy[C]. SEG Technical Program Expanded Abstracts, 2011, 30: 417-421.
|
| [8] |
李建慧, 刘树才, 焦险峰, 等. 地—井瞬变电磁法三维正演研究[J]. 石油地球物理勘探, 2015, 50(3): 556-564. LI Jianhui, LIU Shucai, JIAO Xianfeng, et al. Three-dimensional forward modeling for surface-borehole transient electromagnetic method[J]. Oil Geophysical Prospecting, 2015, 50(3): 556-564. |
| [9] |
COMMER M, HOVERSTEN G M, UM E S. Tran-sient-electromagnetic finite-difference time-domain earth modeling over steel infrastructure[J]. Geophy-sics, 2015, 80(2): E147-E162.. |
| [10] |
SWIDINSKY A, WEISS C J. On coincident loop transient electromagnetic induction logging[J]. Geophysics, 2017, 82(4): E211-E220. DOI:10.1190/geo2017-0134.1 |
| [11] |
李建慧, 胡祥云, 陈斌, 等. 复杂形态回线源激发电磁场的矢量有限元解[J]. 石油地球物理勘探, 2017, 52(6): 1324-1332. LI Jianhui, HU Xiangyun, CHEN Bin, et al. 3D electromagnetic modeling with vector finite element for a complex-shaped loop source[J]. Oil Geophysical Prospecting, 2017, 52(6): 1324-1332. |
| [12] |
段书新, 汪硕, 乔宝强, 等. 井中瞬变电磁旁测范围初探[J]. 地球物理学进展, 2018, 33(4): 1480-1485. DUAN Shuxin, WANG Shuo, QIAO Baoqiang, et al. Side measurement range of bore hole transient electromagnetic method[J]. Progress in Geophysics, 2018, 33(4): 1480-1485. |
| [13] |
MENG Q X, HU X Y, PAN H P, et al. Apparent resistivity for transient electromagnetic induction logging and its correction in radial layer identification[J]. Journal of Applied Geophysics, 2018, 151: 328-342. DOI:10.1016/j.jappgeo.2018.03.001 |
| [14] |
陈卫营, 韩思旭, 薛国强. 电性源地—井瞬变电磁法全分量响应特性与探测能力分析[J]. 地球物理学报, 2019, 62(5): 1969-1980. CHEN Weiying, HAN Sixu, XUE Guoqiang. Analysis on the full-component response and detectability of electric source surface-to-borehole TEM method[J]. Chinese Journal of Geophysics, 2019, 62(5): 1969-1980. |
| [15] |
郭建磊, 姜涛, 郭恒, 等. 轴向各向异性地—井瞬变电磁三分量响应特征[J]. 地球科学与环境学报, 2020, 42(6): 737-748. GUO Jianlei, JIANG Tao, GUO Heng, et al. Characteristics of axial anisotropic borehole transient electromagnetic three-component response[J]. Journal of Earth Sciences and Environment, 2020, 42(6): 737-748. |
| [16] |
UM E S, HARRIS J M, ALUMBAUGH D L. 3D time-domain simulation of electromagnetic diffusion phenomena: a finite-element electric-field approach[J]. Geophysics, 2010, 75(4): F115-F126. DOI:10.1190/1.3473694 |
| [17] |
UM E S, COMMER M, NEWMAN G A, et al. Finite element modelling of transient electromagnetic fields near steel-cased wells[J]. Geophysical Journal International, 2015, 202(2): 901-913. DOI:10.1093/gji/ggv193 |
| [18] |
WANG T, HOHMANN G W. A finite-difference, time-domain solution for three-dimensional electromagnetic modeling[J]. Geophysics, 1993, 58(6): 797-809. DOI:10.1190/1.1443465 |
| [19] |
COMMER M, NEWMAN G A. An accelerated time domain finite difference simulation scheme for three-dimensional transient electromagnetic modeling using geometric multigrid concepts[J]. Radio Science, 2006, 41(3): 1-15. |
| [20] |
许洋铖, 林君, 李肃义, 等. 全波形时间域航空电磁响应三维有限差分数值计算[J]. 地球物理学报, 2012, 55(6): 2105-2114. XU Yangcheng, LIN Jun, LI Suyi, et al. Calculation of full-waveform airborne electromagnetic response with three-dimension finite-difference solution in time-domain[J]. Chinese Journal of Geophysics, 2012, 55(6): 2105-2114. |
| [21] |
殷长春, 任秀艳, 刘云鹤, 等. 航空瞬变电磁法对地下典型目标体的探测能力研究[J]. 地球物理学报, 2015, 58(9): 3370-3379. YIN Changchun, REN Xiuyan, LIU Yunhe, et al. Exploration capability of airborne TEM systems for ty-pical targets in the subsurface[J]. Chinese Journal of Geophysics, 2015, 58(9): 3370-3379. |
| [22] |
陈丁, 程久龙, 王阿明. 矿井全空间孔中瞬变电磁响应积分方程法数值模拟研究[J]. 地球物理学报, 2018, 61(10): 4182-4193. CHEN Ding, CHENG Jiulong, WANG Aming. Numerical simulation of drillhole transient electromagnetic response in mine roadway whole space using integral equation method[J]. Chinese Journal of Geophysics, 2018, 61(10): 4182-4193. DOI:10.6038/cjg2018L0752 |
| [23] |
周建美, 刘文韬, 李貅, 等. 双轴各向异性介质中回线源瞬变电磁三维拟态有限体积正演算法[J]. 地球物理学报, 2018, 61(1): 368-378. ZHOU Jianmei, LIU Wentao, LI Xiu, et al. Research on the 3D mimetic finite volume method for loop-source TEM response in biaxial anisotropic formation[J]. Chinese Journal of Geophysics, 2018, 61(1): 368-378. |
| [24] |
刘亚军, 胡祥云, 彭荣华, 等. 回线源瞬变电磁法有限体积三维任意各向异性正演及分析[J]. 地球物理学报, 2019, 62(5): 1954-1968. LIU Yajun, HU Xiangyun, PENG Ronghua, et al. 3D forward modeling and analysis of the loop-source transient electromagnetic method based on the finite-volume method for an arbitrarily anisotropic medium[J]. Chinese Journal of Geophysics, 2019, 62(5): 1954-1968. |
| [25] |
齐彦福, 殷长春, 刘云鹤, 等. 基于瞬时电流脉冲的三维时间域航空电磁全波形正演模拟[J]. 地球物理学报, 2017, 60(1): 369-382. QI Yanfu, YIN Changchun, LIU Yunhe, et al. 3D time-domain airborne EM full-wave forward modeling based on instantaneous current pulse[J]. Chinese Journal of Geophysics, 2017, 60(1): 369-382. |
| [26] |
赵越, 许枫, 李貅, 等. 浅海瞬变电磁全波形响应特征及探测能力分析[J]. 地球物理学报, 2019, 62(4): 1526-1540. ZHAO Yue, XU Feng, LI Xiu, et al. Exploration capability of transmitter current waveform on shallow water TEM response[J]. Chinese Journal of Geophysics, 2019, 62(4): 1526-1540. |
| [27] |
ZENG S H, HU X Y, LI J H, et al. Effects of full transmitting-current waveforms on transient electromagnetics: insights from modeling the Albany graphi-te deposit[J]. Geophysics, 2019, 84(4): E255-E268. DOI:10.1190/geo2018-0573.1 |
| [28] |
JI Y J, ZHU Y, YU M M, et al. Calculation and application of full-wave airborne transient electromagnetic data in electromagnetic detection[J]. Journal of Central South University, 2019, 26(4): 1011-1020. DOI:10.1007/s11771-019-4067-x |
| [29] |
唐大荣, 张文梁, 崔李丽. 计算直流电测深曲线的有限差分法[J]. 石油地球物理勘探, 1982, 17(4): 65-72. TANG Darong, ZHANG Wenliang, CUI Lili. Finite difference method for calculating D.C.sounding curve[J]. Oil Geophysical Prospecting, 1982, 17(4): 65-72. |



 赵宁,河南省焦作市山阳区世纪大道2001号河南理工大学物理与电子信息学院,454000。Email:
赵宁,河南省焦作市山阳区世纪大道2001号河南理工大学物理与电子信息学院,454000。Email: 