② 核资源与环境国家重点实验室(东华理工大学),江西南昌 330013
② State Key Laboratory of Nuclear Resources and Environment, East China University of Technology, Nanchang, Jiangxi 330013, China
地空频率域电磁法是一种快速有效的电法勘探手段,通过在地面布设电性或者磁性激励源,利用飞行平台在空中接收频率域磁场信号,对地下地质体进行电磁信息研究。该方法具有地面大功率发射、空中非接触式快速测量的优点,具备探测范围大、深度大、探测迅速的能力,其探测效果接近于地面电磁法[1-3]。近年来,随着仪器设备和飞行平台性能的快速发展,各种地空电磁勘探系统得到迅速发展,如基于直升机平台的FLAIRTEM(fixed loop airborne transient electromagnetics)[4]、GREATEM (grou-nded electrical-source airborne transient electro-magnetic)[5-8]、无人飞艇地空电磁探测系统[9]及无人机地空瞬变电磁系统[10]等。随着三分量一体磁场传感器接收技术的日渐成熟,空中三分量磁场测量技术逐步发展,如天然场源的Z-TEM(Z-axis tipper electromagnetic,天然源频率域航空电磁法)系统[11]和Mobile-MT(Mobile electromagnetic)系统[12]。目前频率域地空电磁法数据的处理与解释主要聚焦于单一分量的响应特征研究、视电阻率定义、数据成像与反演等方面[13-15],对多分量磁场观测系统的研究甚少。对于地面电磁勘探系统,可通过研究磁场三分量间的关系得到倾子响应,倾子作为地面频率域电磁法数据处理和解释的重要参数,是提升分辨率和精度的关键。胡文宝等[16]研究了大地电磁勘探中倾子响应特征,结果表明倾子能够反映地下结构的电性横向不均匀性;Berdichevsky等[17]对二维地电模型的倾子资料进行了系统的分析,发现与视电阻率、阻抗相对比,倾子受大地电磁静态位移的影响较小;席振铢[18]定义了人工源频率倾子的概念,利用人工场源激励能够克服天然电磁场信号弱、随机性强、激化不稳定的缺陷,验证了人工源频率域倾子测深法的可行性;邓居智等[19]通过数值模拟研究了三维条件下的大地电磁倾子响应特征,认为利用倾子可有效提高电磁法对地下异常体的横向分辨能力;吴頔等[20]通过分析二维地电模型倾子响应,进一步证明了倾子能够较好地反映地下电性异常体的横向分布;余年等[21]通过有限元法实现了大地电磁二维倾子正演计算,对异常体倾子响应特征的分析表明了倾子对异常体的横向边界反映清楚、纵向边界反映不明显。
综上所述,由于大地电磁倾子横向分辨高、纵向分辨率低,因而对倾子的研究主要集中于方法的横向分辨率,而忽略其测深能力。然而,最新研究表明,可控源电磁倾子不同于大地电磁倾子,前者具备较强的测深能力,但目前尚缺乏对其测深能力和纵向分辨率的系统研究[22]。
近年来,一些学者将倾子参数应用于航空电磁法,提出了航空天然场电磁观测系统[11]。本文以地空电磁法为基础,参照倾子定义方式,提出一种新型地空频率倾子测深法(SAFTSM),推导了有限长接地线源激发下的倾子一维正演公式,并编程实现其方法。本文通过不同层状模型数值模拟分析了地空频率域倾子的响应特征,探讨该方法的测深能力,为地空频率域电磁法的发展提供了理论基础。
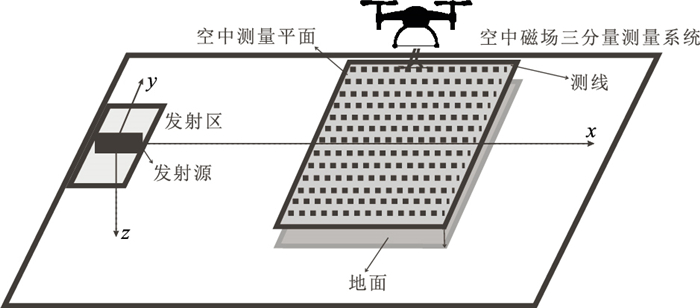
1 方法原理 1.1 方法理论地空频率倾子测深法采用地面大功率发射、空中接收三分量磁场,基于磁场各分量之间的关系分析地下电性结构(图 1)。该方法由地面长导线发射源激励信号,飞行器搭载磁场三分量(Hx、Hy、Hz)测量系统,沿平行于发射源方向的测线飞行,观测10~105Hz的三分量磁信号,以实现大范围、面积性磁场测量,最大勘探深度可达1km。
|
图 1 地空频率倾子测深法工作示意图(据文献[15]修改) |
参照大地电磁法张量倾子的定义,将地空频率倾子T=[Tx Ty]定义为磁场垂直分量与水平分量的比值,有
| $ H_{z}=\boldsymbol{T H}_{\mathrm{n}} $ | (1) |
式中:Hz是地空电磁系统采集的垂直磁场分量;Hn=[Hx Hy]T是地空电磁系统采集的水平磁场分量,其中Hx、Hy分别代表磁场在x、y方向上的分量。将式(1)展开为矩阵形式
| $ H_{z}=\left[\begin{array}{ll} T_{x} & T_{y} \end{array}\right]\left[\begin{array}{l} H_{x} \\ H_{y} \end{array}\right]=T_{x} H_{x}+T_{y} H_{y} $ | (2) |
| $ \left\{\begin{array}{l} T_{x}=\frac{\left|H_{z}\right|}{\left|H_{x}\right|} \\ T_{y}=\frac{\left|H_{z}\right|}{\left|H_{y}\right|} \end{array}\right. $ | (3) |
建立图 2所示地空频率域电磁探测一维均匀水平层状模型,采用直角坐标系,z轴垂直地面向下。各层电阻率表示为ρn(n=1, 2, …),对应的层厚度为hn,这里n表示地层数。电偶极子源布设在地面(z=0),源的中心位于坐标原点O,沿x轴正方向布设,长度为dl,发射电流为I。挂载接收系统的飞行器飞行高度为zF。根据朴化荣[23]推导的电偶极子源磁场表达式可得空中磁场表达式为
| $ \left\{ \begin{array}{l} H_{x}=\frac{I \mathrm{~d} l}{2 {\rm{ \mathsf{ π} }}} \sin \varphi \cos \varphi \int_{0}^{\infty} \frac{\lambda^{2}}{\lambda+\frac{u_{1}}{R}} \mathrm{e}^{\lambda z_{\mathrm{F}}} J_{0}(\lambda r) \mathrm{d} \lambda-\\ \ \ \ \ \ \ \ \ \ \frac{I \mathrm{~d} l}{2 {\rm{ \mathsf{ π} }}} \frac{\sin \varphi \cos \varphi}{r} \int_{0}^{\infty} \frac{2 \lambda}{\lambda+\frac{u_{1}}{R}} \mathrm{e}^{\lambda z_{\mathrm{F}}} J_{1}(\lambda r) \mathrm{d} \lambda\\ H_{y}= \frac{I \mathrm{~d} l}{2 {\rm{ \mathsf{ π} }}} \sin ^{2} \varphi \int_{0}^{\infty} \frac{\lambda^{2}}{\lambda+\frac{u_{1}}{R}} \mathrm{e}^{\lambda z_{\mathrm{F}}} J_{0}(\lambda r) \mathrm{d} \lambda+\\ \ \ \ \ \ \ \ \ \ \frac{I \mathrm{~d} l}{2 {\rm{ \mathsf{ π} }}} \frac{\cos ^{2} \varphi-\sin ^{2} \varphi}{r} \int_{0}^{\infty} \frac{\lambda}{\lambda+\frac{u_{1}}{R}} \mathrm{e}^{\lambda z_{\mathrm{F}}} J_{1}(\lambda r) \mathrm{d} \lambda \\ H_{z}=\frac{I \mathrm{~d} l}{2 {\rm{ \mathsf{ π} }}} \sin \varphi \int_{0}^{\infty} \frac{\lambda^{2}}{\lambda+\frac{u_{1}}{R}} \mathrm{e}^{\lambda z_{\mathrm{F}}} J_{1}(\lambda r) \mathrm{d} \lambda\\ R=\operatorname{cth}\left[u_{1} h_{1}+\operatorname{arcth} \frac{u_{1}}{u_{2}} \operatorname{cth}\left(u_{2} h_{2}+\cdots+\operatorname{arcth} \frac{u_{n-1}}{u_{n}}\right)\right] \end{array} \right. $ | (4) |

|
图 2 频率域地空电磁探测一维层状模型 |
式中:Idl为电偶极矩;r是测点P在地面上的投影点P0距电偶极子中点的距离,即偏移距;φ是连线OP0与x轴的夹角;λ表示波长;
将式(4)代入式(3),可得层状介质模型的空中倾子表达式
| $\left\{\begin{aligned} T_{x} &=\frac{\left|H_{z}\right|}{\left|H_{x}\right|}=\frac{r F_{1}(\lambda)}{\cos \varphi\left[r F_{3}(\lambda)-2 F_{2}(\lambda)\right]} \\ T_{y} &=\frac{\left|H_{z}\right|}{\left|H_{y}\right|} \\ &=\frac{r F_{1}(\lambda)}{2\left(\cos ^{2} \varphi-\sin ^{2} \varphi\right) F_{2}(\lambda)-r \sin ^{2} \varphi F_{3}(\lambda)} \end{aligned}\right. $ | (5) |
其中
| $ \left\{\begin{array}{l} F_{1}(\lambda)=\int_{0}^{\infty} \frac{\lambda^{2}}{\lambda+\frac{u_{1}}{R}} \mathrm{e}^{\lambda z_{\mathrm{F}}} J_{1}(\lambda r) \mathrm{d} \lambda \\ F_{2}(\lambda)=\int_{0}^{\infty} \frac{\lambda}{\lambda+\frac{u_{1}}{R}} \mathrm{e}^{\lambda z_{\mathrm{F}}} J_{1}(\lambda r) \mathrm{d} \lambda \\ F_{3}(\lambda)=\int_{0}^{\infty} \frac{\lambda^{2}}{\lambda+\frac{u_{1}}{R}} \mathrm{e}^{\lambda z_{\mathrm{F}}} J_{0}(\lambda r) \mathrm{d} \lambda \end{array}\right. $ |
从式(4)和式(5)可以看出,对于水平层状介质模型,垂直磁场和水平磁场分量具有相同的电流项(Idl/2π),计算倾子时,两者的电流项可约除,因此地空频率域倾子对发射源的电偶距和电流变化灵敏度较低,仅与收发点的空间几何关系有关。但在三维地质模型和场源条件复杂的情况下,场源电流大小对倾子的影响不可忽略。为此,基于传统地空频率域电磁法具有受场源形态和发射电流影响小的特点,地空频率倾子测深法只要能够观测到足够强的三分量磁场,就可无需记录场源信息,这在一定程度上提高了地空频率域电磁法的探测精度。
在实际工作中,接地长导线发射源长达数千米,不能将其视为电偶极子,因此采用剖分→叠加→求和的方法,即将发射源等距剖分为m段,分别计算m个电偶极子在P点产生的地空频率倾子响应,再将所有的电偶极子在P点的倾子响应叠加,其结果可近似为接地长导线发射源在P点的倾子响应,即
| $ \left\{\begin{array}{l} T_{x}=\sum\limits_{i=1}^{m} T_{x}^{i}=\sum\limits_{i=1}^{m} \frac{\left|H_{z}^{i}\right|}{\left|H_{x}^{i}\right|} \\ T_{y}=\sum\limits_{i=1}^{m} T_{y}^{i}=\sum\limits_{i=1}^{m} \frac{\left|H_{z}^{i}\right|}{\left|H_{y}^{i}\right|} \end{array}\right. $ | (6) |
将式(5)代入式(6)即得到层状大地模型地空频率域倾子的表达式。式(6)主要包括两部分,第一部分为汉克尔积分,第二部分为电偶极子倾子响应的叠加。令汉克尔积分表达式为
| $ F(\xi)=\int_{0}^{\infty} G(\xi) J_{v}(\xi r) \mathrm{d} \xi \quad v=0, 1 $ | (7) |
式中G为核函数。由于上式中的贝塞尔函数是高频振荡慢衰减函数,汉克尔积分难以得到解析解,因此采用数值积分算法进行计算。本文采用Gupta-sarma等[24]提出的线性数值滤波方法,其计算公式为
| $ r f(r)=\sum\limits_{j=-d}^{d} G\left(\xi_{j}\right) W_{j} $ | (8) |
| $ \xi_{j}=\frac{10[a+(j-1) s]}{r} $ | (9) |
式中:d为积分区间长度;a为积分常数;ξj为抽样点的位置;Wj为滤波系数;s为积分因子,本文用241点滤波系数进行快速汉克尔数值滤波计算。
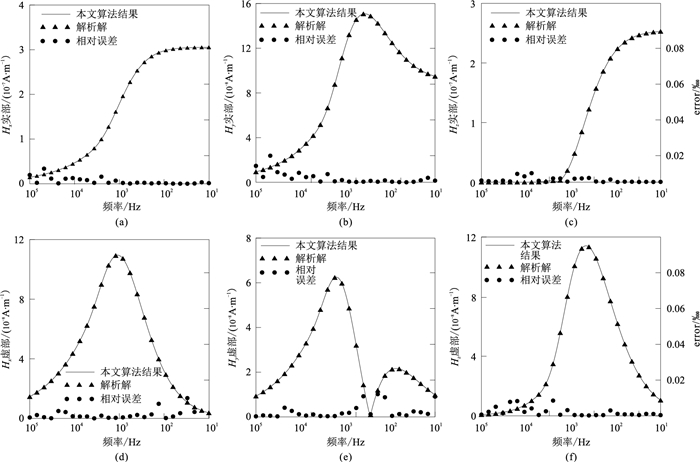
1.2 算法验证目前未见关于人工源地空电磁倾子正演模拟研究的相关文献,因此无法通过对比方式验证算法的准确性,但倾子是由三个磁场分量计算得来的,因此只需验证三个磁场分量的准确性就能验证倾子计算的准确性。为此,设计均匀半空间模型,模拟计算其磁分量,并与电偶极子在均匀大地地表处频率域磁场的三分量解析解对比,解析解见文献[25]。假设均匀半空间模型的电阻率为100Ω·m,电偶极子中心点位于坐标原点,接收点位于地面,坐标为(300m, 400m, 0),计算频率为10~105Hz。图 3为均匀半空间模型磁场三分量一维正演结果与解析解的对比。采用下式计算相对误差
| $ \text { error }=\frac{\left|H_{\mathrm{a}}-H_{0}\right|}{H_{0}} \times 100 \% $ |
|
图 3 均匀半空间模型地表频率域三分量磁场本文方法计算结果、解析解及其相对误差 (a)、(d)Hx实部、虚部;(b)、(e)Hy实部、虚部;(c)、(f)Hz实部、虚部 |
式中:Ha代表本文算法计算的电磁场响应;H0代表解析解结果。由图 3可见,不论实部还是虚部,磁场三分量一维模拟结果与解析解基本吻合,两者相对误差error远小于1%,验证了本文倾子算法的准确性。
2 均匀半空间模型倾子响应特征 2.1 不同频率下倾子平面分布特征为研究地空频率倾子响应特征,分析地空频率倾子在不同频率下的扩散、分布规律,设计电阻率为10Ω·m的均匀半空间模型进行模拟。接地长导线发射源中心位于直角坐标系的原点,长度为1km,沿x轴正方向布设,飞行高度zF=50m。分别研究发射频率为10、1000Hz时的倾子平面分布特征。
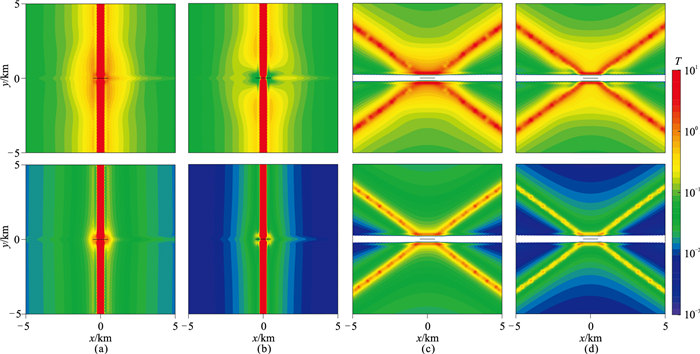
图 4是10Hz和1000Hz的地空倾子Tx和Ty的平面分布图。可以看出,1000Hz时倾子Tx的实部和虚部均沿场源中轴线y轴呈现对称分布;随着收发距增大,Tx幅值沿x轴方向快速衰减,沿y轴方向逐渐缓慢衰减,在远离源的区域逐渐趋于稳定。在场源中轴线附近,倾子Tx实部以x轴为中心向两边逐渐减小,并在场源轴线上出现高值畸变带,这是由于Hx在场源中轴线存在极小值。还可以看出,Ty的实部与虚部整体关于x轴和y轴对称,并随着收发距增大而快速衰减,较大收发距时场值在y轴两边沿x方向基本保持不变,出现稳定幅值的区域;沿场源方向出现极小值,在±38°方向存在“X”形高值畸变带,这是因为Hy场值在场源方向存在极大值,在±38°方向附近存在过渡带低值区。10Hz时倾子Tx和Ty变化规律与1000Hz的情况类似,仅有的区别是10Hz情况下的Tx和Ty分量的衰减慢于1000Hz的情况,变化更加平缓,这是因为高频磁场在有损介质中衰减更快。因此,为了减小场源的影响,开展半航空倾子观测时一般需设置较大的收发距,选择观测Tx分量,Ty在场源垂直方向±38°范围内测量。
|
图 4 频率为10Hz(上)和1000Hz(下)的倾子响应平面分布图 (a)、(b)Tx实部、虚部;(c)、(d)Ty实部、虚部。图中黑色线段表示接地长导线源。 |
从式(5)可以看出,地空频率域倾子测深法一维响应与接收点水平位置和飞行高度相关,为进一步分析测点位置影响规律,设计一个均匀半空间模型,电阻率为100Ω·m,电偶极子中点位于坐标原点,计算不同偏移距和不同飞行高度的倾子响应并分析其特征。
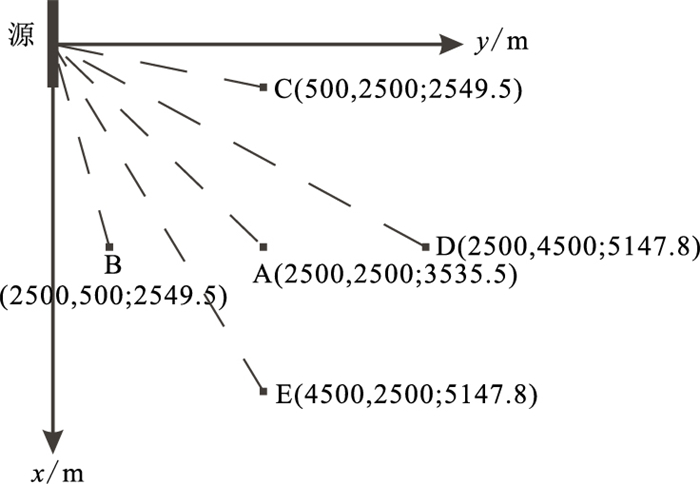
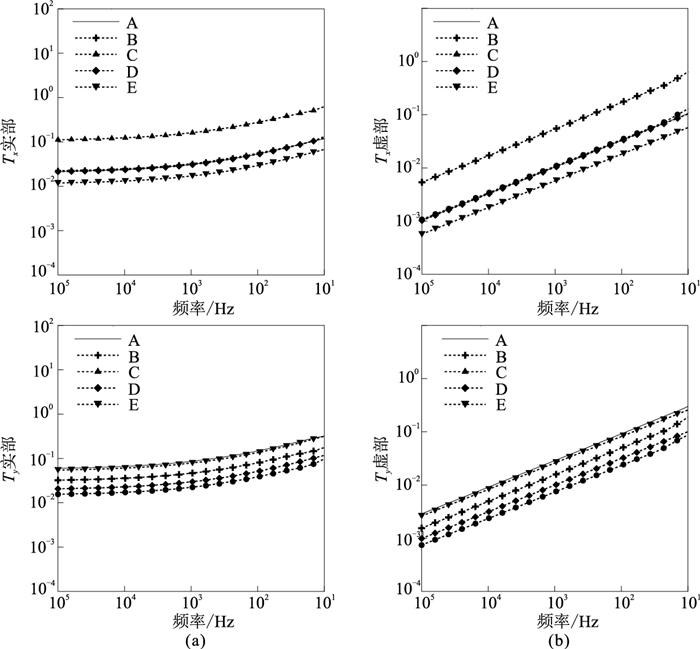
2.2.1 不同偏移距倾子响应特征为了全面分析不同测点位置的响应特征,考虑到倾子响应的对称性,仅在第一象限设计5个测点A、B、C、D、E(图 5),飞行高度均设置为50m。图 6为不同测点倾子响应的实部和虚部曲线,由图可见:在双对数坐标系下,随着频率的降低,倾子Tx与Ty的实部单调增加,虚部呈线性单调递增,斜率近似为0.5;随着偏移距的变化,不同测点的倾子曲线形态基本保持不变,但响应幅值随偏移距的增大而减小。还可以看出,由于倾子Tx响应主要沿场源平行方向快速衰减,而垂直场源方向衰减较慢,因而其响应在场源平行方向受偏移距的影响大于场源垂直方向,如观测点C、A、E;由于Ty分量在±38°方向存在“X”形高值畸变带,因此其响应幅值沿平行场源方向随偏移距的增大呈现先增大后减小的趋势。因此,开展地空频率域倾子测深野外施工时,需准确记录发射点和接收点的位置信息,同时在满足勘探深度的前提下采用尽可能小的收发距,以能保证观测信号的振幅足够强。
|
图 5 测点位置示意图 测点旁边标注的数据是测点在地面投影点的x、y坐标及投影点与坐标原点O的距离 |
|
图 6 不同测点倾子Tx(上)、Ty(下)响应曲线 (a)实部;(b)虚部 |
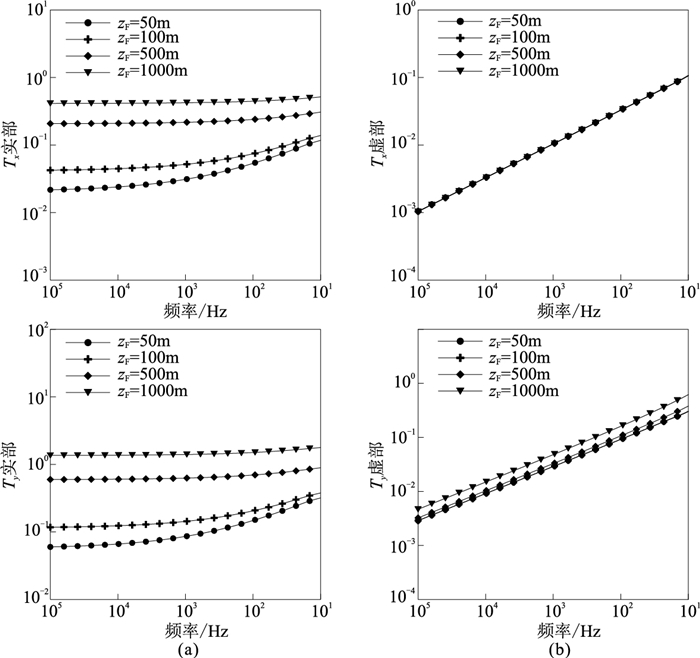
在地空电磁法中,将磁通门搭载在无人机上测量磁信号,由于磁信号在传播过程中会发生扩散,而且空气中分子对电磁波的吸收与折射会对磁信号产生衰减作用,因而测点高度也是影响测量磁信号的重要参数之一。考虑无人飞行器的飞行高度不大于1000m,这里分别取飞行高度为50、100、500、1000m,接收点在地面的投影位置为A点(图 5)。图 7为测点A在不同飞行高度zF下的倾子响应曲线。由图可见,不同接收高度下的倾子响应曲线趋势基本一致,即:倾子振幅随频率的降低而增大;在合理的飞行高度范围内,接收点越高,倾子幅值越大,这是由于磁场分量Hx、Hy的实部随高度的衰减较Hz分量更快,而各磁场分量的虚部随高度的衰减速度基本一致,且实部反映的是空中及沿地面传播的一次电磁场,而虚部反映的是感应(二次)电磁场,因此倾子虚部幅值受飞行高度的影响明显小于实部;当达到一定的飞行高度后,折射波(携带地层电性信息)衰减严重,空中接收到的磁场信号主要是不携带地层电性信息的天波。因而,开展时空频率倾子测深数据采集时应选择尽可能小的飞行高度。
|
图 7 不同接收高度的倾子Tx(上)、Ty(下)响应曲线 (a)实部;(b)虚部 |
为了分析地空频率倾子测深曲线特征,参照直流电阻率测深模型,设计典型的两层和三层地电模型进行倾子模拟,归纳和总结倾子测深法的响应特征,并定性分析倾子测深法的纵向分辨能力。
3.1 两层层状介质模型倾子响应特征设计一个一维两层层状介质地电模型,第一层电阻率ρ1为100Ω·m,厚度为100m;基底介质电阻率ρ2分别设为10、50、100(均匀半空间模型)、200、1000Ω·m,即分别研究D型(ρ1>ρ2)和G型(ρ1 < ρ2)两类地电模型;发射源中心点位于坐标原点,沿x轴正方向布设,长度为1km;飞行高度为50m;接收点地面坐标为(1000m,1000m)。
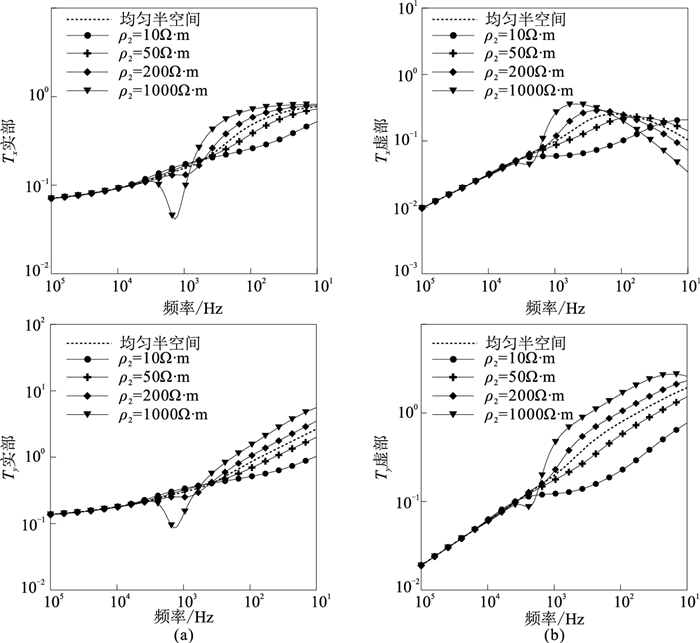
不同基底电阻率模型的倾子计算结果见图 8。可以看出,倾子响应曲线在高频部分基本重合、低频部分呈分散特征,这是由于高频信号反映的是模型的浅部电阻率信息,低频信号反映的是模型的深层电性特征,这说明地空频率倾子响应能够反映纵向上地层电阻率的变化。该模型倾子响应幅值整体上随频率的降低呈增大趋势,仅倾子Tx虚部响应幅值在中低频部分出现一定程度的衰减,这是由于磁场分量Hx虚部随频率的减小呈先减后增趋势;当基底电阻率(ρ2=10、50Ω·m)低于上层电阻率时,中低频段倾子响应幅值明显小于均匀半空间模型;当基底电阻率(ρ2=200、1000Ω·m)大于上层电阻率时,倾子曲线特征相对复杂,高频时曲线基本重合,随着频率减小,曲线逐渐分离,出现明显的幅值减小突变现象,实部响应突变程度较大,且上下两层介质电性差异越大,突变幅度越大,突变峰值点对应的频率也增大,这是由于电磁波在低阻介质折射进入高阻介质时,磁场各分量衰减速度不一致。以上分析说明地空频率倾子对地下电阻率的变化反映更灵敏。
|
图 8 两层介质模型不同ρ2时的倾子Tx(上)、Ty(下)响应曲线 (a)实部;(b)虚部 |
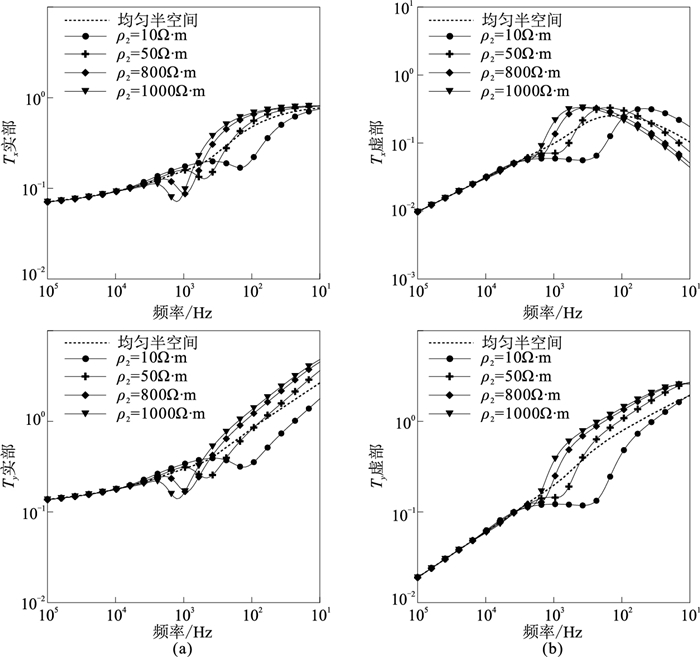
设计一个三层介质模型,上层介质和基底电阻率均为100Ω·m,上层和中间层厚度均为100m,设中间层电阻率ρ2=10、50、100(均匀半空间模型)、800、1000 Ω·m,场源的布设和测点位置同前述两层介质模型。不同中间层电阻率模型的倾子响应计算结果见图 9,可见整体三层模型的倾子响应幅值随频率的变化特征与两层介质模型相似,但前者在低频部分更趋于“聚集”,这是由于三层介质模型的基底电阻率不变。由于中间层电性异于围岩,倾子响应在中间频段出现不同程度幅值减小、突变的现象。当中间层电阻率(ρ2=10、50Ω·m)小于围岩时,倾子响应突变后幅值随频率减小而增大,且其幅值小于均匀半空间模型,最后曲线趋近于均匀半空间模型;当中间层电阻率大于围岩时(ρ2=800、1000Ω·m),倾子响应突变后幅值随频率减小而增大,其幅值大于均匀半空间模型,最后曲线亦趋近于均匀半空间模型。对比四个中间层电阻率变化模型的突变特征可以发现,低阻中间层模型突变出现的频率较高阻中间层模型出现的频率更低,且低阻中间层模型突变程度较高阻中间层模型更大。与均匀半空间模型曲线相比,中间层与围岩的电性差异越大,突变程度越大。以上分析说明地空频率倾子对不同中间层的电性变化表现出不同的响应特征,且地空频率倾子对低阻异常体反映更灵敏。
|
图 9 三层介质模型不同中间层电阻率下的倾子Tx(上)、Ty(下)响应曲线 (a)实部;(b)虚部 |
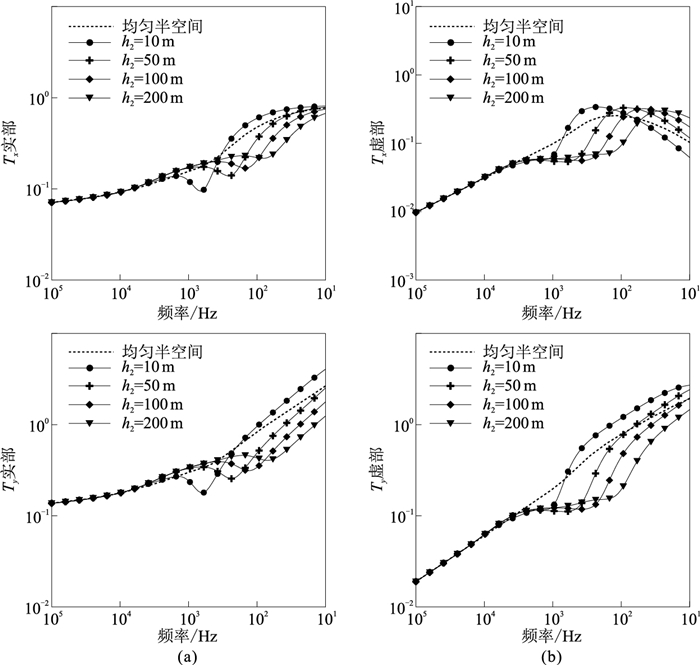
采用前述中间层电阻率ρ2=10 Ω·m的三层介质模型,设中间层厚度h2分别为10、50、100、200m,源的布设和测点位置不变。不同中间层厚度下的倾子响应正演结果见图 10。可以看出,中间层厚度变化时,除了倾子Tx的虚部响应在低频会出现幅值减小的趋势,其他倾子响应曲线的趋势基本相同,即幅值随频率的降低而增大。当中间低阻层厚度为10m时,倾子响应曲线与均匀半空间模型的倾子响应曲线差异较小;随着中间层厚度的增加,倾子响应曲线在中间频段与均匀半空间模型曲线的差异越来越大,由电性界面引起的突变出现的频率越低,且突变程度也越小,这是电磁波在介质中的趋肤深度不同引起的。对比倾子的实、虚部响应曲线可以发现,随着中间层厚度的增大,倾子虚部幅值的差异更大、更明显,因此倾子虚部响应对低阻中间层厚度的变化反应更灵敏。
|
图 10 三层介质模型中间层厚度变化下的倾子Tx(上)、Ty(下)响应曲线 (a)实部;(b)虚部 |
本文提出了一种地空频率倾子测深法,对不同发射频率、偏移距、飞行高度下的地空频率倾子响应进行分析,并对其开展了一维正演模拟,取得以下几点认识。
(1) 地空频率倾子响应沿场源方向和垂直方向基本呈现对称特征,整体上倾子幅值随收发距的增大而快速衰减,其中存在场源畸变和过渡带畸变现象。因而,地空频率域倾子测深法应观测平行于场源方向的Tx分量及与场源垂直方向夹角为±38°内的Ty分量,才能获得有效的倾子数据。
(2) 在中、远收发距内,观测点位置的变化基本不影响地空频率倾子响应曲线的形态,但幅值随收发距的增大而减小;飞行高度的变化基本不会影响倾子虚部振幅,但倾子实部幅值随飞行高度的增大而增大,同时折射波信息会衰减,因而飞行高度的增大会降低测深效果。因此,开展地空频率域倾子测深勘探时尽可能采用低空飞行测量,同时准确记录测点的平面位置和高程信息。
(3) 地空频率倾子响应能够有效反应地下介质电阻率的纵向变化,通过改变观测频率可达到测深目的,当地下存在电性异常体时,倾子响应会呈现“幅值减小、突变”现象,低阻异常体的倾子响应会出现“低幅值”现象,高阻异常体的倾子响应会呈现“高幅值”现象,且对低阻体的纵向分辨率高于高阻体。
| [1] |
SMITH R S, ANNAN A P, MCGOWAN P D. A comparison of data from airborne, semi-airborne, and ground electromagnetic systems[J]. Geophysics, 2001, 66(5): 1379-1385. DOI:10.1190/1.1487084 |
| [2] |
MA Z J, DI Q Y, LEI D, et al. The optimal survey area of the semi-airborne TEM method[J]. Journal of Applied Geophysics, 2020, 172: 103884. DOI:10.1016/j.jappgeo.2019.103884 |
| [3] |
WU X, XUE G Q, FANG G Y, et al. The development and applications of the semi-airborne electromagnetic system in China[J]. IEEE Access, 2019, 7: 104956-104966. DOI:10.1109/ACCESS.2019.2930961 |
| [4] |
ELLIOTT P. The principles and practice of FLAIRTEM[J]. Exploration Geophysics, 1998, 29(1/2): 58-59. |
| [5] |
MOGI T, KUSUNOKI K, KAIEDA H, et al. Grounded electrical-source airborne transient electromagnetic (GREATEM) survey of Mount Bandai, north-eastern Japan[J]. Exploration Geophysics, 2009, 40(1): 1-7. DOI:10.1071/EG08115 |
| [6] |
ITO H, KAIEDA H, MOGI T, et al. Grounded electrical-source airborne transient electromagnetics (GREATEM) survey of Aso Volcano, Japan[J]. Exploration Geophysics, 2014, 45(1): 43-48. DOI:10.1071/EG12074 |
| [7] |
ABD ALLAH S, MOGI T, ITO H, et al. Three-dimensional resistivity modelling of grounded electrical-source airborne transient electromagnetic (GREATEM) survey data from the Nojima Fault, Awaji Island, south-east Japan[J]. Exploration Geophysics, 2014, 45(1): 49-61. DOI:10.1071/EG12086 |
| [8] |
ABD ALLAH S, MOGI T. Three-dimensional resistivity modeling of GREATEM survey data from Ontake Volcano, northwest Japan[J]. Earth Planets and Space, 2016, 68(1): 76. DOI:10.1186/s40623-016-0443-z |
| [9] |
嵇艳鞠, 王远, 徐江, 等. 无人飞艇长导线源时域地空电磁勘探系统及其应用[J]. 地球物理学报, 2013, 56(11): 3640-3650. JI Yanju, WANG Yuan, XU Jiang, et al. Development and application of the grounded long wire source airborne electromagnetic exploration system based on an unmanned airship[J]. Chinese Journal of Geophysics, 2013, 56(11): 3640-3650. DOI:10.6038/cjg20131105 |
| [10] |
方涛, 张建军, 付成群, 等. 无人机地空瞬变电磁系统在冶山地下巷道探测中的应用[J]. 地球物理学进展, 2015, 30(5): 2366-2372. FANG Tao, ZHANG Jianjun, FU Chengqun, et al. Using ground-airborne transient electromagnetic system on unmanned aerial vehicle detecting Yeshan underground tunnels[J]. Progress in Geophysics, 2015, 30(5): 2366-2372. |
| [11] |
LO B, ZANG M. Numerical modeling of Z-TEM (airborne AFMAG) responses to guide exploration stra-tegies[C]. SEG Technical Program Expanded Abstracts, 2008, 27: 1098-1102.
|
| [12] |
SATTEL D, WITHERLY K, KAMINSKI V. A brief analysis of mobile MT data[C]. SEG Technical Program Expanded Abstracts, 2019, 38: 2138-2142.
|
| [13] |
张莹莹. 水平电偶源地空系统瞬变电磁法多分量解释技术及全域视电阻率定义研究[D]. 陕西西安: 长安大学, 2013.
|
| [14] |
李阳阳, 孙怀凤, 杨静, 等. 回线源半航空瞬变电磁响应规律[J]. 煤炭学报, 2019, 44(增刊1): 631-642. LI Yangyang, SUN Huaifeng, YANG Jing, et al. Three-dimensional modeling of semi-airborne tran-sient electromagnetic with loop source[J]. Journal of China Coal Society, 2019, 44(S1): 631-642. |
| [15] |
刘长胜, 朱文杰, 马金发, 等. 地空频率域电磁法探测范围与深度分析[J]. 中国矿业大学学报, 2020, 49(5): 1006-1012. LIU Changsheng, ZHU Wenjie, MA Jinfa, et al. Analysis of detection range and depth of ground-airborne frequency domain electromagnetic method[J]. Journal of China University of Mining & Technology, 2020, 49(5): 1006-1012. |
| [16] |
胡文宝, 苏朱刘, 陈清礼, 等. 倾子资料的特征及应用[J]. 石油地球物理勘探, 1997, 32(2): 202-213. HU Wenbao, SU Zhuliu, CHEN Qingli, et al. Character of tipper data and the application[J]. Oil Geophysical Prospecting, 1997, 32(2): 202-213. |
| [17] |
BERDICHEVSKY M N, DMITRIEV V I, GO-LUBTSOVA N S, et al. Magnetovariational sounding: new possibilities[J]. Izvestiya-Physics of the Solid Earth, 2003, 39(9): 701-727. |
| [18] |
席振铢. 人工源频率倾子测深法[D]. 湖南长沙: 中南大学, 2013.
|
| [19] |
邓居智, 蓝泽鸾, 陈辉, 等. 大地电磁倾子资料的三维正演研究[J]. 地球物理学进展, 2015, 30(4): 1666-1672. DENG Juzhi, LAN Zeluan, CHEN Hui, et al. Research on the 3D magnetotelluric tipper forward mo-deling[J]. Progress in Geophysics, 2015, 30(4): 1666-1672. |
| [20] |
吴頔, 严家斌, 贺文根. 倾子对异常体的分辨能力及影响因素研究[J]. 地球物理学进展, 2012, 27(6): 2656-2663. WU Di, YAN Jiabin, HE Wengen. Study on distinguishing to anomalous bodies by tipper & influencing factor of tipper[J]. Progress in Geophysics, 2012, 27(6): 2656-2663. |
| [21] |
余年, 胡祥云, 王绪本, 等. 大地电磁二维倾子和视倾子模拟及其应用研究[J]. 西南交通大学学报, 2014, 49(2): 268-275. YU Nian, HU Xiangyun, WANG Xuben, et al. Two-dimensional magnetotelluric tipper and apparent tipper: simulation and application[J]. Journal of Southwest Jiaotong University, 2014, 49(2): 268-275. |
| [22] |
徐凤姣, 严良俊, 周磊. 可控源电磁法倾子响应的三维正演[J]. 科学技术与工程, 2019, 19(20): 143-150. XU Fengjiao, YAN Liangjun, ZHOU Lei. Three-dimensional forward for the tipper response of the controlled source electromagnetic method[J]. Science Technology and Engineering, 2019, 19(20): 143-150. |
| [23] |
朴化荣. 电磁测深法原理[M]. 北京: 地质出版社, 1990.
|
| [24] |
Guptasarma D, Singh B. New digital linear filters for Hankel J0 and J1 transforms[J]. Geophysical Prospecting, 1997, 45(5): 745-762. |
| [25] |
纳比吉安. 勘查地球物理电磁法第一卷: 理论[M]. 北京: 地质出版社, 1992.
|



 邓居智,江西省南昌市经开区广兰大道418号东华理工大学地球物理与测控技术学院,330013。Email:
邓居智,江西省南昌市经开区广兰大道418号东华理工大学地球物理与测控技术学院,330013。Email: